Introduction

In the past decade, additive manufacturing attracted interest because of its benefits and flexibility. It made possible the production of designs that were impossible to manufacture using traditional manufacturing techniques and opened the door to the advancement in topology optimization and design efficiency enhancement. Additive manufacturing is a wide technology with many variants. Among them, Selective Laser Melting—SLM—also known as Direct Metal Laser Sintering, that proceeds on a powder bed [1].

SLM consists of a concentrated laser that hits a metal powder layer and melts it according to the slicing of a CAD model. The powder is heated above the liquidus temperature of the metal hence producing parts with properties comparable to those of metal bulk, except in what concerns ductility.

However, due to the extreme process conditions some defects occur, such as cracking [2] and part distortion [3] induced by installed residual stresses [4]. In order to account for these defects, scientists have tried to quantify them using either experimental methods as well as numerical simulation.

Experimentally, two types of measurements are used: with and without contact. In absence of contact, ultrasounds, thermal imaging such as infrared –IR– sensors [5] or X-ray tomography to quantify the part defects such as porosity and cracks [6], are widely considered, among many other techniques. This type of techniques can only inspect external exposed surfaces or its neighborhood inside the material depending on their penetration capability. Contact-based techniques use thermocouple joints to measure the temperature of the substrate (bottom surface or bed) [7] or other sensors enabling accessing to the installed stresses.

To circumvent the shortcomings of the experimental approach, researchers resorted to numerical techniques in an attempt to simulate the printing process. Among the numerical techniques, the finite elements analysis –FEM– is mostly used to simulate the temperature field in additive manufacturing processes [8, 9]. A thermal simulation is then coupled to a mechanical simulation in order to predict the distortion of 3D printed parts. Simulation concerns three different scales: Micro, Meso and Macro.

Microscale analysis focuses on the rich local physics including the interaction between the heat source and the substrate, the phase-change and the associated metallurgical transformations, as well as the localized thermal gradients. The fast cooling and the induced stresses along the printing path is usually described at the mesoscopic scale. These two approaches are usually coupled [10, 11] for reproducing quite well experimental findings. However, the computational cost makes impossible envisaging its application at the part level (macroscopic scale).

In order to validate the numerical results, several approaches are used depending on the considered process. For SLM, the so-called “Twin Cantilever” test shown in Fig. 1 is usually considered. In this experiment a T-shaped part is printed on a support and the tip deflection after removing the support serves to calibrate and/or validate.

Fig. 1
figure 1

The Twin Cantilever experiment setup

Full size image

However in most additive manufacturing processes, distortion is difficult to predict because of the change of the mechanical properties during the process [12]. The high temperatures cause the microstructure to be altered, and the cyclic heating may cause for some materials a thermal fatigue leading to the material embrittlement [13]. These changes are difficult to model and take into account since they depend on the printing parameters such as the laser power and speed, the material itself, the powder characteristics, the heating spot size, ... affecting not only the microstructure but also the interlayer cohesion due to the varying porosity [6].

In these validation experiments, the printing parameters are varied and the distortion is studied. A quite good agreement between the experimental and numerical results are noticed when addressing the thermal modeling. Whereas in what concerns the distortion the error varies depending on the process parameters and materials employed, ranging from 10% to a total mismatch [14, 15].

The present work aims at proposing a thermal simulation of SLM while studying the reheating effect when the heat source re-passes close to a solidified element. In addition, it will present a novel approach for simulating the distortion of a 3D printed part. This approach is used to generate a calibration model from which the stresses will be extracted and used to perform a macroscale simulation that gives the distortion as a function of the temperature reached by the molten metal and of the printing trajectories appropriately parametrized, in real time by using the non-intrusive Proper Generalized Decomposition approach [16, 17], following the rationale initially introduced in [18] where the interested reader can find more references on the advanced simulation of those kind of processes.

The next section defines and implement the thermal model and analyses the effect of the thermal history in the transient temperature field. Section “Thermo-mechanical modelling” establishes a thermomechanical approach, enabling first the calculation of the installed residual stresses and then, its integration in a parametric solution of the manufactured part distortion.

Transient simulation of a moving heat source

This section discusses the finite element thermal modeling associated with a moving heat source hitting a powder bed and moving at a velocity V, as encountered in SLM.

Heat equation

The heat transfer mechanisms in SLM are conduction and natural convection as shown in Fig. 2. Note that radiation can be neglected since metallic materials have an excellent heat conduction ability, hence most of the heat will be diffused by conduction to the surrounding material [19]. In the reduced order modeling that we develops in the present work, the laser-matter interaction is not taken into account, only the effective heat transferred to the material is considered.

Fig. 2
figure 2

Heat transfer mechanisms involved in SLM

Full size image

The transient heat equation that governs the temperature distribution T(x,y,z) reads

$$ \rho Cp \frac{\partial T}{\partial t}= k \left( \frac{\partial^{2} T}{\partial x^{2}}+\frac{\partial^{2} T}{\partial y^{2}}+\frac{\partial^{2} T}{\partial z^{2}} \right) +q_{latent}(x,y,z), $$
(1)

where qlatent is the latent heat, i.e. the heat released by the phase change, Cp refers to the heat capacity and k to the thermal conductivity.

The heat source that acts as a boundary condition, q(r), is considered having a gaussian distribution [19] and hence qsource is expressed by

$$ q(r)=\frac{2P}{\pi {r_{0}^{2}}} e^{-\frac{2r^{2}}{{r_{0}^{2}}}} $$
(2)

in which P is the laser power (W), r0 is the laser spot radius and r is the distance from the spot center.

The initial temperature is given by T(x,t = 0) = 293K and the free convection boundary condition reads \(q=h(T-T_{\infty })\), with h the exchange coefficient.

The implicit semi-discrete formulation reads

$$ \frac{T^{n+1}-T^{n}}{\varDelta t}=\frac{ k}{\rho Cp} \left( \frac{\partial^{2} T^{n+1}}{\partial x^{2}}+\frac{\partial^{2} T^{n+1}}{\partial y^{2}}+\frac{\partial^{2} T^{n+1}}{\partial z^{2}} \right) + q^{\prime} , $$
(3)

in which Tn+ 1 is the temperature field at time step n + 1, i.e. t = (n + 1)Δt, with T0 = 293K, and \(q\prime = q_{latent}/\rho C_{p}\) is assumed temperature dependent according to [20]

$$ q\prime= \left \{ \begin{array}{ll} q^{\prime}=0 & if \quad T>T_{l}\\ q^{\prime}= \frac{\varDelta H}{Cp} \frac{df_{s}}{dT} \frac{\partial T}{\partial t} & if \quad T_{s}<T<T_{l}\\ q^{\prime}=0 & if \quad T<T_{s} \end{array} \right . , $$
(4)

where Tl and Ts are respectively the liquidus and the solidus temperatures, ΔH is the latent heat and fs the solid fraction. The value of ΔH is taken from the literature [20] assuming that the solidification in additive manufacturing is similar to that in casting, even if other expressions considered. The previous equation shows that there is no heat release when cooling in the liquid state or solid state, but only when there is a solid-liquid mixture.

Defining the solid fraction fs from [21]

$$ f_{s}=\frac{(T_{l}-T)+\frac{2}{\pi}(T_{s}-T_{l}) \left( 1-cos \left( \frac{ \pi (T-T_{l})}{2(T_{s}-T_{l})} \right) \right)}{(T-T_{s})(1-2/\pi)} , $$
(5)

its temperature derivative involved in Eq. 4, \(\frac {df_{s}}{dT}\), reads [21]

$$ \frac{df_{s}}{dT}=-\frac{1}{(T_{l}-T_{s})(1-2/ \pi)} \left[1-\sin \left( \frac{ \pi (T-T_{l})}{2(T_{s}-T_{l})} \right) \right] . $$
(6)

In order to simulate the moving heat source, at each time step dt the laser moves a distance dx = Vdt. Hence the FEM discrete problem needs at each time step n, the solution of the linear problem expressed from

$$ \mathbf K^{n} \mathbf T^{n+1}= \mathbf Q^{n,n+1}, $$
(7)

where coefficient matrix at time tn, Kn, depends on the temperature Tn because of the nonlinearity.

Thermal properties

The thermal conductivity is a temperature dependent function and hence it must adapt to the temperature change at each iteration. The used material in the simulation is the 316L stainless steel. In [22] authors found correlations for the thermal conductivity and the temperature

$$ k=a \ T^{b} \ e^{cT} \ e^{d/T} $$
(8)

where T is the temperature in (K) and a, b, c and d are constants corresponding to iron, reported in Table 1. The thermal conductivity is assumed to be the one of the bulk material expressed by Eq. 8 everywhere except in the powder layer in which it is reduced of one order of magnitude for taking into account the effects of porosity in the powder bed.

Table 1 Values of the parameters used in the simulation
Full size table

The heat capacity can be expressed from the mixture rule

$$ C_{p} = \left \{ \begin{array}{ll} C_{p,solid} & if \quad T<T_{s}\\ f_{s} \ C_{p,solid} + (1-f_{s}) \ C_{p,liquid} & if \quad Ts<T<T_{l}\\ C_{p,liquid} & if \quad T>T_{l} \end{array} \right . . $$
(9)

Results and discussion

Numerical simulations are performed by using our own finite element method implementation. For that purpose, the mesh consists of 14553 hexahedral elements (with 66 000 degrees of freedom). The problem is solved using an incremental implicit time integration scheme with a time-step of 1.25 ms. The converged solution (with resperct to the mesh size) using the parameters reported in Table 1, is visualized in the Paraview open source software.

Using these values, the simulation is performed in a thin 3D plate of length 15 mm, width 5 mm and thickness 1 mm, where a temperature snapshot is depicted in Fig. 3.

The objective is to obtain the characteristic temperature time evolution in a representative node.

Fig. 3
figure 3

Temperature field at a given time t, with the source moving from the left boundary towards the right one

Full size image

Heating

When studying the maximum temperature at each point along the laser path, it results the profile depicted in Fig. 4. This result clearly proves that except at the beginning, all the points on the laser trajectory will reach almost the same maximum temperature, for a given heat source that advances with a given velocity.

Fig. 4
figure 4

Maximum temperature (Kelvin) at each position x (in m) that proves that almost all the points in the trajectory reach the same maximum temperazture

Full size image

Then, the cooling profile of every point in this region of uniform maximum temperature is depicted in Fig. 5.

Fig. 5
figure 5

Cooling profile

Full size image

Reheating

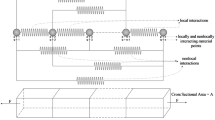
Printing implies considering close trajectories as depicted in Fig. 6. When the heat source comes close to a certain point during the next printing path, this point will be reheated, effect known as neighboring effect.

Fig. 6
figure 6

Printing strategy

Full size image

As shown in Fig. 5, the characteristic cooling time in order to reach a temperature verifying the condition

$$ \frac{T -T_{amb}}{T_{amb}} 100 < 0.5 \%, $$
(10)

is of about 44 ms, time that is referred as critical time tcr.

Thus, if the time elapsed before coming back to the vicinity of a certain point is higher than that critical time tcr, this latter has cooled down to the almost ambient temperature Tamb and it will experience the same reheating as any point in the neighbor path-line, as the marked point in Fig. 7.

Fig. 7
figure 7

Reheating process: the marked point is reheated because the source term moving along a close path-line

Full size image

In these circumstances the temperature evolution of the referred point during its reheating is representative of the reheating of all the points located in the contiguous path-line, and consequently all them experience the same maximum temperature (obviously lower than the one reached when the laser applied directly on them), except at the beginning of the heating path-lines, as shown in Fig. 8, with the associated representative cooling profile given in Fig. 9.

Fig. 8
figure 8

Maximum temperature along x (m) on a parallel close trajectory to the one followed by the laser spot

Full size image
Fig. 9
figure 9

Cooling profile of points on the neighboring line

Full size image

Thus, if the elapsed time between two passes is higher than tcr, the previous analysis proves that all the points start their reheating from an almost ambient temperature and thus will reach almost the same maximum temperature when reheated, and will follow a similar cooling.

However, when the elapsed time between two passes is lower than tcr, reheating applies on a still hot initial state. This situation applies when a printing path starts close to the end of the previous one as illustrated Fig. 10 or when the printed paths are extremely shorts (parts composed of very thin components).

Fig. 10
figure 10

Zig-Zag printing sequence exacerbating neighboring effects

Full size image

The simulation is done on the printing path shown in Fig. 10 in which x = 0 represents the start of the second path. The maximum temperature produced by the reheating exhibits values much higher than the ones obtained when reheating proceeds from the almost ambient temperature. Figure 11 proves that this deviation only applied in the vicinity of x = 0 where the end of one path coincided with the beginning of the next one.

Fig. 11
figure 11

Maximum temperature when t<tcr

Full size image

If we assume that the printing occurs as shown in Fig. 10, tcr/2 = 22 ms corresponds about 2 mm for V = 0.1m/s, then points x > 2 mm will be reheated from the ambient temperature, in agreement with Fig. 11 that clearly states that 2 mm suffice for reaching the temperature characteristic of a reheating from the ambient temperature.

The previous analysis allows neglecting the thermal heterogeneities induced by elapsed times lower than tcr as soon as the printed part are large enough.

Thermo-mechanical modelling

Parametric distortion

In what follows we assume a thermal load ΔT = Tmax − Tamb, with Tmax discussed in the previous section, and the deposition trajectories parametrized as proposed in [18] where the trajectories coincide with the curves Φ = cte, with Φ(x,y) solution of the problem

$$ \varDelta \varPhi(x,y)= \mu_{5} $$
(11)

with (x,y) ∈ ω = [0,L] × [0,H], and where the printed part Ω ⊂ ω.

Equation 11 is solved with the boundary condition expressed from

$$ \left \{ \begin{array}{l} \varPhi (x,y=0) = \mu_{1}+(\mu_{2}-\mu_{1})\frac{x}{L}\\ \varPhi (x,y=H) = \mu_{4}+(\mu_{3}-\mu_{4})\frac{x}{L}\\ \varPhi (x=0,y) = \mu_{1}+(\mu_{4}-\mu_{1})\frac{y}{H}\\ \varPhi (x=L,y) = \mu_{2}+(\mu_{3}-\mu_{2})\frac{y}{H} \end{array} \right . . $$
(12)

In the previous expressions μi, \(i=1, {\dots } , 5\), represent the model parameters, the first four parametrizing the Dirichlet boundary conditions, and μ5 representing the source term in problem (11).

The parametric solution performed by using the so-called Proper Generalized Decomposition –PGD– allows computing \(\varPhi (x,y,\mu _{1}, {\dots } , \mu _{5})\) that as discussed in [18] allows describing most usual printing trajectories.

In [18] authors assume a local residual tension aligned with the deposition trajectory. This means that at each point, if one considers a frame aligned with the deposition trajectory, the one consisting of x0 and y0 depicted in Fig. 12, the resulting tensor \(\sigma _{0} |_{(x_{0},y_{0})}\) will have a single non-zero component.

Fig. 12
figure 12

Local and global frames

Full size image

After expressing the residual stress at each point by using the laboratory frame, and parametrically with respect to μi, \(i=1, {\dots } , 5\), the distortion results from the virtual work principle

$$ {\int}_{\varOmega} \epsilon^{*}:(\sigma-\sigma_{0}) d\varOmega=0 , $$
(13)

or by using the elastic behavior

$$ {\int}_{\varOmega} \epsilon^{*}:\mathbf C: \epsilon d\varOmega = {\int}_{\varOmega} \epsilon^{*} : \sigma_{0} d\varOmega , $$
(14)

with C the fourth order elasticity tensor, and the residual tension scaling with ΔT as discussed in [18].

Thermo-mechanical coupled model

In this section we will present a new macroscale approach to simulate the distortion of a part processed by additive manufacturing. In this approach the cooling of the deposited metal will be divided into two stages: T > Tmelting and T < Tmelting.

In the first stage, the metal is in a liquid phase and no residual stresses are induced because the liquid metal adapts to the substrate deformation that will expand when heated from the ambient temperature. Then, in the second stage, the metal solidifies and hence sticks to the substrate surface. The whole system (deposited later and substrate) continues the cooling from the temperature existing when the deposited layer started its solidification, until reaching the final ambient temperature. The flowchart is presented in Fig. 13. Predictions were validated experimentally as described in the next section.

Fig. 13
figure 13

Simulation flowchart for the calculation of both displacement components d1 and d2 contribution to the total one d

Full size image

Experimental validation

The performed experiment consists of evaluating the distortion of a cantilevered plate with one deposit line on its top surface. The geometry is shown in Fig. 14.

Fig. 14
figure 14

Validation experiment geometry, with prescribed null displacements in the fixed region

Full size image

The experiment is performed using Laser Metal Deposition –LMD–, with the deposit dimensions being: width 0.8 mm, thickness 175 μ m and the substrate thickness 2 mm with its left boundary clamped (all the other remaining free). In addition the material used is stainless steel 316L. The maximum plate deflection is measured after the deposition process finished.

For the thermal simulation, the transient heat transfer equation is solved with a prescribed initial temperature in the deposit layer T(t = 0) = 2000K and T(t = 0) = 293K elsewhere. As discussed in the previous section, the thermal simulation provides the temperature field in the substrate when the deposit-substrate interface reaches the melting temperature Ts. The substrate heating produces the substrate plate deflection depicted in Fig. 15.

Fig. 15
figure 15

Part distortion (m) caused by the substrate heating induced by the deposited molten metal

Full size image

When the metal begins to solidify, both thermal strains, in the substrate and the deposited layer, apply, and result in the deformed part depicted in Fig. 16, that added to the pre-deformed configuration (Fig. 15) results in the final configuration depicted in Fig. 17.

Fig. 16
figure 16

Part distortion (m) caused by the substrate and the deposit cooling

Full size image
Fig. 17
figure 17

Final part distortion obtained by adding the configurations shown in Figs. 15 and 16 (in m)

Full size image

The quantity of interest is the maximum deflection at the tip of the plate. When comparing the simulated results with the experimental measurements of the maximum tip deflection, an excellent agreement was observed. Note that the modulus of elasticity of the deposit is taken to be slightly lower than that of the substrate due to the porosities and phase change during solidification (Edeposit = 175 GPa and Esubstrate = 200 GPa) [13, 23].

Calibration model for the macroscale simulation

In order to perform fast simulations on large scale models, a high-resolution calibration model is proposed from which the residual stresses to be used as local stresses in the whole part (to proceed as discussed in Section “Parametric distortion”) are extracted.

For addressing the solution of the associated thermomechanical problems in the extremely degenerated domains with thicknesses orders of magnitude much smaller that the other in-plane characteristic dimensions, the in-plane-out-of-plane separated representation is considered. The last expresses the displacement field as a finite sum of terms, each involving a function of the in-plane coordinates and the second depending on the thickness coordinate. Thus, extremely rich out-of-plane discretizations can be considered to capture all the 3D effects event in such very degenerated domains, without impacting the computational efficiency.

That separated representation expresses the displacement field according to

$$ \mathbf u (x,y,z) \approx \sum\limits_{i=1}^{\mathtt{N}} {\mathbf{P}}_{i}(x,y) \bullet {\mathbf{T}}_{i}(z), $$
(15)

where ∙ refers to the Hadamard product and Pi and Ti are vectors involving respectively the in-plane and out-of-plane coordinates.

The calibration model geometry consists of three deposited layers with three printed lines per layer as shown in Fig. 18, all of them along direction y. In this model we assume that the deposit of interest, highlighted in red in Fig. 18 of 0.8 mm width and 200 μ m thickness, is a repre sentative one accounting for the effects of the neighboring deposits and hence its stress state can be used at any point in a simulated part.

Fig. 18
figure 18

Calibration model geometry

Full size image

The simulation is performed by adding a deposit after the other to accumulate the distortions and the installed stresses. In the deformed model shown in Fig. 19 we can see that the highest distortion is observed between the tracks and between the layers and mainly on the edges. In addition, in the middle of the representative domain the distortions reached an almost uniform value, meaning that the deposit length is sufficient to extract the installed residual stresses.

Fig. 19
figure 19

Calibration model distortion (m)

Full size image

From the computed strains we can then calculate the stresses and also the Von Mises effective stress. Figure 20 proves that there is a stress concentration on the interface between the layers which is a problem widely encountered in additive manufacturing [24].

Fig. 20
figure 20

Von Mises stress (Pa) distribution

Full size image

Figure 21 extracts the stresses in the deposit of interest. The plot shows a region in the middle of the domain in which stresses are almost uniform and all in-plane stresses vanish. These stresses will be used as local stresses to enrich the parametric model proposed in [18] whose assumption (residual tension aligned with the printing path-line) seems too simplistic when compared with the stresses reported in Fig. 21.

Fig. 21
figure 21

Computed stresses in the deposit of interest along the deposition direction, where the ones representing the residual stresses are extracted at the middle of the deposited length

Full size image

To better appreciate the high-resolution reached by the in-plane-out-of-plane separated representation, Figs. 22 and 23 zoom-in respectively the deformation and the associated equivalent mesh resolution. It is important to note that few minutes in a standard laptop allowed for a resolution equivalent to 2.5 millions of 3D finite elements.

Fig. 22
figure 22

Deformation zoon-in

Full size image
Fig. 23
figure 23

Equivalent 3D finite element mesh associated with the 2D-1D (in-plane-out-of-plane) separated representation resolution

Full size image

Parametric macroscopic modeling of part distortion

In this section we will present the application of the proposed methodology for the simulation of the distortion of a barrel.

Simulated geometry and parametrized trajectories

The simulated part geometry is shown in Fig. 24. The part is made of Titanium Grade 5 and printed on a Titanium substrate.

Fig. 24
figure 24

Case study

Full size image

The cross sectional area being circular we calculate the solution of the Poisson equation (11) in a slightly bigger rectangular domain. Then, the solution will be projected from the rectangular embedding domain onto the part.

In order to obtain circular trajectories, Eq. 11 is solved with μ5 = 1 enforcing Φ = 0 outside the part domain, by using a penalty formulation. Figure 25 shows the penalized domain and the Poisson equation solution.

Fig. 25
figure 25

Penalized domain (black) with Φ = 0 (left) and the Poisson equation solution in the extended domain (right)

Full size image

Hence, after calculating the solution, curves Φ = cte define the trajectories shown in Fig. 26.

Fig. 26
figure 26

Resulting concentric circular trajectories

Full size image

The technique proposed in [18] is extended by incorporating the richer stress state that is parametrized by the deposition temperature T. Thus, a parametric solution representing the part distortion u(μ1,μ2,μ3,μ4,μ5,T) is computed. The deposition temperature can be easily correlated with the process parameters: deposition velocity and laser power. For computing such a parametric solution several runs (about one thousand) for different values of the parameters were performed and the computed results combined for defining the solution for any other choice by interpolation [25].

Moreover, to avoid axial distortion occurring when all trajectories start at the same location, the starting positions will be randomly chosen in each layer. Figure 27 shows the difference between the two cases and it reveals the benefits of randomly choosing the starting point in each layer.

Fig. 27
figure 27

Axial distortion (in m) when all trajectories start at the same position (left) and when that starting point is randomly choosen (right)

Full size image

Figure 28 shows the distortion depending on the temperature of the deposited layer in the case of concentric trajectories with random starting position at each layer. It can be noticed that as the temperature increases from near liquidus temperature the distortion increases up to a certain temperature after which the distortion starts to decrease again.

Fig. 28
figure 28

Part distortion (m) for a T = 2226 K, b T = 2905 K and c T = 4000 K, when considering circular trajectories

Full size image

This behavior can be explained by resorting the consideration discussed when addressing the calibration model, since as the temperature increases the gap between the liquidus temperature and the maximum temperature increases, hence the effect of the pre-heating induced deformation can compensate a cooling induced distortion. Thus, increasing the deposit temperature could be beneficial, however there are other many issues, out of the scope of the present work, pointing in the opposite direction.

Figure 29 shows the distortion in the case of horizontal printing (μ1 = 1 and μ2 = 1 all the others vanishing). In this case the distortion is maximal on the right and left parts of the domain.

Fig. 29
figure 29

Part distortion: printing trajectories (left) and the distortion(m) (right)

Full size image

Figure 30 shows the distortion in the case of vertical printing (μ1 = 1 and μ4 = 1, all the other vanishing). In this case the distortion is maximal on the top and bottom of the domain.

Fig. 30
figure 30

Part distortion: printing trajectories (left) and the distortion (m) (right)

Full size image

Using this parametric solution one can modify the trajectory or process parameters and evaluate their impact in almost real-time.

The methodology performs in larger parts without major difficulties, as the one illustrated in Fig. 31 consisting of a cylinder of inner diameter 35 mm, thickness 10 mm and height 65 mm.

Fig. 31
figure 31

Cylinder distortion (m) printed from concentric circular trajectories, random starting positions and a deposition temperature of 2710 K

Full size image

Conclusion

This paper started by discussing transient thermal simulations of SLM. The reheating effect when the heat source re-passes next to an already printed point of a previous pass was quantified. The analysis proved that if the metal had enough time to cool down to reach the ambient temperature, the heat source will reheat it to an almost representative temperature ensuring a certain uniformity of the mechanical state all along the part.

Then a thermo-mechanical coupled approach for calculating the distortion in a 3D printed part was presented. This model was used to propose a calibration procedure in order to extract the characteristic stresses to be used for calculating the distortion at the part level.

Finally, several simulations were done by varying the trajectory and the temperature of the deposited material to define the parametric part distortion with respect to the process parameters.