Topspin generation in tennis

Abstract

Tennis players impart topspin to the ball by striking the ball in an upwards direction while the racquet head itself is aligned with the string plane approximately vertical. Significantly larger spin can be generated if the racquet head is tilted forward. The amount of spin that can be generated was investigated by measuring the spin off a stationary hand-held racquet, and then calculating the effects of swinging the racquet towards the ball with the racquet head tilted forward. The trajectory of the ball was also calculated to ensure that the resulting spin was consistent with realistic values of the outgoing speed and angle of the ball.

Appendix

1.1 A.1 Racquet at rest equations

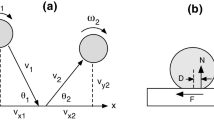
In Fig. 6 the y-axis is taken to be vertical and the x-axis as horizontal so that the x and y components of $v_\text {in}$ and $v_{R}$ are $v_{\text {in}x} = v_\text {in} \cos \theta _\text {in}$, $v_{\text {in}y} = v_\text {in} \sin \theta _\text {in}$, $v_{Rx} = - v_{R} \cos \theta _{R}$ and $v_{Ry} = v_{R} \sin \theta _{R}$. These equations remain valid regardless of whether the ball or the racquet is rising or falling, since $\theta _\text {in}$ and $\theta _{R}$ can be positive or negative. The ball bounces off the court with topspin, so it can be assumed that $\omega _{1}$ is positive in Fig. 6a. On the other hand, the ball could be incident with either topspin or backspin onto the strings, depending on whether the ball is rising or falling and depending on whether the racquet is rising or falling.

In the racquet frame of reference, shown in Fig. 6d, the ball is incident at speed $v_{1}$ onto the stationary racquet, where $v_{1x} = v_{\text {in}x} - v_{Rx}$, $v_{1y} = v_{\text {in}y} - v_{Ry}$, and $v_{1} = (v_{1x}^{2} + v_{1y}^{2})^{1/2}$. For example, if the ball and the racquet are both incident at the same speed and are rising at the same angle, then $v_{1y} = 0$, so in the racquet frame of reference the ball is incident horizontally onto the strings at speed $v_{1x} = 2v_{\text {in}x}$.

Fig. 8

Ball approaching a racquet at rest, at speed $v_{1}$ and angle $\alpha _{1}$

Two different situations are shown in Fig. 8, one where the ball is rising, with $v_{1y}> 0$ and one where it is falling, with $v_{1y} < 0$. The angle of incidence between the incoming ball and the string plane is defined as $\alpha _{1}$, and our main task will be to calculate the bounce angle $\alpha _{2}$, speed $v_{2}$ and spin $\omega _{2}$ off the stationary racquet, using Eqs. (6) and (7). To do that, it is first necessary to calculate the angles $\theta _{1}$ and $\alpha _{1}$ shown in Fig. 8. To simplify the following calculations, it is convenient to define the angles $\theta _{1}$ and $\alpha _{1}$ by

• If $v_{1y} = 0$ then $\theta _{1} = 90^{\circ }$ and $\alpha _{1} = 90 +$Tilt

• If $v_{1y}> 0$ then $\theta _{1} = \,$ Atan$(v_{1x}/v_{1y})$ and $\alpha _{1} = \theta _{1} +$Tilt

• If $v_{1y} < 0$, $\theta _{1} = \,$180 + Atan$(v_{1x}/v_{1y})$ and $\alpha _{1} = \theta _{1} +$Tilt.

The $v_{y} < 0$ case is defined that way since Atan$(v_{1x}/v_{1y})$ is usually computed as a negative number when $v_{1y} < 0$. It is more convenient mathematically to allow the angle of incidence, $\alpha _{1}$ to be greater than $90^{\circ }$ since the above relations also hold when the tilt angle is negative.

Fig. 9

Ball approaching a racquet at rest

Given $v_{1}$ and $\alpha _{1}$, the normal and tangential components of $v_{1}$ with respect to the string plane can be calculated as shown in Fig. 9. Regardless of whether the ball is rising or falling, $v_{n1} = v_{1} \sin \alpha _{1}$ and $v_{t1} = v_{1} \cos \alpha _{1}$, with the result that $v_{t1} < 0$ if $\alpha _{1}> 90^{\circ }$. When deriving the bounce equations in Sec. 2, it was assumed that the ball is incident from left to right. The equations are also valid if the ball is incident right to left, in which case $v_{t1}$ is negative. If the ball is spinning clockwise and travels left to right, it is incident with topspin. If it spins clockwise and travels right to left, it is incident with backspin. However, if the ball travels right to left then the sign of D needs to be changed since N then acts on the opposite side of the ball to that shown in Fig. 1.

Fig. 10

Rebound speed and angle off racquet at rest

The bounce equations are required to calculate the normal and tangential components of the bounce speed $v_{2}$, as shown in Fig. 10. The bounce equations determine whether the ball bounces forward or backward, depending on the sign of $v_{t2}$. If $v_{t2}> 0$, then the bounce angle $\alpha _{2} =$Atan$(v_{n2}/v_{t2})$ is less than $90^{\circ }$. If $v_{t2} < 0$, then it is convenient to define $\alpha _{2} = 180 +$Atan$(v_{n2}/v_{t2})$ so that it is greater than $90^{\circ }$ rather than being a negative angle.

The components of $v_{2}$ in the x-, y-coordinate system are shown in Fig. 11. In that system, the bounce angle $\theta _{2}$ is given by $\theta _{2} = \alpha _{2} +$Tilt. This formula remains valid even if the racquet is tilted backward, with Tilt $< 0$. The x- and y-components of $v_{2}$ are then $v_{2x} = -v_{2} \sin \theta _{2}$ and $v_{2y} = v_{2} \cos \theta _{2}$.

Fig. 11

x- and y-components of $v_{2}$

1.2 A.2 Outgoing ball

To obtain the outgoing speed off the moving racquet, it is necessary to add back the velocity vector $v_{R}$ as shown in Fig. 12. The outgoing speed is then given by $v_\text {out} = (v_{outx}^{2} + v_{outy}^{2})^{1/2}$, and the outgoing angle is given by $\tan \theta _\text {out} = -v_{outy}/v_{outx}$ (since $v_{outx}$ is negative). The outgoing spin $\omega _{2}$ is the same as that given from the bounce calculation. A value $\omega _{2} < 0$ corresponds to outgoing topspin, as indicated in Fig. 12.

Fig. 12

Outgoing ball off moving racquet