Tunable Mechanical Properties of Vectran Liquid Crystal Polymer (LCP) Short Fiber-Reinforced Soft Composite

Abstract

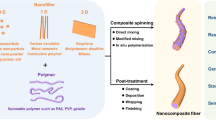
We investigated the tunable mechanical properties of Vectran liquid crystal polymer (LCP) short fiber-reinforced soft composite; we varied the relative foam density and the short fiber loading ratio. The microstructures revealed well-defined pores, matrices, and short fibers. We derived the compressive stress–strain responses and stress relaxations and then performed dynamic mechanical analysis (DMA). To investigate dynamic tunability, the abilities of the soft composites to isolate vibrations from 1 to 300 Hz were assessed. We used the generalized Maxwell model to fit the experimental data and to extract model parameters. We present a simple, versatile, and cost-effective method for the fabrication of LCP short fiber-reinforced soft composites with well-defined and widely tunable mechanical properties. These composites will find applications in many devices.

Appendix

See Figure 18.

In Fig. 18a, the normal stress within the soft composite is [28]:

$$ \sigma \left( t \right) = E_{\infty } \varepsilon \left( t \right) + \int_{0}^{t} {E_{R} \left( {t - \tau } \right)\dot{\varepsilon }\left( \tau \right)d\tau } = E_{\infty } \varepsilon \left( t \right) + \int_{0}^{t} {E_{V} e^{{ - \frac{t - \tau }{{\tau_{V} }}}} \dot{\varepsilon }\left( \tau \right)d\tau } $$

(1)

where ε(t) is the strain, t is the time, $E_{R} \left( t \right) = E_{V} e^{{ - \frac{t}{{\tau_{V} }}}}$ is the relaxation kernel, τ_V = E_V/η_V is the relaxation time, and τ is an integral variable. Then, force F_σ(t) in Fig. 18b is:

$$ F_{\sigma } \left( t \right) = \sigma \left( t \right)A = E_{\infty } A\varepsilon \left( t \right) + \int_{0}^{t} {E_{V} Ae^{{ - \frac{t - \tau }{{\tau_{V} }}}} \dot{\varepsilon }\left( \tau \right)d\tau } $$

(2)

where A is the area of the soft composite.

Because $\varepsilon \left( t \right) = \frac{{x_{1} \left( t \right) - x_{2} \left( t \right)}}{L}$, where x₁(t) and x₂(t) are the displacements of the base (m₁) and the upper (m₂) mass, respectively, and L is the initial thickness of the soft composite, we obtain:

$$ F_{\sigma } \left( t \right) = \frac{{E_{\infty } A}}{L}\left[ {x_{1} \left( t \right) - x_{2} \left( t \right)} \right] + \int_{0}^{t} {\frac{{E_{V} A}}{L}e^{{ - \frac{t - \tau }{{\tau_{V} }}}} \left[ {\dot{x}_{1} \left( \tau \right) - \dot{x}_{2} \left( \tau \right)} \right]d\tau } $$

(3)

By introducing a spring constant $K_{\infty } = \frac{{E_{\infty } A}}{L}$ and the relaxation stiffness $K_{V} = \frac{{E_{V} A}}{L}$, we obtain:

$$ F_{\sigma } \left( t \right) = K_{\infty } \left[ {x_{1} \left( t \right) - x_{2} \left( t \right)} \right] + \int_{0}^{t} {K_{R} \left( {t - \tau } \right)\left[ {\dot{x}_{1} \left( \tau \right) - \dot{x}_{2} \left( \tau \right)} \right]d\tau } $$

(4)

where $K_{R} \left( t \right) = \frac{{E_{V} A}}{L}e^{{ - \frac{t}{{\tau_{V} }}}} = K_{V} e^{{ - \frac{t}{{\tau_{V} }}}}$ is the relaxation kernel [28].

The Fourier transform of Eq. (4) yields:

$$ F_{\sigma } \left( \omega \right) = K_{\infty } \left[ {X_{1} \left( \omega \right) - X_{2} \left( \omega \right)} \right] + j\omega K_{R} \left( \omega \right)\left[ {X_{1} \left( \omega \right) - X_{2} \left( \omega \right)} \right] $$

(5)

where ω is the angular frequency, $j = \sqrt { - 1}$ is the imaginary unit, X₁(ω) and X₂(ω) are the Fourier transforms of x₁(t) and x₂(t), respectively, and jωK_R(ω) is:

$$ j\omega K_{R} \left( \omega \right) = \frac{{K_{V} \omega^{2} \tau_{V}^{2} }}{{1 + \omega^{2} \tau_{V}^{2} }} + j\frac{{K_{V} \omega \tau_{V} }}{{1 + \omega^{2} \tau_{V}^{2} }} = K^{\prime}\left( \omega \right) + jK^{\prime\prime}\left( \omega \right) $$

(6)

By introducing the complex stiffness $K^{*} \left( \omega \right) = K_{\infty } + K^{\prime}\left( \omega \right) + jK^{\prime\prime}\left( \omega \right)$, we obtain:

$$ F_{\sigma } \left( \omega \right) = K^{*} \left( \omega \right)\left[ {X_{1} \left( \omega \right) - X_{2} \left( \omega \right)} \right] $$

(7)

where $K^{\prime}\left( \omega \right) = \frac{{K_{V} \omega^{2} \tau_{V}^{2} }}{{1 + \omega^{2} \tau_{V}^{2} }}$ is the storage stiffness, and $K^{\prime\prime}\left( \omega \right) = \frac{{K_{V} \omega \tau_{V} }}{{1 + \omega^{2} \tau_{V}^{2} }}$ is the loss stiffness.

The equations of motion of the vibration system of Fig. 18(b) are:

$$ \begin{gathered} m_{1} \ddot{x}_{1} \left( t \right) + F_{\sigma } \left( t \right) = F_{e} \left( t \right) \hfill \\ m_{2} \ddot{x}_{2} \left( t \right) - F_{\sigma } \left( t \right) = 0 \hfill \\ \end{gathered} $$

(8)

where F_e(t) denotes the excitation force.

The Fourier transforms of Eq. (8) yield:

$$ \begin{gathered} - m_{1} \omega^{2} X_{1} \left( \omega \right) + F_{\sigma } \left( \omega \right) = F_{e} \left( \omega \right) \hfill \\ - m_{2} \omega^{2} X_{2} \left( \omega \right) - F_{\sigma } \left( \omega \right) = 0 \hfill \\ \end{gathered} $$

(9)

By inserting Eq. (7) into (9) and solving for X₁(ω) and X₂(ω), we obtain:

$$ \begin{gathered} X_{1} \left( \omega \right) = \frac{1}{{\Delta \left( {\omega^{2} } \right)}}\left[ {K^{*} \left( \omega \right) - m_{2} \omega^{2} } \right]F_{e} \left( \omega \right) \hfill \\ X_{2} \left( \omega \right) = \frac{1}{{\Delta \left( {\omega^{2} } \right)}}K^{*} \left( \omega \right)F_{e} \left( \omega \right) \hfill \\ \end{gathered} $$

(10)

where $\Delta \left( {\omega^{2} } \right) = \left[ {K^{*} \left( \omega \right) - m_{1} \omega^{2} } \right]\left[ {K^{*} \left( \omega \right) - m_{2} \omega^{2} } \right] - K^{*} \left( \omega \right)^{2}$.

The transmissibility is then $\frac{{X_{2} \left( \omega \right)}}{{X_{1} \left( \omega \right)}} = \frac{{K^{*} \left( \omega \right)}}{{K^{*} \left( \omega \right) - m_{2} \omega^{2} }}$.

Using $K^{*} \left( \omega \right) = K_{\infty } + \frac{{K_{V} \omega^{2} \tau_{V}^{2} }}{{1 + \omega^{2} \tau_{V}^{2} }} + j\frac{{K_{V} \omega \tau_{V} }}{{1 + \omega^{2} \tau_{V}^{2} }}$, the magnitude $\left| {\frac{{X_{2} \left( \omega \right)}}{{X_{1} \left( \omega \right)}}} \right|$ then becomes:

$$ \left| {\frac{{X_{2} \left( \omega \right)}}{{X_{1} \left( \omega \right)}}} \right| = \sqrt {\frac{{\left[ {K_{\infty } + \frac{{K_{V} \omega^{2} \tau_{V}^{2} }}{{1 + \omega^{2} \tau_{V}^{2} }}} \right]^{2} + \left[ {\frac{{K_{V} \omega \tau_{V} }}{{1 + \omega^{2} \tau_{V}^{2} }}} \right]^{2} }}{{\left[ {K_{\infty } + \frac{{K_{V} \omega^{2} \tau_{V}^{2} }}{{1 + \omega^{2} \tau_{V}^{2} }} - m_{2} \omega^{2} } \right]^{2} + \left[ {\frac{{K_{V} \omega \tau_{V} }}{{1 + \omega^{2} \tau_{V}^{2} }}} \right]^{2} }}} $$

(11)

Finally using $K_{\infty } = \frac{{E_{\infty } A}}{L}$ and $K_{V} = \frac{{E_{V} A}}{L}$, $\left| {\frac{{X_{2} \left( \omega \right)}}{{X_{1} \left( \omega \right)}}} \right|$ is obtained in terms of E_∞, E_V, and τ_V as:

$$ \left| {\frac{{X_{2} \left( \omega \right)}}{{X_{1} \left( \omega \right)}}} \right| = \sqrt {\frac{{\left[ {\frac{{E_{\infty } A}}{L} + \frac{{E_{V} A}}{L}\frac{{\omega^{2} \tau_{V}^{2} }}{{1 + \omega^{2} \tau_{V}^{2} }}} \right]^{2} + \left[ {\frac{{E_{V} A}}{L}\frac{{\omega \tau_{V} }}{{1 + \omega^{2} \tau_{V}^{2} }}} \right]^{2} }}{{\left[ {\frac{{E_{\infty } A}}{L} + \frac{{E_{V} A}}{L}\frac{{\omega^{2} \tau_{V}^{2} }}{{1 + \omega^{2} \tau_{V}^{2} }} - m_{2} \omega^{2} } \right]^{2} + \left[ {\frac{{E_{V} A}}{L}\frac{{\omega \tau_{V} }}{{1 + \omega^{2} \tau_{V}^{2} }}} \right]^{2} }}} $$

(12)

Equation (12) was used to fit the transmissibility data of Fig. 15 by deriving the fitting coefficients E_∞, E_V, and τ_V of Fig. 16.

Fig. 18

a Generalized Maxwell model for a 1-DOF vibration system and b free-body-diagram representation