Some Isoperimetric Inequalities in the Plane with Radial Power Weights

Abstract

We consider the punctured plane with volume density $|x|^\alpha$ and perimeter density $|x|^\beta$. We show that centred balls are uniquely isoperimetric for indices $(\alpha ,\beta )$ which satisfy the conditions $\alpha -\beta +1>0$, $\alpha \le 2\beta$ and $\alpha (\beta +1)\le \beta ^2$ except in the case $\alpha =\beta =0$ which corresponds to the classical isoperimetric inequality. As an application, we verify a conjecture due to Caldiroli and Musina relating to the best constant in the Caffarelli–Kohn–Nirenberg inequality.

1 Introduction

For $\alpha \in \mathbb {R}$ the weighted volume measure $V_\alpha :=|x|^\alpha \mathscr {L}^2$ is defined on the $\mathscr {L}^2$-measurable sets in $\mathbb {R}^2_0:=\mathbb {R}^2\setminus \{0\}$. For $\beta \in \mathbb {R}$ the weighted perimeter of a set of locally finite perimeter E in $\mathbb {R}^2_0$ is defined by

$$\begin{aligned} P_\beta (E):=\int _{\mathbb {R}^2_0}|x|^\beta \,\mathrm{{d}}|D\chi _E|\in [0,\infty ]. \end{aligned}$$

(1.1)

We study minimisers for the weighted isoperimetric problem

$$\begin{aligned} I(v):=\inf \Big \{ P_\beta (E):E\text { is a set with locally finite perimeter in }\mathbb {R}^2_0\text { and }V_\alpha (E)=v\Big \},\nonumber \\ \end{aligned}$$

(1.2)

for $v>0$. Let us introduce the parameter set $\mathcal {P}$ given by

$$\begin{aligned} \mathcal {P}&:=\Big \{(\alpha ,\beta )\in \mathbb {R}^2:\alpha -\beta +1>0,\alpha \le 2\beta \text { and }\alpha (\beta +1)\le \beta ^2\Big \}. \end{aligned}$$

(1.3)

Our main result is the following.

Theorem 1.1

Let $(\alpha ,\beta )\in \mathcal {P}\setminus \{(0,0)\}$ and let $v>0$. Then the centred ball is a unique minimiser for the problem (1.2) up to equivalence.

This result may be formulated alternatively. For $(\alpha ,\beta )\in \mathcal {P}\setminus \{(0,0)\}$,

$$\begin{aligned} P_\beta (E)^{\alpha +2}\ge (2\pi )^{\alpha -\beta +1}(\alpha +2)^{\beta +1}V_\alpha (E)^{\beta +1}, \end{aligned}$$

(1.4)

for any set of locally finite perimeter E in $\mathbb {R}^2_0$ with finite weighted volume and equality holds if and only if E is equivalent to a centred ball.

This result has been formulated in [17] Conjecture 4.22 and [2] Conjecture 5.1. It arises from stability considerations as in [34] Conjecture 3.12. The result has been proved amongst convex competitors in [19] Theorem 3.1. It is proved in part in [2] Theorem 1.1; in particular, for indices $(\alpha ,\beta )$ satisfying $\alpha -\beta +1\ge 0$ as well as $\alpha \le 0\le \beta \le 1/3$ or a more complicated condition with $\beta \ge 1/3$. In [13] Theorem 1.3, the result is proved in the régime $\alpha -\beta +1\ge 0$ and $\alpha \le 2\beta \le 0$.

We remark that centred balls are stable with the radial power perimeter and volume densities above if and only if $\alpha (\beta +1)\le \beta ^2$ as can be seen using [20] Theorem 6.3 (for $\alpha <0$ the condition for existence of isoperimetric minimisers bites rather than stability of centred balls). In short the above result (together with [13] Theorem 1.3) is consistent with the so-called generalised log-convex density conjecture as stated in [19] (though we also refer the reader to [30]).

Apart from its intrinsic interest another motivation to study, this inequality is its application in the theory of Sobolev spaces. In [2], the weighted isoperimetric inequality is used to obtain the best constant in a corresponding Caffarelli–Kohn–Nirenberg inequality (see [2] Theorem 8.3 or [13] for example). We extend this result in Section 14. This verifies a conjecture of Caldirolli and Musina which may be found immediately after the statement of [11] Theorem 1.3.

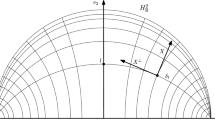
Let us mention some related results. Centred balls are isoperimetric in case $\alpha -\beta +1\le 0$ and $\alpha +2>0$ as shown in [17] Proposition 4.21 (see also [26] Example 3.5 (4)). In [15] Theorem 3.16, it is shown that discs tangent to the origin are isoperimetric in the case $\alpha =\beta >0$. In contrast, isoperimetric minimisers do not exist if $-2<\alpha <0$ and $\alpha =\beta$ according to [12] Proposition 4.2. If $\beta \le \alpha \le 2\beta$ and $\beta \ge 0$ then pinched circles through the origin are isoperimetric. This is contained in [17] Proposition 4.21. The case $\beta \ge 1$ and $\alpha =0$ is treated in [6] Theorem 2.1. A similar isoperimetric problem but with additional constraints is discussed in the case $\alpha =0$ and $\beta <0$ in [14] Theorem 3. According to [17] Conjecture 4.22 the region in the $(\alpha ,\beta )$-plane between the curves $\alpha (\beta +1)=\beta ^2$ and $\alpha =\beta$ should correspond to either undularies or pinched circles through the origin. We refer to Fig. 1.

Fig. 1

In the region between the solid lines and curve centred balls are isoperimetric (see Theorem 1.1 and [17, 26]). The solid curve is given by $\alpha (\beta +1)-\beta ^2=0$ with $\beta \ge 0$. Balls tangent to the origin are isoperimetric on the dotted line (see [15] Theorem 3.16). In the region between the dotted and dashed lines pinched circles through the origin are isoperimetric (see [17] Proposition 4.21). For the region between the solid curve and dotted line see [17] Conjecture 4.22

2 Outline of the Argument

Let us give the bones of the argument.

Select a minimiser E of (1.2). Then E is essentially bounded. Existence and boundedness is guaranteed in Corollary 6.12. Replace E by its spherical cap symmetral $E^{sc}$. This is also a minimiser because the perimeter and volume densities are radial. By choosing a suitable $\mathscr {L}^2$-version of the set $E^{sc}$ we can arrange that its topological boundary is well behaved in a measure-theoretic sense. Call this version $\widetilde{E}$. It has analytic boundary M in $\mathbb {R}^2_0$. So we may choose $\widetilde{E}$ to be open, bounded, spherical cap symmetric and with analytic boundary relative to $\mathbb {R}^2_0$. The altered minimiser $\widetilde{E}$ is related to the original minimiser E via the relation $L_{\widetilde{E}}=L_E$ a.e. on $(0,\infty )$. Here, $L_E(t)$ stands for the $\mathscr {H}^1$-measure of the trace of E on the centred circle with radius $t>0$ (and likewise for $\widetilde{E})$. These facts are contained in Theorem 7.1.

Let n stand for the inner unit normal vector field along M. Choose a tangent vector t in such a way that the pair $\{t,n\}$ is positively oriented. The angle $\sigma$ stands for the angle between the position vector x and the tangent vector t measured in an anticlockwise direction (as in Fig. 2). Define the set $\Omega$ to be the collection of radii for which the centred circle with this radius meets the boundary curve M transversally. This set is open in $(0,\infty )$. The heart of the demonstration is to show that $\Omega$ is empty. In other words centred circles meet the boundary M tangentially if at all. This result is contained in Theorem 13.1. We shall say more about this shortly. With this result in hand we may deduce that $\widetilde{E}$ is a finite union of centred annuli. This leads to the fact that $\widetilde{E}$ is a centred ball. The proof of uniqueness exploits the a.e. relation $L_{\widetilde{E}}=L_E$ mentioned above.

Fig. 2

The inner unit normal along the boundary of E is denoted n. The tangent vector t is chosen in such a way that the pair $\{t,n\}$ is positively oriented. The angle $\sigma$ stands for the angle between the position vector x and the tangent vector t measured in an anticlockwise direction

Let us say a little more about how to show that $\Omega$ is empty. Suppose for a contradiction that $\Omega \ne \emptyset$. The function u at a point $\tau$ in $\Omega$ is defined to be the sine of the angle $\sigma$ introduced above. This function is continuously differentiable on $\Omega$ and there exists a real constant $\lambda$ such that

$$\begin{aligned} u^\prime +\frac{\beta +1}{\tau }u+\lambda \tau ^{\alpha -\beta }&=0, \end{aligned}$$

(2.1)

on $\Omega$. This last is a reformulation of the constant generalised (mean) curvature condition; that is, constancy of the expression

$$\begin{aligned} \tau ^{\beta -\alpha }\Big \{k+\frac{\beta }{\tau }u\Big \}, \end{aligned}$$

along M. The curvature k of M as a function of the radial variable $\tau$ is given by the expression $k=\frac{1}{\tau }(\tau u)^\prime$. This means that the curve M can be reconstructed from the function u up to rotation around the origin. In fact the angular variable admits an explicit integral representation. Suppose that (a, b) is a maximal connected component of $\Omega$. Then the angular variable of a point with polar coordinates $(\tau ,\theta )$ on M is given by

$$\begin{aligned} \theta _u=\theta _u(b)+\int _\cdot ^b\frac{u}{\sqrt{1-u^2}}\frac{\mathrm{{d}}t}{t}, \end{aligned}$$

on (a, b). The angle integral is a hyper-elliptic integral in case the indices $\alpha$ and $\beta$ are integral.

Suppose that the left-hand end-point a is positive. The cosine of $\sigma$ vanishes at the end-points a and b. So u takes values $\pm 1$ there. Suppose first of all that $-u(a)=u(b)=1$ (see Fig. 3). Then $\theta _u(a)\in (0,\pi ]$ by Corollary 9.5 and in fact in $(0,\pi )$. As the sine of $\sigma$ is $-1$ at this point the curvature is $-1/a$; but this conflicts with the curvature obtained from the generalised (mean) curvature equation. Now suppose that $u(a)=u(b)=1$. Then $\theta _u(a)>\pi$ (Corollary 9.11); again a contradiction. We turn to the case $a=0$. Then the weighted perimeter of E relative to the closed centred ball with radius b exceeds that of the centred ball with the same weighted volume. This result is contained in (11.7). This involves a delicate beta function inequality in Theorem 10.1. We refer to the proof of Theorem 13.1 for a discussion of the remaining boundary conditions. We have mentioned two inequalities involving the angle integral. Let us supply a little more detail.

Consider once more the boundary condition $-u(a)=u(b)=1$. The angle integral can be expressed in terms of the distribution function $\mu _{\pm u}$ of $\pm u$ with respect to the measure $\mu$ on $(0,\infty )$ with infinitesimal element $(1/\tau )\,\mathrm{{d}}\tau$; to be more explicit $\mu _u(t)=\mu (\{u>t\})$. In detail,

$$\begin{aligned} \theta _u(b)-\theta _u(a)=-\int _a^b\frac{u}{\sqrt{1-u^2}}\frac{\mathrm{{d}}\tau }{\tau } =-\int _0^1\Big \{\mu _u-\mu _{-u}\Big \}\frac{\mathrm{{d}}t}{(1-t^2)^{3/2}}, \end{aligned}$$

after a change in the order of integration. We aim to show that the right-hand side is strictly negative. This entails that $\theta _u(a)\in (0,\pi ]$ as mentioned in the last paragraph. The difference between the distribution functions can be expressed in terms of their derivatives

$$\begin{aligned} -\Big \{\mu _u(t)-\mu _{-u}(t)\Big \}=\int _{(t,1]}\Big [\mu _u^\prime -\mu _{-u}^\prime \Big ]\,\mathrm{{d}}s. \end{aligned}$$

By the coarea formula

$$\begin{aligned} \mu _u^\prime (t)-\mu _{-u}^\prime (t)=-\int _{\{u=t\}}\frac{1}{u^\prime }\frac{\mathrm{{d}}\mathscr {H}^0}{\tau } +\int _{\{u=-t\}}\frac{1}{u^\prime }\frac{\mathrm{{d}}\mathscr {H}^0}{\tau }. \end{aligned}$$

Let us imagine for a moment that $t=1$ so that $\{u=\pm t\}$ coincides with the point b respectively a. Then this becomes

$$\begin{aligned} \mu _u^\prime (1)-\mu _{-u}^\prime (1)=-\frac{1}{bu^\prime (b)}+\frac{1}{au^\prime (a)}, \end{aligned}$$

As can be seen from the ODE in (2.1) the derivative of u can be expressed in terms of $\lambda$, u and $\tau$. We, thus, require

$$\begin{aligned} -\frac{1}{bu^\prime (b)}+\frac{1}{au^\prime (a)}=\frac{1}{\beta +1+\lambda b^\gamma }+\frac{1}{\beta +1-\lambda a^\gamma }<0, \end{aligned}$$

where $\gamma =\alpha -\beta +1$. The multiplier $\lambda$ depends explicitly on the end-points a and b as well as the parameters $\alpha$ and $\beta$. This results in an algebraic inequality. The necessary inequality is established in Proposition 8.9. Now suppose that $t\in (0,1)$; that is, u takes the values $-t$ and $+t$ at the end-points of the interval $\{|u|<t\}$. The scaled function u/t has boundary values $\pm 1$ and satisfies an ODE similar to (7.8) but with a scaled $\lambda$. Strict negativity of $\mu ^\prime _u(t)-\mu ^\prime _{-u}(t)$ follows as just described.

Now let us turn to the boundary condition $u(a)=u(b)=1$ with again $0<a<b<\infty$. In this case we consider the reciprocal $w:=1/u$ of u. This satisfies the Riccati equation

$$\begin{aligned} w^\prime +\lambda \tau ^{\alpha -\beta }w^2=\frac{\beta +1}{\tau }w, \end{aligned}$$

as can be seen from (2.1) but with boundary conditions $w(a)=w(b)=1$. Likewise the angle integral is

$$\begin{aligned} \theta _u(b)-\theta _u(a)=-\int _a^b\frac{1}{\sqrt{w^2-1}}\frac{\mathrm{{d}}t}{t}. \end{aligned}$$

Expressed in terms of the distribution function we arrive at a formulation that differs from the above

$$\begin{aligned} \int _a^b\frac{1}{\sqrt{w^2-1}}\frac{\mathrm{{d}}\tau }{\tau }=\pi -\int _1^\infty \Big [\mu _w-\mu _{w_0}\Big ]\frac{t}{(t^2-1)^{3/2}}\,\mathrm{{d}}t. \end{aligned}$$

We establish the differential inequality $-\mu _w^\prime >\sigma (t,\mu _w)$ where equality $-\mu _{w_0}^\prime =\sigma (t,\mu _{w_0})$ pertains for the distribution function associated to the case $\alpha =\beta =0$ and corresponds to a semicircle through the points $(-a,0)$ and (b, 0). This differential inequality entails that $\mu _w<\mu _{w_0}$ and the angle integral in the last displayed equation exceeds $\pi$. This results in the contradiction that $\theta _u(a)>\pi$ as mentioned above.

Let us give some indication as how to obtain the last-mentioned differential inequality. Again by the coarea formula

$$\begin{aligned} -\mu _w^\prime (t)+\mu _{w_0}^\prime (t)=\int _{\{w=t\}}\frac{1}{|w^\prime |}\frac{\mathrm{{d}}\mathscr {H}^0}{\tau } -\int _{\{w_0=t\}}\frac{1}{|w_0^\prime |}\frac{\mathrm{{d}}\mathscr {H}^0}{\tau }. \end{aligned}$$

Let us imagine that $t=1$. Then this becomes

$$\begin{aligned} -\mu _w^\prime (1)+\mu _{w_0}^\prime (1) =-\frac{1}{bw^\prime (b)}+\frac{1}{aw^\prime (a)} +\frac{1}{bw_0^\prime (b)}-\frac{1}{aw_0^\prime (a)}. \end{aligned}$$

As before the multiplier $\lambda$ depends explicitly on the end-points a and b as well as the parameters $\alpha$ and $\beta$. This results in an algebraic inequality. The necessary inequality is established in Theorem 8.1 and is somewhat involved. Now suppose that $t\in (0,1)$; that is, w takes the value t at the end-points of the interval $\{w>t\}$. The scaled function w/t has boundary value 1 on an interval contained inside (a, b) and satisfies a Riccati equation there but with a scaled $\lambda$. The above argument leads to the inequality $\mu _w(t)<\mu _{w_0}(t)$.

Finally, we mention that Sects. 3–5 as well as the Appendix Sect. 1 contain some preliminary material that is needed in the proofs of existence and boundedness contained in Sect. 6.

Fig. 3

The diagram on the left gives an illustration of the boundary condition $-u(a)=u(b)=1$; that on the right illustrates the boundary condition $u(a)=u(b)=1$

3 A Tangential Vol’pert Theorem

The main result of this Section is a tangential Vol’pert theorem given in Theorem 3.9. This result appears in [10] Theorem 3.7. This last is couched in the language of integer multiplicity rectifiable currents. We prefer to work here in the framework of sets of locally finite perimeter. The proof is an adaptation of the approach in [5] Theorem 2.4.

Variation on the sphere. The focus of this subsection is a De Giorgi rectifiability theorem on the circle (cf. [3] Theorem 3.59). We use the notation $\mathbb {S}^{1}_\tau$ to stand for the sphere in $\mathbb {R}^2$ with centre at the origin and radius $\tau >0$. We often drop the superscript; $\mathbb {S}$ stands for the unit sphere. The induced Riemannian metric on $\mathbb {S}$ will be denoted by $\langle \cdot ,\cdot \rangle _{\mathbb {S}}$ and the tangential gradient and divergence by $\nabla _\mathbb {S}$ and $\textrm{div}_\mathbb {S}$ (see [3] Section 7.3 for example). Let $\Omega$ be an open set in $\mathbb {S}$. For $u\in L^1(\Omega ,\mathscr {H}^{1})$ define its variation on the sphere by

$$\begin{aligned} V_{\mathbb {S}}(u,\Omega ):= \sup \left\{ \int _{\mathbb {S}}u\,\textrm{div}_{\mathbb {S}}X\,\mathrm{{d}}\mathscr {H}^{1}:X\in C^1_c(\Omega ,\mathbb {R}^2),\Vert X\Vert _\infty \le 1\right\} \in [0,\infty ].\nonumber \\ \end{aligned}$$

(3.1)

We say that u has bounded variation on the sphere if $u\in L^1(\Omega ,\mathscr {H}^{1})$ and $V_{\mathbb {S}}(u,\Omega )<\infty$ and write $u\in \textrm{BV}_{\mathbb {S}}(\Omega )$.

Fix $x\in \mathbb {R}^2$. The projection

$$\begin{aligned} (\pi v)(x)=\pi (x)v:= \left\{ \begin{array}{ll} v - |x|^{-2}\,\langle v,\, x\rangle \,x &{} \quad \text {for }x\ne 0,\\ 0 &{} \quad \text {for }x=0,\\ \end{array} \right. \end{aligned}$$

maps the vector $v\in \mathbb {R}^2$ onto the subspace $x^\perp$ perpendicular to x. Note that $\pi$ is symmetric in the sense that $\langle (\pi v)(x), w\rangle = \langle v,(\pi w)(x)\rangle$ for any $v,\,w\in \mathbb {R}^2$.

Lemma 3.1

Let $\Omega$ be an open set in $\mathbb {S}$. Then

• (i) the functional $u\mapsto V_\mathbb {S}(u,\Omega )$ is lower semicontinuous with respect to convergence in $L^1(\Omega ,\mathscr {H}^{1})$.

Assume that $u\in \textrm{BV}_{\mathbb {S}}(\Omega )$. Then

• (ii) there exists a unique $\mathbb {R}^2$-valued finite Radon measure $D_{\mathbb {S}}u$ on $\Omega$ such that

  $$\begin{aligned} \int _\Omega u\,\textrm{div}_{\mathbb {S}}\,\pi X\,\mathrm{{d}}\mathscr {H}^{1} = -\int _\Omega \langle X,\,dD_{\mathbb {S}}u\rangle _{\mathbb {S}} \text { for any }X\in C^1_c(\Omega ,\mathbb {R}^2), \end{aligned}$$

  and $|D_\mathbb {S} u|(\Omega )=V_\mathbb {S}(u,\Omega )$;

• (iii) $D_\mathbb {S} u=\nabla _\mathbb {S} u\,\mathscr {H}^{1}$ and $|D_\mathbb {S}u|=|\nabla _\mathbb {S} u|\,\mathscr {H}^{1}$ for $u\in C^1(\Omega )\cap \textrm{BV}_\mathbb {S}(\Omega )$.

Proof

(i) follows from [3] Remark 3.5 while (ii) is a consequence of Riesz’s Theorem (see [3] Theorem 1.54). $\square$

Recall that the set E has locally finite perimeter in $\mathbb {R}^2_0$ if $\chi _E$ belongs to $\textrm{BV}_{\textrm{loc}}(\mathbb {R}^2_0)$. The reduced boundary $\mathscr {F}E$ of E is defined by

$$\begin{aligned} \mathscr {F}E:=\Big \{x\in \textrm{supp}|D\chi _E|:\nu _E(x):=\lim _{\rho \downarrow 0}\frac{D\chi _E(B(x,\rho ))}{|D\chi _E|(B(x,\rho ))}\text { exists in }\mathbb {R}^2\text { and }|\nu ^E(x)|=1\Big \}, \end{aligned}$$

as in for example [3] Definition 3.54. Note that $\mathscr {F}E$ is a Borel set and the map $\nu _E:\mathscr {F}E\rightarrow \mathbb {S}$ is Borel (cf. [3] Theorem 2.22).

Lemma 3.2

Let E be a set of locally finite perimeter in $\mathbb {R}^2_0$. Assume that E is scale invariant; that is, $\lambda E=E$ for each $\lambda >0$. Then

• (i) $\mathscr {F}E$ is scale-invariant;

• (ii) $\nu _E(x)=\nu _E(\lambda x)$ for $x\in \mathscr {F}E$ and $\lambda >0$;

• (iii) $\nu _E(x)\perp x$ for each $x\in \mathscr {F}E$.

Proof

(i) A scaling argument gives

$$\begin{aligned} D\chi _E(B(\lambda x,\lambda r))=\lambda D\chi _E(B(x,r)) \text { and } |D\chi _E|(B(\lambda x,\lambda r))=\lambda |D\chi _E|(B(x,r)), \end{aligned}$$

for $x\in \mathbb {R}^2_0$ and $0<r<|x|$. This leads to the first claim. The considerations in (i) entail (ii). (iii) Let $\phi \in C^1_c((0,\infty ))$ and $\psi \in C^1(\mathbb {S})$ and define a $C^1_c$ vector field on $\mathbb {R}^2_0$ by $X(x):=\phi (\tau )\psi (\omega )\omega$ for $x=\tau \omega \in \mathbb {R}^2_0$. Then

$$\begin{aligned}{} & {} -\int _{\mathscr {F}E}\phi \psi \langle \omega ,\nu _E\rangle \,\mathrm{{d}}\mathscr {H}^1 =\int _E\textrm{div}\,X\,\mathrm{{d}}x=\int _E\frac{1}{\tau }(\tau \phi )^\prime \psi \,\mathrm{{d}}x\\{} & {} \quad =\int _\mathbb {S}\int _0^\infty \chi _E(\tau \phi )^\prime \,\mathrm{{d}}\tau \psi \,\mathrm{{d}}\mathscr {H}^1 =0, \end{aligned}$$

upon converting to polar coordinates. The function $\mathbb {S}\rightarrow \mathbb {R};\omega \mapsto \langle \nu _E(\omega ),\omega \rangle$ is Borel. By Lusin’s Theorem (cf. [3] Theorem 1.45) we derive

$$\begin{aligned} \int _{\mathscr {F}E\cap \{\langle \cdot ,\nu _E\rangle >0\}}\phi \langle \omega ,\nu _E\rangle \,\mathrm{{d}}\mathscr {H}^1=0, \end{aligned}$$

from which we infer that the set $\mathscr {F}E\cap \{\langle \cdot ,\nu _E\rangle >0\}$ is an $\mathscr {H}^1$-null set. We arrive at a similar conclusion with the inequality reversed. The result follows. $\square$

For a Borel set E in $\mathbb {R}^2_0$ and $\tau >0$ the $\tau$-section of E is defined by $E_\tau :=\{x\in E: |x|=\tau \}$. For a real-valued Borel function u on $\mathbb {R}^2_0$ define $u_\tau$ to be the restriction of u to $\mathbb {S}_\tau$.

Proposition 3.3

Let E be a set of locally finite perimeter in $\mathbb {R}^2_0$ and let $g:\mathbb {R}^2_0\rightarrow [0,\infty ]$ be a Borel function. Then

$$\begin{aligned} \int _{\mathscr {F}E}g|\nu _E^\omega |\,\mathrm{{d}}\mathscr {H}^{1} =\int _0^\infty \int _{(\mathscr {F}E)_\tau }g\,\mathrm{{d}}\mathscr {H}^{0}\,\mathrm{{d}}\tau , \end{aligned}$$

where $\nu _E^\omega =\pi \nu _E$ stands for the tangential component of the inner unit normal vector $\nu _E$.

Proof

Define $f:\mathbb {R}^2_0\rightarrow (0,\infty )$ via $x\mapsto |x|$. Let $x\in \mathbb {R}^2_0$ and M be a line through x perpendicular to the unit vector v. Then

$$\begin{aligned} C_1d^Mf_x&=(\pi v)(x). \end{aligned}$$

(3.2)

The result follows by the coarea formula [3] Theorem 2.93 and (2.72). $\square$

An $\mathscr {H}^{1}$-measurable set E in $\Omega$ is said to have finite perimeter in $\Omega$ if $\chi _E\in \textrm{BV}_{\mathbb {S}}(\Omega )$. The reduced boundary $\mathscr {F}_{\mathbb {S}}E$ of E consists of the set of points $x\in \textrm{supp}|D_{\mathbb {S}}\chi _E|\cap \Omega$ such that

$$\begin{aligned} \nu _E^{\mathbb {S}}(x):= \lim _{\rho \downarrow 0} \frac{D_{\mathbb {S}}\chi _E(B_\rho (x))}{|D_{\mathbb {S}}\chi _E|(B_\rho (x))}, \end{aligned}$$

exists in $\mathbb {R}^2$ and has unit length. We may now state and prove a De Giorgi rectifiability theorem on the circle (cf. [3] Theorem 3.59).

Theorem 3.4

Let $\Omega$ be an open set in $\mathbb {S}$ and E a set of finite perimeter in $\Omega$. Then

Proof

Let

$$\begin{aligned} \widetilde{\Omega }:=\{x\in \mathbb {R}^2_0:x/|x|\in \Omega \} \end{aligned}$$

be the cone over $\Omega$ and define $\widetilde{E}$ likewise. Let $X\in C^1_c(\widetilde{\Omega },\mathbb {R}^2)$. We first establish the identity

$$\begin{aligned} \int _{\widetilde{\Omega }}\chi _{\widetilde{E}}\,\textrm{div}\,X\,\mathrm{{d}}x&=\int _0^\infty \int _{\Omega }\chi _{E}\,\textrm{div}(\pi \Big [X\circ I^\tau \Big ])\,\mathrm{{d}}\mathscr {H}^1\,\mathrm{{d}}\tau , \end{aligned}$$

(3.3)

where $I^\tau (x)=\tau x$ is the homothety with scale factor $\tau$. It is apparent from this identity that $\widetilde{E}$ is a set of locally finite perimeter in $\widetilde{\Omega }$ because E is a set of finite perimeter in $\Omega$. We decompose $X=\pi X+(I-\pi )X$ and note that $(I-\pi )X=\phi \omega$ where $\phi (x)=\langle X,\omega \rangle$ and $\omega =x/|x|$. Converting to polar coordinates,

$$\begin{aligned} \int _{\widetilde{\Omega }}\chi _{\widetilde{E}}\,\textrm{div}\,X\,\mathrm{{d}}x&=\int _{\widetilde{\Omega }}\chi _{\widetilde{E}}\,\textrm{div}\,\pi X\,\mathrm{{d}}x +\int _{\widetilde{\Omega }}\chi _{\widetilde{E}}\,\textrm{div}(I-\pi )X\,\mathrm{{d}}x\\&=\int _0^\infty \int _{\widetilde{\Omega }_\tau }\chi _{\widetilde{E}}\textrm{div}(\pi X)\,\mathrm{{d}}\mathscr {H}^1\,\mathrm{{d}}\tau +\int _{\Omega }\chi _E\int _0^\infty \partial _\tau (\tau \phi )\,\mathrm{{d}}\tau \,\mathrm{{d}}\mathscr {H}^1\\&=\int _0^\infty \int _{\widetilde{\Omega }_\tau }\chi _{\widetilde{E}}\,\textrm{div}(\pi X)\,\mathrm{{d}}\mathscr {H}^1\,\mathrm{{d}}\tau \\&=\int _0^\infty \int _{\Omega }\chi _{E}\,\textrm{div}\Big (\pi \Big [X\circ I^\tau \Big ]\Big )\,\mathrm{{d}}\mathscr {H}^1\,\mathrm{{d}}\tau , \end{aligned}$$

using the fact that $\textrm{div}(I-\pi )X=\tau ^{-1}\partial _\tau (\tau \phi )$ and $\textrm{div}(\pi X\circ I^\tau )(x)=\tau \,\textrm{div}(\pi X)(\tau x)$. This establishes (3.3).

Let $\phi \in C_c^1((0,\infty ))$. Let Y be an $\mathbb {R}^2$-valued vector field defined on $\Omega$ which is of class $C^1$ with compact support and which is tangential to $\mathbb {S}$. Define $X\in C^1_c(\widetilde{\Omega },\mathbb {R}^2)$ by $X(x):=\phi (\tau ) Y(\omega )$ for $x=\tau \omega \in \widetilde{\Omega }$. The set $\widetilde{E}$ is scale-invariant. So $|\pi \nu _{\widetilde{E}}|=1$ on $\mathscr {F}\widetilde{E}$ by Lemma 3.2 which implies in turn that $|\nu _{\widetilde{E}}^\omega |=1$. By Proposition 3.3 the left-hand side of (3.3) may be written

$$\begin{aligned} \int _{\widetilde{\Omega }}\chi _{\widetilde{E}}\,\textrm{div}\,X\,\mathrm{{d}}x&=-\int _{\mathscr {F}\widetilde{E}}\langle X,\nu _{\widetilde{E}}\rangle \,\mathrm{{d}}\mathscr {H}^1 =-\int _0^\infty \int _{(\mathscr {F}\widetilde{E})_\tau }\langle X,\nu _{\widetilde{E}}\rangle \,\mathrm{{d}}\mathscr {H}^{0}\,\mathrm{{d}}\tau \nonumber \\&=-\int _0^\infty \phi \int _{(\mathscr {F}\widetilde{E})_\tau }\langle Y,\nu _{\widetilde{E}}\rangle \,\mathrm{{d}}\mathscr {H}^0\,\mathrm{{d}}\tau . \end{aligned}$$

(3.4)

The right-hand side of (3.3) may be expressed

$$\begin{aligned} \int _0^\infty \int _{\Omega }\chi _{E}\,\textrm{div}(\pi \Big [X\circ I^\tau \Big ])\,\mathrm{{d}}\mathscr {H}^1\,\mathrm{{d}}\tau&= -\int _0^\infty \int _\Omega \langle X\circ I^\tau ,dD_{\mathbb {S}}\chi _E\rangle _{\mathbb {S}}\,\mathrm{{d}}\tau \nonumber \\&=-\int _0^\infty \phi \int _\Omega \langle Y,dD_{\mathbb {S}}\chi _E\rangle _{\mathbb {S}}\,\mathrm{{d}}\tau , \end{aligned}$$

(3.5)

by Lemma 3.1. On combining (3.4) and (3.5) using (3.3) we may equate

$$\begin{aligned} \int _0^\infty \phi \int _{(\mathscr {F}\widetilde{E})_\tau }\langle Y,\nu _{\widetilde{E}}\rangle \,\mathrm{{d}}\mathscr {H}^0\,\mathrm{{d}}\tau =\int _0^\infty \phi \int _\Omega \langle Y,dD_{\mathbb {S}}\chi _E\rangle _{\mathbb {S}}\,\mathrm{{d}}\tau , \end{aligned}$$

which leads in turn to the identity

$$\begin{aligned} \int _{(\mathscr {F}\widetilde{E})_1}\langle Y,\nu _{\widetilde{E}}\rangle \,\mathrm{{d}}\mathscr {H}^0 = \int _\Omega \langle Y,dD_{\mathbb {S}}\chi _E\rangle _{\mathbb {S}}. \end{aligned}$$

From the uniqueness property in Riesz’s Theorem (cf. [3] Theorem 1.54) we deduce that . We derive that $\mathscr {F}E=(\mathscr {F}\widetilde{E})_1$ and $\nu _E^{\mathbb {S}}=\nu _{\widetilde{E}}$ there. This concludes the proof. $\square$

Spherical variation. Let $\Omega$ be an open set in $\mathbb {R}^2_0$. The spherical variation of $u\in L^1_{\textrm{loc}}(\Omega )$ on $A\subset \subset \Omega$ is defined by

$$\begin{aligned} V_\omega (u,A):=\sup \Big \{\int _A u\,\text {div}(\pi X)\,\mathrm{{d}}x:X\in C^1_c(A,\mathbb {R}^2)\text { and }\Vert X\Vert _\infty \le 1\Big \}\le \infty . \end{aligned}$$

Lemma 3.5

Let $\Omega$ be an open set in $\mathbb {R}^2_0$. Then

• (i) the functional $u\mapsto V_\omega (u,A)$ is lower semicontinuous with respect to convergence in $L^1_{\textrm{loc}}(\Omega )$ for each $A\subset \subset \Omega$.

Assume that $u\in \textrm{BV}_{\textrm{loc}}(\Omega )$. Then

• (ii) there exists a unique $\mathbb {R}^2$-valued Radon measure $D_\omega u$ such that

  $$\begin{aligned} \int _\Omega u\,\textrm{div}(\pi X)\,\mathrm{{d}}x=-\int _\Omega \langle X,\,dD_\omega u\rangle \text { for any } X\in C^1_c(\Omega ,\mathbb {R}^2), \end{aligned}$$

  and $|D_\omega u|(\Omega )=V_\omega (u,\Omega )$;

• (iii) $D_\omega u=(\pi \rho )\,|Du|$ and $|D_\omega u|=|\pi \rho |\,|Du|$ where $Du=\rho \,|Du|$ is the polar decomposition of Du with $\rho$ a unique $\mathbb {S}$-valued function in $L^1(\Omega ,\,|Du|)^2$;

• (iv) $D_\omega u=\nabla _\omega u\,\mathscr {L}^2$ and $|D_\omega u|=|\nabla _\omega u|\,\mathscr {L}^2$ for $u\in C^1(\Omega )\cap \textrm{BV}_{\textrm{loc}}(\Omega )$ where $\nabla _\omega = \pi \nabla$.

Proof

(i) and (ii) follow from [3] Remark 3.5 and Riesz’s Theorem (cf. [3] Theorem 1.54). The fact that u belongs to the class $\textrm{BV}_{\textrm{loc}}(\Omega )$ leads to (iii) and (iv). $\square$

Lemma 3.6

Let $\Omega$ be an open set in $\mathbb {R}^2_0$. Let $u\in BV(\Omega )$ and $U\subset \subset \Omega$ open. Let $(\varphi _\varepsilon )_{\varepsilon >0}$ be a family of mollifiers on $\mathbb {R}^2$ as in [3] Section 2.1. Then $\nabla _\omega (u*\varphi _\varepsilon )=\pi \,(Du*\varphi _\varepsilon )$ on U for small $\varepsilon >0$.

Proof

Let $0<\varepsilon <\textrm{dist}(U,\partial \Omega )$. Let $X\in C^1_c(\Omega ,\mathbb {R}^2)$ with $\textrm{supp}\,X\subset U$. We use the fact that $\textrm{div}(\varphi _\varepsilon *\pi X)=\varphi _\varepsilon *\textrm{div}(\pi X)$ on $\Omega$. Note that the restriction of $u*\varphi _\varepsilon$ to U belongs to $\textrm{BV}(U)$. By symmetry of $\pi$, Lemma 3.5 and the convolution identity [3] (2.3),

$$\begin{aligned} -\int _U\langle \nabla _\omega (u*\varphi _\varepsilon ),X\rangle \,\mathrm{{d}}x&= \int _U(u*\varphi _\varepsilon )\textrm{div}\,\pi X\,\mathrm{{d}}x = \int _\Omega u(\textrm{div}\,\pi X*\varphi _\varepsilon )\,\mathrm{{d}}x\\&= \int _\Omega u\,\textrm{div}(\varphi _\varepsilon *\pi X)\,\mathrm{{d}}x = -\int _\Omega \langle \varphi _\varepsilon *\pi X,\,\mathrm{{d}}Du\rangle \\&= -\int _U\langle \pi (\varphi _\varepsilon *Du),X\rangle \,\mathrm{{d}}x. \end{aligned}$$

The result now follows by the fundamental lemma of the calculus of variations and smoothness of the mollified functions. $\square$

Proposition 3.7

Let $\Omega$ be an open set in $\mathbb {R}^2_0$. Let $u\in \textrm{BV}(\Omega )$ and $U\subset \subset \Omega$ open with the property that $|D u|(\partial U)=0$. Then

$$\begin{aligned} |D_\omega u|(U)= \lim _{\varepsilon \downarrow 0}|D_\omega (u*\varphi _\varepsilon )|(U), \end{aligned}$$

where $(\varphi _\varepsilon )_{\varepsilon >0}$ is a family of mollifiers.

Proof

By lower semicontinuity of the spherical variation (Lemma 3.5),

$$\begin{aligned} |D_\omega u|(U)\le \liminf _{\varepsilon \downarrow 0}|D_\omega (u*\varphi _\varepsilon )|(U). \end{aligned}$$

The bulk of the proof is dedicated to the reverse inequality. Let $0<\varepsilon <\textrm{dist}(U,\partial \Omega )$. By Lemmas 3.5, 3.6 and Fubini’s theorem,

$$\begin{aligned} |D_\omega (u*\varphi _\varepsilon )|(U)= & {} \int _U|\nabla _\omega (u*\varphi _\varepsilon )|\,\mathrm{{d}}x = \int _U|\pi (Du*\varphi _\varepsilon )|\,\mathrm{{d}}x \\\le & {} \int _U\int _{\Omega }\varphi _\varepsilon (x-y)|\pi (x)\rho (y)|\,\mathrm{{d}}|Du|(y)\,\mathrm{{d}}x\\= & {} \int _{\Omega }\int _U\varphi _\varepsilon (x-y)|\pi (x)\rho (y)|\,\mathrm{{d}}x\,\mathrm{{d}}|Du|(y), \end{aligned}$$

for small $\varepsilon >0$. Denoting the integrand by $\phi _\varepsilon$ we may write the right-hand side of the last identity as

$$\begin{aligned} \int _{\Omega }\phi _\varepsilon \,\mathrm{{d}}|Du| = \int _U\phi _\varepsilon \,\mathrm{{d}}|Du| + \int _{\Omega \setminus \overline{U}}\phi _\varepsilon \,\mathrm{{d}}|Du|, \end{aligned}$$

in virtue of the fact that $|D u|(\partial U)=0$ by assumption. The mapping $x\mapsto \pi (x)v$ is continuous on $\mathbb {R}^2_0$ for any $v\in \mathbb {R}^2$. So for $y\in \Omega$,

$$\begin{aligned} \lim _{\varepsilon \downarrow 0}\phi _\varepsilon (y) = \left\{ \begin{array}{lcl} |\pi (y)\rho (y)| &{} \text { if } &{} y\in U,\\ 0 &{} \text { if } &{} y\in \Omega \setminus \overline{U}. \end{array} \right. \end{aligned}$$

By the dominated convergence theorem,

$$\begin{aligned} \limsup _{\varepsilon \downarrow 0}|D_\omega (u*\varphi _\varepsilon )|(U) \le \int _U|\pi \rho |\,\mathrm{{d}}|Du| =|D_\omega u|(U), \end{aligned}$$

by Lemma 3.5. That is, the reverse inequality does indeed hold. $\square$

The next proposition is the spherical variation counterpart to [3] Proposition 3.103.

Proposition 3.8

Let $\Omega$ be an open set in $\mathbb {R}^2_0$ and $u\in \textrm{BV}_{\textrm{loc}}(\Omega )$. Then $u_\tau \in \textrm{BV}_{\mathbb {S}_\tau }(\Omega _\tau )$ for a.e. $\tau >0$ and

$$\begin{aligned} V_\omega (u,\Omega ) = \int _0^\infty V_{\mathbb {S}_\tau }(u_\tau ,\Omega _\tau )\,\mathrm{{d}}\tau . \end{aligned}$$

Proof

First note that equality holds for $u\in C^1(\Omega )\cap \textrm{BV}(\Omega )$. Indeed by Lemma 3.5(iv), switching to polar coordinates and Lemma 3.1(iii),

$$\begin{aligned} |D_\omega u|(\Omega )&=\int _\Omega |\nabla _\omega u|\,\mathrm{{d}}x =\int _0^\infty \int _{\Omega _\tau }|\nabla _\omega u|\,\mathrm{{d}}\mathscr {H}^{1}\,\mathrm{{d}}\tau \nonumber \\&=\int _0^\infty \int _{\Omega _\tau }|\nabla _{\mathbb {S}_\tau } u_\tau |\,\mathrm{{d}}\mathscr {H}^{1}\,\mathrm{{d}}\tau =\int _0^\infty V_{\mathbb {S}_\tau }(u_\tau ,\Omega _\tau )\,\mathrm{{d}}\tau , \end{aligned}$$

(3.6)

as required.

By converting to polar coordinates it can be seen that $u_\tau \in L^1(\Omega _\tau ,\mathscr {H}^{1})$ for a.e. $\tau >0$. For small $t>0$ put

$$\begin{aligned} \Omega ^t:=\Big \{x\in \Omega :\,|x|<1/t\text { and }\textrm{dist}(x,\partial \Omega )>t\Big \}. \end{aligned}$$

It holds that $|D u|(\partial \Omega ^t)=0$ for all but countably many $t>0$ as |Du| is a Radon measure on $\Omega$. For $\varepsilon >0$ small,

$$\begin{aligned} \int _{\Omega ^t}|u*\varphi _\varepsilon - u|\,\mathrm{{d}}x = \int _0^\infty \Vert (u*\varphi _\varepsilon )_\tau - u_\tau \Vert _{L^1((\Omega ^t)_\tau )}\,\mathrm{{d}}\tau , \end{aligned}$$

upon converting to polar coordinates and the left-hand side converges to zero in the limit $\varepsilon \downarrow 0$ by a standard property of mollification. So there exists a subsequence $\varepsilon _h\downarrow 0$ such that with $v_h=u*\varphi _{\varepsilon _h}\in C^\infty _c(\Omega )$,

$$\begin{aligned} (v_h)_\tau \rightarrow u_\tau \text { in }L^1((\Omega ^t)_\tau ,\,\mathscr {H}^{1})\text { for a.e. }\tau >0. \end{aligned}$$

By lower semicontinuity Lemma 3.1, Fatou’s lemma, (3.6) and Proposition 3.7,

$$\begin{aligned} \int _0^\infty V_{\mathbb {S}_\tau }(u_\tau ,(\Omega ^t)_\tau )\,\mathrm{{d}}\tau&\le \int _0^\infty \left\{ \liminf _{h\rightarrow \infty }V_{\mathbb {S}_\tau }((v_h)_\tau ,(\Omega ^t)_\tau )\right\} \,\mathrm{{d}}\tau \\&\le \liminf _{h\rightarrow \infty }\int _0^\infty V_{\mathbb {S}_\tau }((v_h)_\tau ,(\Omega ^t)_\tau ) \,\mathrm{{d}}\tau \\&= \liminf _{h\rightarrow \infty }|D_\omega v_h|(\Omega ^t) = |D_\omega u|(\Omega ^t) \le V_\omega (u,\Omega ). \end{aligned}$$

By the monotone convergence theorem,

$$\begin{aligned} \int _0^\infty V_{\mathbb {S}_\tau }(u_\tau ,\Omega _\tau )\,\mathrm{{d}}\tau \le V_\omega (u,\Omega ), \end{aligned}$$

so that $u_\tau \in \textrm{BV}_{\mathbb {S}_\tau }(\Omega _\tau )$ for a.e. $\tau >0$.

As for the reverse inequality, let $X\in C^1_c(\Omega ,\mathbb {R}^2)$ with $\Vert X\Vert _\infty \le 1$. In polar coordinates

$$\begin{aligned} \int _\Omega u\,\textrm{div}(\pi X)\,\mathrm{{d}}x = \int _{p(\Omega )}\int _{\Omega _\tau }u_\tau \textrm{div}_{\mathbb {S}_\tau }(\pi X)\,\mathrm{{d}}\mathscr {H}^{1} \,\mathrm{{d}}\tau \le \int _{p(\Omega )}V_{\mathbb {S}_\tau }(u_\tau ,\Omega _\tau )\,\mathrm{{d}}\tau , \end{aligned}$$

recalling (3.1). Taking the supremum yields the reverse inequality. $\square$

Let E be a set of locally finite perimeter in $\mathbb {R}^2_0$. In line with Lemma 3.5(iii),

(3.7)

where we write $\nu _E^\omega =\pi \nu _E$ as before. With the foregoing preparation we arrive at the main theorem of this Section. It is a tangential counterpart to [5] Theorem 2.4.

Theorem 3.9

Let E be a set of locally finite perimeter in $\mathbb {R}^2_0$. Then for a.e. $\tau >0$,

• (i) $E_\tau$ is a set of finite perimeter in $\mathbb {S}_\tau$;

• (ii) $\mathscr {H}^0(\mathscr {F}_{\mathbb {S}_\tau }E_\tau \Delta (\mathscr {F}E)_\tau )=0$.

Proof

(i) This follows from Proposition 3.8. (ii) By this last as well as Lemma 3.5 and Lemma 3.1,

$$\begin{aligned} |D_\omega \chi _E|(\Omega ){} & {} =V_\omega (\chi _E,\Omega ) =\int _0^\infty V_{\mathbb {S}_\tau }((\chi _E)_\tau ,\Omega _\tau )\,\mathrm{{d}}\tau \nonumber \\{} & {} =\int _0^\infty |D_{\mathbb {S}_\tau }\chi _{E_\tau }|(\Omega _\tau )\,\mathrm{{d}}\tau , \end{aligned}$$

(3.8)

for any relatively compact open set $\Omega$ contained in $\mathbb {R}^2_0$. Let A stand for the open centred annulus with radii $0<r<R<\infty$. Put

$$\begin{aligned} \mathscr {M}:=\Big \{B\subset A:\,B\text { is a Borel set and } |D_\omega \chi _E|(B) =\int _0^\infty |D_{\mathbb {S}_\tau }\chi _{E_\tau }|(B_\tau )\,\mathrm{{d}}\tau \Big \}. \end{aligned}$$

By (3.8) the collection $\mathscr {M}$ contains all open sets in A; it also has the properties

• (a) $(B_h)_{h\in \mathbb {N}}\subset \mathscr {M},\,B_h\uparrow B\Rightarrow B\in \mathscr {M}$;

• (b) $B,\,B^\prime ,\,B\cup B^\prime \in \mathscr {M}\Rightarrow B\cap B^\prime \in \mathscr {M}$;

• (c) $B\in \mathscr {M}\Rightarrow A\setminus B\in \mathscr {M}$.

$\mathscr {M}$, therefore, coincides with the $\sigma$-algebra of Borel sets in A by [3] Remark 1.9. This entails that the identity in (3.8) holds for each relatively compact Borel set B in $\mathbb {R}^2_0$.

Let B be a relatively compact Borel set in $\mathbb {R}^2_0$. By Proposition 3.3, (3.7), the last observation, and Theorem 3.4,

$$\begin{aligned} \int _0^\infty \int _{(\mathscr {F}E)_\tau }\chi _B\,\mathrm{{d}}\mathscr {H}^{0}\,\mathrm{{d}}\tau&= \int _{\mathscr {F}E}\chi _B|\nu _E^\omega |\,\mathrm{{d}}\mathscr {H}^{1} = |D_\omega \chi _E|(B)\\&=\int _0^\infty |D_{\mathbb {S}_\tau }\chi _{E_\tau }|(B_\tau )\,\mathrm{{d}}\tau = \int _0^\infty \int _{\mathscr {F}_{\mathbb {S}_\tau }E_\tau }\chi _B\,\mathrm{{d}}\mathscr {H}^{0}\,\mathrm{{d}}\tau . \end{aligned}$$

Let $\mathscr {G}$ be a countable base for the $\sigma$-algebra of Borel sets in $\mathbb {S}$. Fix $G\in \mathscr {G}$ and any Borel set $I\subset (0,\infty )$. This last identity holds with $B=\{\tau \omega :\tau \in I\text { and }\omega \in G\}$. We derive that

$$\begin{aligned} \int _{(\mathscr {F}E)_\tau }\chi _G\circ I^{1/\tau }\,\mathrm{{d}}\mathscr {H}^{0} = \int _{\mathscr {F}_{\mathbb {S}_\tau }E_\tau }\chi _G\circ I^{1/\tau }\,\mathrm{{d}}\mathscr {H}^{0}, \end{aligned}$$

(3.9)

for a.e. $\tau >0$. Identity (3.9), therefore, holds for every Borel set G in $\mathbb {S}$ for a.e. $\tau$ in $(0,\infty )$. Item (ii) now follows. $\square$

4 A Radial Vol’pert Theorem

The goal of this Section is to prove a radial Vol’pert theorem in Theorem 4.5; there are similarities with the previous Section. For $x\in \mathbb {R}^2_0$ and $v\in \mathbb {R}^2$ set $(\tilde{\pi } v)(x):=\langle v,\omega \rangle \omega$ where $\omega =x/|x|$. That is, $(\tilde{\pi } v)(x)$ stands for the radial component of v at the point x. Let $\Omega$ be a relatively compact open set in $\mathbb {R}^2_0$. The radial variation of $u\in L^1(\Omega )$ is defined by

$$\begin{aligned} V_{\textrm{rad}}(u,\Omega ):=\sup \Big \{\int _{\Omega }u\,\textrm{div}(r^{-1}\tilde{\pi } X)\,\mathrm{{d}}x:X\in C^1_c(\Omega ,\mathbb {R}^2)\text { and }\Vert X\Vert _\infty \le 1\Big \}. \end{aligned}$$

Lemma 4.1

Let $\Omega$ be a relatively compact open set in $\mathbb {R}^2_0$. Then

• (i) the functional $u\mapsto V_\textrm{rad}(u,\Omega )$ is lower semicontinuous with respect to convergence in $L^1(\Omega )$.

Let $u\in \textrm{BV}(\Omega )$. Then

• (ii) there exists a unique $\mathbb {R}^2$-valued Radon measure $D_\textrm{rad} u$ on $\Omega$ such that

  $$\begin{aligned} \int _{\Omega }u\,\textrm{div}(r^{-1}\tilde{\pi } X)\,\mathrm{{d}}x = -\int _\Omega \langle X,dD_{\textrm{rad}}u\rangle , \end{aligned}$$

  for any $X\in C^1_c(\Omega ,\mathbb {R}^2)$ and $|D_\textrm{rad} u|(\Omega )=V_\textrm{rad}(u,\Omega )$;

• (iii) $D_{\textrm{rad}}u=\frac{1}{r}(\tilde{\pi }\varrho )|Du|$ and $|D_{\textrm{rad}}u|=(1/r)|\langle \varrho ,\omega \rangle ||Du|$ where $Du=\rho \,|Du|$ is the polar decomposition of Du with $\rho$ a unique $\mathbb {S}$-valued function in $L^1(\Omega ,\,|Du|)^2$;

• (iv) $D_{\textrm{rad}}u=\frac{1}{r}(\partial _r u)\mathscr {L}^2$ and $|D_{\textrm{rad}}u|=\frac{1}{r}|\partial _r u|\mathscr {L}^2$ for $u\in C^1(\Omega )\cap \textrm{BV}(\Omega )$.

Proof

(i) follows as in [3] Remark 3.5. (ii) For $X\in C^1_c(\Omega ,\mathbb {R}^2)$ the vector field $r^{-1}\tilde{\pi } X$ belongs to the same class with uniform norm bounded by $\Vert X\Vert _\infty /r_{\textrm{min}}$ where $r_\textrm{min}:=\inf \{|x|:x\in \Omega \}\in (0,\infty )$. This means that $V_{\textrm{rad}}(u,\Omega )$ is finite as $u\in \textrm{BV}(\Omega )$. The assertion now follows from Riesz’s Theorem (cf. [3] Theorem 1.54). The fact that u belongs to the class $\textrm{BV}(\Omega )$ leads to (iii) and (iv). $\square$

Proposition 4.2

Let $\Omega$ be a relatively compact open set in $\mathbb {R}^2_0$ and $u\in \textrm{BV}(\Omega )$. Let $U\subset \subset \Omega$ open with the property that $|D u|(\partial U)=0$. Then

$$\begin{aligned} |D_\textrm{rad} u|(U)= \lim _{\varepsilon \downarrow 0}|D_\textrm{rad}(u*\varphi _\varepsilon )|(U), \end{aligned}$$

where $(\varphi _\varepsilon )_{\varepsilon >0}$ is a family of mollifiers.

Proof

By the lower semicontinuity of the radial variation in Lemma 4.1,

$$\begin{aligned} |D_\textrm{rad} u|(U)\le \liminf _{\varepsilon \downarrow 0}|D_\textrm{rad}(u*\varphi _\varepsilon )|(U). \end{aligned}$$

As for the reverse inequality let us first choose $0<\varepsilon <\textrm{dist}(U,\partial \Omega )$. By Lemma 4.1,

$$\begin{aligned} |D_\textrm{rad}(u*\varphi _\varepsilon )|(U)&=\int _U\frac{1}{|x|}|\langle \nabla (u*\varphi _\varepsilon ),\omega \rangle |\,\mathrm{{d}}x. \end{aligned}$$

As $u\in \textrm{BV}(\Omega )$,

$$\begin{aligned} \left\langle \nabla (u*\varphi _\varepsilon )(x),\omega \right\rangle&=\int _\Omega \left\langle (\nabla \varphi _\varepsilon )(x-y),\frac{x}{|x|}\right\rangle u(y)\,\mathrm{{d}}y =-\int _\Omega \textrm{div}_y\Big (\varphi _\varepsilon (x-\cdot )\frac{x}{|x|}\Big )u(y)\,\mathrm{{d}}y \\&=\int _\Omega \left\langle \varphi _\varepsilon (x-\cdot )\frac{x}{|x|},\mathrm{{d}}Du\right\rangle =\int _\Omega \left\langle \varphi _\varepsilon (x-\cdot )\frac{x}{|x|},\varrho \right\rangle \,\mathrm{{d}}|Du|, \end{aligned}$$

and so

$$\begin{aligned} |\left\langle \nabla (u*\varphi _\varepsilon )(x),\omega \right\rangle |&\le \int _\Omega \varphi _\varepsilon (x-\cdot )|\left\langle \frac{x}{|x|},\varrho \right\rangle |\,\mathrm{{d}}|Du|. \end{aligned}$$

Inserting this estimate into the above equality and using Tonelli’s Theorem leads to

$$\begin{aligned} |D_\textrm{rad}(u*\varphi _\varepsilon )|(U)&\le \int _U\frac{1}{|x|}\int _\Omega \varphi _\varepsilon (x-\cdot )|\left\langle \frac{x}{|x|},\varrho \right\rangle |\,\mathrm{{d}}|Du|\,\mathrm{{d}}x\\&=\int _\Omega \int _U\frac{1}{|x|}\varphi _\varepsilon (x-\cdot )|\left\langle \frac{x}{|x|},\varrho \right\rangle |\,\mathrm{{d}}x\,\mathrm{{d}}|Du| =\int _\Omega \phi _\varepsilon \,\mathrm{{d}}|Du|, \end{aligned}$$

in an obvious notation. We may write the last expression as

$$\begin{aligned} \int _{\Omega }\phi _\varepsilon \,\mathrm{{d}}|Du| = \int _U\phi _\varepsilon \,\mathrm{{d}}|Du| + \int _{\Omega \setminus \overline{U}}\phi _\varepsilon \,\mathrm{{d}}|Du|, \end{aligned}$$

in virtue of the fact that $|D u|(\partial U)=0$ by assumption. For $y\in \Omega \setminus \partial U$,

$$\begin{aligned} \lim _{\varepsilon \downarrow 0}\phi _\varepsilon (y) = \left\{ \begin{array}{ll} \frac{1}{|y|}|\langle \frac{y}{|y|},\varrho (y)\rangle | &{} \text { if }y\in U,\\ 0 &{} \text { if }y\in \Omega \setminus \overline{U}. \end{array} \right. \end{aligned}$$

By the dominated convergence theorem,

$$\begin{aligned} \limsup _{\varepsilon \downarrow 0}|D_\textrm{rad}(u*\varphi _\varepsilon )|(U) \le \int _U\frac{1}{r}|\langle \omega ,\varrho \rangle |\,\mathrm{{d}}|Du| =|D_\textrm{rad} u|(U). \end{aligned}$$

This proves the result. $\square$

For a Borel set E in $\mathbb {R}^2_0$ and $\omega \in \mathbb {S}$ the $\omega$-section of E is defined to be the intersection of E with the open ray $(0,\infty )\omega$ in direction $\omega$. The notation $u_\omega$ refers to the restriction of the function u to $(0,\infty )\omega$.

Proposition 4.3

Let $\Omega$ be a relatively compact open set in $\mathbb {R}^2_0$ and $u\in \textrm{BV}(\Omega )$. Then $u_\omega \in \textrm{BV}(\Omega _\omega )$ for a.e. $\omega \in \mathbb {S}$ and

$$\begin{aligned} V_{\textrm{rad}}(u,\Omega )&=\int _{\mathbb {S}}V(u_\omega ,\Omega _\omega )\,\mathrm{{d}}\mathscr {H}^1. \end{aligned}$$

(4.1)

Proof

Let $u\in C^1_c(\Omega )$. By Lemma 4.1,

$$\begin{aligned} V_{\textrm{rad}}(u,\Omega )&=|D_{\textrm{rad}}u|(\Omega ) =\int _{\Omega }\frac{1}{r}|\partial _r u|\,\mathrm{{d}}x =\int _{\mathbb {S}}\int _{\Omega _\omega }|\partial _\tau u|\,\mathrm{{d}}\tau \,\mathrm{{d}}\mathscr {H}^1\nonumber \\&\quad =\int _{\mathbb {S}}V(u_\omega ,\Omega _\omega )\,\mathrm{{d}}\mathscr {H}^1, \end{aligned}$$

(4.2)

upon switching to polar coordinates.

Now let $u\in \textrm{BV}(\Omega )$. It can be seen that $u_\omega \in L^1(\Omega _\omega ,\mathscr {H}^1)$ for a.e. $\omega \in \mathbb {S}$ by converting to polar coordinates. For small $t>0$ put

$$\begin{aligned} \Omega ^t:=\{x\in \Omega :\textrm{dist}(x,\partial \Omega )>t \}. \end{aligned}$$

It holds that $|D u|(\partial \Omega ^t)=0$ for all but countably many $t>0$ as |Du| is a finite measure on $\Omega$. For $\varepsilon >0$ small,

$$\begin{aligned} \int _{\Omega ^t}|u*\varphi _\varepsilon - u|\,\frac{dx}{|x|} = \int _\mathbb {S}\Vert (u*\varphi _\varepsilon )_\omega - u_\omega \Vert _{L^1((\Omega ^t)_\omega )}\,\mathrm{{d}}\mathscr {H}^1 \end{aligned}$$

and the left-hand side converges to zero in the limit $\varepsilon \downarrow 0$ by a standard property of mollification. So there exists a subsequence $\varepsilon _h\downarrow 0$ such that with $v_h=u*\varphi _{\varepsilon _h}\in C^\infty _c(\Omega )$,

$$\begin{aligned} (v_h)_\omega \rightarrow u_\omega \text { in }L^1((\Omega ^t)_\omega ,\,\mathscr {H}^1)\text { for a.e. }\omega \in \mathbb {S}. \end{aligned}$$

By lower semicontinuity, Fatou’s lemma, (4.2) and Proposition 4.2,

$$\begin{aligned} \int _{\mathbb {S}}V(u_\omega ,(\Omega ^t)_\omega )\,\mathrm{{d}}\mathscr {H}^1&\le \int _{\mathbb {S}}\left\{ \liminf _{h\rightarrow \infty }V((v_h)_\omega ,(\Omega ^t)_\omega )\right\} \,\mathrm{{d}}\mathscr {H}^1\\&\le \liminf _{h\rightarrow \infty }\int _{\mathbb {S}}V((v_h)_\omega ,\,(\Omega ^t)_\omega )\,\mathrm{{d}}\mathscr {H}^1\\&= \liminf _{h\rightarrow \infty }V_{\textrm{rad}}(v_h,\Omega ^t) =V_{\textrm{rad}}(u,\Omega ^t) \le V_{\textrm{rad}}(u,\Omega ). \end{aligned}$$

By the monotone convergence theorem,

$$\begin{aligned} \int _{\mathbb {S}}V(u_\omega ,\Omega _\omega )\,\mathrm{{d}}\mathscr {H}^1 \le V_{\textrm{rad}}(u,\Omega ), \end{aligned}$$

and this permits us to draw the conclusion that $u_\omega \in \textrm{BV}(\Omega _\omega )$ for a.e. $\omega \in \mathbb {S}$.

For the reverse inequality, let $X\in C^1_c(\Omega ,\mathbb {R}^2)$ with $\Vert X\Vert _\infty \le 1$. In polar coordinates

$$\begin{aligned} \int _\Omega u\,\textrm{div}(r^{-1}\tilde{\pi } X)\,\mathrm{{d}}x = \int _{\mathbb {S}}\int _{\Omega _\omega }u_\omega r\,\textrm{div}(r^{-1}\tilde{\pi } X)\,\mathrm{{d}}r\,\mathrm{{d}}\mathscr {H}^1 \le \int _{\mathbb {S}}V(u_\omega ,\Omega _\omega )\,\mathrm{{d}}\mathscr {H}^1, \end{aligned}$$

as $\textrm{div}(r^{-1}\tilde{\pi } X)=r^{-1}\partial _r\langle X,\omega \rangle$ which completes the proof after taking the supremum. $\square$

Proposition 4.4

Let E be a set of locally finite perimeter in $\mathbb {R}^2_0$ and let $g:\mathbb {R}^2_0\rightarrow [0,\infty ]$ be a Borel function. Then

$$\begin{aligned} \int _{\mathscr {F}E}g(1/r)|\langle \nu _E,\omega \rangle |\,\mathrm{{d}}\mathscr {H}^1=\int _{\mathbb {S}}\int _{(\mathscr {F}E)_\omega }g\,\mathrm{{d}}\mathscr {H}^0\,\mathrm{{d}}\mathscr {H}^1. \end{aligned}$$

Proof

Define $f:\mathbb {R}^2_0\rightarrow \mathbb {S}$ via $x\mapsto x/|x|$. Let $x\in \mathbb {R}^2_0$ and M be a line through x in direction $v\in \mathbb {S}$. Then

$$\begin{aligned} J_1d^M f_x=(1/r)|\langle \omega ,v^\perp \rangle |. \end{aligned}$$

Now appeal to the generalised area formula [3] Theorem 2.91. $\square$

The following theorem is a Vol’pert-type theorem; see [5] Theorem 2.4.

Theorem 4.5

Let E be a set of locally finite perimeter in $\mathbb {R}^2_0$. Then for a.e. $\omega \in \mathbb {S}$,

• (i) $E_\omega$ is a set of locally finite perimeter in $(\mathbb {R}^2)_\omega$;

• (ii) $\mathscr {H}^0(\mathscr {F}E_\omega \Delta (\mathscr {F}E)_\omega )=0$.

Proof

(i) This follows from Proposition 4.3. (ii) By Proposition 4.3 and Lemma 4.1,

$$\begin{aligned} |D_\textrm{rad}\chi _E|(\Omega ) =V_\textrm{rad}(\chi _E,\Omega ) =\int _{\mathbb {S}}V((\chi _E)_\omega ,\Omega _\omega )\,\mathrm{{d}}\mathscr {H}^1 =\int _{\mathbb {S}}|D(\chi _E)_\omega |(\Omega _\omega )\,\mathrm{{d}}\mathscr {H}^1,\nonumber \\ \end{aligned}$$

(4.3)

for any relatively compact open set $\Omega \subset \mathbb {R}^2_0$. Let A stand for the open centred annulus with radii $0<r<R<\infty$. Put

$$\begin{aligned} \mathscr {M}:=\Big \{B\subset A:\,B\text { is a Borel set and } |D_\textrm{rad}\chi _E|(B) =\int _{\mathbb {S}}|D(\chi _E)_\omega |(B_\omega )\,\mathrm{{d}}\mathscr {H}^1\Big \}. \end{aligned}$$

By (4.3) the collection $\mathscr {M}$ contains all open sets in A; it also has the properties

• (a) $(B_h)_{h\in \mathbb {N}}\subset \mathscr {M},\,B_h\uparrow B\Rightarrow B\in \mathscr {M}$;

• (b) $B,\,B^\prime ,\,B\cup B^\prime \in \mathscr {M}\Rightarrow B\cap B^\prime \in \mathscr {M}$;

• (c) $B\in \mathscr {M}\Rightarrow A\setminus B\in \mathscr {M}$.

$\mathscr {M}$, therefore, coincides with the $\sigma$-algebra of Borel sets in A by [3] Remark 1.9. This entails that the identity holds for each relatively compact Borel set B in $\mathbb {R}^2_0$. For such a Borel set B in $\mathbb {R}^2_0$,

$$\begin{aligned} \int _{\mathbb {S}}\int _{(\mathscr {F}E)_\omega }\chi _B\,\mathrm{{d}}\mathscr {H}^0\,\mathrm{{d}}\mathscr {H}^1&= \int _{\mathscr {F}E}(1/r)\chi _B|\langle \nu _E,\omega \rangle |\,\mathrm{{d}}\mathscr {H}^1 =|D_{\textrm{rad}}\chi _E|(B) \\&=\int _{\mathbb {S}}|D(\chi _E)_\omega |(B_\omega )\,\mathrm{{d}}\mathscr {H}^1 =\int _{\mathbb {S}}\int _{\mathscr {F}E_\omega }\chi _B\,\mathrm{{d}}\mathscr {H}^0\,\mathrm{{d}}\mathscr {H}^1, \end{aligned}$$

by Proposition 4.4 and the above identity. This leads to (ii). $\square$

5 Further Preliminary Results

In this Section we establish two miscellaneous results for use in the next Section. The first is a standard result which characterises the image of a set of locally finite perimeter under a proper $C^1$ diffeomorphism. The second result in Lemma 5.2 describes a weak regularity property of the boundary of an isoperimetric minimiser. This is used in the proof of the boundedness theorem Theorem 6.10. It is not as deep as the regularity results treated in [36] or [27] Part III for example and we include its proof for completeness.

Lemma 5.1

Let $\Omega$ and $\Omega ^\prime$ be open sets in $\mathbb {R}^2$ and $\Phi :\Omega \rightarrow \Omega ^\prime$ a proper $C^1$ diffeomorphism. Let E be a set of locally finite perimeter in $\Omega$ and put $F:=\Phi (E)$. Then

• (i) F is a set of locally finite perimeter in $\Omega ^\prime$;

• (ii) $(\partial ^* F)\cap \Omega ^\prime =\Phi (\partial ^* E\cap \Omega )$;

• (iii) $\mathscr {F}F\cap \Omega ^\prime$ is $\mathscr {H}^1$-equivalent to $\Phi (\mathscr {F}E\cap \Omega )$.

Proof

Part (i) follows from [3] Theorem 3.16. (ii) We first claim that for each $x\in E^0\cap \Omega$ the point $y:=\Phi (x)$ belongs to $F^0\cap \Omega ^\prime$. Choose open sets $\Omega _1^\prime$ and $\Omega _2^\prime$ in $\Omega ^\prime$ with $\Omega _1^\prime \subset \subset \Omega _2^\prime \subset \subset \Omega ^\prime$. Their inverse images in $\Omega$ are denoted $\Omega _1$ and $\Omega _2$. Let $x\in \Omega _1$. Let K stand for the Lipschitz constant of the restriction of $\Phi ^{-1}$ to $\Omega _2^\prime$. Then $B(y,r)\subset \Phi (B(x,Kr))$ for $r>0$ small. By [3] Theorem 2.53, the fact that $\Phi$ is a bijection, and [3] Proposition 2.49,

$$\begin{aligned} |F\cap B(y,r)|&=\mathscr {H}^2(F\cap B(y,r)) \le \mathscr {H}^2(F\cap \Phi (B(x,Kr))\\&=\mathscr {H}^2(\Phi (E\cap B(x,Kr))\\&\le L^2\mathscr {H}^2(E\cap B(x,Kr)) =L^2|E\cap B(x,Kr)|, \end{aligned}$$

where L stands for the Lipschitz constant of $\Phi$ restricted to the set $\Phi ^{-1}(\Omega _2^\prime )$ noting that this latter set is compactly embedded in $\Omega$ as the mapping $\Phi$ is proper. Noting that $B(x,r)\subset \Phi ^{-1}(B(y,Lr))$ a similar argument shows that $|B(x,r/L)|\le K^2|B(y,r)|$ for r small. This means that

$$\begin{aligned} \frac{|F\cap B(y,r)|}{|B(y,r)|} \le (KL)^2\frac{|E\cap B(x,Kr)|}{|B(x,r/L)|} =(KL)^4\frac{|E\cap B(x,Kr)|}{|B(x,Kr)|}. \end{aligned}$$

This proves the claim. This leads to the identity $\Phi (E^0)=\Phi (E)^0$. The observation that $E^1=(\Omega {\setminus } E)^0$ establishes (ii). Item (iii) follows from Federer’s Theorem [3] Theorem 3.61 and (ii). $\square$

Let $\Omega$ be an open set in $\mathbb {R}^2$. Given positive locally Lipschitz densities f and g on $\Omega$ we shall refer to the variational problem

$$\begin{aligned} I(v):=\inf \Big \{P_g(E):E\text { is a set of locally finite perimeter in }\Omega \text { and }V_f(E)=v\Big \},\nonumber \\ \end{aligned}$$

(5.1)

for $v>0$. In the next result we establish mild regularity of the boundary of an isoperimetric minimiser of (14.6).

Let E be a set of locally finite perimeter in $\Omega$. According to [27] Proposition 12.19 there exists a Borel set F equivalent to E with the property that the topological boundary $\partial F\cap U$ in $\Omega$ satisfies the condition

$$\begin{aligned} \Big \{x\in \Omega :0<|F\cap B(x,r)\cap \Omega |<\pi r^2\text { for all }r>0\Big \}&=\partial F\cap \Omega . \end{aligned}$$

(5.2)

Lemma 5.2

Let $\Omega$ be an open set in $\mathbb {R}^2$ and assume that f and g are positive locally Lipschitz densities on $\Omega$. Let $v>0$ and suppose that the set E is a minimiser of (14.6). Assume that E satisfies the condition in (5.2). Then for each $x\in \partial E\cap \Omega$ there exists $\delta >0$ and a constant $0<c<1/2$ such that

$$\begin{aligned} c\le \frac{|E\cap B(x,r)|}{\pi r^2}\le 1-c \text { for each }0<r<\delta ; \end{aligned}$$

and in particular $\mathscr {H}^1(\partial E\cap \Omega {\setminus }\mathscr {F}E)=0$.

Proof

Let $x\in \Omega$ and $t>0$ such that $B(x,t)\subset \subset \Omega$. An adaptation of the argument in [28] Proposition 3.5 (and [3] Corollary 3.89) leads to the formulae

$$\begin{aligned} P_g(E)&=P_g(E,B(x,t))+\int _{\partial B(x,t)}g|\chi ^{B(x,t)}_E-\chi ^{\Omega \setminus \overline{B}(x,t)}|\,\mathrm{{d}}\mathscr {H}^1\nonumber \\&\quad +P_g(E,\Omega \setminus \overline{B}(x,t)), \end{aligned}$$

(5.3)

and

$$\begin{aligned} P_g(E\cap B(x,t))&=P_g(E,B(x,t))+\int _{\partial B(x,t)}g\chi ^{B(x,t)}_E\,\mathrm{{d}}\mathscr {H}^1. \end{aligned}$$

(5.4)

Let $x\in \partial E\cap \Omega$. By Proposition 15.1 there exist constants $C>0$ and $\delta \in (0,d(x,\partial \Omega ))$ with the following property. For any $0<r<\delta$,

$$\begin{aligned} P_g(E)-P_g(F)\le C\big |V_f(E)-V_f(F)\big |, \end{aligned}$$

(5.5)

where F is any set with locally finite perimeter in $\Omega$ such that $E\Delta F\subset \subset B(x,r)$. Fix $0<r<\delta$ and choose s with $0<r<s<\delta$. Put $F:=E\setminus B(x,r)$. By (14.7) and (5.3),

$$\begin{aligned} P_g(E,B(x,s))&\le P_g(E\setminus B(x,r),B(x,s))+CV_f(E\cap B(x,r))\\&=P_g(E,B(x,s)\setminus \overline{B}(x,r))\\&\quad +\int _{\partial B(x,r)}g\chi ^{\Omega \setminus \overline{B}(x,r)}_E\,\mathrm{{d}}\mathscr {H}^1+CV_f(E\cap B(x,r)). \end{aligned}$$

Upon letting $s\downarrow r$ we obtain

$$\begin{aligned} P_g(E,B(x,r))\le \int _{\partial B(x,r)}g\chi ^{\Omega \setminus \overline{B}(x,r)}_E\,\mathrm{{d}}\mathscr {H}^1 +CV_f(E\cap B(x,r)). \end{aligned}$$

It follows from this last that

$$\begin{aligned} P_g(E\cap B(x,r))\le \int _{\partial B(x,r)}g\Big \{ \chi ^{B(x,r)}_E+\chi ^{\Omega \setminus \overline{B}(x,r)}_E\Big \} +CV_f(E\cap B(x,r)), \end{aligned}$$

with the help of (5.4). From Federer’s Theorem ([3] Theorem 3.60) and the tangential Vol’pert-type theorem (Theorem 3.9),

$$\begin{aligned} \chi _E^{B(x,t)}=\chi _{E^1}\text { }\mathscr {H}^1\text {-a.e. on }\partial B(x,t), \end{aligned}$$

for a.e. $t\in (0,\delta )$ and likewise for $\chi _E^{\Omega \setminus \overline{B}(x,t)}$. So in fact we may write

$$\begin{aligned} P_g(E\cap B(x,t))&\le 2\mathscr {H}^1_g((E^1)_t)+CV_f(E\cap B(x,t)), \end{aligned}$$

(5.6)

for a.e. t in $(0,\delta )$.

Put $m(t):=|E\cap B(x,t)|$ for $t\in (0,\delta )$. The function m is absolutely continuous on $(0,\delta )$ and $m^\prime =\mathscr {H}^1(E^1\cap \partial B(x,t))$ a.e. on $(0,\delta )$. Let $0<c<1$. As both f and g are positive and continuous on $\Omega$ we may choose $0<\delta _1<\delta$ such that

$$\begin{aligned} (1-c)f(x)\le f\le (1+c)f(x) \text { and } (1-c)g(x)\le g\le (1+c)g(x) \text { on }\overline{B}(x,\delta _1). \end{aligned}$$

From (5.6) and the classical isoperimetric inequality we obtain

$$\begin{aligned} \sqrt{4\pi }(1-c)g(x)\le 2(1+c)g(x)\frac{m^\prime }{\sqrt{m}}+C(1+c)f(x)\sqrt{m}, \end{aligned}$$

a.e. on $(0,\delta _1)$. This yields the estimate

$$\begin{aligned} \frac{1-c}{2(1+c)}-\frac{Cf(x)}{8g(x)}t\le \sqrt{\frac{m}{\pi t^2}}, \end{aligned}$$

on $(0,\delta _1)$. This leads to the lower bound in the statement of the Lemma. The upper bound follows from the fact that the complement $\Omega \setminus E$ is a relative isoperimetric minimiser.

The inequality entails that $\partial E\cap \Omega$ is contained in the essential boundary $\partial ^* E\cap \Omega$. This implies the last assertion of the Lemma by Federer’s Theorem (see for example [3] Theorem 3.60). $\square$

6 Existence and Boundedness

In this Section we turn to the topic of existence and boundedness of isoperimetric minimisers. We seek to adapt the existence result contained in [31] Theorem 3.3 in the case of Euclidean space with density to the two-weighted case with radial volume and perimeter densities f respectively g; and we supply a variation of the boundedness result in [31] Theorem 5.9. We mention [16] Theorem 1.2 in passing but we do not pursue this approach here. Our results are contained in Theorem 6.6 and Theorem 6.10. They extend [18] and [19] Theorem 2.3 and Theorem 2.4. We require that the density relative to the metric $\psi$ diverges at infinity as in condition (A.4) below. In the case of radial power weights as considered in this paper this condition fails if $\alpha =2\beta$ with $\beta <0$. We then have recourse to [32] Theorem 1.1 (and [8] Corollary 2.4) through a reparametrisation of the problem.

We begin with this latter result. Let us introduce the index set

$$\begin{aligned} \mathcal {P}^-&:=\Big \{(\alpha ,\beta )\in \mathbb {R}^2:-2<\alpha \le 0\text { and }\alpha =2\beta \Big \}. \end{aligned}$$

For indices in $\mathcal {P}^-$ existence holds as we show shortly. A crucial tool in the proof is the mapping (6.2). This also plays a rôle in preparing the proof of Theorem 6.6 so we choose to introduce this material at an early stage. Towards the end of this Section we show that centred balls are uniquely isoperimetric in Theorem 6.11.

Theorem 6.1

Let $(\alpha ,\beta )\in \mathcal {P}^-\setminus \{0\}$. Then centred balls are minimisers for the problem (1.2) up to equivalence.

We begin with a remark. Choose a pair $(\alpha ,\beta )\in \mathcal {P}^-\setminus \{0\}$. The angle $\gamma \in (0,\pi /2)$ is characterised by the relation $\sin \gamma =\beta +1$. Define a (punctured) cone

$$\begin{aligned} C&=C_\beta :=\Big \{(x,z)\in \mathbb {R}^2_0\times \mathbb {R}:z=(\cot \gamma )|x|\Big \}, \end{aligned}$$

(6.1)

in $\mathbb {R}^3$. The mapping $\phi :\mathbb {R}^2_0\rightarrow C;x\mapsto |x|^\beta (x,(\cot \gamma )|x|)$ has first fundamental form

$$\begin{aligned} \mathrm{{d}}s^2=|x|^{2\beta }(\mathrm{{d}}x_1^2+\mathrm{{d}}x_2^2), \end{aligned}$$

and is a conformal parametrisation of C. In short, the punctured plane equipped with the conformal metric $ds=|z|^\beta |dz|$ is conformally equivalent to the punctured cone C.

Given an index $-1<\beta <0$ we make use of the bijection

$$\begin{aligned}&\Phi :\mathbb {R}^2_0\rightarrow \mathbb {R}^2_0;x\mapsto \frac{1}{\beta +1}|x|^\beta x. \end{aligned}$$

(6.2)

This is the composition of the map $\phi$ above with the map denoted f in the proof of [32] Theorem 1.1. Fix $x\in \mathbb {R}^2_0$ and consider the vector $v=v_\omega \omega +v_{\omega ^\perp }\omega ^\perp$ where $\omega$ and $\omega ^\perp$ are unit vectors, $\omega$ lies in direction x and the pair $\{\omega ,\omega ^\perp \}$ is positively oriented. A calculation gives

$$\begin{aligned} d\Phi _x v=|x|^\beta \Big \{v_\omega \omega +\frac{|x|}{\beta +1}v_{\omega ^\perp }\omega ^\perp \Big \}, \end{aligned}$$

from which it follows that

$$\begin{aligned} J_2d\Phi _x&=\frac{|x|^{2\beta }}{\beta +1}, \end{aligned}$$

(6.3)

and

$$\begin{aligned} J_1d^{x+M}\Phi _x&=\frac{|x|^{\beta }}{\beta +1}\Big \{(\beta +1)^2v_\omega ^2+|x|^2 v_{\omega ^\perp }^2\Big \}^{1/2} \le \frac{|x|^{\beta }}{\beta +1}, \end{aligned}$$

(6.4)

where $M:=\textrm{span}\{v\}$.

Proof of Theorem 6.1

Let E be a set of locally finite perimeter in $\mathbb {R}^2_0$. By (6.3) and the area formula ([3] Theorem 2.71 for example), $V_\alpha (E)=(\beta +1)V_0(\Phi (E))$. By (6.4) and the generalised area formula ( [3] Theorem 2.91 for example), $P_\beta (E)\ge (\beta +1)P_0(\Phi (E))$ with the help of Lemma 5.1. It follows that the centred ball is a minimiser for the problem (1.2) as the inverse of $\Phi$ preserves centred circles. $\square$

We now derive an existence and a boundedness theorem for the isoperimetric problem in the two-weighted situation (namely, Theorems 6.6 and 6.10). Suppose that $\texttt{f}$ and $\texttt{g}$ are continuous positive functions defined on $(0,\infty )$. Put $\zeta :=\texttt{f}/\texttt{g}$ and $\psi :=\texttt{g}^2/\texttt{f}$ on $(0,\infty )$. Assume that

• (A.1) $\int _0^1 t\texttt{f}\,\mathrm{{d}}t<\infty$;

• (A.2) $\int _1^{\infty } t\texttt{f}\,\mathrm{{d}}t=\infty$;

• (A.3) $t^\nu \texttt{g}$ is non-decreasing for some $\nu \in [0,1)$;

• (A.4) $\psi$ diverges as $t\rightarrow \infty$.

Define continuous positive densities f and g on $\mathbb {R}^2_0$ via

$$\begin{aligned}&f:\mathbb {R}^2_0\rightarrow (0,\infty ); x\mapsto \texttt{f}(|x|), \end{aligned}$$

(6.5)

and similarly for g. The weighted f-volume $V_f:=f\mathscr {L}^2$ is defined on the $\mathscr {L}^2$-measurable sets in $\mathbb {R}^2_0$. The weighted g-perimeter of a set E of locally finite perimeter in $\mathbb {R}^2_0$ is defined by

$$\begin{aligned} P_g(E):=\int _{\mathbb {R}^2_0}g\,\mathrm{{d}}|D\chi _E|\in [0,\infty ]. \end{aligned}$$

(6.6)

We refer to the isoperimetric problem (14.6) for $v>0$. We require a number of preparatory results before we reach the existence theorem.

Lemma 6.2

Let $\Omega$ be an open set in $\mathbb {R}^2$ and g a positive continuous function on $\Omega$. Let $(u_h)_{h\in \mathbb {N}}$ be a sequence of functions in $\textrm{BV}_{\textrm{loc}}(\Omega )$ which converge to $u\in L^1_{\textrm{loc}}(\Omega )$ in $L^1_{\textrm{loc}}(\Omega )$. Assume that

$$\begin{aligned} \liminf _{h\rightarrow \infty }\int _\Omega g\,\mathrm{{d}}|Du_h|<\infty . \end{aligned}$$

Then $u\in \textrm{BV}_{\textrm{loc}}(\Omega )$ and

$$\begin{aligned} \int _\Omega g\,\mathrm{{d}}|Du|&\le \liminf _{h\rightarrow \infty }\int _\Omega g\,\mathrm{{d}}|Du_h|. \end{aligned}$$

(6.7)

Proof

Let A be a relatively compact open set in $\Omega$. As g is positive and continuous on $\Omega$ it is bounded away from zero on $\overline{A}$ by a positive constant c. By lower semicontinuity of the variation (see [3] Remark 3.5),

$$\begin{aligned} V(u,A)&\le \liminf _{h\rightarrow \infty }V(u_h,A)\le \frac{1}{c}\liminf _{h\rightarrow \infty }\int _\Omega g\,\mathrm{{d}}|Du_h|. \end{aligned}$$

By [3] Proposition 3.6 the limit function u belongs to $\textrm{BV}_{\textrm{loc}}(\Omega )$. Then gDu is an $\mathbb {R}^2$-valued Radon measure on $\Omega$. By [3] Remark 1.46 and Proposition 1.47,

$$\begin{aligned} |gDu|(A)=\int _A g\,\mathrm{{d}}|Du|. \end{aligned}$$

By [3] Proposition 3.13 the sequence $(u_h)_{h\in \mathbb {N}}$ weakly* converges to u on A. In particular, the finite Radon measures $Du_h\rightarrow Du$ weakly* on A and as a consequence $gDu_h\rightarrow gDu$ weakly* on A as $h\rightarrow \infty$. By [3] Corollary 1.60,

$$\begin{aligned} \int _A g\,\mathrm{{d}}|Du|&=|gDu|(A)\le \liminf _{h\rightarrow \infty }|gDu_h|(A)\\&=\liminf _{h\rightarrow \infty }\int _A g\,\mathrm{{d}}|Du_h| \le \liminf _{h\rightarrow \infty }\int _\Omega g\,\mathrm{{d}}|Du_h|. \end{aligned}$$

The inequality in (6.7) follows from the monotone convergence theorem. $\square$

Let E be a set of locally finite perimeter in $\mathbb {R}^2_0$. We write $E_t:=E\cap \mathbb {S}_t$ for the t-section of E for each $t>0$. Define

$$\begin{aligned} L(t)=L_E(t)&:=\mathscr {H}^1((E^1)_t) \end{aligned}$$

(6.8)

$$\begin{aligned} p(t)=p_E(t)&:=\mathscr {H}^0((\mathscr {F}E)_t). \end{aligned}$$

(6.9)

By the coarea formula ([3] Theorem 2.93) and the De Giorgi structure theorem ([3] Theorem 3.59) the function p is $\mathscr {L}^1$-measurable on $(0,\infty )$. Note that L does not depend on the $\mathscr {L}^2$-version of E.

Let B(t) stand for the open centred ball in $\mathbb {R}^2$ with radius $t\ge 0$; the closed centred ball is denoted $\overline{B}(t)$. Sometimes we simply write $\overline{B}$ for shortness. Let E be a set of locally finite perimeter in $\mathbb {R}^2_0$. Let us define

$$\begin{aligned} V_f(t)&:=V_f(E\cap \mathbb {R}^2_0\setminus \overline{B}(t));\\ P_g(t)&:=\int _{\mathbb {R}^2_0\setminus \overline{B}(t)}g\,\mathrm{{d}}|D\chi _E|; \end{aligned}$$

for $t\ge 0$. In this notation, $V_f(0)=V_f(E)$ and $P_g(0)=P_g(E)$. If $f=g=1$ we add a subscript in the form $V_0$ and $P_0$.

Lemma 6.3

Let $\texttt{f}$ be a positive continuous function on $(0,\infty )$ which satisfies the conditions (A.1)–(A.2) and define f as in (6.5). Let E be a set of locally finite perimeter in $\mathbb {R}^2_0$ with $V_f(E)<\infty$. Then

$$\begin{aligned} P_0(E,\mathbb {R}^2_0\setminus \overline{B}(t))\ge L(t), \end{aligned}$$

for each $t>0$.

Proof

Let us fix $t>0$ and write $\overline{B}$ instead of $\overline{B}(t)$ for shortness. We may assume that E has finite perimeter relative to $\mathbb {R}^2_0\setminus \overline{B}$. Let us first note that $\mathscr {F}E$ is countably 1-rectifiable and

$$\begin{aligned} P_0(E,\mathbb {R}^2_0\setminus \overline{B})=\mathscr {H}^1(\mathscr {F}E\setminus \overline{B}), \end{aligned}$$

as in [3] Theorem 3.59. The map $\alpha :\mathbb {R}^2\setminus \overline{B}\rightarrow \mathbb {S}_t$ defined by $x\mapsto (t/|x|)x$ is 1-Lipschitz. We remark in passing that $\alpha$ admits an extension $\widetilde{\alpha }:\mathbb {R}^2\rightarrow \mathbb {S}_t$ that is $\sqrt{2}$-Lipschitz by [3] Proposition 2.12. By the generalised area formula (cf. [3] Theorem 2.91),

$$\begin{aligned} \int _{\mathbb {R}^2_0}\mathscr {H}^0(\mathscr {F}E\setminus \overline{B}\cap \alpha ^{-1}(\omega ))\,\mathscr {H}^1(d\omega ) = \int _{\mathscr {F}E\setminus \overline{B}}J_1d^{\mathscr {F}E}\alpha _x\,\mathrm{{d}}\mathscr {H}^1 \le \mathscr {H}^1(\mathscr {F}E\setminus \overline{B}). \end{aligned}$$

Put $F:=E^1\setminus \overline{B}$. Consider the set $\Lambda$ of all points $\omega \in \mathbb {S}_t$ which satisfy the properties

• (a) $\omega \in (E^1)_t$;

• (b) $F_\omega$ is a set of locally finite perimeter in $(\mathbb {R}^2)_\omega$;

• (c) $(\mathscr {F}F)_\omega =\mathscr {F}F_\omega$;

• (d) $\omega \in \mathscr {F}F_\omega$.

We argue that $\Lambda$ has full $\mathscr {H}^1$-measure in $(E^1)_t$. First note that the set F is a set of locally finite perimeter in $\mathbb {R}^2_0$ by [3] Corollary 3.89. By Theorem 4.5 the set $F_\omega$ is a set of locally finite perimeter in $(\mathbb {R}^2)_\omega$ and the set $\{\omega :\mathscr {F}F_\omega =(\mathscr {F}F)_\omega \}$ has full measure in $\mathbb {S}_t$ for $\mathscr {H}^1$-a.e. $\omega \in \mathbb {S}_t$. Note that if $\omega \in (E^1)_t$ then $\omega \in F^{1/2}$. By Federer’s Theorem (cf. [3] Theorem 3.61) it follows that $(E^1)_t$ is contained in the reduced boundary of F apart from at most an $\mathscr {H}^1$-null set. These considerations entail that the conditions (a)–(d) hold a.e. in $(E^1)_t$.

Assume for a moment that the set $H:=\Lambda \cap \{\omega :\mathscr {F}F_\omega \setminus \{\omega \}=\emptyset \}$ has positive $\mathscr {H}^1$-measure in $\mathbb {S}_t$. For each $\omega$ in this latter set $F_\omega$ is equivalent to the ray $(1,\infty )\omega$ by [3] Proposition 3.52. We infer that the truncated cone $(1,\infty )H$ is contained within F up to a Lebesgue null set. This truncated cone and hence E has infinite $V_f$-volume on appealing to property (A.2) which contradicts our hypotheses that $V_f(E)<\infty$. We conclude from this that $\Lambda \cap \{\omega :\mathscr {F}F_\omega \setminus \{\omega \}\ne \emptyset \}$ has full measure in $(E^1)_t$.

Suppose that $\omega$ belongs to the set $\Lambda$ and $\mathscr {F}F_\omega \setminus \{\omega \}\ne \emptyset$. By (c), $(\mathscr {F}F)_\omega \setminus \{\omega \}\ne \emptyset$ and this implies in turn that $\omega$ belongs to the range of $\alpha$ restricted to $\mathscr {F}E\setminus \overline{B}$. So

$$\begin{aligned} \int _{\mathbb {R}^2_0}\mathscr {H}^0(\mathscr {F}E\setminus \overline{B}\cap \alpha ^{-1}(\omega ))\,\mathscr {H}^1(d\omega ) \ge \int _{\mathbb {R}^2_0}\chi _{(E^1)_t}\,\mathrm{{d}}\mathscr {H}^1=L(t). \end{aligned}$$

This leads to the result when combined with the above inequality. $\square$

Lemma 6.4

Let $\nu \in [0,1)$ and $\texttt{f}$ be a positive continuous function on $(0,\infty )$ which satisfies the conditions (A.1)–(A.2) and define f as in (6.5). Let E be a set of locally finite perimeter in $\mathbb {R}^2_0$ with $V_f(E)<\infty$. Then

$$\begin{aligned} P_{-\nu }(t)\ge (|\cdot |^{-\nu } L)(t), \end{aligned}$$

for each $t>0$.

Proof

Let $t>0$. By (6.4) and the generalised area formula (cf. [3] Theorem 2.91),

$$\begin{aligned} P_{-\nu }(t)&\ge (-\nu +1)\mathscr {H}^1(\Phi (\mathscr {F}E\setminus \overline{B}))\nonumber \\&=(-\nu +1)\mathscr {H}^1(\mathscr {F}\Phi (E)\setminus \Phi (\overline{B})) =(-\nu +1)P_0(\Phi (E),\mathbb {R}^2_0\setminus \Phi (\overline{B})), \end{aligned}$$

(6.10)

where in the first equality we use the fact that $\Phi (\mathscr {F}E)$ is $\mathscr {H}^1$-a.e. equivalent to $\mathscr {F}\Phi (E)$ according to Lemma 5.1. The push-forward $\Phi _\sharp V_\alpha$ of $V_\alpha$ under $\Phi$ is a non-finite Radon measure on $\mathbb {R}^2_0$ with radial density satisfying (A.1)–(A.2) and $\Phi (E)$ has finite $\Phi _\sharp V_\alpha$-measure. We make use of Lemma 6.3 to continue,

$$\begin{aligned} P_{-\nu }(t) \ge (-\nu +1)\mathscr {H}^1((\Phi (E)^1)_{\frac{t^{-\nu +1}}{-\nu +1}}) =(|\cdot |^{-\nu } L)(t), \end{aligned}$$

where once more we appeal to Lemma 5.1. This establishes the result. $\square$

Proposition 6.5

Suppose that the positive continuous function $\texttt{g}$ satisfies condition (A.3) and the positive continuous function $\texttt{f}$ satisfies conditions (A.1)–(A.2). Let E be a set of locally finite perimeter in $\mathbb {R}^2_0$ with $V_f(E)<\infty$. Assume that $P_g(t)<\infty$ for each $t>0$. Then for each $t>0$,

• (i) $P_g(t)\ge \int _t^\infty \texttt{g}p\,\mathrm{{d}}\tau$;

• (ii) $P_g(t)\ge (\texttt{g}L)(t)$;

and

• (iii) the set $\{L=2\pi \tau \}$ is bounded in $(0,\infty )$.

Moreover if $\texttt{f}$ satisfies condition (A.4) then

• (iv) there exists $T>0$ such that $P_g(t)^2\ge \psi _-(t)V_f(t)$ for each $t>T$;

where $\psi _-(t):=\min _{[t,\infty )}\psi$.

Proof

(i) By Proposition 3.3,

$$\begin{aligned} \int _{\mathscr {F}E\setminus \overline{B}}g|\nu _E^\omega |\,\mathrm{{d}}\mathscr {H}^1 =\int _t^\infty \texttt{g}\mathscr {H}^0((\mathscr {F}E)_\tau )\,\mathrm{{d}}\tau , \end{aligned}$$

for each $t>0$ and the statement follows by the definition in (6.9).

(ii) Choose $\nu \in [0,1)$ as in (A.3). By Lemma 6.4,

$$\begin{aligned} P_g(t)&=\int _{\mathscr {F}E\setminus \overline{B}}(|x|^\nu g)|x|^{-\nu }\,\mathrm{{d}}\mathscr {H}^1 \ge t^\nu \texttt{g}(t)\int _{\mathscr {F}E\setminus \overline{B}}|x|^{-\nu }\,\mathrm{{d}}\mathscr {H}^1\\&=t^\nu \texttt{g}(t)P_{-\nu }(t) \ge (gL)(t). \end{aligned}$$

(iii) For $t>s>0$ we may write $t\texttt{g}(t)=(t^\nu \texttt{g}(t))t^{1-\nu }$ with $\nu \in [0,1)$ as in (A.3). In light of this condition the function $t\texttt{g}$ diverges as $t\uparrow \infty$. Suppose that the set $A:=\{L=2\pi t\}$ is unbounded. By (ii), $P_g(s)\ge P_g(t)\ge (\texttt{g}L)(t)=2\pi t\texttt{g}(t)$ for each $t\in A$. This contradicts the fact that $P_g(s)<\infty$.

(iv) For each $s>t>0$,

$$\begin{aligned} \infty >P_g(s)\ge P_g(t)\ge (\texttt{g}L)(t)=\psi (t)(\zeta L)(t), \end{aligned}$$

by (ii). It follows that $(\zeta L)(t)\rightarrow 0$ as $t\rightarrow \infty$ because $\psi$ diverges according to (A.4). This means in particular that $\zeta L$ is bounded on $[t,\infty )$ for each $t>0$. Put

$$\begin{aligned} M(t):=\sup \Big \{(\zeta L)(\tau ):\tau \ge t\Big \}<\infty . \end{aligned}$$

From the above estimate $P_g(t)\ge \psi _-(t)M(t)$.

Let T be an upper bound for the set A according to (iii). Choose $t>T$. We may assume that $V_f(t)=\int _t^\infty \texttt{f}L\,\mathrm{{d}}\tau >0$ otherwise the inequality follows immediately. This latter condition entails that $M(t)>0$. This in turn implies that $\zeta L/M(t)\le 1$ on $[t,\infty )$. Note that $p\ge 1$ on $\{p>0\}$. With the justification supplied by these comments and (i) we may write

$$\begin{aligned} P_g(t)&\ge \int _t^{\infty }\texttt{g}p\,\mathrm{{d}}\tau =\int _t^{\infty }\chi _{\{p>0\}}\texttt{g}p\,\mathrm{{d}}\tau \ge \int _t^{\infty }\chi _{\{p>0\}}\texttt{g}\,\mathrm{{d}}\tau \\&\ge \frac{1}{M(t)}\int _t^{\infty }\chi _{\{p>0\}}\psi (\zeta ^2 L)\,\mathrm{{d}}\tau \\&=\frac{1}{M(t)}\int _t^{\infty }\chi _{\{L>0\}}\texttt{f}L\,\mathrm{{d}}\tau =\frac{1}{M(t)}\int _t^{\infty }\texttt{f}L\,\mathrm{{d}}\tau =\frac{1}{M(t)}V_f(t). \end{aligned}$$

In the first equality in the second line we make use of the the fact that the sets $\{p>0\}$ and $\{L>0\}$ coincide up to a set of measure zero on $(T,\infty )$. Let us explain this. Let $\Lambda$ signify the set of $t>0$ with the property that both $(E^1)_t$ is a set of finite perimeter in $\mathbb {S}_t$ and $(\mathscr {F}E)_t=\mathscr {F}(E^1)_t$. By Theorem 3.9 this is a set of full measure in $(0,\infty )$. For $t\in \Lambda$,

$$\begin{aligned} L(t)&=\mathscr {H}^1((E^1)_t)\text { and }p(t)=\mathscr {H}^0((\mathscr {F}E)_t)=\mathscr {H}^0(\mathscr {F}(E^1)_t). \end{aligned}$$

(6.11)

Moreover,

$$\begin{aligned} \Lambda \cap \{0<L\}\cap (T,\infty )=\Lambda \cap \{0<L<2\pi t\}\cap (T,\infty ), \end{aligned}$$

and this last coincides with the set $\Lambda \cap \{0<p\}\cap (T,\infty )$.

As a last step the product of the estimates in the first and second paragraphs of this section leads to the result in (iv). $\square$

Theorem 6.6

Suppose that $\texttt{f}$ and $\texttt{g}$ satisfy (A.1)–(A.4). Then (14.6) has a minimiser for each $v>0$.

Proof

We adapt the proof of [31] Theorem 3.3 (or [18] Theorem 2.3). Let $(E_h)_{h\in \mathbb {N}}$ be a minimising sequence for (14.6). By [3] Theorem 3.23 we may assume that the sequence $(u_h)_{h\in \mathbb {N}}$ converges to a function $u\in \textrm{BV}_{\textrm{loc}}(\Omega )$ in $L^1_{\textrm{loc}}(\Omega )$ where $\Omega :=\mathbb {R}^2_0$ and $u_h:=\chi _{E_h}$. By choosing an a.e. convergent subsequence we may assume that the limit function u takes the form $u=\chi _E$ for some Borel set E in $\Omega$. Assume for the moment that

$$\begin{aligned} \lim _{R\rightarrow \infty }\sup _{h\in \mathbb {N}}V_f(E_h\setminus B(R))&=0. \end{aligned}$$

(6.12)

By [3] Proposition 1.27 the collection $\mathscr {F}:=\{u_h:h\in \mathbb {N}\}$ is an equi-integrable subset of $L^1(\Omega ,V_f)$. By the Dunford–Pettis Theorem ( [3] Theorem 1.38 for example) and uniqueness of the weak limit we may assume that $(u_h)_{h\in \mathbb {N}}$ converges to u weakly in $L^1_{\textrm{loc}}(\Omega )$. In particular, $V_f(E)=v$. So E is a minimiser for the variational problem (14.6) by Proposition 6.2.

Let us suppose for a contradiction that the condition (6.12) does not hold; in particular, there exists $\varepsilon >0$ such that for each $t>0$ there exists $h\in \mathbb {N}$ with the property that $V_f(E_h{\setminus } B(t))\ge \varepsilon$. We first remark that there exists $T>0$ with the property that $\{L_h=2\pi t\}\cap (T,\infty )=\emptyset$ for each $h\in \mathbb {N}$ (in an obvious notation). This is a consequence of the fact that the set $\{P_g(E_h):h\in \mathbb {N}\}$ is bounded in $\mathbb {R}$ and the estimate in Proposition 6.5(ii). Let $t>T$ and choose h as above. By Proposition 6.5,

$$\begin{aligned} P_g(E_h)^2\ge \psi _-(t)\varepsilon . \end{aligned}$$

The right-hand side in this inequality diverges as $t\uparrow \infty$ while the left-hand side remains bounded. This gives a contradiction. We conclude that the condition (6.12) holds true. $\square$

Lemma 6.7

Let u be a nonnegative function in $\textrm{BV}_{\textrm{loc}}((0,\infty ))$ with $u\not \equiv 0$. Then there exists a good representative $\overline{u}$ of u with the property that the set $\{\overline{u}>0\}$ is open in $(0,\infty )$.

Proof

Let $\overline{u}$ be a good representative of u (cf. [3] Theorem 3.28). Denote by A the set of atoms of Du; a countable set as |Du| is a Radon measure. Put

$$\begin{aligned} A_1:=\{t\in A:\overline{u}(t-)=0\text { or }\overline{u}(t+)=0\}, \end{aligned}$$

and define $\overline{u}_1:=\chi _{(0,\infty ){\setminus } A_1}\overline{u}$. Then $\overline{u}_1$ is a good representative of $\overline{u}$ by [3] Theorem 3.28. Moreover, the set $\{\overline{u}_1>0\}$ is open in $(0,\infty )$. $\square$

The next is contained in [10] Lemma 4.1. We include its short proof.

Lemma 6.8

Let E be a set of locally finite perimeter in $\mathbb {R}^2_0$. Then $L\in \textrm{BV}_{\textrm{loc}}((0,\infty ))$.

Proof

Let $\phi \in C^1_c((0,\infty ))$. Then

$$\begin{aligned} \int _0^\infty \phi ^\prime (L/t)\,\mathrm{{d}}t=-\int _{\mathscr {F}E}\frac{1}{t}\phi \nu _E^\omega \,\mathrm{{d}}\mathscr {H}^1. \end{aligned}$$

So L/t belongs to $\textrm{BV}_{\textrm{loc}}((0,\infty ))$ and likewise L by [3] Proposition 3.2. $\square$

Lemma 6.9

Suppose that the positive continuous functions $\texttt{f}$ and $\texttt{g}$ on $(0,\infty )$ satisfy the conditions (A.1)-(A.5). Let E be a set of locally finite perimeter in $\mathbb {R}^2_0$ with $V_f(E)<\infty$. Assume $P_g(t)<\infty$ for each $t>0$. Then for each $t>0$ there exists a and b with $t<a<b<\infty$ such that $|E\cap A(a,b)|=0$.

The notation A(a, b) refers to the open annulus with inner radius a and outer radius b.

Proof

First suppose that $\texttt{g}\equiv 1$. In other words, E is a set of locally finite perimeter in $\mathbb {R}^2_0$ with finite $V_f$-measure and $P_0(t)<\infty$ for each $t>0$. Let us decompose $(0,\infty )$ into a disjoint union

$$\begin{aligned} (0,\infty )=\{L=0\}\cup \{0<L<2\pi \tau \}\cup \{L=2\pi \tau \}. \end{aligned}$$

By Proposition 6.5(iii) the set $\{L=2\pi \tau \}$ is bounded and has finite measure. The set $\{0<L<2\pi \tau \}$ is contained in $\{p>0\}$ up to a Lebesgue null set bearing in mind (6.11). Moreover the set $\{p>0\}$ has finite measure in $(0,\infty )$ thanks to Proposition 6.5(i). The upshot of this is that the set $\{0<L<2\pi \tau \}$ has finite measure. Accordingly the set $\{L=0\}$ has infinite measure and so does $\{L=0\}\cap (t,\infty )$ for any $t>0$.

The function L is a nonnegative function in $\textrm{BV}_{\textrm{loc}}((0,\infty ))$ by the previous Lemma 6.8. Choose a good representative $\overline{L}$ of L as in Lemma 6.7. Then the set $\{\overline{L}>0\}$ is open. This latter set is a countable disjoint union of open intervals. Its complement in $(0,\infty )$ is a countable union of disjoint closed intervals relative to $(0,\infty )$. The intersection of this complement with $(t,\infty )$ has infinite measure for each $t>0$. So $\{\overline{L}=0\}$ contains a closed interval [a, b] in $(t,\infty )$ with positive length for any choice of $t>0$. It follows that the intersection of the set E with the annulus A(a, b) has measure zero.

Now suppose that the functions $\texttt{f}$ and $\texttt{g}$ satisfy the conditions (A.1)–(A.4). Let $\nu \in [0,1)$ and $\Phi$ as in (6.2) with $\beta$ replaced by $-\nu$. By (A.3) and (6.10),

$$\begin{aligned} P_g(t)&=\int _{\mathscr {F}E\setminus \overline{B}}g\,\mathrm{{d}}\mathscr {H}^1 \ge t^\nu \texttt{g}(t)P_{-\nu }(t) =(-\nu +1) t^\nu \texttt{g}(t)P_0(\Phi (E),\mathbb {R}^2_0\setminus \Phi (\overline{B})); \end{aligned}$$

that is, the set $\Phi (E)$ has the properties mentioned in the first paragraph of this proof. The set $\Phi (E)$ has finite $\Phi _\sharp V_\alpha$-measure and this measure has radial density satisfying (A.1)–(A.2). By the result for the case $\texttt{g}\equiv 1$ for each $t>0$ there exists a and b with $\frac{t^{-\nu +1}}{-\nu +1}<a<b<\infty$ such that $|\Phi (E)\cap A(a,b))|=0$. As $\Phi$ preserves centred circles a similar result holds for E. $\square$

Theorem 6.10

Suppose that $\texttt{f}$ and $\texttt{g}$ satisfy (A.1)–(A.4). Then for each $v>0$ any minimiser of (14.6) is bounded.

Proof

Let $v>0$ and E be a set of locally finite perimeter in $\mathbb {R}^2_0$ which is a minimiser for (14.6) according to Theorem 6.6. Let us assume that the topological boundary $\partial E\cap \mathbb {R}^2_0$ of E in $\mathbb {R}^2_0$ enjoys the property in (5.2). Assume for a contradiction that E is not bounded. This means that $V_f(t)>0$ for each $t>0$. Choose a centred open ball $B_0$ with weighted volume v. So $\delta :=V_f(B_0\setminus E)>0$. In fact $\delta =V_f(B_0{\setminus } E^1)=V_f(B_0\cap E^0)+V_f(B_0\cap \partial ^*E)=V_f(B_0\cap E^0)>0$ by Federer’s Theorem ([3] Theorem 3.61). Assume for a moment that the interior of the set $B_0\cap E^{0}$ is empty. Then $B_0\cap E^{0}\subset \partial E\cap \mathbb {R}^2_0$. To see this consider a point x in $B_0\cap E^0$. The complement of E has density 1 at x as this point belongs to $E^0$. On the other hand if $E\cap B(x,\rho )$ is empty for some $\rho >0$ then $B_0\cap E^0$ has non-empty interior. This inclusion contradicts Lemma 5.2. So the set $B_0\cap E^{0}$ has non-empty interior.

The upshot of the argument above is that there exists an open ball $B_1$ contained in $B_0$ with the properties $0<V_f(B_1)<\delta$, $|B_1\cap E|=0$ and $0\not \in \overline{B}_1$. Put

$$\begin{aligned} \eta :=\sup \Big \{\frac{P_g(B)^2}{V_f(B)}:B\text { is an open ball contained in }B_1\Big \}<\infty . \end{aligned}$$

Bearing in mind property (A.4) as well as Lemma 6.9 and our hypothesis on the behaviour of $V_f(\cdot )$ we may choose $t>0$ such that

• (a) $\psi _-(t)>\eta$;

• (b) $V_f(t)<V_f(B_1)$;

• (c) there exists $\delta _1>0$ such that $|A(t-\delta _1,t+\delta _1)\cap E|=0$.

Choose an open ball $B_2$ in $B_1$ with $V_f(B_2)=V_f(t)$. Define $E_1:=(E\cap B(t))\cup B_2$. We claim that $P_g(E_1)< P_g(E)$. We first note that

$$\begin{aligned} \frac{P_g(B_2)^2}{V_f(t)}=\frac{P_g(B_2)^2}{V_f(B_2)}\le \eta <\psi _-(t)\le \frac{P_g(E,\mathbb {R}^2\setminus \overline{B}(t))^2}{V_f(t)}, \end{aligned}$$

by Proposition 6.5. By [3] Corollary 3.89,

$$\begin{aligned} P_g(E_1)= P_g(E\cap B(t))+P_g(B_2)<P_g(E\cap B(t))+P_g(E,\mathbb {R}^2\setminus \overline{B}(t))=P_g(E). \end{aligned}$$

This gives rise to the contradiction that the set E is in fact not a minimiser for (14.6). This proves the theorem. $\square$

Fig. 4

The region $\mathcal {Q}$ is enclosed between the solid lines $\alpha +2=0$ and $\alpha -2\beta =0$. The region $\mathcal {P}$ is enclosed between the dashed lines and is contained inside $\mathcal {Q}$

The next result is closely related to [32] Theorem 1.1 (and [8] Corollary 2.4) upon parametrising the cone C in (6.1) using the map $\varphi$.

Theorem 6.11

Let $(\alpha ,\beta )\in \mathcal {P}^-\setminus \{0\}$. Then centred balls are unique minimisers for the problem (1.2) up to equivalence.

Proof

We prove uniqueness. Let B be the centred open ball with volume $V_f(E)=V_f(B)=v$. Assume that $P_\beta (E)=P_\beta (B)$. In this case equality holds in the inequality (6.4) and $\nu _E^\omega =0$ $\mathscr {H}^1$-a.e. on $\mathscr {F}E$. From Proposition 3.3, $(\mathscr {F}E)_t$ is empty for a.e. $t>0$. By Theorem 3.9, $(E^1)_t$ is equivalent to either the empty set $\emptyset$ or $\mathbb {S}_t$ for a.e. $t>0$. Let R stand for the radius of B. Suppose $(E^1)_t$ is equivalent to $\mathbb {S}_t$ for some $t>R$. By Proposition 6.5, $P_\beta (E)\ge P_\beta (t)\ge (|\cdot |^\beta L)(t)=2\pi t^{\beta +1}>2\pi R^{\beta +1}=P_\beta (B)$ as $\beta +1>0$. This is a contradiction. So in fact $(E^1)_t$ is equivalent to the empty set for a.e. $t>0$. This implies that E is equivalent to B. $\square$

Let us now apply the above existence and boundedness theorems to the case of radial power weights which are the focus of this paper. We introduce the parameter set

$$\begin{aligned} \mathcal {Q}&:=\Big \{(\alpha ,\beta )\in \mathbb {R}^2:-2<\alpha \text { and }\alpha \le 2\beta \text { if }\beta \le 0 \text { or }\alpha <2\beta \text { if }\beta >0\Big \}, \end{aligned}$$

(6.13)

illustrated in Fig. 4.

Corollary 6.12

For each $(\alpha ,\beta )\in \mathcal {Q}$ the isoperimetric problem (1.2) has a minimiser for each $v>0$ and any such minimiser is bounded.

Proof

For $(\alpha ,\beta )\in \mathcal {Q}$ with $\alpha <2\beta$ this follows from Theorem 6.6 and Theorem 6.10. Now consider a pair of indices $(\alpha ,\beta )$ satisfying $\alpha =2\beta$ and $-1<\beta <0$. Then existence and boundedness is a special case of Theorem 6.11. The case $(\alpha ,\beta )=(0,0)$ corresponds to the classical isoperimetric inequality. $\square$

The parameter set $\mathcal {P}$ is included in the set $\mathcal {Q}$. This is because

$$\begin{aligned} \alpha =\frac{\beta ^2}{\beta +1}<\beta <2\beta , \end{aligned}$$

whenever $\beta >0$.

7 Regularity, Spherical Cap Symmetry and Curvature

The isoperimetric problem (1.2) has a bounded minimiser after Corollary 6.12 so long as the indices $(\alpha ,\beta )$ belong to the parameter set $\mathcal {Q}$. In this Section we collate some symmetry, regularity and curvature properties of the minimiser. Let us start with spherical cap symmetry and analyticity. The notion of spherical cap symmetry is discussed in for example [28] Section 4.

Theorem 7.1

Let $(\alpha ,\beta )\in \mathcal {Q}$. Let $v>0$ and suppose that E is a bounded minimiser of (1.2). Then there exists an $\mathscr {L}^2$-measurable set $\widetilde{E}$ in $\mathbb {R}^2_0$ with the properties

• (i) $\widetilde{E}$ is a minimiser of (1.2);

• (ii) $L_{\widetilde{E}}=L_E$ a.e. on $(0,\infty )$;

• (iii) $\widetilde{E}$ is open with analytic boundary in $\mathbb {R}^2_0$;

• (iv) $\widetilde{E}=\widetilde{E}^{\textrm{sc}}$.

Proof

Parts (i)-(iv) follow from Theorem 14.8 with analytic replaced by $C^1$ in (iii). A regularity result for manifolds with density is contained in [29] 3.10. In our case the metric may be degenerate or singular at the origin while the density relative to the metric may vanish at the origin (admittedly a minor change). Let us nevertheless demonstrate the analyticity property in (iii). Let E be an isoperimetric set. Consider a point $p\in M$ and assume that the normal to M at p is not parallel to the $x_1$-axis. There exists an open interval G not containing the origin and $u\in C^1(G)$ such that M is locally the graph of u,

$$\begin{aligned} M\cap Q=\{(x_1,u(x_1)):x_1\in G\}, \end{aligned}$$

where Q is the vertical strip $G\times \mathbb {R}$ (making this latter assumption for the sake of simplicity). Let $\zeta \in C^1_c(G)$ and define $X\in C^1_c(\mathbb {R}^2_0,\mathbb {R}^2)$ by $X(x)=\zeta (x_1)\phi (x_2)e_2$ for a suitable cut-off function $\phi \in C^\infty _c(\mathbb {R})$. We may assume that the inner unit normal to $\partial E$ is given locally by

$$\begin{aligned} \nu _E=\frac{(-u^\prime ,1)}{\sqrt{1+(u^\prime )^2}}, \end{aligned}$$

and

$$\begin{aligned} \textrm{div}^M X =\textrm{div}X-\langle \nu _E,D_{\nu _E}X\rangle =-\langle \nu _E,D_{\nu _E}X\rangle =\frac{u^\prime \zeta ^\prime }{1+(u^\prime )^2}, \end{aligned}$$

in a neighbourhood of M in Q. The Jacobean determinant of the parametrisation $\varphi :G\rightarrow M;x_1\mapsto (x_1,u(x_1))$ is $J_1d\varphi =\sqrt{1+(u^\prime )^2}$. As in Proposition 14.9 (for example) and making use of the area formula [3] Theorem 2.71,

$$\begin{aligned} 0&=\int _{M}\langle \nabla g, X\rangle + g\,\textrm{div}^{M}X -\lambda f\langle \nu _E, X\rangle \,\mathrm{{d}}\mathscr {H}^{1}\nonumber \\&=\int _G\big [\partial _{x_2} g(\cdot ,u)\sqrt{1+(u^\prime )^2}-\lambda \,f(\cdot ,u) \big ]\zeta +g(\cdot ,u)\frac{u^\prime \zeta ^\prime }{\sqrt{1+(u^\prime )^2}} \,\mathrm{{d}}x_1. \end{aligned}$$

(7.1)

Define

$$\begin{aligned} I(u,G):=\int _G j(\cdot ,u,u^\prime )\,\mathrm{{d}}x_1 \text { with } j(x_1,z,p):=g(x_1,z)\sqrt{1+p^2}-\lambda \,F(x_1,z), \end{aligned}$$

where the function F is chosen such that $\partial _{x_2} F=f$ on Q. By (7.1), u is a (Lipschitz) extremal in the sense of [33] 1.10 (see also (1.4.7)). Then j is regular and analytic on $G\times \mathbb {R}\times \mathbb {R}$. By [33] Theorem 1.10.4, u is analytic on G. $\square$

Suppose the open set E in $\mathbb {R}^2_0$ has $C^1$ boundary M in $\mathbb {R}^2_0$. Denote by $n:M\rightarrow \mathbb {S}$ the inner unit normal vector field. Given $p\in M$ we choose a tangent vector $t(p)\in \mathbb {S}$ in such a way that the pair $\{t(p),n(p)\}$ forms a positively oriented basis for $\mathbb {R}^2$. For $p\in M$ let $\sigma (p)$ stand for the angle measured anticlockwise from the position vector p to the tangent vector t(p); $\sigma (p)$ is uniquely determined up to integer multiples of $2\pi$. This angle will feature frequently in our considerations.

Let E be an open set in $\mathbb {R}^2_0$ with $C^2$ boundary M in $\mathbb {R}^2_0$. Let $p\in M$. There exists a local parametrisation $\gamma _1:I\rightarrow M$ where $I=(-\delta ,\delta )$ for some $\delta >0$ of class $C^2$ with $\gamma _1(0)=p$. We always assume that $\gamma _1$ is parametrised by arc length and that $\dot{\gamma _1}(0)=t(p)$ where the dot signifies differentiation with respect to arc length. The (geodesic) curvature $k_1$ is defined on I via the relation

$$\begin{aligned} \ddot{\gamma }_1=k_1n_1. \end{aligned}$$

(7.2)

The curvature k of M is defined on M by

$$\begin{aligned} k(x):=k_1(s), \end{aligned}$$

(7.3)

whenever $x=\gamma _1(s)$ for some $s\in I$.

The next important Theorem characterises the generalised (mean) curvature

$$\begin{aligned} \tau ^{\beta -\alpha }\Big \{k+\frac{\beta }{\tau }\sin \sigma \Big \}, \end{aligned}$$

of the boundary of an isoperimetric minimiser in the spherical cap symmetric case.

Theorem 7.2

Let $(\alpha ,\beta )\in \mathcal {Q}$. Given $v>0$ let E be a minimiser of (1.2). Assume that E is a bounded open set with analytic boundary M in $\mathbb {R}^2_0$ and suppose that $E=E^{sc}$. Then there exists $\lambda \in \mathbb {R}$ such that

$$\begin{aligned} k+\frac{\beta }{\tau }\sin \sigma +\lambda \tau ^{\alpha -\beta }=0, \end{aligned}$$

on M.

Proof

We use the notation in Sect. 1. The result follows on the set $M\setminus \overline{\Lambda }_1$ by adapting the proof of [28] Theorem 6.5 (i) and making use of Theorem 14.9. It follows on the set $\overline{\Lambda }_1$ as in (ii)-(iii) of [28] Theorem 6.5 because $g^\prime /g=\beta /\tau$ is continuous. The $\mathscr {H}^1$-a.e. statement in this last can be dropped as M is analytic. $\square$

Let E be an open set with $C^1$ boundary M in $\mathbb {R}^2_0$ and assume that $E=E^{sc}$. Introduce the projection $\pi :\mathbb {R}^2_0\rightarrow (0,\infty );x\mapsto |x|$. The set

$$\begin{aligned} \Omega :=\pi \Big [M\cap \{\cos \sigma \ne 0\}\Big ], \end{aligned}$$

(7.4)

plays an important rôle in the sequel. Bearing in mind [28] Lemma 5.4 we may define

$$\begin{aligned}&\theta _2:\Omega \rightarrow (0,\pi );\tau \mapsto L(\tau )/2\tau ; \end{aligned}$$

(7.5)

$$\begin{aligned}&\gamma :\Omega \rightarrow M;\tau \mapsto (\tau \cos \theta _2(\tau ),\tau \sin \theta _2(\tau )). \end{aligned}$$

(7.6)

The function

$$\begin{aligned}&u:\Omega \rightarrow [-1,1];\tau \mapsto \sin (\sigma (\gamma (\tau ))). \end{aligned}$$

(7.7)

is closely related to the geodesic curvature of M (in fact $k=(1/\tau )(\tau u)^\prime$) and we may rephrase the last Theorem 7.2 as follows.

Theorem 7.3

Let $(\alpha ,\beta )\in \mathcal {Q}$. Given $v>0$ let E be a minimiser of (1.2). Assume that E is a bounded open set with analytic boundary M in $\mathbb {R}^2_0$ and suppose that $E=E^{sc}$. Suppose that $\Omega \ne \emptyset$. Then $u\in C^{1}(\Omega )$ and

$$\begin{aligned} u^\prime +\frac{\beta +1}{\tau }u+\lambda \tau ^{\alpha -\beta }&=0, \end{aligned}$$

(7.8)

on $\Omega$.

Proof

This follows as in [28] Theorem 6.6 using Theorem 7.2. $\square$

Finally we recall [28] Lemma 6.7 which gives an explicit expression for the derivative of the angular coordinate $\theta _2$ of a boundary point involving the function u.

Lemma 7.4

Suppose that E is a bounded open set with $C^1$ boundary M in $\mathbb {R}^2_0$ and that $E=E^{sc}$. Suppose that $\Omega \ne \emptyset$. Then

• (i) $\theta _2\in C^1(\Omega )$;

• (ii) $\theta _2^\prime =-\frac{1}{\tau }\frac{u}{\sqrt{1-u^2}}$ on $\Omega$.

8 Some Algebraic Inequalities

In this Section we obtain two algebraic inequalities. These are used in the next Section to derive some integral inequalities: Theorem 8.1 is used in the proof of Corollary 9.11 while Proposition 8.9 is used in the proof of Corollary 9.5. Let us fix a pair of indices $(\alpha ,\beta )\in \mathcal {P}$ for the time being. The definition of $\mathcal {P}$ entails that $\beta +1<\alpha +2\le 2(\beta +1)$ and in particular $\beta +1>0$ and $\alpha +2>\beta +1>0$. Given positive numbers a and b with $a<b$ define

$$\begin{aligned} m=m(a,b)=m_{\alpha ,\beta }(a,b)&:=(\alpha +2)\frac{b^{\beta +1}-a^{\beta +1}}{b^{\alpha +2}-a^{\alpha +2}}. \end{aligned}$$

(8.1)

We shall make frequent use of the homogeneity property

$$\begin{aligned} m(a,b)&=a^{-(\alpha -\beta +1)}m(t), \end{aligned}$$

(8.2)

where $t:=b/a>1$ and $m(t):=m(1,t)$. The bulk of this Section will be devoted to establishing the following algebraic inequality.

Theorem 8.1

Fix $(\alpha ,\beta )\in \mathcal {P}$. Then for any $0<a<b<\infty$,

$$\begin{aligned}&\frac{1}{1+\beta -ma^{\alpha -\beta +1}}-\frac{1}{1+\beta -mb^{\alpha -\beta +1}}\ge 2\frac{a+b}{b-a}. \end{aligned}$$

(8.3)

If $(\alpha ,\beta )\in \mathcal {P}\setminus \{(0,0)\}$ then strict inequality holds in (8.3) for each $0<a<b<\infty$. If $(\alpha ,\beta )=(0,0)$ then equality holds in (8.3) for each $0<a<b<\infty$.

Let us first mention some landmarks in the proof of this result. We first define the set

$$\begin{aligned} \mathcal {P}^+&:=\Big \{(\alpha ,\beta )\in \mathbb {R}^2:\alpha \ge 0,\beta \ge 0\text { and }\alpha (\beta +1)=\beta ^2\Big \}. \end{aligned}$$

A first step in the proof of Theorem 8.1 is to show that it holds for indices $(\alpha ,\beta )$ belonging to $\mathcal {P}^+\setminus \{(0,0)\}$. With this in hand a monotonicity argument is then used to derive the result for indices in the set $\mathcal {P}\setminus \mathcal {P}^-$. A separate argument deals with the case $\mathcal {P}^-$. To begin we require some preliminary lemmas.

Lemma 8.2

For $\alpha>\beta >0$ the function

$$\begin{aligned} (1,\infty )\rightarrow \mathbb {R};t\mapsto \frac{t^{\beta }-1}{t^\alpha -1}, \end{aligned}$$

is strictly decreasing.

Proof

The derivative of this function is given by

$$\begin{aligned} \frac{\mathrm{{d}}}{\mathrm{{d}}t}\frac{t^\beta -1}{t^\alpha -1}&=\frac{(\beta -\alpha )t^{\alpha +\beta -1}+\alpha t^{\alpha -1}-\beta t^{\beta -1}}{(t^\alpha -1)^2}, \end{aligned}$$

for $t>1$. Put

$$\begin{aligned} p:=\frac{\alpha }{\alpha -\beta }\text { and }q:=\frac{\alpha }{\beta }, \end{aligned}$$

so that $p>1$, $q>1$ and $1/p+1/q=1$. For $t>1$ set

$$\begin{aligned} a:=t^{\frac{\alpha ^2-\beta ^2}{\alpha }}\text { and }b:=t^{\frac{\beta ^2}{\alpha }}, \end{aligned}$$

and apply Young’s inequality to obtain

$$\begin{aligned} t^{\alpha }&=ab\le \frac{a^p}{p}+\frac{b^q}{q} =\frac{\alpha -\beta }{\alpha }t^{\alpha +\beta }+\frac{\beta }{\alpha }t^\beta , \end{aligned}$$

and in fact strict inequality holds as the equality condition in Young’s inequality reads $a^p-b^q=t^{\alpha +\beta }-t^\beta =t^\beta (t^\alpha -1)>0$. This entails that the derivative is strictly negative. $\square$

Lemma 8.3

Let $(\alpha ,\beta )\in \mathcal {P}$, $0<a<b<\infty$ and define m as in (8.1). Then

• (i) $a^{\alpha -\beta +1}m<\beta +1$;

• (ii) $b^{\alpha -\beta +1}m>\beta +1$.

Moreover for each fixed $a>0$,

• (iii) the mapping $b\mapsto m(a,b)$ on $(a,\infty )$ is strictly decreasing;

• (iv) the mapping $b\mapsto b^{\alpha -\beta +1}m(a,b)$ on $(a,\infty )$ is strictly increasing.

Proof

By homogeneity it suffices to consider the case $a=1$ and $b=t>1$. For (i) we require

$$\begin{aligned} \frac{\alpha +2}{\beta +1}\frac{t^{\beta +1}-1}{t^{\alpha +2}-1} =\frac{\int _1^t\tau ^{\beta }\,\mathrm{{d}}\tau }{\int _1^t\tau ^{\alpha +1}\,\mathrm{{d}}\tau } <1, \end{aligned}$$

for each $t>1$ which is the case as $\alpha +1>\beta$. By Cauchy’s mean-value theorem,

$$\begin{aligned} t^{\alpha -\beta +1}\frac{\alpha +2}{\beta +1}\frac{t^{\beta +1}-1}{t^{\alpha +2}-1}&=\Big (\frac{t}{c}\Big )^{\alpha -\beta +1}>1, \end{aligned}$$

for some $c\in (1,t)$ and hence (ii). (iii) This follows using homogeneity and Lemma 8.2. (iv) Using homogeneity we write

$$\begin{aligned} t^{\alpha -\beta +1}m(1,t)&=(\alpha +2)\frac{t^{\alpha +2}-t^{\alpha -\beta +1}}{t^{\alpha +2}-1} =(\alpha +2)\Big \{1-\frac{t^{\alpha -\beta +1}-1}{t^{\alpha +2}-1}\Big \}, \end{aligned}$$

and the claim follows from Lemma 8.2. $\square$

We are now in a position to rephrase the statement of Theorem 8.1 for indices belonging to $\mathcal {P}^+$. The condition mentioned in the next proposition is verified in Lemma 8.5 leading to Corollary 8.6.

Proposition 8.4

Let $(\alpha ,\beta )\in \mathcal {P}^+\setminus \{(0,0)\}$. The following are equivalent:

• (i) for any $0<a<b<\infty$,

  $$\begin{aligned}&\frac{1}{1+\beta -ma^{\alpha -\beta +1}}-\frac{1}{1+\beta -mb^{\alpha -\beta +1}}>2\frac{a+b}{b-a}; \end{aligned}$$

• (ii) for each $\lambda >0$,

  $$\begin{aligned} (1/x)^2\coth (\lambda /2x) +x^2\coth (\lambda x/2) -y^2\coth (\lambda y/2) +y\tanh (\lambda /2)&>0, \end{aligned}$$

  (8.4)

  where $x:=\beta +1$ and $y:=\alpha +2$.

Proof

By homogeneity it suffices to consider the case $a=1$ and $b=t>1$ in which case the inequality (8.3) becomes

$$\begin{aligned}&\frac{1}{1+\beta -m}-\frac{1}{1+\beta -mt^{\alpha -\beta +1}}\ge 2\frac{t+1}{t-1}, \end{aligned}$$

(8.5)

with now

$$\begin{aligned} m=m(t)&:=(\alpha +2)\frac{t^{\beta +1}-1}{t^{\alpha +2}-1}, \end{aligned}$$

(8.6)

as in (8.1). Bearing in mind Lemma 8.3(i) and (ii) the inequality in (8.5) may be rewritten

$$\begin{aligned}&2(t+1)t^{\alpha -\beta +1}m^2+\Big \{(t-1)(t^{\alpha -\beta +1}-1)-2(\beta +1)(t+1)(t^{\alpha -\beta +1}+1)\Big \}m\\&\quad +2(\beta +1)^2(t+1)\ge 0, \end{aligned}$$

as a quadratic in m. Write $\gamma :=\alpha -\beta +1$ and replace m with the expression in (8.6) to obtain

$$\begin{aligned}&2(\alpha +2)^2(t+1)t^{\gamma }(t^{\beta +1}-1)^2 +2(\beta +1)^2(t+1)(t^{\alpha +2}-1)^2\nonumber \\&\quad +(\alpha +2)(t^{\alpha +2}-1)(t^{\beta +1}-1)\Big \{(t-1)(t^{\gamma }-1)-2(\beta +1)(t+1)(t^{\gamma }+1)\Big \} \ge 0. \end{aligned}$$

(8.7)

Let us introduce some further notation. Put $x:=\beta +1$. Because of the constraint $\alpha (\beta +1)=\beta ^2$,

$$\begin{aligned} y:=\alpha +2=\frac{\beta ^2}{\beta +1}+2=\beta +1+\frac{1}{\beta +1}=x+\frac{1}{x}. \end{aligned}$$

In this case $\gamma =y-x=1/x$. In this notation the inequality (8.7) can be rewritten

$$\begin{aligned}&2y^2(t+1)t^{1/x}(t^x-1)^2+2x^2(t+1)(t^{y}-1)^2\\&\quad +y(t^{y}-1)(t^x-1)\Big \{(t-1)(t^{1/x}-1)-2x(t+1)(t^{1/x}+1)\Big \}\ge 0. \end{aligned}$$

As $t>1$ we may put $t=e^\lambda$ for some $\lambda >0$. With this further substitution we obtain

$$\begin{aligned}&2y^2(e^\lambda +1)e^{\lambda /x}(e^{\lambda x}-1)^2 +2x^2(e^\lambda +1)(e^{\lambda y}-1)^2\\&\quad +y(e^{\lambda y}-1)(e^{\lambda x}-1)\Big \{(e^\lambda -1)(e^{\lambda /x}-1)-2x(e^\lambda +1)(e^{\lambda /x}+1)\Big \}\ge 0. \end{aligned}$$

Multiplication by $e^{-\lambda x}$ and $e^{-\lambda /x}$ in turn (or $e^{-\lambda y}$) results in the inequality

$$\begin{aligned}&2y^2(e^\lambda +1)(e^{\lambda x/2}-e^{-\lambda x/2})^2 +2x^2(e^\lambda +1)(e^{\lambda y/2}-e^{-\lambda y/2})^2\\&\quad +y(e^{\lambda y/2}-e^{-\lambda y/2})(e^{\lambda x/2}-e^{-\lambda x/2})\Big \{(e^\lambda -1)(e^{\lambda /2x}-e^{-\lambda /2x})\\&\quad -2x(e^\lambda +1)(e^{\lambda /2x}+e^{-\lambda /2x})\Big \}\ge 0, \end{aligned}$$

or more briefly

$$\begin{aligned}&y^2\cosh (\lambda /2)\sinh ^2(\lambda x/2) +x^2\cosh (\lambda /2)\sinh ^2(\lambda y/2)\\&\quad +y\sinh (\lambda y/2)\sinh (\lambda x/2) \Big \{ \sinh (\lambda /2)\sinh (\lambda /2x) -2x\cosh (\lambda /2)\cosh (\lambda /2x)\Big \}\ge 0. \end{aligned}$$

To continue let us introduce the function

$$\begin{aligned} \phi (x):=\frac{\sinh (\lambda x/2)}{x}, \end{aligned}$$

defined for positive x. The above expression can be written in terms of this function as

$$\begin{aligned} \phi (x)^2+\phi (y)^2-2\cosh (\lambda /2x)\phi (x)\phi (y)+\phi (x)\phi (y)\tanh (\lambda /2)\frac{\sinh (\lambda /2x)}{x}\ge 0, \end{aligned}$$

after dividing by $(xy)^2\cosh (\lambda /2)$. Or equivalently,

$$\begin{aligned} \frac{\phi (x)}{\phi (y)}+\frac{\phi (y)}{\phi (x)}-2\cosh (\lambda /2x)+\tanh (\lambda /2)\frac{\sinh (\lambda /2x)}{x}&\ge 0. \end{aligned}$$

(8.8)

By the addition formula (cf. [1] 4.5.24 for example),

$$\begin{aligned} \frac{\phi (y)}{\phi (x)} =\frac{\sinh (\lambda y/2)}{\sinh (\lambda x/2)}\frac{x}{y} =\Big \{\cosh (\lambda /2x)+\coth (\lambda x/2)\sinh (\lambda /2x)\Big \} \frac{x}{y}, \end{aligned}$$

and its reciprocal is given by

$$\begin{aligned} \frac{\phi (x)}{\phi (y)} =\frac{\sinh (\lambda x/2)}{\sinh (\lambda y/2)}\frac{y}{x} =\Big \{\cosh (\lambda /2x)-\coth (\lambda y/2)\sinh (\lambda /2x)\Big \} \frac{y}{x}. \end{aligned}$$

Inserting these expressions into (8.8) leads to

$$\begin{aligned}&\cosh (\lambda /2x)\Big (\frac{x}{y}+\frac{y}{x}-2\Big ) \\&\quad +\sinh (\lambda /2x)\Big (\coth (\lambda x/2)\frac{x}{y}-\coth (\lambda y/2)\frac{y}{x} +\frac{\tanh (\lambda /2)}{x}\Big )\ge 0; \end{aligned}$$

or upon dividing by $\sinh (\lambda /2x)$ and multiplying by xy,

$$\begin{aligned}&(1/x)^2\coth (\lambda /2x) +x^2\coth (\lambda x/2) -y^2\coth (\lambda y/2) +y\tanh (\lambda /2)\ge 0. \end{aligned}$$

$\square$

Lemma 8.5

Let x and y be positive numbers. Then the inequality (8.4) holds for each $\lambda >0$.

Proof

We first write the left-hand side in (8.4) as

$$\begin{aligned}&x^2\Big \{\coth (\lambda x/2)-\coth (\lambda y/2)\Big \}+(1/x)^2\Big \{\coth (\lambda /2x)-\coth (\lambda y/2)\Big \}\nonumber \\&\quad -2\coth (\lambda y/2)+y\tanh (\lambda /2), \end{aligned}$$

(8.9)

after expanding $y^2$. By the addition formula (cf. [1] 4.5.27 for example),

$$\begin{aligned}&\coth (\lambda x/2)-\coth (\lambda y/2)\\&\quad =\coth (\lambda x/2)-\frac{1+\coth (\lambda x/2)\coth (\lambda /2x)}{\coth (\lambda x/2)+\coth (\lambda /2x)}\\&\quad =\frac{\coth (\lambda x/2)[\coth (\lambda x/2)+\coth (\lambda /2x)]-1-\coth (\lambda x/2)\coth (\lambda /2x)}{\coth (\lambda x/2)+\coth (\lambda /2x)}\\&\quad =\frac{\coth ^2(\lambda x/2)-1}{\coth (\lambda x/2)+\coth (\lambda /2x)} =\frac{\sinh ^{-2}(\lambda x/2)}{\coth (\lambda x/2)+\coth (\lambda /2x)}, \end{aligned}$$

and likewise

$$\begin{aligned} \coth (\lambda /2x)-\coth (\lambda y/2)&=\frac{\sinh ^{-2}(\lambda /2x)}{\coth (\lambda x/2)+\coth (\lambda /2x)}. \end{aligned}$$

The expression (8.9) may be rewritten by completing the square using the addition formula (cf. [1] 4.5.24 for example),

$$\begin{aligned}&\frac{(x/\sinh (\lambda x/2))^2+(1/x\sinh (\lambda /2x))^2}{\coth (\lambda x/2)+\coth (\lambda /2x)} -2\coth (\lambda y/2)+y\tanh (\lambda /2)\\&\quad = \frac{(x/\sinh (\lambda x/2)-1/x\sinh (\lambda /2x))^2}{\coth (\lambda x/2)+\coth (\lambda /2x)} \\&\quad +\frac{2[\sinh (\lambda x/2)\sinh (\lambda /2x)]^{-1}}{\coth (\lambda x/2)+\coth (\lambda /2x)} -2\coth (\lambda y/2)+y\tanh (\lambda /2). \end{aligned}$$

The final three terms in the expression above can be expressed

$$\begin{aligned} \frac{2}{\sinh (\lambda y/2)} -2\coth (\lambda y/2)+y\tanh (\lambda /2) =2\frac{1-\cosh (\lambda y/2)}{\sinh (\lambda y/2)}+y\tanh (\lambda /2) \\ =-2\tanh (\lambda y/4)+y\tanh (\lambda /2) = 2\Big \{-\tanh (\lambda y/4)+(y/2)\tanh (\lambda /2)\Big \}, \end{aligned}$$

where we used the half-angle formula (cf. [1] 4.5.30 for example) in the penultimate line. This means that (8.9) can be written

$$\begin{aligned} \frac{(x/\sinh (\lambda x/2)-1/x\sinh (\lambda /2x))^2}{\coth (\lambda x/2)+\coth (\lambda /2x)} +2\Big \{-\tanh (\lambda y/4)+(y/2)\tanh (\lambda /2)\Big \}. \end{aligned}$$

We now claim that

$$\begin{aligned} -\tanh (\lambda y/4)+(y/2)\tanh (\lambda /2)\ge 0\text { for any }y\ge 2. \end{aligned}$$

At $y=2$ equality holds. Differentiating the left-hand side gives

$$\begin{aligned} -\frac{\lambda }{4}\frac{1}{\cosh ^2(\lambda y/4)}+(1/2)\tanh (\lambda /2)&\ge -\frac{\lambda }{4}\frac{1}{\cosh ^2(\lambda /2)}+(1/2)\tanh (\lambda /2)\\&=\frac{1}{4\cosh ^2(\lambda /2)}\Big \{-\lambda +2\sinh (\lambda /2)\cosh (\lambda /2)\Big \}\\&=\frac{1}{4\cosh ^2(\lambda /2)}\Big \{-\lambda +\sinh (\lambda )\Big \}, \end{aligned}$$

by the double-angle formula (cf. [1] 4.5.31 for example) and this last is positive for $\lambda >0$. $\square$

Corollary 8.6

Let $(\alpha ,\beta )\in \mathcal {P}^+\setminus \{(0,0)\}$. Then for any $0<a<b<\infty$,

$$\begin{aligned}&\frac{1}{1+\beta -ma^{\alpha -\beta +1}}-\frac{1}{1+\beta -mb^{\alpha -\beta +1}}>2\frac{a+b}{b-a}. \end{aligned}$$

Given $(\alpha ,\beta )\in \mathcal {P}$ set

$$\begin{aligned} \zeta&:=\frac{\beta +1}{\alpha -\beta +1}, \end{aligned}$$

(8.10)

and note that $\zeta \ge 1$ in virtue of the property that $\alpha \le 2\beta$. As before we put $\gamma :=\alpha -\beta +1$ and consider this as a function defined on $\mathcal {P}$. For fixed $\zeta \ne 0$ we introduce the line $\ell _\zeta$ in the $(\alpha ,\beta )$-plane given by

$$\begin{aligned}&\ell _\zeta :\mathbb {R}\rightarrow \mathbb {R};\beta \mapsto \ell _\zeta (\beta ):=(1+1/\zeta )\beta +1/\zeta -1. \end{aligned}$$

(8.11)

The graph of this line passes through the point $(-2,-1)$ as well as $(\alpha ,\beta )$.

We have seen that strict inequality in (8.3) holds on $\mathcal {P}^+$. To obtain the inequality in $\mathcal {P}$ we consider the line passing through $(\alpha ,\beta )$ in $\mathcal {P}$ and the point $(-2,-1)$. This meets $\mathcal {P}^+$ in a unique point $(\overline{\alpha },\overline{\beta })$. A monotonicity argument allows us to obtain the inequality at $(\alpha ,\beta )$ by making use of the inequality at $(\overline{\alpha },\overline{\beta })$. See Fig. 5. We now describe the details of this argument. Let us start by fixing some properties of the lines $\ell _\zeta$.

Fig. 5

The region $\mathcal {P}$ is enclosed between the lines $\alpha -\beta +1=0$ and $\alpha -2\beta =0$ and the curve $\alpha (\beta +1)-\beta ^2=0$. This latter curve is marked in bold and corresponds to $\mathcal {P}^+$. Suppose that $(\alpha ,\beta )\in \mathcal {P}$. The line $\ell _\zeta$ that passes through $(-2,-1)$ and $(\alpha ,\beta )$ intersects $\mathcal {P}^+$ in a unique point $(\overline{\alpha },\overline{\beta })$. The gradient of the line $\ell _\zeta$ when considered as a function of $\beta$ is given by $\frac{\alpha +2}{\beta +1}$ and has a value in the interval (1, 2]

Lemma 8.7

For each point $(\alpha ,\beta )\in \mathcal {P}$,

• (i) there exists a unique $\zeta \ge 1$ with the property that $(\alpha ,\beta )$ lies on the graph of $\ell _\zeta$;

• (ii) $\zeta$ is given by (8.10);

and for each $\zeta \in [1,\infty )$,

• (iii) the graph of the line $\ell _\zeta$ meets $\mathcal {P}^+$ exactly once;

• (iv) the function $\beta \mapsto \gamma (\ell _\zeta (\beta ),\beta )$ is increasing on $\mathbb {R}$.

Proof

(i) and (ii). For $(\alpha ,\beta )\in \mathcal {P}$ define $\zeta$ as in (8.10) and observe that

$$\begin{aligned} 1+\frac{1}{\zeta }&=\frac{\alpha +2}{\beta +1}\in (1,2]; \end{aligned}$$

(8.12)

this is the gradient of the line $\ell _\zeta$ when considered as a function of $\beta$. So $\ell _\zeta (\beta )=\alpha$ and $(\ell _\zeta (\beta ),\beta )=(\alpha ,\beta )$; that is, the point $(\alpha ,\beta )$ lies on the graph of $\ell _\zeta$. Conversely, if $\ell _\zeta (\beta )=\alpha$ then $\zeta$ is given by (8.10) and $\zeta \ge 1$ as $(\alpha ,\beta )\in \mathcal {P}$.

(iii) It may be helpful to refer to Fig. 6. Define an affine transformation T mapping the $(\alpha ,\beta )$-plane into the (X, Y)-plane via

$$\begin{aligned} T&:\mathbb {R}^2\rightarrow \mathbb {R}^2;(\alpha ,\beta )\mapsto (X,Y)= \Big (\frac{\alpha +2}{2},\frac{2\beta -\alpha }{2}\Big ). \end{aligned}$$

This has inverse $\alpha =2X-2$ and $\beta =Y+X-1$. Note that

$$\begin{aligned} X^2-Y^2=\alpha (\beta +1)-\beta ^2+1. \end{aligned}$$

The image of $\mathcal {P}^+$ under T is the branch of the hyperbola

$$\begin{aligned} X^2-Y^2&=1, \end{aligned}$$

(8.13)

in the first quadrant of the (X, Y)-plane noting that $X=(\alpha /2)+1$ has range $[1,\infty )$ when restricted to $\mathcal {P}^+$. The centre (0, 0) of the hyperbola (8.13) in the (X, Y)-plane corresponds to the point $(-2,-1)$ in the $(\alpha ,\beta )$-plane; its vertices correspond to the points (0, 0) and $(-4,-2)$; and its asymptotes $X\pm Y=0$ to the lines

$$\begin{aligned} \alpha -\beta +1=0\text { and }\beta +1=0. \end{aligned}$$

Note also that the line $X=1$ corresponds to the line $\alpha =0$ and the line $\alpha -2\beta =0$ corresponds to the line $Y=0$. The graph of the line $\ell _\zeta$ in (8.11) corresponds to the line

$$\begin{aligned} Y&=\frac{\zeta -1}{\zeta +1}X, \end{aligned}$$

in the (X, Y)-plane. Notice that the gradient varies between 0 and 1 as $\zeta$ varies between 1 and $\infty$. This makes evident the claim in (iii).

Fig. 6

The image of $\mathcal {P}$ under the mapping T is enclosed between the lines $Y=0$ and $Y=X$ and the arc of the hyperbola $X^2-Y^2-1=0$ marked in bold. This latter is the image of $\mathcal {P}^+$ under T

(iv) For $\beta \in \mathbb {R}$,

$$\begin{aligned} \gamma (\ell _\zeta (\beta ),\beta )&=\ell _\zeta (\beta )-\beta +1= (1+1/\zeta )\beta +1/\zeta -1-\beta +1=(1/\zeta )(\beta +1), \end{aligned}$$

which increases as $\beta$ increases. $\square$

For $\zeta \ge 1$ define

$$\begin{aligned} M:[1,\infty )\rightarrow \mathbb {R};\tau \mapsto \left\{ \begin{array}{lc} 1&{} \text { for }\tau =1;\\ \frac{\zeta +1}{\zeta }\frac{\tau ^\zeta -1}{\tau ^{\zeta +1}-1} &{} \text { for }\tau >1;\\ \end{array} \right. \end{aligned}$$

(8.14)

so that M is continuous and strictly increasing on $[1,\infty )$ with limit 0 at $\infty$ by Lemma 8.2. Define

$$\begin{aligned} \Lambda :(1,\infty )\rightarrow \mathbb {R};\tau \mapsto \frac{1}{1-M(\tau )}-\frac{1}{1-\tau M(\tau )}. \end{aligned}$$

(8.15)

Lemma 8.8

Let $(\alpha ,\beta )\in \mathcal {P}$. Define $\Lambda$ as in (8.15). Then $\Lambda$ is strictly decreasing on $(1,\infty )$.

Proof

For $\tau >1$,

$$\begin{aligned} \tau M(\tau )=\frac{\zeta +1}{\zeta }\Big \{1-\frac{\tau -1}{\tau ^{\zeta +1}-1}\Big \}. \end{aligned}$$

This is strictly increasing by Lemma 8.2 while M is strictly decreasing as already remarked. Note that $1-\tau M(\tau )<0$ for $\tau >1$ as this is equivalent to $\tau ^{\zeta +1}-(\zeta +1)\tau +\zeta >0$ and this holds by Young’s inequality because $a^p-b^q=\tau ^{\zeta +1}-1>0$. $\square$

Proof of Theorem 8.1

Let $(\alpha ,\beta )\in \mathcal {P}\setminus \mathcal {P}_-$. Define $\zeta$ as in (8.10). It suffices to take $a=1$ and $b=t>1$ by homogeneity. Put $\tau :=t^{\alpha -\beta +1}=t^\gamma$. Then $t^{\beta +1}=\tau ^\zeta$ and $t^{\alpha +2}=\tau ^{\zeta +1}$. So we may write

$$\begin{aligned} m(t)&=(\alpha +2)\frac{t^{\beta +1}-1}{t^{\alpha +2}-1}=(\beta +1)\frac{\zeta +1}{\zeta }\frac{\tau ^\zeta -1}{\tau ^{\zeta +1}-1} =(\beta +1)M(\tau ), \end{aligned}$$

making use of (8.12). This leads to in turn to the identity

$$\begin{aligned} \frac{1}{\beta +1-m}-\frac{1}{\beta +1-t^{\alpha -\beta +1}m}&=\frac{1}{\beta +1}\Big \{\frac{1}{1-M(\tau )}-\frac{1}{1-\tau M(\tau )}\Big \} =\frac{1}{\beta +1}\Lambda (\tau ). \end{aligned}$$

(8.16)

According to Lemma 8.7 the graph of the line $\ell _\zeta$ meets the curve $\mathcal {P}^+\setminus \{(0,0)\}$ at a unique point $(\overline{\alpha },\overline{\beta })$ with $\overline{\alpha }=\ell _\zeta (\overline{\beta })$ where $\beta \le \overline{\beta }$. By (8.16) and Corollary 8.6,

$$\begin{aligned} \frac{1}{\overline{\beta }+1}\Lambda (t^{\overline{\gamma }})= \frac{1}{\overline{\beta }+1-m_{\overline{\alpha },\overline{\beta }}(t)} -\frac{1}{\overline{\beta }+1-t^{\overline{\gamma }}m_{\overline{\alpha },\overline{\beta }}(t)} >2\frac{1+t}{t-1}, \end{aligned}$$

for any $t>1$. Again by (8.16) and Lemma 8.8,

$$\begin{aligned} \frac{1}{\beta +1-m}-\frac{1}{\beta +1-t^{\alpha -\beta +1}m}&=\frac{1}{\beta +1}\Lambda (t^\gamma ) \ge \frac{1}{\overline{\beta }+1}\Lambda (t^{ \overline{\gamma } } )>2\frac{1+t}{t-1} . \end{aligned}$$

where $\overline{\gamma }=\gamma (\ell _\zeta (\overline{\beta }),\overline{\beta })$ because $\gamma \le \overline{\gamma }$ by Lemma 8.7 and $t>1$.

Now suppose that $(\alpha ,\beta )\in \mathcal {P}^-\setminus \{(0,0)\}$. In this case $-1<\beta <0$, $\alpha =2\beta$ and

$$\begin{aligned} m(t)=\frac{2(\beta +1)}{1+t^{\beta +1}}, \end{aligned}$$

for $t>1$. Moreover,

$$\begin{aligned} \frac{1}{1+\beta -m(t)}-\frac{1}{1+\beta -m(t)t^{\alpha -\beta +1}}&=\frac{2}{\beta +1}\frac{t^{\beta +1}+1}{t^{\beta +1}-1}. \end{aligned}$$

(8.17)

Strict inequality holds in (8.3) if and only if

$$\begin{aligned} \beta [t^{\beta +2}-1]+(\beta +2)t[t^\beta -1]<0, \end{aligned}$$

and this holds as $-1<\beta <0$ and $t>1$. Equality holds if $(\alpha ,\beta )=(0,0)$. $\square$

For $(\alpha ,\beta )\in \mathcal {P}$ and $0<a<b<\infty$ define

$$\begin{aligned} \hat{m}&=\hat{m}(a,b)=\hat{m}_{\alpha ,\beta }(a,b):=(\alpha +2)\frac{b^{\beta +1}+a^{\beta +1}}{b^{\alpha +2}-a^{\alpha +2}}. \end{aligned}$$

(8.18)

The corresponding homogeneity property reads

$$\begin{aligned} \hat{m}(a,b)&=a^{-(\alpha -\beta +1)}\hat{m}(t), \end{aligned}$$

(8.19)

where $t:=b/a>1$ and $\hat{m}(t):=\hat{m}(1,t)$.

Proposition 8.9

Let $(\alpha ,\beta )\in \mathcal {P}\setminus \mathcal {P}^-$ and $0<a<b<\infty$ and define $\hat{m}$ as in (8.18). Then

$$\begin{aligned} \hat{m}&<2\frac{\beta +1}{b^{\alpha -\beta +1}-a^{\alpha -\beta +1}}. \end{aligned}$$

Proof

By homogeneity it suffices to show that

$$\begin{aligned} (\alpha +2)\frac{t^{\beta +1}+1}{t^{\alpha +2}-1}<2\frac{\beta +1}{t^{\alpha -\beta +1}-1}, \end{aligned}$$

for each $t>1$. This is equivalent to the inequality

$$\begin{aligned} \frac{\alpha +2}{\beta +1}\Big \{t^{\alpha +2}-1+t^{\alpha -\beta +1}-t^{\beta +1}\Big \} <2(t^{\alpha +2}-1). \end{aligned}$$

Now $\alpha <2\beta$ as $(\alpha ,\beta )\not \in \mathcal {P}^-$ so $\frac{\alpha +2}{\beta +1}<2$ and $0<\alpha -\beta +1<\beta +1$. This proves the result. $\square$

9 Some Integral Inequalities

Recall that the generalised curvature of the boundary of a spherical cap isoperimetric minimiser can be expressed in terms of the function u as in Theorem 7.3. In this Section we study solutions to the differential equation (7.8) subject to two types of Dirichlet boundary condition on a bounded open interval in $(0,\infty )$. The function u determines the angular coordinate as in Lemma 7.4. We obtain estimates for these angular integrals. The main results of this Section are Corollarys 9.5, 9.11 and Corollary 9.14.

Let $\mathscr {L}$ stand for the collection of Lebesgue measurable sets in $[0,\infty )$. Define a measure $\mu$ on $([0,\infty ),\mathscr {L})$ by $\mu (dx):=(1/x)\,\mathrm{{d}}x$. Let $0\le a<b<\infty$. Suppose that $u:[a,b]\rightarrow \mathbb {R}$ is an $\mathscr {L}^1$-measurable function with the property that

$$\begin{aligned} \mu (\{u>t\})&<\infty \text { for each }t>0. \end{aligned}$$

(9.1)

The distribution function $\mu _u:(0,\infty )\rightarrow [0,\infty )$ of u with respect to $\mu$ is given by

$$\begin{aligned} \mu _u(t):=\mu (\{u>t\})\text { for }t>0. \end{aligned}$$

Note that $\mu _u$ is right-continuous and non-increasing on $(0,\infty )$ and $\mu _u(t)\rightarrow 0$ as $t\rightarrow \infty$.

Let $0<a<b<\infty$ and $(\alpha ,\beta )\in \mathcal {P}$. Let $\eta \in \{\pm 1\}^2$. We study solutions $(u,\lambda )$ to the first-order linear ordinary differential equation

$$\begin{aligned} u^\prime +(\beta +1)\tau ^{-1}u+\lambda \tau ^{\alpha -\beta }&=0 \text { on }(a,b)\text { with }u(a)=\eta _1\text { and }u(b)=\eta _2, \end{aligned}$$

(9.2)

where $u\in C^1([a,b])$ and $\lambda \in \mathbb {R}$. In case $(\alpha ,\beta )=(0,0)$ we use the notation $u_0$. This latter is given explicitly by

$$\begin{aligned} u_0(\tau )&=\frac{1}{b-a}\Big \{\tau -\frac{ab}{\tau }\Big \}, \end{aligned}$$

(9.3)

for $\tau \in [a,b]$ and $u_0$ is strictly increasing on [a, b].

Lemma 9.1

Let $(\alpha ,\beta )\in \mathcal {P}$ and $0<a<b<\infty$. Let $\eta \in \{\pm 1\}^2$. Then

• (i) there exists a solution $(u,\lambda )$ of (9.2) with u real analytic and $\lambda =\lambda _\eta \in \mathbb {R}$;

• (ii) the pair $(u,\lambda )$ in (i) is unique;

• (iii) $\lambda _\eta$ is given by

  $$\begin{aligned}&-\lambda _{(1,1)}=\lambda _{(-1,-1)}=m;\,\lambda _{(1,-1)}=-\lambda _{(-1,1)}=\hat{m}; \end{aligned}$$

  with m resp. $\hat{m}$ as in (8.1) resp. (8.18);

• (iv) if $\eta =(1,1)$ or $\eta =(-1,-1)$ then u is uniformly bounded away from zero on [a, b].

Proof

(i) Multiplying by an integrating factor we may rewrite the ordinary differential equation in (9.2) in the form $(\tau ^{\beta +1}u)^\prime +\lambda \tau ^{\alpha +1}=0$ and hence

$$\begin{aligned}&u=\tau ^{-\beta -1}\Big \{c-\frac{\lambda }{\alpha +2}\tau ^{\alpha +2}\Big \}, \end{aligned}$$

(9.4)

for real constants c and $\lambda$. Fitting the boundary conditions we derive

$$\begin{aligned} \lambda&=-m=-(\alpha +2)\frac{b^{\beta +1}-a^{\beta +1}}{b^{\alpha +2}-a^{\alpha +2}}; \end{aligned}$$

(9.5)

$$\begin{aligned} c&=-\frac{m}{\alpha +2}a^{\alpha +2}+a^{\beta +1}; \end{aligned}$$

(9.6)

in case $\eta =(1,1)$ while

$$\begin{aligned} \lambda&=-\hat{m}=-(\alpha +2)\frac{a^{\beta +1}+b^{\beta +1}}{b^{\alpha +2}-a^{\alpha +2}}; \end{aligned}$$

(9.7)

$$\begin{aligned} c&=-\frac{\hat{m}}{\alpha +2}b^{\alpha +2}+b^{\beta +1}; \end{aligned}$$

(9.8)

in case $\eta =(-1,1)$. Similar expressions hold in cases $\eta =(-1,-1)$ and $\eta =(1,-1)$ by linearity. (ii) We consider the case $\eta =(1,1)$. Suppose that $(u_1,\lambda _1)$ resp. $(u_2,\lambda _2)$ solve (9.2). By linearity $u:=u_1-u_2$ solves

$$\begin{aligned} u^\prime +(\beta +1)\tau ^{-1}u+\lambda \tau ^{\alpha -\beta }=0 \text { on }(a,b) \text { with }u(a)=u(b)=0, \end{aligned}$$

where $\lambda =\lambda _1-\lambda _2$. So u takes the form (9.4) for some real constants c and $\lambda$ and the boundary conditions entail that these vanish. The other cases are similar. (iii) follows as in (i). (iv) If $\eta =(1,1)$ then $u>0$ on [a, b] as $c+\frac{m}{\alpha +2}a^{\alpha +2}=a^{\beta +1}>0$. $\square$

The boundary condition $\eta _1\eta _2=-1$.

Lemma 9.2

Let $(\alpha ,\beta )\in \mathcal {P}\setminus \mathcal {P}^-$ and $0<a<b<\infty$. Let $(u,\lambda )$ solve (9.2) with $\eta =(-1,1)$. Put $v:=-u$. Then

• (i) $u^\prime >0$ on [a, b];

• (ii) $\int _{\{v=1\}}\frac{1}{|v^\prime |}\frac{\mathrm{{d}}\mathscr {H}^0}{\tau } < \int _{\{u=1\}}\frac{1}{|u^\prime |}\frac{\mathrm{{d}}\mathscr {H}^0}{\tau }$.

Proof

(i) Write the derivative as $u^\prime =-(\beta +1)\tau ^{-1}u+\hat{m}\tau ^{\alpha -\beta }$ and replace u with the expression in (9.4). Strict positivity of the derivative is equivalent to the condition

$$\begin{aligned} -b^{\alpha +2}\frac{\hat{m}}{\alpha +2}+b^{\beta +1}<\frac{\alpha -\beta +1}{(\alpha +2)(\beta +1)}\tau ^{\alpha +2}\hat{m}, \end{aligned}$$

on substituting the expression for u in (9.4), (9.7) and (9.8). After inserting the definition (8.18) for $\hat{m}$ the left-hand side above becomes

$$\begin{aligned} -\frac{(ab)^{\beta +1}}{b^{\alpha +2}-a^{\alpha +2}}\Big (a^{\alpha -\beta +1}+b^{\alpha -\beta +1}\Big ), \end{aligned}$$

which is plainly negative. This leads to the statement.

(ii) From (9.2),

$$\begin{aligned} \tau u^\prime =-(\beta +1)u+\hat{m}\tau ^{\alpha -\beta +1}, \end{aligned}$$

and in particular,

$$\begin{aligned} bu^\prime (b)&=-(\beta +1)+\hat{m}b^{\alpha -\beta +1}>-(\beta +1)+m b^{\alpha -\beta +1} >0, \end{aligned}$$

as $\hat{m}>m$ and by Lemma 8.3. On the other hand,

$$\begin{aligned} av^\prime (a)&=-au^\prime (a)=-\beta -1-a^{\alpha -\beta +1}\hat{m}<0. \end{aligned}$$

Then

$$\begin{aligned} \int _{\{v=1\}}\frac{1}{|v^\prime |}\frac{\mathrm{{d}}\mathscr {H}^0}{\tau } - \int _{\{u=1\}}\frac{1}{|u^\prime |}\frac{\mathrm{{d}}\mathscr {H}^0}{\tau }&= \frac{1}{au^\prime (a)}-\frac{1}{bu^\prime (b)}\\&=\frac{1}{\beta +1+a^{\alpha -\beta +1}\hat{m}} -\frac{1}{-\beta -1+\hat{m}b^{\alpha -\beta +1}}\\&=\frac{-2(\beta +1)+\hat{m}(b^{\alpha -\beta +1}-a^{\alpha -\beta +1})}{ (\beta +1+\hat{m}a^{\alpha -\beta +1})(-\beta -1+\hat{m}b^{\alpha -\beta +1}) }<0, \end{aligned}$$

by Proposition 8.9. $\square$

Theorem 9.3

Let $(\alpha ,\beta )\in \mathcal {P}\setminus \mathcal {P}^-$ and $0<a<b<\infty$. Let $(u,\lambda )$ solve (9.2) with $\eta =(-1,1)$. Put $v:=-u$. Then

• (i) $-\mu _u^\prime (t)=\int _{\{u=t\}}\frac{1}{|u^\prime |}\frac{\mathrm{{d}}\mathscr {H}^0}{\tau }$ for each $t\in (0,1)$;

• (ii) $-\mu _v^\prime <-\mu _u^\prime$ on (0, 1).

Proof

(i) As $u^\prime >0$ on [a, b] according to Lemma 9.2 the function u possesses a $C^1$ inverse $u^{-1}:[-1,1]\rightarrow [a,b]$. This allows us to write

$$\begin{aligned} \mu _u(t)&=\mu (\{u>t\})=\mu ((u^{-1}(t),b])=\log \Big (\frac{b}{u^{-1}(t)}\Big ), \end{aligned}$$

for $t>1$ and further

$$\begin{aligned} \mu _u^\prime (t)&=-\frac{1}{(\tau u^\prime )(u^{-1}(t))}=-\int _{\{u=t\}}\frac{1}{|u^\prime |}\frac{\mathrm{{d}}\mathscr {H}^0}{\tau }. \end{aligned}$$

(ii) Let $t\in (0,1)$. Put $c:=\min \{v\le t\}=\min \{u\ge -t\}$ and $d:=\min \{u\ge t\}$. By continuity, $a<c<d<b$. Put $\widetilde{u}:=u/t$ and $\widetilde{v}:=v/t$ on [c, d]. Then

$$\begin{aligned} \widetilde{u}^\prime +(\beta +1)\tau ^{-1}\widetilde{u}-(\hat{m}/t)\tau ^{\alpha -\beta }&=0\text { on }(c,d)\text { and }-\widetilde{u}(c)=\widetilde{u}(d)=1;\\ \widetilde{v}^\prime +(\beta +1)\tau ^{-1}\widetilde{v}+(\hat{m}/t)\tau ^{\alpha -\beta }&=0\text { on }(c,d)\text { and }\widetilde{v}(c)=-\widetilde{v}(d)=1. \end{aligned}$$

By Lemma 9.2,

$$\begin{aligned} \int _{\{v=t\}}\frac{1}{|v^\prime |}\frac{\mathrm{{d}}\mathscr {H}^0}{\tau }&=\int _{[c,d]\cap \{v=t\}}\frac{1}{|v^\prime |}\frac{\mathrm{{d}}\mathscr {H}^0}{\tau } =(1/t)\int _{[c,d]\cap \{\widetilde{v}=1\}}\frac{1}{|\widetilde{v}^\prime |}\frac{\mathrm{{d}}\mathscr {H}^0}{\tau }\\&<(1/t)\int _{[c,d]\cap \{\widetilde{u}=1\}}\frac{1}{|\widetilde{u}^\prime |}\frac{\mathrm{{d}}\mathscr {H}^0}{\tau } =\int _{\{u=t\}}\frac{1}{|u^\prime |}\frac{\mathrm{{d}}\mathscr {H}^0}{\tau }. \end{aligned}$$

The claim now follows with the help of (i). $\square$

Corollary 9.4

Let $(\alpha ,\beta )\in \mathcal {P}\setminus \mathcal {P}^-$ and $0<a<b<\infty$. Let $(u,\lambda )$ solve (9.2) with $\eta =(-1,1)$. Put $v:=-u$. Then

$$\begin{aligned} \mu _u(t)>\mu _v(t) for each t\in (0,1). \end{aligned}$$

Proof

By Theorem 9.3,

$$\begin{aligned} \mu _u(t)=\mu _u(t)-\mu _u(1)=-\int _{(t,1]}\mu _u^\prime \,\mathrm{{d}}s, \end{aligned}$$

for each $t\in (0,1)$ as $\mu _u(1)=0$. On the other hand,

$$\begin{aligned} \mu _v(t)=\mu _v(1)+(\mu _v(t)-\mu _v(1)) =\mu _v(1)-\int _{(t,1]}\mu _v^\prime \,\mathrm{{d}}s=-\int _{(t,1]}\mu _v^\prime \,\mathrm{{d}}s, \end{aligned}$$

for each $t\in (0,1)$. The claim follows from Theorem 9.3. $\square$

Corollary 9.5

Let $(\alpha ,\beta )\in \mathcal {P}\setminus \mathcal {P}^-$ and $0<a<b<\infty$. Let $(u,\lambda )$ solve (9.2) with $\eta =(-1,1)$. Let $\varphi \in C^1((-1,1))$ be an odd strictly increasing function with $\varphi \in L^1((-1,1))$. Then

• (i) $\int _{\{u>0\}}\varphi (u)\,\mathrm{{d}}\mu <\infty$;

• (ii) $\int _a^b\varphi (u)\,\mathrm{{d}}\mu >0$;

and in particular,

• (iii) $\int _a^b\frac{u}{\sqrt{1-u^2}}\,\mathrm{{d}}\mu >0$.

Proof

(i) The function u is $C^1$ and $u^\prime$ is bounded away from 0 on [a, b] by Lemma 9.2. Put $I:=\{0<u<1\}$. The restriction of u to the interval I has $C^1$ inverse $v:(0,1)\rightarrow I$ with derivative $v^\prime =1/(u^\prime \circ v)$ and $|v^\prime |$ is uniformly bounded on (0, 1). By a change of variables,

$$\begin{aligned} \int _{\{u>0\}}\varphi (u)\,\mathrm{{d}}\mu&=-\int _0^1\varphi (v^\prime /v)\,\mathrm{{d}}t, \end{aligned}$$

from which the claim is apparent. (ii) The integral is well defined because $\varphi (u)^+=\varphi (u)\chi _{\{u>0\}}\in L^1((a,b),\mu )$ by (i). The set $\{u=0\}$ consists of a singleton and has $\mu$-measure zero. So

$$\begin{aligned} \int _a^b\varphi (u)\,\mathrm{{d}}\mu&=\int _{\{u>0\}}\varphi (u)\,\mathrm{{d}}\mu +\int _{\{u<0\}}\varphi (u)\,\mathrm{{d}}\mu =\int _{\{u>0\}}\varphi (u)\,\mathrm{{d}}\mu -\int _{\{v>0\}}\varphi (v)\,\mathrm{{d}}\mu , \end{aligned}$$

where $v:=-u$ as $\varphi$ is an odd function. We remark that in a similar way as above,

$$\begin{aligned} \int _0^1\varphi ^\prime \mu _u\,\mathrm{{d}}t=\int _{\{u>0\}}\Big \{\varphi (u)-\varphi (0)\Big \}\,\mathrm{{d}}\mu =\int _{\{u>0\}}\varphi (u)\,\mathrm{{d}}\mu , \end{aligned}$$

using oddness of $\varphi$ and an analogous formula holds with v in place of u. Thus, we may write

$$\begin{aligned} \int _a^b\varphi (u)\,\mathrm{{d}}\mu&=\int _0^1\varphi ^\prime \mu _u\,\mathrm{{d}}t-\int _0^1\varphi ^\prime \mu _v\,\mathrm{{d}}t =\int _0^1\varphi ^\prime \Big \{\mu _u-\mu _v\Big \}\,\mathrm{{d}}t>0, \end{aligned}$$

by Corollary 9.4 as $\varphi ^\prime >0$ on (0, 1). (iii) follows from (ii) with the particular choice $\varphi :(-1,1)\rightarrow \mathbb {R};t\mapsto t/\sqrt{1-t^2}$. $\square$

The boundary condition $\eta _1\eta _2=1$. Let $(\alpha ,\beta )\in \mathcal {P}$ and $0<a<b<\infty$. In this subsection study solutions $(w,\lambda )$ of the auxilliary Riccati equation

$$\begin{aligned} w^\prime +\lambda \tau ^{\alpha -\beta }w^2&=\frac{\beta +1}{\tau }w \text { on }(a,b)\text { with }w(a)=w(b)=1; \end{aligned}$$

(9.9)

with w a $C^1$ function on [a, b] and $\lambda \in \mathbb {R}$. If $(\alpha ,\beta )=(0,0)$ then we write $w_0$ instead of w. Suppose $(u,\lambda )$ solves (9.2) with $\eta =(1,1)$. Then $u>0$ on [a, b] by Lemma 9.1 and we may set $w:=1/u$. Then $(w,-\lambda )$ satisfies (9.9).

Lemma 9.6

Let $0<a<b<\infty$ and $(\alpha ,\beta )\in \mathcal {P}$. Then

• (i) there exists a solution $(w,\lambda )$ of (9.9) with w real analytic and $\lambda \in \mathbb {R}$;

• (ii) the pair $(w,\lambda )$ in (i) is unique;

• (iii) $\lambda =m$ with m as in (8.1).

Proof

(i) With c as in (9.6),

$$\begin{aligned} c+\frac{m}{\alpha +2}\tau ^{\alpha +2}\ge c+\frac{m}{\alpha +2}a^{\alpha +2}=a^{\beta +1}>0, \end{aligned}$$

for $\tau \in [a,b]$. It, therefore, makes sense to define $w:[a,b]\rightarrow \mathbb {R}$ by

$$\begin{aligned} w&:=\frac{\tau ^{\beta +1}}{c+\frac{m}{\alpha +2}\tau ^{\alpha +2}}. \end{aligned}$$

(9.10)

Then w is real analytic on [a, b] and (w, m) satisfies (9.9). (ii) We claim that $w>0$ on [a, b] for any solution $(w,\lambda )$ of (9.9). For otherwise, $c:=\min \{w=0\}\in (a,b)$. Then $u:=1/w$ on [a, c) satisfies

$$\begin{aligned} u^\prime +\frac{\beta +1}{\tau }u+\lambda \tau ^{\alpha -\beta }=0 \text { on }(a,c) \text { and }u(a)=1, u(c-)=\infty . \end{aligned}$$

Integrating, we obtain

$$\begin{aligned} \tau ^{\beta +1}u-a^{\beta +1}+\frac{\lambda }{\alpha +2}\Big [\tau ^{\alpha +2}-a^{\alpha +2}\Big ]=0\text { on }[a,c), \end{aligned}$$

and this entails the contradiction that $u(c-)<\infty$. We may now use the uniqueness statement in Lemma 9.1. (iii) follows from (ii) and the particular solution given in (i). $\square$

Lemma 9.7

Let $(\alpha ,\beta )\in \mathcal {P}\setminus \mathcal {P}^-$ and $0<a<b<\infty$. Let $(w,\lambda )$ solve (9.9). Then

• (i) $w^\prime (a)>0$ and $w^\prime (b)<0$;

• (ii) $w>1$ on (a, b);

• (iii) w is unimodal;

• (iv) $\int _{\{w=1\}}\frac{1}{|w^\prime |}\frac{\mathrm{{d}}\mathscr {H}^0}{\tau }>2\coth (\mu ((a,b))/2).$

Proof

(i) follows from Lemma 8.3. (ii) The inequality $w(\tau )>1$ may be rewritten in the form $m_{\alpha ,\beta }(a,\tau )>m_{\alpha ,\beta }(a,b)=m$ upon making use of the expression for w given in (9.10). This last inequality is a consequence of Lemma 8.3. (iii) The reciprocal $u:=1/w$ satisfies (9.2) with $\eta =(1,1)$. The derivative of u vanishes at a point $\tau$ characterised by the condition

$$\begin{aligned} \tau ^{\alpha +2}=\frac{(\alpha +2)(\beta +1)}{\alpha -\beta +1}\frac{c}{m}. \end{aligned}$$

It can be shown using Lemma 8.3 that $\tau \in (a,b)$. It follows that w is unimodal. (iv) By Theorem 8.1,

$$\begin{aligned} \int _{\{w=1\}}\frac{1}{|w^\prime |}\frac{\mathrm{{d}}\mathscr {H}^0}{\tau }&=\frac{1}{1+\beta -ma^{\alpha -\beta +1}}-\frac{1}{1+\beta -mb^{\alpha -\beta +1}} >2\frac{a+b}{b-a}\\&=2\coth (\mu ((a,b))/2). \end{aligned}$$

$\square$

Theorem 9.8

Let $(\alpha ,\beta )\in \mathcal {P}\setminus \mathcal {P}^-$ and $0<a<b<\infty$. Let $(w,\lambda )$ solve (9.9). Then for each $t\in (1,\Vert w\Vert _\infty )$,

• (i) $-\mu _w^\prime =\int _{\{w=t\}}\frac{1}{|w^\prime |}\frac{\mathrm{{d}}\mathscr {H}^0}{\tau }$;

• (ii) $-\mu _w^\prime >(2/t)\coth ((1/2)\mu _w)$.

Proof

(i) This follows from the unimodality property of w in Lemma 9.7. Let c be the unique point in (a, b) such that $w^\prime (c)=0$. The $C^1$ functions $w_1:[a,c]\rightarrow [1,\Vert w\Vert _\infty ]$ resp. $w_2:[c,b]\rightarrow [1,\Vert w\Vert _\infty ]$ have $C^1$ inverses $v_1:[1,\Vert w\Vert _\infty ]\rightarrow [a,c]$ resp. $v_2:[1,\Vert w\Vert _\infty ]\rightarrow [c,b]$. Then

$$\begin{aligned} \mu _w(t)=\mu ((v_1(t),v_2(t))=\log \Big (\frac{v_2(t)}{v_1(t)}\Big ), \end{aligned}$$

and

$$\begin{aligned} \mu _w^\prime (t)=\frac{v_2^\prime (t)}{v_2(t)}-\frac{v_1^\prime (t)}{v_1(t)} =\frac{1}{(\tau w)^\prime (v_2(t))}-\frac{1}{(\tau w)^\prime (v_1(t))} =-\int _{\{w=t\}}\frac{1}{|w^\prime |}\frac{\mathrm{{d}}\mathscr {H}^0}{\tau }, \end{aligned}$$

for each $t\in (1,\Vert w\Vert _\infty )$. (ii) Let $t\in (1,\Vert w\Vert _\infty )$. Put $\widetilde{w}:=w/t$ on $\overline{\{w>t\}}$ so

$$\begin{aligned} \widetilde{w}^\prime +(mt)\tau ^{\alpha -\beta }\widetilde{w}^2&=\frac{\beta +1}{\tau }\widetilde{w} \text { on }\{w>t\}\text { and }\widetilde{w}=1\text { on }\{w=t\}. \end{aligned}$$

By Lemma 9.7,

$$\begin{aligned} (0,\infty )\ni \int _{\{w=t\}}\frac{1}{|w^\prime |}\frac{\mathrm{{d}}\mathscr {H}^0}{\tau }&=(1/t)\int _{\{\widetilde{w}=1\}}\frac{1}{|\widetilde{w}^\prime |}\frac{\mathrm{{d}}\mathscr {H}^0}{\tau }\\&>(2/t)\coth ((1/2)\mu (\{\widetilde{w}>1\}))\\&=(2/t)\coth ((1/2)\mu _w(t)). \end{aligned}$$

The statement now follows from (i). $\square$

We introduce the mapping

$$\begin{aligned} \omega :(0,\infty )\times (0,\infty )\rightarrow \mathbb {R};(t,x)\mapsto -(2/t)\coth (x/2). \end{aligned}$$

For $\xi >0$,

$$\begin{aligned} |\omega (t,x)-\omega (t,y)|&\le \textrm{cosech}^2[\xi /2](1/t)|x-y|, \end{aligned}$$

(9.11)

for $(t,x),(t,y)\in (0,\infty )\times (\xi ,\infty )$ and $\omega$ is locally Lipschitzian in x on $(0,\infty )\times (0,\infty )$ in the sense of [24] I.3. Let $0<a<b<\infty$ and set $\lambda :=A/G>1$. Here, $A=A(a,b)$ stands for the arithmetic mean of a, b as introduced in the previous Section while $G=G(a,b):=\sqrt{|ab|}$ stands for their geometric mean. We refer to the inital value problem

$$\begin{aligned} z^\prime =\omega (t,z)\text { on }(0,\lambda ) \text { and }z(1)=\mu ((a,b)). \end{aligned}$$

(9.12)

Define

$$\begin{aligned} z_0:(0,\lambda )\rightarrow \mathbb {R};t\mapsto 2\log \Big \{\frac{\lambda +\sqrt{\lambda ^2-t^2}}{t}\Big \}. \end{aligned}$$

Lemma 9.9

Let $0<a<b<\infty$. Then

• (i) $w_0(\tau )=\frac{2A\tau }{G^2+\tau ^2}$ for $\tau \in [a,b]$;

• (ii) $\Vert w_0\Vert _\infty =\lambda$;

• (iii) $\mu _{w_0}=z_0$ on $[1,\lambda )$;

• (iv) $z_0$ satisfies (9.12) and this solution is unique;

• (v) $\int _{\{w_0=1\}}\frac{1}{|w_0^\prime |}\,\frac{\mathrm{{d}}\mathscr {H}^0}{\tau }=2\coth (\mu ((a,b))/2)$;

• (vi) $\int _a^b\frac{1}{\sqrt{w_0^2-1}}\,\frac{dx}{x}=\pi$.

Proof

(i) Note that

$$\begin{aligned} m_0=\frac{1+ab}{a+b}. \end{aligned}$$

(i) follows from the representation of $w_0$ in Lemma 9.6 by direct computation. (ii) follows by calculus. (iii) follows by solving the quadratic equation $t\tau ^2-2A\tau +G^2t=0$ for $\tau$ with $t\in (0,\lambda )$. Uniqueness in (iv) follows from [24] Theorem 3.1 as $\omega$ is locally Lipschitzian with respect to x in $(0,\infty )\times (0,\infty )$. For (v) note that $|aw_0^\prime (a)|=1-a/A$ and $|bw_0^\prime (b)|=b/A-1$ and

$$\begin{aligned} 2\coth (\mu ((a,b))/2)=2(a+b)/(b-a). \end{aligned}$$

(vi) We may write

$$\begin{aligned} \int _a^b\frac{1}{\sqrt{w_0^2-1}}\,\frac{\mathrm{{d}}\tau }{\tau }&=\int _a^b\frac{ab+\tau ^2}{\sqrt{(a+b)^2\tau ^2-(ab+\tau ^2)^2}} \frac{\mathrm{{d}}\tau }{\tau }=\int _a^b\frac{ab+\tau ^2}{\sqrt{(\tau ^2-a^2)(b^2-\tau ^2)}} \frac{\mathrm{{d}}\tau }{\tau }. \end{aligned}$$

The substitution $s=\tau ^2$ followed by the Euler substitution (cf. [23] 2.251) $\sqrt{(s-a^2)(b^2-s)}=t(s-a^2)$ gives

$$\begin{aligned} \int _a^b\frac{1}{\sqrt{w_0^2-1}}\,\frac{\mathrm{{d}}\tau }{\tau }&=\int _0^\infty \frac{1}{1+t^2}+\frac{ab}{b^2+a^2t^2}\,\mathrm{{d}}t=\pi . \end{aligned}$$

$\square$

Theorem 9.10

Let $(\alpha ,\beta )\in \mathcal {P}\setminus \mathcal {P}^-$ and $0<a<b<\infty$. Let $(w,\lambda )$ solve (9.9). Then

• (i) $\Vert w\Vert _\infty \le \Vert w_0\Vert _\infty$;

• (ii) $\mu _w(t)<\mu _{w_0}(t)$ for each $t\in (1,\Vert w\Vert _\infty )$.

Proof

(i) From the inequality in Theorem 9.8 we infer that $\mu _w^\prime \le \omega (t,\mu _w)$ on $[1,\Vert w\Vert _\infty ]$ and $\mu _w(1)=\mu ([a,b])$. In virtue of Lemma 9.9, $\mu _{w_0}^\prime =\omega (t,\mu _{w_0})$ on $[1,\Vert w_0\Vert _\infty ]$ and $\mu _{w_0}(1)=\mu ([a,b])$. Put $T:=\min \{\Vert w_0\Vert _\infty ,\Vert w\Vert _\infty \}$. By [24] Theorem 6.1 we deduce that $\mu _w\le \mu _{w_0}$ on [1, T]. This implies that $\Vert w\Vert _\infty \le \Vert w_0\Vert _\infty$. (ii) From Theorem 9.8 we see that $\mu _w^\prime <\omega (t,\mu _w)\le \omega (t,\mu _{w_0})=\mu _{w_0}^\prime$ on $(1,\Vert w\Vert _\infty )$ using the observation that the function $\omega (t,z)$ is strictly increasing in its second argument. This establishes the second claim. $\square$

Corollary 9.11

Let $(\alpha ,\beta )\in \mathcal {P}\setminus \mathcal {P}^-$ and $0<a<b<\infty$. Let $(w,\lambda )$ solve (9.9). Let $0\le \varphi \in C^1((1,\infty ))$ be strictly decreasing with $\int _a^b\varphi (w_0)\,\mathrm{{d}}\mu <\infty$. Then

• (i) $\int _a^b\varphi (w)\,\mathrm{{d}}\mu >\int _a^b\varphi (w_0)\,\mathrm{{d}}\mu$;

and in particular,

• (ii) $\int _a^b\frac{1}{\sqrt{w^2-1}}\,\mathrm{{d}}\mu >\pi$.

Proof

(i) Let $\varphi \ge 0$ be a decreasing function on $(1,\infty )$ which is piecewise $C^1$. Suppose that $\varphi (1+)<\infty$. By Tonelli’s Theorem,

$$\begin{aligned} \int _{(1,\infty )}\varphi ^\prime \mu _w\,\mathrm{{d}}s&=\int _{(1,\infty )}\varphi ^\prime \Big \{\int _{(a,b)}\chi _{\{w>s\}}\,\mathrm{{d}}\mu \Big \}\,\mathrm{{d}}s\\&=\int _{(a,b)}\Big \{\int _{[1,\infty )}\varphi ^\prime \chi _{\{w>s\}}\,\mathrm{{d}}s\Big \}\,\mathrm{{d}}\mu \\&=\int _{(a,b)}\Big \{\varphi (w)-\varphi (1)\Big \}\,\mathrm{{d}}\mu =\int _{(a,b)}\varphi (w)\,\mathrm{{d}}\mu -\varphi (1)\mu ((a,b)), \end{aligned}$$

and a similar identity holds for $\mu _{w_0}$. By Theorem 9.10, $\int _a^b\varphi (w)\,\mathrm{{d}}\mu \ge \int _a^b\varphi (w_0)\,\mathrm{{d}}\mu$. Strict inequality holds if $\varphi$ is nonconstant on $(1,\Vert w\Vert _\infty )$. Now suppose that $\varphi \ge 0$ is a decreasing piecewise $C^1$ function on $(1,\infty )$ with $\int _a^b\varphi (w_0)\,\mathrm{{d}}\mu <\infty$. The inequality holds for the truncated function $\varphi \wedge n$ for each $2\le n\in \mathbb {N}$. An application of the monotone convergence theorem establishes the result result that

$$\begin{aligned} \int _a^b\varphi (w)\,\mathrm{{d}}\mu \ge \int _a^b\varphi (w_0)\,\mathrm{{d}}\mu , \end{aligned}$$

for such $\varphi$.

Let $0\le \varphi \in C^1((1,\infty ))$ be strictly decreasing with $\int _a^b\varphi (w_0)\,\mathrm{{d}}\mu <\infty$. Suppose that equality holds for this $\varphi$. For $c\in (1,\infty )$ put $\varphi _1:=\varphi \vee \varphi (c)-\varphi (c)$ and $\varphi _2:=\varphi \wedge \varphi (c)$. Choose $c\in (1,\Vert w\Vert _\infty )$. By the results of the last paragraph,

$$\begin{aligned} \int _a^b\varphi _1(w)\,\mathrm{{d}}\mu \ge \int _a^b\varphi _1(w_0)\,\mathrm{{d}}\mu \text { while } \int _a^b\varphi _2(w)\,\mathrm{{d}}\mu >\int _a^b\varphi _2(w_0)\,\mathrm{{d}}\mu . \end{aligned}$$

By linearity,

$$\begin{aligned} \int _a^b\varphi _2(w)\,\mathrm{{d}}\mu&=\int _a^b\varphi _1(w)\,\mathrm{{d}}\mu +\int _a^b\varphi _2(w)\,\mathrm{{d}}\mu \\&>\int _a^b\varphi _1(w_0)\,\mathrm{{d}}\mu +\int _a^b\varphi _2(w_0)\,\mathrm{{d}}\mu =\int _a^b\varphi _2(w_0)\,\mathrm{{d}}\mu . \end{aligned}$$

$\square$

The case $a=0$. Let $0<b<\infty$ and $(\alpha ,\beta )\in \mathcal {P}$. We study solutions to the first-order linear ordinary differential equation

$$\begin{aligned} u^\prime +(\beta +1)\tau ^{-1}u+\lambda \tau ^{\alpha -\beta }&=0 \text { on }(0,b)\text { with }u(0)=0\text { and }u(b)=1, \end{aligned}$$

(9.13)

where $u\in C^2([0,b])$ and $\lambda \in \mathbb {R}$. In case $(\alpha ,\beta )=(0,0)$ we use the notation $u_0$.

Lemma 9.12

Let $0<b<\infty$ and $(\alpha ,\beta )\in \mathcal {P}$. The problem (9.13) admits the unique solution

$$\begin{aligned} u(\tau ):=(\tau /b)^{\alpha -\beta +1}\text { for }\tau \in [0,b], \end{aligned}$$

and $\lambda :=-\frac{\alpha +2}{b^{\alpha -\beta +1}}$.

Proof

It is straightforward to check that the pair $(u,\lambda )$ is a solution to (9.13). Let us check uniqueness. Suppose that $(u_1,\lambda _1)$ resp. $(u_2,\lambda _2)$ solve (9.13). By linearity $u:=u_1-u_2$ solves

$$\begin{aligned} u^\prime +(\beta +1)\tau ^{-1}u+\lambda \tau ^{\alpha -\beta }=0 \text { on }(0,b)\text { with }u(0)=0\text { and }u(b)=0, \end{aligned}$$

where $\lambda =\lambda _1-\lambda _2$. Making use of an integrating factor the zero function solves this problem uniquely. $\square$

Lemma 9.13

Let $0<b<\infty$. Then $\int _0^b\frac{u_0}{\sqrt{1-u_0^2}}\,\mathrm{{d}}\mu =\pi /2$.

Proof

The integral is elementary as $u_0(t)=t/b$ for $t\in [0,b]$. $\square$

Corollary 9.14

Let $0<b<\infty$ and $(\alpha ,\beta )\in \mathcal {P}$. Let $(u,\lambda )$ satisfy (9.13). Then

$$\begin{aligned} \int _0^b\frac{u}{\sqrt{1-u^2}}\,\mathrm{{d}}\mu =\frac{\pi }{2\gamma }. \end{aligned}$$

Proof

This follows directly from Lemmas 9.12 and 9.13. $\square$

10 A Beta Function Inequality

Recall from [23] 8.380 that the beta function is defined by

$$\begin{aligned} B(x,y)&:=\int _0^1 t^{x-1}(1-t)^{y-1}\,\mathrm{{d}}t, \end{aligned}$$

(10.1)

for $x,y>0$. The goal of the present Section is to prove the following theorem. This is used in (11.7) to show that a natural competitor domain (spherical cap symmetric whose boundary has a singularity at the origin) is not an isoperimetric minimiser.

Theorem 10.1

For $x\ge 1/2$,

$$\begin{aligned} W(x):=\sqrt{2x}\Big (1+\frac{1}{2x}\Big )^{2x}B(x,1/2)\ge 2\pi , \end{aligned}$$

and equality holds only at $x=1/2$.

Define a function

$$\begin{aligned} \phi (x)&:=\frac{1}{x}-\log x+\psi (x). \end{aligned}$$

(10.2)

for $x>0$ where $\psi$ stands for the digamma function (cf. [1] 6.3) and the logarithm refers to the natural logarithm. According to Binet’s first formula for the logarithm of the gamma function (cf. [37] 12 31),

$$\begin{aligned} \log \Gamma (x)=(x-\frac{1}{2})\log x-x+\frac{1}{2}\log (2\pi )+\int _0^\infty \Big (\frac{1}{2}-\frac{1}{t}+\frac{1}{e^t-1}\Big )\frac{e^{-tx}}{t}\,\mathrm{{d}}t, \end{aligned}$$

for any $x>0$. The partial derivative of the integrand with respect to x is integrable on $(0,\infty )$ so differentiation yields the identity

$$\begin{aligned} \phi (x)&=\int _0^\infty \Big (\frac{1}{t}-\frac{1}{e^t-1}\Big )e^{-tx}\,\mathrm{{d}}t, \end{aligned}$$

(10.3)

for each $x>0$. From this representation it can be seen that the function $\phi$ is positive and completely monotonic; and in particular $\phi$ is convex and strictly decreasing.

Define

$$\begin{aligned} w(x)&:=\phi (x)-\phi (x+1/2)+\log \Big (1+\frac{1}{2x}\Big )-\frac{1}{2x}, \end{aligned}$$

(10.4)

for $x>0$ with $\phi$ as above. A computation reveals that

$$\begin{aligned} \frac{W^\prime }{W}=(\log W)^\prime =w, \end{aligned}$$

on $(0,\infty )$ so that

$$\begin{aligned} (\log W)(x)-(\log W)(1/2)=\int _{1/2}^x w\,\mathrm{{d}}y, \end{aligned}$$

and

$$\begin{aligned} \frac{W(x)}{W(1/2)}=e^{\int _{1/2}^x w\,\mathrm{{d}}y}, \end{aligned}$$

for each $x\ge 1/2$. There are two steps in the proof of Theorem 10.1. We first show in Proposition 10.5 that the integral in the exponent above is positive for $x\ge 1$. In the second step we show that the function w is positive on (1/2, 1) in Proposition 10.9 (see Fig. 7). This gives the conclusion of the Theorem.

Fig. 7

Graph of the function w on the interval [1/2, 20]

Lemma 10.2

For $x\ge 1/2$,

$$\begin{aligned} \int _{1/2}^x w\,\mathrm{{d}}y&=\int _0^\infty \frac{1}{t}\Big (e^{-t/2}-e^{-tx}\Big )\Big [\frac{1}{t}-\frac{1}{e^t-1} +\frac{1}{2}\Big \{\frac{1}{t/2}-\frac{1}{e^{t/2}-1}\Big \}-\frac{1}{2}\Big ]\\&\quad \Big (1-e^{-t/2}\Big )\,\mathrm{{d}}t. \end{aligned}$$

Proof

Note that

$$\begin{aligned} \int _{1/2}^x e^{-ty}\,\mathrm{{d}}y&=\frac{e^{-t/2}-e^{-tx}}{t}, \end{aligned}$$

and

$$\begin{aligned} \int _{1/2}^x e^{-t(y+1/2)}\,\mathrm{{d}}y&=e^{-t/2}\frac{e^{-t/2}-e^{-tx}}{t}, \end{aligned}$$

for $1/2\le x$. From (10.3) and the above,

$$\begin{aligned} \int _{1/2}^x\phi (y)-\phi (y+1/2)\,\mathrm{{d}}y&=\int _0^\infty \Big (\int _{1/2}^x e^{-ty}-e^{-t(y+1/2)}\,\mathrm{{d}}y\Big )\Big (\frac{1}{t}-\frac{1}{e^t-1}\Big )\,\mathrm{{d}}t.\nonumber \\&=\int _0^\infty \frac{1}{t}\Big (e^{-t/2}-e^{-tx}\Big )\Big (\frac{1}{t}-\frac{1}{e^t-1}\Big )\Big (1-e^{-t/2}\Big )\,\mathrm{{d}}t. \end{aligned}$$

(10.5)

On the other hand for $y>0$,

$$\begin{aligned} \log (y+1/2)-\log y&=\int _y^{y+1/2}\frac{1}{t}\,\mathrm{{d}}t=\int _y^{y+1/2}\int _0^\infty e^{-\tau t}\,\mathrm{{d}}\tau \,\mathrm{{d}}t\\&=\int _0^\infty \int _y^{y+1/2}e^{-\tau t}\,\mathrm{{d}}t\,\mathrm{{d}}\tau =\int _0^\infty \frac{e^{-\tau y}-e^{-\tau (y+1/2)}}{\tau }\,\mathrm{{d}}\tau , \end{aligned}$$

We continue

$$\begin{aligned} \int _{1/2}^x\log \Big (1+\frac{1}{2y}\Big )\,\mathrm{{d}}y&=\int _{1/2}^x\log (y+1/2)-\log y\,\mathrm{{d}}y\nonumber \\&=\int _{1/2}^x \int _0^\infty \frac{e^{-\tau y}-e^{-\tau (y+1/2)}}{\tau }\,\mathrm{{d}}\tau \,\mathrm{{d}}y\nonumber \\&=\int _0^\infty \int _{1/2}^x\frac{e^{-\tau y}-e^{-\tau (y+1/2)}}{\tau }\,\mathrm{{d}}y\,\mathrm{{d}}\tau \nonumber \\&=\int _0^\infty \frac{1}{t^2}\Big (e^{-t/2}-e^{-tx}\Big )\Big (1-e^{-t/2}\Big )\,\mathrm{{d}}t. \end{aligned}$$

(10.6)

Finally,

$$\begin{aligned} \int _{1/2}^x\frac{1}{2y}\,\mathrm{{d}}y&=\frac{1}{2}\int _{1/2}^x\int _0^\infty e^{-ty}\,\mathrm{{d}}t\,\mathrm{{d}}y =\frac{1}{2}\int _0^\infty \int _{1/2}^xe^{-ty}\,\mathrm{{d}}y\,\mathrm{{d}}t\nonumber \\&=\frac{1}{2}\int _0^\infty \frac{1}{t}\Big (e^{-t/2}-e^{-tx}\Big )\mathrm{{d}}t. \end{aligned}$$

(10.7)

From (10.5), (10.6) and (10.7),

$$\begin{aligned} \int _{1/2}^x w\,\mathrm{{d}}y&=\int _{1/2}^x\phi (y)-\phi (y+1/2)+\log \Big (1+\frac{1}{2y}\Big )-\frac{1}{2y}\,\mathrm{{d}}y\\&=\int _0^\infty \frac{1}{t}\Big (e^{-t/2}-e^{-tx}\Big )\Big (\frac{2}{t}-\frac{1}{e^t-1}\Big )\Big (1-e^{-t/2}\Big )\,\mathrm{{d}}t\\&\quad -\frac{1}{2}\int _0^\infty \frac{e^{-t/2}-e^{-tx}}{t}\,\mathrm{{d}}t\\&=\int _0^\infty \frac{1}{t}\Big (e^{-t/2}-e^{-tx}\Big )\Big [\Big (\frac{2}{t}-\frac{1}{e^t-1}\Big )\Big (1-e^{-t/2}\Big )-\frac{1}{2}\Big ]\,\mathrm{{d}}t\\&=\int _0^\infty \frac{1}{t}\Big (e^{-t/2}-e^{-tx}\Big )\Big [\frac{1}{t}-\frac{1}{e^t-1} +\frac{1}{t}-\frac{1}{2(1-e^{-t/2})}\Big ]\Big (1-e^{-t/2}\Big )\,\mathrm{{d}}t\\&=\int _0^\infty \frac{1}{t} \Big (e^{-t/2}-e^{-tx}\Big )\Big [\frac{1}{t}-\frac{1}{e^t-1} +\frac{1}{2}\Big \{\frac{1}{t/2}-\frac{1}{e^{t/2}-1}\Big \}-\frac{1}{2}\Big ]\\&\quad \Big (1-e^{-t/2}\Big )\,\mathrm{{d}}t, \end{aligned}$$

as in the statement of the Theorem. $\square$

Define

$$\begin{aligned} h:[0,\infty )\rightarrow \mathbb {R};t\mapsto \left\{ \begin{array}{cl} \frac{1}{t}-\frac{1}{e^t-1} &{} \text { for }t>0;\\ \frac{1}{2} &{} \text { for }t=0; \end{array} \right. \end{aligned}$$

and

$$\begin{aligned} \rho (t)&:=h(t)+\frac{1}{2}h(t/2)-\frac{1}{2}, \end{aligned}$$

(10.8)

for $t\ge 0$.

Lemma 10.3

It holds that

• (i) $\cosh t\le \Big (\frac{\sinh t}{t}\Big )^3$ for each $t>0$;

• (ii) h is continuous and convex on $[0,\infty )$;

• (iii) $\rho$ is continuous and convex on $[0,\infty )$ with exactly one root;

• (iv) $\rho >0$ on [0, 5/2].

Proof

(i) This reduces to the inequality

$$\begin{aligned} \sum _{p=0}^\infty \frac{t^{2p}}{(2p)!}\le \sum _{p=0}^\infty \Big \{\sum _{k+l+m=p}\frac{1}{(2k+1)!(2l+1)!(2m+1)!}\Big \}t^{2p}, \end{aligned}$$

for each $t\ge 0$ after writing in power series. The inequality can be seen after comparing like coefficients. (ii) Continuity at the origin is straightforward. A computation leads to the identity

$$\begin{aligned} h^{\prime \prime }(t)=\frac{2}{t^3}-\frac{1}{4}\frac{\cosh (t/2)}{\sinh ^3(t/2)}, \end{aligned}$$

for each $t>0$. The right-hand side is nonnegative by (i). (iii) The last item entails that the function $\rho$ is convex. Note that $\rho (0)=1/4$ and $\rho (t)\rightarrow -1/2$ as $t\rightarrow \infty$. It follows that $\rho$ has exactly one root. (iv) A calculation shows that $\rho (5/2)>0$. $\square$

We now record two integral identities for later use. First,

$$\begin{aligned}&\int _0^\infty \frac{1}{t}\Big (e^{-t/2}-e^{-tx}\Big )\Big (1-e^{-t/2}\Big )\,\mathrm{{d}}t\nonumber \\&\quad = \int _0^\infty \Big \{ \int _0^\infty e^{-t\tau }\,\mathrm{{d}}\tau \Big \} \Big (e^{-t/2}-e^{-tx}\Big )\Big (1-e^{-t/2}\Big )\,\mathrm{{d}}t\nonumber \\&\quad = \int _0^\infty \Big \{ \int _0^\infty e^{-t\tau } \Big (e^{-t/2}-e^{-tx}\Big )\Big (1-e^{-t/2}\Big )\,\mathrm{{d}}t \Big \}\,\mathrm{{d}}\tau \nonumber \\&\quad = \int _0^\infty \frac{1}{\tau +1/2}-\frac{1}{\tau +1}-\frac{1}{\tau +x}+\frac{1}{\tau +x+1/2}\,\mathrm{{d}}\tau \nonumber \\&\quad =-\log \Big (\frac{x+1/2}{2x}\Big ) =\log \Big (1+\frac{x-1/2}{x+1/2}\Big ). \end{aligned}$$

(10.9)

Secondly,

$$\begin{aligned} \int _0^\infty \Big (e^{-t/2}-e^{-tx}\Big )\Big (1-e^{-t/2}\Big )\,\mathrm{{d}}t&=\frac{x^2+(1/2)x-1/2}{x(x+1/2)}. \end{aligned}$$

(10.10)

Lemma 10.4

For $x\ge 1$,

$$\begin{aligned} \log \Big (1+\frac{x-1/2}{x+1/2}\Big )\ge \frac{2x^2+x-1}{5x(x+1/2)}>0. \end{aligned}$$

Proof

We bound the logarithm from below using the estimate

$$\begin{aligned} \log (1+y)\ge \frac{2y}{2+y}, \end{aligned}$$

for $y\ge 0$ which follows by the Hermite-Hadamard inequality. The resulting algebraic inequality holds if $x^3-x+1/8\ge 0$ and this cubic is positive on $[1,\infty )$. $\square$

Proposition 10.5

For $x\ge 1$,

$$\begin{aligned} \int _{1/2}^x w\,\mathrm{{d}}y&>0. \end{aligned}$$

Proof

Fix $x\ge 1$. We introduce the probability measure $\mathbb {P}$ on $(0,\infty )$ given by

$$\begin{aligned} \mathbb {P}_x(\mathrm{{d}}\tau )= \frac{\frac{1}{\tau }\Big (e^{-\tau /2}-e^{-\tau x}\Big )\Big (1-e^{-\tau /2}\Big )\,\mathrm{{d}}\tau }{\int _0^\infty \frac{1}{t}\Big (e^{-t/2}-e^{-tx}\Big )\Big (1-e^{-t/2}\Big )\,\mathrm{{d}}t}, \end{aligned}$$

and define the random variable $X:(0,\infty )\rightarrow \mathbb {R}$ via $t\mapsto t$. From (10.9) and (10.10) the expectation of X under $\mathbb {P}$ is given by

$$\begin{aligned} Y:=\mathbb {E}X&= \frac{\int _0^\infty \Big (e^{-t/2}-e^{-tx}\Big )\Big (1-e^{-t/2}\Big )\,\mathrm{{d}}t}{\int _0^\infty \frac{1}{t}\Big (e^{-t/2}-e^{-tx}\Big )\Big (1-e^{-t/2}\Big )\,\mathrm{{d}}t} =\frac{\frac{x^2+(1/2)x-1/2}{x(x+1/2)}}{\log \Big (1+\frac{x-1/2}{x+1/2}\Big )}. \end{aligned}$$

By Lemma 10.2, Lemma 10.3 and Jensen’s inequality,

$$\begin{aligned} \frac{\int _{1/2}^x w\,\mathrm{{d}}y}{\log \Big (1+\frac{x-1/2}{x+1/2}\Big )}&=\mathbb {E}\Big [\rho (X)\Big ] \ge \rho (\mathbb {E}[X])=\rho (Y). \end{aligned}$$

By Lemma 10.3, $\rho >0$ on the interval [0, 5/2]; on the other hand, $Y\le 5/2$ by Lemma 10.4. This leads to the result. $\square$

We now turn to the second step in the proof of Theorem 10.1. Recall from [1] 6.4.10,

$$\begin{aligned} \frac{\psi ^{(n)}(x)}{n!}=(-1)^{n+1}\zeta (x,n+1), \end{aligned}$$

for each $x>0$. For $a>0$ and $s>1$,

$$\begin{aligned} \zeta (a,s):=\sum _{p=0}^\infty \frac{1}{(a+p)^s}, \end{aligned}$$

is the Hurwitz zeta function. For $|h|<1/2$,

$$\begin{aligned} \psi (1/2+h)&=\sum _{k=0}^\infty \frac{\psi ^{(k)}(1/2)}{k!}h^k =\psi (1/2)+\sum _{k=1}^\infty (-1)^{k+1}\zeta (1/2,k+1)h^k; \end{aligned}$$

(10.11)

$$\begin{aligned} \psi (1+h)&=\sum _{k=0}^\infty \frac{\psi ^{(k)}(1)}{k!}h^k=\psi (1)+\sum _{k=1}^\infty (-1)^{k+1}\zeta (1,k+1)h^k . \end{aligned}$$

(10.12)

Lemma 10.6

Suppose that f is a positive strictly decreasing function of class $C^1$ defined on $[0,\infty )$ and suppose that both f and $f^\prime$ are integrable. Then

$$\begin{aligned} \sum _{j=1}^\infty \Big \{f(j)-f(j+1/2)\Big \}&=\frac{1}{2}f(1/2)+\frac{1}{2}\sum _{j=0}^\infty (-1)^j\Big \{f(j/2+1)-f(j/2+1/2)\Big \}. \end{aligned}$$

Proof

By the Euler summation formula (see [4] Theorem 3.1 for example),

$$\begin{aligned} \sum _{j=1}^\infty \Big \{f(j)-f(j+1/2)\Big \}&=\int _0^\infty \Big \{f(t)-f(t+1/2)\Big \}\,\mathrm{{d}}t\\&\quad +\int _0^\infty \{t\}\Big [f^\prime (t)-f^\prime (t+1/2)\Big ]\,\mathrm{{d}}t\\&=\int _0^{1/2}f(t)\,\mathrm{{d}}t+\int _0^\infty \{t\}\Big [f^\prime (t)-f^\prime (t+1/2)\Big ]\,\mathrm{{d}}t, \end{aligned}$$

where we use the notation $\{t\}:=t-[t]$ for $t\ge 0$ and $[\cdot ]$ refers to the integer part. Let us observe that for any $t\ge 0$,

$$\begin{aligned} \{t+1/2\}-\{t\}= \left\{ \begin{array}{rcl} 1/2 &{} \text { if } &{} \frac{j}{2}\le t\le \frac{j+1}{2} \text { and }j\in \mathbb {Z}\text { is even};\\ -1/2 &{} \text { if } &{} \frac{j}{2}< t\le \frac{j+1}{2} \text { and }j\in \mathbb {Z}\text { is odd}.\\ \end{array} \right. \end{aligned}$$

Concentrating on the last member in the expression for the sum,

$$\begin{aligned} \int _0^\infty \{t\}\Big [f^\prime (t)-f^\prime (t+1/2)\Big ]\,\mathrm{{d}}t&=\int _0^\infty \{t\}f^\prime (t)-\{t+1/2\}f^\prime (t+1/2)\\&\quad +\Big [\{t+1/2\}-\{t\}\Big ]f^\prime (t+1/2)\,\mathrm{{d}}t \\&=\int _0^{1/2} tf^\prime (t)\,\mathrm{{d}}t+\sum _{j=0}^\infty \int _{\frac{j}{2}}^{\frac{j+1}{2}}\\&\quad \Big [\{t+1/2\}-\{t\}\Big ]f^\prime (t+1/2)\,\mathrm{{d}}t\\&=\int _0^{1/2} tf^\prime (t)\,\mathrm{{d}}t+\frac{1}{2}\sum _{j=0}^\infty (-1)^j\\&\quad \int _{\frac{j}{2}}^{\frac{j+1}{2}}f^\prime (t+1/2)\,\mathrm{{d}}t\\&=\int _0^{1/2} tf^\prime (t)\,\mathrm{{d}}t+\frac{1}{2}\sum _{j=0}^\infty (-1)^j\\&\quad \Big \{f(j/2+1)-f(j/2+1/2)\Big \}. \end{aligned}$$

Lastly let us note that

$$\begin{aligned} \int _0^{1/2}f(t)+tf^\prime (t)\,\mathrm{{d}}t=\int _0^{1/2}(tf)^\prime \,\mathrm{{d}}t=\frac{1}{2}f(1/2). \end{aligned}$$

Combining this with the earlier identities gives the result. $\square$

Corollary 10.7

For $a>0$ and $s>1$,

$$\begin{aligned} \zeta (a,s)-\zeta (a+1/2,s)&= \frac{1}{a^s}-\frac{1}{2}\frac{1}{(a+1/2)^s}\\&\quad +\frac{1}{2}\sum _{j=0}^\infty (-1)^j \Big \{\frac{1}{(a+j/2+1)^s}-\frac{1}{(a+j/2+1/2)^s}\Big \}. \end{aligned}$$

Proof

First note that

$$\begin{aligned} \zeta (a,s)-\zeta (a+1/2,s)&= \frac{1}{a^s}-\frac{1}{(a+1/2)^s} +\sum _{j=1}^\infty \Big [\frac{1}{(a+j)^s}-\frac{1}{(a+1/2+j)^s}\Big ]. \end{aligned}$$

Now apply Lemma 10.6 with $f(t):=(a+t)^{-s}$ to the summation. $\square$

Lemma 10.8

For $|h|<1/2$,

$$\begin{aligned} w(1/2+h)&=2\log \Big (\frac{1+h}{1+2h}\Big )+\frac{h(6h+5)}{2(1+h)(1+2h)}\nonumber \\&\quad -2h\sum _{j=0}^\infty (-1)^j\frac{2j+5+2h}{(j+2)(j+3)(j+2+2h)(j+3+2h)}. \end{aligned}$$

(10.13)

Proof

Making use of the identities (10.11) and (10.12), an application of Corollary 10.7 yields the identity

$$\begin{aligned} \psi (1/2+h)-\psi (1+h)&=\psi (1/2)-\psi (1)+\frac{7h+6h^2}{(1+2h)(2+2h)}\\&-2h\sum _{j=0}^\infty (-1)^j\frac{2j+5+2h}{(j+2)(j+3)(j+2+2h)(j+3+2h)} \end{aligned}$$

after some careful calculation where $|h|<1/2$. We remark that

$$\begin{aligned} w(1/2)&=\psi (1/2)-\psi (1)+2\log 2=0, \end{aligned}$$

(10.14)

after substituting the $\psi$-values in [1] 6.3.2 and 6.3.3. Upon writing $x=1/2+h$ for $|h|<1/2$ we compute

$$\begin{aligned} w(x)&=\phi (x)-\phi (x+1/2)+\log \Big (1+\frac{1}{2x}\Big )-\frac{1}{2x}\\&=2\log \Big (1+\frac{1}{2x}\Big )+\frac{1}{2x}-\frac{1}{x+1/2}+\psi (x)-\psi (x+1/2)\\&=2\log \Big (\frac{2+2h}{1+2h}\Big )-\frac{h}{(1+h)(1+2h)}+\psi (1/2+h)-\psi (1+h)\\&=2\log \Big (\frac{2+2h}{1+2h}\Big )-\frac{h}{(1+h)(1+2h)}+\psi (1/2)-\psi (1)+\frac{7h+6h^2}{(1+2h)(2+2h)}\\&\quad -2h\sum _{j=0}^\infty (-1)^j\frac{2j+5+2h}{(j+2)(j+3)(j+2+2h)(j+3+2h)}\\&=2\log \Big (\frac{1+h}{1+2h}\Big )+\frac{h(6h+5)}{2(1+h)(1+2h)}\\&\quad -2h\sum _{j=0}^\infty (-1)^j\frac{2j+5+2h}{(j+2)(j+3)(j+2+2h)(j+3+2h)}, \end{aligned}$$

where we made use of (10.14) to obtain the last line. $\square$

Proposition 10.9

The function w is positive on the interval (1/2, 1).

Proof

For fixed h in (0, 1/2) the sequence $(a_j)_{j=0}^\infty$ with

$$\begin{aligned} a_j:=\frac{2j+5+2h}{(j+2)(j+3)(j+2+2h)(j+3+2h)}, \end{aligned}$$

is a strictly decreasing null sequence noting that $2j+5+2h=2(j+2+2h)+1-2h$. The alternating series in (10.13) is bounded above by its first term. We, thus, obtain

$$\begin{aligned} w(1/2+h)&\ge 2\log \Big (\frac{1+h}{1+2h}\Big )+\frac{h(6h+5)}{2(1+h)(1+2h)}-\frac{h(5+2h)}{6(1+h)(3+2h)}. \end{aligned}$$

We bound the logarithm from below using the estimate

$$\begin{aligned} \log (1+y)\ge \frac{y(2+y)}{2(1+y)}\text { for }-1<y\le 0. \end{aligned}$$

This follows from the Hermite–Hadamard inequality. Continuing,

$$\begin{aligned} w(1/2+h)&\ge -\frac{h(2+3h)}{(1+h)(1+2h)}+\frac{h(6h+5)}{2(1+h)(1+2h)}-\frac{h(5+2h)}{6(1+h)(3+2h)}\\&=\frac{2h(2+h)(1/2-h)}{3(1+h)(1+2h)(3+2h)}>0, \end{aligned}$$

for $0<h<1/2$. $\square$

11 An Isoperimetric Competitor

There is a natural candidate for isoperimetric minimiser in problem (1.2) which is not a centred ball. This candidate set is spherical cap symmetric and its boundary contains the origin but this fails to be of class $C^1$ there. Our task here is to show that this candidate is not isoperimetric.

Let $(\alpha ,\beta )\in \mathcal {P}$ and $b>0$. As in Lemma 9.12 the constant generalised curvature equation $(\tau ^{\beta +1}u)^\prime +\lambda \tau ^{\alpha +1}=0$ on (0, b) with boundary conditions $u(0)=0$ and $u(b)=1$ has the unique solution $u(\tau )=(\tau /b)^\gamma$ for $\tau \in [0,b]$ where we write $\gamma :=\alpha -\beta +1$. Put

$$\begin{aligned} \theta (\tau )&:=\int _\tau ^b\frac{u}{\sqrt{1-u^2}}\,\mathrm{{d}}\mu = \int _{\tau /b}^1\frac{t^{\gamma -1}}{\sqrt{1-t^{2\gamma }}}\,\mathrm{{d}}t, \end{aligned}$$

(11.1)

for $\tau \in [0,b]$. This angular coordinate may be expressed in more explicit form. Let us explain this briefly - though we do not make further use of this fact. On substituting $s=t^\gamma$ we obtain

$$\begin{aligned} \theta (\tau )=\frac{1}{2\gamma }\int _0^{1-(\tau /b)^{2\gamma }}\frac{\mathrm{{d}}s}{\sqrt{s(1-s)}}. \end{aligned}$$

At this point let us note the integral identity

$$\begin{aligned} \int _x^{1/2}\frac{\mathrm{{d}}s}{\sqrt{s(1-s)}}&=\frac{\pi }{2}-\textrm{arcsin}\sqrt{4x(1-x)}, \end{aligned}$$

(11.2)

which holds for $0\le x\le 1/2$. This can be seen using the substitution $\sqrt{s(1-s)}=z$ as in [23] 2.292. Making use of this last identity (11.2) we alight on a more explicit formula

$$\begin{aligned} \theta (\tau&)= \left\{ \begin{array}{rl} \frac{1}{2\gamma }\Big (\pi -\textrm{arcsin}\Big [2(\tau /b)^\gamma \sqrt{1-(\tau /b)^{2\gamma }}\Big ]\Big ) &{} \text { if }0\le (\tau /b)^{2\gamma }\le 1/2;\\ \frac{1}{2\gamma }\textrm{arcsin}\Big [2(\tau /b)^\gamma \sqrt{1-(\tau /b)^{2\gamma }}\Big ] &{} \text { if }1/2<(\tau /b)^{2\gamma }\le 1; \end{array} \right. \end{aligned}$$

(11.3)

for $\theta (\tau )$. It can be seen that $\theta (0)=\frac{\pi }{2\gamma }$ (though this also follows from the first equality in (11.1) using the substitution $t^\gamma =\sin \theta$).

Fig. 8

Plot of the set E in (11.4) with $\gamma =1/2$ and $b=1$. Its boundary has a cusp at 0. In case $1/2<\gamma <1$ there is a Lipschitz singularity at 0. If $\gamma =1$ and $b=1$ then E is a ball with centre (1/2, 0) and tangent to the origin

In the remainder of this subsection we shall assume that $1/2\le \gamma <1$ so that $\theta (0)\in (\pi /2,\pi ]$. Define the open set

$$\begin{aligned} E&:=\{(\tau \cos \phi ,\tau \sin \phi ):0<\tau<b\text { and }|\phi |<\theta (\tau )\}\subset \mathbb {R}^2_0, \end{aligned}$$

(11.4)

with $\theta$ defined as in (11.1). For $1/2\le \gamma <1$ the boundary of E fails to be $C^1$ at the origin as $\theta (0)\in (\pi /2,\pi ]$. See Fig. 8. Incidentally, the regularity result for an isoperimetric minimiser in [29] 3.10 fails to apply in this setting because the metric $\zeta =r^{\gamma -1}$ has a singularity at the origin and the density $\psi =r^{2\beta -\alpha }$ vanishes at the origin.

Let us now compute the weighted perimeter and volume of the set E. From Lemma 7.4 and Lemma 9.12,

$$\begin{aligned} P_\beta (E)&=2\int _0^b\sqrt{1+t^2(\theta ^\prime )^2}t^\beta \,\mathrm{{d}}t =2b^{\beta +1}\int _0^1\frac{t^\beta }{\sqrt{1-t^{2\gamma }}}\,\mathrm{{d}}t =\frac{b^{\beta +1}}{\gamma }B(x,1/2), \end{aligned}$$

where the beta function is defined as in (10.1) and $x:=\frac{\beta +1}{2\gamma }$. Turning to the weighted volume,

$$\begin{aligned} V_\alpha (E)&=2\int _0^b\theta t^{\alpha +1}\,\mathrm{{d}}t=-2\int _0^b\theta ^\prime \frac{t^{\alpha +2}}{\alpha +2}\,\mathrm{{d}}t =2\int _0^b\frac{1}{t}\frac{(t/b)^\gamma }{\sqrt{1-(t/b)^{2\gamma }}}\frac{t^{\alpha +2}}{\alpha +2}\,\mathrm{{d}}t\\&=\frac{b^{\alpha +2}}{(\alpha +2)\gamma }B(x+1,1/2) =\frac{b^{\alpha +2}}{(2x+1)\gamma ^2}B(x+1,1/2), \end{aligned}$$

with x as before using the relation $\alpha +2=(2x+1)\gamma$. By the recurrence relation for the beta function $B(x+1,1/2)=\frac{x}{x+1/2}B(x,1/2)$ we may write

$$\begin{aligned} V_\alpha (E)&=\frac{b^{\alpha +2}}{\gamma ^2}\frac{2x}{(2x+1)^2}B(x,1/2). \end{aligned}$$

Let us notice here that the ratio

$$\begin{aligned} \frac{P_\beta (E)^{\alpha +2}}{V_\alpha (E)^{\beta +1}}&=\gamma ^{2\beta -\alpha }\Big [\frac{(2x+1)^2}{2x}\Big ]^{\beta +1}B(x,1/2)^\gamma , \end{aligned}$$

(11.5)

does not depend on the choice of b.

Now let B stand for the open centred ball in $\mathbb {R}^2_0$ with radius $r>0$. Then the isoperimetric ratio

$$\begin{aligned} \frac{P_\beta (B)^{\alpha +2}}{V_\alpha (B)^{\beta +1}}&=(2\pi )^\gamma (\alpha +2)^{\beta +1} =(2\pi )^\gamma \gamma ^{\beta +1}(2x+1)^{\beta +1}, \end{aligned}$$

(11.6)

is likewise scale invariant. The main claim of this subsection is that

$$\begin{aligned} \frac{P_\beta (E)^{\alpha +2}}{V_\alpha (E)^{\beta +1}}&>\frac{P_\beta (B)^{\alpha +2}}{V_\alpha (B)^{\beta +1}}. \end{aligned}$$

(11.7)

From (11.5) and (11.6) this holds if and only if

$$\begin{aligned} \gamma ^{-1}\Big (1+\frac{1}{2x}\Big )^{2x}B(x,1/2)&>2\pi . \end{aligned}$$

(11.8)

Comparing the definition of $\zeta$ in (8.10) with the expression for x above we see that $\zeta =2x$. In other words, the expression x which depends on $(\alpha ,\beta )$ in $\mathscr {P}$ is constant on the graph of the line $\ell _{2x}$. From Lemma 8.7, $\gamma$ attains its maximum where the graph of $\ell _{2x}$ meets $\mathcal {P}^+$. Denote this point by $(\overline{\alpha },\overline{\beta })$ as before. The pair $(\overline{\alpha },\overline{\beta })$ satisfies the simultaneous equations

$$\begin{aligned} \left\{ \begin{array}{rcl} \alpha (\beta +1)&{}=&{}\beta ^2;\\ \alpha +2&{}=&{}[1+\frac{1}{2x}](\beta +1).\\ \end{array} \right. \end{aligned}$$

Eliminating $\alpha$ we see that $\overline{\beta }+1=\sqrt{2x}$ using positivity of $\beta +1$ and $\overline{\gamma }=\frac{1}{\sqrt{2x}}$ appealing to the identity $\beta +1=(2x)\gamma$.

Now take $(\alpha ,\beta )\in \mathcal {P}\setminus \mathcal {P}^-$ with $1/2\le \gamma <1$. Then

$$\begin{aligned} \gamma ^{-1}\Big (1+\frac{1}{2x}\Big )^{2x}B(x,1/2)&\ge \overline{\gamma }^{-1}\Big (1+\frac{1}{2x}\Big )^{2x}B(x,1/2)\\&=\sqrt{2x}\Big (1+\frac{1}{2x}\Big )^{2x}B(x,1/2)=W(x), \end{aligned}$$

in the notation of Theorem 10.1. By Lemma 8.7, $\zeta =2x\ge 1$ so that $x\ge 1/2$. The case $x=1/2$ corresponds to $\zeta =1$ and $\alpha =2\beta$ or in other words $(\alpha ,\beta )\in \mathcal {P}^-$ which we are here excluding so $x>1/2$. By Theorem 10.1 the right-hand side above is positive. This establishes the claim in (11.7).

12 A Necessary Condition for Spherical Cap Symmetry

In this short Section we record two results which will be used in the proof of Theorem 13.1; namely, Lemma 12.2 and Proposition 12.3.

Lemma 12.1

Let E be a bounded open set with $C^2$ boundary M in $\mathbb {R}^2_0$ and assume that $E=E^{sc}$. Put $R:=\sup \{|x|:x\in M\}>0$ and $x:=(R,0)$. Then the curvature of M at x satisfies the estimate $k(x)\ge 1/R$.

Proof

Let $\gamma _1:I\rightarrow M$ be a $C^2$ local parametrisation of $\gamma$ with $\gamma _1(0)=x$ as in Sect. 7. Put $r_1:=|\gamma _1|$. By [28] (2.9) (for example), $\dot{r}_1=\cos \sigma _1$ and differentiating once more $\ddot{r}_1=-\sin \sigma _1\Big (k_1-\frac{\sin \sigma _1}{r_1}\Big )$ on I using the decomposition $\sigma _1=\alpha _1-\theta _1$ and [28] (2.10). In particular, $\ddot{r}_1(0)=-k(x)+1/R$. As $r_1$ has a global maximum on I at $s=0$ it follows by the second derivative test that $-k(x)+1/R\le 0$. $\square$

Let

$$\begin{aligned} H:=\{x=(x_1,x_2)\in \mathbb {R}^2:x_2>0\}, \end{aligned}$$

stand for the open upper half-plane in $\mathbb {R}^2$.

Lemma 12.2

Let E be an open set with $C^2$ boundary $M:=\partial E\cap \mathbb {R}^2_0$ in $\mathbb {R}^2_0$. Assume that $E=E^{sc}$. Suppose

• (i) $x\in M\cap H$;

• (ii) $\sin (\sigma (x))=-1$.

Then $k(x)+1/a=0$ where $a:=|x|$.

Proof

Let $\gamma _1:I\rightarrow M$ be a $C^2$ parametrisation of M in a neighbourhood of x with $\gamma _1(0)=x$ as above. We use the same notation as before. At $s=0$, $\dot{r}_1(0)=0$ and $\ddot{r}_1(0)=k_1(0)+1/a$. By Taylor’s Theorem,

$$\begin{aligned} r_1(s)=r_1(0)+\dot{r}_1(0)s+\frac{\ddot{r}_1(c)}{2}s^2 =a-(1/2)s^2\Big (\sin \sigma _1\Big [k_1-\frac{\sin \sigma _1}{r_1}\Big ]\Big )(c), \end{aligned}$$

for $s\in I$ and some c between 0 and s. At $s=0$ the expression in round brackets takes the value $k(x)+1/a$. If $k(x)+1/a>0$ then $r_1>a$ in a neighbourhood of $s=0$. This contradicts spherical cap symmetry. If the expression $k(x)+1/a$ happens to be strictly negative on the other hand then the above expansion implies that $r_1<a$ near 0. This contradicts the fact that $r_1\ge a$ on $I\cap \{s<0\}$. This is because $\cos \sigma _1\le 0$ on I by [28] Lemma 5.4 as well as the above expression for the derivative of $r_1$. See Fig. 9. $\square$

Fig. 9

At the point $x\in \partial E$ the sine of $\sigma$ is $-1$. The inward unit normal to E at x is the vector n. The curvature at x is $-1/a$

Proposition 12.3

Let $(\alpha ,\beta )\in \mathcal {Q}$. Given $v>0$ let E be a minimiser of (1.2). Assume that E is a bounded open set with analytic boundary M in $\mathbb {R}^2_0$ and suppose that $E=E^{sc}$. Let $\lambda$ be as in Theorem 7.2. Then $\lambda <0$.

Proof

Let R be as in Lemma 12.1 and put $x:=(R,0)$ as before. By Lemma 12.1, $k(x)\ge 1/R$. By Theorem 7.2, $k(x)=-\frac{\beta }{R}-\lambda R^{\alpha -\beta }\ge 1/R$; that is, $\lambda \le -(\beta +1)R^{-\alpha +\beta -1}<0$. $\square$

13 Proof of Main Result

This Section contains the proof of Theorem 1.1. Recall the set $\Omega$ defined in (7.4). This set comprises all those radii where the boundary curve crosses the foliation of centred circles transversally. The first step in the proof is to show that this set is empty.

Theorem 13.1

Let $(\alpha ,\beta )\in \mathcal {P}\setminus \mathcal {P}^-$. Given $v>0$ let E be a bounded minimiser of (1.2). Assume that E is open in $\mathbb {R}^2_0$, $M:=\partial E\cap \mathbb {R}^2_0$ is an analytic hypersurface in $\mathbb {R}^2_0$ and $E=E^{\textrm{sc}}$. Then $\Omega =\emptyset$.

Proof

Suppose that $\Omega \ne \emptyset$. The set $\Omega$ is open in $(0,\infty )$ by [28] Lemma 5.6. So we may write $\Omega$ as a countable union of disjoint open intervals in $(0,\infty )$. By a suitable choice of one of these intervals we may assume that the interval (a, b) is a connected component of $\Omega$ for some $0\le a<b<\infty$. Let us assume for the time being that $a>0$. As M is analytic, $[a,b]\subset \pi (M)$ and $\cos \sigma$ vanishes on $M_a\cup M_b$. Let $\lambda \in \mathbb {R}$ be as in Theorem 7.2.

Let $u:\Omega \rightarrow [-1,1]$ be as in (7.7). Then u has a continuous extension to [a, b] and $u=\pm 1$ at $\tau =a,b$. This may be seen as follows. For $\tau \in (a,b)$ the set $M_\tau \cap H$ consists of a singleton by [28] Lemma 5.4. The limit $x:=\lim _{\tau \downarrow a}M_\tau \cap H\in \mathbb {S}_a\cap \overline{H}$ exists as the boundary M is analytic in $\mathbb {R}^2_0$. In other words, $\gamma (\tau )\rightarrow x$ as $\tau \downarrow a$. Observe that $\cos \sigma (x)=0$ by openness of $\Omega$ and hence $\sin \sigma (x)=\pm 1$. The tangent vector varies continuously along M. So $\sigma (\gamma (\tau ))\rightarrow \sigma (x)$ and hence $\sin (\sigma (\gamma (\tau )))\rightarrow \sin (\sigma (x))$ as $\tau \downarrow a$. This shows that $u\rightarrow \pm 1$ as $\tau \downarrow a$. The argument at b is similar.

Put $\eta _1:=u(a)$ and $\eta _2:=u(b)$. Let us consider the case $\eta =(\eta _1,\eta _2)=(1,1)$. Note that $u<1$ on (a, b) for otherwise $\cos (\sigma \circ \gamma )$ vanishes at some point in (a, b) contradicting the definition of $\Omega$. By Theorem 7.3 the pair $(u,\lambda )$ satisfies (9.2) with $\eta =(1,1)$. By Lemma 9.1, $u>0$ on [a, b]. Put $w:=1/u$. Then $(w,-\lambda )$ satisfies (9.9) and $w>1$ on (a, b). By Lemma 7.4,

$$\begin{aligned} \theta _2(b)-\theta _2(a)=\int _a^b\theta _2^\prime \,\mathrm{{d}}\tau =-\int _a^b\frac{u}{\sqrt{1-u^2}}\,\frac{\mathrm{{d}}\tau }{\tau } =-\int _a^b\frac{1}{\sqrt{w^2-1}}\,\frac{\mathrm{{d}}\tau }{\tau }. \end{aligned}$$

By Corollary 9.11, $|\theta _2(b)-\theta _2(a)|>\pi$. But this contradicts the definition of $\theta _2$ in (7.5) as $\theta _2$ takes values in $(0,\pi )$ on (a, b) according to [28] Lemma 5.4. If $\eta =(-1,-1)$ then $\lambda >0$ by Lemma 9.1; this contradicts Proposition 12.3.

Now let us consider the case $\eta =(-1,1)$. As before the limit $x:=\lim _{\tau \downarrow a}M_\tau \cap H\in \mathbb {S}_a\cap \overline{H}$ exists as M is $C^1$ in $\mathbb {R}^2_0$ and $u(a)=\sin \sigma (x)=-1$. Using the same formula as above, $\theta _2(b)-\theta _2(a)<0$ by Corollary 9.5. This means that $\theta _2(a)\in (0,\pi ]$. We may assume that $\theta _2(a)\in (0,\pi )$. For if $\theta _2(a)=\pi$ then $x=(-a,0)$ and the tangent vector to M at x is pointing into the upper half-plane. This implies that $\theta _2$ exceeds $\pi$ near a and contradicts the definition of $\theta _2$ in (7.5). We proceed on the basis of this assumption. By Theorem 7.2 the curvature at a is given by

$$\begin{aligned} k=\frac{\beta }{a}-\lambda a^{\alpha -\beta }=\frac{1}{a}\Big \{\beta -\lambda a^{\alpha -\beta +1}\Big \} =\frac{1}{a}\Big \{\beta +\hat{m}a^{\alpha -\beta +1}\Big \}, \end{aligned}$$

and

$$\begin{aligned} k+1/a=\frac{1}{a}\Big \{\beta +1+\hat{m}a^{\alpha -\beta +1}\Big \}>0. \end{aligned}$$

This contradicts Lemma 12.2. If $\eta =(1,-1)$ then $\lambda >0$ by Lemma 9.1. This contradicts Proposition 12.3.

Suppose finally that $a=0$. Then u satisfies the ordinary differential equation (7.8) on (0, b) for some $\lambda \in \mathbb {R}$. This may be rewritten $(\tau ^{\beta +1}u)^\prime +\lambda \tau ^{\alpha +1}=0$ or integrating

$$\begin{aligned} u+\frac{\lambda }{\alpha +2}\tau ^{\alpha -\beta +1}+c\tau ^{-(\beta +1)}=0\text { on }(0,b), \end{aligned}$$

for some constant $c\in \mathbb {R}$. The first two terms are bounded on (0, b) while the third is unbounded if $c\ne 0$. This entails that $c=0$ and hence that $u(0+)=0$.

Let us assume that $u(b)=1$. From the earlier part of the proof the set $\Omega$ coincides with (0, b). Notice that $\theta _2$ takes values in $(0,\pi )$ on (0, b). As in Sect. 11, $\theta (0+)=\frac{\pi }{2\gamma }$. If $\gamma \in (0,1/2)$ this last exceeds $\pi$ strictly. This contradicts the definition of $\theta _2$ because $\theta$ coincides with $\theta _2$. Suppose then that $\gamma \in [1/2,1)$. We claim that $\theta _2(b)=0$. Suppose for a contradiction that $\theta _2(b)\in (0,\pi )$. Then the boundary M of E in $\mathbb {R}^2_0$ includes a centred circular arc with radius b. From the parametric formulae [28] (2.9) and (2.10) (for example),

$$\begin{aligned} \frac{\mathrm{{d}}\tau }{\mathrm{{d}}\theta _2}=\frac{\dot{r}_1}{\dot{\theta }_1}=-\tau \frac{\sqrt{1-u^2}}{u}, \end{aligned}$$

on the image of (0, b) under $\theta _2$. By scale-invariance we may assume that $b=1$. We derive that

$$\begin{aligned} \frac{\mathrm{{d}}\tau }{\mathrm{{d}}\theta }= \left\{ \begin{array}{lcl} 0 &{} \text { if } &{} 0<\theta<\theta _2(b);\\ -\tau ^{1-\gamma }\sqrt{1-\tau ^{2\gamma }} &{} \text { if } &{}\theta _2(b)<\tau <\theta _2(0);\\ \end{array} \right. \end{aligned}$$

using Lemma 9.12. It is then apparent that the boundary M fails to be analytic at the point with polar coordinates $(b,\theta _2(b))$ which contradicts a hypothesis of the Theorem. This shows that $\theta _2(b)=0$. Let us continue with the argument. Let B stand for the centred ball which has the same weighted area as E. According to the claim in (11.7) the set B has smaller weighted perimeter compared to the set E. This contradicts the fact that E is an isoperimetric minimiser.

Now consider the case in which $u(b)=-1$. We may choose x in M in the closed upper half-plane; and in fact x may be chosen in the open upper half-pane H because of the condition $u(b)=-1$. By Theorem 7.2,

$$\begin{aligned} k-\frac{\beta }{b}+\lambda b^{\alpha -\beta }=0, \end{aligned}$$

at x. By Lemma 12.2, $k(x)=-1/b$. Substituting into the expression above we obtain that $\lambda =(\beta +1)b^{-\gamma }>0$. This contradicts Proposition 12.3. $\square$

Lemma 13.2

Let $(\alpha ,\beta )\in \mathcal {P}\setminus \mathcal {P}^-$. Given $v>0$ let E be a bounded minimiser of (1.2). Assume that E is open in $\mathbb {R}^2_0$, $M:=\partial E$ is an analytic hypersurface in $\mathbb {R}^2_0$ and $E=E^{sc}$. Then M consists of an at most countable union of disjoint centred circles which accumulate at the origin if at all.

Proof

The set E is open and bounded so $M\ne \emptyset$ and hence $\emptyset \ne \pi (M)=\pi (M)\setminus \Omega$ by Theorem 13.1. By definition of $\Omega$, $\cos \sigma =0$ on M. Let $0<\tau \in \pi (M)$. We claim that $M_\tau =\mathbb {S}_\tau$. Suppose for a contradiction that $M_\tau \ne \mathbb {S}_\tau$. By [28] Lemma 5.2, $M_\tau$ is the union of two closed spherical arcs in $\mathbb {S}_\tau$. Let x be a point on the boundary of one of these spherical arcs relative to $\mathbb {S}_\tau$. There exists an analytic parametrisation $\gamma _1:I\rightarrow M$ of M in a neighbourhood of x with $\gamma _1(0)=x$ with conventions as mentioned in Sect. 7. By [28] (2.9), $\dot{r}_1=0$ on I as $\cos \sigma _1=0$ on I because $\cos \sigma =0$ on M; that is, $r_1$ is constant on I. This means that $\gamma _1(I)\subset \mathbb {S}_\tau$. As the function $\sin \sigma _1$ is continuous on I it takes the value $\pm 1$ there. By [28] (2.10), $r_1\dot{\theta }_1=\sin \sigma _1=\pm 1$ on I. This means that $\theta _1$ is either strictly decreasing or strictly increasing on I. This entails that the point x is not a boundary point of $M_\tau$ in $\mathbb {S}_\tau$ and this proves the claim. $\square$

Proof of Theorem 1.1

The result follows from [32] Theorem 1.1 in case $(\alpha ,\beta )\in \mathcal {P}^-\setminus \{(0,0)\}$. Let us assume then that $(\alpha ,\beta )\in \mathcal {P}\setminus \mathcal {P}^-$.

Existence. By Corollary 6.12 the variational problem (1.2) admits a bounded minimiser E. By Theorem 7.1 we may assume that E is open in $\mathbb {R}^2_0$, $M:=\partial E$ is an analytic hypersurface in $\mathbb {R}^2_0$ and $E=E^{sc}$. By Lemma 13.2M consists of an at most countable union of disjoint centred circles which accumulate at the origin if at all. As such we may write

$$\begin{aligned} E=\bigcup _{h=0}^NA((a_{2h+1},a_{2h})), \end{aligned}$$

where $N\in \mathbb {N}\cup \{\infty \}$ and $\infty>a_0>a_1>\cdots>a_{2N}>a_{2N+1}>\cdots >0$. Define

$$\begin{aligned}&F:[0,\infty )\rightarrow \mathbb {R};t\mapsto V_\alpha (B(0,t))=2\pi \frac{t^{\alpha +2}}{\alpha +2}. \end{aligned}$$

Define the strictly increasing function

$$\begin{aligned}&J:[0,\infty )\rightarrow \mathbb {R};t\mapsto P_\beta (B(0,F^{-1}(t))=\Big [(2\pi )^\gamma (\alpha +2)^{\beta +1}\Big ]^{\frac{1}{\alpha +2}}t^{\frac{\beta +1}{\alpha +2}}. \end{aligned}$$

The function J is continuous, strictly increasing and $J(0)=0$. Put $t_h:=F(a_h)$ for $h=0,1,\ldots$. Then $\infty>t_0>t_1>\cdots >0$. Put $B:=B(0,r)$ where $r:=F^{-1}(v)$ so that $V_f(B)=v$. Note that

$$\begin{aligned} v=V_f(E)=\sum _{h=0}^N\Big \{F(a_{2h})-F(a_{2h+1})\Big \}=\sum _{h=0}^{2N+1}(-1)^{h}t_h. \end{aligned}$$

By [28] Lemma 10.5,

$$\begin{aligned} P_\beta (E)=2\pi \sum _{h=0}^{2N+1}a_h^{\beta +1}=\sum _{h=0}^{2N+1}J(t_h) \ge J\left( \sum _{h=0}^{2N+1}(-1)^h t_h\right) =J(v)=P_\beta (B). \end{aligned}$$

This shows that the centred ball B is a minimiser for (1.2).

Uniqueness. Let $v>0$ and E be any minimiser for (1.2); this is essentially bounded by Corollary 6.12. By Theorem 7.1 there exists an $\mathscr {L}^2$-measurable set $\widetilde{E}$ with the properties

• (a) $\widetilde{E}$ is a minimiser of (1.2);

• (b) $L_{\widetilde{E}}=L_E$ a.e. on $(0,\infty )$;

• (c) $\widetilde{E}$ is open with analytic boundary in $\mathbb {R}^2_0$;

• (d) $\widetilde{E}=\widetilde{E}^{\textrm{sc}}$.

Let B be the open centred ball with the property that $V_\alpha (B)=V_\alpha (E)=v$ and denote its radius by $r>0$. Suppose that $\widetilde{E}\setminus B\ne \emptyset$. By Lemma 13.2 there exists $t>r$ such that $\mathbb {S}_t\subset \widetilde{M}$. So $P_\beta (E)=P_\beta (\widetilde{E})\ge 2\pi t^{\beta +1}>2\pi r^{\beta +1}=P_\beta (B)$. This contradicts the fact that E is a minimiser for (1.2). Consequently, $\widetilde{E}=B$. We infer that $L_E=L_B$ a.e. on $(0,\infty )$; in particular, $|E\Delta B|=0$. This entails that E is equivalent to B. $\square$

14 On the Caffarelli–Kohn–Nirenberg Inequality

For $1\le p<\infty$ define

$$\begin{aligned} p^*:= \left\{ \begin{array}{rcl} \frac{2p}{2-p} &{} \text { if } &{} p<2;\\ \infty &{} \text { if } &{} p\ge 2.\\ \end{array} \right. \end{aligned}$$

Choose a and q with

$$\begin{aligned}&1<p<q<p^*, \end{aligned}$$

(14.1)

and

$$\begin{aligned}&a>1-\frac{2}{p}, \end{aligned}$$

(14.2)

and put

$$\begin{aligned} b&:=2\Big (\frac{1}{p}-\frac{1}{q}\Big )+a-1. \end{aligned}$$

(14.3)

According to a special case of the Caffarelli–Kohn–Nirenberg inequality [9] there exists a positive constant C with the property that

$$\begin{aligned} C\Vert |x|^b u\Vert _q&\le \Vert |x|^a|\nabla u|\Vert _p, \end{aligned}$$

(14.4)

for any $u\in C_c^\infty (\mathbb {R}^2)$.

Given $a\in \mathbb {R}$ the notation $\mu _a$ refers to the measure $|\cdot |^{a}\mathscr {L}^2$ on $\mathbb {R}^2_0$. For $u\in C_c^\infty (\mathbb {R}_0^2)$ define

$$\begin{aligned} \Vert u\Vert :=\Big (\int _{\mathbb {R}^2_0}|\nabla u|^p\,\mathrm{{d}}\mu _{ap}\Big )^{1/p}. \end{aligned}$$

This is a norm on $C_c^\infty (\mathbb {R}^2_0)$ because of (14.4). Let $\mathscr {D}^{1,p}(\mathbb {R}^2_0,\mu _{ap})$ stand for the abstract completion of $C_c^\infty (\mathbb {R}_0^2)$ with respect to this norm. This latter may be viewed as a subset of $L^q(\mathbb {R}^2_0,\mu _{bq})$. In this case the completion contains $C_c^\infty (\mathbb {R}^2)$ in an obvious sense. We may write

$$\begin{aligned} \mathscr {D}^{1,p}(\mathbb {R}^2_0,\mu _{ap})=\Big \{u\in L^q(\mathbb {R}^2_0,\mu _{bq}):u\text { is weakly differentiable and }|\nabla u|\in L^p(\mathbb {R}^2_0,\mu _{ap})\Big \}. \end{aligned}$$

The best constant in (14.4) is given by the relation

$$\begin{aligned} C^p=S(a,p,q)&:=\inf \Big \{\frac{\Vert |x|^a|\nabla u|\Vert _p^p}{\Vert |x|^b u\Vert _q^p}:u\in \mathscr {D}^{1,p}(\mathbb {R}^2_0,\mu _{ap})\text { and }u\ne 0\Big \}. \end{aligned}$$

The infimum is attained by [21] Theorem 0.1 and [25] Theorem 3.4. According to [11] Theorem 1.3 there exists $a_\star >1-\frac{2}{p}$ with the property that

(i):

there exists a radial extremal for S(a, p, q) for any $a\le a_\star$; and

(ii):

no extremal for S(a, p, q) is radial for $a>a_\star$.

In fact, $a_\star \ge 0$. Let us now introduce the unique $a^*$ lying in $(1-\frac{2}{p},\infty )$ which satisfies

$$\begin{aligned} \Big (\frac{2}{p}-1+a^*\Big )^2&=\frac{1}{q-p}-\frac{1}{q+p^\prime }, \end{aligned}$$

(14.5)

where $p^\prime$ is the conjugate index to p. This $a^\star$ is positive. According to [11] Theorem 1.1, $a_\star \le a^\star$. We prove that in fact $a_*=a^*$. This latter equality was conjectured in [11]. The proof shares much in common with that of [2] Theorem 8.3.

Theorem 14.1

Let p, q and a be as in (14.1) and (14.2). Then $a_*=a^*$.

Proof

It suffices to show that $a_*\ge a^*$. Choose $a\in (1-\frac{2}{p},a^*]$ and define b as in (14.3). Set

$$\begin{aligned} \alpha :=bq\text { and }\beta :=a+\Big (1-\frac{1}{p}\Big )\alpha . \end{aligned}$$

The lower bound on a ensures that $\alpha >-2$. Suppose that $-2<\alpha <0$. We claim that $\alpha <2\beta$. In fact this statement is equivalent to the inequality

$$\begin{aligned} 0<\Big (1-2\Big [\frac{1}{p}-\frac{1}{q}\Big ]\Big )\Big (a-1+\frac{2}{p}\Big ), \end{aligned}$$

where both factors are positive in light of the condition $q<p^*$.

Suppose that $\alpha \ge 0$. We claim that $\beta ^2\ge \alpha (\beta +1)$. Expressing b in terms of $\alpha$ and $\beta$,

$$\begin{aligned} \beta +1=\Big (1-\frac{1}{p}+\frac{1}{q}\Big )(\alpha +2); \text { and } a+\frac{2}{p}-1=\frac{1}{q}(\alpha +2). \end{aligned}$$

From this last,

$$\begin{aligned} \frac{1}{(\alpha +2)^2}&=\frac{1}{q^2\Big (a+\frac{2}{p}-1\Big )^2} \ge \frac{1}{q^2\Big (a^*+\frac{2}{p}-1\Big )^2} =\Big (\frac{1}{p}-\frac{1}{q}\Big )\Big (1-\frac{1}{p}+\frac{1}{q}\Big ), \end{aligned}$$

upon substituting the identity in (14.5). On the other hand,

$$\begin{aligned} \frac{\beta +1}{\alpha +2}\Big (1-\frac{\beta +1}{\alpha +2}\Big )=\Big (\frac{1}{p}-\frac{1}{q}\Big )\Big (1-\frac{1}{p}+\frac{1}{q}\Big ), \end{aligned}$$

and this leads to the claimed inequality.

Arguing as in [2] Lemma 8.1,

$$\begin{aligned} \frac{\Vert |x|^a\nabla u|\Vert _p^p}{\Vert |x|^b u\Vert _q^p}&\ge \frac{\Vert |x|^a\nabla u^\star |\Vert _p^p}{\Vert |x|^b u^\star \Vert _q^p}, \end{aligned}$$

for any $u\in W^{1,p}_0(\mathbb {R}^2_0,\mu _{ap})\setminus \{0\}$. The star $\star$ refers to the $\mu _{ap}$-symmetrisation of the function u. This makes use of Theorem 1.1 as well as [26] Theorem 3.1. This leads to the inequality $a_*\ge a^*$. $\square$

Appendix

In this Appendix we discuss a number of results used in Sect. 7. These are adapted from [28] and where possible we refer to this source for details.

1.1 Regularity

Let U be an open set in $\mathbb {R}^2$. Given positive locally Lipschitz densities f and g on U we consider the variational problem

$$\begin{aligned} I(v):=\inf \Big \{P_g(E):E\text { is a set of finite perimeter in }U\text { and }V_f(E)=v\Big \},\nonumber \\ \end{aligned}$$

(14.6)

for $v>0$.

Proposition 14.2

Assume that f and g are positive locally Lipschitz densities on U. Let $v>0$ and suppose that the set E is a minimiser of (14.6). Let V be a relatively compact open set in U. There exist constants $C>0$ and $\delta \in (0,d(V,\partial U))$ with the following property. For any $x\in V$ and $0<r<\delta$,

$$\begin{aligned} P_g(E)-P_g(F)\le C\big |V_f(E)-V_f(F)\big |, \end{aligned}$$

(14.7)

where F is any set with finite perimeter in U such that $E\Delta F\subset \subset B(x,r)$.

Proof

The proof follows that of [29] Proposition 3.1. In detail, the proof proceeds as in [28] Proposition 3.6 by replacing $\Delta _f$ by $\Delta _g$ and $P_f$ by $P_g$. $\square$

Theorem 14.3

Assume that f and g are positive locally Lipschitz densities on U. Let $v>0$ and assume that the set E is a minimiser of (14.6). Then the boundary of E is almost minimal in U.

Proof

The notion of almost minimal can be found in [36] Definition 1.5 (and stated in [28] before the last-mentioned Theorem). The proof follows [28] Theorem 3.7 with minor changes. We spell out these changes for the sake of convenience.

Let V be a relatively compact open set in U and $C>0$ and $\delta >0$ as in Proposition 14.2. The open $\delta$-neighbourhood of V is denoted $I_\delta (V)$; put $W:=I_{\delta }(V)$. Let $x\in V$ and $r\in (0,\delta )$. For the sake of brevity write $m:=\inf _{B(x,r)}g$ and $M:=\sup _{B(x,r)}g$. Let F be a set of finite perimeter in U such that $F\Delta E\subset \subset B(x,r)$. By Proposition 14.2,

$$\begin{aligned}&P(E,B(x,r))-P(F,B(x,r))\\&\quad \le \frac{1}{m}P_g(E,B(x,r))-\frac{1}{M}P_g(F,B(x,r))\\&\quad =\frac{1}{m} \Big ( P_g(E,B(x,r))-P_g(F,B(x,r)) \Big )+ \Big (\frac{1}{m}-\frac{1}{M} \Big ) P_g(F,B(x,r))\\&\quad \le \frac{1}{m} \Big ( P_g(E,B(x,r))-P_g(F,B(x,r)) \Big )+ \frac{M-m}{m^2} P_g(F,B(x,r))\\&\quad \le \frac{C}{\inf _W g}|V_f(E)-V_f(F)| + (2Lr)\frac{\sup _W g}{(\inf _W g)^2}P(F,B(x,r))\\&\quad \le C\pi r^2\frac{\sup _W f}{\inf _W g} + (2Lr)\frac{\sup _W g}{(\inf _W g)^2}P(F,B(x,r)), \end{aligned}$$

where L stands for the Lipschitz constant of the restriction of g to W. We then derive that

$$\begin{aligned} \psi (E,B(x,r))\le C\pi r^2\frac{\sup _W f}{\inf _W g} + (2Lr)\frac{\sup _W g}{(\inf _W g)^2} \nu (E,B(x,r)), \end{aligned}$$

in the notation of [28] (3.12). By [22] (5.14), $\nu (E,B(x,r))\le \pi r$. The inequality in [28] (3.13) now follows. $\square$

Theorem 14.4

Assume that f and g are positive locally Lipschitz densities on U. Let $v>0$ and suppose that E is a minimiser of (14.6). Then there exists a set $\widetilde{E}\subset U$ such that

• (i) $\widetilde{E}$ is a minimiser of (14.6);

• (ii) $\widetilde{E}$ is equivalent to E;

• (iii) $\widetilde{E}$ is open and $\partial \widetilde{E}\cap U$ is a $C^1$ hypersurface in U.

Proof

The proof follows as in [28] Theorem 3.8 making use of the last Theorem. $\square$

1.2 Spherical Cap Symmetry

In this Section we work in $\mathbb {R}^2_0$. Denote by $\mathbb {S}^1_\tau$ the centred circle in $\mathbb {R}^2$ with radius $\tau >0$. We sometimes write $\mathbb {S}^1$ for $\mathbb {S}^1_1$. Given $x\in \mathbb {R}^2$, $v\in \mathbb {S}^1$ and $\alpha \in (0,\pi ]$ the open cone with vertex x, axis v and opening angle $2\alpha$ is the set

$$\begin{aligned} C(x,v,\alpha ):=\Big \{y\in \mathbb {R}^2:\langle y-x,v\rangle >|y-x|\cos \alpha \Big \}. \end{aligned}$$

Let E be an $\mathscr {L}^2$-measurable set in $\mathbb {R}^2_0$ and $\tau >0$. The $\tau$-section $E_\tau$ of E is the set $E_\tau :=E\cap \mathbb {S}^1_\tau$. Put

$$\begin{aligned} L(\tau )=L_E(\tau ):=\mathscr {H}^1(E_\tau )\text { for }\tau >0, \end{aligned}$$

(14.8)

and $p(E):= \{\tau \in (0,\infty ):L(\tau )>0\}$. The function L is $\mathscr {L}^1$-measurable by [3] Theorem 2.93. Given $\tau \in (0,\infty )$ and $0<\alpha \le \pi$ the spherical cap $C(\tau ,\alpha )$ is the set

$$\begin{aligned} C(\tau ,\alpha ):= \left\{ \begin{array}{ll} \mathbb {S}^1_\tau \cap C(0,e_1,\alpha ) &{} \text { if }0<\alpha <\pi ;\\ \mathbb {S}^1_\tau &{} \text { if }\alpha =\pi ;\\ \end{array} \right. \end{aligned}$$

and has $\mathscr {H}^1$-measure $s(\tau ,\alpha ):=2\alpha \tau$. The spherical cap symmetral $E^{sc}$ of the set E is defined by

$$\begin{aligned} E^{sc}:=\bigcup _{\tau \in p(E)}C(\tau ,\alpha ), \end{aligned}$$

(14.9)

where $\alpha \in (0,\pi ]$ is determined by $s(\tau ,\,\alpha )=L(\tau )$. Observe that $E^{sc}$ is a $\mathscr {L}^2$-measurable set in $\mathbb {R}^2_0$ and $V_f(E^{sc})=V_f(E)$. Note also that if B is a centred open (punctured) ball in $\mathbb {R}^2_0$ then $B^{sc}=B\setminus \{0\}$. We say that E is spherical cap symmetric if $\mathscr {H}^1((E\Delta E^{sc})_\tau )=0$ for each $\tau \in (0,\infty )$. This definition is broad but suits our purposes.

The result below is stated in [31] Theorem 6.2 and a sketch proof given. A proof along the lines of [5] Theorem 1.1 can be found in [5]. First, let B be a Borel set in $(0,\infty )$; then the annulus A(B) over B is the set $A(B):=\{x\in \mathbb {R}^2_0:|x|\in B\}$.

Theorem 14.5

Let E be a set of finite perimeter in $\mathbb {R}^2_0$. Then $E^{sc}$ is a set of finite perimeter in $\mathbb {R}^2_0$ and

$$\begin{aligned} P(E^{sc},A(B))\le P(E,A(B)), \end{aligned}$$

(14.10)

for any Borel set $B\subset (0,\infty )$ and the same inequality holds with $E^{sc}$ replaced by any set F that is $\mathscr {L}^2$-equivalent to $E^{sc}$.

Corollary 14.6

Let g be a positive lower semi-continuous radial function on U. Let E be a set of finite perimeter in U. Then $P_g(E^{sc})\le P_g(E)$.

Proof

See [28] Corollary 4.3 for example. $\square$

Lemma 14.7

Let E be an $\mathscr {L}^2$-measurable set in $\mathbb {R}^2_0$ such that $E=E^{sc}$. Then there exists an $\mathscr {L}^2$-measurable set F in $\mathbb {R}^2_0$ equivalent to E such that

• (i) $\partial F\cap \mathbb {R}^2_0=\{x\in \mathbb {R}^2_0:0<|F\cap B(x,\rho )|<|B(x,\rho )|\text { for small }\rho >0\}$;

• (ii) $F=F_1\cup Y$ where $F_1:=\{x\in \mathbb {R}^2_0:|F\cap B(x,\rho )|=|B(x,\rho )|\text { for some }\rho >0\}$ and $Y\subset \partial F\cap \mathbb {R}^2_0$;

• (iii) F is spherical cap symmetric.

Proof

The proof of (i) and (iii) follows as in [28] Lemma 4.4. In the notation of this last, $F=E_1\cup (E{\setminus } E_0)=E_1\cup [E{\setminus }(E_0\cup E_1)]=F_1\cup Y$ where $Y:=E{\setminus }(E_0\cup E_1)\subset \partial F\cap \mathbb {R}^2_0$. This leads to (ii). $\square$

Theorem 14.8

Assume that f and g are positive locally Lipschitz densities on $\mathbb {R}^2_0$. Let $v>0$ and suppose that E is a minimiser for (14.6). Then there exists an $\mathscr {L}^2$-measurable set $\widetilde{E}$ in $\mathbb {R}^2_0$ with the properties

• (i) $\widetilde{E}$ is a minimiser of (14.6);

• (ii) $L_{\widetilde{E}}=L$ a.e. on $(0,\infty )$;

• (iii) $\widetilde{E}$ is open and has $C^1$ boundary in $\mathbb {R}^2_0$;

• (iv) $\widetilde{E}=\widetilde{E}^{sc}$.

Proof

The proof proceeds as in [28] Theorem 4.5 and making use of the above results Corollary 14.6, Lemma 14.7 and Theorem 14.4 in place of those mentioned in [28]. $\square$

1.3 Generalised (Mean) Curvature

Let E be a relatively compact open set in $\mathbb {R}^2_0$ with $C^1$ boundary M in $\mathbb {R}^2_0$. Let us recall some notation from Sect. 2. Denote by $n:M\rightarrow \mathbb {S}^1$ the inner unit normal vector field. Given $p\in M$ we choose a tangent vector $t(p)\in \mathbb {S}^1$ in such a way that the pair $\{t(p),n(p)\}$ forms a positively oriented basis for $\mathbb {R}^2$. If $p\in M$ let $\sigma (p)$ stand for the angle measured anti-clockwise from the position vector p to the tangent vector t(p); $\sigma (p)$ is uniquely determined up to integer multiples of $2\pi$.

Define $\Lambda :=M\cap \{\cos \sigma =0\}$ and

$$\begin{aligned} \Lambda _1&:=\{x\in M:\mathscr {H}^1(\Lambda \cap B(x,\rho ))=\mathscr {H}^1(M\cap B(x,\rho ))\text { for some }\rho >0\}. \end{aligned}$$

(14.11)

This set corresponds to the union of open centred circular arcs contained in the boundary M. The notation $\Lambda _1^{\pm }:=\Lambda _1\cap \{x\in M:\pm \langle x,n\rangle >0\}$ will also be used.

Proposition 14.9

Let f and g be positive radial densities on $\mathbb {R}^2_0$ of class $C^1$. Given $v>0$ suppose that E is a minimiser of (14.6). Assume that E is a relatively compact open set in $\mathbb {R}^2_0$ with $C^1$ boundary M in $\mathbb {R}^2_0$ and suppose that $E=E^{sc}$. Suppose that $M\setminus \overline{\Lambda _1}\ne \emptyset$. Then there exists $\lambda \in \mathbb {R}$ such that for any $X\in C^1_c(\mathbb {R}^2_0,\mathbb {R}^2)$,

$$\begin{aligned} 0=\int _M\Big \{\langle \nabla g,X\rangle + g\,\textrm{div}^M X-\lambda f\langle n, X\rangle \Big \} \,\mathrm{{d}}\mathscr {H}^1. \end{aligned}$$

Proof

This result is essentially well known. The proof of [28] Proposition 6.4 ( for example) can be adapted to obtain this result by replacing $P_f$ by $P_g$. $\square$