Thermocapillary Flow and Coalescences of Heterogeneous Bubble Size Diameter in a Rotating Cylinder: 3D Study

Abstract

Two dimensional axisymmetric and three-dimensional VOF simulations of gas/liquid transient flow were performed using a multiphase flow algorithm based on the finite-volume method. The results for motion of a multiple bubbles of a heterogeneous sizes aligned horizontally and perpendicular to a hot surface incorporating thermocapillary forces in a rotating liquid in a zero-gravity environment have been presented for the first time. No bubbles broke in any of the cases observed. The results also show that collision and agglomeration of bubbles of unequal sizes diameter are different from those of similar size diameters presented from earlier research work of Alhendal et al. Acta Astronaut. 117, 484–496 (2015). Different flow patterns such as thermocapillary bubble migration, collision, and stream function were observed and presented for the 2-D and 3-D models.

Introduction

Very little is known about bubble collision and agglomeration in zero-gravity conditions, due to the relative complexity of conducting experiments under such conditions. In addition, the literature reveals the complexity of modelling three-dimensional geometries to simulate the thermocapillary flow of bubbles/droplets in cylindrical coordinates. Understanding thermocapillary bubble flow and the interaction between bubbles is very important for future research and for designing useful experiments; indeed, an understanding of these phenomena is highly desirable for the future design of space shuttles and equipment that might be employed in zero-gravity environments, besides some bubbles cannot be raised thermocapillary due to their small sizes and must be merged together to form a larger bubble size in order to migrate toward the hotter side (Top wall). Based on previous analyses of the bubble shape and motion, Colin et al. (2008) bubbles are spherical, and have rectilinear trajectories. The momentum of an actual rotating cylinder usually causes the merging of gas bubbles as they move towards the axis of rotation. This merging increases the bubble size, and may lead to a reduction in the gas holdup, at the main time, thermocapillary (Marangoni) force migrates the bubbles toward the hotter side. Bubbles then can be removing by cutting the upper part or by any other operation. However, even with the advent of modern science, the motion of a single and a group of bubbles in a rotating flow field is yet to be fully understood. “In particular, the spin force acting on a small bubble is not clearly identified, and it is not easy to predict optimum conditions for bubble removal” Yamaguchi et al. (2004). Thereby explaining not only the motion of small bubbles but also their coalescence into one large bubble. A rotating fluid provides a gyrostatic pressure field which causes

less dense material such as bubbles to move inward toward the rotation axis” Subramanian and Cole (1979). Annamalai et al. (1982) states that in a rotating field, fluid particles with a lower density than the surrounding media migrate inwards, i.e. towards the axis of rotations. Adding additional forces, such as the centrifugal force, is one way to enhance bubble-bubble interaction, in the same time shows potential applications in micro-gravitational science and technology. The same centrifugal force method can be used in the glass-manufacturing processes by controlling bubble coalescence, which may improve gas bubble distribution. A useful method for bubble removing, non-metallic inclusions removal Annamalai et al. (1982) and in microgravity is centrifugal fining Yamaguchi et al. (2004). In this process rotation of the melt is followed by thermocapillary migration of the coalesced Annamalai et al. (1982). Previous studies have shown that there is much still to be understood about thermocapillary flows and the interaction of a group of bubbles Alhendal et al. (2013), and due to the lack of information available on the interaction of a group of bubbles/droplets, the objective of this paper is therefore to extend the previous 2D and 3D study Alhendal et al. (2015), Alhendal and Turaan (2015) and to investigate in detail the merging process of bubbles having diverse size diameter inside a rotating cylinder under zero-gravity conditions. Three dimensional numerical results of the motion of a singular and multiple bubbles incorporating thermocapillary forces in a rotating liquid in a zero-gravity environment have been presented for the first time by Alhendal et al. (2015). Previous studies have shown that there is much still to be understood about thermocapillary flows and the interaction of a group of bubbles (Young et al. 1959), there still appears to be insufficient information available with regard to thermocapillary flow contribution to heat transfer, Radulescu and Robinson (2008). Kang et al. (2008) state that bubble and/or drop dynamics has become a hot point of research, and the phenomenon of motion of gas bubbles or insoluble fluid drops inserted into non-isothermal liquids was first discovered by Young et al. (1959) using a linear model (Bratukhin et al. 2005):

$$ V_{YGB} =\frac{2\left| {\frac{d\sigma} {dT}} \right|r_{b} \lambda \frac{dT}{dx}}{(2\mu +3{\mu}^{\prime})(2\lambda +\lambda^{\prime})} $$

(1)

commonly called the YGB model, which is suitable for small Reynolds and Marangoni numbers:

$$ Re_{T} =\frac{r_{b} V_{T}} {\nu} $$

(2)

$$ Ma_{T} =\frac{r_{b} V_{T}} {\alpha} =Re_{T} .\Pr $$

(3)

where Prandtl number is the ratio of kinematic viscosity to thermal diffusivity:

$$ \Pr =\frac{\nu} {\alpha} $$

(4)

and ν is the kinematic viscosity in m²/s:

$$ \nu =\frac{\mu} {\rho} $$

(5)

The velocity V _T derived from the tangential stress balance at the free surface is used for scaling the migration velocity (m/s) in Eqs. 2 and 3:

$$ V_{T} =\frac{\frac{d\sigma} {dT}.\frac{dT}{dx}.r_{b}} {\mu} $$

(6)

Where μ and μ ^′, λ and λ ^′ are the dynamic viscosity and thermal conductivity of continuous phase and gas, respectively. ρ is the density and r _b is the radius of the bubble. The constant dσ/dT or σ _T is the rate of change of interfacial tension and dT/dx is the temperature gradient imposed in the continuous phase fluid.

VOF Model and Computational Procedure

The governing continuum conservation equations for two-phase flow were solved using the ANSYS-FLUENT commercial software package Ansys-Fluent (2013), and the volume of fluid (VOF) method was used to track the liquid/gas interface. This method deals with completely separated phases with no diffusion, and has been used extensively to calculate the hydrodynamics of bubbles rising in a liquid by Kawaji and colleagues (Kawaji et al. 1997). The previous authors reported new findings for the two-dimensional simulation of a Taylor bubble rising in a stagnant liquid-filled tube. Larkin (1970) was possibly the first to numerically investigate Marangoni convection caused by the presence of a bubble situated on a heated wall (O’Shaughnessy and Robinson 2008). Alhendal et al. (2010) illustrated the capability of VOF model to accurately simulate the bubble shape. The simulated shapes were found to agree well with the published experimental data. The geometric reconstruction scheme, based on the piece-wise linear interface calculation (PLIC) method of Youngs (1982) in Ansys-Fluent, was chosen for the current investigation. Geo-reconstruction is an added module to the already existing VOF scheme that allows for a more accurate definition of the free surface Hirt and Nichols (1981).The movement of the gas–liquid interface is tracked based on the distribution of the volume fraction of the gas, i.e. α _G , in a computational cell, where the value of α _G is 0 for the liquid phase and 1 for the gas phase. Therefore, the gas–liquid interface exists in the cell where α _G lies between 0 and 1. A single momentum equation, which is solved throughout the domain and shared by all the phases, is given by:

$$ \frac{\partial} {\partial t}(\rho \vec{{\nu} })+\nabla .(\rho \vec{{\nu} }\vec{{\nu} })=-\nabla p+\nabla .[\mu (\nabla \vec{{\nu} }+\nabla \vec{{\nu} }^{T})]+\vec{{F}} $$

(7)

where v is treated as the mass-averaged variable:

$$ \vec{{v}}=\frac{\alpha_{G} \rho_{G} \vec{{v}}_{G} +\alpha_{L} \rho_{L} \vec{{v}}_{L}} {\rho} $$

(8)

In Eq. 7, $\vec {{F}}$ represents volumetric forces at the interface, resulting from the surface tension force per unit volume. The continuum surface force (CSF) model proposed by Brackbill et al. (1992) is used to compute the surface tension force for the cells containing the gas–liquid interface:

$$ \vec{{F}}=\sigma \frac{\rho k\vec{{n}}}{\frac{1}{2}(\rho_{L} +\rho_{G} )} $$

(9)

where σ is the coefficient of surface tension,

$$ \sigma =\sigma_{0} +\sigma_{T} (T_{0} -T) $$

(10)

and σ ₀ is the surface tension at a reference temperature T _o , T is the liquid temperature, n is the surface normal which is estimated from the gradient of volume fraction, and κ is the local surface curvature, given as:

$$ k=-(\nabla \vec{{n}})=\frac{1}{\vec{{n}}}\left[ {\frac{\vec{{n}}}{\left| n \right|}\nabla \left| n \right|-(\nabla .\vec{{n}})} \right] $$

(11)

The tracking of the interface between the gas and liquid is accomplished by the solution of a continuity equation for the volume fraction of gas:

$$ \frac{\partial} {\partial t}(\alpha_{G} \rho_{G} )+\nabla \cdot (\alpha_{G} \rho_{G} \vec{{v}}_{G} )=0 $$

(12)

The volume fraction equation is not solved for the liquid; rather, the liquid volume fraction is computed based on the following constraint:

$$ \alpha_{G} +\alpha_{L} =1 $$

(13)

Where α _G and α _L are the volume fractions of the gas and liquid phases respectively. The transport equation properties are determined by the presence of the component phases in each control volume and are calculated as volume-averaged values. The density of each cell at the interface is computed by application of the following equations:

$$ \rho =\alpha_{G} \rho_{G} +(1-\alpha_{G} )\rho_{L} $$

(14)

Viscosity is computed same manner as shown in Eq. 14 for the density properties due to algebraically simpler and is more effective at immiscible fluids mixture.

$$ \mu =\alpha_{G} \mu_{G} +(1-\alpha_{G} )\mu_{L} $$

(15)

Where ρ, μ and α _G are the density, viscosity and volume fraction of the different phases respectively. The energy equation is also shared among the phases:

$$ \frac{\partial} {\partial t}(\rho E)+\nabla .[\vec{{\nu} }(\rho E)+p)]=\nabla .(\kappa_{eff} \nabla T) $$

(16)

The VOF model treats energy (E) and temperature (T) as mass-averaged variables:

$$ E=\frac{\sum\limits_{q=1}^{n} {\alpha_{q} \rho_{q} E_{q}}} {\sum\limits_{q=1}^{n} {\alpha_{q} \rho_{q}} } $$

(17)

Where Eq. 17 for each phase is based on the specific heat of that phase and the shared temperature. The properties ρ and κ _{e f f} (effective thermal conductivity) are also shared by the phases.

The computations were performed using a pressure-based, segregated, implicit solver. Pressure–velocity coupling is accomplished by the pressure implicit with the splitting of operators (PISO) function, which performs both neighbour and skewness corrections. The pressure-staggering option (PRESTO) scheme is used for pressure interpolation, and the momentum and the energy equations were discretised using a second-order upwind differencing scheme. Other spatial discretisation schemes, such as QUICK, were also tested, and no differences in results were observed. Nevertheless, simulations using non-iterative methods were found to be considerably computationally faster than the iterative ones. It should be noted that the non-iterative time advancement with time steps of 2.5×10⁻³s was used to obtain convergence, no gravitational force was imposed in the simulation, and all cases were run with double precision.

Two-Dimensional Axisymmetry Validation Against Previous Experimental Work

For the initial boundary condition and validation against previous experimental work of bubble dynamics in a 2D axisymmetric domain, two different test cases for a nitrogen bubble with a diameter of 6 mm in ethanol and a diameter of 8 mm in silicon oil was considered for comparison of the present numerical results with the experiments available in literature. Predictions provided for a good qualitative agreement with the available experimental data regarding Marangoni bubble motion in zero gravity supplied by Thompson et al. (1980) as shown in Table 1 and Figs. 1 and 2. Please refer to Alhendal et al. (2013, 2015, 2016) for further figures and tables.

Fig. 1

Schematic of bubble migration in a uniform temperature gradient

Fig. 2

validation of VOF-model with previous experimental data for bubble diameters, d=6 and 8 mm in ethanol (Pr=16.3) and silicon oil (Pr=138) respectively

Table 1 Physical properties of the liquid employed in the simulation at T_o = 300K and sample results of bubble diameters = 6 and 8 mm for (Pr =16.3) and (Pr =138), respectively

The effect of different liquid temperature upon bubble migration was also consider on the same article in which a linear temperature distribution was prescribed between the upper and lower walls to monitor the bubble velocity as it moved from the cold to the hot wall. A direct relationship between the temperature gradient and the bubble speed, as the temperature gradient increases, so does the migration velocity as shown in Figs. 3 and 4.

Fig. 3

Temperature contours (bottom -K) and streamlines (top-Kg/s) for N₂ =8. a Temperature contours (left) and streamlines (right-Kg/s) for N₂ =8 mm diameter at t=9 s, with bottom wall temperature=300K and top wall temperature =320K. b Temperature contours (left) and streamlines (right-Kg/s) for N₂ =8 mm diameter at t=9 s, with bottom wall temperature=300K and top wall temperature =322.5K. c Temperature contours (left) and streamlines (right-Kg/s) for N₂ =8 mm diameter at t=9 s, with bottom wall temperature=300K and top wall temperature =325K

Fig. 4

Relation between migration time and displacement of N₂ = 8 mm diameter migrates in Ethanol (Pr =16.28) for different temperature gradient

Grid Resolution Study for a two-Dimensional Axisymmetry

The objective of a grid independence study is to ensure that the simulation results are independent of the grid density. Grid independence was achieved by increasing the number of region adaption cells from 72 to 406 per bubble radius by increasing the grid cells in both the X and Y directions, and plotting the convergence of certain parameters of interest such as bubble migration time towards the hotter side and migration distance to ensure that the solution remains independent of grid size. Concerning the number of cells in the present study, a non-uniform grid with grid lines clustered towards the centre was used in order to keep cell count down and to avoid the drawback of increasing memory and CPU time. The grid sensitivity test was simulated with the parameters outlined in Table 1. Another important point is that, when using an axisymmetric solver, a mesh need only be created for half of the domain, thus drastically reducing the number of cells used and consequently the time of calculation.

Five different grids were used to study the grid size dependency. Each of the grids was used to simulate the thermocapillary bubble migration under zero-gravity conditions. Since the bubble translation behaviour is of interest to this study, five simulations using each of the five grids developed in Table 2 are presented in Fig. 5 and the mesh size with streamline resolutions was tested using Tecplot software to simulate the 2D representation of the domain, as seen in Fig. 6. The profiles of bubbles with diameter of 8 mm were extracted across half of the 2D axis domain at a time = 9s at different distances from the cold lower side. These figures show only a very small difference in the calculated bubble motion profiles using the 23200 mesh (grid-4) and the 31200 mesh (grid-5) of the domain, which give 278 and 406 cells per bubble radius respectively. As seen from the results, it was expected that the greater grid density would give more accurate simulation results as finer grids reduce the distance over which variables in the computation are interpolated. However, as the 31200 mesh is computationally expensive, it is desirable to use the 23200 mesh to produce the desired results. In this grid study, the number of computational cells in the horizontal and vertical directions was increased while maintaining a square computational cell. This is achieved by changing the grid to uniform control volume (Δx/ Δy=1), which is more satiable for accurate schemes at higher orders, avoiding numerical aliasing errors.

Table 2 Grid sensitivity check for a bubble diameter =8 mm for 2-d-axis models

Fig. 5

Show the rise distance of bubble nose for five different grid sizes vs. time (s)

Fig. 6

The rising distance of a bubble for five different grid sizes at t=9 s from the start of the bubble migration

Bubble Dynamics in a 3D Domain

Given the promising 2D results from earlier works of Alhendal and Al-Mazidi (2015) and Alhendal and Turan (2012), it was decided to extend the simulations to a 3D scenario. The 3D geometry consisted of a cylinder with a diameter of 120 mm and a height of 120 mm, where the grid consisted of over 324,000 hexahedral cells. Again, an investigation of grid size dependency was performed and grid independence was achieved by increasing the number of region adaption cells from 40 to 304 per bubble diameter. The grid size was increased in the X, Y and Z directions from 20 x 20 x 80 (96,000 cells) to 30 x 30 x 120 (324,000 cells) and 40 x 40 x 160 (768,000 cells), respectively. Ultimately, the medium mesh with dimensions of 30 x 30 x 120 (324000 cells) was chosen for all further testing, as it was both time-consuming and had reasonable comparisons to the previous 2D results as can been seen in Fig. 7. Some results from the chosen 3D case are shown in Fig. 8 and Alhendal et al. (2015).

Fig. 7

Three dimension grid sensitivity check and comparison with 2d axis

Fig. 8

Migration distance of the bubble (11mm) inside ethanol (Pr=16.2) towards the hotter side (Y-direction), versus time for the three tested meshes

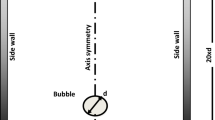
Fluids and Initial Conditions: Description of Parameters and Domain

A cylindrical vessel measuring 120 mm high (H) x 120 mm diameter (D) was filled with liquid Ethanol (Pr =16.28). The origin of the cylindrical coordinate system was placed on the centre of the lower plate, and the vertical axis, y, was directed upward. Nitrogen bubbles were patched into liquid contained in a cylinder and subjected to a vertical temperature gradient, ∇T. The velocity is set to zero, with a no-slip boundary used for the walls of the vessel. This signifies that no flow passes across the wall boundary and the flow does not slip along the wall, as well as meaning that no heat is lost or gained from the wall. The physical parameters used for the three-dimensional simulation are similar to the two-dimensional simulations in Alhendal et al. (2015) and Table 1.

Distribution of Tangential Velocity Component, Pressure, and Temperature of the Surrounding Liquid

The three-dimensional Navier-Stokes equation for incompressible fluid flow in a system rotating about a vertical axis reads from Eq. 6:

$$\frac{\partial} {\partial t}(\rho \vec{{\nu} })+\nabla .(\rho \vec{{\nu} }\vec{{\nu} })=-\nabla P-2\omega .\vec{{\nu} }+\nabla .[\mu (\nabla \vec{{\nu} }+\nabla \vec{{\nu} }^{T})]+\vec{{F}} $$

Where ω is the angular velocity of the system and P is the modified pressure accounting for centrifugal force:$P=p-\frac {1}{2}\rho \omega ^{2}R^{2}$.

To check the procedure, the simple problem of ω= 0.5 rad/sec was first examined as the baseline case. To confirm the accuracy of the simulation, after a steady state was established, the tangential velocity component, pressure and temperature gradient of the host liquid were measured. Figure 9a-d shows the distributions of the tangential velocity component,v, along with the temperature and pressure within the computational domain after reaching the steady state condition. Here, the cylinder has a rotational velocity of 0.5 rad/sec and a temperature differential of 25 K between the lower and the upper faces. The results in Fig. 9a illustrate that the radial distributions of the tangential velocity component measured on the horizontal planes (R =60 mm) obey the v=Rω relationship at every axial measurement position.

Fig. 9

a Tangential velocity along the radius. b Tangential velocity (mm/s). c Distribution of static pressure (Pa). d temperature gradient (K)

The steady state results shows that the tangential velocity increases linearly from the cylinder’s axis of rotation to the walls of the cylinder. It also indicates that the minimum and maximum values of total pressure are found at the centre and the outside walls of the cylinder, respectively. The temperature also shows a linear behaviour from the lower to the upper face of the cylinder. Thus, the steady state result shown in Fig. 9, verifies that the present CFD measurements are accurate.

Single Bubble Dynamics in a Rotating Cylinder

The results obtained from the steady state simulation of the rotating cylinder were used to predict the behaviour of a single bubble within such a cylinder. A bubble was placed at the location of 5d, 1.5d and 0d in the X, Y and Z directions respectively, where “d” is the diameter of the bubble.

The transient simulation result in plot Fig. 10a presents the location profiles of the bubble in the x, y and z directions at different time intervals. It is evident from the figure that two important forces affect the thermocapillary bubble dynamics. This induces Marangoni flow in the surrounding liquid, which may affect the bubble migration by subjecting it to additional forces. Since the applied thermal gradient (and hence the thermocapillary motion) is parallel to the rotational axis, i.e. the y-axis, the bubble dynamics can be simplified into motion along the transverse plane (x-z plane) and motion in the axial direction, where the bubble can be expected to be asymmetrically placed. Since the transverse plane motion for a bubble is an inward-spiralling trajectory and the vertical thermocapillary motion is a straight line (from the cooler to the warmer region), qualitatively, the bubble trajectory should follow a helical path, as is observed from figure curves in plots Figs. 10b, c and 11 for ω = 0.5 rad/sec. The radius and the pitch of the helix will depend on the relative magnitude of the temperature gradient that causes the vertical motion and the rotation rate that governs that rate of inward-spiralling motion. From the same figures, it can also be concluded that the gas bubble trajectory under the current rotating conditions is significantly different from that of a non-rotating case presented in Alhendal et al. (2015). That is, the centrifugal force due to the rotation of the cylinder is the more dominant factor than the inertial force caused by the Marangoni flow where the deflection is strongly influenced by the rotation rates.

Fig. 10

a The X and Y directions of a single bubble vs. time (s). b The Z-direction of a single bubble vs. time (s). c The radial and angular directions of a single bubble vs. time (s)

Fig. 11

Three-dimensional numerical solution of a bubble trajectory in XYZ when ω = 0.5 rad/sec, d_b = 10mm, ?? T=0.208 K/mm

Thermocapillary Flow and Coagulation of Bubbles of Equal Sizes

The results presented in Figs. 12a, b and 13a, b show a comparison of two cylinders each containing 4 bubbles of equal diameter located at a distance of 50 mm from the axis of rotation and 90 mm apart from each other in the angular direction. The cylinder measured 120 mm in diameter and rotated at an angular velocity of 0.5 rad/sec, filled with a liquid with a Prandtl number of 16.28. The temperature was 300 K at the lower surface for all cases and 325 K at the upper surface of the cylinder. For given conditions, the temperature gradient measured 0.208 K/mm and thermocapillary Reynolds and Marangoni numbers were 257 and 4188 respectively. The computed results in this section compare two bubble diameters (10 mm and 11mm) migrating under the same conditions. The merging for the bubbles with diameter equal to 11 mm occurred at the top of the cylinder, as seen in the time sequence in Figs. 13a and b. On the other hand, no collision was noticed for lower bubble size diameter, 10mm. These two figures show the possibility of controlling bubble agglomeration by adjusting the angular velocity, and demonstrate that the merging process between the equal bubbles size diameter could occur at the same level on the axis of ration. Furthermore, bubble collision and agglomeration under such condition change with the changing bubble size diameter.

Fig. 12

Snap-shot in time showing for equal and unequal bubbles diameter moving toward the warmer region. a Migration time= 6 s. b Migration time= 10 s. c Bubble diameter=10 mm

Fig. 13

Snap-shot in time showing for equal and unequal bubbles diameter moving toward the warmer region. a Migration time = 6 s. b Migration time = 8 s. c Bubble diameter=11 mm

Simulation of Heterogeneous Bubble Sizes in a Rotating Cylinder

Finally, in order to further confirm that the merging process is affected by the diameter of the bubbles involved, a simulation of four different bubble sizes were carried out in a single cylinder at the same time. The diameters of the bubbles measured 9, 10, 11 and 12 mm and the bubbles were located at a distance of 50 mm from the axis of rotation and 90 mm apart from each other in the angular direction. The bubbles were placed axially at a distance of one and a half times the diameter of the bubble from the base of the cylinder (cooler region). The size of the computational domain and the fluid parameters were kept the same as in the previous sections of the study, and the bubbles were patched after obtaining the steady state condition against a constant temperature gradient of 0.208 K/mm and a rotational velocity of 0.5 rad/sec. Figure 14a-b show that the bubbles migrate towards the centre and the hotter side of the cylinder, while maintaining a steady state velocity with a slight different between them. The plots in Fig. 15a, b and c show that bubbles with a larger diameter reached the axis of ration and the warmer side faster than those with smaller diameters. On the other hand, the bubbles with smaller diameters exhibited a taller helix than the other bubbles. The final configuration can be explained by the fact that in order to simulate the merging process between bubbles, we apply angular velocity to the cylinder containing bubbles. This rotational rate forces the bubbles to move closer to the axis of rotation, leading to coalescence. Bubble with the larger diameter could merge at a level lower than those of smaller diameter, and acts different of those having diverse bubble size diameter.

Fig. 14

Snap-shot in time showing for equal and unequal bubbles diameter moving toward the warmer region. a Time step = 6 s. b Time step =10 s. c Bubble diameters =9, 10,11 and 12 mm

Fig. 15

a Displacement of the four bubbles towards the warmer region. b Plot of bubble motion around the axis of rotation

Conclusion

Motion of a singular and multiple bubbles of equal and a heterogeneous sizes incorporating thermocapillary forces in a rotating liquid in a zero-gravity environment have been presented for the first time. Results of centrifugal forces is an example of external phenomena that may be used to control bubble agglomeration and can play an important role in the dynamics and collision of bubbles in zero-gravity conditions. The results also show that collision and agglomeration could occur at a higher level at the axis of rotation for larger bubble size diameters unlike smaller and varied bubble size diameter. No bubbles broke was noticed in any of the cases. Different flow patterns such as thermocapillary bubble migration, stream function, and thermal gradients were observed for the 2D and 3D models under the effects of zero gravity. Since zero gravity is difficult to achieve in a laboratory setting, one can demonstrate the relevant phenomena using numerical simulations, which allows one to study the effects of altering the sensitivities of different parameters.

With computer simulations proving their worth as a valuable tool to study the complex problems in zero-gravity conditions, from the results of this paper one can observe the credentials of numerical modelling to simulate realistic 3D Marangoni cases.