Skip to main content
SpringerLink
Log in

Sufficient stability condition for fractional-order nonlinear systems

  • Published:
Journal of Mechanical Science and Technology Aims and scope Submit manuscript

Abstract

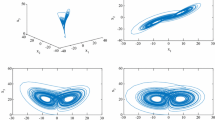
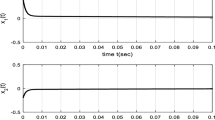
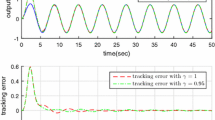
This study examines the stabilization control problem for Fractional-order nonlinear systems (FONS). Based on the frequency distribution model of the fraction-order integrator, a sufficient stability condition is presented for the Riemann-Liouville FONS. The stability of the FONS is proven using Lyapunov stability theory. An improved sufficient stability condition is also proposed with Linear matrix inequalities (LMIs) techniques. A novel control law to stabilize the FONS is put forward. Numerical simulation examples are provided to verify the proposed approaches.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. I. Podlubny, Fractional differential equations: An introduction to fractional derivatives, fractional differential equations, to methods of their solution and some of their applications, Academic press (1998).

    MATH  Google Scholar 

  2. N. H. T. Lemes, V. A. Simpao and J. P. C. dos Santos, A speculative study of non-linear Arrhenius plot by using fractional calculus, Physics. chem-ph (2016).

    Google Scholar 

  3. D. Baleanu, Z. B. Güvenç and J. A. Tenreiro Machado, New trends in nanotechnology and fractional calculus applications, Springer Science+Business Media B.V. (2010).

    Book  MATH  Google Scholar 

  4. A. S. Sheoran, K. K. Kalkal and S. Deswal, Fractional order thermo-viscoelastic problem with temperature dependent modilis of elasticity, Mechanics of Advanced Materials and Structures (2015).

    Google Scholar 

  5. B. Ducharne, B. Zhang, D. Guyomar and G. Sebald, Fractional derivative operators for modeling piezoceramic polarization behaviors under dynamic mechanical stress excitation, Sensors and Actuators. A: Physical (2013).

    Google Scholar 

  6. M. Ichise, Y. Nagayanagi and T. Kojima, An analog simulation of noninteger order transfer functions for analysis of electrode process, J. Electroanal. Chem., 33 (1971) 253–265.

    Article  Google Scholar 

  7. J. A. Stratton, Electromagnetic theory, John Wiley & Sons (2007).

    MATH  Google Scholar 

  8. N. Laskin, Fractional market dynamics, Physica A: Statistical Mechanics and its Applications, 287 (2000) 482–492.

    Article  MathSciNet  Google Scholar 

  9. D. Kusnezov, A. Bulgac and G. D. Dang, Quantum levy processes and fractional kinetics, Phys. Rev. Lett., 82 (1999) 1136–1139.

    Article  Google Scholar 

  10. J. C. Trigeassou et al., Modelling and identification of a non-integer order system, ECC’99 European Control Conference, Karlsruhe, Germany 1999 2453–2458.

    Google Scholar 

  11. J. C. Trigeassou and N. Maamri, State-space modelling of fractional differential equations and the initial condition problem, IEEE SSD’09, Djerba, Tunisia 2009 1–7.

    Google Scholar 

  12. J. C. Trigeassou and N. Maamri, The initial conditions of Riemman-Liouville and Caputo derivatives: An integrator interpretation, Proceeding of the FDA’2010 Conference, October, Badajoz, Spain (2010).

    Google Scholar 

  13. J. C. Trigeassou and N. Maamri, Initial conditions and initialization of linear fractional differential equations, Signal Processing, 91 (3) (2011) 427–436.

    Article  MATH  Google Scholar 

  14. J. Sabatier et al., On a representation of fractional order systems: Interests for the initial condition problem, Proceeding of the 3rd IFAC workshop on Fractional Differentiation and its Applications, Ankara, Turkey 2008 5–7.

    Google Scholar 

  15. H. Li, W. Yan and Y. Shi, Continuous-time model predictive control of under-actuated spacecraft with bounded control torques, Automatica, 75 (2017) 144–153.

    Article  MathSciNet  MATH  Google Scholar 

  16. J. Sabatier, M. Merveillaut, R. Malti and A. Oustaloup, How to impose physically coherent initial conditions to a fractional system?, Communications in Nonlinear Science and Numerical Simulation, 15 (2010) 1318–1326.

    Article  MathSciNet  MATH  Google Scholar 

  17. J. Sabatier, M. Merveillaut, L. Feneteau and A. Oustaloup, On observability of fractional order systems, Proceedings of the ASME IDET-CIE Conferences, San Diego, California, USA 2009 253–260.

    Google Scholar 

  18. J. Sabatier, C. Farges, M. Merveillaut and L. Feneteau, On observability and pseudo state estimation of fractional order system, European Journal of Control, 18 (2012) 260–271.

    Article  MathSciNet  MATH  Google Scholar 

  19. T. Poinot and J. C. Trigeassou, A method for modelling and simulation of fractional systems, Signal Processing, 83 (2003) 2319–2333.

    Article  MATH  Google Scholar 

  20. J. Lin, T. Poinot and J. C. Trigeassou, Parameter estimation of fractional systems: Application to the modelling of a leadacid battery, Proceeding of the 12th IFAC Symposium on System Identification, SYSID 2000, USA (2000).

    Google Scholar 

  21. X. Tang, Y. Shi and L. Wang, A new framework for solving fractional optimal control problems using fractional pseudospectral methods, Automatica (accepted for publication).

  22. J. Lin, Modélisation et identification des systèmes d’ordre non entier, Thèse de doctorat, Université de Poitiers, France (2001).

    Google Scholar 

  23. J. Lin, T. Poinot and J. C. Trigeassou, Parameter estimation of fractional systems. Application to heat transfer, European Control Conference ECC 2001, Porto Portugal 2001 2644–2649.

    Google Scholar 

  24. T. Poinot and J. C. Trigeassou, Parameter estimation of fractional models: Application to the modelling of diffusive systems, 15th IFAC World Congress, Barcelona, Spain (2002).

    Google Scholar 

  25. J. C Trigeassou, N. Maamri, J. Sabatier and A. Oustaloup, A Lyapunov approach to the stability of fractional differential equations, Signal Processing, 91 (2011) 437–445.

    Article  MATH  Google Scholar 

  26. Y. Li, Y. Q. Chen and I. Podlubny, Mittag-Leffler stability of fractional order nonlinear dynamic systems, Automatica, 45 (8) (2009) 1965–1969.

    Article  MathSciNet  MATH  Google Scholar 

  27. S. J. Sadati, D. Baleanu, D. A. Ranjbar, R. Ghaderi and T. Abdeljawad, Mittag-Leffler stability theorem for fractional nonlinear systems with delay, Abstract Appl. Anal. 108 (2010) 651–1-7.

    MathSciNet  MATH  Google Scholar 

  28. X. J. Wen, Z. M. Wu and J. G. Lu, Stability analysis of a class of nonlinear fractional-order systems, IEEE Trans. Circuits Syst. II, Exp. Briefs, 55 (11) (2008) 1178–1182.

    Google Scholar 

  29. W. H. Deng, Smoothness and stability of the solutions for nonlinear fractional differential equations, Nonlinear Anal. TMA, 72 (3/4) (2010) 1768–1777.

    Article  MathSciNet  MATH  Google Scholar 

  30. A. E. Matouk and A. A. Elsadany, Achieving synchronization between the fractional-order hyperchaotic Novel and Chen systems via a new nonlinear control technique, Applied Mathematics Letters, 29 (2014) 30–35.

    Article  MathSciNet  MATH  Google Scholar 

  31. M. Srivastava et al., Anti-synchronization between identical and non-identical fractional-order chaotic systems using active control method, Nonlinear Dyn., 76 (2014) 905–914.

    Article  MathSciNet  Google Scholar 

  32. L. Chao and X. Wang, Chaos in the fractional-order complex Lorenz system and its Synchronization, Nonlinear Dyn., 71 (2013) 241–257.

    Article  MathSciNet  MATH  Google Scholar 

  33. G.-C. Wu and D. Baleanu, Chaos synchronization of the discrete fractional logistic map, Signal Processing, 102 (2014) 96–99.

    Article  Google Scholar 

  34. G. Si, Z.-Y. Sun and Y.-B. Zhang, A general method for synchronizing an integer-order chaotic system and a fractional-order chaotic system, Chin. Phys. B, 20 (8) (2011) 080505–1-7.

    Article  Google Scholar 

  35. D. Heleschewitz and D. Matignon, Diffusive realizations of fractional integro-differential operators: structural analysis under approxi-mation, Conference IFAC, System, Structure and Control, Nantes, France, 2 (1998) 243–248.

    Google Scholar 

  36. G. Montseny, Diffusive representation of pseudo differential time operators, Proc. ESSAIM 5 (1998) 159–175.

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Electrical and Information Engineering, Northeast Petroleum University, Daqing, 163318, China

    Keyong Shao

  2. School of Marine Science and Technology, Northwestern Polytechnical University, Xi’an, 710072, China

    Lei Zuo

Authors
  1. Keyong Shao
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Lei Zuo
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Keyong Shao.

Additional information

Recommended by Associate Editor Yang Shi

Keyong Shao is currently a Pofessor in School of Electrical and Information Engineering, Northeast Petroleum University. He was born in Huainan, Henan Province, China in 1970. He received his B.E. degree from Daqing Northeast Petroleum Institute in 1992, his M.E. degree from Northeast University, Shenyang, China, in 2000, his Ph.D. in Control Theory and Control Engineering from Northeast University, Shenyang, China, in 2003. His main research interests include robust control and fractional-order system theory.

Lei Zuo is currently a Ph.D. candidate in School of Marine Science and Technology, Northwestern Polytechnical University, China. He received his B.Eng. degree from NWPU in 2011 and directly began his Ph.D. program in Control Theory and Control Application. He is interested in adaptive control, coverage control and optimization. His current research interests are focus on the coverage control for underwater vehicles in unknown environment.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Shao, K., Zuo, L. Sufficient stability condition for fractional-order nonlinear systems. J Mech Sci Technol 31, 3531–3537 (2017). https://doi.org/10.1007/s12206-017-0641-z

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12206-017-0641-z

Keywords

Search

Navigation