Qualitative analysis of second-order fuzzy difference equation with quadratic term

Abstract

In this paper, we explore the qualitative features of a second-order fuzzy difference equation with quadratic term

$$\begin{aligned} x_{n+1}=A+\frac{Bx_{n}}{x_{n-1}^2},\ \ n=0,1,\ldots . \end{aligned}$$

Here the parameters $A, B\in \Re _F^+$ and the initial values $x_0, x_{-1}\in \Re _F^+$. Utilizing a generalization of division (g-division) of fuzzy numbers, we obtain some sufficient condition on the qualitative features including boundedness, persistence, and convergence of positive fuzzy solution of the model, Moreover two simulation examples are presented to verify our theoretical analysis.

1 Introduction

Difference equation is one of the most important dynamical model. It is the analogue of corresponding differential equation and delay differential equation having an extensive applications in computer science, control engineering, chemistry, biology, economics, etc. (see [1,2,3,4,5,6,7,8,9,10,11]). Recently, many authors are interested in studying qualitative features of rational difference equation. For example, Bešo et al. [12] proposed a second-order rational difference equation with quadratic term

$$\begin{aligned} x_{n+1}=\gamma +\delta \frac{x_n}{x_{n-1}^2}, n=0,1,\ldots , \end{aligned}$$

(1)

where $\gamma>0, \delta >0$, and the initial values $x_0>0, x_{-1}>0$.

In 2017, Khyat et al. [13] explored a similar model with quadratic term in both the numerator and denominator

$$\begin{aligned} x_{n+1}=a+ \frac{x_n^2}{x_{n-1}^2}, n=0,1,\ldots . \end{aligned}$$

(2)

Furthermore, they obtained the globally asymptotically stability of (2) and the direction of the Neimark–Sacker bifurcation.

In the last few decades, there are many publications on the stability, oscillatory, periodicity, and boundedness of nonlinear rational difference equations. Moreover a lot of similar qualitative features also appear in nonlinear rational difference equation systems (see [14,15,16,17]).

Although these models are very simple in their forms, we can not understand fully the qualitative features of their solutions. In fact, these models inevitably implicit inherent uncertainty or vague. It is well known that fuzzy set is a powerful tool to cope with these uncertainties or subjective information in mathematical model. Therefore, it is a natural method to explore dynamical model with uncertainty or impression by establishing fuzzy difference equation (FDE) or fuzzy differential equation.

FDE is a special kind of difference equation whose coefficients and the initial condition are fuzzy numbers, and its’ solution is a sequence of fuzzy number. Due to the advantage of FDE in dealing with inherent imprecision, the study on qualitative features of these models has become an important research topic both from theoretical viewpoint and in applications. Therefore, in the last decades, there has been an increasing results on the study of FDE (see [18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33]). It is found that fuzzy set theory has potential in the application of fuzzy differential equations and fuzzy time series (see [34,35,36,37,38,39,40]).

Inspired by previous works, in this paper, utilizing a generalization of division (g-division) of fuzzy numbers, we explore the qualitative features of positive fuzzy solution to the following FDE with quadratic term

$$\begin{aligned} x_{n+1}=A+\frac{Bx_n}{x_{n-1}^2},\ n=0,1,\ldots , \end{aligned}$$

(3)

where the initial condition $x_{-1}, x_0$, and the parameters A, B are positive fuzzy numbers.

The organization of this paper is arranged as follows. Section 2 gives some basic concepts of fuzzy numbers used throughout the paper. In Sect. 3, the qualitative features of the positive fuzzy solution to FDE (3) are obtained by virtue of g-division of fuzzy numbers. Section 4 presents two illustrative examples to verify our theoretic results. A general conclusion and discussion are drawn in Sect. 5.

2 Preliminary and definitions

In this section, we first review some basic concepts and definitions to be used in the sequel. These particular descriptions are found in many publications [20,21,22].

A function defined as $U: R\rightarrow [0,1]$ is called a fuzzy number if it is normal, fuzzy convex, upper semi-continuous, and compactly support on R.

For $\alpha \in (0,1]$, we denote the $\alpha -$cuts of U by $[U]_\alpha =\{x\in R: U(x)\ge \alpha \}$, and for $\alpha =0$, the support of U is written as $\text{ supp }U=[U]_0=\overline{\{x\in R: U(x)>0\}}$.

It is easy to see that the $[U]_\alpha$ is a closed interval. Provided that $\text{ supp } U\subset (0,\infty ),$ then U is said to be a positive fuzzy number. Particularly, if U is a positive real number, then it is said to be a trivial fuzzy number, i.e., $[U]_\alpha =[U, U], \alpha \in (0,1].$

Let U, V be fuzzy numbers, $[U]_\alpha =[U_{l,\alpha },U_{r,\alpha }],[V]_\alpha =[V_{l,\alpha },V_{r,\alpha }],\alpha \in [0,1]$, $k>0$. Addition and multiplication of fuzzy numbers are defined as follows.

$$\begin{aligned}{}[U+V]_\alpha= & {} [U_{l,\alpha }+V_{l,\alpha },U_{r,\alpha }+V_{r,\alpha }], \end{aligned}$$

(4)

$$\begin{aligned}{}[kU]_\alpha= & {} [kU_{l,\alpha },kU_{r,\alpha }]. \end{aligned}$$

(5)

The family of fuzzy numbers with addition and multiplication defined by Eqs. (4) and (5) is written as $\Re _F$. Particularly, the family of positive (resp. negative) fuzzy numbers is denoted by $\Re _F^+$( resp. $\Re _F^-$).

Definition 2.1

Let $U,V\in \Re _F$, the metric is defined as follows.

$$\begin{aligned} D(U,V)=\sup _{\alpha \in [0,1]}\max \{\mid U_{l,\alpha }-V_{l,\alpha }\mid ,\mid U_{r,\alpha }-V_{r,\alpha }\mid \}. \end{aligned}$$

(6)

Obviously, $(\Re _F,D)$ is a complete metric space.

Definition 2.2

[41] Let $U, V\in \Re _F$, $[U]_\alpha =[U_{l,\alpha }, U_{r,\alpha }], [V]_\alpha =[V_{l,\alpha }, V_{r,\alpha }]$, $0\notin [V]_\alpha , \forall \alpha \in [0,1]$. The g-division $\div _g$ of the fuzzy numbers is written as $W=U\div _gV$ with $\alpha -$cuts $[W]_\alpha =[W_{l,\alpha },W_{r,\alpha }]$( $[W]_\alpha ^{-1}=[1/W_{r,\alpha },1/W_{l,\alpha }]$), where

$$\begin{aligned}{}[W]_\alpha =[U]_\alpha \div _g[V]_\alpha \Longleftrightarrow \left\{ \begin{array}{ll} (i) &{} [U]_\alpha =[V]_\alpha [W]_\alpha ,\\ &{}\\ (ii)&{} [V]_\alpha =[U]_\alpha [W]_\alpha ^{-1}, \end{array} \right. \end{aligned}$$

(7)

if W is a proper fuzzy number.

Remark 2.1

According to [41], Let $U,V\in \Re _F^+$, if $U\div _g V=W\in \Re _F^+$ exists, then there are two cases

Case (i). if $U_{l,\alpha }V_{r,\alpha }\le U_{r,\alpha }V_{l,\alpha },\forall \alpha \in [0,1],$ then $W_{l,\alpha }=\frac{U_{l,\alpha }}{V_{l,\alpha }}, W_{r,\alpha }=\frac{U_{r,\alpha }}{V{r,\alpha }},$

Case (ii). if $U_{l,\alpha }V_{r,\alpha }\ge U_{r,\alpha }V_{l,\alpha },\forall \alpha \in [0,1],$ then $W_{l,\alpha }=\frac{U_{r,\alpha }}{V_{r,\alpha }}, W_{r,\alpha }=\frac{U_{l,\alpha }}{V{l,\alpha }}.$

Definition 2.3

Let $x_n\in \Re _F^+, n=1, 2, \ldots$, $(x_n)$ is said to be persistence (resp. bounded) provided that there is $M>0$ (resp. $N>0$) satisfying

$$\begin{aligned} \text{ supp }\ x_n\subset [M,\infty ) (\text{ resp }.\ \text{ supp }\ x_n\subset (0,N]). \end{aligned}$$

The sequence $(x_n)$ is bounded and persistence if there are $M, N>0$ satisfying

$$\begin{aligned} \text{ supp }\ x_n\subset [M,N], n=1, 2, \ldots . \end{aligned}$$

The sequence $(x_n)$ is unbounded if the norm of $x_n$, $\Vert x_n\Vert ,n=1,2,\ldots ,$ is unbounded.

Definition 2.4

If a sequence $(x_n)$ of positive fuzzy numbers is satisfied with FDE (3), then $x_n$ is said to be a positive solution of FDE (3). $x\in \Re _F^+$ is called a positive equilibrium of FDE (3) if

$$\begin{aligned} x=A+\frac{Bx}{x^2}. \end{aligned}$$

Let $x_n,x\in \Re _F^+, n=0,1,2,\ldots ,$ we say $x_n$ converges to x as $n\rightarrow \infty$ if $\lim _{n\rightarrow \infty }D(x_n,x)=0$.

Lemma 2.1

Let $g: R^+\times R^+\times R^+\times R^+\rightarrow R^+$ be continuous, $A, B, C, D\in \Re _F^+$. Then

$$\begin{aligned}{}[g(A,B,C,D)]_\alpha =g([A]_\alpha ,[B]_\alpha ,[C]_\alpha ,[D]_\alpha ),\ \ \alpha \in (0,1]. \end{aligned}$$

(8)

Lemma 2.2

[8] Let $I_x, I_y$ be some intervals of real numbers and let $f: I_x^2\times I_y^2\rightarrow I_x,$, $g:I_x^2\times I_y^2\rightarrow I_y$ be continuously differentiable functions. Then for every initial conditions $(x_i,y_i)\in I_x\times I_y (i=-1,0)$, the following system of difference equations

$$\begin{aligned} \left\{ \begin{array}{ccc} x_{n+1}=f(x_n,x_{n-1},y_n,y_{n-1}),&{}\\ &{} n=0,1,2,\ldots ,\\ y_{n+1}=g(x_n,x_{n-1},y_n,y_{n-1}).&{} \end{array} \right. \end{aligned}$$

(9)

has a unique solution $\{(x_i,y_i)\}_{n=-1}^{+\infty }$.

Definition 2.5

[8] A point $({\overline{x}},{\overline{y}})$ is called an equilibrium point of system (9) if

$$\begin{aligned} {\overline{x}}=f({\overline{x}},{\overline{x}},{\overline{y}},{\overline{y}}),\ \ {\overline{y}}=g({\overline{x}},{\overline{x}},{\overline{y}},{\overline{y}}). \end{aligned}$$

That is, $(x_n,y_n)=({\overline{x}},{\overline{y}})$ for $n\ge 0$ is the solution of (9), or equivalently, $({\overline{x}},{\overline{y}})$ is a fixed point of the vector map (f, g).

Definition 2.6

[8] Let $({\overline{x}},{\overline{y}})$ be an equilibrium point of (9). (i) The equilibrium point $({\overline{x}},{\overline{y}})$ is called locally stable if for every $\varepsilon >0$, there exists $\delta >0$ such that for all $(x_i,y_i)\in I_x\times I_y(i=-1,0)$, with $\mid x_{-1}-{\overline{x}}\mid +\mid x_0-{\overline{x}}\mid<\delta , \mid y_{-1}-{\overline{y}}\mid +\mid y_0-{\overline{y}}\mid <\delta ,$ we have $\mid x_n-{\overline{x}}\mid<\varepsilon , \mid y_n-{\overline{y}}\mid <\varepsilon ,$ for $n\ge 0.$

(ii) The equilibrium $({\overline{x}},{\overline{y}})$ of (9) is called locally asymptotically stable if it is locally stable, and if there exists $\gamma >0$, such that for all $(x_i,y_i)\in I_x\times I_y(i=-1,0)$, with $\mid x_{-1}-{\overline{x}}\mid +\mid x_0-{\overline{x}}\mid<\gamma , \mid y_{-1}-{\overline{y}}\mid +\mid y_0-{\overline{y}}\mid <\gamma ,$ we have

$$\begin{aligned} \lim _{n\rightarrow \infty }x_n={\overline{x}},\ \ \lim _{n\rightarrow \infty }y_n={\overline{y}}. \end{aligned}$$

(iii) The equilibrium $({\overline{x}},{\overline{y}})$ of (9) is called a global attractor if for every $(x_i,y_i)\in I_x\times I_y(i=-1,0)$, we have

$$\begin{aligned} \lim _{n\rightarrow \infty }x_n={\overline{x}},\ \ \lim _{n\rightarrow \infty }y_n={\overline{y}}. \end{aligned}$$

(iv) The equilibrium $({\overline{x}},{\overline{y}})$ of (9) is called globally asymptotically stable if it is locally stable and a global attractor.

(v) The equilibrium $({\overline{x}},{\overline{y}})$ of (9) is called unstable if it is not stable.

3 Main results

3.1 Existence of positive fuzzy solution

In this section, we first discuss the existence of the positive fuzzy solution of FDE (3).

Theorem 3.1

Consider FDE (3), where $A, B\in \Re _F^+$, then there is a unique positive fuzzy solution $x_n$ of FDE (3), for $x_{-1},x_0\in \Re _F^+$.

Proof

The proof of Theorem is similar to those of Proposition 2.1 [19]. Assume that $(x_n)$ is a sequence of fuzzy numbers and satisfies FDE (3) with initial values $x_{-1}, x_0.$ Consider the $\alpha -$cuts, $\alpha \in (0,1], n\in N^+$

$$\begin{aligned} \left\{ \begin{array}{lll} {[}x_n]_\alpha &{}=&{}[L_{n,\alpha },R_{n,\alpha }], \\ &{}&{}\\ {[}A]_\alpha &{}=&{} [A_{l,\alpha }, A_{r,\alpha }], \\ &{}&{}\\ {[}B]_\alpha &{}=&{} [B_{l,\alpha },B_{r,\alpha }]. \end{array} \right. \end{aligned}$$

(10)

Applying Lemma 2.1, it follows from (3) and (10) that

$$\begin{aligned}{}[x_{n+1}]_\alpha= & {} [L_{n+1,\alpha },R_{n+1,\alpha }]=\left[ A+\frac{Bx_n}{x_{n-1}^2}\right] _\alpha =[A]_\alpha +\frac{[B]_\alpha \times [x_n]_\alpha }{[x_{n-1}^2]_\alpha }\\= & {} [A_{l,\alpha },A_{r\alpha }]+\frac{[B_{l,\alpha }L_{n,\alpha },B_{r,\alpha }R_{n,\alpha }]}{[L_{n-1,\alpha }^2, R_{n-1,\alpha }^2]}. \end{aligned}$$

Utilizing g-division of fuzzy numbers, one of the following two cases occurs.

Case (i)

$$\begin{aligned}{}[x_{n+1}]_\alpha =[L_{n+1,\alpha },R_{n+1,\alpha }]=\left[ A_{l,\alpha }+\frac{B_{l,\alpha }L_{n,\alpha }}{L_{n-1,\alpha }^2}, A_{r,\alpha }+\frac{B_{r,\alpha }R_{n,\alpha }}{R_{n-1,\alpha }^2}\right] . \end{aligned}$$

(11)

Case (ii)

$$\begin{aligned}{}[x_{n+1}]_\alpha =[L_{n+1,\alpha },R_{n+1,\alpha }]=\left[ A_{l,\alpha }+\frac{B_{r,\alpha }R_{n,\alpha }}{R_{n-1,\alpha }^2}, A_{r,\alpha }+\frac{B_{l,\alpha }L_{n,\alpha }}{L_{n-1,\alpha }^2}\right] . \end{aligned}$$

(12)

If Case (i) holds true, from (11), one gets, for $\alpha \in (0,1], n\in \{0,1,2,\ldots \},$

$$\begin{aligned} L_{n+1,\alpha }=A_{l,\alpha }+\frac{B_{l,\alpha }L_{n,\alpha }}{L_{n-1,\alpha }^2},\ \ R_{n+1,\alpha }=A_{r,\alpha }+\frac{B_{r,\alpha }R_{n,\alpha }}{R_{n-1,\alpha }^2}. \end{aligned}$$

(13)

It is clear that there is a unique solution $(L_{n,\alpha },R_{n,\alpha })$ for any initial value $(L_{k,\alpha },R_{k,\alpha }),k=-1,0,\alpha \in (0,1]$. We only need to show that, for $\alpha \in (0,1],\ n\in N^+$, $[L_{n,\alpha },R_{n,\alpha }]$ makes certain the positive fuzzy solution $x_n$ of FDE (3) with the initial condition $x_{i}, i=0,-1$, and

$$\begin{aligned}{}[x_n]_\alpha =[L_{n,\alpha },R_{n,\alpha }]. \end{aligned}$$

(14)

From [18], since $x_j\in \Re _F^+,j=-1,0$, for $\alpha _i\in (0,1], i=1,2,$ and $\alpha _1\le \alpha _2$, it has

$$\begin{aligned} 0<L_{j,\alpha _1}\le L_{j,\alpha _2}\le R_{j,\alpha _2}\le R_{j,\alpha _1},j=-1, 0. \end{aligned}$$

(15)

We declare that, for $n=0,1,2,\ldots ,$

$$\begin{aligned} L_{n,\alpha _1}\le L_{n,\alpha _2}\le R_{n,\alpha _2}\le R_{n,\alpha _1}. \end{aligned}$$

(16)

By mathematical induction. From (15), for $n=0,1$, it is true. Suppose that, for $n\le k, k\in N^+$, (16) holds true, then it follows from (13) and (16) that, for $n=k+1$,

$$\begin{aligned} L_{k+1,\alpha _1}= & {} A_{l,\alpha _1}+\frac{B_{l,\alpha _1}L_{k,\alpha _1}}{L_{k-1,\alpha _1}^2} \le A_{l,\alpha _2}+\frac{B_{l,\alpha _2}L_{k,\alpha _2}}{L_{k-1,\alpha _2}^2}=L_{k+1,\alpha _2}\\= & {} A_{l,\alpha _2}+\frac{B_{l,\alpha _2}L_{k,\alpha _2}}{L_{k-1,\alpha _2}^2}\le A_{r,\alpha _2} +\frac{B_{r,\alpha _2}R_{k,\alpha _2}}{R_{k-1,\alpha _2}^2}=R_{k+1,\alpha _2}\\= & {} A_{r,\alpha _2}+\frac{B_{r,\alpha _2}R_{k,\alpha _2}}{R_{k-1,\alpha _2}^2}\le A_{r,\alpha _1}+\frac{B_{r,\alpha _1}R_{k,\alpha _1}}{R_{k-1,\alpha _1}^2}=R_{k+1,\alpha _1} \end{aligned}$$

So (16) holds true. Also, from (13), it has

$$\begin{aligned} L_{1,\alpha }=A_{l,\alpha }+\frac{B_{l,\alpha }L_{0,\alpha }}{L_{-1,\alpha }^2},\ \ R_{1,\alpha }=A_{r,\alpha }+\frac{B_{r,\alpha }R_{0,\alpha }}{R_{-1,\alpha }^2},\ \ \alpha \in (0,1]. \end{aligned}$$

(17)

Since $x_j\in \Re _F^+, j=-1, 0$, and $A, B\in \Re _F^+$ , then $L_{i,\alpha },R_{i,\alpha },i=0,-1,$ are left continuous. So, one gets from (17) that $L_{1,\alpha },R_{1,\alpha }$ are also left continuous. By inductively, we can show that, for $n\ge 1$, $L_{n,\alpha }$ and $R_{n,\alpha }$ are left continuous.

Secondly, we will prove that $\text{ supp } x_n=\overline{\bigcup _{\alpha \in (0,1]}[L_{n,\alpha },R_{n,\alpha }]}$ is compact. It need to show that $\bigcup _{\alpha \in (0,1]}[L_{n,\alpha },R_{n,\alpha }]$ is bounded. Since $x_j\in \Re _F^+,j=-1,0$, and $A,B\in \Re _F^+$, there exist $M_A>0,N_A>0,N_B>0, M_B>0, M_j>0,N_j>0,j=-1,0,$ such that, $\forall \alpha \in (0,1]$,

$$\begin{aligned} \left\{ \begin{array}{l} [A_{l,\alpha },A_{r,\alpha }]\subset [M_A,N_A],\\ \\ {[}B_{l,\alpha },B_{r,\alpha }]\subset [M_B,N_B], \\ \\ {[}L_{j,\alpha },R_{j,\alpha }]\subset [M_j,N_j]. \end{array} \right. \end{aligned}$$

(18)

Hence from (17) and (18), one can get, for $n=1$,

$$\begin{aligned} {[}L_{1,\alpha },R_{1,\alpha }]\subset \left[ M_A+\frac{M_BM_0}{M_{-1}^2},N_A+\frac{N_BN_0}{N_{-1}^2}\right] ,\alpha \in (0,1]. \end{aligned}$$

(19)

From which, it follows that

$$\begin{aligned} \bigcup _{\alpha \in (0,1]}[L_{1,\alpha },R_{1,\alpha }]\subset \left[ M_A+\frac{M_BM_0}{M_{-1}^2}, N_A+\frac{N_BN_0}{N_{-1}^2}\right] ,\ \ \alpha \in (0,1]. \end{aligned}$$

(20)

Hence, $\overline{\bigcup _{\alpha \in (0,1]}[L_{1,\alpha },R_{1,\alpha }]}$ is compact, and $\overline{\bigcup _{\alpha \in (0,1]}[L_{1,\alpha },R_{1,\alpha }]}\subset (0,\infty )$. Deducing inductively, one can get that $\overline{\bigcup _{\alpha \in (0,1]}[L_{n,\alpha }, R_{n,\alpha }]}$ is compact, moreover, for $n=1,2,\ldots ,$

$$\begin{aligned} \overline{\bigcup _{\alpha \in (0,1]}[L_{n,\alpha },R_{n,\alpha }]}\subset (0,\infty ). \end{aligned}$$

(21)

And since $L_{n,\alpha }, R_{n,\alpha }$ are left continuous, from (16) and (21), we get that $[L_{n,\alpha }, R_{n,\alpha }]$ makes certain a positive sequence $x_n$ satisfying (14).

Now we show that, for the initial conditions $x_{i} (i=0,-1)$, $x_n$ is the solution of (3). Since, $\forall \alpha \in (0,1]$,

$$\begin{aligned}{}[x_{n+1}]_\alpha= & {} [L_{n+1,\alpha },R_{n+1,\alpha }]\\= & {} \left[ A_{l,\alpha }+\frac{B_{l,\alpha }L_{n,\alpha }}{L_{n-1,\alpha }^2}, A_{r,\alpha }+\frac{B_{r,\alpha }R_{n,\alpha }}{R_{n-1,\alpha }^2}\right] =\left[ A+\frac{Bx_{n}}{x_{n-1}^2}\right] _\alpha . \end{aligned}$$

Therefore, $x_n$ is the solution of FDE (3) with initial conditions $x_{i}, i=0, -1$.

Suppose that, for the initial values $x_{i}\in \Re _F^+, i=0,-1$, ${\overline{x}}_n$ is another solution of (3). Then, deducing as above, it has, for $n\in N^+$

$$\begin{aligned}{}[{\overline{x}}_n]_\alpha =[L_{n,\alpha },R_{n,\alpha }],\ \ \ \alpha \in (0,1].\ \ \ \end{aligned}$$

(22)

Then, (14) and (22) imply that $[x_n]_\alpha =[{\overline{x}}_n]_\alpha , \alpha \in (0,1],n\in N^+,$ so $x_n={\overline{x}}_n.$

If Case (ii) occurs, The proof is similar to the proof above. This completes the proof of Theorem 3.1. $\square$

3.2 Dynamics of FDE (3)

In order to obtain results on qualitative features of the positive solutions, Case (i) and Case (ii) are considered respectively.

If Case (i) occurs, the following lemma is required.

Lemma 3.1

Consider the following difference equations

$$\begin{aligned} y_{n+1}=p+\frac{cy_n}{y_{n-1}^2},\ \ n=0,1,\ldots , \end{aligned}$$

(23)

where $p^2>c>0, y_{i}\in (0,+\infty ), i=0,-1$. Then

$$\begin{aligned} p\le y_n\le \frac{p^3}{p^2-c}+y_3, \ \ n\ge 4. \end{aligned}$$

(24)

Proof

It is clear that, for $n\ge 1$, $y_n>p, z_n>q$ from (23). Moreover, for $n\ge 4$,

$$\begin{aligned} y_n=p+\frac{cy_{n-1}}{y_{n-2}^2}\le p+\frac{c}{p^2}y_{n-1}, \end{aligned}$$

(25)

By induction, it can get that, for $n-k\ge 3$

$$\begin{aligned} y_n\le & {} p+\frac{c}{p}+\frac{c}{p^4}y_{n-2}\le p+\frac{c}{p}+\frac{c^2}{p^3}+\frac{c^3}{p^6}y_{n-3} \le p+\frac{c}{p}+\frac{c^2}{p^3}+\frac{c^3}{p^5}+\frac{c^4}{p^8}y_{n-4}\nonumber \\\le & {} \cdots \le \sum _{i=1}^{k}\frac{c^{i-1}}{p^{2i-3}}+\frac{c^k}{p^{2k}}y_{n-k} =\frac{p}{1-c/p^2}\left[ 1-\left( \frac{c}{p^2}\right) ^{k}\right] +\frac{c^k}{p^{2k}}y_{n-k}\nonumber \\\le & {} \frac{p^3}{p^2-c}+y_{n-k} \end{aligned}$$

(26)

Noting $n-k\ge 3$ is equal to $k\le n-3$. The proposition is true. $\square$

Theorem 3.2

Consider FDE (3), where $A, B\in \Re _F^+$, and $x_{-1},x_0\in \Re _F^+$. Suppose that there exist $M_A>0, N_A>0, M_B>0, N_B>0$, $\forall \alpha \in (0,1]$, such that

$$\begin{aligned} \left\{ \begin{array}{l} M_A\le A_{l,\alpha }\le A_{r,\alpha }\le N_A, \\ \\ \ M_B\le B_{l,\alpha }\le B_{r,\alpha }\le N_B,\\ \\ M_A^2>M_B,\ \ N_A^2>N_B. \end{array} \right. \end{aligned}$$

(27)

Then every positive fuzzy solution $x_n$ of FDE (3) is bounded and persists.

Proof

If Case (i) occurs. Let $x_n$ be a positive fuzzy solution of FDE (3). It is obvious from (11) that, for $n=1,2,\ldots ,\ \ \alpha \in (0,1],$

$$\begin{aligned} M_A\le L_{n,\alpha },\ \ M_A\le R_{n,\alpha }. \end{aligned}$$

(28)

Then, from (21), Lemma 3.1, and $A_{l,\alpha }\ge M_A$, it has, for $n\ge 5,$

$$\begin{aligned}{}[L_{n,\alpha },R_{n,\alpha }]\subset [M_A, T_\alpha ], \end{aligned}$$

(29)

where

$$\begin{aligned} T_\alpha = \frac{N_A^3}{N_A^2-N_B}+R_{3,\alpha }. \end{aligned}$$

Then since $x_n\in \Re _F^+$, there exists $T>0$, satisfying,

$$\begin{aligned} T_\alpha \le T,\ \ \ \forall \alpha \in (0,1]. \end{aligned}$$

(30)

Therefore, (29) and (30) imply that $[L_{n,\alpha },R_{n,\alpha }]\subset [M_A,T],$ then, for $n\ge 4, \bigcup _{\alpha \in (0,1]}[L_{n,\alpha },R_{n,\alpha }]\subset [M_A,T]$, so $\overline{\bigcup _{\alpha \in (0,1]}[L_{n,\alpha },R_{n,\alpha }]}\subseteq [M_A,T]$. Thus the positive fuzzy solution $x_n$ is bounded and persists.

To show that the convergence of positive fuzzy solution $x_n$, we give the following lemmas. $\square$

Lemma 3.2

Consider the following difference equation

$$\begin{aligned} y_{n+1}=p+\frac{cy_n}{y_{n-1}^2},\ n=0,1,2,\ldots , \end{aligned}$$

(31)

Assume $p^2>\frac{4c}{3}$. Then the equilibrium ${\overline{y}}$ of (31) is locally asymptotically stable.

Proof

Let ${\overline{y}}$ be an equilibrium of (31), we obtain that ${\overline{y}}=\frac{p+\sqrt{p^2+4c}}{2}.$ The linearized equation of (31) at equilibrium ${\overline{y}}$ is

$$\begin{aligned} y_{n+1}-\frac{2c}{p^2+2c+p\sqrt{p^2+4c}}y_n+\frac{4c}{p^2+2c+p\sqrt{p^2+4c}}y_{n-1}=0, \end{aligned}$$

(32)

Since $p^2>\frac{4c}{3}$, it can get

$$\begin{aligned} \frac{6c}{p^2+2c+p\sqrt{p^2+4c}}<1. \end{aligned}$$

By virtue of Theorem 1.3.7 [8], the equilibrium ${\overline{y}}$ of (31) is locally asymptotically stable. $\square$

Lemma 3.3

Consider Eq. (23), if $p^2>\frac{4c}{3}$. Then every positive solution $(y_n)$ of (23) tends to the positive equilibrium

$$\begin{aligned} {\overline{y}}=\frac{p+\sqrt{p^2+4c}}{2}. \end{aligned}$$

Proof

From system (23), we obtain a unique equilibrium ${\overline{y}}=\frac{p+\sqrt{p^2+4c}}{2}.$ If $(y_n)$ is a positive solution of (23). Let

$$\begin{aligned} \Lambda _1=\lim _{n\rightarrow \infty }\sup y_n,\ \ \lambda _1=\lim _{n\rightarrow \infty }\inf y_n. \end{aligned}$$

Applying Lemma 3.1, we get $0<p<\lambda _1\le \Lambda _1<\infty .$ From (23), it implies that

$$\begin{aligned} \Lambda _1\le p+\frac{c\Lambda _1}{\lambda _1^2}, \ \ \lambda _1\ge p+\frac{c\lambda _1}{\Lambda _1^2}. \end{aligned}$$

This can derive that

$$\begin{aligned} \Lambda _1\le \lambda _1. \end{aligned}$$

Thus $\Lambda _1=\lambda _1$. Namely $\lim _{n\rightarrow \infty }y_n$ exists. Since ${\overline{y}}$ of (23) is the unique positive equilibrium, then $\lim _{n\rightarrow \infty }y_n={\overline{y}}$.

Combining two lemmas above, we have the following theorem $\square$

Theorem 3.3

Consider Eq. (23), if $p^2>\frac{4c}{3}$, then the unique positive equilibrium ${\overline{y}}$ of (23) is globally asymptotically stable.

Theorem 3.4

If $A_{l,\alpha }^2>\frac{4}{3}B_{l,\alpha }, A_{r,\alpha }^2>\frac{4}{3}B_{r,\alpha }$, for all $\alpha \in (0,1],$ then every positive fuzzy solution $x_n$ of FDE (3) converges to the fuzzy positive equilibrium x as $n\rightarrow \infty .$

Proof

Suppose that there is a fuzzy number x satisfying

$$\begin{aligned} x=A+\frac{Bx}{x^2},\ \ [x]_\alpha =[L_\alpha ,R_\alpha ],\ \ \alpha \in (0,1]. \end{aligned}$$

(33)

in which $L_\alpha , R_\alpha \ge 0$. Then, from (33), one gets

$$\begin{aligned} L_\alpha =A_{l,\alpha }+\frac{B_{l,\alpha }L_\alpha }{L_\alpha ^2},\ \ R_\alpha =A_{r,\alpha }+\frac{B_{r,\alpha }R_\alpha }{R_\alpha ^2}. \end{aligned}$$

(34)

Hence we have from (34) that

$$\begin{aligned} L_\alpha =\frac{A_{l,\alpha }+\sqrt{A_{l,\alpha }^2+4B_{l,\alpha }}}{2},\ \ R_\alpha =\frac{A_{r,\alpha }+\sqrt{A_{r,\alpha }^2+4B_{r,\alpha }}}{2}. \end{aligned}$$

Let $x_n$ be a positive fuzzy solution of FDE (3) satisfying (11). Since $A_{l,\alpha }^2>\frac{4}{3}B_{l,\alpha }, A_{r,\alpha }^2>\frac{4}{3}B_{r,\alpha }, \alpha \in (0,1]$. Utilizing Lemma 3.3 to system (13), then

$$\begin{aligned} \lim _{n\rightarrow \infty }L_{n,\alpha }=L_\alpha ,\ \ \lim _{n\rightarrow \infty }R_{n,\alpha }=R_\alpha , \end{aligned}$$

(35)

Then, from (35), it has

$$\begin{aligned} \lim _{n\rightarrow \infty }D(x_n,x)=\lim _{n\rightarrow \infty }\sup _{\alpha \in (0,1]}\{\max \{\mid L_{n,\alpha }-L_\alpha \mid , \mid R_{n,\alpha }-R_\alpha \mid \}\}=0. \end{aligned}$$

The proof of the theorem is completed.

Secondly, if Case (ii) occurs, i.e., for $n\in \{0,1,2,\ldots \},$

$$\begin{aligned} L_{n+1,\alpha }=A_{l,\alpha }+\frac{B_{r,\alpha }R_{n,\alpha }}{R_{n-1,\alpha }^2},\ \ R_{n+1,\alpha }=A_{r,\alpha }+\frac{B_{l,\alpha }L_{n,\alpha }}{L_{n-1,\alpha }^2}, \ \alpha \in (0,1]. \end{aligned}$$

(36)

The following lemmas are required. $\square$

Lemma 3.4

Consider the following difference equations system.

$$\begin{aligned} y_{n+1}=p+\frac{dz_n}{z_{n-1}^2},\ \ z_{n+1}=q+\frac{cy_n}{y_{n-1}^2},\ \ n=0,1,\ldots , \end{aligned}$$

(37)

where $y_{i}, z_{i}\in (0,+\infty ), i=-1,0$. If

$$\begin{aligned} p>d>1,\ \ q>c>1. \end{aligned}$$

(38)

Then, for $n\ge 4$,

$$\begin{aligned} p\le y_n\le \frac{p(p^2q^2+pqd)}{p^2q^2-cd}+y_2,\ \ q\le z_n\le \frac{q(p^2q^2+pqc)}{p^2q^2-cd}+z_2. \end{aligned}$$

(39)

Proof

Let $Y_n=\frac{y_n}{p}, Z_n=\frac{z_n}{q}$, then Eq. (37) can be transformed into the following systems

$$\begin{aligned} Y_{n+1}=1+\frac{d}{pq}\frac{Z_n}{Z_{n-1}^2},\ \ Z_{n+1}=1+\frac{c}{pq}\frac{Y_n}{Y_{n-1}^2},\ n=0,1,2,\ldots , \end{aligned}$$

(40)

From (40), we have $Y_n\ge 1, Z_n\ge 1,$ for $n\ge 1.$ And, for $n\ge 4$,

$$\begin{aligned} \left\{ \begin{array}{l} Y_n\le 1+\frac{d}{pq}Z_{n-1}\le 1+\frac{d}{pq}+\frac{cd}{p^2q^2}Y_{n-2},\\ \\ Z_n\le 1+\frac{c}{pq}Y_{n-1}\le 1+\frac{c}{pq}+\frac{cd}{p^2q^2}Z_{n-2}. \end{array} \right. \end{aligned}$$

(41)

Deducing inductively, it can conclude that, for $n-2k\ge 2$,

$$\begin{aligned} Y_n\le & {} 1+\frac{d}{pq}+\frac{cd}{p^2q^2}Y_{n-2}\le 1+\frac{d}{pq}+\frac{cd}{p^2q^2}+\frac{cd^2}{p^3q^3}Z_{n-3}\nonumber \\\le & {} 1+\frac{d}{pq}+\frac{cd}{p^2q^2}+\frac{cd^2}{p^3q^3}+\frac{c^2d^2}{p^4q^4}Y_{n-4}\nonumber \\\le & {} \cdots \le 1+\frac{d}{pq}+\frac{cd}{p^2q^2}+\frac{cd^2}{p^3q^3}+\frac{c^2d^2}{p^4q^4}+\cdots +\frac{c^{2k-1}d^{2k}}{p^{2k-1}q^{2k-1}}+\frac{c^{2k}d^{2k}}{p^{2k}q^{2k}}Y_{n-2k}\nonumber \\= & {} \frac{1}{1-\frac{cd}{p^2q^2}}\left[ 1-\left( \frac{cd}{p^2q^2}\right) ^{k-1}\right] +\frac{\frac{d}{pq}}{1-\frac{cd}{p^2q^2}}\left[ 1-\left( \frac{cd}{p^2q^2}\right) ^k\right] +\frac{c^{2k}d^{2k}}{p^{2k}q^{2k}}Y_{n-2k}\nonumber \\\le & {} \frac{p^2q^2+pqd}{p^2q^2-cd}+Y_{n-2k}. \end{aligned}$$

(42)

$$\begin{aligned} Z_n\le & {} 1+\frac{c}{pq}+\frac{cd}{p^2q^2}Z_{n-2}\le 1+\frac{c}{pq}+\frac{cd}{p^2q^2}+\frac{c^2d}{p^3q^3}Y_{n-3}\nonumber \\\le & {} 1+\frac{c}{pq}+\frac{cd}{p^2q^2}+\frac{c^2d}{p^3q^3}+\frac{c^2d^2}{p^4q^4}Z_{n-4}\nonumber \\\le & {} \cdots \le 1+\frac{c}{pq}+\frac{cd}{p^2q^2}+\frac{c^2d}{p^3q^3}+\frac{c^2d^2}{p^4q^4}+\cdots +\frac{c^{2k}d^{2k-1}}{p^{2k-1}q^{2k-1}}+\frac{c^{2k}d^{2k}}{p^{2k}q^{2k}}Z_{n-2k}\nonumber \\= & {} \frac{1}{1-\frac{cd}{p^2q^2}}\left[ 1-\left( \frac{cd}{p^2q^2}\right) ^{k-1}\right] +\frac{\frac{c}{pq}}{1-\frac{cd}{p^2q^2}}\left[ 1-\left( \frac{cd}{p^2q^2}\right) ^k\right] +\frac{c^{2k}d^{2k}}{p^{2k}q^{2k}}Z_{n-2k}\nonumber \\\le & {} \frac{p^2q^2+pqc}{p^2q^2-cd}+Z_{n-2k}. \end{aligned}$$

(43)

Noting $n-2k\ge 2$ is equal to $k\le (n-2)/2$. The proposition is true. $\square$

Lemma 3.5

Consider Eq. (37), if condition (38) holds true, then the unique positive equilibrium point $({\overline{y}},{\overline{z}})$ of (37) is locally asymptotically stable.

Proof

From (37), we obtain a positive equilibrium $({\overline{y}},{\overline{z}})=$

$$\begin{aligned} \left( \frac{pq-d+c+\sqrt{(pq-d+c)^2+4pqd}}{2p}, \frac{pq-c+d+\sqrt{(pq-c+d)^2+4pqc}}{2q}\right) . \end{aligned}$$

The linearized equation of (37) at the equilibrium $({\overline{y}},{\overline{z}})$ is

$$\begin{aligned} \Psi _{n+1}=B\Psi _n, \end{aligned}$$

(44)

here $\Psi _n=(y_n,y_{n-1},z_n,z_{n-1})^T$,

$$\begin{aligned} B=\left( \begin{array}{cccc} 0&{} 0&{} \frac{d}{{\overline{z}}^2} &{}-\frac{2d}{{\overline{z}}^2}\\ 1&{} 0 &{}0 &{}0 \\ \frac{c}{{\overline{y}}^2}&{} -\frac{2c}{{\overline{y}}^2}&{}0&{} 0\\ 0&{}0&{}1&{}0 \end{array} \right) . \end{aligned}$$

Let $\lambda _i,i=1,2,3,4$ be the eigenvalues of matrix B, $L=\text{ diag }(l_1,l_2,l_3,l_4)$ be a diagonal matrix, $l_1=l_3=1,d_i=d_{2+i}=1-i\varepsilon (i=2),$ and

$$\begin{aligned} 0<\varepsilon <\min \left\{ \frac{1}{2}-\frac{3d}{2{\overline{z}}^2}, \frac{1}{2}-\frac{3c}{2{\overline{y}}^2}\right\} . \end{aligned}$$

(45)

Clearly, L is an invertible matrix. Calculating $LBL^{-1}$, one has

$$\begin{aligned} LBL^{-1}= \left( \begin{array}{cccc} 0&{}0&{}\frac{d}{{\overline{z}}^2}l_1l_3^{-1}&{}-\frac{2d}{{\overline{z}}^2}l_1l_4^{-1}\\ l_2l_1^{-1}&{}0&{}0&{}0\\ \frac{c}{{\overline{y}}^2}l_3l_1^{-1}&{}-\frac{2c}{{\overline{y}}^2}l_3l_2^{-1}&{}0&{}0\\ 0&{}0&{}l_4l_3^{-1}&{}0 \end{array} \right) \end{aligned}$$

From $l_1>l_2>0, l_3>l_4>0$, it implies that

$$\begin{aligned} l_2l_1^{-1}<1, l_4l_3^{-1}<1. \end{aligned}$$

Furthermore, noting (45), we have

$$\begin{aligned} \frac{d}{{\overline{z}}^2}l_1l_3^{-1} +\frac{2d}{{\overline{z}}^2}l_1l_4^{-1} =\frac{d}{{\overline{z}}^2} \left( 1+\frac{2}{1-2\varepsilon }\right)<\frac{3d}{{\overline{z}}^2(1-2\varepsilon )}<1, \\ \frac{c}{{\overline{y}}^2}l_3l_1^{-1} +\frac{2c}{{\overline{z}}^2}l_3l_2^{-1} =\frac{c}{{\overline{y}}^2} \left( 1+\frac{2}{1-2\varepsilon }\right)<\frac{3c}{{\overline{y}}^2(1-2\varepsilon )}<1. \end{aligned}$$

It is clear that B has the same eigenvalues as $LBL^{-1}$, and

$$\begin{aligned} \max _{1\le i\le 4}\mid \lambda _i\mid\le & {} \Vert LBL^{-1}\Vert _\infty \\= & {} \max \left\{ l_2l_1^{-1}, l_4l_3^{-1}, \frac{d}{{\overline{z}}^2}l_1l_3^{-1}+\frac{2d}{{\overline{z}}^2}l_1l_4^{-1}, \frac{c}{{\overline{y}}^2}l_3l_1^{-1}+\frac{2c}{{\overline{y}}^2}l_3l_2^{-1}\right\} <1. \end{aligned}$$

Therefore the equilibrium $({\overline{y}}, {\overline{z}})$ of (37) is locally asymptotically stable. $\square$

Lemma 3.6

Consider Eq. (37), if (38) hold true, then every positive solution $(y_n,z_n)$ of (37) converges to the equilibrium point $({\overline{y}},{\overline{z}}).$

Proof

From (37), we obtain positive equilibrium $({\overline{y}},{\overline{z}})=$

$$\begin{aligned} \left( \frac{pq-d+c+\sqrt{(pq-d+c)^2+4pqd}}{2p}, \frac{pq-c+d+\sqrt{(pq-c+d)^2+4pqc}}{2q}\right) . \end{aligned}$$

Suppose that $(y_n,z_n)$ is an arbitrary positive solution of (37). Noting (35)–(37), one has

$$\begin{aligned} \lim _{n\rightarrow \infty }\sup y_n=H_1,\lim _{n\rightarrow \infty }\inf y_n=h_1,\ \ \lim _{n\rightarrow \infty }\sup z_n=H_2,\ \ \ \lim _{n\rightarrow \infty }\inf z_n=h_2. \end{aligned}$$

(46)

where $h_i, H_i\in (0,+\infty ), i=1,2.$ Then, noting (37) and (46), we have

$$\begin{aligned} H_1\le p+\frac{dH_2}{h_2^2}, \ \ h_1\ge p+\frac{dh_2}{H_2^2},\ \ \ H_2\le q+\frac{cH_1}{h_1^2},\ \ h_2\ge q+\frac{ch_1}{H_1^2}. \end{aligned}$$

From which we have

$$\begin{aligned} H_1-h_1\le d\left( \frac{h_2}{H_2^2}-\frac{H_2}{h_2^2}\right) ,\ \ \ H_2-h_2\le c\left( \frac{h_1}{H_1^2}-\frac{H_1}{h_1^2}\right) . \end{aligned}$$

(47)

We claim that

$$\begin{aligned} H_1=h_1,\ \ H_2=h_2. \end{aligned}$$

(48)

Suppose contrarily that $H_1>h_1$, then from the first inequality of (47), it can conclude $h_2>H_2$, which is a contradiction. So $H_1=h_1$. Similarly we can get $H_2=h_2$. Noting (37) and (48), then $\lim _{n\rightarrow \infty }y_n={\overline{y}}, \lim _{n\rightarrow \infty }z_n={\overline{z}}.$ The proof of Lemma 3.6 is completed.

Combining Lemma 3.5 with Lemma 3.6. We have the following theorem. $\square$

Theorem 3.5

Consider Eq. (37). If relation (38) holds true, then the unique positive equilibrium $({\overline{y}},{\overline{z}})$ is globally asymptotically stable.

Theorem 3.6

If

$$\begin{aligned} A_{l,\alpha }>B_{r,\alpha }>1, \ \ A_{r,\alpha }>B_{l,\alpha }>1, \ \forall \alpha \in (0,1]. \end{aligned}$$

(49)

and, for $n=0,1,2,\ldots ,$

$$\begin{aligned} \frac{R_{n,\alpha }L_{n-1,\alpha }^2}{L_{n,\alpha }R_{n-1,\alpha }^2}\le \frac{B_{l,\alpha }}{B_r,\alpha }, \forall \alpha \in (0,1]. \end{aligned}$$

(50)

Then every positive fuzzy solution of FDE (3) converges to the positive fuzzy equilibrium x as $n\rightarrow +\infty .$

Proof

The proof is similar to those of Theorem 3.4. Assume that there is a positive fuzzy number x satisfying (33). From (33), condition (49) and (50), we can get

$$\begin{aligned} L_\alpha =A_{l,\alpha }+\frac{B_{r,\alpha } R_\alpha }{R_\alpha ^2},\ \ R_\alpha =A_{r,\alpha }+\frac{B_{l,\alpha }L_\alpha }{L_\alpha ^2}. \end{aligned}$$

(51)

Hence we can from (51) have that

$$\begin{aligned} \left\{ \begin{array}{c} L_\alpha =\frac{A_{l,\alpha }A_{r,\alpha }+B_{r,\alpha }-B_{l,\alpha } +\sqrt{(A_{l,\alpha }A_{r,\alpha }+B_{r,\alpha }-B_{l,\alpha })^2+4A_{l,\alpha }A_{r,\alpha }B_{l,\alpha }}}{2A_{r,\alpha }},\\ \\ R_\alpha =\frac{A_{l,\alpha }A_{r,\alpha }+B_{l,\alpha }-B_{r,\alpha } +\sqrt{(A_{l,\alpha }A_{r,\alpha }+B_{l,\alpha }-B_{r,\alpha })^2+4A_{l,\alpha }A_{r,\alpha }B_{r,\alpha }}}{2A_{l,\alpha }}. \end{array} \right. \end{aligned}$$

(52)

Suppose that $x_n$ is a positive fuzzy solution of FDE (3) such that (10) holds. Noting (50) and (51), utilizing Lemma 3.5 and Lemma 3.6 to (36), we have

$$\begin{aligned} \lim _{n\rightarrow \infty }L_{n,\alpha }=L_\alpha ,\ \ \lim _{n\rightarrow \infty }R_{n,\alpha }=R_\alpha , \end{aligned}$$

(53)

Then

$$\begin{aligned} \lim _{n\rightarrow \infty }D(x_n,x)=\lim _{n\rightarrow \infty }\sup _{\alpha \in (0,1]}\{\max \{\mid L_{n,\alpha }-L_\alpha \mid , \mid R_{n,\alpha }-R_\alpha \mid \}\}=0. \end{aligned}$$

The proof of the theorem is completed. $\square$

Remark 3.1

In fuzzy discrete dynamical systems. To find qualitative behavior of solutions for discrete fuzzy difference equation, it is very vital to utilize which operations such as addition, scalar multiplication, division of fuzzy numbers. In [19,20,21,22, 25, 26, 28,29,30,31], Using Zadeh extension principle, the authors obtained dynamical behaviors of some fuzzy difference equations. However, utilizing g-division of fuzzy numbers, Zhang et al. [23, 24] studied the dynamical behaviors of some nonlinear fuzzy difference equations. Compared with the former, The advantage is that the support sets of positive fuzzy solution of latter is smaller than those of former. In fact, it is obvious that the degree of fuzzy uncertainty is reduced by virtue of g-division of fuzzy numbers. Based on this fact above, Therefore, we consider the qualitative behaviors of the fuzzy difference equation with quadratic term by virtue of g-division of fuzzy numbers.

4 Numerical examples

In this section, two illustrative examples are presented to verify the effectiveness of theoretic results.

Example 4.1

Consider the following fuzzy difference equation

$$\begin{aligned} x_{n+1}=A+\frac{Bx_n}{x_{n-1}^2},\ n=0,1,\ldots , \end{aligned}$$

(54)

where $A, B\in \Re _F^+$ and the initial conditions $x_{i}\in \Re _F^+, i=0,-1$ are as follows

$$\begin{aligned}&\begin{array}{ll} A(x)=\left\{ \begin{array}{ll} x-3,&{} 3\le x\le 4\\ &{}\\ -x+5,&{} 4\le x\le 5 \end{array} \right. , &{} B(x)=\left\{ \begin{array}{ll} x-4,&{} 4\le x\le 5\\ &{}\\ -x+6,&{} 5\le x\le 6 \end{array} \right. \end{array} \end{aligned}$$

(55)

$$\begin{aligned}&\begin{array}{ll} x_{-1}(x)=\left\{ \begin{array}{ll} 2x-4,&{} 2\le x\le 2.5\\ &{}\\ -2x+6,&{} 2.5\le x\le 3 \end{array} \right. , &{} x_{0}(x)=\left\{ \begin{array}{ll} x-1,&{} 1\le x\le 2\\ &{}\\ -x+3,&{} 2\le x\le 3 \end{array} \right. \end{array} \end{aligned}$$

(56)

From (55), one has

$$\begin{aligned}{}[A]_\alpha =\left[ 3+\alpha ,5-\alpha \right] ,\ [B]_\alpha =\left[ 4+\alpha ,6-\alpha \right] ,\ \alpha \in (0,1]. \end{aligned}$$

(57)

From (56), one has

$$\begin{aligned}{}[x_{-1}]_\alpha =[2+\frac{1}{2}\alpha ,3-\frac{1}{2}\alpha ],\ \ [x_{0}]_\alpha =[1+\alpha ,3-\alpha ],\ \alpha \in (0,1]. \end{aligned}$$

(58)

Therefore, it follows that

$$\begin{aligned} \left\{ \begin{array}{cc} \overline{\bigcup _{\alpha \in (0,1]}[A]_\alpha }=[3,5], &{} \overline{\bigcup _{\alpha \in (0,1]}[B]_\alpha }=[4,6],\\ &{} \\ \overline{\bigcup _{\alpha \in (0,1]}[x_{-1}]_\alpha }=[2,3],&{} \overline{\bigcup _{\alpha \in (0,1]}[x_{0}]_\alpha }=[1,3]. \end{array} \right. \end{aligned}$$

(59)

It is clear that Case (i) occurs, so Eq. (54) can results in a difference equation system with parameter $\alpha ,$

$$\begin{aligned} L_{n+1,\alpha }=A_{l,\alpha }+\frac{B_{l,\alpha }L_{n,\alpha }}{L_{n-1,\alpha }^2},\ \ R_{n+1,\alpha }=A_{r,\alpha }+\frac{B_{r,\alpha }R_{n,\alpha }}{R_{n-1,\alpha }^2},\ \alpha \in (0,1]. \end{aligned}$$

(60)

Therefore, $A_{l,\alpha }^2>\frac{4}{3}B_{l,\alpha }, A_{r,\alpha }^2>\frac{4}{3}B_{r,\alpha } \forall \alpha \in (0,1],$ and the initial value $x_{i}\in \Re _F^+,(i=0,-1)$, so applying Theorem  3.2, then every positive solution $x_n$ of Eq. (54) is bounded and persistent.

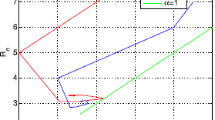
In addition, from Theorem 3.4, there is a unique positive equilibrium ${\overline{x}}=(4,5,6)$. Moreover every positive fuzzy solution $x_n$ of Eq. (54) converges to ${\overline{x}}$ with respect to D as $n\rightarrow \infty$ (see Figs. 1, 2, 3).

Fig. 1

The dynamics of system (60)

Fig. 2

The solution of system (60) at $\alpha =0$ and $\alpha =0.25$

Fig. 3

The solution of system (60) at $\alpha =0.75$ and $\alpha =1$

Example 4.2

Consider Eq. (54), where $A, B\in \Re _F^+$ and the initial value $x_{i}\in \Re _F^+, i=0,-1$ are as follows

$$\begin{aligned} \begin{array}{ll} A(x)=\left\{ \begin{array}{ll} x-6,&{} 6\le x\le 7\\ &{}\\ -2x+15,&{} 7\le x\le 7.5 \end{array} \right. , &{} B(x)=\left\{ \begin{array}{ll} 2x-3,&{} 1.5\le x\le 2\\ &{}\\ -x+3,&{} 2\le x\le 3 \end{array} \right. \end{array} \end{aligned}$$

(61)

$$\begin{aligned} \begin{array}{ll} x_{-1}(x)=\left\{ \begin{array}{ll} 2x-4,&{} 2\le x\le 2.5\\ &{}\\ -2x+6,&{} 2.5\le x\le 3 \end{array} \right. , &{} x_{0}(x)=\left\{ \begin{array}{ll} x-1,&{} 1\le x\le 2\\ &{}\\ -x+3,&{} 2\le x\le 3 \end{array} \right. \end{array} \end{aligned}$$

(62)

From (61), one has

$$\begin{aligned}{}[A]_\alpha =\left[ 6+\alpha ,7.5-\frac{1}{2}\alpha \right] ,\ [B]_\alpha =\left[ 1.5+\frac{1}{2}\alpha ,3-\alpha \right] ,\ \alpha \in (0,1]. \end{aligned}$$

(63)

From (62), one has

$$\begin{aligned}{}[x_{-1}]_\alpha =\left[ 2+\frac{1}{2}\alpha ,3-\frac{1}{2}\alpha \right] ,\ \ [x_{0}]_\alpha =[1+\alpha ,3-\alpha ],\ \alpha \in (0,1]. \end{aligned}$$

(64)

Therefore, it follows that

$$\begin{aligned}&\overline{\bigcup _{\alpha \in (0,1]}[A]_\alpha }=[6,7.5], \ \overline{\bigcup _{\alpha \in (0,1]}[B]_\alpha }=[1.5,3],\ \overline{\bigcup _{\alpha \in (0,1]}[x_{-1}]_\alpha }=[2,3], \nonumber \\&\overline{\bigcup _{\alpha \in (0,1]}[x_0]_\alpha }=[1,3]. \end{aligned}$$

(65)

It is clear that Case (ii) occurs, so Eq. (54) can result in a difference equation systems with parameter $\alpha ,$

$$\begin{aligned} L_{n+1,\alpha }=A_{l,\alpha }+\frac{B_{r,\alpha }R_{n,\alpha }}{R_{n-1,\alpha }^2},\ \ R_{n+1,\alpha }=A_{r,\alpha }+\frac{B_{l,\alpha }L_{n,\alpha }}{L_{n-1,\alpha }^2},\ \alpha \in (0,1]. \end{aligned}$$

(66)

It is clear that the initial value $x_{i}\in \Re _F^+(i=0,-1)$, and (47) is satisfied, so applying Theorem 3.6, there is a unique positive equilibrium ${\overline{x}}=(6.3879,7.2749,7.7348)$. Moreover every positive fuzzy solution $x_n$ of Eq. (54) converges ${\overline{x}}$ with respect to D as $n\rightarrow \infty .$ (see Figs. 4, 5, 6)

Fig. 4

The Dynamics of system (66)

Fig. 5

The solution of system (66) at $\alpha =0$ and $\alpha =0.25$

Fig. 6

The solution of system (66) at $\alpha =0.75$ and $\alpha =1$

5 Conclusion

In this work, utilizing g-division of fuzzy numbers, the qualitative features of second-order FDE $x_{n+1}=A+\frac{Bx_{n}}{x_{n-1}^2}$ are studied. The main theoretic results are as follows.

(i) The existence and uniqueness of positive fuzzy solution of FDE (3) are obtained under the positive initial values $x_{-1},x_0$.

(ii) The positive fuzzy solution is bounded and persistence either Case (i) or Case (ii) occurs. Moreover, every positive fuzzy solution $x_n$ tend to the unique equilibrium x as $n\rightarrow \infty$, if $A_{l,\alpha }^2>\frac{4}{3}B_{l,\alpha }, A_{r,\alpha }^2>\frac{4}{3}B_{r,\alpha }, \alpha \in (0,1]$. And also, every positive fuzzy solution $x_n$ of FDE (3) converges to the unique equilibrium x as $n\rightarrow \infty .$ if $A_{l,\alpha }>B_{r,\alpha }>1, A_{r,\alpha }>B_{1,\alpha }>1$ and $\frac{R_{n,\alpha }L_{n-1,\alpha }^2}{L_{n,\alpha }R_{n-1,\alpha }^2}\le \frac{B_{l,\alpha }}{B_{r,\alpha }},\alpha \in (0,1], n=0,1,2,\ldots$.