Further development of F-index for fuzzy graph and its application in Indian railway crime

Abstract

From the mid-nineteenth century, the railway network has been the most important mode of conveying people and goods in India. 22.15 million passengers used this network and 3.32 million metric tons of goods were also shipped daily from 2019 to 2020. The national rail network comprised 126,366 km of track over a route of 67,368 km and 7,325 stations. It is the fourth-largest national railway network globally after the United States, Russia and China. But with the passage, they pose a threat to the general public while travelling, being the instances of crimes rising fourfold in rails. The ongoing railway crime has become a cause of concern for the common passenger now. In this article, F-index for fuzzy graphs is used to analyze the railway crimes in India and compared with three other topological indices. F-index for fuzzy graphs and the first Zagreb index for fuzzy graphs provide similar results whereas F-index for fuzzy graphs provides better realistic results than F-index for crisp graphs and first Zagreb index for crisp graphs to detect the crime in Indian railway. Also, this index is studied for several operations such as Cartesian product, composition, union and join of two fuzzy graphs. Some interesting relations of F-index are established during fuzzy graph transformations. Using those transformation, it is shown that n-vertex star has maximum F-index among the n-vertex trees. Also, maximal n-vertex unicyclic fuzzy graph having r cycle is determined with respect to F-index.

1 Introduction

1.1 Research background

Nowadays, due to the vast applications of fuzzy graph theory, many researchers are working on topological indices (TIs) on fuzzy graphs. In the year 1965, the concept of uncertainty in a classical set was firstly introduced by Zadeh [45] and called it fuzzy set. In 1975, inspired by this, Rosenfeld [37] introduced the fuzzyness for a graph and called the graph is the fuzzy graph (FG). Generalized the neutrosophic planer graph [23] and link prediction in the neutrosophic graph [24] are studied by Mahapatra et al. A telecommunication system based on fuzzy graphs [40] and a social network system based on fuzzy graphs [41] is studied by Samanta and Pal. Bipolar fuzzy graph [3], fuzzy soft graph [4], m-polar fuzzy graph [5], generalized m-polar fuzzy graph [43], bipolar fuzzy soft hypergraph [42] and measures of connectivity in rough fuzzy network [6] are studied by Akram et al. Rashmanlou et al. [38] studied the product of bipolar fuzzy graphs with their degree. In 2016, Rashmanlou and Borzooei studied vague graph in [39]. The degree of a vertex in a FG is also discussed in [33] and also discussed strong degree, strong neighbour of a FG. In [5, 32, 33], one can see for more generalization of a FG and related results.

Table 1 Review of related works

In the field of mathematical chemistry, molecular topology and chemical graph theory, TIs are molecular descriptors that are calculated on the molecular graph of a chemical compound. These TIs are numerical quantities of a graph that describe its topology. Vertex represents an atom and an edge represents the bond between two atoms in a molecular graph. In 1947, the Wiener index (WI) was introduced by Wiener, which is used to calculate the boiling point of paraffins. Zagreb index (ZI) is degree-based TI established by Gutman and Trinajstic in 1972 [15] and used to calculate $\pi$-electron energy of a conjugate system. In 2015, Fortula and Gutman defined another degree-based topological index called forgotten topological index (F-index) [14]. Amin and Nayeem studied the F-index and F-coindex of subdivision graph and line graph in [7]. In 2017, Abdo et al. [1] studied the extremal trees (crisp) with respect to F-index. Extremal unicyclic and bicyclic graphs (crisp) with respect to F-index is determined by Akhtar et al. De et al. [13] studied F-index for some crisp graph operations.

In 2019, Binu et al. [8, 10, 11] introduced connectivity index, average connectivity index, connectivity status and cyclic connectivity index of a FG. Motivated from these articles, recently, Binu et al. [9] introduced Wiener index of a FG and Islam and Pal also studied Wiener index for FG in [16]. In 2021, Islam and Pal also introduced hyper-Wiener index [19], hyper-connectivity index [20], first Zagreb index [17] and F-index [18] for fuzzy graphs. In [22], Mahapatra et al. provided the RSM index in fuzzy graph. Poulik et al. studied Cretain index [34], Wiener absolute index [35] and Randic index [36] for bipolar fuzzy graphs. In [21] Kalathian et al. also introduced so many index for fuzzy graphs.

1.2 Motivation

Topological indices have an important role in molecular chemistry, chemical graph theory, spectral graph theory, network theory, etc. Zagreb index (ZI) is one such TIs which is degree-based TI and established by Gutman and Trinajstic in 1972 [15] and these TIs are used to calculate $\pi$-electron energy of a conjugate system. Followed by this topological index, in 2015, Fortula and Gutman defined another degree-based topological index called forgotten topological index (F-index) [14] and they proved that first ZI and F-index have the almost same entropy, predictive ability and acentric factor and F-index obtain correlation coefficients greater than 0.95. So this TI is very much useful in molecular chemistry, spectral graph theory, network theory, and several fields of mathematics and chemistry. Some neighbourhood degree-based topological indices are introduced and studied their correlations between the physico-chemical properties of some chemical compounds by Mondal et al. [26, 27]. In [29] they also studied neighbourhood Zagreb index of product graph and analyzed QSPR of some novel degree-based topological descriptors [30]. In [28, 31], they also studied molecular descriptors of some chemicals that prevent COVID-19. But, those indices are defined in the crisp graph only. Recently, in 2021, Islam and Pal [18] introduced and studied F-index for fuzzy graphs. Also, they introduced so many interesting results on F-index for various fuzzy graphs like path, cycle, star, complete fuzzy graph, etc. Motivated by this article, we start research on further developing the F-index for fuzzy graphs. F-index is used not only for application but also for theoretical purposes. Abdo et al. determined the extremal n-vertex trees (Crisp) with respect to the F-index and Akhtar et al. [2] determined the extremal n-vertex unicyclic and bicyclic graphs with respect to the F-index. Still, those results for the fuzzy graph have been unsolved till now. In this article, We established that n-vertex star has maximal F-index among the class of n-vertex trees (fuzzy) and determined the n-vertex unicyclic fuzzy graph with cycle length r having maximal F-index, which are partially generalization of the article [1] and [2], respectively. De et al. [13] studied F-index of some graph (crisp) operations. Motivated by this article, we also studied this index of some fuzzy graph operations (Cartesian product, composition, join and union of fuzzy graphs).

1.3 Significance and objective of the article

Topological indices for a crisp graph has huge applications in real life. Also, laboratory testing of chemicals to understand their different properties are costly. To overcome this, many topological indices have been presented in theoretical chemistry. But sometimes it is seen that most real-life problems cannot be modelled using crisp graphs. Those topological indices are needed to define in a fuzzy graph for these circumstances. In 2021, Islam and Pal [18] introduced and studied F-index for fuzzy graphs. In this paper, some bounds on F-index are provided for several fuzzy graph operations such as Cartesian product, composition, union and join of two fuzzy graphs. Some interesting relations of the F-index are established during fuzzy graph transformations. Using those transformations, it is shown that n-vertex star has maximal F-index among the class of n-vertex trees (fuzzy) and determined the n-vertex unicyclic fuzzy graph with cycle length r having maximal F-index, which are partially generalization of the article [1] and [2], respectively. At the end of this article, railway crime in India is studied, and F-index is used to analyze the crimes rate in the railway in India and compared with three other topological indices. Also, F-index for fuzzy graphs and the first Zagreb index for fuzzy graphs provide similar results and F-index for fuzzy graphs provides better realistic results than F-index for crisp graphs and first Zagreb index for crisp graphs to detect the crime in Indian railway.

1.4 Framework of the article

The article’s structure is as follows: Section 2 provides some basic definitions that are essential to developing our main results. In Sect. 3, some bounds on F-index are provided for several fuzzy graph operations such as Cartesian product, composition, union and join of two fuzzy graphs. In Sect. 4, some interesting relations of the F-index are established during fuzzy graph transformations. Using those transformation, it is also shown that, $n-$vertex star hs maximum F-index among the n-vertex trees. Also, maximal n-vertex unicyclic fuzzy graph with r cycle is determined with respect to this index. In Sect. 5, this index is used to analyze the crimes in railway in India and compared with three other topological indices. Also, it is shown that the F-index for fuzzy graphs and the first Zagreb index for fuzzy graphs provide similar results and F-index for fuzzy graphs provides better realistic results than F-index for crisp graphs and first Zagreb index for crisp graphs to detect the crime in Indian railway.

Table 2 The list of abbreviation

2 Preliminaries

In this portion, some basic definitions are provided which are essential to develop our results are given, most of them one can be found in [32, 33].

Let X be a universal set. A FS S on X is a mapping $\mu : X \rightarrow [0,1]$. Here $\mu$ is called the membership function of the FS S. Generally a FS is denoted by $S = (x,\mu )$.

Definition 1

Let $X(\ne \phi )$ be a given finite set. The FG is a triplet, $G=(V,E)$, where V is nonempty finite subset of X with $\sigma : V \rightarrow [0,1]$ and $\mu : V\times V \rightarrow [0,1]$ satisfying $\mu (x,y) \le \sigma (x)\wedge \sigma (y)$, where $\wedge$ represents the minimum.

The set V is the set of vertices and $E := \{(x,y): \mu (x,y)>0\}$ is the set of edge of the FG. $\sigma (x)$ represents the vertex MV of x and $\mu (x,y)$ represents the edge MV of (x, y) (or simply xy).

Definition 2

Let $v\in V$ then degree of v is denoted by $d_G(v)$ or simply d(v) and defined as $d(v) = \sum _{x\in V}^{} \mu (xv).$

Let $\Delta (G)$ or $\Delta$ be the maximum degree of G and defined as $\Delta = \vee _{v\in V}d(v)$ and $\delta (G)$ or $\delta$ be the minimum degree of G and defined as $\delta = \wedge _{v\in V} d(v)$. The total degree of G is denoted by T(G) or simply T, i.e. $T = \sum _{v\in V}^{}d(v) = 2 \sum _{uv\in E}^{}\mu (uv) \le 2\cdot m,$ where $m =$ no. of edges.

Throughout this article, we consider, $G_1 = (V_1, E_1)$ with $n_1$-vertices, $m_1$-edges and $G_2 = (V_2, E_2)$ with $n_2$-vertices, $m_2$-edges be two FGs and $\Delta _1= \Delta (G_1), \Delta _2= \Delta (G_2), \delta _1= \delta (G_1), \delta _2= \delta (G_2).$

Cartesian product of two FGs are defined below:

Definition 3

[32] Cartesian product of $G_1$ and $G_2$ is a FG $G_1\times G_2 = (V, E)$, where $V= V_1\times V_2$, $(u,v), (u_1,v_1), (u_2, v_2) \in V, \sigma (u,v) = \wedge \{\sigma _1(u), \sigma _2(v)\}$ and

$$\begin{aligned} \mu ((u_1,v_1),(u_2, v_2)) = {\left\{ \begin{array}{ll} \wedge \{\sigma _1(u_1) , \mu _2(v_1,v_2)\} \text { if }~ u_1= u_2, \\ v_1 v_2\in E_2\\ \wedge \{\sigma _2(v_1) , \mu _1(u_1,u_2)\} \text { if }~ u_1 u_2\in E_1,\\ v_1 = v_2\\ 0 \text {otherwise.} \end{array}\right. } \end{aligned}$$

Composition of two FGs are defined below:

Definition 4

[32] Let $G_1 = (V_1, E_1), G_2 = (V_2, E_2)$ be two FGs. Then the composition of $G_1$ and $G_2$ is a FG $G_1[G_2] = (V, E)$, where $V= V_1\times V_2$, $(u,v), (u_1,v_1), (u_2, v_2) \in V, \sigma (u,v) = \wedge \{\sigma _1(u), \sigma _2(v)\}$ and

$$\begin{aligned} \mu ((u_1,v_1),(u_2, v_2)) = {\left\{ \begin{array}{ll} \wedge \{\sigma _1(u_1) , \mu _2(v_1,v_2)\} \text {if}~ u_1= u_2 \, ~\text {and}~ \, v_1 v_2\in E_2\\ \wedge \{\sigma _2(v_1) , \sigma _2(v_2), \mu _1(u_1,u_2)\} \text {if}~ u_1 \, u_2\in E_1\\ 0 \text {otherwise.} \end{array}\right. } \end{aligned}$$

Join of two FGs are defined below:

Definition 5

[32] Let $G_1 = (V_1, E_1), G_2 = (V_2, E_2)$ be two FGs. Then the join of $G_1$ and $G_2$ is a FG $G_1+ G_2 = (V, E)$, where $V= V_1\cup V_2$, $u,v,u_1,v_1 \in V$,

$$\begin{aligned} \sigma (u) = {\left\{ \begin{array}{ll} \sigma _1(u), \text {if}~ u\in V_1\\ \sigma _2(u), \text {if}~ u\in V_2 \end{array}\right. } \end{aligned}$$

and

$$\begin{aligned} \mu (u,v) = {\left\{ \begin{array}{ll} \wedge \{\sigma _1(u) , \sigma _2(v)\} \text { if } u\in V_1 \text { and } v\in V_2\\ \mu _1(u,v) \text { if } uv\in E_1\\ \mu _2(u,v) \text { if } uv\in E_2\\ 0 \text {otherwise.} \end{array}\right. } \end{aligned}$$

Union of two FGs are defined below:

Definition 6

[32] Let $G_1 = (V_1, E_1), G_2 = (V_2, E_2)$ be two FGs. Then the union of $G_1$ and $G_2$ is a FG $G_1\cup G_2 = (V, E)$, where $V= V_1\cup V_2$, $u,v \in V$,

$$\begin{aligned} \sigma (u) = {\left\{ \begin{array}{ll} \sigma _1(u), \text {if } u\in V_1{\setminus } V_2\\ \sigma _2(u), \text {if } u\in V_2{\setminus } V_1\\ \max \{\sigma _1(u), \sigma _2(u)\}, \text {if } u\in V_1\cap V_2 \end{array}\right. } \end{aligned}$$

and

$$\begin{aligned} \mu (u,v) = {\left\{ \begin{array}{ll} \mu _1(u,v) \text { if } uv\in E_1{\setminus } E_2\\ \mu _2(u,v) \text { if } uv\in E_2{\setminus } E_1\\ \vee \{\sigma _1(u,v) , \sigma _2(u,v)\} \text { if } (u,v)\in E_1\cap E_2\\ 0 \text {otherwise.} \end{array}\right. } \end{aligned}$$

Topological indices has an important role in molecular chemistry, chemical graph theory, spectral graph theory, network theory, etc. Zagreb index (ZI) is one such TIs which is degree-based TI and established by Gutman and Trinajstic in 1972 [15] and this TIs are used to calculate $\pi$-electron energy of a conjugate system. The first and second ZI for crisp graph is defined as follows:

Definition 7

[15] Let $G = (V,E)$ be a crisp graph. Then the first ZI of the graph G is denoted by $M_1(G)$ and is defined by:

$$\begin{aligned} M_1(G) = \sum _{v\in V}^{} d^2(v). \end{aligned}$$

Definition 8

[15] Let $G = (V,E)$ be a crisp graph. Then the second ZI of the G is denoted by $M_2(G)$ and is defined by:

$$\begin{aligned} M_2(G) = \sum _{uv\in E}^{} d(u)d(v). \end{aligned}$$

This two TIs are degree based TIs. Followed by this two topological indices, in 2015, Fortula and Gutman defined another degree based topological indices called forgotten topological index (F-index) [14] and they proved that first ZI and F-index have the almost same entropy, predictive ability and acentric factor and F-index obtain correlation coefficients greater than 0.95. So this TI is very much useful in molecular chemistry and used in spectral graph theory, network theory, and several field of mathematics. F-index for crisp graph is defined as follows:

Definition 9

[14] Suppose $G = (V,E)$ be a graph (crisp). F-index of G is indicated by F(G) and is defined by:

$$\begin{aligned} F( G) = \sum _{v\in V}^{} d^3(v). \end{aligned}$$

Those indices are defined in crisp graph only. In 2020, Kalathian et al. [21] studied first and second ZI for a FG as follows:

Definition 10

[21] Suppose $G = (V, E, \mu )$ be a FG. Then first ZI of the FG G is indicated by M(G) and is defined by:

$$\begin{aligned} M(G) = \sum _{v\in V}^{} \sigma (v) d^2(v). \end{aligned}$$

Definition 11

[21] Suppose $G = (V, E)$ be a FG. Then the second ZI of the FG G is indicated by $ZF_2(G)$ and is defined by:

$$\begin{aligned} ZF_2(G) = \sum _{uv\in E}^{} \sigma (u) d(u) \sigma (v) d(v). \end{aligned}$$

In 2021, the definition of the first ZI for a FG was modified by Islam and Pal [17].

Definition 12

[17] Suppose $G = (V, E)$ be a FG. Then first ZI of the FG G is indicated by $ZF_1(G)$ and is defined by:

$$\begin{aligned} ZF_1(G) = \sum _{v\in V}^{} [\sigma (v) d(v)]^2. \end{aligned}$$

In 2021, Islam and Pal [18] introduced F-index for a FG.

Definition 13

[18] Suppose $G = (V, E)$ be a FG. Then F-index of the FG G is indicated by FF(G) and is defined by:

$$\begin{aligned} FF( G) = \sum _{v\in V}^{} [\sigma (v) d(v)]^3. \end{aligned}$$

In [18], Islam and Pal provided the upper and lower bounds of F-index for connected n-vertex fuzzy graph with m-edges.

Theorem 1

[18] $\frac{n\delta ^6}{m^3} \le FF( G)\le n\Delta ^3$.

In [18], Islam and Pal provided a relation of F-index between fuzzy graph and its partial fuzzy subgraph.

Proposition 1

[18] Let H be a PFSG of a FG G. Then $FF(H)\le FF( G)$.

Here, relation between F-index and first ZI are studied.

3 Bounds of F-index during fuzzy graph operations

In this section, some bounds of F-index are discussed during FG operations.

Theorem 2

$FF( G_1\times G_2) \le n_2 FF( G_1) + n_1 FF( G_2) + 3n_1 n_2 \Delta _1 \Delta _2 (\Delta _1 + \Delta _2).$

Proof

As $G_1\times G_2$ is CP of $G_1$ and $G_2$, then for $(u,v), (u_1,v_1) \in V, \sigma (u,v) = \wedge \{\sigma _1(u), \sigma _2(v)\}$ and

$$\begin{aligned} \mu ((u,v),(u_1, v_1)) = {\left\{ \begin{array}{ll} \wedge \{\sigma _1(u) , \mu _2(v,v_1)\} \text { if } u= u_1 \text { and } v v_1\in E_2\\ \wedge \{\sigma _2(v) , \mu _1(u,u_1)\} \text { if } u u_1\in E_1 \text { and } v = v_1\\ 0 \text {otherwise.} \end{array}\right. } \end{aligned}$$

Then degree of the vertex (u, v) is given below:

$$\begin{aligned} d_{G_1\times G_2}(u,v)&= \sum _{v_i v\in E_2}^{} \mu \{(u,v),(u,v_i)\} + \sum _{u_i u\in E_1}^{} \mu \{(u,v),(u_i,v)\}\\&\quad = \sum _{v_i v\in E_2}^{} \wedge \{\sigma _1(u) , \mu _2(v,v_i)\} + \sum _{u_i u \in E_1}^{} \wedge \{\sigma _2(v) , \mu _1(u,u_i)\}\\&\quad \le \sum _{v_i v\in E_2}^{} \mu _2(v,v_i) + \sum _{u_i u\in E_1}^{} \mu _1(u,u_i)\\&\quad = d_{G_1}(u) + d_{G_2}(v). \end{aligned}$$

Then F-index of $G_1 \times G_2$ is:

$$\begin{aligned} ZF_1( G_1 \times G_2)&= \sum _{(u,v)\in V}^{} [\sigma (u,v)d_{G_1 \times G_2}(u,v)]^3\\&\quad \le \sum _{(u,v)\in V}^{} \left[ \wedge \{\sigma _1(u), \sigma _2(v)\} \{d_{G_1}(u) + d_{G_2}(v)\}\right] ^3\\&\quad \le \sum _{(u,v)\in V}^{} \left[ \sigma _1(u)d_{G_1}(u) + \sigma _2(v)d_{G_2}(v)\right] ^3\\&\quad = \sum _{(u,v)\in V}^{} [\sigma _1(u)d_{G_1}(u)]^3 + \sum _{(u,v)\in V}^{} \left[ \sigma _2(v)d_{G_2}(v)\right] ^3 \\&\quad + 3\sum _{(u,v)\in V}^{} \sigma _1(u)\sigma _2(v)d_{G_1}(u)d_{G_2}(v)[\sigma _1(u) d_{G_1}(u)+ \sigma _2(v) d_{G_2}(v)]\\&\quad \le \sum _{v\in V_2}^{} FF( G_1) + \sum _{u\in V_1}^{} FF( G_2) + 3\sum _{(u,v)\in V}^{} \Delta _1 \Delta _2 (\Delta _1 + \Delta _2)\\&\quad = n_2 FF( G_1) + n_1 FF( G_2) + 3n_1 n_2 \Delta _1 \Delta _2 (\Delta _1 + \Delta _2). \end{aligned}$$

Hence the result. $\square$

Corollary 1

(i) $FF( G_1\times G_2) \le n_1n_2(\Delta _1+ \Delta _2)^3,$ (ii) $FF( G_1\times G_2) \le n_1n_2(n_1+ n_2-2)^3,$ (iii) $FF( G_1\times G_2) \le 8m_1^3n_1^3n_2 + 8m_2^3n_2^3n_1 + 2n_1n_2(n_1-1)(n_2-1)(n_1+n_2-2).$

Proof

(i) From theoremrem 2 and theoremrem 1, the following inequalities are holds:

$$\begin{aligned} FF( G_1\times G_2)&\le n_2 FF( G_1) + n_1 FF( G_2) + 3n_1 n_2 \Delta _1 \Delta _2 (\Delta _1 + \Delta _2)\\&\quad \le n_1n_2\Delta _1^3 + n_1n_2\Delta _2^3 +3n_1n_2\Delta _1\Delta _2(\Delta _1 + \Delta _2)\\&\quad = n_1n_2 (\Delta _1+ \Delta _2)^3. \end{aligned}$$

(ii) Using (i) and the facts $\Delta _1 \le n_1-1$ and $\Delta _2 \le n_2-1$, the result follow.

(iii) From theoremrem 2, Proposition 1 and the facts $\Delta _1 \le n_1-1$ and $\Delta _2 \le n_2-1$, the required inequality hold. $\square$

Theorem 3

$FF( G_1[G_2]) \le n^4_2 FF( G_1) + n_1FF( G_2)+ 3n_1 n^2_2 \Delta _1 \Delta _2(\Delta _1 + \Delta _2).$

Proof

As $G_1[G_2]$ is composition graph of $G_1$ and $G_2$, then for $(u,v), (u_1,v_1) \in V, \sigma (u,v) = \wedge \{\sigma _1(u), \sigma _2(v)\}$ and

$$\begin{aligned} \mu ((u,v),(u_1, v_1)) = {\left\{ \begin{array}{ll} \wedge \{\sigma _1(u) , \mu _2(v,v_1)\} \text { if } u= u_1 \text { and } v v_1\in E_2\\ \wedge \{\sigma _2(v) , \sigma _2(v_1), \mu _1(u,u_1)\} \text { if } u u_1\in E_1\\ 0 \text {otherwise.} \end{array}\right. } \end{aligned}$$

Then,

$$\begin{aligned} d_{G_1[G_2]}(u,v)&= \sum _{v_i v\in E_2}^{} \mu \{(u,v),(u,v_i)\} + \sum _{u_i u\in E_1, v_j\in V_2}^{} \mu \{(u,v),(u_i,v_j)\}\\&\quad = \sum _{v_i v\in E_2}^{} \wedge \{\sigma _1(u) , \mu _2(v,v_i)\} + \sum _{u_i u\in E_1, v_j \in V_2}^{} \wedge \{\sigma _2(v),\sigma _2(v_j) \mu _1(u,u_i)\}\\&\quad \le \sum _{v_i v\in E_2}^{} \mu _2(v,v_i) + \sum _{u_i u\in E_1, v_j \in V_2}^{} \mu _1(u,u_i)\\&\quad = n_2 d_{G_1}(u) + d_{G_2}(v). \end{aligned}$$

Then F-index of $G_1[G_2]$ is:

$$\begin{aligned} FF( G_1[G_2])&= \sum _{(u,v)\in V}^{} [\sigma (u,v)d_{G_1[G_2]}(u,v)]^3\\&\quad \le \sum _{(u,v)\in V}^{} [\wedge \{\sigma _1(u), \sigma _2(v)\} \{n_2 d_{G_1}(u) + d_{G_2}(v)\}]^3\\&\quad \le \sum _{(u,v)\in V}^{} [n_2 \sigma _1(u)d_{G_1}(u) + \sigma _2(v)d_{G_2}(v)]^3\\&\quad = n^2_3\sum _{(u,v)\in V}^{} [\sigma _1(u)d_{G_1}(u)]^3 + \sum _{(u,v)\in V}^{} \left[ \sigma _2(v)d_{G_2}(v)\right] ^2 \\&\qquad + 3 n_2 \sum _{(u,v)\in V}^{} \sigma _1(u)\sigma _2(v)d_{G_1}(u)d_{G_2}(v)[n_2 \sigma _1(u)d_{G_1}(u) + \sigma _2(v)d_{G_2}(v)]\\&\quad \le n^2_3 \sum _{v\in V_2}^{} FF( G_1) + \sum _{u\in V_1}^{} FF( G_2) + 3 n_2 \sum _{(u,v)\in V}^{} \Delta _1 \Delta _2(n_2\Delta _1 + \Delta _2)\\&\quad = n^4_2 FF( G_1) + n_1 FF( G_2) + 3 n_1 n^2_2 \Delta _1 \Delta _2(n_2\Delta _1 + \Delta _2). \end{aligned}$$

Hence the result. $\square$

Corollary 2

(i) $FF( G_1[G_2]) \le n_1n_2^4(n_1-1)^3 + n_1n_2(n_2-1)^3 + 3n_1n_2^2(n_1-1)(n_2-1)(n_1n_2-1)$ and

(ii) $FF( G_1[G_2]) \le 8n_1^3n_2^4m_1^3 + 8n_1n_2^3m_2^3 + n_1n_2(n_2-1)^3 + 3n_1n_2^2(n_1-1)(n_2-1)(n_1n_2-1)$.

Theorem 4

$$\begin{aligned}&FF( G_1) + FF( G_2) \le FF( G_1+ G_2) \le FF( G_1) + FF( G_2) + n_1n_2(n_1^2+n_2^2) \\&\quad + 3n_1 n_2 (\Delta _1^2 +\Delta _2^2 + n_2\Delta _1 + n_1\Delta _2). \end{aligned}$$

Proof

As $G_1+ G_2$ is join graph of $G_1$ and $G_2$, then for $u,v,u_1,v_1 \in V$,

$$\begin{aligned} \sigma (u) = {\left\{ \begin{array}{ll} \sigma _1(u), u\in V_1\\ \sigma _2(u), u\in V_2 \end{array}\right. } \end{aligned}$$

and

$$\begin{aligned} \mu (u,v) = {\left\{ \begin{array}{ll} \wedge \{\sigma _1(u) , \sigma _2(v)\} u\in V_1 \text { and } v\in V_2\\ \mu _1(u,v) uv\in E_1\\ \mu _2(u,v) uv\in E_2\\ 0 \text {otherwise.} \end{array}\right. } \end{aligned}$$

Then,

$$\begin{aligned} d_{G_1+ G_2}(u)&= {\left\{ \begin{array}{ll} d_{G_1}(u) + \sum _{v\in V_2}^{} \wedge \{\sigma _1(u), \sigma _2(v)\}, u\in V_1\\ d_{G_2}(u) + \sum _{v\in V_1}^{} \wedge \{\sigma _2(u), \sigma _1(v)\}, u\in V_2 \end{array}\right. } \end{aligned}$$

(1)

$$\begin{aligned}&\ge {\left\{ \begin{array}{ll} d_{G_1}(u), u\in V_1\\ d_{G_2}(u), u\in V_2. \end{array}\right. } \end{aligned}$$

(2)

Again, from Eq. (1), the following hold:

$$\begin{aligned} d_{G_1+ G_2}(u)&\le {\left\{ \begin{array}{ll} d_{G_1}(u) + \sum _{v\in V_2}^{}\sigma _1(u), u\in V_1\\ d_{G_2}(u) + \sum _{v\in V_1}^{}\sigma _2(u), u\in V_2 \end{array}\right. } \end{aligned}$$

(3)

$$\begin{aligned}&\le {\left\{ \begin{array}{ll} d_{G_1}(u) + n_2\sigma _1(u), u\in V_1\\ d_{G_2}(u) + n_1\sigma _2(u), u\in V_2 \end{array}\right. } \end{aligned}$$

(4)

Then F-index of $G_1+ G_2$ is:

$$\begin{aligned} FF( G_1+ G_2)&= \sum _{u\in V}^{} [\sigma (u)d_{G_1+ G_2}(u)]^3\\&\quad = \sum _{u\in V_1}^{} [\sigma _1(u)d_{G_1+ G_2}(u)]^3 + \sum _{u\in V_2}^{} \left[ \sigma _2(u)d_{G_1+ G_2}(u)\right] ^3\\&\quad \ge \sum _{u\in V_1}^{} [\sigma _1(u)d_{G_1}(u)]^3 + \sum _{u\in V_2}^{} \left[ \sigma _2(u)d_{G_2}(u)\right] ^3 \text {[by (2)]}\\&\quad = FF( G_1) + FF( G_2). \end{aligned}$$

Now,

$$\begin{aligned} ZF_1( G_1+ G_2)&= \sum _{u\in V}^{} \left[ \sigma (u)d_{G_1+ G_2}(u)\right] ^3\\&\quad = \sum _{u\in V_1}^{} \left[ \sigma _1(u)d_{G_1+ G_2}(u)\right] ^3 + \sum _{u\in V_2}^{} \left[ \sigma _2(u)d_{G_1+ G_2}(u)\right] ^3\\&\quad \le \sum _{u\in V_1}^{} \left[ \sigma _1(u)\{d_{G_1}(u) + n_2 \sigma _1(u)\}\right] ^3 \\&\qquad + \sum _{u\in V_2}^{} \left[ \sigma _2(u)\{d_{G_2}(u) + n_2 \sigma _2(u)\}\right] ^3 \text {[ by (4)]}\\&\quad = K_1 + K_2, \end{aligned}$$

where $K_1 = \sum _{u\in V_1}^{} [\sigma _1(u)\{d_{G_1}(u)+ n_2 \sigma _1(u)\}]^3$ and $K_2 = \sum _{u\in V_2}^{} [\sigma _2(u)\{d_{G_2}(u) + n_2 \sigma _2(u)\}]^3$ Now

$$\begin{aligned} K_1&= \sum _{u\in V_1}^{} \left[ \sigma _1(u)\{d_{G_1}(u)+ n_2 \sigma _1(u)\}\right] ^3\\&\quad = \sum _{u\in V_1}^{} [\sigma _1(u)d_{G_1}(u)]^3 +n_2^3 \sum _{u\in V_1}^{} \left[ \sigma _1(u)\right] ^6 \\&\qquad + 3 n_2\sum _{u\in V_1}^{} \sigma ^4_1(u)d_{G_1}(u)\left[ d_{G_1}(u) + n_2 \sigma _1(u)\right] \\&\quad \le FF( G_1) + n_1 n_2^3 + 3n_1n_2\Delta _1 (\Delta _1 + n_2). \end{aligned}$$

Similarly, $K_2 \le FF( G_2) + n_1^3 n_2 + 3n_1n_2 \Delta _2(\Delta _2 + n_1).$ Therefore,

$$\begin{aligned} FF( G_1+ G_2)&\le K_1 +K_2\\ \quad&\le FF( G_1) + FF( G_2) + n_1n_2(n_1^2+n_2^2) \\&\quad + 3n_1 n_2 (\Delta _1^2 +\Delta _2^2 + n_2\Delta _1 + n_1\Delta _2). \end{aligned}$$

Hence the result. $\square$

Corollary 3

• (i) $FF( G_1+ G_2) \le n_1(n_1-1)^3 + n_2(n_2-1)^3 + n_1n_2(n_1^2 +n_2^2) + 3n_1n_2[(n_1-1)^2 + (n_2-1)^2 +2n_1n_2 -n_1 -n_2]$ and

• (ii) $FF( G_1+ G_2) \le 8n_1^3m_1^3 + 8n_2^3m_2^3 + n_1n_2(n_1^2 +n_2^2) + 3n_1n_2[(n_1-1)^2 + (n_2-1)^2 +2n_1n_2 -n_1 -n_2]$.

Theorem 5

$FF( G_1\cup G_2) \ge FF( G_1) + FF( G_2) -k\Delta ^3$, where $k = |V_1\cap V_2|, \Delta = \max \{\Delta _1,\Delta _2\}$.

Proof

As $G_1 \cup G_2$ is union of $G_1$ and $G_2$, then for any $u,v\in V,$

$$\begin{aligned} \sigma (u)&= {\left\{ \begin{array}{ll} \sigma _1(u), \text { if } u\in V_1{\setminus } V_2\\ \sigma _2(u), \text { if } u\in V_2{\setminus } V_1\\ \vee \{\sigma _1(u),\sigma _2(u)\}, \text { if } u\in V_1\cap V_2 \end{array}\right. }\\ \text { and } \mu (uv)&= {\left\{ \begin{array}{ll} \mu _1(uv), \text { if } uv\in E_1{\setminus } E_2\\ \mu _2(uv), \text { if } uv\in E_2{\setminus } E_1\\ \vee \{\mu _1(uv), \mu _2(uv)\}, \text { if } uv\in E_1\cap E_2\\ 0 \text { otherwise.} \end{array}\right. } \end{aligned}$$

Then the degree of a vertex u is given below:

$$\begin{aligned} d_{G_1\cup G_2}(u) \ge {\left\{ \begin{array}{ll} d_1(u), \text { if } u\in V_1{\setminus } V_2\\ d_2(u), \text { if } u\in V_2{\setminus } V_1\\ d_1(u) \text { or } d_2(u), \text { if } u\in V_1\cap V_2. \end{array}\right. } \end{aligned}$$

Hence,

$$\begin{aligned} FF(G_1\cup G_2)&= \sum _{u\in V}^{}[\sigma (u)d_{G_1\cup G_2}(u)]^3\\&\quad = \sum _{u\in V_1}^{}[\sigma _1(u)d_{G_1}(u)]^3 + \sum _{u\in V_2}^{}[\sigma _2(u)d_{G_2}(u)]^3 \\&\qquad - \sum _{u\in V_1\cap V_2}^{}[\sigma (u)d_{G_1\cup G_2}(u)]^3\\&\quad \ge FF(G_1) + FF(G_2) - k\Delta ^3. \end{aligned}$$

$\square$

4 F-index for fuzzy graph transformation

Transformation A: Let $X_1$ be a fuzzy graph shown in Fig. 1. Now the fuzzy graph $X_2$ is obtained by $X_1$ whose vertex set is same as the vertex set $X_1$ and edge set is $E(X_2) = E(X_1)\cup \{v_1v_n\}{\setminus } \{v_{n-1}v_n\}$ with $\sigma _{X_2}(x) = \sigma _{X_1}(x) = \sigma (x), \forall x\in V(X_2),$ and $xy\in E(X_2)$

$$\begin{aligned} \mu _{X_2}(xy) = {\left\{ \begin{array}{ll} \mu _{X_2}(xy) \text { if } xy\in E(X_1)\\ \sigma (v_1) \wedge \mu (v_{n-1}v_n) \text { if } xy=v_{n-1}v_n. \end{array}\right. } \end{aligned}$$

Fig. 1

Transformation A

Theorem 6

If $\sigma (v_1) \ge \sigma (v_i)$ for $i = n-1,n$, then $FF(X_2) \ge FF(X_1).$

Proof

$$\begin{aligned} FF(X_2) - FF(X_1)&= \sigma ^3(v_1)[d^3_{X_2}(v_1)-d^3_{X_1}(v_1)] \\&\qquad + \sigma ^3(v_{n-1}) \left[ d^3_{X_2}(v_{n-1})-d^3_{X_1}(v_{n-1})\right] \\&\quad = \sigma ^3(v_1)[(d_{X_1}(v_1) + \mu (v_{n-1}v_n))^3-d^3_{X_1}(v_1)] \\&\qquad + \sigma ^3(v_{n-1})\left[ (d_{X_2}(v_{n-1}) - \mu (v_{n-1}v_n))^3-d^3_{X_1}(v_{n-1})\right] \\&\ge 0. \end{aligned}$$

$\square$

Fig. 2

Transformation B

Transformation B: Let $X_3$ be a fuzzy graph shown in Fig. 2. Now the fuzzy graph $X_4$ is obtained by $X_3$ whose vertex set is same as the vertex set $X_3$ and edge set is $E(X_4) = E(X_3)\cup \{v_1v_n\}{\setminus } \{v_{n-1}v_n\}$ with $\sigma _{X_4}(x) = \sigma _{X_3}(x) = \sigma (x), \forall x\in V(X_4),$ and $xy\in E(X_4)$

$$\begin{aligned} \mu _{X_4}(xy) = {\left\{ \begin{array}{ll} \mu _{X_4}(xy) \text { if } xy\in E(X_3)\\ \sigma (v_1) \wedge \mu (v_{n-1}v_n) \text { if } xy=v_{n-1}v_n. \end{array}\right. } \end{aligned}$$

Theorem 7

If $\sigma (v_1) \ge \sigma (v_i)$ for $i = n-1,n$, then $FF(X_4) \ge FF(X_3).$

Proof

Similar as the proof of Theorem 6. $\square$

Theorem 8

The n-vertex star (S) with each vertex and edge has membership value 1 has maximum F-index among the $n-$vertex tree (fuzzy).

Proof

Suppose T be any n-vertex tree (fuzzy). Then, by repeated applying of Theorem 6, 7 and by the Proposition 1, one can easily get, $FF(T) \le FF(S)$.

In this section, some fuzzy graph transformation is defined and studied F-index for those transformation.

Transformation C: Let $T_1$ be a fuzzy graph shown in Fig. 3. Now the fuzzy graph $T_2$ is obtained by $T_1$ whose vertex set is the same as the vertex set $T_1$ and edge set is

$$\begin{aligned} E(T_2) = E(G_1) \cup \{uv\} \cup \{uy: vy\in E(G_2)\} \cup \{xy: xy\in E(G_2), x,y \ne v\} \end{aligned}$$

with $\sigma _{T_2}(x) = \sigma _{T_1}(x) = \sigma (x), v\in V(T_2)$ and $xy\in E(T_2)$

$$\begin{aligned} \mu _{T_2}(xy) = {\left\{ \begin{array}{ll} \mu _{T_1}(xy), xy\in E(G_1)\\ \mu _{T_1}(uv) = \mu , xy=uv\\ \sigma (u) \wedge \mu _{T_1}(vy), xy=uy\\ \mu _{T_1}(xy), xy\in E(G_2), x,y\ne v.\\ \end{array}\right. } \end{aligned}$$

$\square$

Fig. 3

Transformation C

Theorem 9

If $\sigma (u) \ge \sigma (v)$, then $FF(T_2) \ge FF(T_1).$

Proof

$$\begin{aligned} FF(T_2) - FF(T_1)&= \sigma ^3(u)d^3_{T_2}(u) + \sigma ^3(v)d^3_{T_2}(v) - \sigma ^3(u)d^3_{T_1}(u) - \sigma ^3(v)d^3_{T_1}(v)\\&\quad = \sigma ^3(u) \left[ d_{G_1}(u) + d_{G_2}(v) + \mu \right] ^3 + \sigma ^3(v) \mu ^3 \\&\quad - \sigma ^3(u) \left[ d_{G_1}(u) + \mu \right] ^3 - \sigma ^3(v) \left[ d_{G_2}(v) + \mu \right] ^3\\&\quad = \sigma ^3(u)[\{d_{G_1}(u) + \mu \}^3 + 3 d_{G_2}(v) \{d_{G_1}(u) + \mu \}^2 \\&\qquad + 3 d^2_{G_2}(v) \{d_{G_1}(u) + \mu \} + d^3_{G_2}(v)] + \sigma ^3(v) \mu ^3 - \sigma ^3(u) [d_{G_1}(u) \\&\qquad + \mu ]^3 - \sigma ^3(v) [d^3_{G_2}(v) + 3\mu d^2_{G_2}(v) + 3\mu ^2 d_{G_2}(v) + \mu ^3]\\&\quad = \left[ \sigma ^3(u) - \sigma ^3(v)\right] \left[ d^3_{G_2}(v) + 3\mu d^2_{G_2}(v) + 3\mu ^2 d_{G_2}(v)\right] \\&\qquad + \sigma ^3(u)\left[ 3 d^2_{G_1}(u)d_{G_2}(v) + 6\mu d_{G_1}(u)d_{G_2}(v) + 3 d_{G_1}(u)d^2_{G_2}(v)\right] . \end{aligned}$$

As $\sigma (u) \ge \sigma (v)$, the result follows. $\square$

Fig. 4

$FF(U_3) \le FF(U_4)$

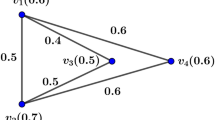
Example 1

Let $U_1$ be a fuzzy graph shown in Fig. 4 whose each vertex has membership value 1 and edge membership value has shown in Fig. 4. Then $U_2$ is obtained by $U_1$ by using the Transformation C. Now, F-index of $U_1$ and $U_2$ are given below:

$$\begin{aligned} FF(U_1)&= \sum _{u\in V(U_1)}^{} \left[ \sigma (u)d(u)\right] ^3\\&\quad = 1.5^3 + 1.2^3 + 1.9^3 + 1.7^3 + 1.0^3 + 1.3^3\\&\quad = 20.072.\\ FF(U_2)&\quad = \sum _{u\in V(U_2)}^{} \left[ \sigma (u)d(u)\right] ^3\\&\quad = 1.5^3 + 1.2^3 + 3.0^3 + 0.6^3 + 1.0^3 + 1.3^3\\&\quad = 35.516. \end{aligned}$$

Hence, $FF(U_1) \le FF(U_2)$. Therefore, the Theorem 9 is valid for the fuzzy graph $U_1$ and $U_2$.

Transformation D: Let $T_3$ be a fuzzy graph shown in Fig. 5. Now the fuzzy graph $T_4$ is obtained by $T_3$ whose vertex set is the same as the vertex set $T_3$ and edge set is

$$\begin{aligned} E(T_4) = E(G) \cup \{uv\} \cup \{uv_i: i=1,2,\cdots , r\} \end{aligned}$$

with $\sigma _{T_4}(x) = \sigma _{T_3}(x) = \sigma (x), v\in V(T_4)$ and $xy\in E(T_4)$

$$\begin{aligned} \mu _{T_4}(xy) = {\left\{ \begin{array}{ll} \mu _{T_3}(xy), xy\in E(G)\\ \mu _{T_3}(uv) = \mu , xy=uv\\ \sigma (u) \wedge \mu _{T_3}(vv_i)=\mu _i, xy=uv_i.\\ \end{array}\right. } \end{aligned}$$

Fig. 5

Transformation D

Theorem 10

If $\sigma (u) \ge \sigma (v)$, then $FF(T_4) \ge FF(T_3).$

Proof

$$\begin{aligned} FF(T_4) - FF(T_3)&= \sigma ^3(u)d^3_{T_4}(u) + \sigma ^3(v)d^3_{T_4}(v) - \sigma ^3(u)d^3_{T_3}(u) - \sigma ^3(v)d^3_{T_3}(v)\\&\quad = \sigma ^3(u) \left[ d_{G}(u) + \mu + \sum _{i=1}^{r}\mu _iz\right] ^3 + \sigma ^3(v) \mu ^3\\&\qquad - \sigma ^3(u) \left[ d_{G}(u) + \mu \right] ^3 - \sigma ^3(v) \left[ \mu + \sum _{i=1}^{r} \mu _i\right] ^3\\&\quad = \sigma ^3(u)[\{d_{G}(u) + \mu \}^3 + 3 d_{G}(u)(\sum _{i=1}^{r} \mu _i)^2 + 3 \mu (\sum _{i=1}^{r} \mu _i)^2 + 3 \mu ^2\\&\quad (\sum _{i=1}^{r} \mu _i) + 3\{d^2_{G}(u) + 2\mu d_{G}(u)\}(\sum _{i=1}^{r} \mu _i) + (\sum _{i=1}^{r} \mu _i)^3] + \sigma ^3(v) \mu ^3\\&\qquad - \sigma ^3(u) \left[ d_{G}(u) + \mu \right] ^3 - \sigma ^3(v) \left[ \mu ^3 + 3\mu (\sum _{i=1}^{r} \mu _i)^2 +3\mu ^2 (\sum _{i=1}^{r} \mu _i)\right] \\&\quad = \left[ \sigma ^3(u) - \sigma ^3(v)\right] \left[ 3 \mu (\sum _{i=1}^{r} \mu _i)^2 + 3 \mu ^2 (\sum _{i=1}^{r} \mu _i)\right] + \sigma ^3(u)\\&\quad \left[ 3 d_{G}(u)(\sum _{i=1}^{r} \mu _i)^2 + 3\{d^2_{G}(u) + 2\mu d_{G}(u)\}(\sum _{i=1}^{r} \mu _i) + (\sum _{i=1}^{r} \mu _i)^3\right] . \end{aligned}$$

As $\sigma (u) \ge \sigma (v)$, the result follows. $\square$

Fig. 6

$FF(U_3) \le FF(U_4)$

Example 2

Let $U_3$ be a fuzzy graph shown in Fig. 6 whose each vertex has membership is 1 and edge membership value is shown in Fig. 6. Then $U_4$ is obtained by $U_3$ by using the Transformation D. Now, F-index of $U_3$ and $U_4$ are given below:

$$\begin{aligned} FF(U_3)&= \sum _{u\in V(U_3)}^{} \left[ \sigma (u)d(u)\right] ^3\\&= 1.5^3 + 1.2^3 + 1.9^3 + 1.7^3 + 0.4^3 + 0.7^3\\&= 17.282.\\ FF(U_4)&= \sum _{u\in V(U_4)}^{} \left[ \sigma (u)d(u)\right] ^3\\&= 1.5^3 + 1.2^3 + 3.0^3 + 0.6^3 + 0.4^3 + 0.7^3\\&= 32.726. \end{aligned}$$

Hence, $FF(U_3) \le FF(U_4)$. Therefore, the Theorem 10 is valid for the fuzzy graph $U_3$ and $U_4$.

Transformation E: Let $T_5$ be a fuzzy graph shown in Fig. 7. Now the fuzzy graph $T_6$ is obtained by $T_5$ whose vertex set is the same as the vertex set $T_5$ and edge set is

$$\begin{aligned} E(T_6) = E(G) \cup \{uu_i: i=1,2,\cdots , s\} \cup \{uv_i: i=1,2,\cdots , t\} \end{aligned}$$

with $\sigma _{T_6}(x) = \sigma _{T_5}(x) = \sigma (x), v\in V(T_6)$ and $xy\in E(T_6)$

$$\begin{aligned} \mu _{T_6}(xy) = {\left\{ \begin{array}{ll} \mu _{T_5}(xy), xy\in E(G)\\ \mu _{T_5}(uu_1) = \mu _i, xy=uu_i\\ \sigma (u) \wedge \mu _{T_5}(vv_i)=G_i, xy=uv_i.\\ \end{array}\right. } \end{aligned}$$

Fig. 7

Transformation E

Theorem 11

If $\sigma (u) \ge \sigma (v)$ and $d_G(u) \ge d_G(v)$, then $FF(T_6) \ge FF(T_5).$

Proof

$$\begin{aligned} FF(T_6) - FF(T_5)&= \sigma ^3(u)d^3_{T_6}(u) + \sigma ^3(v)d^3_{T_6}(v) - \sigma ^3(u)d^3_{T_5}(u) - \sigma ^3(v)d^3_{T_5}(v)\\&\quad = \sigma ^3(u) \left[ d_{G}(u) + \sum _{i=1}^{s}\mu _i + \sum _{i=1}^{t}\gamma _i\right] ^3 + \sigma ^3(v) d^3_G(v) \\&\qquad - \sigma ^3(u) \left[ d_{G}(u) + \sum _{i=1}^{s}\mu _i\right] ^3 - \sigma ^3(v) \left[ d_{G}(v) + \sum _{i=1}^{t} \gamma _i\right] ^3\\&\quad = \sigma ^3(u) [\{d_{G}(u) + \sum _{i=1}^{s}\mu _i\}^3 + \{\sum _{i=1}^{t}\gamma _i\}^3 + 3\{d_{G}(u) \\&\qquad + \sum _{i=1}^{s}\mu _i\}^2 \sum _{i=1}^{t}\gamma _i + 3\{d_{G}(u) + \sum _{i=1}^{s}\mu _i\} \{\sum _{i=1}^{t}\gamma _i\}^2 + \{\sum _{i=1}^{t}\gamma _i\}^3] \\&\qquad + \sigma ^3(v) d^3_G(v) - \sigma ^3(u) \left[ d_{G}(u) + \sum _{i=1}^{s}\mu _i\right] ^3 - \sigma ^3(v) [d^3_{G}(v) \\&\qquad + 3 d^2_{G}(v) \sum _{i=1}^{t} \gamma _i + 3 d_{G}(v) \{\sum _{i=1}^{t} \gamma _i\}^2 + \{\sum _{i=1}^{t} \gamma _i\}^3]. \end{aligned}$$

As $\sigma (u) \ge \sigma (v)$ and $d_G(u) \ge d_G(v)$, the result follows. $\square$

Fig. 8

$FF(U_5) \le FF(U_6)$

Example 3

Let $U_5$ be a fuzzy graph shown in Fig. 8 whose each vertex has membership is 1 and edge membership value is shown in Fig. 8. Then $U_6$ is obtained by $U_5$ by using the Transformation E. Now, F-index of $U_5$ and $U_6$ are given below:

$$\begin{aligned} FF(U_5)&= \sum _{u\in V(U_5)}^{} \left[ \sigma (u)d(u)\right] ^3\\&\quad = 2.3^3 + 1.2^3 + 1.9^3 + 0.4^3 + 0.8^3 + 0.6^3\\&\quad = 21.546.\\ FF(U_6)&= \sum _{u\in V(U_6)}^{} \left[ \sigma (u)d(u)\right] ^3\\&= 2.9^3 + 1.2^3 + 1.3^3 + 0.4^3 + 0.8^3 + 0.6^3\\&= 29.106. \end{aligned}$$

Hence, $FF(U_5) \le FF(U_6)$. Therefore, the Theorem 11 is valid for the fuzzy graph $U_5$ and $U_6$.

Transformation F: Let $T_7$ be a fuzzy graph shown in Fig. 9. Now the fuzzy graph $T_8$ is obtained by $T_7$ whose vertex set is the same as the vertex set $T_7$ and edge set is

$$\begin{aligned} E(T_8) = E(G) \cup \{uu_i: i=1,2,\cdots , r\} \cup \{u_1u_2\} \end{aligned}$$

with $\sigma _{T_8}(x) = \sigma _{T_7}(x) = \sigma (x), v\in V(T_8)$ and $xy\in E(T_8)$

$$\begin{aligned} \mu _{T_8}(xy) = {\left\{ \begin{array}{ll} \mu _{T_7}(xy), xy\in E(G)\\ \mu _{T_7}(uu_i) = \mu _i, i = 2, 3, \cdots , r\\ \sigma (u_2) \wedge \mu _{T_7}(u_1u_2) = \mu _1 xy=u_1u_2.\\ \end{array}\right. } \end{aligned}$$

Fig. 9

Transformation F

Theorem 12

If $\sigma (u_1) \le \sigma (u_2) \le \sigma (u)$, then $FF(T_7) \ge FF(T_8).$

Proof

$$\begin{aligned} FF(T_7) - FF(T_8)&= \sigma ^3(u)d^3_{T_7}(u) + \sigma ^3(u_2)d^3_{T_7}(u_2) - \sigma ^3(u)d^3_{T_8}(u) - \sigma ^3(u_2)d^3_{T_8}(u_2)\\&\quad = \sigma ^3(u)\left[ d_G(u) + \sum _{i=1}^{r} \mu _i\right] ^3 - \sigma ^3(u)\left[ d_G(u) + \sum _{i=2}^{r} \mu _i\right] ^3\\&\qquad + \sigma ^3(u_2)\mu ^3_2 - \sigma ^3(u_2)(\mu _1 + \mu _2)^3\\&\quad = \sigma ^3(u) [\{d_G(u) + \sum _{i=2}^{r} \mu _i\}^3 + \mu _1^3 + 3\mu _1^2 \{d_G(u) + \sum _{i=2}^{r} \mu _i\} \\&\qquad + 3 \mu _1 \{d_G(u) + \sum _{i=2}^{r} \mu _i\}^2] - \sigma ^3(u)\left[ d_G(u) + \sum _{i=2}^{r} \mu _i\right] ^3 + \sigma ^3(u_2)\mu ^3_2\\&\qquad - \sigma ^3(u_2)\left[ \mu ^3_1 + \mu ^3_2 + 3 \mu ^2_1\mu _2 + 3 \mu _1\mu ^2_2\right] ^3 \end{aligned}$$

As $\sigma (u) \ge \sigma (u_2)$, the result follows. $\square$

Transformation G: Let $T_9$ be a fuzzy graph shown in Fig. 10. Now the fuzzy graph $T_{10}$ is obtained by $T_9$ whose vertex set is the same as the vertex set $T_9$ and edge set is

$$\begin{aligned} E(T_{10}) = E(G) \cup \{uu_i: i=1,2,\cdots , r\} \cup \{u_1v_1\} \end{aligned}$$

with $\sigma _{T_{10}}(x) = \sigma _{T_9}(x) = \sigma (x), v\in V(T_{10})$ and $xy\in E(T_{10})$

$$\begin{aligned} \mu _{T_{10}}(xy) = {\left\{ \begin{array}{ll} \mu _{T_9}(xy), xy\in E(G)\\ \mu _{T_9}(uu_i) = \mu _i, i = 2, 3, \cdots , r\\ \sigma (u_1) \wedge \mu _{T_9}(vv_1) = \gamma _1 xy=u_1v_1.\\ \end{array}\right. } \end{aligned}$$

Theorem 13

If $\sigma (v) \ge \sigma (u_1)$ and $d_G(v) \ge \mu _1$, then $FF(T_9) \ge FF(T_{10}).$

Fig. 10

Transformation G

Proof

$$\begin{aligned} FF(T_9) - FF(T_{10})&= \sigma ^3(u_1)d^3_{T_9}(u_1) + \sigma ^3(v)d^3_{T_9}(v) \\&\quad - \sigma ^3(u_1)d^3_{T_{10}}(u_1) - \sigma ^3(v)d^3_{T_{10}}(v)\\&=\sigma ^3(u_1) \mu _1^3 + \sigma ^3(v)\left[ d^3_G(v) + \gamma ^3_1 + 3 \gamma _1 d^2_G(v) + 3 \gamma ^2_1 d_G(v)\right] \\&\quad - \sigma ^3(u_1)\left[ \mu ^3_1 + \gamma ^3_1 + 3 \mu ^2_1 \gamma _1 + 3 \mu _1 \gamma ^2_1\right] - \sigma ^3(v)d^3_G(v)\\&= \sigma ^3(v)\left[ \gamma ^3_1 + 3 \gamma _1 d^2_G(v) + 3 \gamma ^2_1 d_G(v)\right] \\&\quad - \sigma ^3(u_1)\left[ \gamma ^3_1 + 3 \mu ^2_1 \gamma _1 + 3 \mu _1 \gamma ^2_1\right] \end{aligned}$$

As $\sigma (v) \ge \sigma (u_1)$ and $d_G(v) \ge \mu _1$, the result follows. $\square$

Theorem 14

Let ${\mathbb {U}}(n,r)$ be the unicyclic fuzzy graph with n vertices and the length of the cycle is r. Suppose $U \in {\mathbb {U}}(n,r)$ such that ($n-r$) pendant vertices are joined at a fixed vertex and each vertex and edge has membership value 1. Then U has maximum F-index among the ${\mathbb {U}}(n,r)$.

Proof

Suppose, $U \in {\mathbb {U}}_{n,r}(V,\sigma ,E_m)$ be any unicyclic graph. Then by using Theorem 8 and repeated applying of Theorem 10, 11, 12 and the Proposition 1, one can easily get, $FF(U) \le FF({\mathbb {U}}(n,r))$. $\square$

Fig. 11

Railways network in India

Fig. 12

Fuzzy graph representation of the railway network in India

5 Application of F-index for fuzzy graphs to detect crime in Indian railways

From the mid-nineteenth century, railways network is the most important mode of the conveyance of people and goods in India. About 22.15 million passengers used this network and 3.32 million metric tons of good was also shipped by this network daily in the year 2019 to 2020. The national rail network comprised 126,366 km of track over a route of 67,368 km and 7,325 stations. It is the fourth-largest national railway network in the world after United States, Russia and China. But with the passage they are posing as a threat for the general public at large while traveling, being the instances of crimes rising fourfold in rails. The ongoing railway crime has become a cause of concern for the common passenger now. So the objective of this section is to find out the railway where the most crime occurs.

Now, we consider the railways network graph in Fig. 11, where an state is considered as a vertex and if there is rail communication between the neighboring states then an edge is consider between the states. The railways crime share percentage and population share percentage in the year 2019 (last updated data) of each state are listed in the table 3 and railway distance between the main station of the neighboring states are listed in Table 4. Now the vertex membership value of a state S is denoted by $\sigma (\text {S})$ and is calculated by the formula:

$$\begin{aligned} \wedge \left\{ 1,\frac{\text {Railways crime share percentage of the state S}}{\text {Population share percentage of the state S}}\right\} . \end{aligned}$$

Clearly, $\sigma (\text {S}) \in [0,1]$ and if $\sigma (\text {S}_1) \ge \sigma (\text {S}_2)$ then the number of railway crimes of S$_1$ is higher than the number of railway crimes of S$_2$ per one lakh populations. If there is an edge between the states S$_1$ and S$_2$, the edge membership value is denoted by $\mu$(S$_1$S$_2$)and is calculated by the formula:

$$\begin{aligned}&\wedge \left\{ \sigma (\text {S}_1), \sigma (\text {S}_2)\right\} \times \\&\quad \frac{\text {Railway distance between the main station of the states S}_1 \text {and S}_2}{\text {Maximum railway distance between the main station of the neighboring states}}. \end{aligned}$$

The vertex membership values are listed in 3 and the edge membership values are listed in 5. Now, the fuzzy graph representation of the railway network in India is shown in Fig. 12. Now degree of each vertex is listed in Table 3 and which is calculated by the formula:

$$\begin{aligned} d(S) = \sum _{SS_i\in E}^{}\mu (SS_i). \end{aligned}$$

Now F-index of the fuzzy graph shown in Fig. 12 is calculated by the formula:

$$\begin{aligned} FF(G) = \sum _{S \in V}^{}\left[ \sigma (S)d(S)\right] ^3. \end{aligned}$$

Using this formula and Table 3, one can easily determined the value of F-index for the fuzzy graph representation of the railway network in India shown in Fig. 12 and the value is 4.395103.

Table 3 Vertex membership value of each state

Table 4 Railway distance between the main station of the neighboring states

Table 5 Edge membership value

Now a fuzzy subgraph $G_{S_1S_2}$ is constructed from the fuzzy graph shown in Fig. 12 by deleting an edge S$_1$S$_2$. Again by similar manner one can calculate the F-index of the fuzzy subgraph $G_{S_1S_2}$. In Table 6, F-index for all single edge deleted fuzzy subgraph is listed.

Table 6 F-index of edge deleted fuzzy subgraph

Now F-index of an edge S$_1$S$_2$ is defined by the formula:

$$\begin{aligned} FF(\text {S}_1\text {S}_2) = FF(G) - FF(G_{S_1S_2}). \end{aligned}$$

F-index of each edges is listed in Table 7.

Table 7 F-index of edges

Now score of an edge S$_1$S$_2$ is defined by the formula:

$$\begin{aligned} Sc(\text {S}_1\text {S}_2) = \left[ \frac{FF(\text {S}_1\text {S}_2)}{\vee _{ e \in E } FF(e)}\right] ^{\frac{1}{3}}. \end{aligned}$$

In Table 8, score of each edge is listed.

More score value of an edge reduces the safety. Note that, score of the edge MP-Mah is highest imply most railway crimes occurs per population in the railway in India. Also, most crime free railway per population in India is Ass-WB railway.

Table 8 Score of edges for different topological indices

Fig. 13

Linear and parabolic curves fitting of the scores obtained by first Zagreb index for fuzzy graphs with F-index for fuzzy graphs

5.1 Comparative analysis

For the comparison, other topological indices: first Zagreb index for crisp graphs, F-index for crisp graphs, first Zagreb index for fuzzy graphs are considered to determine the railway in India where most crime occurs. Note that, the topological indices defined only for the crisp graph, does not depend on the nature of the vertex or nature of its neighbour vertices, i.e. those topological indices do not depend on the number of crimes in any state and its neighbour. Hence, the topological indices for crisp graphs cannot predict the actual crime for any railways. Therefore, fuzziness is required to predict such consideration. Here, F-index for fuzzy graphs depends not only on the number of crimes of each state but also on the total number of crimes of neighbour states for each state. So this index always provides realistic results compared to the other existing indices. The score of each edge for those indices is shown in Table 8. From Table 8, each index provides the edge “MP-Mah" has the highest score, which implies the railway crime is highest on that railway track in India. But the first two indices, defined for crisp graphs, also provide the highest score value for the edges: AP-Kar, Bih-Chh, Bih-WB, Chh-MP, Chh-Mah, Kar-Mah. If the decision-maker used the indices for a crisp graph, they could not distinguish among those edges. But, the other two indices, which are defined for fuzzy graphs, provide different scores for different edges. Hence, from this point of view, the topological indices defined in crisp graphs also need to be introduced in fuzzy graphs. We also fit linear and parabolic curves between the score values obtained by the first Zagreb index for fuzzy graphs and F-index for the fuzzy graphs (See Fig. 13). Here $X-$axis represents the value of the score obtained using the first Zagreb index for fuzzy graphs, and $Y-$axis represents the value of the score obtained using the F-index for fuzzy graphs. The relation between those scores are shown below:

$$\begin{aligned} & (\text {Linear fitting}) Y= 0.8995X+0.2176, R = 0.9338 \text {and}\\ & (\text { Parabolic fitting}) Y = 1.0789X^2+1.9045X + 0.1319, R = 0.9841. \end{aligned}$$

From the correlation coefficient value (R), it is clear that the score obtained from F-index for fuzzy graphs is closely related to the score obtained from the first Zagreb index for fuzzy graphs.

6 Conclusion

F-index has a vital role in the chemical graph, spectral graph, network theory, molecular chemistry, FG theory, etc. In this article, F-index is studied for several operations such as Cartesian product, composition, union and join of two fuzzy graphs. Some exciting relations of the F-index are established during fuzzy graph transformations. Using those transformations shows that n-vertex star has a maximum F-index among the class of n-vertex trees. Also, maximal n-vertex unicyclic fuzzy graph having r cycle is determined with respect to F-index. At the end of the article, this index analyses the crime in Indian railways and compares it with three other topological indices. Also, it is shown that F-index for fuzzy graphs and the first Zagreb index for fuzzy graphs provide similar results. F-index for fuzzy graphs provides better realistic results than F-index for crisp graphs and first Zagreb index for crisp graphs to detect the crime in Indian railway. The future scopes of the research are:

• (i) In this article, it is shown that n-vertex star has a maximum F-index among the class of n-vertex trees. But, for which $n-$vertex tree (fuzzy) has the minimum F-index?

• (ii) Also, maximal n-vertex unicyclic fuzzy graph with r cycle is determined with respect to F-index. But, a minimal n-vertex unicyclic fuzzy graph with r cycle is not determined with respect to F-index.

• (iii) In this article, some good relations are established for the Cartesian product, composition, union and join of two fuzzy graphs. But, we cannot provide the exact values of those fuzzy graph operations.