Thermal decay rate of a metastable state with two degrees of freedom: Dynamical modelling versus approximate analytical formula

Abstract

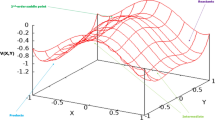
Accuracy of the Kramers approximate formula for the thermal decay rate of the metastable state is studied for the two-dimensional potential pocket. This is done by comparing with the quasistationary rate resulting from the dynamical modelling. It is shown that the Kramers rate is in agreement with the quasistationary rate within the statistical errors provided the absorptive border is far enough from the potential ridge restricting the metastable state. As the absorptive border (or its part) gets closer to the ridge, the Kramers formula underestimates the quasistationary rate. The difference reaches approximately the factor of 2 when the absorptive border coincides with the ridge.

Appendices

Appendix A

Numerical modelling of the random motion of a Brownian particle is based on a pseudorandom number generator. Results of this modelling is a sequence of $N_{\mathrm{tot}}$ trajectories, each terminated not later than at $t_\mathrm{D}$. The trajectories which have reached the absorptive border during this time lapse contribute to the decay rate $R_{\mathrm{at}}$ calculating according to eq. (21) (see also figure 4). The time dependence of $R_{\mathrm {at}}$ can be separated into a nonlinear transition part and a quasistationary part although significant fluctuations may be present. We are interested in the quasistationary value of the rate, $R_\mathrm{D}$, which is calculated as an average value of $R_{\mathrm{at}}$ over the quasistationary part

$$\begin{aligned} R_\mathrm{D} =\frac{1}{k}\mathop \sum \limits _{j=L-k+1}^L R_{\mathrm{at}}({t_j }). \end{aligned}$$

(A1)

Here $L=t_\mathrm{D} /\Delta t$ is the total number of bins, $\Delta t$ is the bin width, k is the number of bins used for finding $R_\mathrm{D}$. The initial $\left( {L-k} \right)$ bins are disregarded. The aim of this Appendix is to show that the value of $R_\mathrm{D}$ does not depend (within the statistical errors) on $\Delta t$, k, and $N_{\mathrm {tot}}$. The statistical error of $R_\mathrm{D}$ reads as

$$\begin{aligned} \varepsilon _\mathrm{R} =\frac{1}{R_\mathrm{D} \sqrt{k}}\sqrt{\frac{1}{k-1}\mathop \sum \limits _{j=L-k+1}^L ( {R_{\mathrm{at}}({t_j})-R_\mathrm{D} } )^{2}}. \end{aligned}$$

(A2)

It must decrease as $\sqrt{k}$.

Checking these properties of $R_\mathrm{D}$ and $\varepsilon _\mathrm{R}$ is of importance due to the well-known periodic character of any pseudorandom number generator. The larger is the number of trajectories (and presumably the smaller is $\varepsilon _\mathrm{R} )$ the larger is the probability of catching this periodicity.

Fig. A2

Same as in figure A1 but vs. the total number of trajectories $N_{\mathrm{tot}}$. The curve without symbols in panel b represents the $N_{\mathrm{tot}}^{-1/2}$ dependence and has been adjusted to $\varepsilon _\mathrm{R}$ at some intermediate points. See parameters of the calculations in table B1.

It is convenient to analyse not the QDR itself but its fractional difference from the Kramers rate $\xi$ defined by eq. (24). This fractional difference and its absolute error which is equal to $\varepsilon _\mathrm{R}$ are shown in figure A1. In the upper panels we see that as the interval of time-averaging $\left( {k\Delta t} \right)$ increases, $\xi$ somewhat decreases and then stays stable, fluctuating within 1%. When ${k\Delta t}$ exceeds the duration of the quasistationary stage, $\xi$ begins to grow sharply, indicating that $R_\mathrm{D}$ gets smaller. This is expected because the transient stage (where $R_{\mathrm {at}}$ is significantly smaller than QDR) becomes involved in the calculation. In the lower panels of figure A1 the relative error of $R_\mathrm{D}$, $\varepsilon _\mathrm{R}$, is shown. It evolves with ${k\Delta t}$ according to $k^{-1/2}$ law. As the transient stage starts to be involved, $\varepsilon _\mathrm{R}$ sharply increases. The curves without symbols in lower panels correspond to $\left( {k\Delta t} \right) ^{-1/2}$ dependence and have been adjusted to $\varepsilon _\mathrm{R}$ at some intermediate points. One sees that all these conclusions are unchangeable with respect to the value of $\Delta t$ (compare the left and right columns).

In figure A2 we present the dependence of $R_\mathrm{D}$ and $\varepsilon _\mathrm{R}$ on the number of trajectories. It is seen that as this number increases, $R_\mathrm{D}$ approaches its constant value and the relative error decreases like $N_{\mathrm{tot}}^{-1/2}$ as it is expected. Note that even at very small number of trajectories ($N_{\mathrm{tot}} =100\div 500)$ when the number of useful trajectories reaching the absorptive border is extremely small, our algorithm produces $R_\mathrm{D}$ which is only 20–30% away from the more correct value corresponding to $2\cdot 10^{5}$ trajectories. Therefore, using this algorithm one can obtain a rough estimate of $R_\mathrm{D}$ very quickly.

Thus, we conclude that all the results of the present paper are valid and no evidence of generator periodicity is seen.

Appendix 2

See table B1.