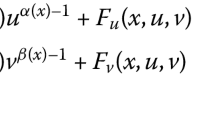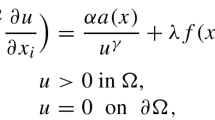Skip to main content
SpringerLink
Log in

Multiple solutions for two general classes of anisotropic systems with variable exponents

  • Published:
Journal d'Analyse Mathématique Aims and scope

Abstract

We are concerned with the weak solvability of two anisotropic systems with variable exponents: one with no-flux boundary condition, on a rectangular-like domain, and the other with zero Dirichlet boundary condition, on a general bounded domain. Both systems involve Leray–Lions type operators and a function F satisfying sublinear conditions at zero and infinity. By particularizing these general operators we can arrive at generalized Laplace operators, at generalized orthotropic Laplace operators, at Laplace-type operators that originated from a capillary phenomenon, or at generalized mean curvature operators. Our hypotheses are taken such that our situation cannot be covered by single equations and the examples provided for F show just that. The multiplicity results are obtained via the critical point theory.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. G. A. Afrouzi, N. T. Chung and S. Mahdavi, Existence and multiplicity of solutions for anisotropic elliptic systems with non-standard growth conditions, Electron. J. Differential Equations 2012 (2012), Article no. 32.

  2. G. A. Afrouzi, M. Kirane and S. Shokooh, Infinitely many weak solutions for p(x)-Laplacian-like problems with Neumann condition, Complex Var. Elliptic Equ. 63 (2018), 23–36.

    Article  MathSciNet  MATH  Google Scholar 

  3. G. A. Afrouzi, M. Mirzapour and V. D. Rădulescu, The variational analysis of a nonlinear anisotropic problem with no-flux boundary condition, Rev. R. Acad. Cienc. Exactas Fís. Nat. Ser. A Math. RACSAM 109 (2015), 581–595.

    Article  MathSciNet  MATH  Google Scholar 

  4. M. Avci, Ni-Serrin type equations arising from capillarity phenomena with non-standard growth, Bound. Value Probl. 2013 (2013), Article no. 55.

  5. S. N. Antontsev and J. F. Rodrigues, On stationary thermo-rheological viscous flows, Ann. Univ. Ferrara Sez. VII Sci. Mat. 52 (2006), 19–36.

    Article  MathSciNet  MATH  Google Scholar 

  6. G. Bonanno, Some remarks on a three critical points theorem, Nonlinear Anal. 54 (2003), 651–665.

    Article  MathSciNet  MATH  Google Scholar 

  7. G. Bonanno and G. Molica Bisci, Three weak solutions for elliptic Dirichlet problems, J. Math. Anal. Appl. 382 (2011), 1–8.

    Article  MathSciNet  MATH  Google Scholar 

  8. M.-M. Boureanu, On some variable exponent problems with no-flux boundary condition, in Current Trends in Mathematical Analysis and Its Interdisciplinary Applications, Birkhäuser/Springer, Cham, 2019, pp. 253–285.

    Chapter  Google Scholar 

  9. M.-M. Boureanu, A new class of nonhomogeneous differential operator and applications to anisotropic systems, Complex Var. Elliptic Equ. 61 (2016), 712–730.

    Article  MathSciNet  MATH  Google Scholar 

  10. M.-M. Boureanu, Infinitely many solutions for a class of degenerate anisotropic elliptic problems with variable exponent, Taiwanese J. Math. 15 (2011), 2291–2310.

    Article  MathSciNet  MATH  Google Scholar 

  11. M.-M. Boureanu, A. Matei and M. Sofonea, Nonlinear problems with p(·)-growth conditions and applications to antiplane contact models, Adv. Nonlinear Stud. 14 (2014), 295–313.

    Article  MathSciNet  MATH  Google Scholar 

  12. M.-M. Boureanu and C. Udrea, No-flux boundary value problems with anisotropic variable exponents, Commun. Pure Appl. Anal. 14 (2015), 881–896.

    Article  MathSciNet  MATH  Google Scholar 

  13. M.-M. Boureanu, C. Udrea and D.-N. Udrea, Anisotropic problems with variable exponents and constant Dirichlet condition, Electron. J. Differential Equations 2013 (2013), Article no. 220.

  14. M.-M. Boureanu and D. N. Udrea, Existence and multiplicity results for elliptic problems with p(·) - growth conditions, Nonlinear Anal. Real World Appl. 14 (2013), 1829–1844.

    Article  MathSciNet  MATH  Google Scholar 

  15. M.-M. Boureanu and A. Vélez-Santiago, Fine regularity for elliptic and parabolic anisotropic Robin problems with variable exponents, J. Differential Equations 266 (2019), 8164–8232.

    Article  MathSciNet  MATH  Google Scholar 

  16. P. Bousquet and L. Brasco, C1regularity of orthotropic p-harmonic functions in the plane, Anal. PDE 11 (2018), 813–854.

    Article  MathSciNet  MATH  Google Scholar 

  17. L. Brasco and G. Carlier, On certain anisotropic elliptic equations arising in congested optimal transport: local gradient bounds, Adv. Calc. Var. 7 (2014), 379–407.

    Article  MathSciNet  MATH  Google Scholar 

  18. E. Cabanillas Lapa, V. Pardo Rivera and J. Quique Broncano, No-flux boundary problems involving p(x)-Laplacian-like operators, Electron. J. Differential Equations 2015 (2015), Article no. 219.

  19. Y. Chen, S. Levine and R. Rao, Variable exponent, linear growth functionals in image restoration, SIAM J. Appl. Math. 66 (2006), 1383–1406.

    Article  MathSciNet  MATH  Google Scholar 

  20. M. Chermisi and E. Valdinoci, A symmetry result for a general class of divergence form PDEs in fibered media, Nonlinear Anal. 73 (2010), 695–703.

    Article  MathSciNet  MATH  Google Scholar 

  21. N. T. Chung, H. Q. Toan, On a class of anisotropic elliptic equations without Ambrosetti–Rabinowitz type conditions, Nonlinear Anal. Real World Appl. 16 (2014), 132–145.

    Article  MathSciNet  MATH  Google Scholar 

  22. D. G. Costa, An Invitation to Variational Methods in Differential Equations, Birkhäuser, Boston, MA, 2007.

    Book  MATH  Google Scholar 

  23. B. Dacorogna, Direct Methods in the Calculus of Variations Springer, New York, 2008.

    MATH  Google Scholar 

  24. L. Diening, P. Harjulehto, P. Hästö and M. Ru̇žička, Lebesgue and Sobolev Spaces with Variable Exponents, Springer, Heidelberg, 2011.

    Book  MATH  Google Scholar 

  25. M. S. B. Elemine Vall and A. Ahmed, Multiplicity of solutions for a class of Neumann elliptic systems in anisotropic Sobolev spaces with variable exponent, Adv. Oper. Theory 4 (2019), 497–513.

    Article  MathSciNet  MATH  Google Scholar 

  26. X. Fan, Anisotropic variable exponent Sobolev spaces and \(\overrightarrow p ( \cdot )\)-Laplacian equations, Complex Var. Elliptic Equ. 56 (2011), 623–642.

    Article  MathSciNet  MATH  Google Scholar 

  27. X. Fan and D. Zhao, On the spaces Lp(x)(Ω) and Wm,p(x)(Ω), J. Math. Anal. Appl. 263 (2001), 424–446.

    Article  MathSciNet  Google Scholar 

  28. G. Fragnelli, Positive periodic solutions for a system of anisotropic parabolic equations, J. Math. Anal. Appl. 367 (2010), 204–228.

    Article  MathSciNet  MATH  Google Scholar 

  29. T. C. Halsey, Electrorheological fluids, Science 258 (1992), 761–766.

    Article  Google Scholar 

  30. J. Henríquez-Amador and A. Vélez-Santiago, Generalized anisotropic Neumann problems of Ambrosetti–Prodi type with nonstandard growth conditions, J. Math. Anal. Appl. 494 (2021), Article no. 124668.

  31. K. Ho and I. Sim, Existence results for degenerate p(x)-Laplace equations with Leray-Lions type operators, Sci. China Math. 60 (2017), 133–146.

    Article  MathSciNet  MATH  Google Scholar 

  32. K. Ho and I. Sim, A-priori bounds and existence for solutions of weighted elliptic equations with a convection term, Adv. Nonlinear Anal. 6 (2017), 427–445.

    Article  MathSciNet  MATH  Google Scholar 

  33. I. H. Kim, Y. H. Kim and K. Park, Existence of three solutions for equations of p(x)-Laplace type operators with nonlinear Neumann boundary conditions, Bound. Value Probl. (2016), Article no. 185.

  34. B. Kone, S. Ouaro and S. Traore, Weak solutions for anisotropic nonlinear elliptic equations with variable exponents, Electron. J. Differential Equations 2009 (2009), Article no. 144.

  35. O. Kováčik and J. Rákosník, On spaces Lp(x) and Wk,p(x), Czechoslovak Math. J. 41 (116) (1991), 592–618.

    Article  MathSciNet  MATH  Google Scholar 

  36. A. J. Kurdila and M. Zabarankin, Convex Functional Analysis, Birkhäuser, Basel, 2005.

    MATH  Google Scholar 

  37. V. K. Le, On a sub-supersolution method for variational inequalities with Leray-Lions operators in variable exponent spaces, Nonlinear Anal. 71 (2009), 3305–3321.

    Article  MathSciNet  MATH  Google Scholar 

  38. Y. Liu, R. Davidson and P. Taylor, Investigation of the touch sensitivity of ER fluid based tactile display, in Smart Structures and Materials 2005: Smart Structures and Integrated Systems SPIE, Bellingham, WA, 2005, pp. 92–99.

    Chapter  Google Scholar 

  39. M. Mihăilescu, P. Pucci and V. Rădulescu, Eigenvalue problems for anisotropic quasilinear elliptic equations with variable exponent, J. Math. Anal. Appl. 340 (2008), 687–698.

    Article  MathSciNet  MATH  Google Scholar 

  40. K. R. Rajagopal and M. Ru̇žička, Mathematical modelling of electrorheological fluids, Contin. Mech. Thermodyn. 13 (2001), 59–78.

    Article  Google Scholar 

  41. V. Rădulescu and D. Repovš, Partial Differential Equations with Variable Exponents, CRC Press, Boca Raton, FL, 2015.

    Book  MATH  Google Scholar 

  42. M. M. Rodrigues, Multiplicity of solutions on a nonlinear eigenvalue problem for p(x)-Laplacian-like operators, Mediterr. J. Math. 9 (2012), 211–223.

    Article  MathSciNet  MATH  Google Scholar 

  43. H. L. Royden and P. M. Fitzpatrick, Real Analysis, China Machine Press, Beijing, 2010.

    MATH  Google Scholar 

  44. M. Ru̇žička, Electrorheological Fluids: Modeling and Mathematical Theory, Springer, Berlin, 2000.

    Book  Google Scholar 

  45. R. Stanway, J. L. Sproston, and A. K. El-Wahed, Applications of electrorheological fluids in vibration control: a survey, Smart Mater. Struct. 5 (1996), 464–482.

    Article  Google Scholar 

  46. R. Temam, Remarks on a free boundary value problem arising in plasma physics, Comm. Partial Differential Equations 2 (1977), 563–585.

    Article  MathSciNet  MATH  Google Scholar 

  47. R. Temam, A non-linear eigenvalue problem: the shape at equilibrium of a confined plasma, Arch. Rational Mech. Anal. 60 (1975), 51–73.

    Article  MathSciNet  MATH  Google Scholar 

  48. A. Vélez-Santiago, Embedding and trace results for variable exponent Sobolev and Maz’ya spaces on non–smooth domains, Glasg. Math. J. 58 (2016), 471–489.

    Article  MathSciNet  MATH  Google Scholar 

  49. C. Vetro, Weak solutions to Dirichlet boundary value problem driven by p(x)-Laplacian-like operator, Electron. J. Qual. Theory Differ. Equ. (2017), Article no. 98.

  50. I. M. Višik, Solubility of boundary-value problems for quasi-linear parabolic equations of higher orders, Mat. Sbornik (N.S.) 59 (1962), 289–325.

    MathSciNet  Google Scholar 

  51. I. M. Višik, Quasi-linear strongly elliptic systems of differential equations in divergence form, Trans. Moscow. Math. Soc. 12 (1963), 140–208.

    Google Scholar 

  52. E. Zeidler, Nonlinear Functional Analysis and its Applications II/B, Springer, New York, 1990.

    MATH  Google Scholar 

  53. Q. Zhang, Y. Guo and G. Chen, Existence and multiple solutions for a variable exponent system, Nonlinear Anal. 73 (2010), 3788–3804.

    Article  MathSciNet  MATH  Google Scholar 

  54. V. V. Zhikov, Averaging of functionals in the calculus of variations and elasticity, Math. USSR Izv. 29 (1987), 33–66.

    Article  MATH  Google Scholar 

  55. Q. M. Zhou, On the superlinear problem involving p(x)-Laplacian-like operators without AR-condition, Nonlinear Anal. Real World Appl. 21 (2015), 161–169.

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgments

This research was supported by the Horizon2020-2017-RISE-777911 project. Part of this research was conducted while M. M. Boureanu was visiting Universidade de São Paulo, a São Carlos, Brazil and the author is very grateful to Prof. Regilene D. S. Oliveira and to her colleagues for their kindness and for the interesting discussions.

Author information

Authors and Affiliations

  1. Department of Applied Mathematics, University of Craiova, 200585, Craiova, Romania

    Maria-Magdalena Boureanu

Authors
  1. Maria-Magdalena Boureanu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Maria-Magdalena Boureanu.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Boureanu, MM. Multiple solutions for two general classes of anisotropic systems with variable exponents. JAMA 150, 685–735 (2023). https://doi.org/10.1007/s11854-023-0287-y

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11854-023-0287-y

Search

Navigation