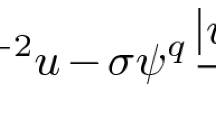Skip to main content
SpringerLink
Log in

Weighted critical Hénon equations with p-Laplacian on the unit ball in ℝN

  • Published:
Journal d'Analyse Mathématique Aims and scope

Abstract

In this paper we study the p-Hénon equations involving weighted critical exponents on the unit ball B in ℝN with 1 < p < N. It has been proved in [34] that the number \({q^ \ast }\left( \alpha \right) = {{p\left( {N + \alpha } \right)} \over {N - p}}\) with α > −p is exactly the critical exponent for the embedding from \(W_{0,r}^{1,p}\left( B \right)\) into Lq(B; ∣x∣α) and q*(α) is named as the Hénon—Sobolev critical exponent for α > 0. This important fact allows us to apply the great ideas of Brézis and Nirenberg [5] to study the existence of nontrivial radial solutions of the p-Hénon equations involving weighted critical exponent and weighted subcritical perturbations. We establish the existence of solutions of the problems with single or multiple critical exponents including Hardy—Sobolev, Sobolev and Hénon—Sobolev critical exponents. We also present to the interested readers the regularity and non-existence results for the p-Laplacian equation with multiple weighted critical terms.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. A. Ambrosetti and P. H. Rabinowitz, Dual variational methods in critical point theory and applications, J. Funct. Anal. 14 (1973), 349–381.

    Article  MathSciNet  MATH  Google Scholar 

  2. S. Bae, H. C. Choi and D. H. Pahk, Existence of nodal solutions of nonlinear elliptic equations, Proc. Roy. Soc. Edinburgh Sect. A 137 (2007), 1135–1155.

    Article  MathSciNet  MATH  Google Scholar 

  3. L. Boccardo and F. Murat, Almost everywhere convergence of the gradients of solutions to elliptic and parabolic equations, Nonlinear Anal. 19 (1992), 581–597.

    Article  MathSciNet  MATH  Google Scholar 

  4. H. Brézis and E. Lieb, A relation between pointwise convergence of functions and convergence of functionals, Proc. Amer. Math. Soc. 88 (1983), 486–490.

    Article  MathSciNet  MATH  Google Scholar 

  5. H. Brézis and L. Nirenberg, Positive solutions of nonlinear elliptic equations involving critical Sobolev exponents, Comm. Pure Appl. Math. 36 (1983), 437–477.

    Article  MathSciNet  MATH  Google Scholar 

  6. L. Caffarelli, R. Kohn and L. Nirenberg, First order interpolation inequalities with weights, Compositio Math. 53 (1984), 259–275.

    MathSciNet  MATH  Google Scholar 

  7. F. Catrina and Z.-Q. Wang, On the Caffarelli—Kohn—Nirenberg inequalities: sharp constants, existence (and nonexistence), and symmetry of extremal functions, Comm. Pure Appl. Math. 54 (2001), 229–258.

    Article  MathSciNet  MATH  Google Scholar 

  8. F. Catrina and Z.-Q. Wang, A one-dimensional nonlinear degenerate elliptic equation, in Proceedings of the USA-Chile Workshop on Nonlinear Analysis (Viña del Mar-Valparaiso, 2000), Southwest Texas State University, San Marcos, TX, 2001, pp. 89–99.

    Google Scholar 

  9. J.-L. Chern and C.-S. Lin, Minimizers of Caffarelli—Kohn—Nirenberg inequalities with the singularity on the boundary, Arch. Ration. Mech. Anal. 197 (2010), 401–432.

    Article  MathSciNet  MATH  Google Scholar 

  10. D. G. de Figueiredo, E. M. dos Santos and O. H. Miyagaki, Sobolev spaces of symmetric functions and applications, J. Funct. Anal. 261 (2011), 3735–3770.

    Article  MathSciNet  MATH  Google Scholar 

  11. P. Drábek and Y. X. Huang, Multiplicity of positive solutions for some quasilinear elliptic equation in ℝN with critical Sobolev exponent, J. Differential Equations 140 (1997), 106–132.

    Article  MathSciNet  MATH  Google Scholar 

  12. J. P. García Azorero and I. Peral Alonso, Hardy inequalities and some critical elliptic and parabolic problems, J. Differential Equations 144 (1998), 441–476.

    Article  MathSciNet  MATH  Google Scholar 

  13. N. Ghoussoub and X. Kang, Hardy—Sobolev critical elliptic equations with boundary singularities, Ann. Inst. H. Poincaré Anal. Non Linéaire 21 (2004), 767–793.

    Article  MathSciNet  MATH  Google Scholar 

  14. N. Ghoussoub and C. Yuan, Multiple solutions for quasi-linear PDEs involving the critical Sobolev and Hardy exponents, Trans. Amer. Math. Soc. 352 (2000), 5703–5743.

    Article  MathSciNet  MATH  Google Scholar 

  15. F. Gladiali, M. Grossi and S. L. N. Neves, Nonradial solutions for the Hénon equation in ℝN, Adv. Math. 249 (2013), 1–36.

    Article  MathSciNet  MATH  Google Scholar 

  16. M. Guedda and L. Véron, Quasilinear elliptic equations involving critical Sobolev exponents, Nonlinear Anal. 13 (1989), 879–902.

    Article  MathSciNet  MATH  Google Scholar 

  17. M. Hénon, Numerical experiments on the stability oh spherical stellar systems, Astronom. Astrophys. 24 (1973), 229–238.

    Google Scholar 

  18. T. Horiuchi, Best constant in weighted Sobolev inequality with weights being powers of distance from the origin, J. Inequal. Appl. 1 (1997), 275–292.

    MathSciNet  MATH  Google Scholar 

  19. C.-H. Hsia, C.-S. Lin and H. Wadade, Revisiting an idea of Brézis and Nirenberg, J. Funct. Anal. 259 (2010), 1816–1849.

    Article  MathSciNet  MATH  Google Scholar 

  20. L. Iturriaga, E. Moreira dos Santos and P. Ubilla, Local minimizers in spaces of symmetric functions and applications, J. Math. Anal. Appl. 429 (2015), 27–56.

    Article  MathSciNet  MATH  Google Scholar 

  21. E. Lieb, Sharp constants in the Hardy—Littlewood—Sobolev and related inequalities, Ann. of Math. (2) 118 (1983), 349–374.

    Article  MathSciNet  MATH  Google Scholar 

  22. Y. Y. Li and C.-S. Lin, A nonlinear elliptic PDE and two Sobolev-Hardy critical exponents, Arch. Ration. Mech. Anal. 203 (2012), 943–968.

    Article  MathSciNet  MATH  Google Scholar 

  23. W. M. Ni, A nonlinear Dirichlet problem on the unit ball and its applications, Indiana Univ. Math. J. 31 (1982), 801–807.

    Article  MathSciNet  MATH  Google Scholar 

  24. I. Peral, Multiplicity of Solutions for the p-Laplacian, https://matematicas.uam.es/~ireneo.peral/ICTP.pdf.

  25. P. Pucci and R. Servadei, Regularity of weak solutions of homogeneous or inhomogeneous quasi-linear elliptic equations, Indiana Univ. Math. J. 57 (2008), 3329–3363.

    Article  MathSciNet  MATH  Google Scholar 

  26. P. Pucci and R. Servadei, Existence, non-existence and regularity of radial ground states for p-Laplacain equations with singular weights, Ann. Inst. H. Poincaré Anal. Non Linéaire 25 (2008), 505–537.

    Article  MathSciNet  MATH  Google Scholar 

  27. E. A. B. Silva and M. S. Xavier, Multiplicity of solutions for quasilinear elliptic problems involving critical Sobolev exponents, Ann. Inst. H. Poincaré Anal. Non Linéaire 20 (2003), 341–358.

    Article  MathSciNet  MATH  Google Scholar 

  28. D. Smets, J. Su and M. Willem, Non-radial ground states for the Hénon equation, Commun. Contemp. Math. 4 (2002), 467–480.

    Article  MathSciNet  MATH  Google Scholar 

  29. J. Su, Z.-Q. Wang and M. Willem, Nonlinear Schrödinger equations with unbounded and decaying radial potentials, Commun. Contemp. Math. 9 (2007), 571–583.

    Article  MathSciNet  MATH  Google Scholar 

  30. J. Su, Z.-Q. Wang and M. Willem, Weighted Sobolev embedding with unbounded and decaying radial potential, J. Differential Equations 238 (2007), 201–219.

    Article  MathSciNet  MATH  Google Scholar 

  31. J. Su and Z.-Q. Wang, Sobolev type embedding and quasilinear elliptic equations with radial potentials, J. Differential Equations 250 (2011), 223–242.

    Article  MathSciNet  MATH  Google Scholar 

  32. G. Talenti, Best constant in Sobolev inequality, Ann. Mat. Pura Appl. 110 (1976), 353–372.

    Article  MathSciNet  MATH  Google Scholar 

  33. J. L. Vázquez, A strong maximum principle for some quasilinear elliptic equations, Appl. Math. Optim. 12 (1984), 191–202.

    Article  MathSciNet  MATH  Google Scholar 

  34. C. Wang and J. Su, Critical exponents of weighted Sobolev embeddings for radial functions, Appl. Math. Lett. 107 (2020), 106484.

    Article  MathSciNet  MATH  Google Scholar 

  35. C. Wang and J. Su, Positive radial solutions of critical Hénon equations on the unit ball in ℝN, Math. Methods Appl. Sci. 45 (2022), 11769–11806.

    Article  MathSciNet  Google Scholar 

  36. C. Wang and J. Su, The existence of ground state solutions for critical Hénon equation in ℝN, preprint.

  37. C. Wang and J. Su, The ground state solutions of Hénon equation with upper weighted critical exponents, J. Differential Equations 302 (2021), 444–173.

    Article  MathSciNet  MATH  Google Scholar 

  38. C. Wang and J. Su, The ground states of Hénon equations for p-Laplacian in ℝN involving upper weighted critical exponents, preprint.

Download references

Acknowledgment

The authors would like to thank the referees for carefully reading the manuscript and giving valuable comments to improve the exposition of the paper.

Author information

Authors and Affiliations

  1. School of Mathematical Sciences, Capital Normal University, Beijing, 100048, People’s Republic of China

    Cong Wang & Jiabao Su

Authors
  1. Cong Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jiabao Su
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jiabao Su.

Additional information

Supported by KZ202010028048 and NSFC(12271373, 11771302, 12171326).

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wang, C., Su, J. Weighted critical Hénon equations with p-Laplacian on the unit ball in ℝN. JAMA 149, 643–676 (2023). https://doi.org/10.1007/s11854-022-0262-z

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11854-022-0262-z

Search

Navigation