Skip to main content
SpringerLink
Log in

State-of-the-Art of Research on Optimization of Shell and Tube Heat Exchangers by Methods of Evolutionary Computation

  • Original Paper
  • Published:
Archives of Computational Methods in Engineering Aims and scope Submit manuscript

Abstract

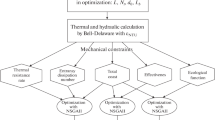
This paper presents a comprehensive state-of-the-art review of optimization by evolutionary computation methods of shell and tubes heat exchangers (STHE) of single segmental baffles. It is seen that the heat transfer coefficient to the shell side is calculated by the Kern method or by the Bell Delaware method, and that the pressure drop to the shell side is calculated by the Kern method or by the Bell Delaware method or by the Peters and Timmershaus method. It is verified the use of evolutionary computation algorithms in single-objective and multiobjective optimization of STHE, and that most related work used the total cost function of STHE. And among the contributions presented, there were implementations and applications of different evolutionary computation algorithms, or study of the STHE optimization problem by different objective functions, such as ecological, entransy dissipation, field synergy, and cost of the life cycle. Also, it was possible to verify some gaps in the work related to STHE optimization, among them, can be cited the need for greater application of decision-making methods that relate technical, economic and managerial aspects applied to the solution of the STHE. And it is suggested for future work the development of the STHE model subject to delimited uncertainties; and the formalization of a standard STHE optimization problem, so that it can serve as a reference for comparing the different optimization algorithms, and applying metrics to evaluate the advantages that are obtained when using a new algorithm for the same problem.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1

Similar content being viewed by others

Abbreviations

ABC:

Artificial bee colony

ACO:

Ant colony optimization

ARGA:

Adaptive range genetic algorithm

BA:

Bat algorithm

BBO:

Biogeography-based algorithm

BSA:

Backtracking search algorithm

BF:

Brute force

CC:

Capital cost

CEGA:

Controlled elitist genetic algorithm

CI:

Cohort intelligence

CSA:

Cuckoo search algorithm

CSO:

Civilized swarm optimization

DE:

Differential evolution

DEACO:

Differential evolution and ant colony optimization

EA:

Evolutionary algorithms

EDNFF:

Entransy dissipation number to fluid friction

EDNHC:

Entransy dissipation number to heat conduction

EI:

Economic index

E-JA:

Elitist-Jaya algorithm

ENI:

Environmental index

FA:

Firefly algorithm

FOA:

Falcon optimization algorithm

GA:

Genetic algorithm

GSA:

Gravitational search algorithm

HSA:

Harmony search algorithm

ICA:

Imperialist competitive algorithm

ITHS:

Intelligent tuned harmony search

I-ITHS:

Improved intelligent tuned harmony search

JA:

Jaya algorithm

LCC:

Life cycle cost

MCS:

Monte Carlo simulation

MOO:

Multiobjective optimization

MOPSO:

Multi-objective particle swarm optimization

MTLBO:

Modified teaching–learning-based optimization algorithm

NSGA II:

Non-dominated sorting genetic algorithm II

NR:

Not reported

OC:

Operating cost

PP:

Predador prey

PROMETHEE:

Preference ranking organization method for enrichment evaluations

PSO:

Particle swarm optimization

QPSO:

Quantum particle swarm optimization

QPSOZ:

Quantum particle swarm optimization combined with Zaslavskii chaotic map sequences

SA:

Simulated annealing

SCA:

Sine–cosine algorithm

SCAOCE:

Sum of annual operating cost and exergetic cost

SI:

Sustainability index

SOI:

Social index

SOO:

Single-objective optimization

SSFSN:

Shell side field synergy number

STHE:

Shell and tube heat exchanger

TC:

Total cost

TDE:

Tsallis differential evolution

TEDN:

Total entransy dissipation number

TEMA:

Tubular Exchanger Manufacturers Association

TOPSIS:

Technique for order performance by similarity to the ideal solution

A :

Area, or cross flow area (m\(^2\))

a :

Tube layout

AA :

First term of the Bhatti and Shah correlation

BB :

Second term of the Bhatti and Shah correlation, this factor multiplies the Reynolds number of the flow inside the tubes

bc :

Baffle cut (%)

cc :

Dittus-Bolter correlation constant

CL :

Tube layout constant

CTP :

Tube count constant

d :

Diameter (m)

D :

Diameter (m)

esp :

Wall thickness of the tubes (m)

f :

Friction factor in the flow in the shell

FF :

Correction factor for logarithmic mean temperature difference

FQPT :

Pressure drop factor in the tubes

G :

Fluid mass velocity based on the minimum free area (kg/m\(^2\) s)

h :

Heat transfer coefficient (W/m\(^2\) K)

k :

Thermal conductivity of fluid (W/m K)

L :

Spacing or length (m)

\(\dot{m}\) :

Mass flow rate (kg/s)

N :

Number of sealing strips or number of tubes or number of baffles

np :

Number of passes

Nu:

Nusselt number

P :

Pitch (m) or pumping power (W)

Pr:

Prandtl number

Q :

Heat transfer rate (W)

Re:

Reynolds number

v :

Flow velocity (m/s)

\(\delta\) :

Clearance (m)

\(\Delta P\) :

Pressure drop (Pa)

\(\varepsilon\) :

Effectiveness

\(\theta\) :

Angle between two radii intersected at the inside shell wall with the baffle cut (radians)

\(\phi\) :

Viscosity correction factor.

\(\rho\) :

Density (kg/m\(^3\))

\(\sigma\) :

Ratio of minimum free flow area to frontal area

b :

Baffles

e :

Equivalent

i :

Inside the tube

o :

Outside the tube

p :

Pattern

s :

Shell side

t :

Tubes side

otl :

Tube bundle

ss :

Sealing strips

s, t :

Shell side and tubes side

\(c_1\) :

Empirical coefficient

\(f_{alocat}\) :

Fluid allocation

\(f_{ss}\) :

Friction factor

\(E_{E}'\) :

Ecological (W)

\(k_c\) :

Contraction loss coefficient at tube entrance

\(k_e\) :

Expansion loss coefficient at tube outlet

\(I_s\) :

Area increment

\(j_{hs}\) :

Thermal factor

\(m_1\) :

Empirical coefficient

\(r_d\) :

Fouling factor \((\hbox {m}^{2}\,^{\circ }\hbox {C}/\hbox {W})\)

\(R_{fall}\) :

Allowed fouling resistance \((\hbox {m}^2\,^{\circ }\hbox {C}/\hbox {W})\)

\(sh_{types}\) :

Shell head types

\(T_{c,o}\) :

Cold side fluid output temperature \((^{\circ }\hbox {C})\)

\(t_{mat}\) :

Tube material

References

  1. Shah RK, Sekulic DP (2003) Fundamentals of heat exchanger design. Wiley

  2. TEMA (2007) Standards of the Tubular Exchanger Manufacturers Association and others. Tubular Exchanger Manufacturers Association Inc., Tarrytown

  3. ASME (2013) Boiler and pressure vessel codes: section VIII rules for construction of pressure vessels. The American Society of Mechanical Engineers, Two Park Avenue, New York

  4. Kern DQ (1950) Process heat transfer. Tata McGraw-Hill Education, New York

    Google Scholar 

  5. Tinker T (1951) Shell-side characteristic of shell-and-tube heat exchangers, Parts i, ii, and iii. General Discussion on Heat Transfer. In: Proceedings of institute of mechanical engineers, London, pp 89–116

  6. Tinker T (1958) Shell side characteristics of shell and tube heat exchangers: a simplified rating system for commercial heat exchangers. Trans ASME 80:36–52

    Google Scholar 

  7. Bell KJ (1963) Final report of the cooperative research program on shell and tube heat exchangers. University of Delaware, Engineering Experimental Station, Newark

    Google Scholar 

  8. Palen J, Taborek J (1969) Solution of shell side flow pressure drop and heat transfer by stream analysis method. Chem Eng Prog Symp Ser 65:53–63

    Google Scholar 

  9. Ribeiro MCC (1984) Comparação de métodos de cálculo termo-hidraulico para trocadores de calor casco e tubo, sem mudança de fase. Master’s thesis, Universidade Estadual de Campinas

  10. Bell KJ (2004) Heat exchanger design for the process industries. In: ASME 2004 heat transfer/fluids engineering summer conference. American Society of Mechanical Engineers, pp 921–959

  11. Peters MS, Timmerhaus KD (1991) Plant design and economics for chemical engineers. McGraw-Hill

  12. Patel VK, Rao RV (2010) Design optimization of shell-and-tube heat exchanger using particle swarm optimization technique. Appl Therm Eng 30(11–12):1417–1425. https://doi.org/10.1016/j.applthermaleng.2010.03.001

    Article  Google Scholar 

  13. Selbaş R, Kızılkan Ö, Reppich M (2006) A new design approach for shell-and-tube heat exchangers using genetic algorithms from economic point of view. Chem Eng Process Process Intensif 45(4):268–275

    Google Scholar 

  14. Wildi-Tremblay P, Gosselin L (2007) Minimizing shell-and-tube heat exchanger cost with genetic algorithms and considering maintenance. Int J Energy Res 31(9):867–885

    Google Scholar 

  15. Babu BV, Munawar S (2007) Differential evolution strategies for optimal design of shell-and-tube heat exchangers. Chem Eng Sci 62(14):3720–3739. https://doi.org/10.1016/j.ces.2007.03.039

    Article  Google Scholar 

  16. Caputo AC, Pelagagge PM, Salini P (2008) Heat exchanger design based on economic optimisation. Appl Therm Eng 28(10):1151–1159

    Google Scholar 

  17. Fesanghary M, Damangir E, Soleimani I (2009) Design optimization of shell and tube heat exchangers using global sensitivity analysis and harmony search algorithm. Appl Therm Eng 29(5–6):1026–1031. https://doi.org/10.1016/j.applthermaleng.2008.05.018

    Article  Google Scholar 

  18. Ravagnani MASS, Silva AP, Biscaia EC, Caballero JA (2009) Optimal design of shell-and-tube heat exchangers using particle swarm optimization. Ind Eng Chem Res 48(6):2927–2935. https://doi.org/10.1021/ie800728n

    Article  Google Scholar 

  19. Guo J, Xu M, Cheng L (2009) The application of field synergy number in shell-and-tube heat exchanger optimization design. Appl Energy 86(10):2079–2087. https://doi.org/10.1016/j.apenergy.2009.01.013

    Article  Google Scholar 

  20. Guo J, Xu M (2012) The application of entransy dissipation theory in optimization design of heat exchanger. Appl Therm Eng 36(1):227–235. https://doi.org/10.1016/j.applthermaleng.2011.12.043

    Article  Google Scholar 

  21. Şahin AŞ, Kılıç B, Kılıç U (2011) Design and economic optimization of shell and tube heat exchangers using artificial bee colony (abc) algorithm. Energy Convers Manag 52(11):3356–3362

    Google Scholar 

  22. Cocco V, Rodrigo A, Duck K, Alessandro F, Coelho S, Venkata R (2012) A chaotic quantum-behaved particle swarm approach applied to optimization of heat exchangers. Appl Therm Eng 42:119–128. https://doi.org/10.1016/j.applthermaleng.2012.03.022

    Article  Google Scholar 

  23. Caputo AC, Pelagagge PM, Salini P (2011) Joint economic optimization of heat exchanger design and maintenance policy. Appl Therm Eng 31(8–9):1381–1392

    Google Scholar 

  24. Sanaye S, Hajabdollahi H (2010) Multi-objective optimization of shell and tube heat exchangers. Appl Therm Eng 30(14–15):1937–1945. https://doi.org/10.1016/j.applthermaleng.2010.04.018

    Article  Google Scholar 

  25. Hadidi A, Hadidi M, Nazari A (2013) A new design approach for shell-and-tube heat exchangers using imperialist competitive algorithm (ICA) from economic point of view. Energy Convers Manag 67:66–74. https://doi.org/10.1016/j.enconman.2012.11.017

    Article  Google Scholar 

  26. Hadidi A, Nazari A (2013) Design and economic optimization of shell-and-tube heat exchangers using biogeography-based (BBO) algorithm. Appl Therm Eng 51(1–2):1263–1272. https://doi.org/10.1016/j.applthermaleng.2012.12.002

    Article  Google Scholar 

  27. Rao RV, Patel V (2013) Multi-objective optimization of heat exchangers using a modified teaching-learning-based optimization algorithm. Appl Math Model 37(3):1147–1162. https://doi.org/10.1016/j.apm.2012.03.043

    Article  MathSciNet  MATH  Google Scholar 

  28. Fettaka S, Thibault J, Gupta Y (2013) Design of shell-and-tube heat exchangers using multiobjective optimization. Int J Heat Mass Transf 60(1):343–354. https://doi.org/10.1016/j.ijheatmasstransfer.2012.12.047

    Article  Google Scholar 

  29. Ghanei A, Assareh E, Biglari M, Ghanbarzadeh A, Noghrehabadi AR (2014) Thermal-economic multi-objective optimization of shell and tube heat exchanger using particle swarm optimization (PSO). Heat Mass Transf. https://doi.org/10.1007/s00231-014-1340-2

    Article  Google Scholar 

  30. Amini M, Bazargan M (2014) Two objective optimization in shell-and-tube heat exchangers using genetic algorithm. Appl Therm Eng 69(1–2):278–285. https://doi.org/10.1016/j.applthermaleng.2013.11.034

    Article  Google Scholar 

  31. Asadi M, Song Y, Sunden B, Xie G (2014) Economic optimization design of shell-and-tube heat exchangers by a cuckoo-search-algorithm. Appl Therm Eng 73(1):1032–1040. https://doi.org/10.1016/j.applthermaleng.2014.08.061

    Article  Google Scholar 

  32. Mohanty DK (2016a) Application of firefly algorithm for design optimization of a shell and tube heat exchanger from economic point of view. Int J Therm Sci 102:228–238

    Google Scholar 

  33. Mohanty DK (2016b) Gravitational search algorithm for economic optimization design of a shell and tube heat exchanger. Appl Therm Eng 107:184–193

    Google Scholar 

  34. Tharakeshwar T, Seetharamu K, Prasad BD (2017) Multi-objective optimization using bat algorithm for shell and tube heat exchangers. Appl Therm Eng 110:1029–1038

    Google Scholar 

  35. Rao RV, Saroj A (2017) Economic optimization of shell-and-tube heat exchanger using jaya algorithm with maintenance consideration. Appl Therm Eng 116:473–487

    Google Scholar 

  36. de Vasconcelos Segundo EH, Amoroso AL, Mariani VC, dos Santos Coelho L (2017) Economic optimization design for shell-and-tube heat exchangers by a tsallis differential evolution. Appl Therm Eng 111:143–151

    Google Scholar 

  37. Barros JJC, Coira ML, de la Cruz López MP, del Caño GA (2018) Sustainability optimisation of shell and tube heat exchanger, using a new integrated methodology. J Clean Prod 200:552–567

    Google Scholar 

  38. Saldanha W, Soares G, Machado-Coelho T, dos Santos E, Ekel P (2017) Choosing the best evolutionary algorithm to optimize the multiobjective shell-and-tube heat exchanger design problem using promethee. Appl Therm Eng 127:1049–1061. https://doi.org/10.1016/j.applthermaleng.2017.08.052

    Article  Google Scholar 

  39. Iyer VH, Mahesh S, Malpani R, Sapre M, Kulkarni AJ (2019) Adaptive range genetic algorithm: a hybrid optimization approach and its application in the design and economic optimization of shell-and-tube heat exchanger. Eng Appl Artif Intell 85:444–461

    Google Scholar 

  40. de Vasconcelos Segundo EH, Mariani VC, dos Santos Coelho L (2019) Design of heat exchangers using falcon optimization algorithm. Appl Therm Eng 156:119–144

    Google Scholar 

  41. Rodríguez MBR, Rodríguez JLM, Fontes CHDO (2019) Thermo ecological optimization of shell and tube heat exchangers using NSGA II. Appl Therm Eng 156:91–98

    Google Scholar 

  42. Turgut OE, Turgut MS, Coban MT (2014) Design and economic investigation of shell and tube heat exchangers using improved intelligent tuned Harmony Search algorithm. Ain Shams Eng J 5(4):1215–1231. https://doi.org/10.1016/j.asej.2014.05.007 http://linkinghub.elsevier.com/retrieve/pii/S2090447914000756

    Article  Google Scholar 

  43. Dhavle SV, Kulkarni AJ, Shastri A, Kale IR (2018) Design and economic optimization of shell-and-tube heat exchanger using cohort intelligence algorithm. Neural Comput Appl 30(1):111–125

    Google Scholar 

  44. Özçelik Y (2007) Exergetic optimization of shell and tube heat exchangers using a genetic based algorithm. Appl Therm Eng 27:1849–1856. https://doi.org/10.1016/j.applthermaleng.2007.01.007

    Article  Google Scholar 

  45. Rao RV, Saroj A (2017) Constrained economic optimization of shell-and-tube heat exchangers using elitist-jaya algorithm. Energy 128:785–800

    Google Scholar 

  46. Rao R, Patel V (2011) Design optimization of shell and tube heat exchangers using swarm optimization algorithms. Proc Inst Mech Eng Part A J Power Energy 225(5):619–634

    Google Scholar 

  47. Wong JY, Sharma S, Rangaiah G (2016) Design of shell-and-tube heat exchangers for multiple objectives using elitist non-dominated sorting genetic algorithm with termination criteria. Appl Therm Eng 93:888–899

    Google Scholar 

  48. Hajabdollahi H, Ahmadi P, Dincer I (2012) Exergetic optimization of shell-and-tube heat exchangers using NSGA-II. Heat Transf Eng 33(7):618–628

    Google Scholar 

  49. Lahiri SK, Khalfe NM, Wadhwa SK (2012) Particle swarm optimization technique for the optimal design of shell and tube heat exchangers. Chem Prod Process Model 7(1):1–38

    Google Scholar 

  50. Lahiri SK, Khalfe N (2014) Improve shell and tube heat exchangers design by hybrid differential evolution and ant colony optimization technique. Asia Pac J Chem Eng 9(3):431–448

    Google Scholar 

  51. Fraas AP (1989) Heat exchanger design. Wiley

  52. Kakac S, Liu H (2012) Heat exchangers: selection, rating, and thermal design. CRC Press, Boca Raton

    MATH  Google Scholar 

  53. Turgut OE (2017) Thermal and economical optimization of a shell and tube evaporator using hybrid backtracking search-sine–cosine algorithm. Arab J Sci Eng 42(5):2105–2123

    Google Scholar 

  54. Serth RW, Lestina T (2014) Process heat transfer: principles, applications and rules of thumb. Academic Press, London

    Google Scholar 

  55. Towler G, Sinnott R (2008) Chemical engineering design: principles, practice and economics of plant and process design. Elsevier, Amsterdam

    Google Scholar 

  56. Sinnott R, Richardson JF, Coulson J (1989) Chemical engineering: an introduction to chemical engineering design. Elsevier, Amsterdam

    Google Scholar 

  57. Thakore SB, Bhatt BI (2007) Introduction to process engineering and design. McGraw-Hill Education, New York

    Google Scholar 

  58. Wills M, Johnston D, Harwell A (1984) A new and accurate hand calculation method for shell-side pressure drop and flow distribution. In: 22nd national heat transfer conference, HTD, ASME, vol 36

  59. Mirzaei M, Hajabdollahi H, Fadakar H (2017) Multi-objective optimization of shell-and-tube heat exchanger by constructal theory. Appl Therm Eng 125:9–19

    Google Scholar 

  60. Lee PS, Garimella SV, Liu D (2005) Investigation of heat transfer in rectangular microchannels. Int J Heat Mass Transf 48(9):1688–1704

    Google Scholar 

  61. Sadeghzadeh H, Aliehyaei M, Rosen MA (2015) Optimization of a finned shell and tube heat exchanger using a multi-objective optimization genetic algorithm. Sustainability 7(9):11679–11695

    Google Scholar 

  62. Incropera FP, Lavine AS, Bergman TL, DeWitt DP (2007) Fundamentals of heat and mass transfer. Wiley, Hoboken

    Google Scholar 

  63. Hewitt GF (1998) Heat exchanger design handbook, 1998. Begell House, New York

    Google Scholar 

  64. Saunders E (1988) Heat exchangers: selection. Design and construction. Longman Scientific and Technical, London

    Google Scholar 

  65. Rao RV, Saroj A (2018) Constrained economic optimization of shell-and-tube heat exchangers using a self-adaptive multipopulation elitist-jaya algorithm. J Therm Sci Eng Appl 10(4):041001

    Google Scholar 

  66. Shi M, Wang Z (1996) Principia and design of heat transfer device. Southeast University Press [in Chinese]

  67. Taal M, Bulatov I, Klemeš J, Stehlik P (2003) Cost estimation and energy price forecasts for economic evaluation of retrofit projects. Appl Therm Eng 23(14):1819–1835

    Google Scholar 

  68. Purohit G (1983) Estimating costs of shell-and-tube heat exchangers. Chem Eng 90(17):56–67

    Google Scholar 

  69. Caputo AC, Pelagagge PM, Salini P (2016) Manufacturing cost model for heat exchangers optimization. Appl Therm Eng 94:513–533

    Google Scholar 

  70. Nasr MJ, Polley G (2000) An algorithm for cost comparison of optimized shell-and-tube heat exchangers with tube inserts and plain tubes. Chem Eng Technol Ind Chem Plant Equip Process Eng Biotechnol 23(3):267–272

    Google Scholar 

  71. Azad AV, Amidpour M (2011) Economic optimization of shell and tube heat exchanger based on constructal theory. Energy 36(2):1087–1096. https://doi.org/10.1016/j.energy.2010.11.041

    Article  Google Scholar 

  72. Yang J, Fan A, Liu W, Jacobi AM (2014) Optimization of shell-and-tube heat exchangers conforming to TEMA standards with designs motivated by constructal theory. Energy Convers Manag 78:468–476. https://doi.org/10.1016/j.enconman.2013.11.008

    Article  Google Scholar 

  73. Caputo AC, Salini P (2012) Robust approach for shell and tube exchangers optimization under uncertain heat transfer estimation. In: Proceedings of ENCIT 2012

  74. Hajabdollahi H, Ahmadi P, Dincer I (2011) Thermoeconomic optimization of a shell and tube condenser using both genetic algorithm and particle swarm. Int J Refrig 34(4):1066–1076

    Google Scholar 

  75. Yang J, Oh SR, Liu W (2014) Optimization of shell-and-tube heat exchangers using a general design approach motivated by constructal theory. Int J Heat Mass Transf 77:1144–1154

    Google Scholar 

  76. Genceli O (1999) Heat exchangers. Birsen Book Company, Istanbul

    Google Scholar 

  77. Kakaç S (1996) Heat exchanger design course. Fundamentals and applications, vol 3. ITU Faculty of Mechanical Engineering, Istanbul

    Google Scholar 

  78. Schlunder EU (1983) Heat exchanger design handbook. Hemisphere Publishing, New York

    Google Scholar 

  79. Sinnot R (1996) Coulson & Richardson’s chemical engineering. Butterworth-Heinemann, Oxford

    Google Scholar 

  80. Smith RM (2005) Chemical process: design and integration. Wiley, Hoboken

    Google Scholar 

  81. Allen B, Gosselin L (2008) Optimal geometry and flow arrangement for minimizing the cost of shell-and-tube condensers. Int J Energy Res 32(10):958–969

    Google Scholar 

  82. Zarei O, Fesanghary M, Farshi B, Saffar RJ, Razfar M (2009) Optimization of multi-pass face-milling via harmony search algorithm. J Mater Process Technol 209(5):2386–2392

    Google Scholar 

  83. Turton R, Bailie RC, Whiting WB, Shaeiwitz JA (2008) Analysis, synthesis and design of chemical processes. Pearson Education, London

    Google Scholar 

  84. Ponce-Ortega JM, Serna-González M, Jiménez-Gutiérrez A (2009) Use of genetic algorithms for the optimal design of shell-and-tube heat exchangers. Appl Therm Eng 29(2–3):203–209. https://doi.org/10.1016/j.applthermaleng.2007.06.040

    Article  Google Scholar 

  85. Peters MS, Timmerhaus KD, West RE, Timmerhaus K, West R (1980) Plant design and economics for chemical engineers. McGraw-Hill New York, New York

    Google Scholar 

  86. Chaudhuri PD, Diwekar UM (1997) An automated approach for the optimal design of heat exchangers. Ind Eng Chem Res 36:3685–3693. https://doi.org/10.1021/ie970010h

    Article  Google Scholar 

  87. Tayal MC, Fu Y, Diwekar UM (1999) Optimal design of heat exchangers: a genetic algorithm framework. Ind Eng Chem Res 38(2):456–467. https://doi.org/10.1021/ie980308n

    Article  Google Scholar 

  88. Ozden E, Tari I (2010) Shell side cfd analysis of a small shell-and-tube heat exchanger. Energy Convers Manag 51(5):1004–1014

    Google Scholar 

  89. Pal E, Kumar I, Joshi JB, Maheshwari N (2016) Cfd simulations of shell-side flow in a shell-and-tube type heat exchanger with and without baffles. Chem Eng Sci 143:314–340

    Google Scholar 

  90. Wang Q, Chen Q, Chen G, Zeng M (2009) Numerical investigation on combined multiple shell-pass shell-and-tube heat exchanger with continuous helical baffles. Int J Heat Mass Transf 52(5):1214–1222

    MATH  Google Scholar 

  91. Zhang JF, He YL, Tao WQ (2009) 3d numerical simulation on shell-and-tube heat exchangers with middle-overlapped helical baffles and continuous baffles-part i: Numerical model and results of whole heat exchanger with middle-overlapped helical baffles. Int J Heat Mass Transf 52(23):5371–5380

    MATH  Google Scholar 

  92. Wang S, Xiao J, Wang J, Jian G, Wen J, Zhang Z (2018) Application of response surface method and multi-objective genetic algorithm to configuration optimization of shell-and-tube heat exchanger with fold helical baffles. Appl Therm Eng 129:512–520

    Google Scholar 

  93. Wen J, Yang H, Jian G, Tong X, Li K, Wang S (2016) Energy and cost optimization of shell and tube heat exchanger with helical baffles using kriging metamodel based on moga. Int J Heat Mass Transf 98:29–39

    Google Scholar 

  94. Wen J, Gu X, Wang M, Wang S, Tu J (2017) Numerical investigation on the multi-objective optimization of a shell-and-tube heat exchanger with helical baffles. Int Commun Heat Mass Transf 89:91–97

    Google Scholar 

  95. Gu X, Wang M, Liu Y, Wang S et al (2018) Multi-parameter optimization of shell-and-tube heat exchanger with helical baffles based on entransy theory. Appl Therm Eng 130:804–813

    Google Scholar 

  96. Shahril S, Quadir G, Amin N, Badruddin IA (2017) Thermo hydraulic performance analysis of a shell-and-double concentric tube heat exchanger using cfd. Int J Heat Mass Transf 105:781–798

    Google Scholar 

  97. You Y, Fan A, Huang S, Liu W (2012) Numerical modeling and experimental validation of heat transfer and flow resistance on the shell side of a shell-and-tube heat exchanger with flower baffles. Int J Heat Mass Transf 55(25):7561–7569

    Google Scholar 

  98. You Y, Chen Y, Xie M, Luo X, Jiao L, Huang S (2015) Numerical simulation and performance improvement for a small size shell-and-tube heat exchanger with trefoil-hole baffles. Appl Therm Eng 89:220–228

    Google Scholar 

  99. Tan XH, Zhu DS, Zhou GY, Zeng LD (2012) Experimental and numerical study of convective heat transfer and fluid flow in twisted oval tubes. Int J Heat Mass Transf 55(17):4701–4710

    Google Scholar 

  100. Yang J, Liu W (2015) Numerical investigation on a novel shell-and-tube heat exchanger with plate baffles and experimental validation. Energy Convers Manag 101:689–696

    Google Scholar 

  101. Dong Q, Wang Y, Liu M (2008) Numerical and experimental investigation of shellside characteristics for rodbaffle heat exchanger. Appl Therm Eng 28(7):651–660

    Google Scholar 

  102. Wang X, Zheng N, Liu Z, Liu W (2018) Numerical analysis and optimization study on shell-side performances of a shell and tube heat exchanger with staggered baffles. Int J Heat Mass Transf 124:247–259

    Google Scholar 

  103. Bhutta MMA, Hayat N, Bashir MH, Khan AR, Ahmad KN, Khan S (2012) Cfd applications in various heat exchangers design: a review. Appl Therm Eng 32:1–12

    Google Scholar 

  104. Pedrycz W, Ekel P, Parreiras R (2011) Fuzzy multicriteria decision-making: models, methods and applications. Wiley, Hoboken

    MATH  Google Scholar 

  105. Sobol IM (1993) Sensitivity estimates for nonlinear mathematical models. Math Model Comput Exp 1(4):407–414

    MathSciNet  MATH  Google Scholar 

  106. Caputo AC, Pelagagge PM, Salini P (2008) Heat exchanger design based on economic optimisation. Appl Therm Eng 28(10):1151–1159. https://doi.org/10.1016/j.applthermaleng.2007.08.010

    Article  Google Scholar 

  107. Muralikrishna K, Shenoy U (2000) Heat exchanger design targets for minimum area and cost. Chem Eng Res Des 78(2):161–167

    Google Scholar 

  108. Sinnott CJRK, Richardson J (1996) Chemical enginering design, vol 6. Elsevier, Amsterdam

    Google Scholar 

  109. Turgut OE, Turgut MS, Coban MT (2014) Design and economic investigation of shell and tube heat exchangers using improved intelligent tuned harmony search algorithm. Ain Shams Eng J 5(4):1215–1231

    Google Scholar 

  110. Khosravi R, Khosravi A, Nahavandi S, Hajabdollahi H (2015) Effectiveness of evolutionary algorithms for optimization of heat exchangers. Energy Convers Manag 89:281–288

    Google Scholar 

  111. Mariani VC, Duck ARK, Guerra FA, dos Santos Coelho L, Rao RV (2012) A chaotic quantum-behaved particle swarm approach applied to optimization of heat exchangers. Appl Therm Eng 42:119–128

    Google Scholar 

  112. Sadeghzadeh H, Ehyaei M, Rosen M (2015) Techno-economic optimization of a shell and tube heat exchanger by genetic and particle swarm algorithms. Energy Convers Manag 93:84–91. https://doi.org/10.1016/j.enconman.2015.01.007

    Article  Google Scholar 

  113. Deb K (2001) Multi-objective optimization using evolutionary algorithms. Wiley, Chichester

    MATH  Google Scholar 

  114. Riquelme N, Von, (2015) Lücken C, Baran B (2015) Performance metrics in multi-objective optimization. In: Computing conference (CLEI). Latin American, IEEE, pp 1–11

  115. Martin BAC (2016) MCDM: multi-criteria decision making methods for crisp data, r package version 1.2. https://CRAN.R-project.org/package=MCDM

  116. Guo Z, Li D, Wang B (1998) A novel concept for convective heat transfer enhancement. Int J Heat Mass Transf 41(14):2221–2225

    MathSciNet  MATH  Google Scholar 

  117. Guo ZY, Tao WQ, Shah R (2005) The field synergy (coordination) principle and its applications in enhancing single phase convective heat transfer. Int J Heat Mass Transf 48(9):1797–1807

    MATH  Google Scholar 

  118. Guo J, Cheng L, Xu M (2009) Entransy dissipation number and its application to heat exchanger performance evaluation. Chin Sci Bull 54(15):2708–2713

    Google Scholar 

  119. Angulo-Brown F (1991) An ecological optimization criterion for finite-time heat engines. J Appl Phys 69(11):7465–7469

    Google Scholar 

  120. Eryener D (2006) Thermoeconomic optimization of baffle spacing for shell and tube heat exchangers. Energy Convers Manag 47(11–12):1478–1489

    Google Scholar 

  121. Bejan A (2000) Shape and structure, from engineering to nature. Cambridge University Press, Cambridge

    MATH  Google Scholar 

  122. Sinnott R (2005) Heat transfer equipment, Coulson & Richardson’s chemical engineering. Butterworth-Heinemann

  123. Branke J, Branke J, Deb K, Miettinen K, Slowiński R (2008) Multiobjective optimization: interactive and evolutionary approaches, vol 5252. Springer, Berlin

    MATH  Google Scholar 

  124. Cho SM (1987) Uncertainty analysis of heat exchanger thermal-hydraulic designs. Heat Transf Eng 8(2):63–74

    Google Scholar 

  125. Badar MA, Zubair SM, Sheikh AK (1993) Uncertainty analysis of heat-exchanger thermal designs using the monte carlo simulation technique. Energy 18(8):859–866

    Google Scholar 

  126. Knetsch T, Hauptmanns U (2005) Integration of stochastic effects and data uncertainties into the design of process equipment. Risk Anal Int J 25(1):189–198

    Google Scholar 

  127. Clarke D, Vasquez V, Whiting W, Greiner M (2001) Sensitivity and uncertainty analysis of heat-exchanger designs to physical properties estimation. Appl Therm Eng 21(10):993–1017

    Google Scholar 

  128. Haseler L, Owen R, Sardesai R (1983) The sensitivity of heat exchanger calculations to uncertainties in the physical properties of the process fluids. Proc Inst Mech Eng Part A Power Process Eng 197(3):171–178

    Google Scholar 

  129. Shilling RL, Rudy MP, Rudy TM (2011) Risk-based design margin selection for heat exchangers. Heat Transf Eng 32(3–4):307–313

    Google Scholar 

  130. Zhiqiang X (2009) Multiobjective design of shell-and-tube heat exchangers under uncertainty. Master’s thesis, National Tsing-Hua University, Taiwan

  131. Paul H (1982) An application of geometric programming to heat exchanger design. Comput Ind Eng 6(2):103–114

    Google Scholar 

  132. Paul H (1986) An application of stochastic geometric programming to heat exchanger design. Comput Ind Eng 10(3):253–262

    Google Scholar 

  133. Unuvar A, Kargici S (2004) An approach for the optimum design of heat exchangers. Int J Energy Res 28(15):1379–1392

    Google Scholar 

  134. Onishi VC, Ravagnani MASS, Caballero JA (2013) Mathematical programming model for heat exchanger design through optimization of partial objectives. Energy Convers Manag 74:60–69. https://doi.org/10.1016/j.enconman.2013.05.011

    Article  Google Scholar 

  135. Gonçalves CdO, Costa AL, Bagajewicz MJ (2019) Linear method for the design of shell and tube heat exchangers using the Bell–Delaware method. AIChE J 65(8):1–16

    Google Scholar 

  136. Lemos JC, Costa AL, Bagajewicz MJ (2017) Linear method for the design of shell and tube heat exchangers including fouling modeling. Appl Therm Eng 125:1345–1353

    Google Scholar 

  137. Saldanha WH, Junior PA (2017) General pattern search applied to the optimization of the shell and tube heat exchanger. Int J Adv Eng Res Sci 4(11)

  138. De Jong KA (2006) Evolutionary computation: a unified approach. MIT Press, Cambridge

    MATH  Google Scholar 

  139. Bartz-Beielstein T (2006) Experimental research in evolutionary computation: the new experimentalism (Natural computing series). Springer, Berlin

    MATH  Google Scholar 

  140. Houck CR, Joines J, Kay MG (1995) A genetic algorithm for function optimization: a matlab implementation. Ncsu-ie tr 95(09):1–10

    Google Scholar 

Download references

Acknowledgements

”This study was financed in part by the Coordenação de Aperfeiçãoamento de Pessoal de Nível Superior - Brasil (CAPES) - Finance Code 001”.

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, PUC-MG, Belo Horizonte, Brasil

    Wagner Henrique Saldanha & Felipe Raul Ponce Arrieta

  2. IBMEC - Belo Horizonte, 300 Rio Grande do Norte Street, Funcionários, Belo Horizonte, MG, 30.130-130, Brasil

    Felipe Raul Ponce Arrieta

  3. Department of Electrical Engineering, PUC-MG, Belo Horizonte, Brasil

    Gustavo Luís Soares

Authors
  1. Wagner Henrique Saldanha
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Felipe Raul Ponce Arrieta
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Gustavo Luís Soares
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Wagner Henrique Saldanha.

Ethics declarations

Conflict of interest

On behalf of all authors, the corresponding author states that there is no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix: Variables related to STHE optimization problems

Appendix: Variables related to STHE optimization problems

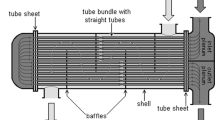
The variables used in the related works are presented in Tables 9 and 10, they are: tube layout pattern (\(a_p\)), number of passes (np), length of the tubes (\(L_t\)), wall thickness of the tubes (esp), outer diameter of the tubes (\(d_o\)), inner diameter of tubes (\(d_i\)), baffle spacing (\(L_b\)), baffle cut (bc), tube-to-baffle diametrical clearance (\(\delta _{tb}\)), shell-to-baffle diametrical clearance (\(\delta _{sb}\)), inner diameter of the shell (\(D_s\)), outer diameter of the tube bundle (\(D_{otl}\)), tube pitch (\(P_t\)), number of tubes (\(N_{t}\)), number of baffles (\(N_b\)), number of sealing strips (\(N_{ss}\)), cold side fluid output temperature (\(T_{c,o}\)), angle between two radii intersected at the inside shell wall with the baffle cut (\(\theta _{b}\)), allowed fouling resistance (\(R_{fall}\)), tube material (\(t_{mat}\)), shell head types (\(sh_{types}\)), fluid allocation (\(f_{alocat}\)).

Table 9 Variables related to the main optimization problems of STHE—part 1
Full size table
Table 10 Variables related to the main optimization problems of STHE—part 2
Full size table

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Saldanha, W.H., Arrieta, F.R.P. & Soares, G.L. State-of-the-Art of Research on Optimization of Shell and Tube Heat Exchangers by Methods of Evolutionary Computation. Arch Computat Methods Eng 28, 2761–2783 (2021). https://doi.org/10.1007/s11831-020-09476-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11831-020-09476-4

Keywords

Search

Navigation