1 Introduction

Synthetic aperture sonar (SAS) is a prominent technique used for underwater high-resolution and optical-like imaging of the seafloor. Using coherent combined multiple pings from a moving platform, SAS systems create a long synthetic aperture and provide a frequency- and range-independent resolution in acoustic imagery. This advantage of SAS distinguishes it from traditional imaging sonars, including the side-scan sonar, and makes it an appropriate technique for many underwater applications including target recognition, search for small objects, and inspection (Hayes and Gough 2009; Hansen and Kolev 2011) (Galusha et al. 2018; Tesfaye et al. 2019). Figure 1 compares side-scan sonar with SAS in terms of the image quality of a towrope on the seabed. The SAS technology can create an image with higher resolution compared with the side-scan sonar system. An SAS image is an intensity representation of the scattered acoustic energy at the SAS receiver; therefore, acoustic scattering is the main parameter in sonar equations.

Figure 1
figure 1

Comparison of image quality between a side-scan sonar and a SAS system of a 20-m towrope on the seabed (Marine technology news 2019)

Full size image

Acoustic scattering due to an arbitrary object in free space is defined as the irregular refraction of an incident acoustic wave. The scattered fields are propagated along different directions according to the object geometry, with varying intensities (Dashen et al. 1990). An underwater acoustic scattering model is an important parameter in different types of sonar-system applications including SAS imaging, underwater inspection, and target detection (Qin et al. 2018) (Fischell and Schmidt 2017; Zhang et al. 2017). Acoustic scattering due to underwater objects is the most important factor that embodies the characteristics of objects to find interesting targets in the ocean environment, in military, scientific, and commercial domains (Li et al. 2018).

Therefore, a precise model that describes scattered fields of the scattered surface is essential. Theoretical researches on acoustic scattering are extended from underwater targets with simple shapes to those with increasingly complex geometric shapes; the scattered fields contain the characteristic information of the target, and this information is used for underwater target structure modeling. The interesting objects in this field are commonly occurring natural objects (e.g., marine life and bobbles) and artificial objects (e.g., pipelines, mines, and submarines) (Flax et al. 1978; Yang and Li 2016).

Many researches have been conducted to develop acoustic scattering models. Generally, scattering models are grouped into two basic categories: numerical and analytical, both of which differ from each other in terms of efficient frequency range, accuracy, and required computational resources (Bonomo et al. 2015). High-accuracy full-field theories, such as finite element method (FEM) and boundary element method (BEM), numerically solve the Helmholtz integral equation to the degree of discretization (Hunt et al. 1975; Karimi et al. 2016). BEM requires the surface discretization of a scatterer, which is commonly represented using triangular and quadrilateral elements, while FEM performs the discretization of a full-volume scatterer. Although numerical models are sufficiently accurate, they are often not feasible for large objects or far-field scattering because of increased computational load.

Analytical models, however, reduce the computational load of full-field methods by making some assumptions. These methods do not require large complex systems of equations and rather use approximate solutions to compute scattered pressures. Additionally, they are often appropriate for mid- and high-frequency range and for scatterers with special structures (Nolte et al. 2015). However, they are not efficient for accurate acoustic scattering computations, except for objects with simple geometry. Although numerical methods provide accurate predictions, their computational costs increase with the size and complexity of the scatterers (Chandler-Wilde and Langdon 2007).

Underwater acoustic scattering modeling is an important field in SAS system design and algorithm development. In real aperture sonars, the scattering from each ping is individually processed, while in the SAS system, the scattering combination of multiple hits-on-target upon target scattering is processed. Thus, it is desirable to have an accurate scattering model with low computation cost. The existing scattering models in SAS simulators utilize point- or facet-based models with smooth primitive facets or elements.

In this paper, we propose a new model for computing acoustic waves scattering from underwater arbitrary objects; the model obtains scattered pressure using a new discretization method that employs non-uniform texture facets as primitive elements in the Helmholtz Kirchhoff (HK) integral equation. The proposed model, called texture element method (TEM), uses statistical local binary pattern (LBP) descriptors for the discretization of the target surface domain into many non-uniform elements so that the region that belongs to any element has the same statistical and roughness properties as those of a known roughness class. The proposed model can be more useful and efficient, especially in image-reconstruction algorithms. The following are the main contributions of this paper:

  • An efficient acoustic scattering model, called TEM, which is based on a new discretization method that uses object surface texture descriptions is proposed.

  • A new structured surface discretization method is proposed that uses non-uniform element–based LBP descriptors that efficiently reduce computational time and cost.

  • The size and number of non-uniform elements are related to the surface roughness; for a given surface, few elements with large size are required for smooth portions, and for more complex portions, large numbers of elements with small size are required.

  • The proposed discretization method can efficiently improve scattering models such as BEM and FEM.

  • The performance of the proposed model is evaluated and compared with those of BEM and analytical methods in terms of sonar parameters to prove the effectiveness of the proposed model.

  • The proposed model can be utilized as an efficient scattering method in SAS system design and algorithm development.

The rest of this paper is organized as follows. In Section 2, some related works regarding the scattering problem are reviewed. The scattering problem formulation is described in Section 3. In Section 4, the architecture of the proposed scattering model is introduced. In Section 5, experimental results are presented. Finally, conclusions are drawn in Section 6.

2 Review of Acoustic Scattering Methods

The acoustic fields scattered from underwater targets reflect their characteristics. Therefore, they are crucial for the target-recognition process. Many methods have been proposed for the scattering problem, and they include the boundary integral method (Schenck 1968), BEM (Copley 1967), FEM (Ihlenburg 2006), Kirchhoff approximate method (Gaunaurd 1985), and T-matrix method (Waterman 1969). These methods can be categorized into numerical and analytical types. The analytical models are appropriate only for targets with significantly simple geometries. Thus, there is a great focus on the numerical methods for solving acoustic scattering problems.

Ju et al. proposed a numerical calculation model for the acoustic scattering from underwater targets in low-frequency-based FEM. Three-dimensional mesh finite element meshes were transformed into two-dimensional ones to increase computing speed. The underwater targets were considered to have axisymmetric structure (Ju et al. 2018).

Bonomo et al. used FEM to model the acoustic scattering from a one-dimensional rough elastic surface. The scattering strength was compared with analytic models to evaluate the effectiveness. An agreement was observed between small-slope approximation and FEM in all the studied cases (Bonomo et al. 2015).

Okumura et al. applied BEM to calculate the frequency dependence of the target strength (TS) at any incident angle. The scattering amplitude was calculated for four types of prolate-spheroids using BEM and prolate-spheroid model, respectively. A comparison of results confirmed the accuracy of BEM (Okumura et al. 2003).

Nolte et al. presented a physical model that involved sound-propagation measurement and numerical simulation. BEM and ray tracing methods were used to predict the scattering pressure due to underwater objects and TS (Nolte et al. 2015).

Zampolli et al. used a hybrid model that comprised FEM and a discrete representation of Helmholtz integral based on Green’s function for rough targets acoustic scattering. The hybrid model reduced the three-dimensional scattering problem into a series of independent two-dimensional scattering problems and was appropriate for axisymmetric targets (Zampolli et al. 2012).

Kargl et al. considered two models including FEM and a fast ray model for free field scattering amplitude of targets on a water–sediment interface. The fast ray model was used to decrease the computational burden of FEM. Target scattering was achieved by the convolution of an incident field and a free field scattering amplitude at a solid aluminum surface (Kargl et al. 2014).

Richard et al. proposed an enclosing surface acoustic scattering method via pressure and particle velocity measurements. Scattering was characterized by the acoustic samples far-field estimation under an incident plane wave. The numerical results showed the far-field pattern estimated via near-field measurements (Richard et al. 2018).

Song et al. used combination FEM and an automatic matched layer technique to calculate the TS of composite and steel materials. The acoustic scattering properties of steel and composite materials were evaluated (Song et al. 2017).

Chai et al. used a hybrid two-dimensional acoustic scattering model, called HS-FEM-DtN, based on a smooth FEM and Dirichlet–Neuman boundary condition for an underwater rigid cylinder. The underwater targets were presented with triangular elements (Chai et al. 2016).

BEM and FEM are popular numerical methods in solving the acoustic scattering problem. BEM offers certain advantages including boundary conditions being considered on curved surfaces and acoustic problems being studied in the infinite domain. However, its main constraint is a homogeneous or half homogeneous scatterer (Wu 2000; Okumura et al. 2003).

Usually, mesh density and element quality considerably affect the solution accuracy and calculation time in numerical models. A small mesh size results in accurate solutions with high computational time, while a large mesh size leads to less accurate results but with decreased computational time. Liu and Dutt investigated the effect of element quality and mesh size on the numerical models to select the appropriate mesh size (Liu and Glass 2013; Dutt 2015).

The main drawback of almost all the above-mentioned papers is computational intensity, which increases with object size and shape. Moreover, a smooth surface with uniform discretization is considered in most scattering methods, whose accuracy and computational complexity increase with the number of mesh elements, however requiring many computational resources and days.

The textures in sonar images contain important information regarding the target and are thus used as the main features in different sonar applications including target detection and recognition (Nabelek et al. 2018). In the existing acoustic scattering models, the texture properties of the target surface are not considered for target modeling. In this paper, for the first time, a scattering model is proposed based on the texture properties of the target surface for the realistic modeling of arbitrary targets. Our proposed model efficiently computes the acoustic scattering due to the concerned object in fluid media such as oceans. The basic ingredient of the proposed model is a new representation of acoustic scattering, and the model is described as an object surface non-uniform discretization method based on characterized information via LBP descriptors. Moreover, scattered fields are obtained via the HK integral. The proposed model can solve the target acoustic scattering problem using less computational cost and resources compared with other numerical models.

3 Acoustic Scattering Problem

The acoustic scattering problem has special importance in underwater applications including sonar imaging. Target scattering is the result of the interaction between transmitted and received acoustic signals from active sonar and underwater target, respectively. Target scattering characterization is necessary for effective underwater target detection and recognition in active sonar systems.

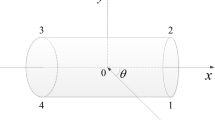
Consider an arbitrary, finite-sized object bounded by a surface S in free space. Let the object be influenced by an incident acoustic pressure, as depicted in Figure 2. The incident acoustic pressure is considered a plane wave (black arrow). The object re-radiates the incident field in the water, the so-called scattered fields, which propagate away from the object along all directions (blue arrows). The acoustic pressure p(x) at an arbitrary point x located outside the object satisfies the well-known Helmholtz Equation (Nennig et al. 2011) as follows and is expressed using Eq. (1):

Figure 2
figure 2

Acoustic scattering geometry

Full size image
$$ \left({\nabla}^2+{k}^2\right)p(x)=0\kern0.75em \mathrm{in}\ D\subset {\mathrm{\mathbb{R}}}^d $$
(1)

where D and d denote the propagation domain and problem dimension, respectively. The symbol ∇2 denotes Laplacian operator. Additionally, k denotes the wave number (a positive quantity), which is associated with wavelength λ, angular frequency ω, and speed of sound c in the media, as follows:

$$ k=\frac{\omega }{c}=\frac{2\pi }{\lambda } $$
(2)
$$ P(x)={P}_{\mathrm{in}}(x)+{P}_{\mathrm{scat}}(x) $$
(3)

where Pin denotes the incident acoustic pressure and Pscat the scattered acoustic pressure. The scattered pressure Pscat at point x is calculated using the HK integral (Pierce 1989) as follows:

$$ {P}_{\mathrm{scat}}(x)=\int \left(\frac{\partial G\left(x,{x}^{\prime}\right)}{\partial n}\ p\left({x}^{\prime}\right)-G\left(x,{x}^{\prime}\right)\frac{\partial p\left({x}^{\prime}\right)}{\partial n}\right)\mathrm{d}S\left({x}^{\prime}\right) $$
(4)

where the integral is over the surface S, and x′ is a point on S. The acoustic pressure p(x′) and its normal derivative \( \frac{\partial p\left({x}^{\prime}\right)}{\partial n} \) on surface S are unknown and should be identified using analytical/numerical models or experimental measurements. The function G(x, x′) is the free space Green’s function between points x and point x′ on the surface of the background medium in which sound waves propagate in the underwater environment with no target presence. The free space Green’s function (Zampolli et al. 2008) is expressed as follows:

$$ G\left(x,{x}^{\prime}\right)=\frac{{\mathrm{e}}^{-\mathrm{i}k\left|x-{x}^{\prime}\right|}}{4\uppi \left|x-{x}^{\prime}\right|} $$
(5)

where \( \mathrm{i}=\sqrt{-1} \). To achieve a unique solution in the solution space, it is assumed that the acoustic field p satisfies the Sommerfeld radiation condition (Pignier et al. 2015) at infinity with appropriate boundary conditions (Faran Jr 1951; Dashen et al. 1990). The Sommerfeld radiation condition is expressed as follows:

$$ \frac{\partial P}{\partial n}+\mathrm{i} k\beta P=0 $$
(6)

where the constant β corresponds directly to medium impedance and inversely to surface impedance, and β = 0 in Neumann boundary or sound hard condition. The HK integral reduces the Helmholtz equation to a surface integral evaluation. For example, the three-dimensional Helmholtz equation is reduced to two-dimensional surface integral estimation. Commonly, in many free field scattering problems, two assumptions are made; the interface between the object and ocean floor does not affect the scattering pressure, and the possibility of multiple scattering is ignored (Kargl et al. 2014).

4 Proposed Scattering Model

Underwater target detection and recognition process is particularly important in SAS system applications, which require a comprehensive characterization of target scattering for performing acoustic imaging and improving feature extraction. Different methods were suggested for target surface modeling and computing the acoustic scattering using the HK integral, in which the target surface was represented by smooth primitive elements and the discrete representation of integral Eq. (4) was computed as a sum of contributions from the primitive elements or facets. However, many computations and significant storage space are required to achieve an accurate scattering method, especially in the SAS system. However, in this paper, a new model for computing scattered pressure from a finite-sized target using target surface statistical description is proposed. The proposed model accurately estimates the scattering pressure with computational cost less than those of numerical scattering models including BEM.

In this section, the proposed model is described. Additionally, it will be explained how the non-uniform discretization method can be used to compute scattered pressures. First, an LBP descriptor is introduced for object surface characterization. Second, the acoustic scattering pressures are computed at an observation point outside the object by modeling the object surface using the proposed model.

4.1 Surface Texture Descriptors

The accuracy of underwater object acoustic scattering modeling depends on the accuracy of object surface modeling. Texture is an important feature to characterize a large- or small-sized object surface in a far or near distance. In sonar images, as an essential feature that contains important information regarding the scene and concerned targets, texture is usually utilized in underwater applications including segmentation, and target detection and recognition (Nabelek et al. 2018).

LBP is one of the most distinguished texture descriptors (Ojala et al. 2002). As a non-parametric method, it characterizes the texture using primitive elements with their statistical descriptions. LBP descriptors offer the following prominent advantages:

  • Computational simplicity

  • Low computational complexity

  • Invariance to changes in scale and illumination changes

  • Discriminative power of discriminating different textures

LBP descriptors have attracted significant attention in various fields of image processing and computer vision (Liu et al. 2016). The LBP operator labels image pixels with decimal values that result from LBP codes using neighborhoods of different sizes (Ojala et al. 2002). The neighborhood system is determined as a set of equally spaced pixels P on a circle with radius R to the center of the pixel to be labeled. Figure 3 depicts an example of the LBP operator with a neighborhood of P pixels on a circle of radius R in which the image pixels are labeled by encoding the local structure around each pixel. The original LBP operator for a given pixel at (xc, yc) is expressed (Huang et al. 2011) as follows:

$$ {\mathrm{LBP}}_{R.P}\left({x}_c,{y}_c\right)=\sum \limits_{p=0}^{P-1}S\left({i}_p-{i}_c\right){2}^p $$
(7)

where ic and ip denote the intensity values of the central pixel and neighbor pixels, respectively. The term p denotes the neighbor pixels that correspond to the neighborhood system with size R. The term S(ip − ic) denotes the sign function is expressed as follows:

$$ S\left({i}_p-{i}_c\right)=\left\{\begin{array}{c}1\ \mathrm{if}\ {i}_p\ge {i}_c\\ {}0\ \mathrm{otherwise}\end{array}\right. $$
(8)

When the target image is rotated, the neighbor pixel values ip will correspondingly move around the central pixel ic, and the LBPR.P operator generates different LBP values. In this paper, a rotation-invariant LBP, denoted as \( {\mathrm{LBP}}_{R.P}^{\mathrm{riu}2} \)(Ojala et al. 2002), is used for achieving robustness to image rotation. The rotation-invariant LBP is used for uniform patterns by introducing a uniformity measure U, which corresponds to the number of bitwise transitions from 0 to 1 or vice versa in LBP, as follows (Liu et al. 2016):

$$ U\left({\mathrm{LBP}}_{R.P}\right)={\sum}_{p=0}^{P-1}\left|S\left({i}_p-{i}_c\right)-S\left({i}_{\operatorname{mod}\left(p+1,P\right)}-{i}_c\right)\right| $$
(9)
Figure 3
figure 3

Examples of LBP operators with (R. P) neighborhood

Full size image

An LBP with the U value of at most two is considered uniform. Notably, uniform patterns represent fundamental texture microstructures, and the rotation-invariant LBP is defined as (Liu et al. 2016) follows:

$$ {\mathrm{LBP}}_{R.P}^{\mathrm{riu}2}=\left\{\begin{array}{c}{\sum}_{p=0}^{P-1}S\left({i}_p-{i}_c\right)\kern0.5em \mathrm{if}\ U\left({\mathrm{LBP}}_{R.P}\right)\le 2\\ {}P+1\ \mathrm{otherwise}\end{array}\right. $$
(10)

4.2 Acoustic Scattering Based on LBP-Elements

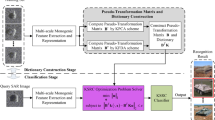
The discretization of the target surface into many uniform primitive elements or facets is a common approach to solving acoustic scattering problems in SAS systems; however, it leads to high computational costs and resource usage. In this paper, a new model based on LBP descriptors is proposed; in the proposed model, the object surface is decomposed into a few structured elements. Figure 4 depicts the block diagram of the proposed model. For a given object, LBP codes are calculated using Eq. (10) in a determined neighboring space, where the surface is decomposed into many different-sized elements called LBP-Elements.

Figure 4
figure 4

Proposed model

Full size image

Our model offers the following two primary advantages: first, a fewer number of elements are required than those required by popular scattering methods, and surface modeling is performed with smooth surface regions modeled using a few LBP-Elements versus rough regions. Second, the regions that belong to an LBP-Element have the same texture features and roughness. However, all the LBP-Elements with similar features have the same decimal value with useful properties that can be used in complex object modeling and image formation algorithms.

Figure 5 depicts a pipeline newly installed on the seabed (BfN 2019). We will continue our description with this example. Pipeline decomposition based on LBP descriptors is depicted in Figure 6.

Figure 5
figure 5

Newly installed pipeline on the seabed

Full size image
Figure 6
figure 6

Example of surface discretization using the LBP operator

Full size image

Figure 6b depicts LBP-Elements, each decimal value being illustrated in the same color. The number of colors can be determined by the size of the neighborhood system and object complexity. The center of all the LBP-Elements is illustrated in Figure 6c. Additionally, the center of the LBP-Elements for three decimal values with different pipeline characteristics is depicted in Figure 6d–6f.

After modeling the target surface using the LBP operator, the acoustic pressure sampled at the points that belong to LBP-Elements \( {x}_j^{\prime } \) is then propagated to an observation point or receiver located at x outside the surface S by using the discrete representation of the HK integral (see Eq. (4)) as follows:

$$ {P}_{\mathrm{scat}}(x)={\sum}_j\left(\frac{\partial G\left(x,{x}_j^{\prime}\right)}{\partial {n}_j}\ p\left({x}_j^{\prime}\right)-G\left(x,{x}_j^{\prime}\right)\frac{\partial p\left({x}_j^{\prime}\right)}{\partial {n}_j}\right)\mathrm{d}{L}_j $$
(11)

where index j denotes a point on surface S. The term dLj denotes the LBP-Element on S associated with the jth point \( \left({x}_j^{\prime}\right), \) whose pressure \( p\left({x}_j^{\prime}\right) \) and normal derivative \( \frac{\partial p\left({x}_j^{\prime}\right)}{\partial {n}_j} \) are sampled. The boundary condition can be used to replace \( \frac{\partial p}{\partial n} \)by –ikβp, following which Eq. (11) is reformulated as follows:

$$ {P}_{\mathrm{scat}}(x)={\sum}_j\left(\frac{\partial G\left(x,{x}_j^{\prime}\right)}{\partial {n}_j}+\mathrm{i} k\beta\ G\left(x,{x}_j^{\prime}\right)\right)p\left({x}_j^{\prime}\right)\mathrm{d}{L}_j $$
(12)

Targets with rigid and absorbing surfaces are modeled wherever β = 0 or β contains a positive real part, respectively. This is necessary, once the scattered pressure determined at points x on surface S and then the scattered pressure are computed at any observation point.

5 Performance Evaluation

In this section, the acoustic scattering model is simulated. The results are then analyzed to evaluate the efficiency of the proposed model against other presented scattering methods. The simulation parameters are listed in Table 1. Two well-known models are compared: the full-wave theory using BEM and the following analytical model.

Table 1 Model simulation parameters
Full size table

5.1 Boundary Element Method

BEM is one of the most common approaches for computing acoustic scattering from closed objects. It numerically solves the scattering problem of a scatterer surface. It applies finite element discretization to a formulation of the scattering problem boundary integral. It generally represents the object surface as a tiny uniform mesh with smooth elements, typically triangular, rectangular, or curvilinear boundary elements, and then the scattered pressure p(x) is approximated for each element (Chandler-Wilde and Langdon , 2007).

5.2 Analytical Solution

The acoustic scattering problem can be represented as a set of spherical functions (Faran 1951) as follows:

$$ {P}_{\mathrm{scat}}\left(x,\theta \right)={\sum}_{n=1}^{\infty }{c}_n\left({j}_n(kx)-i{y}_n(kx)\right){p}_n\left(\hat{k}.\hat{x}\cos \theta \right) $$
(13)

where jn and yn denote the spherical Bessel functions of the first and second kinds, respectively; additionally, pn denotes a Legendre polynomial of order n. The coefficients cn are determined using the boundary conditions considered in the problem. For a sphere with radius a, in a sound-soft case with p = 0 on the boundary and in Neumann boundary conditions, in which normal displacement at the boundary is equal to zero, the scattered pressure is calculated using Eqs. (14) and (15), respectively (Pignier et al. 2015) One has

$$ {P}_{\mathrm{scat}}\left(x,\theta \right)=-{\sum}_{n=1}^{\infty}\left(2n+1\right){i}^n{h}_n(kx)\frac{j_n(ka)}{h_n(ka)}\ {p}_n\left(\cos \theta \right) $$
(14)
$$ {P}_{\mathrm{scat}}\left(x,\theta \right)=-{\sum}_{n=1}^{\infty}\left(2n+1\right){i}^n{h}_n(kx)\frac{j_n^{\prime }(ka)}{h_n^{\prime }(ka)}\ {p}_n\left(\cos \theta \right) $$
(15)

where \( {j}_n^{\prime } \) and \( {h}_n^{\prime } \) denote the derivatives of the spherical Bessel and Hankel function of the first kind, respectively.

5.3 Experimental Results

In this section, some experimental results outlined upon comparing the proposed model with two other well-known numerical and analytical models are discussed. To compute the acoustic scattering in the proposed model (TEM), the concerned object surface is initially discretized into non-uniform elements using the LBP operator of Eq. (10). Subsequently, pressure on the LBP-Elements and its normal derivative are calculated, and the scattered pressure at the observation point is calculated using Eq. (12). BEM divides the concerned object boundary into boundary elements, where the mesh size is important and closely related to accuracy of BEM. However, the mesh size directly determines the complexity of the method.

In this paper, to evaluate the performance, the proposed model and BEM are applied to a rigid cylinder with the radius of a = 0.5, which is insonified by a plane incident acoustic wave. The 2D scattered pressure fields are calculated over a frequency band of f = 100 to 50 kHz at the increments of 100 Hz. Figure 7 depicts the estimated scattering pressure as a function of frequency estimated using the BEM model with different numbers of boundary elements and the proposed model, respectively, at observation points at a distance r = 2a, 5a, and 10a. Although the proposed model has a good agreement with the BEM model for the highest number of elements, it uses a fewer number of elements (approximately half). For more details, the real and imaginary parts of the scattered pressure as a function of the wavenumber at a point with polar angle θ = π/4 in r = 5a are plotted in Figure 8.

Figure 7
figure 7

Scattering pressure as a function of the frequency given by the proposed model (TEM) and BEM, with 100, 200, 300, and 400 elements in observation points at different distances TEM with 210 elements has a good agreement with BEM with 400 elements

Full size image
Figure 8
figure 8

Imaginary and real parts of the scattered pressure as a function of the wavenumber given by the proposed model TEM with 210 elements and BEM with 400 elements, respectively, in different distances

Full size image

One of the important quantities in sonar equations and acoustic applications is TS, which determines the reflection ability of targets (Zhang et al. 2014). TS is expressed in terms of the target-scattered pressure at a distance r relative to the incoming pressure as

$$ \mathrm{TS}=20\times {\log}_{10}\left(r\left|{P}_{\mathrm{scat}}\right|/\left|{P}_{\mathrm{in}}\right|\right) $$
(16)

where Pin denotes the incoming plane wave and its amplitude is considered |P_in| = 1. Figure 9 depicts the TS results of BEM and TEM for the cylinder as a function of frequency in r = 2a. An excellent agreement is observed between both the models.

Figure 9
figure 9

TS as a function of the frequency. Comparison between the results obtained with using the proposed model, i.e., TEM with 210 elements, and BEM with 400 elements, at r = 2a

Full size image

To clearly investigate the experimental results, Figure 10 depicts the average relative error between the exact solution and the BEM solution for different mesh sizes, as well as the average relative error between the exact solution and that obtained using the proposed model for different distances. From the results, it can be realized that the accuracy increases with the mesh size. The proposed model with a discretization method based on surface texture descriptor yields accuracy similar to that of BEM with 400 elements while only using 210 elements.

Figure 10
figure 10

Average relative error in a semi-log y plot between BEM with 100, 200, 300, 400, and 500 elements and TEM with 210 elements for the rigid circular cylinder at distances r = 2a, 5a, and 10a and over a frequency band of f = 100 to 50 kHz

Full size image

Accurate target modeling is related to accurate target surface modeling. In the proposed model, a new discretization method is based on the statistical characteristics of the surface. Therefore, the points at an element have the same features, making the scattering pressure across the entire element equal and proportional to its area. The proposed model can accurately estimate acoustic scattering using a few elements.

Another experiment is performed to draw a comparison between the proposed model and analytical model for a sphere with radius a and various range values r under different boundary conditions. The scattered pressure results for a sound-soft sphere with radius a = 2 wavelengths in range r = 2a, 3a, and 4a for different scattering angles are depicted in Figure 11. Additionally, the scattered fields of the sphere with Neumann boundary conditions are depicted in Figure 12. The directivity plots show that both the models well predicted the scattered fields in all directions and that the proposed model has a good agreement with the analytical method.

Figure 11
figure 11

Scattered field of a rigid sphere for a = 2 wavelengths given by TEM and analytic method, respectively, for different scattering angles

Full size image
Figure 12
figure 12

Scattered field of a sound-soft sphere for a = 2 wavelengths given by TEM and analytic method, respectively, for different scattering angles

Full size image

The TS estimations of a rigid sphere and a sound-soft sphere using the proposed and analytical models with radius a = 2 and 3 in range r = 2a as a function of the scattering angles are depicted in Figures 13 and 14, respectively. The scattered pressures of a rigid sphere with radius a = 0.5 in r = 2a at different wavenumbers are also depicted in Figure 15. The estimated results for various radius values and ranges at different boundary conditions show an accurate agreement between the proposed and analytic models.

Figure 13
figure 13

Comparison of TS estimates using TEM and analytical method for a sound-soft sphere and rigid sphere in a radius of a = 2 and a range of r = 2a for different scattering angles

Full size image
Figure 14
figure 14

Comparison of TS estimates using TEM and analytical method for a sound-soft sphere and rigid sphere in a radius of a = 3 and a range of r = 2a for different scattering angles

Full size image
Figure 15
figure 15

Comparison of scattering fields using TEM and analytical method of a rigid sphere in a radius of a = 0.5 wavelengths and a range of r = 2a for different wavenumbers

Full size image

A detailed comparison of accuracy and computational efficiency between the proposed method, i.e., TEM, and the two other comparative methods are given in the following; Max error and computing time are used as the metrics for comparison. Max error is defined as the maximum absolute error as follows:

$$ \operatorname{Max}\ \mathrm{error}=\max \left|\left|{P}_{\mathrm{scat}}\right|-\left|{P}_{\mathrm{exact}}\right|\right| $$
(17)

where Pscat and Pexact denote the predicted and exact scattered fields, respectively. The computational efficiency is defined as the computing time required by each method in terms of the average CPU time. All the method simulations were conducted using a PC with CPU Intel 2.5 G and 4 G memory.

The Max error and the computing time for the proposed method and the BEM method with the different number of elements in at the range of r = 2a for varying frequency values between 100 Hz and 50 kHz are presented in Table 2. Evidently, TEM method with 210 elements has accuracy similar to that of BEM with 400 elements while spending significantly less computing time. This demonstrates that the proposed method more efficiently reduces the computational cost compared with the numerical methods.

Table 2 Comparison of the Max error and computational efficiency between TEM and BEM with different number of elements at distance r = 2a and varying frequency values from 100 to 50 kHz
Full size table

Additionally, the Max error and computing time comparisons between the proposed and analytical methods on a sphere with a radius of a = 0.5 wavelengths in the range of r = 2a, 3a, 5a, and 10a for varying k values [1, 50] and different scattering angles −π < θ < π are presented in Table 3. The analytical method is an accurate analytical scattering method for computing the acoustic scattering of a sphere; its computational cost increases with the wave number. Table 3 demonstrates a good agreement between the proposed model, i.e., TEM, and analytical method, while the former spends less computing time than the latter.

Table 3 Comparison of Max error and computational efficiency between TEM and analytical method in a range of r = 2a, 3a, 5a, and 10a for varying k values with different scattering angles −π < θ < π
Full size table

One must use a small mesh size to obtain accurate scattering information using numerical models that require high computation and resource usage, essentially in 3D space. Additionally, sampling in uniform discretization is of m-order, where m is related to the total number of nodes in the mesh. For the same target, half of the samples are approximately required in the proposed non-uniform discretization method. Therefore, the proposed model can effectively reduce the computational complexity. Moreover, an efficient discretization method improves the scattering models.

Meanwhile, the texture is the main feature in sonar images, as it reflects important information regarding targets. Target modeling based on surface texture properties results in realistic target modeling, which can be useful in sonar and SAS algorithm design and improvement.

6 Conclusions

Underwater acoustic scattering is an important factor in SAS imaging systems and their applications. Underwater target characteristics are inferred from the target-scattered fields; therefore, an accurate scattering model of an acoustic field incident on the target is essential for actual target modeling. Most scattering methods including FEM, BLM, and analytical models decompose the scattering target into many uniform primitive elements without considering the surface features. Consequently, the accuracy of scattering modeling depends on mesh size and results in high computational cost and resources.

We proposed a new scattering model that uses an efficient discretization method based on statistical target surface texture information to achieve an accurate acoustic scattering model with less computational cost and resources. The proposed model is a new representation of acoustic scattering, and it uses non-uniform elements described by LBP descriptors as an influential and fine-scale descriptor for different textures. The scattered pressure is computed on texture elements and arrived in observation point via the discrete representation of the HK integral. The experimental results demonstrated an excellent agreement between the proposed model with two well-known BLM and analytic models, although it required fewer elements. By using the surface texture information, the proposed model could model the target with low computational complexity, which is especially useful in improving the scattering models and coherence process in real-time SAS design and related applications