Bootstrap-based model selection criteria for beta regressions

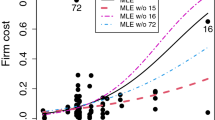
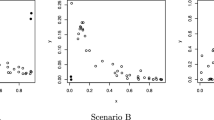
Abstract

This paper addresses the issue of model selection in the beta regression model focused on small samples. The Akaike information criterion (AIC) is a model selection criterion widely used in practical applications. The AIC is an estimator of the expected log-likelihood value, and measures the discrepancy between the true model and the estimated model. In small samples, the AIC is biased and tends to select overparameterized models. To circumvent that problem, we propose two new selection criteria, namely: the bootstrapped likelihood quasi-CV and its 632QCV variant. We use Monte Carlo simulation to compare the finite sample performances of the two proposed criteria to those of the AIC and its variations that use the bootstrapped log-likelihood in the class of varying dispersion beta regressions. The numerical evidence shows that the proposed model selection criteria perform well in small samples. We also present and discuss and empirical application.

Appendix A: score function and information matrix of the beta regression model with varying dispersion

This appendix presents the score function and Fisher’s information matrix for the varying dispersion beta regression model described in Sect. 3.

The score function is obtained by differentiating the log-likelihood function with respect to the unknown parameters. The score function of $\log f(Y|\theta _{k})$ with respect to ${\beta }$ is given by

$$\begin{aligned} U_{\!\beta }({\beta },{\gamma })!= X^{\top } \Phi \, T({y}^{*}-{\mu }^{*}), \end{aligned}$$

where $\Phi \!= \!\text {diag}\! \left\{ \frac{1\!-\! \sigma ^2_1}{\sigma ^2_1},\ldots ,\frac{1\!-\sigma ^2_n}{\sigma ^2_n} \right\}$, $T \!=\! \text {diag}\left\{ \frac{1}{g^{\prime }(\mu _1)},\ldots ,\frac{1}{g^{\prime }(\mu _n)}\right\}$, ${y}^{*}\!=\!(y^{*}_1,\ldots ,y^{*}_n)^{\top }$, ${\mu }^{*}\!=\!(\mu ^{*}_1,\ldots ,\mu ^{*}_n)^{\top }$, $y^{*}_t \! = \log \left( \frac{y_t}{1-y_t} \right)$, $\mu ^{*}_t= \psi \left( \mu _t\left( \frac{1-\sigma ^2_t}{\sigma ^2_t}\right) \right) - \psi \left( (1-\mu _t)\left( \frac{1-\sigma ^2_t}{\sigma ^2_t}\right) \right)$ and $\psi (\cdot )$ is the digamma function, i.e., $\psi (u)\!=\frac{\partial \log \Gamma (u)}{\partial u}$, for $u>0$. The score function of $\log f(Y|\theta _{k})$ with respect to ${\gamma }$ is

$$\begin{aligned} U_{\!\gamma }({\beta },{\gamma })=Z^{\top }H {a}, \end{aligned}$$

where $H\! = \!\text {diag} \!\left\{ \! \frac{1}{h^{\prime }(\sigma _1)}, \ldots , \frac{1}{h^{\prime }(\sigma _n)} \!\right\}$ and ${a}= ( a_1,$ $\ldots ,a_n)^{\top }$, the $t$th element of $a$ being $a_t = -\frac{2}{\sigma ^3_t} \left\{ \mu _t \left( y^*_t - \mu ^*_t \right) + \log (1-y_t) - \psi \left( (1-\mu _t)(1-\sigma ^2_t)/\sigma ^2_t \right) + \psi \right. \left. \left( (1-\sigma ^2_t) / \sigma ^2_t \right) \right\}$.

Fisher’s information matrix for ${\beta }$ and ${\gamma }$ is given by

$$\begin{aligned} K({\beta },{\gamma }) = \left( \begin{array}{cc} K_{({\beta },{\beta })} &{}\quad K_{({\beta },{\gamma })} \\ K_{({\gamma },{\beta })} &{}\quad K_{({\gamma },{\gamma })} \end{array} \right) , \end{aligned}$$

where $K_{({\beta },{\beta })} = X^{\top }\Phi WX$, $K_{({\beta },{\gamma })} = (K_{({\gamma },{\beta })})^{\top }=X^{\top }CTHZ$ and $K_{({\gamma },{\gamma })}=Z^{\top }DZ$. Also, we have $W = \text {diag}\{w_1,\ldots ,w_n\}$, $C = \text {diag}\{c_1,\ldots ,c_n\}$ and $D = \text {diag}\{d_1,\ldots ,d_n\}$, where

$$\begin{aligned} w_t&= \frac{(1-\sigma _t^2)}{\sigma _t^2}\left[ \psi ' \left( \frac{\mu _t(1-\sigma _t^2)}{\sigma _t^2}\right) + \psi ' \left( \frac{(1-\mu _t)(1-\sigma _t^2)}{\sigma _t^2}\right) \right] \frac{1}{\left[ g'(\mu _t)\right] ^2}, \\ c_t&= \frac{(2-2\sigma _t^2)}{\sigma _t^5}\left[ \mu _t\psi ' \left( \frac{\mu _t(1-\sigma _t^2)}{\sigma _t^2}\right) -(1-\mu _t) \psi ' \left( \frac{(1-\mu _t)(1-\sigma _t^2)}{\sigma _t^2}\right) \right] , \text { and } \\ d_t&= \frac{4}{\sigma _t^6}\!\left[ \!\mu _t^2\psi ' \left( \!\frac{\mu _t(1\!-\!\sigma _t^2)}{\sigma _t^2}\!\right) \!\! -(1\!-\!\mu _t)^2 \psi ' \left( \!\frac{(1\!-\!\mu _t)(1\!-\!\sigma _t^2)}{\sigma _t^2}\!\right) \!\!-\psi ' \left( \!\frac{(1\!-\!\sigma _t^2)}{\sigma _t^2}\!\right) \!\right] \\&\quad \times \frac{1}{\left[ h'(\sigma _t)\right] ^2}. \end{aligned}$$