Enhancing Fatigue Life of Thick-Walled Cylinders through a Hybrid Rotational-Swage Autofrettage-Induced Residual Stresses

Abstract

Enhancing fatigue life of thick-walled cylinders used for high-pressure application is an important design task. Cylindrical vessels find applications in oil and gas industries, food and chemical industries, nuclear reactors and gun barrels. They are susceptible to cracking due to high tensile stress caused by internal pressurization at their inner side during operation. Compressive residual stress can potentially help in suppressing inner cracks in such components to safeguard against any awkward situations. In this work, a hybrid rotational-swage autofrettage method is proposed to induce beneficial compressive residual stresses at the interior wall of a thick-walled cylinder. An analytical model is developed to determine the residual stresses in the process using Tresca yield criterion and its associated flow rule for non-hardening material behavior. The compressive residual stress generated in the hybrid autofrettage process is assessed for increase in the fatigue life of pressurized cylinders. To exemplify the process, cylinders of two different materials, viz. SS316 and Al7075-T6, are considered to be rotated while interfering at their inner side with an axially driven oversized AISI4340 mandrel. The design speeds of the cylinders for each material are obtained as a function of the swaging mandrel interference without contact separation during the process. The residual stresses in the cylinders are evaluated numerically, and the performance of the cylinders on enhancing the fatigue life under in-service internal pressurization is investigated using Paris law.

1 Introduction

Residual stresses play an important role in the design of any structural component. The existence of residual stresses in a component greatly influences the material performance in terms of strength, life, surface hardness (Ref 1,2,3,4) and resistance to stress corrosion cracking (Ref 5). Contrary to the tensile residual stresses, the compressive residual stresses have beneficial impact on the strength and life of materials. The beneficial effect of residual stresses is successfully utilized in the design of thick-walled cylinders used for high-pressure applications to increase their pressure carrying capacity and fatigue life. Commonly, the beneficial residual stresses in thick-walled cylinders are generated by employing a metal working process called autofrettage (Ref 6). In autofrettage process, the interior wall of the cylinder is deliberately subjected to plastic deformation by the application of sufficiently high magnitude of loading to the cylinder in various forms. In the next stage, the plastically deforming load is released to induce significantly large compressive residual stresses at the interior wall of the cylinder. Toward the exterior wall of the cylinder, the process induces small tensile residual stresses due to self-equilibrating nature of the residual stresses. The compressive residual stress induced by autofrettage at the cylinder interior wall contributes to offset the maximum in-service stress level in the cylinder extending its operating pressure carrying capacity. Further, the compressive residual stress helps in suppressing inner cracks enhancing the fatigue life of the cylinder. Therefore, the autofrettage analysis for thick-walled cylinders primarily focuses on two aspects—increasing the in-service pressure bearing capacity and fatigue life due to induced residual stress field.

From the early age of inception of the process to the present, various autofrettage processes have been proposed to take the advantage of compressive residual stresses in thick-walled cylinders. The types of autofrettage process vary in the type of loading applied to cylinder to induce plasticity. For instance, if the applied loading is an internal hydraulic pressure, it is called hydraulic autofrettage (Ref 6). It is called swage autofrettage, if the cylinder is loaded with a mechanical interference by driving a solid cylindrical mandrel through its interior (Ref 7). In the recent, it was proposed to achieve autofrettage by loading the cylinder with a radial temperature difference, called thermal autofrettage (Ref 8) and by axisymmetric high speed rotation of the cylinder, called rotational autofrettage (Ref 9). The detailed analysis of all the known autofrettage processes can be found in Ref 10.

Both the hydraulic and swage autofrettage process have received significant attention of the researchers to predict the advantageous residual stress field resulting in extended in-service pressure bearing capacity. Numerous analytical, numerical and experimental works on the hydraulic autofrettage have been reported in the literature (e.g., Ref. 11,12,13,14,15). These analyses are based on different yield criterions: Tresca or von Mises, hardening models: isotropic or kinematic and choice of experimental methods to assess residual stresses. Most of the works reported in literature on swage autofrettage are based on numerical finite element method (Ref 16,17,18) and experimental investigation (Ref 19, 20) due to the complex nature of the interaction between the swage mandrel and cylinder interior. Nevertheless, a simple plane strain analysis of swage autofrettage was also reported (Ref 21) based on Tresca yield criterion and elastic-perfectly plastic material model. A few analytical, numerical as well as experimental investigations were carried out to apprise the residual stresses induced by the method of thermal autofrettage (Ref 3, 8, 22). The recent rotational autofrettage process have been analyzed either analytically or numerically using Tresca or von Mises yield criterion (Ref 9, 23, 24).

The beneficial effect of autofrettage-induced residual stresses in enhancing the fatigue life of thick-walled cylinders under cyclic pressure loading have been considered by several researchers. One of the earliest work on the investigation of the effect of autofrettage on the fatigue life of internally pressurized thick-walled cylinders was credited to Davidson et al. (Ref 25). They experimentally determined the fatigue life of high strength 4340-type steel autofrettaged cylinders of different diameter ratios and observed significant improvements in fatigue life as compared to non-autofrettaged cylinders. A simple numerical method for the prediction of fatigue life of autofrettaged cylinders was proposed by Kendall (Ref 26) based on the numerical integration of fatigue crack propagation rate equation due to Paris and Erdogan (Ref 27). Some other notable contributions on the prediction of fatigue life of autofrettaged cylinders were made by Rees (Ref 28, 29), Parker and Underwood (Ref 30), and Jahed et al. (Ref 31). In all the above referred works, the authors assumed the autofrettaged cylinder with initial single or multiple cracks of various geometries (straight fronted, elliptical or semi-elliptical) emanating from the interior wall. The range of Mode-I crack tip stress intensity factors (SIFs) for a given cyclic pressure was evaluated using or modifying existing approximate solutions for SIFs available in various studies (e.g., Ref 32,33,34) and then incorporated in Paris law (Ref 27) for calculating fatigue life. A combined effect of internal pressure and overstraining on the fatigue life of internally cracked smooth gun barrel subjected to hydraulic and swage autofrettage was analyzed by Perl and Saley (Ref 35) using three-dimensional Mode-I stress SIFs along the front of a single inner radial semi elliptical crack. The effect of autofrettage-induced residual stresses on the high cycle fatigue life of notched S355 low carbon steel specimen was investigated by Okorokov (Ref 36) using FEM analysis in the framework of a cyclic plasticity material model. Recently Perl and Saley (Ref 37) carried out an extensive analysis of fatigue life of a typical modern smoothbore hydraulic and swage autofrettaged barrel subjected to overstrain levels of 70% and 100%.

Some researchers have proposed hybrid processes by combining different autofrettage methods or combing autofrettage method to other self-hooping techniques. For example, Shufen and Dixit (Ref 38) proposed a hybrid process combining hydraulic and thermal autofrettage and analyzed it using FEM-based package ABAQUS. It was shown that the proposed hybrid process is capable of increasing the desired pressure carrying capacity of a typical cylinder at relatively low autofrettage pressure than the individual hydraulic autofrettage. A theoretical study of thermal autofrettage combined with shrink-fit was also carried out (Ref 39, 40) to enhance pressure carrying capacity and fatigue life in the compound cylinder as compared to a monobloc cylinder autofrettaged only by thermal autofrettage. There are examples where the hydraulic autofrettage is combined with wire-winding (Ref 41, 42) to increase the desired level of compressive residual hoop stress in cylinder. In Ref 41, the residual stresses generated in hybrid wire-wound hydraulic autofrettage process was analyzed, while the fatigue life was studied in Ref 42.

In this work, a new hybrid rotational-swage autofrettage method is proposed by combining the recently proposed rotational and well-established swage autofrettage techniques into one process. The stand-alone rotational autofrettage process requires very high angular speed of rotation to generate desired level of compressive residual stress in a cylinder (Ref 9, 23). By combining the rotational autofrettage with swage autofrettage, it is intended to reduce the required high speed rotation of the cylinder for a specified compressive residual hoop stress and fatigue life. The proposed hybrid process is analyzed using Tresca yield criteria and its associated flow rule for non-hardening material behavior. The analytical solution for residual stresses are developed and numerically evaluated for SS316 and Al7075-T6 cylinders undergoing hybrid rotational-swage autofrettage process interacting with AISI4340 mandrel. The fatigue life analysis of the cylinder after autofrettage is assessed under in-service pressurization and depressurization. The fatigue life estimation is based on the evaluation of Mode-I crack tip stress intensity factors for an inner straight-fronted axial crack and incorporating them in Paris law for a range of in-service pressures.

2 The Proposed Method of Hybrid Rotational-Swage Autofrettage

A hybrid method of rotational-swage autofrettage is proposed here combining the principles exploited in a recently conceived rotational autofrettage process (Ref 9) and about six-decade swage autofrettage process (Ref 7). The method of rotational autofrettage is based on the principle of inducing compressive residual stress at the interior of a thick-walled cylindrical component by applying a plastically deforming centrifugal load and suppressing it subsequently. The centrifugal load is induced through the axisymmetric rotation of the cylinder. The swage autofrettage method employs an oversized tapered mandrel to push through the bore of the cylinder. While pushing the mandrel, it interferes with the material at the interior wall of the cylinder causing localized plastic deformation. Upon completely forcing out the mandrel from the cylinder, the interior wall is induced with compressive residual stresses. This work proposes combining the rotational and swage autofrettage processes to form a single process called the hybrid rotational-swage autofrettage. The process is depicted in Fig. 1 schematically. The advantage of achieving autofrettage by the effect of rotation as well as mechanical interference is exploited. As shown in Fig. 1, the cylinder considered to be subjected to autofrettage is rotated at certain angular speed while simultaneously an oversized tapered mandrel is being driven through its bore from one end to the other. For the ease of loading and unloading, the geometry of the swage mandrel is provided with tapers at its front and back with a very small length of uniform diameter, which is slightly larger than the inner diameter of the rotating cylinder to maintain interference. The simultaneous action of angular speed and mechanical interference should induce plasticity at the interior of the cylinder without the contact separation between the mandrel and the cylinder interior wall during loading. It is considered that the material of the mandrel is strong enough and does not undergo any plastic deformation during the process. Once the mandrel is completely forced out through the interior wall of the rotating partially plastic cylinder, the rotation of the cylinder is stopped bringing the angular speed to zero. This amounts to the unloading of the procedure. At this instant, compressive residual stresses are set up at the interior wall of the cylinder penetrating to a certain radial depth. Due to self-equilibrating nature of the residual stresses, the exterior portion of the cylinder wall gets induced with tensile residual stresses. The analysis of the proposed method is presented in Sect. 3.

Fig. 1

Schematic of a hybrid rotational-swage autofrettage method

3 Analysis of Hybrid Rotational-Swage Autofrettage Method

A cylinder with internal radius a and external radius b is considered to be rotated along with the pushing of an oversized non-rotating solid cylindrical tapered mandrel through the bore for achieving the hybrid rotational-swage autofrettage of the cylinder. The angular speed of rotation of the cylinder is taken as ω and the mechanical interference between the solid mandrel and the interior wall of the cylinder is taken as δ. It is considered that E and ν are the Young’s modulus of elasticity and Poisson’s ratio of the cylinder material and the corresponding values for the material of the mandrel are E₁ and ν₁, respectively. The whole assembly is assumed to be axisymmetric. Two-dimensional plane strain condition (axial strain ε_z = 0) and Tresca yield criteria are used to analyze the stresses during the hybrid rotational-swage autofrettage process. The present analysis assumes the elastic-perfectly plastic material model in the framework of small-strain plasticity. In a recent analytical study of rotational autofrettage for ASTM A723 and SS316 cylinders, Kamal and Perl (Ref 43) found that the effect of strain hardening is not very significant. The justification was based on the comparison of autofrettage-induced stresses obtained through an analytical model without strain hardening and a three-dimensional finite element model incorporating Ramberg-Osgood power-law strain hardening model. The maximum deviations of equivalent stress with and without strain hardening in the ASTM A723 and SS316 cylinders were 1.8% and 4.3%, respectively. Thus, in the present analytical modelling, it is reasonable to consider the elastic-perfectly plastic material model to predict the first-hand solution for the proposed hybrid autofrettage process.

3.1 Elastic Analysis

When the angular speed of the cylinder and interference between the swage mandrel and the cylinder are small, the stress states in the cylinder remains elastic. The elasticity in the cylinder and the swage mandrel is governed by the generalized Hooke’s law. In Sects. 3.1.1 and 3.1.2, the elastic analysis of the cylinder and the swage mandrel is presented.

3.1.1 The Cylinder

For the cylinder with Young’s modulus of elasticity E and Poisson’s ratio ν, the generalized Hooke’s law due to plane strain assumption can be written as (Ref 44)

$$\varepsilon_{r} = \,\frac{1 + \nu }{E}\left\{ {\left( {1 - \nu } \right)\sigma_{r} - \nu \sigma_{\theta } } \right\}.$$

(1)

$$\varepsilon_{\theta } = \,\frac{1 + \nu }{E}\left\{ {\left( {1 - \nu } \right)\sigma_{\theta } - \nu \sigma_{r} } \right\}.$$

(2)

$$\sigma_{z} \, = \,\nu \,\left( {\sigma_{r} + \,\sigma_{\theta } } \right),$$

(3)

where ε_r, ε_θ are the radial and hoop strain components and σ_r, σ_θ, σ_z are the radial, hoop and axial stress components, respectively. The axisymmetric strain-displacement relations are given by (Ref 44)

$$\varepsilon_{r} = \frac{{{\text{d}}u}}{{{\text{d}}r}},\,\,\,\,\,\varepsilon_{\theta } = \frac{u}{r},$$

(4)

where u is the radial displacement. The axisymmetric rotation of the cylinder is governed by the following equilibrium equation (Ref 44):

$$\frac{{{\text{d}}\sigma_{r} }}{{{\text{d}}r}} + \frac{{\sigma_{r} - \sigma_{\theta } }}{r} + \rho r\omega^{2} = 0,$$

(5)

where ρ is the density of the cylinder material and ω is the angular speed of rotation of the cylinder. Using the strain-displacement relations from Eq. (4), the expressions for σ_r and σ_θ from Eq. (1) and (2) are substituted in Eq. (5) and the resulting differential equation is solved to obtain the following solution for the radial displacement:

$$u = - \frac{{\left( {1 + \nu } \right)\left( {1 - 2\nu } \right)}}{E}\frac{{\rho \omega^{2} r^{3} }}{8(1 - \nu )} + C_{1} r + \frac{{C_{2} }}{r},$$

(6)

where C₁ and C₂ are the constants of integration. Using Eq. 4 and the value of u from Eq. 6 in Eq. 1 and 2, the solutions for radial and hoop stresses in the elastic cylinder are obtained as

$$\sigma_{r} = - \frac{{\rho \omega^{2} r^{2} }}{{8\left( {1 - \nu } \right)}}\left( {3 - 2\nu } \right) + \frac{{EC_{1} }}{{\left( {1 + \nu } \right)\left( {1 - 2\nu } \right)}} - \frac{{EC_{2} }}{{\left( {1 + \nu } \right)r^{2} }}.$$

(7)

$$\sigma_{\theta } = - \frac{{\rho \omega^{2} r^{2} }}{{8\left( {1 - \nu } \right)}}\left( {1 + 2\nu } \right) + \frac{{EC_{1} }}{{\left( {1 + \nu } \right)\left( {1 - 2\nu } \right)}} + \frac{{EC_{2} }}{{\left( {1 + \nu } \right)r^{2} }}.$$

(8)

Once the radial and hoop stress distribution is known from Eq. 7 and 8, the elastic axial stress distribution can be obtained from Eq. 3.

3.1.2 The Swage Mandrel

Denoting the Young’s modulus of elasticity by E₁ and Poisson’s ratio by ν₁, the generalized Hooke’s law for the swage mandrel is given by the expressions stated in Eq. 1-3. For the solid cylindrical axisymmetric and non-rotating mandrel, which is interfering with the interior wall of the rotating cylinder, the equilibrium equation can be written as

$$\frac{{{\text{d}}\sigma_{r} }}{{{\text{d}}r}} + \frac{{\sigma_{r} - \sigma_{\theta } }}{r} = 0.$$

(9)

Following the same procedure as that for the cylinder, the radial displacement and state of stress in the solid swage mandrel are obtained as

$$u = C_{3} r + \frac{{C_{4} }}{r},$$

(10)

$$\sigma_{r} = \frac{{E_{1} }}{{\left( {1 + \nu_{1} } \right)\left( {1 - 2\nu_{1} } \right)}}\left\{ {C_{3} - \left( {1 - 2\nu_{1} } \right)\frac{{C_{4} }}{{r^{2} }}} \right\},$$

(11)

$$\sigma_{\theta } = \frac{{E_{1} }}{{\left( {1 + \nu_{1} } \right)\left( {1 - 2\nu_{1} } \right)}}\left\{ {C_{3} + \left( {1 - 2\nu_{1} } \right)\frac{{C_{4} }}{{r^{2} }}} \right\},$$

(12)

where C₃ and C₄ are integration constants.

3.1.3 Evaluation of Integration Constants C ₁ , C ₂ , C ₃ and C ₄

The integration constants involved in the equations presented in Sect. 3.1.1 and 3.1.2 can be determined using the following boundary conditions:

• (i) At the outer surface of the outer cylinder, i.e., at $r = b$,

  $$\left( {\sigma_{r} } \right)_{{_{r = b} }}^{{{\text{cylinder}}}} = 0.\,\,\,\,\,\,$$

  (13)

• (ii) At the center of the swage mandrel,

  $$\left( u \right)_{r = 0}^{{{\text{mandrel}}}} = 0.$$

  (14)

• (iii) At the interface between the swage mandrel and the cylinder i.e. at $r = a$,

  $$\left( {\sigma_{r} } \right)_{r = a}^{{\,{\text{cylinder}}}} = \left( {\sigma_{r} } \right)_{r = a}^{{{\text{mandrel}}}} .$$

  (15)

• (iv) The difference between the radial displacements of the cylinder interior wall and the outer surface of the swage mandrel equals to the interference δ:

  $$\left( u \right)_{r = a}^{{{\text{cylinder}}}} - \left( u \right)_{r = a}^{{{\text{mandrel}}}} = \delta .$$

  (16)

In order to have a finite value of the radial displacement u at the centre of the swage mandrel, Eq. 14 dictates that C₄ must vanish. Using the rest of the boundary conditions, i.e., Eq. 13, 15 and 16, the other integration constants are determined as

$$\begin{gathered} \frac{{EC_{1} }}{{\left( {1 + \nu } \right)\left( {1 - 2\nu } \right)}} = \frac{{\frac{E\delta }{{\left( {1 + \nu } \right)\left( {1 - 2\nu } \right)a}}\left( {\frac{1}{{a^{2} }} - \frac{1}{{b^{2} }}} \right) - \frac{{\rho \omega^{2} }}{{8\left( {1 - \nu } \right)}}\left\{ {\left( {3 - 2\nu } \right)\left( {\frac{{b^{2} }}{{a^{2} }} - \frac{{a^{2} }}{{b^{2} }}} \right) + \left( {\frac{3 - 2\nu }{{1 - 2\nu }}} \right)\left( {\frac{{b^{2} }}{{a^{2} }} - 1} \right) + \frac{{a^{2} }}{{b^{2} }} - 1} \right\}}}{{b^{2} \left( {\frac{1}{{b^{2} }} - \frac{1}{{a^{2} }}} \right)\left( {\frac{1}{{b^{2} }} + \frac{1}{{\left( {1 - 2\nu } \right)a^{2} }}} \right) - b^{2} \left( {\frac{{E_{1} }}{E}} \right)\frac{{\left( {1 + \nu } \right)\left( {1 - 2\nu } \right)}}{{\left( {1 + \nu_{1} } \right)\left( {1 - 2\nu_{1} } \right)}}\left\{ {\frac{1}{{b^{2} }} + \frac{1}{{\left( {1 - 2\nu } \right)a^{2} }}} \right\}^{2} }} \hfill \\ \,\,\,\,\, + \frac{E\delta }{{\left( {1 + \nu } \right)}}\left\{ {\frac{a}{{\left( {1 - 2\nu } \right)a^{2} + b^{2} }}} \right\} - \frac{{\rho \omega^{2} }}{{8\left( {1 - \nu } \right)}}\left\{ {\frac{{a^{2} \left( {1 - 2\nu } \right)}}{{\left( {1 - 2\nu } \right)a^{2} + b^{2} }}} \right\}\left\{ {b^{2} \left( {3 - 2\nu } \right) - a^{2} } \right\} + \frac{{\rho \omega^{2} b^{2} }}{{8\left( {1 - \nu } \right)}}\left( {3 - 2\nu } \right), \hfill \\ \,\,\,\, \hfill \\ \end{gathered}$$

(17)

$$\begin{gathered} \frac{{EC_{2} }}{{\left( {1 + \nu } \right)}} = \,\,\frac{{\frac{E\delta }{{\left( {1 + \nu } \right)\left( {1 - 2\nu } \right)a}}\left( {\frac{1}{{a^{2} }} - \frac{1}{{b^{2} }}} \right) - \frac{{\rho \omega^{2} }}{{8\left( {1 - \nu } \right)}}\left\{ {\left( {3 - 2\nu } \right)\left( {\frac{{b^{2} }}{{a^{2} }} - \frac{{a^{2} }}{{b^{2} }}} \right) + \left( {\frac{3 - 2\nu }{{1 - 2\nu }}} \right)\left( {\frac{{b^{2} }}{{a^{2} }} - 1} \right) + \frac{{a^{2} }}{{b^{2} }} - 1} \right\}}}{{\left( {\frac{1}{{b^{2} }} - \frac{1}{{a^{2} }}} \right)\left( {\frac{1}{{b^{2} }} + \frac{1}{{\left( {1 - 2\nu } \right)a^{2} }}} \right) - \left( {\frac{{E_{1} }}{E}} \right)\frac{{\left( {1 + \nu } \right)\left( {1 - 2\nu } \right)}}{{\left( {1 + \nu_{1} } \right)\left( {1 - 2\nu_{1} } \right)}}\left\{ {\frac{1}{{b^{2} }} + \frac{1}{{\left( {1 - 2\nu } \right)a^{2} }}} \right\}^{2} }} \hfill \\ \,\,\,\,\, + \frac{E\delta }{{\left( {1 + \nu } \right)}}\left\{ {\frac{{ab^{2} }}{{\left( {1 - 2\nu } \right)a^{2} + b^{2} }}} \right\} - \frac{{\rho \omega^{2} }}{{8\left( {1 - \nu } \right)}}\left\{ {\frac{{a^{2} b^{2} \left( {1 - 2\nu } \right)}}{{\left( {1 - 2\nu } \right)a^{2} + b^{2} }}} \right\}\left\{ {b^{2} \left( {3 - 2\nu } \right) - a^{2} } \right\}, \hfill \\ \end{gathered}$$

(18)

$$C_{3} = \frac{{\frac{E\delta }{{\left( {1 + \nu } \right)\left( {1 - 2\nu } \right)a}}\left( {\frac{1}{{a^{2} }} - \frac{1}{{b^{2} }}} \right) - \frac{{\rho \omega^{2} }}{{8\left( {1 - \nu } \right)}}\left\{ {\left( {3 - 2\nu } \right)\left( {\frac{{b^{2} }}{{a^{2} }} - \frac{{a^{2} }}{{b^{2} }}} \right) + \left( {\frac{3 - 2\nu }{{1 - 2\nu }}} \right)\left( {\frac{{b^{2} }}{{a^{2} }} - 1} \right) + \frac{{a^{2} }}{{b^{2} }} - 1} \right\}}}{{\frac{E}{{\left( {1 + \nu } \right)\left( {1 - 2\nu } \right)}}\left( {\frac{1}{{b^{2} }} - \frac{1}{{a^{2} }}} \right) - \frac{{E_{1} }}{{\left( {1 + \nu_{1} } \right)\left( {1 - 2\nu_{1} } \right)}}\left\{ {\frac{1}{{b^{2} }} + \frac{1}{{\left( {1 - 2\nu } \right)a^{2} }}} \right\}}}.$$

(19)

Substituting the values of the constants C₁ and C₂ from Eq. 17 and 18, the resulting stress distribution in the cylinder can be obtained from Eq. 7 and 8 and the radial displacement from Eq. 6. Inserting C₄ = 0 and C₃ from Eq. 19, the resulting radial displacement and stress distribution in the swage mandrel can be obtained from Eq. 10-12. As C₄ vanishes, the radial and hoop stress distributions are of constant magnitudes and same in the mandrel as evident from Eq. 11 and 12.

3.2 Analysis of Yield Onset

It is assumed that the yielding in the cylinder commences according to Tresca yield criteria. Under the combined effect of rotation and interference without contact separation, the tensile hoop stress is the highest and the radial stress being compressive is the minimum at the inner radius. Thus, for yielding to commence at the inner radius as per Tresca yield criterion, the following condition needs to be satisfied:

$$\left. {\left( {\sigma_{\theta } - \sigma_{r} } \right)} \right|_{r = a}^{{{\text{Rotating}}\,{\text{cylinder}}}} = \sigma_{{\text{Y}}} ,$$

(20)

where σ_Y is the yield stress of the cylinder. It is important to note that while the cylinder is rotating, the contact between the swage mandrel and the cylinder interior wall should not be lost. Thus, to avoid the contact separation between the swage mandrel and the cylinder interior wall,

$$\left. {\left( {\sigma_{r} } \right)} \right|_{r = a} \le 0.$$

(21)

For the onset of yielding at the inner radius, Eq. 20 must be satisfied along with Eq. 21 to ensure interference of the mandrel with the interior wall of the rotating cylinder. As the stress distributions given by Eq. 7 and 8 remain valid at the onset of yielding, substituting them in Eq. 20, the angular speed of the cylinder corresponding to the yield onset is obtained as

$$\omega_{Y} = \sqrt {\left\{ {\frac{{4\left( {1 - \nu } \right)}}{\rho }} \right\}\left[ {\frac{{\sigma_{Y} - \frac{2E\delta }{{\left( {1 + \nu } \right)a}}\left\{ {\frac{1}{{\left( {1 - 2\nu } \right)}}\left( {\frac{1}{{a^{2} }} - \frac{1}{{b^{2} }}} \right)\left( {\frac{1}{{Aa^{2} }}} \right) + \frac{{b^{2} }}{{\left( {1 - 2\nu } \right)a^{2} + b^{2} }}} \right\}}}{{a^{2} \left\{ {\left( {1 - 2\nu } \right) - \left( {\frac{B}{{Aa^{4} }}} \right)} \right\} - b^{4} \left\{ {\frac{{\left( {1 - 2\nu } \right)}}{{\left( {1 - 2\nu } \right)a^{2} + b^{2} }}} \right\}\left\{ {\left( {3 - 2\nu } \right) - \frac{{a^{2} }}{{b^{2} }}} \right\}}}} \right]} ,$$

(22)

where

$$A = \left( {\frac{1}{{b^{2} }} - \frac{1}{{a^{2} }}} \right)\left( {\frac{1}{{b^{2} }} + \frac{1}{{\left( {1 - 2\nu } \right)a^{2} }}} \right) - \left( {\frac{{E_{1} }}{E}} \right)\frac{{\left( {1 + \nu } \right)\left( {1 - 2\nu } \right)}}{{\left( {1 + \nu_{1} } \right)\left( {1 - 2\nu_{1} } \right)}}\left\{ {\frac{1}{{b^{2} }} + \frac{1}{{\left( {1 - 2\nu } \right)a^{2} }}} \right\}^{2} ,$$

(23)

$$B = \left\{ {\left( {3 - 2\nu } \right)\left( {\frac{{b^{2} }}{{a^{2} }} - \frac{{a^{2} }}{{b^{2} }}} \right) + \left( {\frac{3 - 2\nu }{{1 - 2\nu }}} \right)\left( {\frac{{b^{2} }}{{a^{2} }} - 1} \right) + \frac{{a^{2} }}{{b^{2} }} - 1} \right\}.$$

(24)

It can be seen from Eq. 22 that ω vanishes if

$$\frac{2E\delta }{{\left( {1 + \nu } \right)a}}\left\{ {\frac{1}{{\left( {1 - 2\nu } \right)}}\left( {\frac{1}{{a^{2} }} - \frac{1}{{b^{2} }}} \right)\left( {\frac{1}{{Aa^{2} }}} \right) + \frac{{b^{2} }}{{\left( {1 - 2\nu } \right)a^{2} + b^{2} }}} \right\} = \sigma_{Y} .$$

(25)

Upon satisfaction of Eq. 25, the yielding in the cylinder initiates just by interference and the corresponding value of interference δ can be obtained from Eq. 25. As b > a, it is evident from Eq. 22 that to avoid complex root of ω_Y, the value of interference δ should satisfy the following inequality:

$$\delta > \frac{{\sigma_{Y} \left( {1 + \nu } \right)a}}{{2E\left\{ {\frac{1}{{\left( {1 - 2\nu } \right)}}\left( {\frac{1}{{a^{2} }} - \frac{1}{{b^{2} }}} \right)\left( {\frac{1}{{Aa^{2} }}} \right) + \frac{{b^{2} }}{{\left( {1 - 2\nu } \right)a^{2} + b^{2} }}} \right\}}}.$$

(26)

It is desirable that at the onset of yielding, the mandrel interference is not lost with the rotating cylinder. For this, one needs to ensure the satisfaction of Eq. 21. The critical condition for contact separation between the swage mandrel and the cylinder interior wall is given by the equality of Eq. 21. Using the value of σ_r from Eq. 7 in Eq. 21, the critical value of angular speed corresponding to the contact separation as

$$\omega_{s} = \sqrt {\frac{{8\left( {1 - \nu } \right)}}{\rho }\left[ {\frac{{\frac{E\delta }{{\left( {1 + \nu } \right)a}}\left\{ {\frac{1}{{\left( {1 - 2\nu } \right)a^{2} + b^{2} }} - \frac{1}{{\left( {1 - 2\nu } \right)A}}\left( {\frac{1}{{a^{2} b^{2} }}} \right)\left( {\frac{1}{{b^{2} }} - \frac{1}{{a^{2} }}} \right)} \right\}}}{{\left( {3 - 2\nu } \right) + \left( \frac{B}{A} \right)\left( {\frac{1}{{a^{2} b^{2} }}} \right) + \left\{ {\frac{{\left( {1 - 2\nu } \right)}}{{\left( {1 - 2\nu } \right)a^{2} + b^{2} }}} \right\}\left\{ {b^{2} \left( {3 - 2\nu } \right) - a^{2} } \right\}}}} \right]} ,$$

(27)

where A and B are given by Eq. 23 and 24, respectively. Equating Eq. 22 and 27 provides the critical value of interference δ corresponding to the contact separation at the onset of yielding of the rotating cylinder as

$$\left( \delta \right)_{{{\text{lost}}\,\,{\text{interference}}}} = \frac{{\left( {1 + \nu } \right)a\sigma_{{\text{Y}}} N}}{{2E\left( {{\text{PQ}} + {\text{MN}}} \right)}},$$

(28)

where

$$M = \left\{ {\frac{1}{{\left( {1 - 2\nu } \right)}}\left( {\frac{1}{{a^{2} }} - \frac{1}{{b^{2} }}} \right)\left( {\frac{1}{{Aa^{2} }}} \right) + \frac{{b^{2} }}{{\left( {1 - 2\nu } \right)a^{2} + b^{2} }}} \right\},$$

(29)

$$N = \left( {3 - 2\nu } \right) + \left( \frac{B}{A} \right)\left( {\frac{1}{{a^{2} b^{2} }}} \right) + \left\{ {\frac{{\left( {1 - 2\nu } \right)}}{{\left( {1 - 2\nu } \right)a^{2} + b^{2} }}} \right\}\left\{ {b^{2} \left( {3 - 2\nu } \right) - a^{2} } \right\},$$

(30)

$$P = \left\{ {\frac{1}{{\left( {1 - 2\nu } \right)a^{2} + b^{2} }} - \frac{1}{{\left( {1 - 2\nu } \right)A}}\left( {\frac{1}{{a^{2} b^{2} }}} \right)\left( {\frac{1}{{b^{2} }} - \frac{1}{{a^{2} }}} \right)} \right\},$$

(31)

$$Q = \left( {1 - 2\nu } \right)a^{2} - \left( {\frac{B}{{Aa^{2} }}} \right) - \left\{ {\frac{{b^{2} \left( {1 - 2\nu } \right)}}{{\left( {1 - 2\nu } \right)a^{2} + b^{2} }}} \right\}\left\{ {b^{2} \left( {3 - 2\nu } \right) - a^{2} } \right\}.$$

(32)

Now, the range of the interference values δ corresponding to the initiation of yielding in the rotating cylinder can be given by

$$\frac{{\sigma_{Y} \left( {1 + \nu } \right)a}}{{2E\left\{ {\frac{1}{{\left( {1 - 2\nu } \right)}}\left( {\frac{1}{{a^{2} }} - \frac{1}{{b^{2} }}} \right)\left( {\frac{1}{{Aa^{2} }}} \right) + \frac{{b^{2} }}{{\left( {1 - 2\nu } \right)a^{2} + b^{2} }}} \right\}}} < \delta < \frac{{\left( {1 + \nu } \right)a\sigma_{Y} N}}{{2E\left( {PQ + MN} \right)}}.$$

(33)

For the range of values of δ given by Eq. 33, the corresponding yield onset angular speeds ω_Y of the cylinder can be determined from Eq. 22.

3.3 Analysis of the Elastic–Plastic Loading Stage

The combination of (δ, ω_Y) at the onset of yielding can be determined from Eq. 33 and 22. If the cylinder is loaded with certain combination of (δ, ω) that exceeds the combinations corresponding to the yield onset, then the rotating cylinder becomes partially plastic. This loading situation is referred as the loading stage of the hybrid rotational-swage autofrettage. In the loading stage, the interior wall of the rotating cylinder deforms plastically up to a certain intermediate radius c creating an inner plastic zone a ≤ r ≤ c and the portion of the exterior wall of the cylinder c ≤ r ≤ b forms the outer elastic zone as shown in Fig. 2.

Fig. 2

The elastic and plastic zones in the cylinder created during the loading stage of hybrid rotational-swage autofrettage

3.3.1 The Elastic Zone, c ≤ r ≤ b

When the cylinder becomes partially plastic, in the elastic zone c ≤ r ≤ b, the stress distributions given by Eq. 7 and 8 remain valid in the elastic zone with the change of the values of the integration constants C₁ and C₂. Employing the boundary conditions of vanishing radial stress at the outer radius of the cylinder (Eq. 13) along with the boundary condition: $\left. {\left( {\sigma_{\theta } - \sigma_{r} } \right)} \right|_{r = c} = \sigma_{{\text{Y}}} ,$ the changed integration constants C₁ and C₂ in Eq. 7 and 8 are obtained as

$$\frac{{EC_{1} }}{{\left( {1 + \nu } \right)\left( {1 - 2\nu } \right)}} = \frac{{\sigma_{Y} }}{2}\left( {\frac{{c^{2} }}{{b^{2} }}} \right) - \frac{{\rho \omega^{2} }}{{8\left( {1 - \nu } \right)}}\left\{ {\frac{{c^{4} }}{{b^{2} }}\left( {1 - 2\nu } \right) - b^{2} \left( {3 - 2\nu } \right)} \right\},$$

(34)

$$\frac{{EC_{2} }}{{\left( {1 + \nu } \right)}} = \frac{{\sigma_{Y} }}{2}c^{2} - \frac{{\rho \omega^{2} c^{4} }}{{8\left( {1 - \nu } \right)}}\left( {1 - 2\nu } \right).$$

(35)

Substituting Eq. 34 and 35 in Eq. 7 and 8, one obtains the resulting stress distributions in the elastic zone as

$$\sigma_{r} = \frac{{\sigma_{Y} }}{2}c^{2} \left( {\frac{1}{{b^{2} }} - \frac{1}{{r^{2} }}} \right) - \frac{{\rho \omega^{2} }}{{8\left( {1 - \nu } \right)}}\left\{ {c^{4} \left( {1 - 2\nu } \right)\left( {\frac{1}{{b^{2} }} - \frac{1}{{r^{2} }}} \right) - \left( {3 - 2\nu } \right)\left( {b^{2} - r^{2} } \right)} \right\}.$$

(36)

$$\sigma_{\theta } = \frac{{\sigma_{Y} }}{2}c^{2} \left( {\frac{1}{{b^{2} }} + \frac{1}{{r^{2} }}} \right) - \frac{{\rho \omega^{2} }}{{8\left( {1 - \nu } \right)}}\left\{ {c^{4} \left( {1 - 2\nu } \right)\left( {\frac{1}{{b^{2} }} + \frac{1}{{r^{2} }}} \right) - b^{2} \left( {3 - 2\nu } \right) + r^{2} \left( {1 + 2\nu } \right)} \right\}.$$

(37)

The axial stress distribution in the elastic zone is obtained from Eq. 3, where σ_r and σ_θ are given by Eq. 36 and 37, respectively.

The radial displacement u in the elastic zone is obtained by substituting the values of C₁ and C₂ from Eq. 34 and 35 in Eq. 6 and is expressed as

$$\begin{gathered} u = \frac{{\left( {1 + \nu } \right)\left( {1 - 2\nu } \right)}}{E}r\left[ {\frac{{\sigma_{{\text{Y}}} }}{2}\left( {\frac{{c^{2} }}{{b^{2} }}} \right) - \frac{{\rho \omega^{2} }}{{8\left( {1 - \nu } \right)}}\left\{ {\frac{{c^{4} }}{{b^{2} }}\left( {1 - 2\nu } \right) - b^{2} \left( {3 - 2\nu } \right)} \right\} - \frac{{\rho \omega^{2} r^{2} }}{8(1 - \nu )}} \right] \hfill \\ \,\,\,\,\,\, + \frac{{\left( {1 + \nu } \right)}}{Er}\left\{ {\frac{{\sigma_{{\text{Y}}} }}{2}c^{2} - \frac{{\rho \omega^{2} c^{4} }}{{8\left( {1 - \nu } \right)}}\left( {1 - 2\nu } \right)} \right\}. \hfill \\ \end{gathered}$$

(38)

3.3.2 The Plastic Zone, a ≤ r ≤ c

In the plastic zone, the yielding takes place according to Tresca yield criteria given by

$$\sigma_{\theta } - \sigma_{r} = \sigma_{Y}$$

(39)

Employing Eq. 39 in differential equation of equilibrium (Eq. 5) and solving it with the boundary condition of continuity of radial stress at the elastic–Plastic interface radius c: $\left. {\left( {\sigma_{r} } \right)} \right|_{r = c}^{{{\text{plastic}}\,{\text{zone}}}} = \left. {\left( {\sigma_{r} } \right)} \right|_{r = c}^{{{\text{elastic}}\,{\text{zone}}}} ,$ the solution for radial stress in the plastic zone is obtained as

$$\begin{gathered} \sigma_{r} = \sigma_{{\text{Y}}} \ln \left( \frac{r}{c} \right) + \frac{{\rho \omega^{2} }}{2}\left( {c^{2} - r^{2} } \right) + \frac{{\sigma_{Y} }}{2}c^{2} \left( {\frac{1}{{b^{2} }} - \frac{1}{{c^{2} }}} \right) \hfill \\ \,\,\,\,\,\,\,\,\,\, - \frac{{\rho \omega^{2} }}{{8\left( {1 - \nu } \right)}}\left\{ {c^{4} \left( {1 - 2\nu } \right)\left( {\frac{1}{{b^{2} }} - \frac{1}{{c^{2} }}} \right) - \left( {3 - 2\nu } \right)\left( {b^{2} - c^{2} } \right)} \right\}. \hfill \\ \end{gathered}$$

(40)

Substituting the expression for σ_r in Eq. (39), the hoop stress distribution in the plastic zone is obtained as

$$\begin{gathered} \sigma_{\theta } = \sigma_{Y} \left\{ {1 + \ln \left( \frac{r}{c} \right)} \right\} + \frac{{\rho \omega^{2} }}{2}\left( {c^{2} - r^{2} } \right) + \frac{{\sigma_{Y} }}{2}c^{2} \left( {\frac{1}{{b^{2} }} - \frac{1}{{c^{2} }}} \right) \hfill \\ \,\,\,\,\,\,\,\,\,\, - \frac{{\rho \omega^{2} }}{{8\left( {1 - \nu } \right)}}\left\{ {c^{4} \left( {1 - 2\nu } \right)\left( {\frac{1}{{b^{2} }} - \frac{1}{{c^{2} }}} \right) - \left( {3 - 2\nu } \right)\left( {b^{2} - c^{2} } \right)} \right\}. \hfill \\ \end{gathered}$$

(41)

Due to plane strain condition, the axial stress distribution in the plastic zone can be obtained from Eq. 3, where σ_r and σ_θ are given by Eq. 40 and 41. Incorporating Tresca-associated flow rule and plastic incompressibility, one can express the sum of the total radial and hoop strain in the plastic zone as

$$\varepsilon_{r} + \varepsilon_{\theta } = \varepsilon_{r}^{e} + \varepsilon_{\theta }^{e} ,$$

(42)

where $\varepsilon_{r}^{e}$ and $\varepsilon_{\theta }^{e}$ are the elastic parts of the radial and hoop strains, which are given by Eq. 1 and 2, respectively. Using the strain displacement relations from Eq. 4 and 1, 2 along with Eq. 40, 41 in Eq. 42 one obtains a differential equation, the solution of which provides the radial displacement distribution u as

$$u = \frac{1}{E}\left( {1 - \nu - 2\nu^{2} } \right)\left[ \begin{gathered} \sigma_{{\text{Y}}} r\ln \left( \frac{r}{c} \right) + \rho \omega^{2} \left( {\frac{{c^{2} r}}{2} - \frac{{r^{3} }}{4}} \right) + \sigma_{Y} \frac{{c^{2} r}}{2}\left( {\frac{1}{{b^{2} }} - \frac{1}{{c^{2} }}} \right) \hfill \\ - \frac{{\rho \omega^{2} r}}{{8\left( {1 - \nu } \right)}}\left\{ {c^{4} \left( {1 - 2\nu } \right)\left( {\frac{1}{{b^{2} }} - \frac{1}{{c^{2} }}} \right) - \left( {3 - 2\nu } \right)\left( {b^{2} - c^{2} } \right)} \right\} \hfill \\ \end{gathered} \right] + \frac{{C_{5} }}{r},$$

(43)

where C₅ is a constant of integration and can be determined applying appropriate boundary condition.

3.3.3 Analysis of Elastic Mandrel When the Rotating Cylinder Becomes Partially Plastic

It is to be noted that even when the cylinder becomes plastic in the vicinity of its interior wall, the swage mandrel remains in the fully elastic state. Thus, the radial displacement and stresses in the swage mandrel are still given by Eq. 10-12 and the integration constants involved in these equations can be determined by applying boundary conditions given by Eq. 14 and 15. Use of Eq. 14 yields C₄ = 0. In applying boundary condition Eq. 15, the corresponding values of $\left( {\sigma_{r} } \right)_{r = a}^{{\,{\text{cylinder}}}}$ needs to be evaluated using Eq. (40) of the plastic zone to determine the value of C₃. The integration constants so obtained are then substituted back to Eq. 10-12 to obtain the resulting distribution of radial displacement and stresses in the elastic mandrel when the rotating cylinder becomes partially plastic as

$$u = \frac{{\left( {1 + \nu_{1} } \right)\left( {1 - 2\nu_{1} } \right)}}{{E_{1} }}r\left[ \begin{gathered} \sigma_{{\text{Y}}} \ln \left( \frac{a}{c} \right) + \frac{{\rho \omega^{2} }}{2}\left( {c^{2} - a^{2} } \right) + \frac{{\sigma_{{\text{Y}}} }}{2}c^{2} \left( {\frac{1}{{b^{2} }} - \frac{1}{{c^{2} }}} \right) \hfill \\ \, - \frac{{\rho \omega^{2} }}{{8\left( {1 - \nu } \right)}}\left\{ {c^{4} \left( {1 - 2\nu } \right)\left( {\frac{1}{{b^{2} }} - \frac{1}{{c^{2} }}} \right) - \left( {3 - 2\nu } \right)\left( {b^{2} - c^{2} } \right)} \right\} \hfill \\ \end{gathered} \right],$$

(44)

$$\begin{gathered} \sigma_{r} = \sigma_{\theta } = \sigma_{{\text{Y}}} \ln \left( \frac{a}{c} \right) + \frac{{\rho \omega^{2} }}{2}\left( {c^{2} - a^{2} } \right) + \frac{{\sigma_{{\text{Y}}} }}{2}c^{2} \left( {\frac{1}{{b^{2} }} - \frac{1}{{c^{2} }}} \right) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - \frac{{\rho \omega^{2} }}{{8\left( {1 - \nu } \right)}}\left\{ {c^{4} \left( {1 - 2\nu } \right)\left( {\frac{1}{{b^{2} }} - \frac{1}{{c^{2} }}} \right) - \left( {3 - 2\nu } \right)\left( {b^{2} - c^{2} } \right)} \right\}. \hfill \\ \end{gathered}$$

(45)

Once the radial displacement distribution is known from Eq. 44, the incorporation of boundary condition Eq. 16 provides the integration constant C₅ involved in Eq. 43. Thus, knowing C₅, the radial displacement in the plastic zone can be evaluated as a function of radius r from Eq. 43.

3.3.4 Determination of the Elastic–Plastic Interface Radius c and Critical Speeds Corresponding to Contact Separation and Plastic Collapse

The unknown elastic–Plastic interface radius c can be determined by using the following boundary condition:

$$\left. {\left( u \right)} \right|_{r = c}^{{{\text{plastic}}\,\,{\text{zone}}}} = \left. {\left( u \right)} \right|_{r = c}^{{{\text{elastic}}\,\,{\text{zone}}}} .$$

(46)

Evaluating $\left. {\left( u \right)} \right|_{r = c}^{{{\text{plastic}}\,\,{\text{zone}}}}$ using Eq. 43 and $\left. {\left( u \right)} \right|_{r = c}^{{{\text{elastic}}\,\,{\text{zone}}}}$ using Eq. 38, and then substituting them in Eq. 46 provides

$$\begin{gathered} \frac{{\left( {1 + \nu } \right)\left( {1 - 2\nu } \right)}}{E}\left( {\frac{{\rho \omega^{2} c^{3} }}{4} - \frac{{\sigma_{{\text{Y}}} c}}{2} - \frac{{\rho \omega^{2} a^{4} }}{4c}} \right) - \frac{{\left( {1 + \nu } \right)}}{E}\left( {\frac{{\sigma_{{\text{Y}}} c}}{2}} \right) + \frac{\delta a}{c} \hfill \\ + \left[ \begin{gathered} \sigma_{{\text{Y}}} \ln \left( \frac{a}{c} \right) + \frac{{\rho \omega^{2} }}{2}\left( {c^{2} - a^{2} } \right) + \frac{{\sigma_{{\text{Y}}} }}{2}c^{2} \left( {\frac{1}{{b^{2} }} - \frac{1}{{c^{2} }}} \right) \hfill \\ \, - \frac{{\rho \omega^{2} }}{{8\left( {1 - \nu } \right)}}\left\{ {c^{4} \left( {1 - 2\nu } \right)\left( {\frac{1}{{b^{2} }} - \frac{1}{{c^{2} }}} \right) - \left( {3 - 2\nu } \right)\left( {b^{2} - c^{2} } \right)} \right\} \hfill \\ \end{gathered} \right] \hfill \\ \times \left( {\frac{{a^{2} }}{c}} \right)\left\{ {\frac{{\left( {1 + \nu_{1} } \right)\left( {1 - 2\nu_{1} } \right)}}{{E_{1} }} - \frac{{\left( {1 + \nu } \right)\left( {1 - 2\nu } \right)}}{E}} \right\} = 0. \hfill \\ \end{gathered}$$

(47)

Equation 47 is solved using numerical methods, e.g., bisection method to estimate the elastic–Plastic interface radius c for the combination of plastically deforming (δ, ω). It is worth noting that for a chosen suitable value of interference δ, the angular speed ω of the cylinder should be limited to avoid the contact separation between the swage mandrel and the interior wall of the cylinder.

For avoiding the loss of contact between the swage mandrel and the rotating cylinder during loading, the following condition need to be satisfied:

$$\left. {\left( {\sigma_{r} } \right)} \right|_{r = a}^{{{\text{plastic}}\,{\text{zone}}}} \le 0.$$

(48)

The equality of Eq. 48 provides the critical condition corresponding to the contact separation. Thus, substituting Eq. 40 in Eq. 48 and using equality sign, the critical speed ω_s corresponding to the contact separation between the swage mandrel and the interior wall of the cylinder is obtained as

$$\omega_{s} = \sigma_{Y} \left\{ {\frac{{8\left( {1 - \nu } \right)}}{\rho }} \right\}\frac{{\left\{ {\ln \left( {\frac{a}{{c_{s} }}} \right) + \frac{{\sigma_{Y} }}{2}c_{s}^{2} \left( {\frac{1}{{b^{2} }} - \frac{1}{{c_{s}^{2} }}} \right)} \right\}}}{{\left\{ {c_{s}^{4} \left( {1 - 2\nu } \right)\left( {\frac{1}{{b^{2} }} - \frac{1}{{c_{s}^{2} }}} \right) - \left( {3 - 2\nu } \right)\left( {b^{2} - c_{s}^{2} } \right) - 4\left( {1 - \nu } \right)\left( {c_{s}^{2} - a^{2} } \right)} \right\}}},$$

(49)

where c_s is the critical radius of elastic–Plastic interface radius corresponding to the condition of contact separation.

Now, for the critical condition of contact separation, Eq. 47 can be rewritten as

$$\begin{gathered} \frac{{\left( {1 + \nu } \right)\left( {1 - 2\nu } \right)}}{E}\left( {\frac{{\rho \omega_{{\text{s}}}^{2} c_{s}^{3} }}{4} - \frac{{\sigma_{Y} c_{s} }}{2} - \frac{{\rho \omega_{{\text{s}}}^{2} a^{4} }}{{4c_{s} }}} \right) - \frac{{\left( {1 + \nu } \right)}}{E}\left( {\frac{{\sigma_{Y} c_{s} }}{2}} \right) + \frac{\delta a}{{c_{s} }} \hfill \\ + \left[ \begin{gathered} \sigma_{Y} \ln \left( {\frac{a}{{c_{s} }}} \right) + \frac{{\rho \omega_{s}^{2} }}{2}\left( {c_{s}^{2} - a^{2} } \right) + \frac{{\sigma_{Y} }}{2}c_{s}^{2} \left( {\frac{1}{{b^{2} }} - \frac{1}{{c_{s}^{2} }}} \right) \hfill \\ \, - \frac{{\rho \omega_{s}^{2} }}{{8\left( {1 - \nu } \right)}}\left\{ {c_{s}^{4} \left( {1 - 2\nu } \right)\left( {\frac{1}{{b^{2} }} - \frac{1}{{c_{s}^{2} }}} \right) - \left( {3 - 2\nu } \right)\left( {b^{2} - c_{s}^{2} } \right)} \right\} \hfill \\ \end{gathered} \right] \hfill \\ \times \left( {\frac{{a^{2} }}{{c_{s} }}} \right)\left\{ {\frac{{\left( {1 + \nu_{1} } \right)\left( {1 - 2\nu_{1} } \right)}}{{E_{1} }} - \frac{{\left( {1 + \nu } \right)\left( {1 - 2\nu } \right)}}{E}} \right\} = 0. \hfill \\ \end{gathered}$$

(50)

Solving Eq. 49 and 50, one can obtain the critical angular speed ω_s and the critical elastic–Plastic interface radius c_s for a range of selected suitable values of δ.

If one continues to increase the angular speed beyond ω_s, the contact between the swage mandrel and the cylinder interior wall no longer remains and upon reaching a certain value of angular speed, the cylinder wall deforms fully plastically. At this stage, the elastic–Plastic boundary radius c becomes equal to b. If the corresponding rotational speed causing this full plastic deformation of the cylinder is denoted as ω_f then, substituting c = b in Eq. 47, one obtains

$$\begin{gathered} \frac{{\left( {1 + \nu } \right)\left( {1 - 2\nu } \right)}}{E}\left( {\frac{{\rho \omega_{f}^{2} b^{3} }}{4} - \frac{{\sigma_{Y} b}}{2} - \frac{{\rho \omega_{f}^{2} a^{4} }}{4b}} \right) - \frac{{\left( {1 + \nu } \right)}}{E}\left( {\frac{{\sigma_{Y} b}}{2}} \right) + \frac{\delta a}{b} \hfill \\ + \left\{ {\sigma_{Y} \ln \left( \frac{a}{b} \right) + \frac{{\rho \omega_{f}^{2} }}{2}\left( {b^{2} - a^{2} } \right)} \right\}\left( {\frac{{a^{2} }}{b}} \right)\left\{ {\frac{{\left( {1 + \nu_{1} } \right)\left( {1 - 2\nu_{1} } \right)}}{{E_{1} }} - \frac{{\left( {1 + \nu } \right)\left( {1 - 2\nu } \right)}}{E}} \right\} = 0. \hfill \\ \end{gathered}$$

(51)

Solving Eq. 51 one can obtain the values of ω_f as a function of interference δ.

3.4 Analysis of the Unloading Stage

In the loading stage, once the estimated level of plastic deformation of the cylinder interior wall is reached, the complete unloading of the interference and the centrifugal force is executed. The unloading process is carried out by completely driving out the swage mandrel through the interior of the rotating cylinder from one end to the other followed by stopping the rotation of the cylinder. As the unloading procedure is assumed to be purely elastic, the stress state in the elastic mandrel during unloading is given by the same Eq. 45 associating a negative sign with it.

For elastic unloading of the cylinder, the equation of equilibrium can be expressed as (Ref 9)

$$\frac{{{\text{d}}\sigma_{r} }}{{{\text{d}}r}} + \frac{{\sigma_{r} - \sigma_{\theta } }}{r} - \rho r\omega^{2} = 0.$$

(52)

With the help of strain-displacement relations (Eq. 4) and elastic constitutive relations (Eq. 1 and 2) incorporated in Eq. 52 along with the boundary conditions of the continuity of radial stresses at the inner radius between the swage mandrel-cylinder assembly and vanishing radial stress at the outer radius of the cylinder during unloading, the solution for unloading stresses are obtained as

$$\begin{gathered} \sigma_{r} = \left( {\frac{{a^{2} }}{{a^{2} - b^{2} }}} \right)\left( {1 - \frac{{b^{2} }}{{r^{2} }}} \right)\left[ \begin{gathered} \frac{{\rho \omega^{2} }}{{8\left( {1 - \nu } \right)}}\left\{ {c^{4} \left( {1 - 2\nu } \right)\left( {\frac{1}{{b^{2} }} - \frac{1}{{c^{2} }}} \right) - \left( {3 - 2\nu } \right)\left( {b^{2} - c^{2} } \right)} \right\} \hfill \\ - \frac{{\sigma_{Y} }}{2}c^{2} \left( {\frac{1}{{b^{2} }} - \frac{1}{{c^{2} }}} \right) - \sigma_{Y} \ln \left( \frac{a}{c} \right) - \frac{{\rho \omega^{2} }}{2}\left( {c^{2} - a^{2} } \right) \hfill \\ + \frac{{\rho \omega^{2} }}{{8\left( {1 - \nu } \right)}}\left( {3 - 2\nu } \right)\left( {b^{2} - a^{2} } \right) \hfill \\ \end{gathered} \right] \hfill \\ \,\,\,\,\,\,\,\, + \frac{{\rho \omega^{2} }}{{8\left( {1 - \nu } \right)}}\left( {3 - 2\nu } \right)\left( {r^{2} - b^{2} } \right), \hfill \\ \end{gathered}$$

(53)

$$\begin{gathered} \sigma_{\theta } = \left( {\frac{{a^{2} }}{{a^{2} - b^{2} }}} \right)\left( {1 + \frac{{b^{2} }}{{r^{2} }}} \right)\left[ \begin{gathered} \frac{{\rho \omega^{2} }}{{8\left( {1 - \nu } \right)}}\left\{ {c^{4} \left( {1 - 2\nu } \right)\left( {\frac{1}{{b^{2} }} - \frac{1}{{c^{2} }}} \right) - \left( {3 - 2\nu } \right)\left( {b^{2} - c^{2} } \right)} \right\} \hfill \\ - \sigma_{Y} \ln \left( \frac{a}{c} \right) - \frac{{\rho \omega^{2} }}{2}\left( {c^{2} - a^{2} } \right) - \frac{{\sigma_{Y} }}{2}c^{2} \left( {\frac{1}{{b^{2} }} - \frac{1}{{c^{2} }}} \right) \hfill \\ + \frac{{\rho \omega^{2} }}{{8\left( {1 - \nu } \right)}}\left( {3 - 2\nu } \right)\left( {b^{2} - a^{2} } \right) \hfill \\ \end{gathered} \right] \hfill \\ \,\,\,\,\,\,\, + \frac{{\rho \omega^{2} }}{{8\left( {1 - \nu } \right)}}\left\{ {\left( {1 + 2\nu } \right)r^{2} - \left( {3 - 2\nu } \right)b^{2} } \right\}. \hfill \\ \,\,\,\,\, \hfill \\ \end{gathered}$$

(54)

The unloading axial stress can be obtained from Eq. 3 after substituting Eq. 53 and 54 in it.

3.5 Analysis of Residual Stresses

The cylinder that has undergone elastic–plastic deformation during loading retains residual stresses after unloading. The elastic mandrel however completely springs back to its initial configuration without any residual stresses in it. The residual stresses in the plastic zone, a ≤ r ≤ c of the cylinder are obtained by the superposition of Eq. 40 and 41 with Eq. 53 and 54 and are given by

$$\begin{aligned} \left( {\sigma_{r} } \right)_{R}^{{{\text{Plastic}}\,{\text{zone}}}} = & \left( {\frac{{a^{2} }}{{a^{2} - b^{2} }}} \right)\left( {1 - \frac{{b^{2} }}{{r^{2} }}} \right)\left[ \begin{gathered} \frac{{\rho \omega^{2} }}{{8\left( {1 - \nu } \right)}}\left\{ {c^{4} \left( {1 - 2\nu } \right)\left( {\frac{1}{{b^{2} }} - \frac{1}{{c^{2} }}} \right) - \left( {3 - 2\nu } \right)\left( {b^{2} - c^{2} } \right)} \right\} \hfill \\ - \frac{{\sigma_{Y} }}{2}c^{2} \left( {\frac{1}{{b^{2} }} - \frac{1}{{c^{2} }}} \right) - \sigma_{Y} \ln \left( \frac{a}{c} \right) - \frac{{\rho \omega^{2} }}{2}\left( {c^{2} - a^{2} } \right) \hfill \\ + \frac{{\rho \omega^{2} }}{{8\left( {1 - \nu } \right)}}\left( {3 - 2\nu } \right)\left( {b^{2} - a^{2} } \right) \hfill \\ \end{gathered} \right] \\ & \;\; - \frac{{\rho \omega^{2} }}{{8\left( {1 - \nu } \right)}}\left\{ {c^{4} \left( {1 - 2\nu } \right)\left( {\frac{1}{{b^{2} }} - \frac{1}{{c^{2} }}} \right) - \left( {3 - 2\nu } \right)\left( {b^{2} - c^{2} } \right) - \left( {3 - 2\nu } \right)\left( {r^{2} - b^{2} } \right)} \right\} \\ & \;\; + \sigma_{Y} \ln \left( \frac{r}{c} \right) + \frac{{\rho \omega^{2} }}{2}\left( {c^{2} - r^{2} } \right) + \frac{{\sigma_{Y} }}{2}c^{2} \left( {\frac{1}{{b^{2} }} - \frac{1}{{c^{2} }}} \right), \\ \end{aligned}$$

(55)

$$\begin{aligned} \left( {\sigma_{\theta } } \right)_{R}^{{{\text{Plastic}}\,{\text{zone}}}} = & \left( {\frac{{a^{2} }}{{a^{2} - b^{2} }}} \right)\left( {1 + \frac{{b^{2} }}{{r^{2} }}} \right)\left[ \begin{gathered} \frac{{\rho \omega^{2} }}{{8\left( {1 - \nu } \right)}}\left\{ {c^{4} \left( {1 - 2\nu } \right)\left( {\frac{1}{{b^{2} }} - \frac{1}{{c^{2} }}} \right) - \left( {3 - 2\nu } \right)\left( {b^{2} - c^{2} } \right)} \right\} \hfill \\ - \sigma_{Y} \ln \left( \frac{a}{c} \right) - \frac{{\rho \omega^{2} }}{2}\left( {c^{2} - a^{2} } \right) - \frac{{\sigma_{Y} }}{2}c^{2} \left( {\frac{1}{{b^{2} }} - \frac{1}{{c^{2} }}} \right) \hfill \\ + \frac{{\rho \omega^{2} }}{{8\left( {1 - \nu } \right)}}\left( {3 - 2\nu } \right)\left( {b^{2} - a^{2} } \right) \hfill \\ \end{gathered} \right] \\ & \;\; - \frac{{\rho \omega^{2} }}{{8\left( {1 - \nu } \right)}}\left\{ {c^{4} \left( {1 - 2\nu } \right)\left( {\frac{1}{{b^{2} }} - \frac{1}{{c^{2} }}} \right) - \left( {3 - 2\nu } \right)\left( {b^{2} - c^{2} } \right) - \left( {1 + 2\nu } \right)r^{2} + \left( {3 - 2\nu } \right)b^{2} } \right\} \\ & \;\; + \sigma_{Y} \left\{ {1 + \ln \left( \frac{r}{c} \right)} \right\} + \frac{{\rho \omega^{2} }}{2}\left( {c^{2} - r^{2} } \right) + \frac{{\sigma_{Y} }}{2}c^{2} \left( {\frac{1}{{b^{2} }} - \frac{1}{{c^{2} }}} \right). \\ \end{aligned}$$

(56)

In the elastic zone, c ≤ r ≤ b of the cylinder, the induced residual stresses can be obtained by the superposition of Eq. 36 and 37 with Eq. 53 and 54 and the resulting expressions are given by

$$\begin{aligned} \left( {\sigma_{r} } \right)_{R}^{{{\text{Elastic}}\,{\text{zone}}}} = & \left( {\frac{{a^{2} }}{{a^{2} - b^{2} }}} \right)\left( {1 - \frac{{b^{2} }}{{r^{2} }}} \right)\left[ \begin{gathered} \frac{{\rho \omega^{2} }}{{8\left( {1 - \nu } \right)}}\left\{ {c^{4} \left( {1 - 2\nu } \right)\left( {\frac{1}{{b^{2} }} - \frac{1}{{c^{2} }}} \right) - \left( {3 - 2\nu } \right)\left( {b^{2} - c^{2} } \right)} \right\} \hfill \\ - \frac{{\sigma_{Y} }}{2}c^{2} \left( {\frac{1}{{b^{2} }} - \frac{1}{{c^{2} }}} \right) - \sigma_{Y} \ln \left( \frac{a}{c} \right) - \frac{{\rho \omega^{2} }}{2}\left( {c^{2} - a^{2} } \right) \hfill \\ + \frac{{\rho \omega^{2} }}{{8\left( {1 - \nu } \right)}}\left( {3 - 2\nu } \right)\left( {b^{2} - a^{2} } \right) \hfill \\ \end{gathered} \right] \\ & \;\; - \frac{{\rho \omega^{2} }}{{8\left( {1 - \nu } \right)}}\left\{ {c^{4} \left( {1 - 2\nu } \right)\left( {\frac{1}{{b^{2} }} - \frac{1}{{r^{2} }}} \right) - \left( {3 - 2\nu } \right)\left( {b^{2} - r^{2} } \right) - \left( {3 - 2\nu } \right)\left( {r^{2} - b^{2} } \right)} \right\}\,\, \\ & \;\; + \frac{{\sigma_{Y} }}{2}c^{2} \left( {\frac{1}{{b^{2} }} - \frac{1}{{r^{2} }}} \right), \\ \end{aligned}$$

(57)

$$\begin{aligned} \,\left( {\sigma_{\theta } } \right)_{R}^{{{\text{Elastic}}\,{\text{zone}}}} = & \left( {\frac{{a^{2} }}{{a^{2} - b^{2} }}} \right)\left( {1 + \frac{{b^{2} }}{{r^{2} }}} \right)\left[ \begin{gathered} \frac{{\rho \omega^{2} }}{{8\left( {1 - \nu } \right)}}\left\{ {c^{4} \left( {1 - 2\nu } \right)\left( {\frac{1}{{b^{2} }} - \frac{1}{{c^{2} }}} \right) - \left( {3 - 2\nu } \right)\left( {b^{2} - c^{2} } \right)} \right\} \hfill \\ - \sigma_{Y} \ln \left( \frac{a}{c} \right) - \frac{{\rho \omega^{2} }}{2}\left( {c^{2} - a^{2} } \right) - \frac{{\sigma_{Y} }}{2}c^{2} \left( {\frac{1}{{b^{2} }} - \frac{1}{{c^{2} }}} \right) \hfill \\ + \frac{{\rho \omega^{2} }}{{8\left( {1 - \nu } \right)}}\left( {3 - 2\nu } \right)\left( {b^{2} - a^{2} } \right) \hfill \\ \end{gathered} \right] \\ & \;\; - \frac{{\rho \omega^{2} }}{{8\left( {1 - \nu } \right)}}\left\{ {c^{4} \left( {1 - 2\nu } \right)\left( {\frac{1}{{b^{2} }} + \frac{1}{{r^{2} }}} \right) - b^{2} \left( {3 - 2\nu } \right) + r^{2} \left( {1 + 2\nu } \right) - \left( {1 + 2\nu } \right)r^{2} + \left( {3 - 2\nu } \right)b^{2} } \right\} \\ & \;\; + \frac{{\sigma_{Y} }}{2}c^{2} \left( {\frac{1}{{b^{2} }} + \frac{1}{{r^{2} }}} \right). \\ \end{aligned}$$

(58)

4 Numerical Evaluation of Residual Stresses

To exemplify the residual stresses induced by the proposed method of hybrid rotational-swage autofrettage, two hollow cylinders of different materials, viz., SS316 and Al7075-T6 are considered with a solid swage mandrel of AISI4340 steel. The material properties of the cylinder and mandrel materials are presented in Table 1.

Table 1 Material properties of SS316, Al7075 cylinders and AISI4340 mandrel

The radial dimensions of the SS316 cylinder are taken as a = 30 mm, b = 60 mm and that of the Al7075-T6 cylinder are taken as a = 20 mm, b = 50 mm. The outer radius of the swage mandrel is considered as a + δ, where δ is the amount of interference between the mandrel and interior wall of the cylinders. For numerical evaluation of residual stresses in both the cylinders when subjected to hybrid rotational-swage autofrettage, first a permissible range of operating (δ, ω) responsible for causing plastic deformation without contact separation during the process is obtained. Then one typical permissible combination of such (δ, ω) is chosen for each cylinder-mandrel assembly for the operation of the process and the elastic–plastic interface radius for each cylinder is obtained. The elastic–plastic loading stresses in the cylinder along with the stress distribution in the elastic mandrel are numerically evaluated followed by the evaluation of residual stresses in the cylinders after unloading as a function of radii.

4.1 Determination of Permissible Operating Range of Interference and Angular Speed to Achieve Autofrettage without Contact Separation

To satisfy this requirement of no contact separation between the mandrel outer surface and the interior wall of the cylinders while rotating during loading, a permissible operating zone with combinations of cylinder angular speed and mandrel interference is obtained. To determine a permissible operating zone, the values of the different threshold angular speeds with mandrel interference corresponding to yield initiation, contact separation and plastic collapse are plotted in Fig. 3 for the SS316 and Al7075-T6 cylinders. The curve obtained by joining the different combinations of angular speed and interference corresponding to the yield onset in the cylinder in the space of δ-ω is referred as the yield line (solid line in Fig. 3). The curve obtained by joining the points (δ, ω) corresponding the separation of rotating cylinder from mandrel is referred as the separation line (the dashed line in Fig. 3) and the points (δ, ω) corresponding to the complete plastic deformation of the cylinder are joined together to form the plastic collapse line (the centred dash line in Fig. 3). The values of angular speed ω_Y that initiates yielding with interference in the cylinder are obtained from Eq. 22. While evaluating ω_Y, the corresponding range of values of δ for each mandrel-cylinder assembly are evaluated from Eq. 33. For SS316, this range of mandrel interference δ (in mm) is obtained as 0.04071 < δ < 0.04102 and that for Al7075-T6 cylinder, it is obtained as 0.0833 < δ < 0.0952. The critical angular speeds of the cylinders corresponding to contact separation between the swage mandrel and the rotating cylinders ω_s are determined as a function of δ from Eq. 28 up to the onset of yielding in the cylinder. Once the cylinder becomes elastic–plastic, the critical angular speeds corresponding to the contact separation between the swage mandrel and the rotating cylinders ω_s and the corresponding radii of elastic–plastic boundary c_s are obtained by solving Eq. 49 and 50 simultaneously. The critical values of plastic collapse speed ω_f i.e., speeds corresponding to the full plastic deformation of the cylinders as a function of δ are obtained from Eq. 51.

Fig. 3

Rotational speed (ω) vs. interference (d) plot to determine the permissible operating zone to achieve hybrid rotational-swage autofrettage in (a) SS316 and (b) Al7075-T6 cylinders

The intersection of the yield line and the separation line provide the critical combination of cylinder angular speed and mandrel interference corresponding to contact separation at the onset of yielding. For the present cases, this point is marked as A (0.0410207, 106.20) in Fig. 3(a) for SS316 cylinder and B (0.0952, 247) in Fig. 3(b) for Al7075-T6 cylinder, where the first coordinate δ is measured in mm and the second coordinate ω is measured in rad/s. The plastic collapse line intersects the line of contact separation at point C (0.1234, 136.53) for SS316 cylinders and at point D (0.4345, 344.9) for Al7075-T6 cylinder. The points C and D in Fig. 3(a) and (b), respectively, describe the critical condition for the contact separation corresponding to the full plastic deformation of the wall of the cylinders. It can be concluded from Fig. 3(a) and (b) that the region bounded by the yield line and the separation line in the space of (δ, ω), represented by hatched lines, dictates the permissible operating zones for achieving the hybrid rotational-swage autofrettage in the present cylinders. If one considers to load the cylinder-mandrel assembly choosing any combination of (δ, ω) from the permissible zones, interference of mandrel is maintained along with the rotation of the cylinders throughout the operation.

4.2 Elastic–Plastic Stresses in the Cylinders and Elastic Stresses in the Mandrel During Loading

The SS316 and Al7075-T6 cylinders are considered to be loaded with a suitable combination of (δ, ω) chosen from the permissible operating zones as presented in Fig. 3(a) and (b), respectively, to achieve hybrid rotational-swage autofrettage. For instance, the SS316 cylinder is considered to be loaded with δ = 0.088 mm, ω = 131 rad/s and that the Al7075-T6 is considered to be loaded with δ = 0.35 mm, ω = 335 rad/s.

At δ = 0.088 mm and ω = 131 rad/s, the interior wall of the SS316 cylinder deforms plastically up to radius c = 46.9596 mm as obtained by solving Eq. 47. Thus, the overstrain level achieved in the SS316 cylinder can be obtained by $\varepsilon = {{(c - a)} \mathord{\left/ {\vphantom {{(c - a)} {(b - a)}}} \right. \kern-0pt} {(b - a)}} = 56.53\%$. Similarly, for Al7075-T6, the elastic–plastic interface radius c is obtained as 42.3658 mm when loaded with δ = 0.35 mm, ω = 335 rad/s, achieving an overstrain level of 74.55%. Knowing the value of the elastic–plastic interface radius c for the respective cylinders, the elastic–plastic stresses as a function of radius are determined using the stress solutions developed in Sect. 3.3.1 and 3.3.2. The elastic stress distribution in the corresponding AISI4340 mandrels are also obtained using Eq. 45 and 3. The evaluated elastic–plastic stress distribution in the SS316 and Al7075-T6 cylinders along with the mandrel stress distribution are shown in Fig. 4(a) and (b), respectively. It is observed that the radial stress at the interface between the swage mandrel and the cylinders i.e., at the inner radius of the cylinders remain compressive ensuring no contact separation. The radial stress vanishes at the outer radius of the cylinders. The hoop and axial stresses are tensile from the inner to outer radius of the cylinders.

Fig. 4

Elastic–plastic stress distribution during loading in (a) SS316 cylinder for d = 0.088 mm and δ = 131 rad/s and (b) Al7075-T6 cylinder for d = 0.035 mm and ω = 335 rad/s along with the elastic stress distribution in the mandrel

4.3 Residual Stress Distribution in the Cylinders After Unloading

The residual stresses after unloading of the mandrel interference and the rotational centrifugal force from the cylinders are evaluated using Eq. (55)-(58) and are plotted as a function of radius in Fig. 5(a) and (b) for SS316 and Al7075-T6 cylinders, respectively. It is observed that significantly large compressive residual hoop stresses are generated at the interior wall of both the cylinders. After unloading the whole mandrel becomes stress free as it was deformed purely elastically during loading. With the generation of compressive residual hoop stresses in the cylinders, the procedure for the method of hybrid rotational-swage autofrettage is completed.

Fig. 5

Residual stress distribution after unloading in (a) SS316 and (b) Al7075-T6 cylinders

The residual hoop stress induced at the inner radius of the SS316 cylinder is –167.5 MPa (− 0.58σ_Y) as observed from Fig. 5(a). Figure 5(b) shows the generation of residual hoop stress of the order of − 355.5 MPa (− 0.93σ_Y) at the inner radius of the Al7075-T6 cylinder. The residual hoop stress in the SS316 becomes compressive up to a radial depth of 10.78 mm and that in the Al7075-T6 cylinder the compressive residual hoop stress spreads up to a radial depth of 11.58 mm at the interior wall. Thereafter, the residual hoop stresses induced in the cylinders change to tensile. The residual radial stress distribution is smaller in magnitude and compressive across the wall thickness vanishing at both the extreme radii. The residual axial stress in the cylinders are moderately compressive at the interior wall up to some intermediate radius and it then it becomes tensile up to the outer radius. It is to be noted that the tensile residual hoop and axial stresses toward the exterior surface of the cylinders are significantly smaller in magnitude and follow a decreasing trend.

The large compressive residual hoop stresses induced at the interior of the cylinders contribute to the significant reduction in the equivalent stress when internally pressurized in actual service condition. This enables the autofrettaged cylinders to withstand more pressure as compared to the corresponding single non-autofrettaged monobloc cylinders. The maximum pressure carrying capacity of the autofrettaged cylinders can be determined by the superposition of Lamé stresses (Ref 44) due to in-service internal pressurization to the residual stresses and then employing the criterion of yield onset. For the present autofrettaged SS316 cylinder, the maximum pressure carrying capacity is obtained as 171.55 MPa. The corresponding non-autofrettaged monobloc SS316 cylinder can withstand the maximum pressure of 108.75 MPa. This shows an enhancement of 57.7% in the maximum pressure carrying capacity of SS316 cylinder due the hybrid rotational-swage autofrettage-induced residual stresses. In the autofrettaged Al7075-T6 cylinder, the maximum pressure carrying capacity achieved is obtained as 310.2 MPa. The corresponding non-autofrettaged monobloc Al7075 cylinder can withstand the maximum pressure of 160.86 MPa only. Thus, the enhancement in the maximum pressure carrying capacity achieved in the Al7075-T6 cylinder due to the present hybrid rotational-swage autofrettage is 92.8%. The large compressive residual hoop stress generated due to autofrettage contributes to the significant enhancement of the fatigue life of high-pressure cylinders. The beneficial effect of compressive residual hoop stress induced by the present method of hybrid-rotational autofrettage is analyzed in Sect. 5.

5 Analysis of Fatigue Life

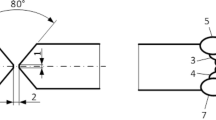
A fracture mechanics-based approach is used to analyze the fatigue life of the cylinders subjected to hybrid rotational-swage autofrettage. A straight-fronted longitudinal crack is considered emanating from the interior wall of the autofrettaged cylinders. The crack geometry is schematically represented in Fig. 6. The stress intensity factors (SIFs) at the crack tip are calculated using the solution given by Underwood (Ref 33), as described in Sect. 5.1. Based on the calculated SIFs, the fatigue life of the cylinders is estimated employing Paris law.

Fig. 6

Schematic representation of a straight-fronted axial crack emanating from interior wall of the cylinder

5.1 Calculation of Stress Intensity Factors

The Mode-I SIF for a straight-fronted longitudinal crack shown in Fig. 6 due to Underwood (Ref 33) is given by

$$K_{{\text{I}}} = 1.12\sigma_{\theta } \sqrt {\pi l} + 1.13p\sqrt {\pi l} + 1.12\left( {\sigma_{\theta } } \right)_{R} \sqrt {\pi l} ,\,\,\,\,\,\,\,\,\,\frac{l}{t} < 0.25$$

(59)

where σ_θ is the hoop stress due to working internal pressure p, (σ_θ)_R is the residual hoop stress, l is the crack length and t is the wall thickness of the cylinder. Underwood (Ref 33) formed the approximate solution of K_I for a long axial, straight-fronted shallow crack given by Eq. 59 by combining known K_I solutions available in literature. The first term of Eq. 59 corresponds to the K_I solution for an edge notch in a semi-infinite plate (Ref 45) and the second term corresponds to Bueckner’s solution (Ref 46) of K_I for a pressurized edge notch in a half space. The third term was added similar to the first term to take into account the effect of residual stress on the crack tip SIF. Like the hoop stress σ_θ at the interior of the cylinder due to internal pressurization in the first term is responsible for Mode-I opening of crack, the compressive residual hoop stress (σ_θ)_R at the cylinder interior wall involved in the third term is the corresponding mitigating effect on Mode-I opening.

If the cylinder is subjected to a cyclic pressure, the range of SIF, ΔK_I can be given by

$$\Delta K_{{\text{I}}} = \left( {K_{{\text{I}}} } \right)_{\max } - \left( {K_{{\text{I}}} } \right)_{\min } ,$$

(60)

where $\left( {K_{{\text{I}}} } \right)_{\max }$ and $\left( {K_{{\text{I}}} } \right)_{\min }$ denote the maximum and minimum SIFs, respectively, and can be given by using Eq. (59) as

$$\left( {K_{{\text{I}}} } \right)_{\max } = 1.12\left( {\sigma_{\theta } } \right)_{\max } \sqrt {\pi l} + 1.13p_{\max } \sqrt {\pi l} + 1.12\left( {\sigma_{\theta } } \right)_{R} \sqrt {\pi l} ,$$

(61)

$$\left( {K_{{\text{I}}} } \right)_{\min } = 1.12\left( {\sigma_{\theta } } \right)_{\min } \sqrt {\pi l} + 1.13p_{\min } \sqrt {\pi l} + 1.12\left( {\sigma_{\theta } } \right)_{R} \sqrt {\pi l} ,$$

(62)

where p_max and p_min are the maximum and minimum in-service internal pressure in the cycle. Equation 62 may provide negative values of $\left( {K_{{\text{I}}} } \right)_{\min }$ if the induced residual stress in the cylinder is large compressive. As negative SIFs indicate the closing of cracks, one may set $\left( {K_{{\text{I}}} } \right)_{\min } = 0$. Thus, the range of SIF can be given by $\Delta K_{{\text{I}}} = \left( {K_{{\text{I}}} } \right)_{\max }$ using Eq. 60. For this case, ΔK_I can be expressed as

$$\Delta K_{{\text{I}}} = 1.12\Delta \sigma_{\theta } \sqrt {\pi l} + 1.13\Delta p\sqrt {\pi l} + 1.12\left( {\sigma_{\theta } } \right)_{R} \sqrt {\pi l} .$$

(63)

In Eq. 63, the range of hoop stress Δσ_θ for the range of internal pressure Δp as a function of radius r is given by Lamé’s solution as

$$\Delta \sigma_{\theta } = \frac{{\Delta p\left( {1 + \frac{{b^{2} }}{{r^{2} }}} \right)}}{{\left( {\frac{{b^{2} }}{{a^{2} }} - 1} \right)}}.$$

(64)

Substituting Eq. 64 in Eq. 63 and defining $\Delta K_{o} = \Delta p\sqrt {\pi l}$, the range of SIF in normalized form can be expressed as

$$\frac{{\Delta K_{{\text{I}}} }}{{\Delta K_{o} }} = 1.12\left\{ {\frac{{\left( {1 + \frac{{b^{2} }}{{r^{2} }}} \right)}}{{\left( {\frac{{b^{2} }}{{a^{2} }} - 1} \right)}} + 1.009 + \frac{{\left( {\sigma_{\theta } } \right)_{R} }}{\Delta p}} \right\}.$$

(65)

The normalized crack length l/t for a given crack of length l can be defined as

$$\frac{l}{t} = \frac{r - a}{{b - a}},$$

(66)

where r is the radial location up to which the crack is propagated. One can recast the value of r from Eq. 66 in terms of l/t and substitute in Eq. 65 to obtain the range of normalized SIFs as a function of normalized crack length l/t, i.e., $\frac{{\Delta K_{{\text{I}}} }}{{\Delta K_{o} }} = f\left( \frac{l}{t} \right)$. The normalized SIFs in non-autofrettaged cylinders can also be evaluated using Eq. 65. For this, one has to set $\left( {\sigma_{\theta } } \right)_{R} = 0.$

5.2 Estimation of Fatigue Life

It has been shown by Paris and Erdogan (Ref 27) that the rate of fatigue crack propagation can be determined as a function of Mode-I SIF ΔK_I given by the following equation, popularly known as Paris law:

$$\frac{{{\text{d}}l}}{{{\text{d}}N}} = C\left( {\Delta K_{{\text{I}}} } \right)^{m} ,$$

(67)

where l is the length of the crack, N is the number of cycles applied during fatigue loading and C and m are the material constants. In Eq. 67, the fatigue crack propagation rate $\frac{{{\text{d}}l}}{{{\text{d}}N}}$ is measured in m/cycle and ΔK_I in ${\text{MPa}}\sqrt m$. Since, $\frac{{\Delta K_{{\text{I}}} }}{{\Delta K_{{\text{o}}} }} = f\left( \frac{l}{t} \right),$ one reiterate Eq. 67 in the following form:

$$\Delta K_{{\text{I}}} = \Delta K_{{\text{o}}} f\left( \frac{l}{t} \right) = \Delta p\sqrt {\pi l} f\left( \frac{l}{t} \right).$$

(68)

Substituting Eq. 68 in Eq. 67 one obtains

$$\frac{{{\text{d}}l}}{{{\text{d}}N}}\,\, = C\left( \pi \right)^{\frac{m}{2}} \left( {\Delta p} \right)^{m} \left( l \right)^{\frac{m}{2}} \left\{ {f\left( \frac{l}{t} \right)} \right\}^{m} .$$

(69)

The number of fatigue life cycles N for a thick-walled cylinder subjected to internal pressurization can be estimated by numerical integration of Eq. 69. In applying Eq. 69 for the estimation of fatigue life of thick-walled cylinder, the following are considered here:

• (a) The thick-walled cylinder contains a crack, the length of which is assumed as the initial crack length.

• (b) An allowable final crack length is calculated in accordance with ASME Pressure Vessel Code (Ref. 47).

• (c) The material constants C and m for the material of the cylinder are known.

• (d) The range of normalized SIF can be calculated as a function of normalized crack length l/t.

Equation 69 can be expressed in terms of normalized crack length by dividing both sides of Eq. 69 by t. The resulting expression is then integrated from the normalized initial crack size to the normalized allowable final crack size to obtain the number of fatigue cycles as

$$N = \frac{{t^{{1 - \frac{m}{2}}} }}{{C\left( \pi \right)^{\frac{m}{2}} \left( {\Delta p} \right)^{m} }}\int\limits_{{\left( \frac{l}{t} \right)_{i} }}^{{\left( \frac{l}{t} \right)_{f} }} {\frac{{{\text{d}}\left( \frac{l}{t} \right)}}{{\left( \frac{l}{t} \right)^{\frac{m}{2}} \left\{ {f\left( \frac{l}{t} \right)} \right\}^{m} }}} .$$

(70)

In Eq. 70, the integration limits $\left( \frac{l}{t} \right)_{i}$ and $\left( \frac{l}{t} \right)_{f}$ denote the initial and final normalized crack lengths, respectively. The integral term of Eq. 70 can be evaluated numerically using a suitable method, e.g., Simpson’s 1/3rd rule.

5.3 Numerical Example

The fatigue life of thick-walled cylinders considered in Section 4 subjected to hybrid rotational-swage autofrettage method is numerically exemplified in this section using the fracture mechanics-based approach discussed in Sect. 5.1 and 5.2. The numerical evaluation of residual stresses induced in both the SS316 and Al7075-T6 cylinders due to hybrid rotational-swage autofrettage method are carried out in Sect. 4.3 and is shown in Fig. 5. For the analysis of fatigue life in both the cylinders, single straight-fronted axial crack is assumed to emanate from the interior surface. The initial normalized crack length is taken as (l/t)_i = 0.001 (Ref 28) and the allowable final normalized crack length is calculated using KD-412.1 ASME pressure vessel code (Ref 47) as (l/t)_f = 0.25. The material constants C and m used for both the materials are provided in Table 2.

Table 2 Material constants C and m appearing in Paris law for SS316 and Al7075-T6

The autofrettaged cylinders are considered to be subjected to different individual maximum pressures, which are less than or equal to their maximum pressure carrying capacity during service fatigue cycle. The minimum pressure in the cycle is assumed to be zero. For the present consideration, (K_I)_min values are negative as provided by Eq. 62 and thus, (K_I)_min can be taken as zero and the range of Mode-I SIFs can be calculated using Eq. 63 for each in-service maximum pressure in the cycle. The normalized range of Mode-I SIFs are evaluated using Eq. 65 for the autofrettaged cylinders and the same equation is employed to evaluate the SIFs in the corresponding non-autofrettaged cylinders setting $\left( {\sigma_{\theta } } \right)_{R} = 0$.

For instance, the autofrettaged SS316 cylinder is considered to be subjected to individual in-service maximum pressures p_max (in MPa) = 70, 90, 108.75, 140 and 171.55. It is to be noted that the pressure 108.75 MPa is the maximum pressure carrying capacity of the non-autofrettaged SS316 cylinder and 171.55 MPa is the maximum pressure carrying capacity of the present autofrettaged SS316 cylinder. The autofrettaged Al7075-T6 cylinder is considered to be subjected to p_max (in MPa) = 150, 160.86, 200 and 310.2, where 160.86 MPa is the maximum pressure carrying capacity of the non-autofrettaged Al7075-T6 cylinder and 310.2 MPa is the maximum pressure carrying capacity of the autofrettaged cylinder. The normalized range of SIFs evaluated for the different in-service pressures in the SS316 and Al7075-T6 cylinders as a function of normalized crack length are shown in Fig. 7(a) and (b), respectively. It is observed from Fig. 7 that the normalized SIFs in both the cylinders subjected to hybrid rotational-swage autofrettage is the minimum at the initial normalized crack length for different in-service pressures and it increases gradually to the allowable final normalized crack length. It can be concluded that as the in-service pressure is increased the corresponding normalized SIFs also increases at the corresponding normalized crack lengths. In the non-autofrettaged cylinders, the normalized SIF is the maximum at the initial normalized crack length and it gradually decreases up to the allowable final normalized crack length. The normalized SIFs in the non-autofrettaged cylinder remains the highest as compared to the normalized SIFs in the autofrettaged cylinders for all permissible internal in-service pressures.

Fig. 7

Normalized SIFs in autofrettaged (a) SS316 s and (b) Al7075-T6 cylinders for different in-service pressures along with the corresponding values in its non-autofrettaged counter parts

The number of fatigue life cycles required to propagate the crack from l/t = 0.001 to l/t = 0.25 in the autofrettaged SS316 and Al7075-T6 cylinders are estimated using Eq. (70) for all the considered in-service internal pressures and are presented in Table 3 and 4, respectively. In calculating the fatigue lives of the cylinders, the normalized SIFs $\frac{{\Delta K_{{\text{I}}} }}{{\Delta K_{{\text{o}}} }} = f\left( \frac{l}{t} \right)$ for SS316 are taken from Fig. 7(a) and that for the Al7075-T6 are taken from Fig. 7(b). For comparison, the corresponding fatigue life of the cylinders subjected to stand-alone rotational autofrettage as well as their non-autofrettaged counterparts are also estimated and presented in the respective tables. When the cylinders are considered to be subjected to stand-alone rotational autofrettage, it is assumed that they reach the same level of overstrain, i.e., the plastic deformation in the cylinders propagate to the same radial depth as that of the proposed hybrid method. However, to achieve the same level of overstrain in the cylinders by the stand-alone rotational autofrettage, the rotational speed requirement is much higher than that required in the proposed hybrid rotational-swage autofrettage process. For example, to achieve an overstrain level of 56.53%, the stand-alone rotational autofrettage requires a very high speed of 4212 rad/s. Contrary to this, the proposed hybrid rotational-swage autofrettage requires only a speed of 131 rad/s along with an interference of 0.088 mm. The fatigue life of both the SS316 and Al7075-T6 cylinders subjected to hybrid rotational-swage autofrettage method is significantly increased as compared to the corresponding non-autofrettaged cylinders for the given in-service internal pressure. Table 3 dictates that for the in-service internal pressure of 70 MPa, the fatigue life of the autofrettaged SS316 cylinder is increased by a factor 1201 as compared to that of the corresponding non-autofrettaged cylinder. If the same autofrettaged cylinder is considered to work under the internal pressures of 90 MPa and 108.75 MPa, its fatigue life is enhanced by a factor of 44.12 and 15.37, respectively. The autofrettaged SS316 cylinder still can bear significant number of fatigue cycles even if it is subjected to pressures beyond 108.75 MPa (the yield onset pressure of non-autofrettaged cylinder) up to 171.55 MPa (the yield onset pressure of autofrettaged cylinder). For example, for 140 MPa in-service internal pressure, the autofrettaged SS316 cylinder can sustain 1.27 × 10⁶ cycles for the present crack propagation, which is still 2.88 times the number of cycles that its non-autofrettaged counterpart can sustain. Comparing the fatigue life results of the proposed hybrid rotational-swage autofrettage with that of the stand-alone rotational autofrettage for the SS316 cylinder subjected to the same internal pressures, it is observed that the fatigue life enhancement is higher in the present hybrid autofrettage process. At the maximum pressure carrying capacity of the SS316 cylinder subjected to the hybrid process, i.e., at p = 171.55 MPa, the cylinder which is subjected to rotational autofrettage fails providing zero fatigue life. The same cylinder if it is autofrettaged by the hybrid rotational-swage autofrettage process, it can withstand the maximum pressure p = 171.55 MPa, sustaining a fatigue life of 4.15 × 10⁵ cycles. In the autofrettaged Al7075-T6 cylinder, the fatigue life enhances by a factor of 3.09 × 10⁴ and 377.33 for the in-service internal pressures of 150 MPa and 160.86 MPa, respectively, as evident from results presented in Table 4. As the in-service internal pressure is increased, the fatigue life of the cylinders is decreased. At the yield onset pressures of the autofrettaged and non-autofrettaged cylinders, the fatigue life is the minimum. Further, comparing the fatigue life improvement in the corresponding AL7075-T6 cylinder subjected to the stand-alone rotational autofrettage for the same internal pressures, it is noticed that the present hybrid rotational-swage autofrettage process provides higher fatigue life. At the yield onset pressure p = 310.2 MPa, of the Al7075-T6 cylinder subjected to hybrid rotational-swage autofrettage process, it has the fatigue life of 13 cycles. However, the corresponding rotationally autofrettaged cylinder cannot withstand the above pressure, making the fatigue life zero.

Table 3 Fatigue life of SS316 cylinder subjected to in-service internal pressure

Table 4 Fatigue life of Al7075-T6 cylinder subjected to in-service internal pressure

6 Conclusions

In this work, a hybrid rotational-swage autofrettage method is proposed to induce compressive residual stresses at the interior wall of a thick-walled cylinder. The analytical solutions for stresses during loading, unloading and residual stresses are obtained. The analysis is expected to provide only approximate results because the transient nature of the process is ignored; it is assumed that the mandrel is fully inserted before the rotation commences. However, the analysis can be used for approximate prediction and can serve as a guide for checking the accuracy of simulation results. The hybrid process is exemplified for SS316 and Al7075-T6 cylinders using a mandrel of AISI4340 considering typical radial dimensions. The critical angular speeds as a function of mandrel interference corresponding to yield onset, contact separation and plastic collapse are obtained to identify a permissible operating zone for both the cylinders. Considering a typical combination of angular speed and mandrel interference from the safe zone, each cylinder is loaded to create an inner plastic zone and outer elastic zone within the wall of the cylinder keeping the mandrel in the elastic state. The elastic–plastic interface radius is obtained for the cylinders and the elastic–plastic loading stresses as well as post unloading residual stresses are plotted as a function of radius from the interior to the exterior wall of the cylinders. It is observed that the compressive residual hoop stress generated at the interior of the autofrettaged SS316 cylinder is − 0.58σ_Y and that in the Al7075-T6 is − 0.93σ_Y. The beneficial effect of compressive residual stresses induced by hybrid rotational-swage autofrettage in enhancing the fatigue life of the cylinders due to in-service internal pressurization is investigated for a range of internal pressures. The fatigue life is estimated by numerical integration of Paris law. It is found that the fatigue life of autofrettaged SS316 cylinder is increased by 15.37 times and that of the Al7075-T6 cylinder is increased by 377.33 times as compared to their non-autofrettaged counterparts when operated at pressure corresponding to the maximum pressure carrying capacity of the respective non-autofrettaged cylinders.