Modeling of the Kinetics of Carbonitride Precipitation Process in High-Strength Low-Alloy Steels Using Cellular Automata Method

Abstract

Proposition of a cellular automata (CA) model of carbonitride precipitation to simulate image of microstructure in HSLA steels and to predict the mechanical properties is presented in the paper. CA model proved to be very efficient in modeling various phenomena in material science. Numerical modeling played an important role in development of new processing technologies taking advantage of precipitation. By modeling, we mean a mathematical description of the relation between the main process variables and the resulting material properties, based on sound physical principles. In microalloyed steels, the microalloying elements Ti, Nb and V are added in order to control their microstructure and mechanical properties. High chemical affinity of these elements for interstitials (C, N) results in precipitation of binary compound, nitrides and carbides and products of their mutual solubility—carbonitrides. The model accounts for an increase in dislocation density due to plastic deformation and predicts kinetics of precipitation as well as shape of precipitates.

Introduction

Carbonitrides precipitations of microalloying elements V, Nb and Ti strongly influence the microstructure and mechanical properties of high-strength low-alloy (HSLA) steels. To predict the mechanical properties of these steels, parameters of precipitates such as size (mean radius) and content (volume fraction) are required. Understanding and modeling microstructure evolution is a major concern in the scientific and engineering fields. Due to the difficulty of directly incorporating topological features into mathematical models, together with the difficulty in providing a space–time description, there has been increasing interest in using computer simulation to study and predict the microstructure evolution in a range of technologically important materials. Numerous researches were carried out, and development of the microalloyed steels was one of the most spectacular practical effects of these researches. Numerical modeling played an important role in development of new processing technologies taking advantage of precipitation. Modeling means a mathematical description of the relation between the main process variables and the resulting material properties (Ref 1). Most of the thermodynamics models were developed in the second half of the twentieth century, for example, the model of carbonitrides precipitation in microalloyed steels of Dutta and Sellars (Ref 2), Dutta et al. (Ref 3), Dutta et al. (Ref 4). The models are based on the algebraic equations describing the nucleation and growth kinetics of precipitates. One of the available tools to simulate the precipitation processes is the method of cellular automata (CA). The CA method offers a reasonable balance between its computational simplicity and ability to provide quantitative results. CA model of carbonitrides precipitation in microalloyed steels containing such elements as Ti, Nb or V is presented in the paper. The model predicts kinetics of precipitation as well as stereological parameters of precipitates.

The Effect of Carbonitrides on Microstructure and Mechanical Properties of HSLA Steels

Microalloyed steels with ferrite-pearlite microstructure are an important group of structural steels, where high mechanical properties are achieved through small additions of elements such as Ti, Nb, V, introduced separately or comprehensively. High chemical affinity of these elements for interstitials (N, C) results in precipitation of binary compound, nitrides and carbides and products of their mutual solubility—carbonitrides. In steel containing one of the microalloying elements (Ti, Nb, V), the carbonitride described by chemical formula MC_yN_1−y is formed, where y means atomic fraction of carbon in carbonitride.

These compounds have a dual role. The carbonitrides undissolved at austenitization temperature inhibit the growth of austenite grains, providing a fine grain of supercooled austenite transformation products.

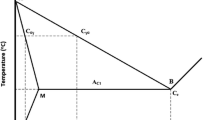
Effect of the carbonitride parameters, volume fraction, V_V, and the average radius of the precipitations, r, on the average radius of the austenite grains, R_a, describes the Smith–Zener equation (Ref 5):

$$R_{a} = \frac{4r}{{3V_{v} }}$$

(1)

The second most important factor influencing the mechanical properties of microalloyed steel is the effect of strengthening of ferrite by dispersed carbonitrides precipitations formed during the transformation austenite-ferrite as a result of reactions between elements dissolved in austenite. This effect is described by Ashby i Orowan model (Ref 5):

$$\Delta \sigma_{e} = \frac{{10.8\sqrt {V_{v} } }}{d}\ln \left( {\frac{d}{{6.125 \cdot 10^{ - 4} }}} \right)$$

(2)

where Δσ_e, increase in yield point, MPa; d, mean diameter of carbonitride particles, μm.

Knowledge of parameters carbonitrides precipitations, both undissolved in austenite at high temperatures and formed in ferrite during phase transformations of undercooled austenite allows to predict the mechanical properties after manufacturing process using the knowledge of the steel chemical composition and process parameters. Carbonitride precipitations parameters, their contents, V_V and size distribution of precipitates can be calculated using mathematical models (Ref 6,7,8,9).

Model of the Kinetics of Carbonitride Precipitation Process

To calculate the kinetics of the carbonitrides precipitation process in the HSLA steel, a model based on the classical theory of nucleation and growth (CNGT) was developed. CNGT is based on the change in free energy, ΔG, associated with the formation of an embryo in a supersaturated solid solution. In the process of carbonitrides precipitation, there are three stages: nucleation, growth and coalescence, which can occur simultaneously. The nucleation rate $V_{n}$, is described by the equation (Ref 7):

$$V_{n} = \frac{dN}{dt} = N_{0} Z\beta^{*} \exp \left( { - \frac{{\Delta G^{*} }}{kT}} \right)\exp \left( { - \frac{\tau }{t}} \right)$$

(3)

where $\beta^{*}$, the condensation rate of solute atoms in cluster of critical size; Z, Zeldovich parameter; $N_{0}$, number of nucleation sites per unit volume; $\Delta G^{*}$, critical Gibbs free energy for nucleus formation; k, Boltzmann constant; T, temperature; τ, incubation time; t, time.

Embryo critical radius $r^{*}$ and parameters $\beta^{*}$ and Z represent the following equations (Ref 7):

$$r^{*} = - \frac{2\gamma }{{\Delta G_{v} }}$$

(4)

$$\beta^{*} = \frac{{4\pi r^{*2} DX}}{{a^{4} }}$$

(5)

$$Z = \frac{{v_{at}^{p} }}{{2\pi r^{*2} }}\sqrt {\frac{\gamma }{kt}}$$

(6)

The incubation time, τ, is given by equation (Ref 7):

$$\tau = \frac{4}{{2\pi \beta^{*} Z^{2} }}$$

(7)

where γ, interphase boundaries energy; $\Delta G_{v}$, the driving force for precipitation per unit volume; D, diffusion coefficient of the metallic element; X, a fraction of the atomic metallic element dissolved in matrix; a, lattice parameter; v ^p _at , the average volume of an atom in precipitation.

In the case of the formation of precipitates of carbonitrides, described by formula MC_yN_1−y, driving force of nucleation is equal to (Ref 7):

$$\Delta G_{v} = - \frac{RT}{{V_{MCN} }}\left[ {\ln \left( {\frac{{X_{M}^{S} }}{{X_{M}^{e} }}} \right) + y\ln \left( {\frac{{X_{C}^{S} }}{{X_{C}^{e} }}} \right) + \left( {1 - y} \right)\ln \left( {\frac{{X_{N}^{S} }}{{X_{N}^{e} }}} \right)} \right]$$

(8)

where X ^s _i , the atomic fraction of the component X in the solution i; X ^e _i , equilibrium atomic fraction of component X in solution; V_MCN, molar volume of carbonitride MC_yN_1−y.

Growth rate, V_gr, is described by equation (Ref 7):

$$V_{gr} = \frac{dr}{dt} = \frac{D}{r}\left( {\frac{{X - X^{i} \left( r \right)}}{{\alpha X^{p} - X^{i} \left( r \right)}}} \right)$$

(9)

where D, diffusion coefficient of metal M, X, X^p, atomic fractions of X in matrix and in precipitate; Xⁱ(r), equilibrium solute fraction of X at precipitate/matrix interface taking into account the Gibbs–Thomson effect; α = v ^M _at /v ^p _at , ratio of matrix to precipitate volumes.

Calculation of the chemical composition of the surface layer of carbonitride precipitation MC_yN_1−y is carried out by solving the following system of equations (Ref 7):

$$yK_{MC} \left( r \right) = X_{M}^{i} \cdot X_{C}^{i}$$

(10)

$$\left( {1 - y} \right)K_{MN} \left( r \right) = X_{M}^{i} \cdot X_{N}^{i}$$

(11)

$$D_{C} \left( {X_{C}^{i} - X_{C} } \right) = yD_{M} \left( {X_{M}^{i} - X_{M} } \right)$$

(12)

$$D_{N} \left( {X_{N}^{i} - X_{N} } \right) = \left( {1 - y} \right)D_{M} \left( {X_{M}^{i} - X_{M} } \right)$$

(13)

where X_M, X_C, X_N represent atomic fractions of elements M, C, N dissolved in the matrix, while X ⁱ _M , X ⁱ _C , X ⁱ _N represent the atomic fraction of elements at precipitate/matrix interface; D_M, D_N, D_C are diffusion coefficients of elements M, C, N in matrix, K_MC(r) i K_MN(r) denote the solubility products of the compounds of the MN and MC corrected for the Gibbs–Thomson effect describes the effect of radius of curvature, r, on the conditions of thermodynamic equilibrium (Ref 7).

$$K_{MC} \left( r \right) = K_{MC} \exp \left( {\frac{{2\gamma V_{MCN} }}{rRT}} \right)$$

(14)

$$K_{MN} \left( r \right) = K_{MN} \exp \left( {\frac{{2\gamma V_{MCN} }}{rRT}} \right)$$

(15)

In the last stage, the precipitations undergo the coagulation process involving of dissolution of small precipitates and growing of large precipitation at constant V_V and $\bar{r} = r^{*}$. The coarsening process of precipitates is described by equation (Ref 7):

$$V_{coarse} = \frac{{d\bar{r}}}{dt} = \frac{4}{27}\left( {\frac{{X^{i} }}{{\alpha X^{p} - X^{i} }}} \right)\frac{{2\gamma v_{at}^{p} }}{kT}\frac{D}{{\bar{r}^{2} }}$$

(16)

Consequently, mean radius, $\bar{r}$, of precipitates is an increasing function of time. As a result, the particle density, N_V, decreases and size distribution as a probability density function, g(r), with a negative asymmetry moves toward larger particle size.

CA Model

CA are mathematical tools that can be used to model physical systems. The main principles of the applications of the CA method in materials science were discussed by Raabe (Ref 10). Modeling microstructure evolution is the most frequent application of the CA. In general, any CA is described by a quadruplet: <L, S, F, N>, where L is a lattice (spatial ordering) of the cells, S is a state of the cell, F is a state transition rule governing an evolution of the state in consecutive time steps, and N is a definition of neighborhood describing a range of local interactions between the cells (Ref 10).

Idea of the cellular automata technique is to divide a specific part of the material into one-, two-, or three-dimensional lattices of finite cells. Each cell in this CA space is called a cellular automaton, while the lattice of the cells is known as cellular automata space. Each cell is surrounded by neighbors, which affect one another. Neighborhoods can be specified in one-, two- and three-dimensional spaces. The most popular examples are the von Neumann and the Moore neighborhoods (Ref 10), where in the 2D case each cell is surrounded by either four or eight neighboring cells, respectively (Fig. 1).

Fig. 1

Von Neumann and Moore neighborhoods

Each cell in the CA space is characterized by its state and by values of internal variables. The cells interactions within the CA space are based on the knowledge defined while studying a particular phenomenon. In every time step, the state of each cell in the lattice is determined by the previous states of its neighbors and the cell itself on a basis of a set of precisely defined transition rules:

$$Y_{i,j}^{t + 1} = \left\{ {\begin{array}{*{20}l} {{\text{if}}\,\left( \varLambda \right) \Rightarrow {\text{new}}\,{\text{state}}} \hfill \\ {{\text{else}} \Rightarrow Y_{i,j}^{t} } \hfill \\ \end{array} } \right\}$$

(17)

where $Y_{i,j}^{t + 1} , Y_{i,j}^{t}$, state of the cell i,j in the current and previous time steps, respectively; Λ, logical function, which describes the condition when the state of the cell changes. Function Λ depends on:

$$\varLambda = \varLambda \left( {Y_{i,j}^{t} , Y_{k,l}^{t} , \varvec{p},\varvec{ q}} \right)$$

(18)

where $Y_{k,l}^{t}$, state of the cell k,l, which is a neighbor to the cell i,j, in the previous time step, p, vector containing external variables, e.g., temperature, q, vector containing internal variables, e.g., carbon concentration.

The logical function, $\varLambda$, is a type of function that can only, as a result, returns the value of true or false. Result of this function depends on few arguments: state of cell and its neighbors, external and internal variables. For example, function $\varLambda$ returns value of true as a result when the external, internal variables and neighborhoods of current cell allow to change its state to the new one. When the $\varLambda$ is true or false, the formula (17) will be activate. When true, then the state of current cell changes to the new state. When false, then the state of current cell does not change.

Since the transition rules control the cells behavior during calculations (i.e., during the deformation and precipitation processes), the proper definition of these rules in designing a CA model critically affects the accuracy of this approach. The transition rules of the developed CA model of precipitation are based on the knowledge of experts, scientists, experimental observations and available literature knowledge.

CA Precipitation Model

Publications dealing with modeling of precipitation using the CA are scarce. Objective of the present work was to apply CA technique to simulate strain-induced transport of carbon, niobium, titanium or vanadium in steel and further formation and growth of carbonitride precipitates and predict the image of microstructure in HSLA steels.

CA—States of Cells and Variables

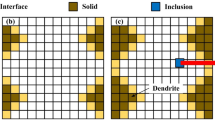
Two-dimensional CA space was created. Two alternative neighbors were tested: Moore—as neighbors, assume all cells, the cells lying on the sides and in the corners, von Neumann—as neighbors, take only the cells lying on the sides of the cell. Since dimensions of precipitates are few orders magnitude smaller than the grain size, the modeling process was carried out in a domain, which represented very small part of the material. Three possible states of the cell were introduced: austenite (γ), precipitate (P) and boundary (γ − P). Beyond this, each cell was characterized by the internal variables: nucleation rate (V_N), dislocation density (ρ). The following external variables were assumed: concentration of carbon, nitride and microalloying element in steel ([C], [N], [MA]), current radius of the precipitate (r).

CA Model—Transition Rules and Flow of Calculation

The transition rules transfer the mathematical model and the knowledge regarding precipitation into the CA space. CA model allows three main transition rules to define the CA space. The cell, which belongs to the austenite grain, γ, will become a nucleus of a precipitate, with certain probability if:

• it has a dislocation density exceeding critical value ρ_cr, which is a function of the temperature (decrease in the temperature results in a decrease in a critical dislocation density).

The cell, which belongs to the austenite grain, γ, will become a precipitate if:

• it has at least one neighbor, which is a precipitate, and the displacement of the γ - P interface is larger than the distance between the cells and the content of MA in this cell is above equilibrium level.

The cell, which is a precipitate, P, will coagulate if:

• it has at least one neighbor, which is also a precipitate and the increase in the radius, r is larger than the distance between the cells.

In each time step, calculations begin with determination of the increment of the dislocation density. This increment is distributed randomly between all the cells, except the cells which are precipitate. Dislocations are allowed to migrate randomly, but they cannot cross austenite grain boundaries. In consequence, random distribution of dislocation density is obtained with higher density close to the grain boundary and lower density inside the grains.

The nucleation rate, V_n, is significantly influenced by the amount of plastic deformation that increases the density of dislocations. The average dislocation density in a given time step is calculated from the formula (Ref 11):

$$\rho_{A } = \frac{A}{B} + \left( {1 - \frac{A}{B}} \right)\exp \left( { - Bt} \right) + \rho^{0}$$

(19)

where t, time; $\rho^{0}$, dislocation density in previous time step.

$$A = \frac{{\dot{\varepsilon }M}}{Bl}$$

(20)

$$B = c_{1} \dot{\varepsilon }\exp \left( { - \frac{Q}{RT}} \right)$$

(21)

where $\dot{\varepsilon }$, strain rate; b, Burgers vector; l, dislocation length; M, Taylor constant; c₁, constant (30); Q, activation energy of recovery; R, gas constant, T, temperature.

Dislocation density is allocated to each cell in the CA, excluding cells that are precipitate. Assuming u as the number of all cells in the CA, u_p—number of cells that are new precipitate, Δρ—increase in dislocation density in time, then the package of dislocation density, P_p, that can be attributed to each of the other cells in the CA is calculated using:

$$P_{P} = \frac{\Delta \rho }{{u - u_{p} }}$$

(22)

The distribution of packages in the CA is random. Preferred are the cells that are a phase boundary. The model introduced the probability of receiving the package, Ω_i. The cell in CA becomes an nucleus, in time step, if the dislocation density value in it, is greater than the ρ_cr and Ω_i> Ω (Ω—random number between 0 and 1).

The following transition rule was formulated for nucleation of the precipitate:

$$Y_{i,j}^{t + 1} = \left\{ {\begin{array}{*{20}l} {{\text{if}}\,\left( \varLambda \right) \Rightarrow {\text{Precipitate}}} \hfill \\ {{\text{else }} \Rightarrow Y_{i,j}^{t} } \hfill \\ \end{array} } \right\}$$

(23)

where:

$$\varLambda = Y_{i,j}^{t} \equiv \gamma \wedge \rho_{i,j} > \rho_{cr} \wedge l_{{\left( {0,1} \right)}} < P_{N1}$$

(24)

P_N1, probability of nucleation (random number between 0.3 and 0.5); l_(0,1), an arbitrary number between 0 and 1; ρ_cr, critical dislocation density to create strain-induced precipitate (10¹⁰ m⁻²).

Logical function, $\varLambda$ (24), returns value of true as the result when state of current cell is austenite grain, γ, and its internal variable, dislocation density is higher than critical value, and its arbitrary number is lower than value of probability of nucleation. Arbitrary number and probability of nucleation are random numbers, they are only use to put some probability and randomize the CA space. Only when those three conditions (state of cell is austenite grain, value of dislocation density inside the cell is higher than critical value and exists the probability of nucleation) are true, the logical function, $\varLambda$, returns true. Even if only one condition is false, the $\varLambda$ is false. The formula (23) is activated by logical function (24) and depends on it. When (24) is true, the state of current cell changes to precipitate; when (24) is false, the state of cell does not change. The next step after nucleation is growth of the precipitates.

Microalloying element and interstitials are removed from the neighbor cells to the precipitate. The transition rule for the nucleation is checked next. The following logical function Λ for a transition rule was proposed for growth of the precipitate:

$$\varLambda = Y_{i,j}^{t} \equiv \gamma \wedge \rho_{i,j} > \rho_{cr} \wedge Y_{k,l}^{t} \equiv P \wedge l_{{\left( {0,1} \right)}} \langle P_{N2} \wedge [MA]_{i,j} \rangle [MA]_{cr} \wedge \Delta r > d$$

(25)

where P_N2, probability of growth (random number between 0.3 and 0.5); [MA]_cr, critical content of microalloying element in a cell to form a precipitate; Δr, increase in the precipitate, d, cell size (nm).

Formula (25) is quite the same as formula (24), it is used to activate the transition rule (23). Logical function, $\varLambda$ (25), returns value of true as the result when state of current cell is austenite grain, γ, and its internal variable, dislocation density is higher than critical value, and neighbor of current cell is precipitate, and its arbitrary number is lower than value of probability of growth, and content of microalloying element in current cell is higher than some critical value, and the increase in the precipitate is higher than current cell size. Only when those six conditions (state of cell is austenite grain, value of dislocation density inside the cell is higher than critical value, the current cell has at least one neighbor whose state is precipitate, exists the probability of growth, the content of microalloying element inside the cell is higher than some critical value, and the increase in the precipitate is higher than cell size) are true, the logical function, $\varLambda$, is true. Even if only one condition is false, the $\varLambda$ is false. The formula (23) is activated by function (25) and depends on it. When (25) is true, the precipitate is growing; when (25) is false, nothing changes.

When deformation is finished, the dislocation density remains constant, which means that the model at this stage does not account for the recovery. This relation has to be added in each cell separately, because recovery depends on the current level of the dislocation density. Calculations are stopped when the content of microalloying element in steel is too low to form new precipitate cells.

In C# was written and implemented in the Visual Studio 2010 the MPCA (Marynowski Przemysław Cellular Automata) program. Graphical interface was added. The following input data are introduced through the interface: content of niobium, titanium or vanadium, carbon and nitrogen in steel, temperature, strain rate and size of the CA space. The following parameters are calculated by the model: distribution of the dislocation density, distribution function for the size of precipitates and an average size of precipitates and composition of austenite. The model contains several parameters, which are not known a priori. These parameters are: critical dislocation density, microalloying element content necessary to create a precipitate. General scheme of calculations in developed computer program is presented in Fig. 2.

Fig. 2

The schematic diagram of calculation of carbonitrides precipitation process using CA model. T_H, temperature of first step austenitization (dissolution of compounds); T_P, precipitation temperature; time_A, actual time; time_S, start time; time_F, finish time; V_N, nucleation rate; V_Np, nucleation rate in the previous step

Example of Modeling of Carbonitride Precipitation

Developed computer program, MPCA, was used to simulate the image of carbonitride precipitates, Nb(C,N) and V(C,N), in microalloyed steel. Simulation of Nb(C,N) precipitation process was carried out for steel containing 0.11% C, 0.03% Nb and 0.01% N subjected to heat treatment austenitization at 1250 °C with the following holding at T = 900 and 950 °C for time, t, from t = 0.00001 to 10000 s. Results of the simulations were compared with the experimental data of the average radius of precipitates, measured after similar temperature of austenitization with holding at 900 and 950 °C for 100, 1000 and 10,000 s (Ref 4, 12).

Simulation of V(C,N) precipitation process was carried out for steel containing 0.36% C, 1.88% Cr, 0.078% V and 0.0412% N subjected to austenitization at 1200 °C with following holding at T = 850 °C for 20 h and quenching in water. Investigation of steel microstructure after heat treatment was carried out using transmission electron microscope, JEM 200CX (Ref 13). The observed image was compared with the microstructure image obtained as a result of modeling the V(C, N) evolution process using the MPCA program.

For the simulations, the input data used during calculations are presented in Table 1.

Table 1 Main parameters used in simulations

Calculated images of carbonitride Nb(C,N) are presented in Fig. 3(a) and (b).

Fig. 3

Simulated microstructures with precipitations of carbonitrides in microalloyed niobium steel after heat treatment: austenitization at 1250 °C with following isothermal holding at 900 °C (a) and 950 °C (b) for 10,000 s

Comparison of calculated mean radius, $\bar{r}$, of precipitation with experimental data (Ref 4, 12) is presented in Fig. 4.

Fig. 4

Comparison of the calculated mean radius, $\bar{r}$, of precipitation with experimental data (Ref 4, 12), at T = 900 °C, T = 950 °C for t = 10,000 s

At temperature 900 °C, experimental data lie slightly above calculated curve $\bar{r}$ = f (time). At temperature 950 °C, $\bar{r}$ precipitates lie below calculated curve. Larger difference between the compared values occurs at 100 s. At 1000 and 10,000 s, the compared values are quite close. The comparison of calculated and experimental data shows a satisfactory convergence, which proves that the developed computer program can be a useful tool supporting the design of heat treatment parameters, providing the desired mechanical properties of steel.

Comparison of experimental and simulated images of microstructure of steel containing 0.36% C, 1.88% Cr, 0.078% V and 0.0412% N is presented in Fig. 5. Compared images show satisfied similarity, although the particle size of the simulated image is slightly smaller compared to real particles.

Fig. 5

Experimental and simulated images of V(C,N) precipitations in steel containing 0.3% C, 0.078% V 1.88% Cr and 0.0412% N, (a) experimental microstructure, (b) diffraction image of V(C,N), (c) solution of diffraction patterns (zone axis: [011] V(C,N)), (d) simulated image

Conclusion

A particular advantage of the model is the ability to distinguish and track the individual stages of the carbonitride precipitation process (nucleation, growth, coagulation). It enables to calculate the size distribution of carbonitrides existing in austenite and influencing its grain size as well as size distribution of carbonitrides precipitated in ferrite during decomposition of undercooled austenite and influencing the mechanical properties of ferrite by the strengthening precipitation effect.

On the computer with processor Intel i7, 4th generation with 4 cores/8 threads, total real time of one simulation is about 4 min. This time depends on the speed and frequency of the processor. The MPCA program is not a paralleled program, therefore the number of the processor cores/threads does not affect the total calculation time. One simulation means simply run the MPCA program with time set to 10,000 s. Total real time of simulation depends also on maximum time of simulation put in program interface. If higher virtual time we put, the real time of simulation will be longer.

Derived model can be a useful tool for chemical composition of steel and heat treatment parameters optimization for obtaining the required high mechanical properties.

The model needs further development, which should include:

• extending the range of chemical composition of steel for case of simultaneous addition of several microalloying elements in steel, on the carbonitride precipitation process

• including of calculation of the temperature field during heat treatment processes and its effect on size distribution of carbonitride particles

• calculation of final mechanical properties of steel after heat treatment.