Introduction

Gas turbines operate at high temperatures where phenomena such as oxidation and creep occur readily. Thermal barrier coating (TBC) systems have become common in gas turbines as they lower the temperature of the underlying substrate and provide protection against high-temperature degradation of the substrate materials (Ref 1). TBC systems thus prolong the life of structural parts, as well as increase the gas turbine efficiency by enabling higher combustion temperatures (Ref 2-4). The requirements to improve jet engine efficiencies have proved to be a big driving force to improve the thermal barrier coating technology by novel compositions and improved production techniques for subsequent improvement in microstructure and thus enhance thermo-mechanical performance of TBCs. Yttria-stabilized zirconia (YSZ) is the present industrial standard topcoat material in TBC system, which can operate long term at temperatures below 1200 °C (Ref 5, 6). However, two flaws, including phase transformation and sintering, have been reported when YSZ is exposed to high temperature (above 1200 °C) for long time. Met stable tetragonal phase decomposes into tetragonal and cubic phase above 1200 °C. Upon cooling, tetragonal phase transforms to monoclinic phase, causing about 3.5% volume change and resulting in crack formation in the TBCs. In addition, volume fraction of pores decreases due to the significant sintering of YSZ at high temperature, which leads to an increase in the thermal conductivity as well as the in-plane stiffness and thus decreases the strain compliance of TBCs (Ref 7-9). The limited capability of YSZ above 1200 °C necessitates its substitution with some novel compositions capable of handling higher temperatures with better stability in advanced gas turbines (Ref 10, 11).

A number of oxide ceramics have been proposed as novel thermal barrier coatings during the last few years. These novel compositions cover especially doped zirconia (Ref 12, 13), pyrochlores (Ref 14, 15), aluminates (Ref 16, 17), and perovskites (Ref 10). Recently, Sm2Ce2O7 has been investigated as one TBC candidate material because of its better thermal properties (Ref 18). In order to enhance the performance of this A2B2O7 compounds, co-doping on the A-site by one or more oxide has been proposed to reduce the thermal conductivity (Ref 19-22). Ying doped La2Zr2O7 with Yb2O3 (Ref 14), and G. Z. Liu doped Gd2Zr2O7 with Nd2O3 (Ref 15), and their thermal conductivities were further reduced after doping. Clarke and coworkers also pointed out that substituted atoms at site B create mass disorder on the cation sublattice, which results in the lowering of thermal conductivity (Ref 23). Ying investigated the thermophysical properties of Ce-doped La2Zr2O7, and found that the doped ceramics (La0.7Yb0.3)2(Zr0.7Ce0.3)2O7 and (La0.2Yb0.8)2(Zr0.7Ce0.3)2 have lower thermal conductivity than La2Zr2O7, whereas their thermal expansion coefficient are higher than La2Zr2O7 (Ref 14). Wan found that Ti substitution for Zr can reduce significantly thermal conductivity at lower temperatures, and the maximum value of thermal expansion coefficient is obtained at x = 0.2 (Ref 24). Ling indicated that Sm2Zr2O7 co-doped with La2O3, Yb2O3, and CeO2 has lower thermal conductivity and high thermal expansion coefficient as compared to Sm2Zr2O7 (Ref 25). However, no research has been conducted concerning B-site substitution of SmCe2O7. In this paper, the Gd3+ and Zr4+ were selected to partially substitute the Sm3+ and Ce4+ in order to provide a general insight into the involvement of thermophysical properties on B-site doping of A2Ce2O7-type fluorite.

Experimental

In this paper, the polycrystalline samples of the (Sm0.5Gd0.5)2(Ce1−x Zr x )2O7 ceramics were synthesized by a solid-state reaction method. Sm2O3, Gd2O3, ZrO2, and CeO2 with purity 99.9% were used as starting materials, and all oxides were dried before use. The stoichiometric amounts of precursors were ground in acetone for 6 h to obtain uniformly distributed mixtures. The mixture slurry was dried at 120 °C for 2 h for complete removal of acetone. The dried powders were pressed into small columns at 50 MPa followed by cold isostatic pressing with 150 MPa. Finally, the bulks were pressureless sintered at 1600 °C for 10 h in air.

The phase structure of (Sm0.5Gd0.5)2(Ce1−x Zr x )2O7 oxides was identified by x-ray diffraction (XRD, Rigaku D/Max 2500, Japan) with Ni-filtered Cu Ka radiation (0.1542 nm) at the scanning rate of 4°/min. The microstructure of the pellets was observed using field emission scanning electron microscopy (SEM, Model Hitachi S-4800, Japan). The specimens were polished with 1-μm diamond paste, and then thermally etched at 1500 °C for 2 h in air for SEM observations. Qualitative x-ray element analysis of various phases was carried out using SEM equipped with energy dispersive spectroscopy (EDS). For heat-treated samples, the actual densities (ρ) were measured by using Archimedes method with an immersion medium of deionized water.

The thermal expansion coefficients of these ceramics were determined with a high-temperature dilatometer (Netzsch DIL402C/7, Germany) from ambient temperature to 1000 °C at a heating rate of 5°/min in argon atmosphere. The size of sample was 25 mm × 3 mm × 4 mm. The specific heat capacities (C P) were calculated from constituent oxides according to the Neumann-Kopp rule based on the reference specific heat values of Sm2O3, Gd2O3, CeO2, and ZrO2 (Ref 26). The thermal diffusivity (λ) was measured from 200 to 1000°C using a laser flash apparatus (FlashLineTM3000, USA) in an argon gas atmosphere. The specimen dimension was about 12.7 mm in diameter and about 1.2 mm in thickness. The thermal conductivity was then calculated according to the relation:

$$ k = \uplambda \cdot \uprho \cdot C_{\text{P}}. $$
(1)

Because the sintered specimen was not fully dense, the measured thermal conductivity was modified for the actual value k 0 using Eq 2, where ϕ is the fractional porosity and the coefficient 4/3 is used to eliminate the effect of porosity on actual thermal conductivity (Ref 17).

$$ {\raise0.7ex\hbox{$k$} \!\mathord{\left/ {\vphantom {k {k_{0} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${k_{0} }$}} = 1 - \frac{4}{3}\upphi. $$
(2)

Results and Discussions

Phase Structure

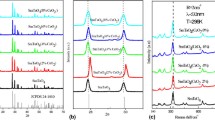
The XRD patterns of all the products in (Sm0.5Gd0.5)2(Ce1−x Zr x )2O7 were recorded in Fig. 1 and analyzed. Detailed analysis indicates that all XRD patterns match well with the standard cubic defect fluorite phase of CeO2. The diffraction peaks of (Sm0.5Gd0.5)2(Ce0.7Zr0.3)2O7 located at 28.33°, 32.85°, 47.28°, and 56.21° can be well indexed to the (111), (200), (220), and (311) planes of a cubic fluorite structure, respectively (Ref 27). In XRD patterns of other oxides, the defect fluorite structure can be identified by the scarce of super-lattice peaks at 2θ values between 32.85° and 47.28°. These two peaks could help us to distinguish the fluorite and pyrochlore structures (Ref 28). Furthermore, no peaks corresponding to the individual oxides are observed. This disparate feature can be attributed to the formation of (Sm0.5Gd0.5)2(Ce1−x Zr x )2O7 ceramics.

Fig. 1
figure 1

XRD patters of (Sm0.5Gd0.5)2(Ce1−x Zr x )2O7 ceramics

Full size image

In the A2B2O7 system, the crystal structure is mainly determined by the ionic radius ratio \( r(A^{3 + } )/r(B^{3 + } ) \) of A and B cations. The stable pyrochlore structure is limited to the range of \( 1.46 \le r(A^{3 + } )/r(B^{3 + } ) \le 1.78 \), and the fluorite oxide will form if the \( r(A^{3 + } )/r(B^{3 + } ) \) is lower than 1.40 (Ref 29). For the complex rare-earth cerium oxides, the ionic radius can be estimated from the ionic radius of the component ions and the chemical composition using the following equation.

$$ \frac{{r(A_{{{\text{av}}.}}^{3 + } )}}{{r(B_{\text{av}}^{4 + } )}} = \frac{{[0.5r({\text{Sm}}^{3 + } ) + 0.5r({\text{Gd}}^{3 + } )]}}{{[(1 - x)r({\text{Ce}}^{4 + } ) + xr({\text{Zr}}^{4 + } )]}}, $$
(3)

where 0.5, 1 − x, and x are the composition of each atom. The ionic radii of Sm3+ and Gd3+ are 1.079 and 1.053 Å, while the Zr4+ and Ce4+ are 0.72 and 0.97 Å, respectively. The values of \( {{r(A_{\text{av}}^{3 + } )} \mathord{\left/ {\vphantom {{r(A_{\text{av}}^{3 + } )} {r(B_{\text{av}}^{4 + } )}}} \right. \kern-0pt} {r(B_{\text{av}}^{4 + } )}} \) for (Sm0.5Gd0.5)2 (Ce1−x Zr x )2O7 oxides can be calculated by the Eq 3 with above mentioned ionic radiuses, and the values are equal to 1.11, 1.13, 1.156, and 1.189 with x increasing from zero to 0.3. The ionic ratios of (Sm0.5Gd0.5)2(Ce1−x Zr x )2O7 are smaller than 1.40 due to the co-doping in the Sm and Ce sites, which reveals that the co-doping in Sm2Ce2O7 cannot change the crystal structure.

Microstructure

The typical microstructure of (Sm0.5Gd0.5)2(Ce1−x Zr x )2O7 ceramics is shown in Fig. 2. The average grain size of (Sm0.5Gd0.5)2(Ce1−x Zr x )2O7 ceramics is several micrometers. The interfaces between grains are very clean, the gap is very small, and no other inter-phases and unreacted oxides existed in boundaries between grains. The chemical compositions and relative density of the synthesized (Sm0.5Gd0.5)2(Ce1−x Zr x )2O7 ceramics are listed in Table 1. As can be seen from Table 1, the mole ratios of different elements in (Sm0.5Gd0.5)2(Ce1−x Zr x )2O7 ceramics are very close to their stoichiometries, and each specimen has a high relative density due to the high-temperature sintering.

Fig. 2
figure 2

Morphologies of (Sm0.5Gd0.5)2(Ce1−x Zr x )2O7 ceramics (a) x = 0, (b) x = 0.1, (c) x = 0.2, (d) x = 0.3

Full size image
Table 1 Element mole ratio, relative density, and lattice parameter of (Sm0.5Gd0.5)2(Ce1−x Zr x )2O7 ceramics
Full size table

Thermal Expansion Coefficient

The dilatometric measurement results of (Sm0.5Gd0.5)2(Ce1−x Zr x )2O7 ceramics with calibration are plotted in Fig. 3. The typical linear expansions can be observed for (Sm0.5Gd0.5)2(Ce1−x Zr x )2O7 ceramics in the temperature range of 20-1000 °C. Clearly, there is no phase transformation for (Sm0.5Gd0.5)2(Ce1−x Zr x )2O7 ceramics in the temperature range. The technical thermal expansion coefficient is defined as

$$ \upalpha_{\text{tech}} = \frac{1}{{L_{0} }}\frac{{\Delta L_{\text{k}} - \Delta L_{0} }}{{T_{\text{k}} - T_{0} }}, $$
(4)

where L 0 is the length of the specimen at T 0 (20 °C), ΔL 0 is the change in length at T 0, and ΔL k is the corresponding length change at temperature T k.

Fig. 3
figure 3

Calibrated dilatometric data of (Sm0.5Gd0.5)2(Ce1−x Zr x )2O7 ceramics as function of temperature

Full size image

Their calculated technical thermal expansion coefficients against temperature are plotted in Fig. 4, together with the data of YSZ. Fig 4 shows that their thermal expansion coefficients increase smoothly with temperature up to 1000 °C, which is attributed to the increasing atomic spacing at elevated temperatures. As also can be seen in Fig. 4, the thermal expansion coefficient decreases gradually with increasing x from 0 to 0.3 at identical temperature levels. It is well known that the thermal expansion coefficient is inverse the crystal energy (U). The crystal (U) of an ionic compound can be expressed as (Ref 30).

$$ U = \frac{{N_{0} Az^{ + } z^{ - } e^{2} }}{{r_{0} }}\left( {1 - \frac{1}{n}} \right), $$
(5)

where N 0, A, z, r 0, e, and n represent Avogadro’s number, the Madelung constant, the ionic charge, the inter-ionic distance, the charge of an electron, and Born exponent, respectively. From the lattice parameters listed in Table 1, it can be known that the substitution of Zr4+ for Ce4+ results in a slight contraction in the unit cell, indicating a decrease in the average inter-ionic distance, \( r_{0} \). This would lead to an increase in the crystal energy of the (Sm0.5Gd0.5)2(Ce1−x Zr x )2O7 ceramics, which represents the decrease of thermal expansion coefficient. Alternatively, there are some structure defects, such as substitutional or interstitial cations and other imperfections in the lattice or varying properties in thermal expansion along with different orientations that have significant effect on the overall thermal expansion coefficient of A2B2O7 oxides (Ref 31, 32). In the fluorite-type A2Ce2O7 system, oxygen vacancies are randomly distributed in disordered fluorite structure; therefore, it facilitates formation of the ionic vacancy clustering, which represents to some extent the decrease in thermal expansion. The structure disorder degree of fluorite-type A2Ce2O7 is inverse to value of \( {{r(A_{\text{av}}^{3 + } )} \mathord{\left/ {\vphantom {{r(A_{\text{av}}^{3 + } )} {r(B_{\text{av}}^{4 + } )}}} \right. \kern-0pt} {r(B_{\text{av}}^{4 + } )}} \) (Ref 29), and the increasing value of \( {{r(A_{\text{av}}^{3 + } )} \mathord{\left/ {\vphantom {{r(A_{\text{av}}^{3 + } )} {r(B_{\text{av}}^{4 + } )}}} \right. \kern-0pt} {r(B_{\text{av}}^{4 + } )}} \) in (Sm0.5Gd0.5)2(Ce1−x Zr x )2O7 ceramics represents the increase of thermal expansion coefficient. Hence, the decrease of thermal expansion coefficients with increasing ZrO2 content in (Sm0.5Gd0.5) 2(Ce1−x Zr x )2O7 ceramics reveals that the influence of crystal energy is greater than oxygen vacancy (Ref 29, 33). These thermal expansion coefficients are obviously higher than 7 wt.% yttria-stabilized zirconia [10.7 × 10−6/K at 1000 °C (Ref 10)] and are good enough to be used as thermal barrier coating materials in the industry condition.

Fig. 4
figure 4

Thermal expansion coefficients of (Sm0.5Gd0.5)2(Ce1−x Zr x )2O7 ceramics

Full size image

Thermal Conductivity

The specific heat capacities of the (Sm0.5Gd0.5)2(Ce1−x Zr x )2O7 ceramics at different temperatures were calculated according to the Neumann-Kopp rule based on the reference specific heat values of Sm2O3, Gd2O3, CeO2 and ZrO2. As can be seen in Fig. 5, the specific heat capacity of the (Sm0.5Gd0.5)2(Ce1−x Zr x )2O7 ceramics increases with increasing temperature from room temperature to 1000 °C, and the calculated specific heat capacity of the (Sm0.5Gd0.5)2(Ce1−x Zr x )2O7 ceramics slightly increases from x = 0 to 0.3 at identical temperature levels.

Fig. 5
figure 5

The calculated specific heat capacities as a function of temperature for (Sm0.5Gd0.5)2(Ce1−x Zr x )2O7 ceramics

Full size image

Fig 6 shows the composition-dependent thermal diffusivities of the (Sm0.5Gd0.5)2(Ce1−x Zr x )2O7 ceramics measured by laser flash method. The values of thermal diffusivity are the arithmetic mean of three measurements. Since the error derived from the mean standard deviation of the three measurements for each specimen is <1.5%, the error bars in Fig. 6 are omitted for all thermal diffusivity date because they are smaller than symbols. As can be seen in Fig. 6, the thermal diffusivity of the (Sm0.5Gd0.5)2(Ce1−x Zr x )2O7 ceramics exhibits inverse temperature dependence, which suggests a dominant phonon conduction behavior in most polycrystalline materials (Ref 32, 33). Furthermore, the thermal diffusivity remarkably decreases with increasing Zr4+ fraction, and (Sm0.5Gd0.5)2 (Ce0.7Zr0.3)2O7 exhibits the lowest thermal diffusivity among all the ceramics investigated.

Fig. 6
figure 6

Composition-dependent thermal diffusivities of (Sm0.5Gd0.5)2(Ce1−x Zr x )2O7 ceramics at different temperatures

Full size image

The thermal conductivities were calculated using Eq 1 and calibrated with Eq 2 to represent fully dense samples, as plotted in Fig. 7. The error bars are omitted because they are smaller than the symbols. The thermal conductivity of the synthesized samples also decreases with increasing ZrO2 content. It decreases from 1.69 W/m K for Sm2Ce2O7 to 1.22 W/m K for (Sm0.5Gd0.5)2(Ce0.7Zr0.3)2O7 at 1000°C. The composition with x = 0.3 exhibits the lowest at all temperatures, and the thermal conductivities of (Sm0.5Gd0.5)2 (Ce1−x Zr x )2O7 ceramics are obviously lower than those of fully dense 7 wt.%YSZ [3.0 at room temperature to 2.3 W/m K at 700 °C reported by Wu et al (Ref 31)]. In electronic insulator crystalline solids, heat is transferred by lattice vibrations. The quanta of lattice vibrations are defined as phonons, and the thermal conductivity is proportional to the phonon mean free path \( l(\upomega ,t) \), which can be approximately described as reported in (Ref 33).

$$ \frac{1}{l(\upomega ,t)} = \frac{1}{{l_{\text{i}} (\upomega ,t)}} + \frac{1}{{l_{\text{p}} (\upomega ,t)}} + \frac{1}{{l_{\text{v}} (\upomega ,t)}} + \frac{1}{{l_{\text{gb}} }}, $$
(6)

where \( l_{\text{i}} (\upomega ,t) \), \( l_{\text{p}} (\upomega ,t) \), \( l_{\text{v}} (\upomega ,t), \) and \( l_{\text{gb}} \) are the phonon mean free path due to interstitials scattering, point defect scattering, vacancies scattering, and grain boundary scattering, respectively. Since the phonon mean free path is several orders of magnitude smaller than the grain size for the (Sm0.5Gd0.5)2(Ce1−x Zr x )2O7 ceramics, the grain boundary scattering can be omitted (Ref 34). The small phonon mean free path contributes to strong phonon scattering in the crystal cell. First, the special and complex crystal structure of fluorite-type (Sm0.5Gd0.5)2 (Ce1−x Zr x )2O7 ceramics can reduce the phonon mean free path. The second factor is the intrinsic oxygen vacancies existed in the crystal lattice. The (Sm0.5Gd0.5)2 (Ce1−x Zr x )2O7 ceramics could be regarded as the solid solution of Zr4+ taking the site of Ce4+ in (Sm0.5Gd0.5)2Ce2O7 ceramics. Thus, the last factor is the substitutional atoms existing in the lattice of (Sm0.5Gd0.5)2Ce2O7, which can also reduce the mean free path of phonon. Atomic substitution causes lattice distortion, increases phonon scattering, and decreases phonon mean free path, according to Eq 7 (Ref 35). On the other hand, the phonon mean free path is proportional to the square of atomic weight difference between the solute and host cations, according to Eq 8 (Ref 35):

$$ \frac{1}{l(\upomega ,t)} = \frac{{2ca^{3} \upomega^{4} }}{{\pi v^{4} }}J^{2} \upgamma^{2} \left( {\frac{\Delta R}{R}} \right)^{2} $$
(7)
$$ \frac{1}{l(\upomega ,t)} = \frac{{a^{3} }}{{4\uppi v^{4} }}\upomega^{4} c\left( {\frac{\Delta M}{M}} \right)^{2}, $$
(8)

where a 3 is the volume per atom, \( v \) the transverse wave speed, \( \upomega \) the phonon frequency, \( c \) the concentration per atom, \( J \) the constant, \( \upgamma \) the Grüneisen parameter, \( M \) and \( R \) the average mass and ionic radius of the host atom, respectively, and \( \Delta M \) and \( \Delta R \) are the differences of masses and ionic radius between the substituted and substituting atoms, respectively. Because the atomic weights of Zr and Ce are 91.22 and 140.1, respectively. The effective ionic radii of Zr4+ and Ce4+ are 0.72 and 0.97 Å, and the effective phonon scattering of the substitutional atoms contributes to the lower thermal conductivity. Thus, thermal conductivity of (Sm0.5Gd0.5)2 (Ce1−x Zr x )2O7 ceramics decreases with increasing ZrO2 content at identical temperature levels. The low thermal conductivity indicates that the (Sm0.5Gd0.5)2 (Ce1−x Zr x )2O7 ceramics can be explored as potential candidates for thermal barrier coating applications.

Fig. 7
figure 7

Composition-dependent thermal conductivities of (Sm0.5Gd0.5)2(Ce1−x Zr x )2O7 ceramics

Full size image

Conclusions

Pure (Sm0.5Gd0.5)2(Ce1−x Zr x )2O7 ceramics with fluorite structure were successfully prepared by solid-state reaction method and sintered at 1600 °C for 10 h using Sm2O3, Gd2O3, ZrO2 and CeO2 as raw materials. Their microstructure is very dense and there are no other inter-phases or unreacted oxides existing at the boundaries between grains. The thermal conductivity of (Sm0.5Gd0.5)2(Ce1−x Zr x )2O7 ceramics decreases with increasing ZrO2 content at identical temperature levels, and phonon scattering caused by the substitutional atoms contributes to the low thermal conductivity. The thermal expansion coefficient of (Sm0.5Gd0.5)2(Ce1−x Zr x )2O7 ceramics decreases with increasing Zr4+ ions, and these thermal expansion coefficients are obviously higher than 7 wt.% yttria-stabilized zirconia. The synthesized (Sm0.5Gd0.5)2(Ce1−x Zr x )2O7 ceramics can be explored as potential candidates for thermal barrier coatings.