Scrap Dissolution in Molten Iron Containing Carbon for the Case of Coupled Heat and Mass Transfer Control

Abstract

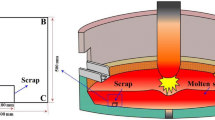
The scrap dissolution in an actual process like the BOF is affected both by mass transfer and heat transfer. In this paper, the mass transfer of carbon in liquid melt is considered along with heat transfer. The approaches used in this paper to model the scrap dissolution phenomenon include the application of Green’s function, quasi-static, integral profile, and the finite difference approach for different Biot numbers. Mass transfer coefficients are calculated using the Chilton–Colburn’s analogy for the case of forced convection. Since the quasi-static approach requires the least computational time, it is used for a detailed parametric study, including the effect of other parameters like different scrap ratios and heating rates of liquid melt. The region of control of heat transfer vs mass transfer is also identified. The dissolution of mixed scrap (light and heavy scrap) is investigated for different scrap ratios and the autogenous heating rates of liquid melt, with the help of mathematical models. The heat transfer coefficient is estimated as a function of mixing energy and the mass transfer coefficient by invoking the Chilton–Colburn analogy. The permissible limits of light scrap, which can be charged into the BOF, are also suggested from the results of this model. The Artificial Neural Network (ANN) model is trained on the dataset (patterns) generated by the coupled heat and mass transfer model. The accuracy of the results obtained using different ANN topologies is discussed followed by a recommendation for selecting the best approach.

Appendices

Appendix A: Estimation of Heat and Mass Transfer Coefficients as a Function of Velocity of the Moving Interface

Stagnant concentration and thermal boundary layers in liquid melt are assumed to exist adjacent to the interface. The heat transfer in the boundary layer takes place only through conduction, whereas the mass transfer occurs through diffusion.

Governing Mathematical Equations for Mass Transfer

It is assumed that the mass transfer in the boundary layer occurs only due to the diffusion process. The mass transfer equation in 1-D in the liquid melt adjacent to the scrap interface is given by

$$ D\frac{{d^{2} C}}{{dX^{2} }} + v\frac{dC}{dX} = 0 $$

(A1)

with the following boundary conditions:

$$ C = C_{\text{i}} \;\;\;\;{\text{at}}\;x = 0 $$

$$ C = C_{\text{b}} \;\;\;\;{\text{at}}\;x = \delta_{\text{C}} $$

where the thickness of the concentration boundary layer $\delta_{\text{c}}$ is estimated from

$$ D\frac{{C_{\text{b}} - C_{\text{i}} }}{{\delta_{\text{C}} }} = \beta_{\text{o}} (C_{\text{b}} - C_{\text{i}} ) $$

which means that the thickness of the boundary layer is given by

$$ \delta_{\text{C}} = \frac{D}{{\beta_{\text{o}} }} $$

(A2)

where D is the diffusion coefficient for mass transfer in the liquid melt and $\beta_{0}$ is the mass transfer coefficient.

The solution of Eq. [A1] is

$$ \frac{{C - C_{\text{i}} }}{{C_{\text{b}} - C_{\text{i}} }} = \frac{\exp ( - vX/D) - 1.0}{{\exp ( - v\delta_{\text{C}} /D) - 1.0}}. $$

(A3)

The mass transfer of carbon from the melt to the interface per unit time unit area is calculated from

${\text{Mass}}\;{\text{flux}}\;{\text{of}}\;{\text{carbon}}\;\left( {{\text{unit}}\;{\text{time}}\;{\text{unit}}\;{\text{area}}} \right) = \left. {D\frac{dC}{dX}} \right|_{X = 0} = D(C_{\text{b}} - C_{\text{i}} )\left( \frac{v}{D} \right)\left. {\frac{\exp ( - vX/D)}{{1 - \exp ( - v\delta_{\text{C}} /D)}}} \right|_{X = 0} = (C_{\text{b}} - C_{\text{i}} )\frac{v}{1 - \exp ( - v\delta /D)}.$

Substituting the value of $\delta_{\text{C}}$,

the mass flux of carbon can be calculated from

$$ J_{\text{C}} = (C_{\text{b}} - C_{\text{i}} )\frac{v}{{1 - \exp ( - v/\beta_{\text{o}} )}}. $$

(A4)

Equation [A4] can be rewritten as

$$ J_{\text{C}} = \beta (C_{\text{b}} - C_{\text{i}} ) $$

(A5)

where β is the mass transfer coefficient for the case of the moving boundary.

From Eqs. [A4] and [A5], the mass transfer coefficient for the moving boundary is estimated from

$$ \beta = \frac{v}{{1 - \exp ( - v/\beta_{0} )}}. $$

(A6)

Governing Equation for Heat Transfer

It is assumed that the heat transfer in the boundary layer occurs due to conduction. The heat transfer equation in 1-D in the liquid melt adjacent to the scrap interface is given by

$$ \alpha \frac{{d^{2} C}}{{dX^{2} }} + v\frac{dC}{dX} = 0 $$

(A7)

where

$$ \alpha = \frac{k}{{\rho C_{\text{p}} }} $$

with following conditions:

$$ T = T_{\text{m}} \;\;\;\;{\text{at}}\;x = 0 $$

$$ T = T_{\text{b}} \;\;\;\;{\text{at}}\;x = \delta_{T} $$

where $\delta_{T}$ is the thickness of the thermal boundary layer which is estimated from the following equation:

$$ k\frac{{T_{\text{b}} - T_{\text{m}} }}{{\delta_{T} }} = h_{\text{o}} (T_{\text{b}} - T_{\text{m}} ). $$

It implies that the thickness of the boundary layer is given by

$$ \delta_{T} = \frac{k}{{h_{\text{o}} }} $$

(A8)

where k is the thermal conductivity in the liquid melt and $h_{\text{o}}$ is the heat transfer coefficient.

The solution of Eq. [A7] is

$$ \frac{{T - T_{\text{m}} }}{{T_{\text{b}} - T_{\text{m}} }} = \frac{\exp ( - vX/\alpha ) - 1.0}{{\exp ( - v\delta_{T} /\alpha ) - 1.0}}. $$

(A9)

The heat transfer flux at the interface (J _H) is given by

$$ J_{\text{H}} = \left. {k\frac{dT}{dX}} \right|_{X = 0} = (T_{\text{b}} - T_{\text{m}} )(kv/\alpha )\left. {\frac{\exp ( - vX/\alpha )}{{1 - \exp ( - v\delta_{T} /\alpha )}}} \right|_{X = 0} = (T_{\text{b}} - T_{\text{m}} )(kv/\alpha )\frac{1.0}{{1 - \exp ( - v\delta_{T} /\alpha )}}. $$

Putting the value of $\delta_{T}$ and $\alpha$,

$$ J_{\text{H}} = (T_{\text{b}} - T_{\text{m}} )(\lambda v/\alpha )\frac{1.0}{{1 - \exp ( - \rho Cpv/h_{\text{o}} )}}. $$

(A10)

Equation [A10] may be rewritten as

$$ J_{\text{H}} = h(T_{\text{b}} - T_{\text{m}} ) $$

(A11)

where h is the heat transfer coefficient for the moving boundary.

From Eqs. [A8], [A10], and [A11], the heat transfer coefficient for the moving boundary can be estimated from

$$ h = \frac{{\rho C_{\text{p}} v}}{{1 - \exp ( - \rho C_{\text{p}} v/h_{0} )}}. $$

(A12)

Heat and Mass Balance at the Interface

Heat balance at the interface is given as

$$ \rho \nu \Updelta H_{0} = \left[ {\left. {k\frac{\partial T}{\partial x}} \right|_{\text{interface}} - h(T_{\text{b}} - T_{\text{m}} )} \right]. $$

(A13)

On substituting the value of h from Eq. [A12], the above equation can be written as

$$ \rho \nu \Updelta H_{0} = \left[ {\left. {k\frac{\partial T}{\partial x}} \right|_{\text{interface}} - \frac{{\rho C_{\text{p}} \nu }}{{\left( {1 - \exp \left( { - \frac{{\rho C_{\text{p}} v}}{{h_{\text{o}} }}} \right)} \right)}}(T_{\text{b}} - T_{\text{m}} )} \right]. $$

(A14)

Mass balance of carbon at the interface is given by

$$ v(C_{\text{i}} - C_{\text{sc}} ) = \beta (C_{\text{i}} - C_{\text{b}} ). $$

(A15)

On substituting the value of β from Eq. [A6], the above equation becomes

$$ \nu = \beta_{\text{o}} \ln \left( {\frac{{C_{\text{i}} - C_{\text{sc}} }}{{C_{\text{b}} - C_{\text{sc}} }}} \right). $$

(A16)

Equations [A14] and [A16] are coupled together as

$$ \nu = \beta_{\text{o}} \ln \left( {\frac{{C_{\text{i}} - C_{\text{sc}} }}{{C_{\text{b}} - C_{\text{sc}} }}} \right) = \frac{1}{{\rho \Updelta H_{\text{o}} }}\left[ {\left. {k\frac{\partial T}{\partial x}} \right|_{\text{interface}} - \frac{{\rho C_{\text{p}} \nu }}{{\left( {1 - \exp \left( { - \frac{{\rho C_{\text{p}} v}}{{h_{\text{o}} }}} \right)} \right)}}\left( {T_{\text{b}} - T_{\text{m}} } \right)} \right]. $$

(A17)

Appendix B

Estimation of Heat Transfer Coefficient as a Function of Total Mixing Energy to the BOF Steelmaking System[25,26]

The following equations are used to estimate heat transfer coefficient as a function of total mixing energy to the BOF steelmaking system which is considered under combined influence of top lance, bottom stirring flow rate, and decarburization reaction.

$$ \begin{gathered} E_{t}^{0} = 6.32 \times 10^{ - 7} \cos \phi \frac{{Q_{t}^{3} M}}{{Wn^{2} d_{\text{t}}^{3} X}} \hfill \\ Q_{\text{decarb}} = \frac{d[C]}{dt}W\frac{{10^{6} \times 22.4 \times 60}}{12} \hfill \\ E_{\text{decarb}}^{0} = 6.18 \times \frac{{Q_{\text{decarb}} T_{\text{l}} }}{W}\left( {\ln \left[ {1 + \frac{{\rho g{\text{H}}h\_{\text{frac}}}}{{p_{\text{atm}} }}} \right] + \left[ {1 - \frac{{T_{0} }}{{T_{\text{l}} }}} \right]} \right) \hfill \\ E_{\text{b}}^{0} = 6.18 \times \frac{{Q_{\text{bottom}} T_{\text{l}} }}{W}\left( {\ln \left[ {1 + \frac{\rho gH}{{p_{\text{atm}} }}} \right] + \left[ {1 - \frac{{T_{\text{o}} }}{{T_{\text{l}} }}} \right]} \right) \hfill \\ E_{\text{total}}^{0} = E_{\text{top}}^{0} \times 0.10 + E_{\text{b}}^{0} + E_{\text{decarb}}^{0} \hfill \\ h = 5000\left( {7.0E_{\text{total}}^{0} } \right)^{0.20} \hfill \\ \end{gathered} $$

where $\phi$ is the angle of the lance tip from vertical, $Q_{\text{t}}$ is the oxygen flow rate, W is the weight of steel, n is the number of openings of the lance, X is the lance height above the metal bath during blowing, H is the bath depth, h_frac is the average depth fraction at which CO bubble formation takes place, $d_{\text{t}}$ is the throat diameter, $T_{\text{o}}$ is the temperature of the bottom stirring gas at input, $T_{\text{l}}$ is the average temperature of the liquid steel, $p_{\text{atm}}$ is the atmospheric pressure, and h is the heat transfer coefficient.

Process Conditions Used in Simulation

Lance angle = 14 deg Number of openings in lance = 6 Throat diameter = 2.46 cm Bath depth = 1.30 m

bottom stirring flow rate = 2 Nm3/min (first 30 pct and last 30 pct of the blow) blowing pattern is defined as follows: oxygen flow rate = 500 NM3/min if 0 < t < 180 seconds; Lance height = 2.20 m if 180 < t < 300 seconds; Lance height = 2.00 m if 300 < t < 400 seconds; Lance height = 1.80 m if t > 400 seconds; Lance height = 1.60

Appendix C: Artificial Neural Network

The concept of ANN originally comes from the mechanisms for information processing in the human brain system. ANN models have been applied to a wide range of complex metallurgical processes[27–30] and proved to be successful due to their ability to develop nonlinear relationships. ANNs are the mathematical patterns constructed by several neurons arranged in different layers interconnected through the complex networks. The layers are defined as input layer, output layer, and at least one hidden layer. A multilayer feed forward backpropagation ANN network has been used in the present work. The typical ANN topology is presented in Figure A1.

Fig. A1

Architecture of feed forward backpropagation ANN

The output of a neuron (k) in the network (y _k ) is the summation of all signals from a previous layer multiplied by weights (w _k,j ) and a bias (b _k ) which is activated by a transfer function (tanh sigmoid) in the following way:

$$ y_{k} = f\left( {\sum\limits_{j = 1}^{N} {\left( {w_{k,j} x_{j} } \right) + b_{k} } } \right)\;\;\;\;{\text{where}}\;f(z) = \frac{2}{1 - \exp ( - 2z)} - 1. $$

(A18)

The sum of the square of the errors (between the training output data and output data obtained using ANN) is minimized for getting the correct values of weights.