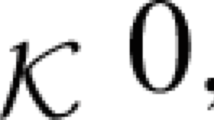1 Introduction

Interior-point algorithms (IPAs) provide an efficient tool for solving different optimization problems. Important references related to IPAs for solving linear programming (LP) problems are the monographs of Roos, Terlaky and Vial [30], Wright [36] and Ye [37]. IPAs have been also extended to LCPs, see [9, 10, 15,16,17, 20, 21]. Note that LCPs belong to the class of NP-complete problems [7]. In spite of this fact, Kojima et al. [21] showed that if the problem’s matrix possesses the \(P_*(\kappa )\)-property, then IPAs for LCPs have polynomial iteration complexity in the size of the problem, bit length of the data and in the parameter \(\kappa\). IPAs have been generalized to Cartesian symmetric cone linear complementarity problems (SCLCPs) in [23, 24] and Cartesian symmetric cone horizontal linear complementarity problems (SCHLCPs) in [4]. Anitescu et al. [1] showed the equivalence between different formulations of the LCPs. It should be mentioned that LP, convex quadratic optimization (CQO), LCPs, second-order cone optimization (SOCO), symmetric cone optimization (SCO) and semidefinite programming (SDP) problems can be formulated as special cases of SCHLCP. Mohammadi et al. [25] proposed an infeasible IPA taking full NT steps for solving SCHLCPs. In [3], the authors presented an IPA for solving Cartesian SCHLCP which uses the search directions proposed in [8]. Later on, Asadi et al. [2] proposed a new IPA for solving Cartesian SCHLCP which is based on a positive-asymptotic barrier function. In [5], a feasible IPA for solving \(P_*(\kappa )\)-SCHLCP using a wide neighbourhood of the central path was proposed.

The way we determine the search directions plays a crucial role in this paper. Note that there exist several approaches for defining search directions in case of IPAs. Peng et al. [27] introduced large-update IPAs for LP by using self-regular barriers. In [22], the authors provided a unified analysis of kernel-based IPAs for \(P_*(\kappa )\)-LCPs. Vieira [34] also proposed different IPAs for SCO problems that use kernel functions for determining search directions. Tunçel and Todd [33] gave a reparametrization of the central path system. Karimi et al. [19] dealt with entropy-based search directions for LP. Subsequently, Darvay introduced a new technique for determining search directions for LP problems [8]. This method has become known as algebraic equivalent transformation (AET) technique. In [28], different IPAs for LP, SCO and \(P_*(\kappa )\)-LCPs using the AET technique have been proposed. Haddou et al. [14] proposed a class of concave functions in the AET technique to define IPAs for solving monotone LCPs. However, they used other type of transformation of the central path system. In 2022, Illés et al. [18] introduced a new class of AET functions and they defined IPAs for \(P_*(\kappa )\)-LCPs. It needs to be mentioned that this new class differs from the class of concave functions proposed by Haddou et al. Moreover, there exist functions belonging to the new class of AET functions proposed by Illés et al. [18], for which the corresponding kernel functions are neither eligible, nor self-regular kernel functions.

The aim of this paper is to generalize the algorithms presented in [18] to Cartesian SCHLCP possessing the \(P_*(\kappa )\)-property. In addition, we propose a modification of the class of AET functions proposed in [18]. We also present the complexity analysis of the proposed IPA and we provide some technical lemmas that will be useful in the analysis. In [18], the authors gave a relationship between the parameters appearing in the definition of the class of AET functions in order to prove that the IPA is well defined. In this paper we prove that the IPA is well defined without any relationship between the parameters. Hence, we provide a wider class of AET functions. We prove that the derived iteration bound matches the best known iteration bounds for IPAs solving these types of problems.

The paper is organized in the following way. Section 2 contains the description of the Cartesian \(P_*(\kappa )\)-SCHLCP. In Sect. 3 we present the class of AET functions used in this paper and we give the generalization of the AET technique to Cartesian \(P_*(\kappa )\)-SCHLCP. In Sect. 4 the new IPA is defined for Cartesian \(P_*(\kappa )\)-SCHLCPs. Section 5 is devoted to the complexity analysis of the proposed IPA. In Sect. 6 we list several concluding remarks and the possible related future research topics. Appendix contains several results from the theory of Euclidean Jordan algebras and symmetric cones relevant for the analysis of the proposed IPA.

2 Cartesian \(P_*(\kappa )\)-symmetric cone horizontal linear complementarity problem and the central path

In the Appendix we provide a more detailed presentation of the theory of Euclidean Jordan algebras and symmetric cones. We denote by \(\mathcal {V}:=\mathcal {V}_1\times \mathcal {V}_2\times \cdots \times \mathcal {V}_m\) the Cartesian product space, where each space \(\mathcal {V}_{i}\) is a Euclidean Jordan algebra. The corresponding cone of squares is denoted by \(\mathcal {K}:=\mathcal {K}_1\times \mathcal {K}_2\times \cdots \times \mathcal {K}_m\), where each \(\mathcal {K}_i\) is the corresponding cone of squares of \(\mathcal {V}_{i}\). Let \(x=\left(x^{(1)},\,x^{(2)},\,\cdots ,\,x^{(m)}\right)^T\in \mathcal {V}\) and \(s=\left(s^{(1)},\,s^{(2)},\,\cdots ,\,s^{(m)}\right)^T\in \mathcal {V}\). The trace, the determinant and the minimal and maximal eigenvalues of the element x are given as

$$\begin{aligned} \textrm{tr}(x)=\sum _{i=1}^{m}\textrm{tr}\left( x^{{(i)}}\right) ,~~\det (x)=\prod _{i=1}^{m}\det \left( x^{{(i)}}\right) , ~~~~~~~~~~~~~~~~~~~~~~~\\ \lambda _{\min }(x)=\min _{1\le i \le m}\left\{ \lambda _{\min }\left( x^{{(i)}}\right) \right\} ,~~~\lambda _{\max }(x)=\max _{1\le i \le m}\left\{ \lambda _{\max }\left( x^{{(i)}}\right) \right\} .~~~ \end{aligned}$$

Furthermore,

$$\begin{aligned} x\circ s=\left(x^{(1)}\circ s^{(1)},\,x^{(2)}\circ s^{(2)},\,\cdots ,\,x^{(m)}\circ s^{(m)}\right)^{T},~~ \langle x,\,s\rangle =\sum _{i=1}^{m}\langle x^{(i)},\,s^{(i)}\rangle . \end{aligned}$$

The Lyapunov transformation and the quadratic representation of x is defined in the following way:

$$\begin{aligned} L(x)=\textrm{diag}\,\!\!\left(L(x^{(1)}),\,L(x^{(2)}),\,\cdots ,\,L\left( x^{(m)}\right) \right),\\ P(x)=\textrm{diag}\,\!\!\left(P(x^{(1)}),\,P(x^{(2)}),\,\cdots ,\,P\left( x^{(m)}\right) \right). \end{aligned}$$

The Frobenius norm of x is given as \(\left\Vert x \right\Vert _F=\left(\sum _{i=1}^{m}\left\Vert x^{(i)} \right\Vert ^2_F\right)^{1/2}\).

In the Cartesian SCHLCP a vector pair \((x,s) \in \mathcal {V}\times \mathcal {V}\) should be found which satisfies

$$\begin{aligned}{} & {} Qx+Rs = q, \quad \langle x,s \rangle = 0, \quad x \succeq _K 0, \quad s \succeq _K 0,\quad \quad \quad \quad (SCLCP) \end{aligned}$$

where \(q \in \mathcal {V}\), \(Q,R: \mathcal {V}\rightarrow \mathcal {V}\) are linear operators and \(\mathcal {K}\) is the symmetric cone of squares of the Cartesian product space \(\mathcal {V}\). Let \(\kappa \ge 0\). We say that the pair \(\left(Q,\,R\right)\) possesses the \(P_*(\kappa )\)-property if for all \((x,s)\in \mathcal {V}\times \mathcal {V}\)

$$\begin{aligned} Qx+Rs=0 ~~\text {implies}~~ (1+4\kappa )\sum _{i\in I_+}\langle x^{(i)},\,s^{(i)}\rangle +\sum _{i\in I_-}\langle x^{(i)},\,s^{(i)}\rangle \ge 0, \end{aligned}$$

where \(I_+=\{i~:~\langle x^{(i)},\,s^{(i)}\rangle >0\}\) and \(I_-=\{i~:~\langle x^{(i)},\,s^{(i)}\rangle <0\}\).

In developing our IPA we assume that the pair \(\left(Q,\,R\right)\) possesses the \(P_*(\kappa )\)-property and the interior-point condition (IPC) holds, which means that there exists \(( x^0, s^0)\), such that

$$\begin{aligned} Q x^0 + R s^0&=q, \\ x^0 \succ _ K 0, \; s^0 &\succ _K& 0.\quad \quad \quad \quad \qquad \qquad \qquad (IPC) \end{aligned} $$

The central path system is characterized by

$$\begin{aligned} \begin{aligned} Q x+ R s= & {} q,\qquad x \succeq _K 0,\\ x \circ s= & {} \mu e,\qquad s \succeq _K 0, \end{aligned} \end{aligned}$$
(1)

where \(\mu > 0\). It has been shown that if the pair \(\left(Q,\,R\right)\) possesses the \(P_*(\kappa )\)-property and the (IPC) holds, then system (1) has unique solution, for each \(\mu >0\), see [4] and [24].

For the strictly feasible \(x \in \text {int}\,\mathcal {K}\) and \(s \in \text {int}\,\mathcal {K}\) our aim is to find the search directions \((\Delta x, \Delta s)\) such that

$$\begin{aligned} \begin{aligned} Q \Delta x+ R \Delta s= & {} 0,~~~~~~~~~~\\ x \circ \Delta s + s \circ \Delta x= & {} \mu e - x \circ s, \end{aligned} \end{aligned}$$
(2)

where \(\mu > 0\). Note that system (2) does not necessarily have a unique solution, because in general, x and s do not operator commute. Hence, a scaling scheme is needed in order to fix this problem. In this paper, we deal with the Monteiro-Zhang [26] class of scaling schemes:

$$\begin{aligned} C(x,s)=\left\{ u|u \text { is invertible and } L(P(u)x) L(P(u)^{-1}s)=L(P(u)^{-1}s) L(P(u)x) \right\} . \end{aligned}$$

Faybusovich [13] generalized this to the symmetric cones case and Alizadeh and Schmieta further analysed this question [31]. The following lemma plays important role in the determination of the search directions.

Lemma 1

(Lemma 28 in [31]) Let \(u \in \text {int}\,\mathcal {K}.\) Then,

$$\begin{aligned} x \circ s = \mu e \quad \Leftrightarrow \quad P(u)x \circ P(u)^{-1}s=\mu e. \end{aligned}$$

Let \(u \in C(x,s)\), \(\widetilde{Q} = Q P(u)^{-1}\), \(\widetilde{R}=RP(u)\). In the paper we consider the NT-scaling scheme. Let \(u=w^{-\frac{1}{2}}\), where w is called the NT-scaling point of x and s:

$$\begin{aligned} w=P(x)^{\frac{1}{2}}\left( P(x)^{\frac{1}{2}}s\right) ^{-\frac{1}{2}} =P(s)^{-\frac{1}{2}}\left( P(s)^{\frac{1}{2}}x \right) ^{\frac{1}{2}}. \end{aligned}$$
(3)

By using Lemma 1, system (1) can be written as

$$\begin{aligned} \begin{aligned} \widetilde{Q}P(u) x+\widetilde{R} P(u)^{-1}s= & {} q, \qquad \quad P(u)x \succeq _K 0,\\ P(u)x \circ P(u)^{-1}s= & {} \mu e,\qquad P(u)^{-1}s \succeq _K 0. \end{aligned} \end{aligned}$$
(4)

System (4) has unique solution for each \(\mu >0\), if the (IPC) holds, see [4] and [24].

3 New class of AET functions for Cartesian \(P_*(\kappa )\)-SCHLCPs

In this section the generalization of the AET technique derived in [8] to \(P_*(\kappa )\)-SCHLCP is presented by using techniques and results in [2, 29]. Below we define a new class of AET functions that is a modification of the class of AET functions proposed in Definition 2.4 of [18]. The main difference is that only two conditions are used instead of three as it is the case in [18]. Furthermore, in [18], a relationship between the parameters appearing in the definition of the class of AET functions was given in order to prove that the IPA is well defined. In this paper we prove that the IPA is well defined without any relationship between the parameters.

Definition 1

Let \(\varphi :(\xi , \infty ) \rightarrow \mathbb {R}\) be a continuously differentiable, invertible function, such that \(\varphi '(t)> 0, \; \forall t> \xi\), where \(0 \le \xi <1\). All functions \(\varphi\) satisfying the following two conditions belong to the new class of AET functions. There exist two positive real numbers \(L_1 > 0\) and \(L_2 > 0\), such that the inequalities

$$\begin{aligned} \left| \frac{\varphi (1) - \varphi (t^2)}{2t \varphi '(t^2)}\right| \le L_1 \left| 1-t^2 \right| ,\quad \quad \quad \quad (AET1) \end{aligned}$$

and

$$\begin{gathered} 4t^{2} (\varphi (1) - \varphi (t^{2} ))\varphi ^{\prime}(t^{2} ) - L_{2} \left( {\varphi (1) - \varphi (t^{2} )} \right)^{2} \le 4t^{2} (1 - t^{2} )\left( {\varphi ^{\prime}(t^{2} )} \right)^{2} \hfill \\ \quad \le 4t^{2} (\varphi (1) - \varphi (t^{2} ))\varphi ^{\prime}(t^{2} ) + \left( {\varphi (1) - \varphi (t^{2} )} \right)^{2} \quad \quad \quad \quad (AET2) \hfill \\ \end{gathered}$$

hold for all \(t> \xi\).

Corollary 1

If condition (AET2) is satisfied, then there exists \(L_3 > 0\), such that

$$\begin{aligned} \left| 4 t^2 \varphi '(t^2) \left( (1-t^2) \varphi '(t^2) - \varphi (1) + \varphi (t^2) \right) \right| \le L_3 \left( \varphi (1) - \varphi (t^2) \right) ^2,\quad \quad \quad \quad (AET2b) \end{aligned}$$

for all \(t>\xi\).

Proof

Suppose that (AET2) holds and let \(L_3 = \max \{1,L_2\}\). Then, the inequality (AET2b) is also satisfied. \(\square\)

Consider the continuously differentiable function \(\varphi :(\xi , \infty ) \rightarrow \mathbb {R}\) satisfying (AET1) and (AET2). Let \(x = \sum _{i=1}^{r}\lambda _i(x)c_i\), where \(\{c_1,\ldots ,c_r\}\) is the corresponding Jordan frame. We define the function \(\varphi\) for the elements of the Euclidean Jordan algebra in the following way

$$\begin{aligned} \varphi (x):=\varphi (\lambda _1(x))c_1+\ldots +\varphi (\lambda _r(x))c_r. \end{aligned}$$
(5)

In this way, (4) can be written as follows:

$$\begin{aligned} \begin{aligned} \widetilde{Q}P(u) x+\widetilde{R} P(u)^{-1}s= & {} q,\qquad \quad P(u)x \succeq _K 0,\\ \varphi \left( \frac{P(u)x \circ P(u)^{-1}s}{\mu } \right)= & {} \varphi (e),\qquad P(u)^{-1}s \succeq _K 0. \end{aligned} \end{aligned}$$
(6)

To determine the search directions we use the method given in [29, 35]. For the strictly feasible \(x \in \text {int}\, K\) and \(s \in \text {int}\, K\) our aim is to find the search directions \((\Delta x, \Delta s)\) that satisfy the system

$$\begin{aligned} \begin{aligned} \widetilde{Q}P(u) \Delta x+\widetilde{R} P(u)^{-1} \Delta s= & {} 0,\qquad \quad P(u)x \succeq _K 0,\\ P(u)x \circ P(u)^{-1} \Delta s + P(u)^{-1} s \circ P(u) \Delta x= & {} a_{\varphi },\qquad P(u)^{-1}s \succeq _K 0, \end{aligned} \end{aligned}$$
(7)

where

$$\begin{aligned} a_{\varphi } = \mu \left( \varphi ' \left( \frac{P(u)x \circ P(u)^{-1}s}{\mu } \right) ^{-1} \right) \circ \left( \varphi (e)-\varphi \left( \frac{P(u)x \circ P(u)^{-1}s}{\mu } \right) \right) , \end{aligned}$$

and \(\varphi\) belongs to the class given in Definition 1.

We use the following notations:

$$\begin{aligned} v:=\frac{P(w)^{-\frac{1}{2}}x}{\sqrt{\mu }} = \frac{P(w)^{\frac{1}{2}}s}{\sqrt{\mu }}, \quad d_x:=\frac{P(w)^{-\frac{1}{2}} \Delta x}{\sqrt{\mu }}, \quad d_s:=\frac{P(w)^{\frac{1}{2}} \Delta s}{\sqrt{\mu }}, \end{aligned}$$
(8)

where w is the NT-scaling point defined in (3). From (8) we obtain the scaled system

$$\begin{aligned} \begin{aligned} \sqrt{\mu } Q P(w)^{\frac{1}{2}} d_x + \sqrt{\mu } R P(w)^{-\frac{1}{2}} d_s= & {} 0,\\ d_x+d_s= & {} p_v, \end{aligned} \end{aligned}$$
(9)

where

$$\begin{aligned} p_v = v^{-1} \circ (\varphi '(v \circ v))^{-1} \circ (\varphi (e)-\varphi (v \circ v)). \end{aligned}$$
(10)

If we define the function \(f:(\xi ,\infty ) \rightarrow \mathbb {R}\)

$$\begin{aligned} f(t) = \frac{\varphi (1) - \varphi (t^2)}{t(\varphi '(t^2))}, \end{aligned}$$
(11)

then the conditions presented in Definition 1 can be written in the following form.

Proposition 1

The conditions (AET1) and (AET2) can be formulated in the following equivalent form. There exist \(L_1 > 0\) and \(L_2 > 0\) such that the inequalities

$$\begin{aligned} \left| f(t) \right|&\le 2L_1 \left| 1-t^2 \right| ,\quad \quad \quad \quad (AETa)\\ -L_2 \frac{f(t)^2}{4}&\le 1-t^2-t f(t) \le \frac{f(t)^2}{4},\quad \quad \quad \quad (AETb) \end{aligned}$$

hold for all \(t> \xi\).

Corollary 2

If condition (AETb) is satisfied, then there exists \(L_3 > 0\) such that

$$\begin{aligned} |1-t^2-tf(t)| \le L_3 \frac{f(t)^2}{4}\quad \quad \quad \quad (AETb2) \end{aligned}$$

holds for all \(t> \xi\).

Proof

Suppose that (AETb) holds and let \(L_3 = \max \{1,L_2\}\). Then the inequality (AETb2) is also satisfied. \(\square\)

It needs to be mentioned that most of the functions used in the literature belong to the new class of AET functions, in particular the AET functions used in [8, 11, 20]. The intervals on which the functions \(\varphi\) are defined are important in this approach. For example, \(\varphi (t)=t\) belongs to this new class of AET functions only if it is defined on a \((\xi ,\infty )\) interval, where \(\xi\) is strictly positive.

Now, we present the class of AET functions proposed in [18] for determining search directions in case of IPAs for solving \(P_*(\kappa )\)-LCPs.

Definition 2

(Definition 2.4 in [18]) Let \(\varphi :(\xi , \infty ) \rightarrow \mathbb {R}\) be a continuously differentiable, invertible function, such that \(\varphi '(t)> 0, \; \forall t> \xi\), where \(0 \le \xi <1\). All functions \(\varphi\) satisfying the conditions

  1. AETi.

    \(\exists \; \bar{c}_1 > 0\), such that

    $$\begin{aligned} \left| \frac{\varphi (1) - \varphi (t^2)}{2t(1-t^2)\varphi '(t^2)} \right| \le \bar{c}_1, \end{aligned}$$

    for all \(t>\xi\).

  2. AETii.

    \(\exists \; \bar{c}_2 > 0\), such that

    $$\begin{aligned} \left| \frac{4 t^2 \varphi '(t^2) \left[ (1-t^2) \varphi '(t^2) - \varphi (1) + \varphi (t^2) \right] }{(\varphi (1)-\varphi (t^2))^2} \right| \le \bar{c}_2, \end{aligned}$$

    for all \(t>\xi\).

  3. AETiii.

    \(\exists \; \bar{c}_3 > 0\) such that the inequality

    $$\begin{aligned}{} & {} 4t^2(\varphi (1)-\varphi (t^2)) \varphi '(t^2) - \bar{c}_3 \left( \varphi (1) - \varphi (t^2) \right) ^2 \le 4t^2 (1-t^2) \left( \varphi '(t^2) \right) ^2 \\\le & {} 4t^2(\varphi (1)-\varphi (t^2)) \varphi '(t^2) + \left( \varphi (1) - \varphi (t^2) \right) ^2 \end{aligned}$$

    holds for all \(t> \xi\),

belong to the class of AET functions.

It can be seen that Definition 1 is a modification of Definition 2.4 in [18].

Remark 1

Note that parameter \(L_1\) from Definition 1 corresponds to \(\bar{c}_1\) from Definition 2. Furthermore, \(L_2\) corresponds to \(\bar{c}_3\) from Definition 2 and \(L_3\) from Corollary 1 corresponds to \(\bar{c}_2\) from Definition 2. Hence, in this paper we modify the conditions proposed in [18] in the sense that we delete condition (AETii) from Definition 2 and we prove that it holds in Corollary 1.

Remark 2

In [18] the complexity analysis of the proposed IPA is presented for \(\bar{c_2} > \frac{1}{2}\), \(\bar{c}_1 < \frac{100\bar{c}_2-4}{41\bar{c}_2+50}\) and \(\bar{c}_3 < 16\bar{c}_2^2-1\). In this paper we generalize the primal-dual IPA proposed in [18] to \(P_*(\kappa )\)-horizontal LCPs over Cartesian product of symmetric cones. However, we prove that the IPA is well defined without any relationship between the parameters. Hence, we provide a wider class of functions in the sense, that the complexity analysis of the IPA in this paper works for a wider class of parameters.

Example 1

If we take \(\varphi (t)=t\), then due to condition \(\bar{c}_1 < \frac{100\bar{c}_2-4}{41\bar{c}_2+50}\) given in [18], the function \(\varphi (t) = t\) defined on \((\xi ,\infty )\), where \(\xi > 0.205\) belongs to the class of AET function proposed in Definition 2. This follows from condition (AETi) of Definition 2, where \(\xi\) can be chosen as \(\xi = \frac{1}{2\bar{c}_1} > \frac{41}{200} = 0.205\). However, in this paper we do not have any relationship between the parameters, hence \(\varphi (t)=t\) defined on \((\xi ,\infty )\), where \(\xi > 0\) belongs to the class of AET functions given in Definition 1. Therefore, we consider a wider class of functions than the one used in [18].

The class of AET functions can be compared to the class of eligible kernel functions and self-regular functions, see [6, 27]. Lešaja et al. [23] presented IPAs for \(P_*(\kappa )\)-LCPs over symmetric cones based on eligible kernel functions. A detailed description about the comparison of the class of AET functions given in Definition 1 to the class of eligible kernel and self-regular functions is provided in [18].

4 Interior-point algorithm for solving Cartesian \(P_*(\kappa )\)-SCHLCPs

In this section, we present a generic IPA based on the new class of AET functions given in Definition 1. The proximity measure to the central path is defined as

$$\begin{aligned} \delta (v)= \delta (x,s;\mu ) := \frac{\Vert p_v\Vert _F}{2} . \end{aligned}$$
(12)

The \(\tau\)-neighbourhood of a fixed point on the central path is given by

$$\begin{aligned} \mathcal {N}(\tau ,\mu ):= \{(x,s) \in \mathcal {V}\times \mathcal {V}: Qx+Rs = q, \; x \succeq _K 0, \; s \succeq _K 0: \; \delta (x,s;\mu ) \le \tau \}, \end{aligned}$$

where \(\mu >0\) is fixed and \(\tau\) is a threshold parameter.

We determine the search directions using system (9) with functions \(\varphi\) satisfying (AET1) and (AET2).

We can calculate the search directions \(\Delta x\) and \(\Delta s\) from

$$\begin{aligned} \Delta x = \sqrt{\mu } P(w)^{\frac{1}{2}} d_x, \quad \Delta s = \sqrt{\mu } P(w)^{-\frac{1}{2}} d_s. \end{aligned}$$
(13)

Let \(x^{+}=x+ \Delta x\) and \(s^{+}=s + \Delta s\) be the point after a full NT-step.

Our IPA starts with \((x^0,s^0) \in \mathcal {N}(\tau ,\mu )\).

In Algorithm 4.1 we present a generic IPA for solving Cartesian \(P_*(\kappa )\)-SCHLCP based on the new class of AET functions given in Definition 1.

figure a

The next section is devoted to the complexity analysis of the proposed IPA.

5 Analysis of Algorithm 4.1

In the first part of this section we provide technical lemmas that are necessary for the analysis of the IPA. Let

$$\begin{aligned} q_v=d_x-d_s, \end{aligned}$$
(14)

hence

$$\begin{aligned} d_x =\frac{p_v+q_v}{2},~~ d_s =\frac{p_v-q_v}{2},~~~d_x \circ d_s=\frac{p_v^2-q_v^2}{4}. \end{aligned}$$
(15)

In Lemma 2 we get an upper bound for \(\left\Vert q_v \right\Vert _F\) in terms of \(\left\Vert p_v \right\Vert _F\).

Lemma 2

(Lemma 5.1 in [2])We have \(~\left\Vert q_v \right\Vert _F\le \sqrt{1+4\kappa }~\left\Vert p_v \right\Vert _F\).

Let \(x,\,s\in \text {int}\;\mathcal {K}\), \(\mu >0\) and w be the scaling point of x and s. Consider

$$\begin{aligned} x(\alpha ) = x+ \alpha \Delta x, \qquad s(\alpha ) = s + \alpha \Delta s, \end{aligned}$$
(16)

where \(0\le \alpha \le 1.\) We have

$$\begin{aligned} \begin{array}{ccc}x^+:= x(1)=x+\Delta x=\sqrt{\mu }P(w)^{1/2}(v+d_x),~\\ s^+:=s(1)=s+\Delta s=\sqrt{\mu }P(w)^{-1/2}(v+d_s).\end{array} \end{aligned}$$
(17)

Note that \(x^+, s^+ \in \text {int}\;\mathcal {K}\) if and only if \(v+d_x, v+d_s \in \text {int}\;\mathcal {K}\). This follows from the fact that \(P(w)^{1/2}\) and \(P(w)^{-1/2}\) are automorphisms of \(\text {int}\;\mathcal {K}\), see Proposition 2 part (ii) from Appendix. Using (17) we have

$$\begin{aligned} x^+ \circ s^+ = \mu (v+d_x) \circ (v+d_s). \end{aligned}$$
(18)

The next lemma is a technical one which will be used when we prove the strict feasibility of the full-NT step.

Lemma 3

[cf. Lemma 4.1 of [35]] Let \(x=x(0) \in int \; \mathcal {K}\), \(s=s(0)\in int \; \mathcal {K}\) and for \(0\le \alpha \le \bar{\alpha }\), \(x(\alpha )\circ s(\alpha )\in\) int \(\mathcal {K}\). Then, we have \(x(\bar{\alpha })\in int \; \mathcal {K}~\text {and}~ s(\bar{\alpha })\in int \; \mathcal {K}\).

In the following lemma the strict feasibility of the full NT-step is proven.

Lemma 4

Let \(x \succ _K 0\), \(s \succ _K 0\) and \(\delta :=\delta (x,s;\mu )<\frac{1}{\sqrt{1+4\kappa }}\) and suppose that \(\lambda _{\min } \left( v \right) >\xi\). For any function satisfying (AET2), after a full-NT step we have \(x^+ \succ _K 0\) and \(s^+ \succ _K 0\).

Proof

For \(0\le \alpha \le 1\), let

$$\begin{aligned} v_x(\alpha ):=v+\alpha d_x~~ \text {and}~~ v_s(\alpha ):=v+\alpha d_s. \end{aligned}$$

From the second equation of the system (9), we get

$$\begin{aligned} v_x(\alpha )\circ v_s(\alpha )=\; & {} v^2+\alpha v\circ (d_x+d_s)+\alpha ^2(d_x\circ d_s)\nonumber \\= \;& {} (1-\alpha )v^2+\alpha \left(v^2+v\circ p_v\right)+\alpha ^2\frac{p_v^{2}{- } q_v^{2}}{4}\nonumber \\=\; & {} (1-\alpha )v^2+\alpha \left(v^2+v\circ p_v-e+\frac{p_v^2}{4}\right)\nonumber \\+ & {} \alpha \left(e-(1-\alpha )\frac{p_v^2}{4}-\alpha \frac{q_v^2}{4}\right). \end{aligned}$$
(19)

The right hand side of (AET2) of Proposition 1 yields \(v^2+v\circ p_v-e+\frac{p_v^2}{4} \in \mathcal {K}\). Using Lemma 2 we have:

$$\begin{aligned} \left\Vert (1-\alpha )\frac{p_v^{2}}{4}+\alpha \frac{q_v^{2}}{4} \right\Vert _F\le \;& {} (1-\alpha )\left\Vert \frac{p_v^2}{4} \right\Vert _F+\alpha \left\Vert \frac{q_v^2}{4} \right\Vert _F\le \;(1-\alpha )\frac{\left\Vert p_v \right\Vert ^2_F}{4}+\alpha \frac{\left\Vert q_v \right\Vert ^2_F}{4}\nonumber \\ {}\le & {} (1-\alpha )\frac{\left\Vert p_v \right\Vert ^2_F}{4} +\alpha (1+4\kappa ) \frac{\left\Vert p_v \right\Vert ^2_F}{4} \nonumber \\=\; & {} ((1-\alpha )+\alpha (1+4\kappa ))\delta ^2=(1+4\alpha \kappa )\delta ^2\nonumber \\\le\; & {} (1+4\kappa )\delta ^2. \end{aligned}$$
(20)

Using (20) and the assumption \(\delta <\frac{1}{\sqrt{1+4\kappa }}\) we obtain

$$\begin{aligned} \left\Vert (1-\alpha )\frac{p_v^{2}}{4}+\alpha \frac{q_v^{2}}{4} \right\Vert _F<1. \end{aligned}$$

Lemma 12 from Appendix implies

$$\begin{aligned} e-(1-\alpha )\frac{p_v^{2}}{4}-\alpha \frac{q_v^{2}}{4} \in \text{ int } \mathcal {K}. \end{aligned}$$
(21)

We know that \((1-\alpha )v^2 \in \text{ int } \mathcal {K}\) for \(0 \le \alpha <1\). Using (19) we get that \(v_x(\alpha )\circ v_s(\alpha )\in \text{ int } \mathcal {K}\), for \(\alpha \in [0,1]\). If we substitute \(\alpha =1\) in Lemma 3, we obtain \(v+d_x\in \text{ int } \mathcal {K}\) and \(v+d_s\in \text{ int } \mathcal {K}\). Using (17) and Proposition 2, part (ii) from Appendix, the proof of the lemma follows. \(\square\)

The following lemma will be used later in the complexity analysis of the IPA.

Lemma 5

Let \(\bar{f}:{(\bar{d},+\infty )}\rightarrow \mathbb {R}_+\) be a function, where \(\bar{d} > 0\) and \(|\bar{f}(t)|\le \bar{k} \left| 1-t^2 \right|\), for \(t > \bar{d}\) and \(\bar{k}>0\). Assume that \(v\in \mathcal {V}\). Then,

$$\begin{aligned} \left\Vert \bar{f}(v) \right\Vert _F\le \bar{k} \left\Vert e-v^2 \right\Vert _F {.} \end{aligned}$$

Proof

Using Theorem 2 from Appendix, we assume that \(v=\sum _{i=1}^{r} \lambda _i(v) c_i\). Then, \(\bar{f}(v)=\sum _{i=1}^r \bar{f}(\lambda _i(v))c_i\) and we have

$$\begin{aligned} \left\Vert \bar{f}(v) \right\Vert _F = \sqrt{\sum _{i=1}^{r} \left( \bar{f}(\lambda _i(v))\right) ^2} \le \bar{k} \sqrt{\sum _{i=1}^{r} \left( \lambda _i(e-v^2)\right) ^2} = \bar{k} \left\Vert e-v^2 \right\Vert _F {,} \end{aligned}$$

which gives the result. \(\square\)

Assume that \(x^+\) and \(s^+\) are the iterates after taking a full-NT step, and \(w^+\) is their corresponding NT scaling point. The v-vector after a ful-NT step is given by

$$\begin{aligned} \bar{v}:=\frac{P(w^+)^{-1/2}x^+}{\sqrt{\mu }}~~\left[=\frac{P(w^+)^{1/2}s^+}{\sqrt{\mu }}\right]. \end{aligned}$$
(22)

Lemma 6 gives an upper bound for the proximity measure after a full-NT step.

Lemma 6

Let \((x,s) \in {\mathcal {F}}^+\), where \({\mathcal{F}}^+\) is the set of strictly feasible solutions and suppose that \(\delta := \delta (x,s;\mu ) < \sqrt{\frac{1-\xi ^2}{1+4\kappa }}\) and \(\lambda _{\min } \left( v \right) >\xi\). For any function \(\varphi\) satisfying (AET1) and (AET2), we show that after a full-NT step we have \(\lambda _{\min } \left( \bar{v} \right) >\xi\) and

$$\begin{aligned} \delta (x^+,s^+;\mu ) \le L_1 (L_3 + 2 + 4\kappa )\delta (x,s;\mu )^2, \end{aligned}$$

where \(L_1 >0\), \(L_2 >0\) and \(L_3 = \max \{1,L_2\}.\)

Proof

By using the proof of Lemma 5.6 in [2] and the right hand side of condition (AETb), we get

$$\begin{aligned} \lambda _{\min } \left( \bar{v} \right) \ge \sqrt{1 - (1 + 4 \kappa ) \delta ^2}. \end{aligned}$$

From this and \(\delta < \sqrt{\frac{1-\xi ^2}{1+4\kappa }}\), we obtain \(\lambda _{\min } \left( \bar{v} \right) >\xi\). Using (12) we have

$$\begin{aligned} \delta (x^+,s^+;\mu ) := \frac{\Vert p_{\bar{v}}\Vert _F}{2} = \frac{\left\| f(\bar{v})\right\| _F}{2}, \end{aligned}$$
(23)

where the function f is given as in (5) using (11). Using (AETa) of Proposition 1 and Lemma 5 we get

$$\begin{aligned} \delta (x^+,s^+;\mu ) \le L_1 \left\| e-\bar{v}^2\right\| _F. \end{aligned}$$
(24)

Substituting \(\alpha =1\) in (19), we get

$$\begin{aligned} \begin{aligned} \left\| e - \bar{v}^2\right\| _F&= \left\| e-v^2 - v \circ p_v - \dfrac{p_v^2}{4} + \dfrac{q_v^2}{4}\right\| _F. \\ \end{aligned} \end{aligned}$$
(25)

From condition (AETb) of Proposition 1 we obtain that condition (AETb2) of Corollary 2 also holds. Using this, (25) and Lemmas 2 and 5 we get

$$\begin{aligned} \left\| e - \bar{v}^2\right\| _F\le & {} \left\| e - v^2 - v \circ p_v\right\| _F + \left\| \frac{p_v^2}{4}\right\| _F + \left\| \frac{q_v^2}{4}\right\| _F \nonumber \\\le & {} (2 + L_3 + 4\kappa ) \delta ^2. \end{aligned}$$
(26)

From (24) and (26) we have

$$\begin{aligned} \delta (x^+,s^+;\mu ) \le L_1 (L_3 + 2 + 4\kappa )\delta (x,s;\mu )^2, \end{aligned}$$

and the lemma is proven. \(\square\)

Lemma 7

(Lemma 5.7 in [2]) Let \(d_x\) and \(d_s\) be the solutions of the system (9) with \(p_v\) defined as in (10), and \(\delta :=\delta (x,s; \mu )\). Then \(\left\langle d_x,d_s\right\rangle \le \delta ^2\).

We provide an upper bound for the duality gap after a full-NT step.

Lemma 8

Let \(\delta =\delta (x,s; \mu )\) and \(x^+\) and \(s^+\) be obtained after a full NT-step. For any function \(\varphi\) satisfying (AET2) of Definition 1 with \(L_2 >0\), we have

$$\begin{aligned} \langle x^+, s^+ \rangle \le \mu \left( r + (L_2 +1)\delta ^2\right) . \end{aligned}$$

Proof

In the proof only the left hand side of (AETb) from Proposition 1 will be used, namely

$$\begin{aligned} t f(t) - L_2 \frac{f(t)^2}{4} \le 1-t^2, \quad t > \xi , \end{aligned}$$
(27)

where \(L_2 > 0\). Using Corollary 2 we have that condition (AETb2) is also satisfied. Using this, (18), (19) and (27) we get

$$\begin{aligned} \dfrac{1}{\mu } x^+ \circ s^+ = v^2 + v \circ p_v +d_x \circ d_s \preceq _K e + \frac{L_2}{4} p_v^2 + d_x \circ d_s. \end{aligned}$$
(28)

Using (28) and Lemma 7 we have

$$\begin{aligned} \langle x^+, s^+ \rangle= \;& {} \langle e, x^+ \circ s^+ \rangle \le \mu \langle e, e + \frac{L_2}{4} p_v^2 + d_x \circ d_s \rangle \nonumber \\\le\; & {} \mu \left( r + L_2 \delta ^2 + \langle d_x, d_s \rangle \right) \le \mu \left( r + (L_2+1)\delta ^2\right) , \end{aligned}$$
(29)

and the proof is complete. \(\square\)

The next lemma explains the effect of a \(\mu\)-update on the proximity of the new iterates to the central path.

Lemma 9

Suppose that \(\delta := \delta (x,s;\mu ) < \sqrt{\frac{1-\xi ^2}{1+4\kappa }}\), \(\lambda _{\min } \left( v \right) >\xi\) and \(\mu ^+ = (1-\theta )\mu\). Let \(v^+ = \frac{\bar{v}}{\sqrt{1-\theta }}\) be the scaled vector v after the full-NT step and the \(\mu\)-update. For any function \(\varphi\) satisfying (AET1) and (AET2) with \(L_1 > 0\), \(L_2 > 0\), we have \(\lambda _{\min } \left( v^+ \right) >\xi\) and

$$\begin{aligned} \delta (x^+,s^+;\mu ^+) \le \frac{L_1}{1-\theta } \left( \theta \sqrt{r} + (L_3+2+ 4\kappa ) \delta ^2 \right) , \end{aligned}$$

where \(L_3 = \max \{1,L_2\}.\)

Proof

Using Lemma 6 we have \(\lambda _{\min } \left( \bar{v} \right) >\xi\). From this and \(0< \theta < 1\) we obtain \(\lambda _{\min } \left( v^+ \right) >\xi\). From (12) we get

$$\begin{aligned} \delta (x^+,s^+;\mu ^+)&= \frac{\left\| f\left( v^+\right) \right\| _F}{2}. \end{aligned}$$

Using condition (AETa) of Proposition 1 and Lemma 5, we have

$$\begin{aligned} \delta (x^+,s^+;\mu ^+) \le L_1 \left\| e-\left( v^{+}\right) {^2}\right\| _F. \end{aligned}$$
(30)

Using (18) and (19) we get

$$\begin{aligned} \left\| e - (v^+)^2\right\| _F= \;& {} \left\| e - \dfrac{x^+ \circ s^+}{(1-\theta )\mu }\right\| _F \nonumber \\ {}= \;& {} \left\| e-\dfrac{1}{1-\theta }\left( v^2 + v \circ p_v+ \dfrac{p_v^2}{4} - \dfrac{q_v^2}{4}\right) \right\| _F \nonumber \\=\; & {} \dfrac{1}{1-\theta }\left\| -\theta e+e - v^2 - v \circ p_v - \dfrac{p_v^2}{4} + \dfrac{q_v^2}{4}\right\| _F. \end{aligned}$$
(31)

From (30), (31), condition (AETb) of Proposition 1 and Lemma 5 we obtain

$$\begin{aligned} \delta (x^+,s^+;\mu ^+)\le & {} \frac{L_1}{1-\theta } \left( \left\| \theta e \right\| _F + \left\| e-v^2 -v \circ p_v \right\| _F + \left\| \dfrac{p_v^2}{4}\right\| _F + \left\| \dfrac{q_v^2}{4}\right\| _F \right) \nonumber \\ {}\le & {} \frac{L_1}{1-\theta } \left( \theta \sqrt{r} + (L_3+2+ 4\kappa ) \delta ^2 \right) , \end{aligned}$$
(32)

and the lemma is proven. \(\square\)

We will set the values of the parameters \(\theta\) and \(\tau\) and we show that for these values the IPA using the new class of AET functions is well defined.

Lemma 10

Assume that \(\varphi : (\xi ,\infty ) \rightarrow \mathbb {R}\) satisfies (AET1) and (AET2). Consider \(L_4=\max \{L_1,\frac{1}{4}\}\), \(\tau =\frac{\sqrt{1-\xi ^2}}{4L_4 (L_3+2+4\kappa )}\), \(\theta = \frac{\sqrt{1-\xi ^2}}{16L_4^2(L_3+2+4\kappa )\sqrt{r}}\). Assume also that \(\delta (x,s;\mu ) \le \tau\). Then, we have

$$\begin{aligned} \delta (x^+,s^+;\mu ^+) \le \tau , \end{aligned}$$

hence the IPA defined in Algorithm 4.1 is well defined.

Proof

By using \(\kappa \ge 0\), \(L_4=\max \{L_1,\frac{1}{4}\}\) and \(L_3=\max \{1, L_2\}\), we have \(\tau =\frac{\sqrt{1-\xi ^2}}{4L_4 (L_3+2+4\kappa )}< \frac{1}{\sqrt{1+4 \kappa }}.\) Using this and the assumption conditions (AET1) and (AET2), from Lemma 4 we get that \((x^{+},s^{+}) \in {\mathcal {F}}^+\), where \({\mathcal{F}}^+\) is the set of strictly feasible solutions.

By using Lemma 9 and \(L_1 \le L_4\), we have

$$\begin{aligned} \delta (x^+,s^+;\mu ^+)\le & {} \frac{L_4}{1-\theta } \left( \theta \sqrt{r} + (L_3+2+ 4\kappa ) \delta ^2 \right) . \end{aligned}$$
(33)

From \(\kappa \ge 0\), \(r \ge 1\), \(L_4=\max \{L_1,\frac{1}{4}\}\) and \(L_3=\max \{1, L_2\}\) we conclude that \(\theta = \frac{\sqrt{1-\xi ^2}}{16L_4^2(L_3+2+4\kappa )\sqrt{r}} \le \frac{1}{2}\) and \(\frac{1}{1-\theta } \le 2\). Using this and the values of \(\tau\) and \(\theta\) we have

$$\begin{aligned} \frac{L_4 \theta \sqrt{r}}{1-\theta } \le \frac{2 L_4\sqrt{1-\xi ^2}}{16L_4^2(L_3+2+4\kappa )} \le \frac{1}{2} \tau . \end{aligned}$$
(34)

Furthermore, from \(\frac{1}{1-\theta } \le 2\) and \(\tau =\frac{\sqrt{1-\xi ^2}}{4L_4(L_3+2+4\kappa )}\) we obtain

$$\begin{aligned} \frac{L_4 (L_3+2+4\kappa )\delta ^2}{1-\theta } \le 2L_4(L_3+2+4\kappa ) \frac{1-\xi ^2}{16L_4^2(L_3+2+4\kappa )^2} \le \frac{1}{2} \tau . \end{aligned}$$
(35)

From (33), (34) and (35) we obtain

$$\begin{aligned} \delta (x^+,s^+;\mu ^+) \le \tau , \end{aligned}$$
(36)

proving the lemma \(\square\)

The following lemma gives upper bound on the number of iterations.

Lemma 11

Assume that \(\varphi : (\xi ,\infty ) \rightarrow \mathbb {R}\) satisfies (AET1) and (AET2). Consider \(L_4=\max \{L_1,\frac{1}{4}\}\), \(\tau =\frac{\sqrt{1-\xi ^2}}{4L_4 (L_3+2+4\kappa )}\), \(L_3=\max \{L_2,1\}\) and \(\theta = \frac{\sqrt{1-\xi ^2}}{16L_4^2(L_3+2+4\kappa )\sqrt{r}}\). We assume that the pair \((x^0,s^0)\) is strictly feasible, \(\mu ^0 = \frac{\langle x^0, s^0 \rangle }{r}\) and \(\delta (x^0,s^0;\mu ^0) \le \tau\). Let \(x^k\) and \(s^k\) be the \(k\)-th iteration of Algorithm 4.1. Then, for

$$\begin{aligned} k \ge \Bigg \lceil \dfrac{1}{\theta }\log {\dfrac{\mu ^0\left( r + \frac{L_2+1}{9}\right) }{\varepsilon }}\Bigg \rceil \end{aligned}$$

we have \(\langle x^k, s^k \rangle < \varepsilon\).

Proof

By using \(L_3=\max \{L_2,1\}\), \(\kappa \ge 0\), we have

$$\begin{aligned} \tau < \frac{1}{4L_4(L_3+2+4\kappa )} \le \frac{1}{3}. \end{aligned}$$
(37)

From (37) and Lemma 8 we have

$$\begin{aligned} \langle x^k, s^k \rangle\le & {} \mu ^k\left( r + \frac{L_2+1}{9} \right) = (1-\theta )^k \mu ^0\left( r + \frac{L_2+1}{9}\right) . \end{aligned}$$

The condition \(\langle x^k, s^k \rangle < \varepsilon\) holds if

$$\begin{aligned} (1-\theta )^k\mu ^0\left( r + \frac{L_2+1}{9}\right) < \varepsilon . \end{aligned}$$
(38)

We take the logarithm of both sides of (38) and we get

$$\begin{aligned} k\log {(1-\theta )}+\log {\left( \mu ^0\left( r + \frac{L_2+1}{9}\right) \right) } < \log {\varepsilon }. \end{aligned}$$
(39)

From \(-\log {(1-\theta )} \ge \theta\) we have that (39) holds if

$$\begin{aligned}k\theta \ge \log {\left( \mu ^0\left( r + \frac{L_2+1}{9}\right) \right) } - \log {\varepsilon } = \log {\dfrac{\mu ^0(r + \frac{L_2+1}{9})}{\varepsilon }}, \end{aligned}$$

which proves the lemma. \(\square\)

The results in this section are summarized in the following main theorem.

Theorem 1

Assume that \(\varphi : (\xi ,\infty ) \rightarrow \mathbb {R}\) satisfies (AET1) and (AET2). Consider \(L_4=\max \{L_1,\frac{1}{4}\}\), \(\tau =\frac{\sqrt{1-\xi ^2}}{4L_4 (L_3+2+4\kappa )}\), \(L_3=\max \{L_2,1\}\) and \(\theta = \frac{\sqrt{1-\xi ^2}}{16L_4^2(L_3+2+4\kappa )\sqrt{r}}\). We assume that the pair \((x^0,s^0)\) is strictly feasible, \(\mu ^0 = \frac{\langle x^0, s^0 \rangle }{r}\) and \(\delta (x^0,s^0;\mu ^0) \le \tau\). Then, the IPA given in Algorithm 4.1 requires no more than

$$\begin{aligned} \Bigg \lceil \frac{16L_4^2(L_3+2+4\kappa )}{\sqrt{1-\xi ^2}} \sqrt{r} \log {\dfrac{\mu ^0\left( r + \frac{L_2+1}{9}\right) }{\varepsilon }}\Bigg \rceil \end{aligned}$$

interior-point iterations.

6 Concluding remarks

In this paper, we generalized a full-NT step feasible IPA proposed in [18] to Cartesian \(P_*(\kappa )\)-horizontal LCPs. We also extended and modified the class of AET functions defined in [18] to a new class of AET functions defined in Definition 1 and applied it to the Cartesian \(P_*(\kappa )\)-SCHCP framework by using the theory of Euclidean Jordan algebras and symmetric cones. We designed and analyzed an IPA in Algorithm 4.1 based on a general AET function belonging to the class in Definition 1. Hence, we obtain a class of IPAs, that is, for each AET function we get a specific variant of generic IPA. The complexity analysis of the proposed IPA is presented and it is proved that the derived iteration bound matches the best known iteration bound for IPAs solving these types of problems. Furthermore, it is proved that Algorithm 4.1 is well defined without any relationship between the parameters \(L_1\) and \(L_2\) from Definition 1, which was not the case in the analysis of the IPA in [18]. Hence, the class of AET functions in Definition 1 is wider than the one used in [18].

We briefly mention few possible topics for further research. One interesting topic would be to extend the obtained results to non-symmetric cone optimization and to nonlinear complementarity problems over symmetric cones. Furthermore, it would be worth considering a more general framework where we do not assume the \(P_*(\kappa )\)-property of the pair (Q, R), but rather consider problems similar to general LCPs given in [16, 17].