Skip to main content
SpringerLink
Log in

Auxiliary particle filtering with lookahead support for univariate state space models

  • Published:
ANNALI DELL'UNIVERSITA' DI FERRARA Aims and scope Submit manuscript

Abstract

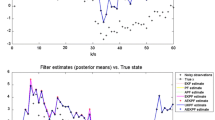
An essential type of Bayesian recursive filters known as the sequential Monte Carlo (alias, the particle filter) is used to estimate hidden Markov target states from noisy sensor data. Utilising sensor data and a collection of weighted particles, the filter makes an approximation of the posterior probability density of the target state. These particles are made to recursively propagate in time and are then updated using the incoming sensor information. The auxiliary particle filter improves over the traditional particle filter by guiding particles into regions of importance of the probability density using a lookahead scheme. This facilitates in the use of fewer particles and improved accuracy. However, when the sensor observations are extremely informative and the state transition noise is strong, the filter suffers badly. This is because the high state transition noise causes the particles that are determined to be important by the lookahead step could guide themselves to unimportant regions of the posterior in the final sampling process. Recent improvements of the auxiliary particle filter explored better weighting strategies but the said problem has not been explored closely. This paper seeks to solve the problem by adopting an auxiliary lookahead technique with two predictive support points to estimate the particles that will be located in regions of high importance after final sampling. The proposed method is successfully tested using a nonlinear model using simulations.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Algorithm 1
Algorithm 2
Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

Data Availability

Not applicable.

Notes

  1. This paper assumes additive noise model.

References

  1. Bar-Shalom, Y., Rong Li, X., Kirubarajan, T.: Estimation with Applications to Tracking and Navigation: Theory Algorithms and Software. Wiley, New York (2004)

    Google Scholar 

  2. Mahler, R.P.S.: Advances in Statistical Multisource-Multitarget Information Fusion. Norwood, Artech House (2014)

    Google Scholar 

  3. Choppala, P.: Bayesian Multiple Target Tracking, PhD tThesis. Victoria University of Wellington, New Zealand (2014)

  4. Geweke, John: Using simulation methods for Bayesian econometric models: inference, development, and communication. J. Econom. Rev. 18(1), 1–73 (1999)

    Article  MathSciNet  Google Scholar 

  5. Ashik, M., Manapuram, R.P., Choppala, P.B.: 2023 Observation leveraged resampling-free particle filter for tracking of rhythmic biomedical signals. Int. J. Intell. Syst. Appl. Eng. (Scopus indexed) 11(4s), 616–624 (2023)

    Google Scholar 

  6. Dissanayake, M.G., Newman, P., Clark, S., Durrant-Whyte, H., Csorba, M.: A solution to the simultaneous localization and map building (SLAM) problem. IEEE Trans. Robot. Autom. 17(3), 229–241 (2001)

    Article  Google Scholar 

  7. Huo, Q., Ma, Z., Zhao, X., Zhang, T., Zhang, Y.: Bayesian network based state-of-health estimation for battery on electric vehicle application and its validation through real-world data. J. IEEE Access 9, 11328–11341 (2021)

    Article  Google Scholar 

  8. Kalman, R.E.: A new approach to linear filtering and prediction problems. ASME J. Basic Eng. 82(1), 35–45 (1960)

    Article  MathSciNet  Google Scholar 

  9. Gordon, N., Salmond, D.J., Smith, A.F.M.: Novel approach to nonlinear/non-Gaussian Bayesian state estimation. IEE Proc. F (Radar. Signal Process.) 140(2), 107–113 (1993)

    Article  Google Scholar 

  10. Arulampalam, M.S., Maskell, S., Gordon, N., Clapp, T.: A tutorial on particle filters for online nonlinear/non-Gaussian Bayesian tracking. IEEE Trans. Signal Proc. 50(2), 174–188 (2002)

    Article  Google Scholar 

  11. Douc, R., Cappe, O.: Comparison of resampling schemes for particle filtering. In: Proceedings IEEE International Symposium on Image and Signal Processing and Analysis, pp. 64–69 (2005)

  12. Hol, J.D., Schon, T.B., Gustafsson, F.: On resampling algorithms for particle filters. In: Proceedings of the 2006 IEEE Workshop on Nonlinear Statistical Signal Processing, pp. 79–82 (2006)

  13. Pitt, M., Shephard, N.: Filtering via simulation: auxiliary particle filters. J. Am. Stat. Assoc. 94(446), 590–599 (1999)

    Article  MathSciNet  Google Scholar 

  14. Charalampidis, A.C., Papavassilopoulos, G. P.: Improved auxiliary and unscented particle filter variants. In: Proceedings of the 52nd IEEE Conference on Decision and Control, pp. 7040 – 7046 (2013)

  15. Xue, L., Chunning, N., Yulan, H.: Improved auxiliary particle filter for SINS/SAR navigation. J. Hindawi Math. Problems Eng. pp. 1–9 (2021)

  16. Elvira, V., Martino, L., Bugallo, M.F., Djuric, P.M.: In search for improved auxiliary particle filters. In: Proceedings of the IEEE European Signal Processing Conference (EUSIPCO), pp. 1637–1641 (2018)

  17. Elvira, V., Martino, L., Bugallo, M., Djuric, P.M.: Elucidating the auxiliary particle filter via multiple importance sampling. IEEE Signal Process. Mag. 36(6), 145–152 (2019)

    Article  Google Scholar 

  18. Norton, J.P., Veres, G.V.: Improvement of the particle filter by better choice of the predicted sample set. Proc. IFAC 35(1), 365–370 (2002)

    Google Scholar 

  19. Lin, M., Chen, R., Liu, J.S.: Lookahead strategies for sequential Monte Carlo. J. Stat. Sci. 28(1), 69–94 (2013)

    MathSciNet  Google Scholar 

  20. Rehman, M., Dass, S.C., Asirvadam, V.S.: A weighted likelihood criteria for learning importance densities in particle filtering. EURASIP J. Adv. Signal Proc. 1, 1–19 (2018)

    Google Scholar 

  21. Choppala, P.B., Teal, P.D., Frean, M.R.: Soft systematic resampling for accurate posterior approximation and increased information retention in particle filtering. In: Proceedings of the IEEE Workshop on Statistical Signal Processing, pp. 260–263 (2014)

  22. Choppala, P.B., Teal, P.D., Frean, M.R.: Resampling and network theory. IEEE Trans. Signal Inf. Process. Over Netw. 08, 106–119 (2022)

    Article  MathSciNet  Google Scholar 

  23. Branchini, N., Elvira, V.: Optimized auxiliary particle filters: adapting mixture proposals via convex optimization. In: Proceedings of the Thirty-Seventh Conference on Uncertainty in Artificial Intelligence, PMLR, vol. 161, pp. 1289–1299 (2021)

Download references

Funding

Not applicable.

Author information

Authors and Affiliations

  1. Department of E.C.E., Andhra University, Visakhapatnam, A.P., 530003, India

    Praveen B. Choppala

Authors
  1. Praveen B. Choppala
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

NDU was responsible for running the simulations and proof-reading of the manuscript. PBC developed the proposed idea, designed the code and prepared the manuscript.

Corresponding author

Correspondence to Praveen B. Choppala.

Ethics declarations

Conflict of interest

The authors declare no competing interests.

Ethical approval

Not applicable.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Choppala, P.B. Auxiliary particle filtering with lookahead support for univariate state space models. Ann Univ Ferrara 70, 515–532 (2024). https://doi.org/10.1007/s11565-024-00487-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11565-024-00487-8

Keywords

Search

Navigation