Local Identifiability Analysis, Parameter Subset Selection and Verification for a Minimal Brain PBPK Model

Abstract

Physiologically-based pharmacokinetic (PBPK) modeling is important for studying drug delivery in the central nervous system, including determining antibody exposure, predicting chemical concentrations at target locations, and ensuring accurate dosages. The complexity of PBPK models, involving many variables and parameters, requires a consideration of parameter identifiability; i.e., which parameters can be uniquely determined from data for a specified set of concentrations. We introduce the use of a local sensitivity-based parameter subset selection algorithm in the context of a minimal PBPK (mPBPK) model of the brain for antibody therapeutics. This algorithm is augmented by verification techniques, based on response distributions and energy statistics, to provide a systematic and robust technique to determine identifiable parameter subsets in a PBPK model across a specified time domain of interest. The accuracy of our approach is evaluated for three key concentrations in the mPBPK model for plasma, brain interstitial fluid and brain cerebrospinal fluid. The determination of accurate identifiable parameter subsets is important for model reduction and uncertainty quantification for PBPK models.

Appendix A

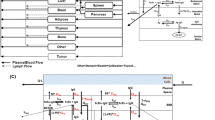
The brain minimal PBPK (mPBPK) model (Bloomingdale et al. (2021)) comprises the following system of ordinary differential equations for the 16 antibody concentrations:

• 1. Plasma ($C_P$)

  $$\begin{aligned} V_{P} \cdot \frac{dC_P}{dt}= & {} (Q_T-L_T)\cdot C_{T_{V}}+(Q_B-L_B)\cdot C_{B_{V}}+(L_T+L_B)\cdot C_L\nonumber \\{} & {} -Q_T\cdot C_P-Q_B \cdot C_P \end{aligned}$$

  (15)

  Table 5 Parameter values for human in the model of Bloomingdale et al. 2021

• 2. Tissue vascular ($C_{T_{V}}$)

  $$\begin{aligned} V_{T_{V}} \cdot \frac{dC_{T_{V}}}{dt}= & {} Q_T\cdot C_P-(Q_T-L_T)\cdot C_{T_{V}}-((1-\sigma _{T_{V}})\cdot L_T\cdot C_{T_{V}})\nonumber \\{} & {} -CLUP_{T}\cdot C_{T_{V}} +CLUP_T\cdot FR\cdot C_{T_{E,B}} \end{aligned}$$

  (16)

• 3. Tissue endosome (unbound) $(C_{T_{E,U}})$

  $$\begin{aligned} V_{T_{E}} \cdot \frac{C_{T_{E,U}}}{dt}= & {} CLUP_T\cdot (C_{T_{V}}+C_{T_{I}})-V_{T_{E}}\cdot (kon_{FcRn}\cdot C_{T_{E,U}} \cdot C_{T_{FcRn,U}}\nonumber \\{} & {} -koff_{FcRn}\cdot C_{T_{E,B}}+k_{deg} \cdot C_{T_{E,U}}) \end{aligned}$$

  (17)

• 4. Tissue endosome (FcRnbound) $(C_{T_{E,B}})$

  $$\begin{aligned} V_{T_{E}} \cdot \frac{C_{T_{E,B}}}{dt}= & {} V_{T_{E}}\cdot (kon_{FcRn}\cdot C_{T_{E,U}} \cdot C_{T_{FcRn,U}}-koff_{FcRn}\cdot C_{T_{E,B}})\nonumber \\{} & {} -CLUP_T\cdot C_{T_{E,B}} \end{aligned}$$

  (18)

• 5. Tissue interstitium $(C_{T_{I}})$

  $$\begin{aligned} V_{T_{I}} \cdot \frac{C_{T_{I}}}{dt}= & {} (1-\sigma _{T_{V}})\cdot L_T\cdot C_{T_{V}}-(1-\sigma _{T_{L}})\cdot L_T\cdot C_{T_{I}}\nonumber \\{} & {} +CLUP_{T}\cdot (1-FR)\cdot C_{T_{E,B}}-CLUP_T\cdot C_{T_{I}} \end{aligned}$$

  (19)

• 6. Brain vascular ($C_{B_{V}}$)

  $$\begin{aligned} V_{B_{V}} \cdot \frac{C_{B_{V}}}{dt}= & {} Q_B\cdot C_P-(Q_B-L_B)\cdot C_{B_{V}}-(1-\sigma _{BBB})\cdot Q_{B_{ECF}}\cdot C_{B_{V}} \nonumber \\{} & {} -(1-\sigma _{BCSFB}) \cdot Q_{B_{CSF}}\cdot C_{B_{V}} -CLUP_B\cdot C_{B_{V}} \nonumber \\{} & {} + CLUP_{BBB}\cdot FR_{B} \cdot C_{B_{EBBB,B}} \nonumber \\{} & {} + CLUP_{BCSFB}\cdot FR_{B}\cdot C_{B_{EBCSFB,B}} \end{aligned}$$

  (20)

• 7. BBB endosome (unbound) ($C_{B_{EBBB,U}}$)

  $$\begin{aligned} V_{B_{EBBB}} \cdot \frac{C_{B_{EBBB,U}}}{dt}= & {} CLUP_{BBB}\cdot (C_{B_{V}}+C_{B_{I}})+V_{B_{EBBB}} \cdot (-kon_{FcRn}\cdot \nonumber \\{} & {} C_{B_{EBBB,U}}\cdot C_{B_{BBBFcRn,U}}+koff_{FcRn}\cdot C_{B_{EBBB,B}} \nonumber \\{} & {} -k_{deg}\cdot C_{B_{EBBB,U}}) \end{aligned}$$

  (21)

• 8. BBB endosome (FcRnbound) ($C_{B_{EBB,B}}$)

  $$\begin{aligned} V_{B_{EBBB}} \cdot \frac{C_{B_{EBBB,B}}}{dt}= & {} V_{B_{EBBB}} \cdot (kon_{FcRn}\cdot C_{B_{EBBB,U}}\cdot C_{B_{BBBFcRn,U}}\nonumber \\{} & {} -koff_{FcRn}\cdot C_{B_{EBBB,B}})\nonumber \\{} & {} -CLUP_{BBB}\cdot C_{B_{EBBB,B}} \end{aligned}$$

  (22)

• 9. Brain interstitium ($C_{B_{{I}}}$)

  $$\begin{aligned} V_{B_{I}} \cdot \frac{C_{B_{I}}}{dt}= & {} (1-\sigma _{BBB})\cdot Q_{B_{ECF}}\cdot C_{B_{V}}-(1-\sigma _{B_{ISF}})\cdot Q_{B_{ECF}}\cdot C_{B_{I}}\nonumber \\{} & {} +CLUP_{BBB}\cdot (1-FR_B)\cdot C_{B_{EBBB,B}} -CLUP_{BBB}\cdot C_{B_{I}}\nonumber \\{} & {} -Q_{B_{ECF}}\cdot C_{B_{I}} +Q_{B_{ECF}}\cdot C_{B_{CSF}} \end{aligned}$$

  (23)

• 10. BCSFB endosome (unbound) ($C_{B_{EBCSFB,U}}$)

  $$\begin{aligned} V_{B_{EBCSFB}}\cdot \frac{C_{B_{EBCSFB,U}}}{dt}= & {} CLUP_{BCSFB}\cdot C_{B_{V}}+CLUP_{BCSFB} \cdot C_{B_{CSF}}\nonumber \\{} & {} +V_{B_{EBCSFB}}\cdot (-kon_{FcRn}\cdot C_{B_{EBCSFB,U}}\nonumber \\{} & {} \cdot C_{B_{BCSFBFcRn,U}}+koff_{FcRn}\cdot C_{B_{EBCSFB,B}}\nonumber \\{} & {} -k_{deg}\cdot C_{B_{EBCSFB,U}}) \end{aligned}$$

  (24)

• 11. BCSFB endosome (FcRnbound) ($C_{B_{EBCSFB,B}}$)

  $$\begin{aligned} V_{B_{EBCSFB}}\cdot \frac{C_{B_{EBCSFB,B}}}{dt}= & {} V_{B_{EBCSFB}}\cdot (kon_{FcRn}\cdot C_{B_{EBCSFB,U}}\nonumber \\{} & {} \cdot C_{B_{BCSFBFcRn,U}}-koff_{FcRn}\cdot C_{B_{EBCSFB,B}})\nonumber \\{} & {} -CLUP_{BCSFB}\cdot C_{B_{EBCSFB,B}} \end{aligned}$$

  (25)

• 12. Brain CSF ($C_{B_{CSF}}$)

  $$\begin{aligned} V_{B_{CSF}}\cdot \frac{C_{B_{CSF}}}{dt}= & {} (1-\sigma _{BCSFB})\cdot Q_{B_{CSF}}\cdot C_{B_{V}}-CLUP_{BCSFB} \cdot C_{B_{CSF}}\nonumber \\{} & {} +CLUP_{BCSFB}\cdot (1-FR_B) \cdot C_{B_{EBCSFB,B}} +Q_{B_{ECF}}\cdot C_{B_{I}}\nonumber \\{} & {} -(1-\sigma _{B_{CSF}})\cdot Q_{B_{CSF}} \cdot C_{B_{CSF}}- Q_{B_{ECF}} \cdot C_{B_{CSF}} \end{aligned}$$

  (26)

• 13. Lymph ($C_L$)

  $$\begin{aligned} V_{L}\cdot \frac{C_{L}}{dt}= & {} (1-\sigma _{T_{L}})\cdot L_T\cdot C_{T_{I}}+(1-\sigma _{B_{CSF}})\cdot Q_{B_{CSF}} \cdot C_{B_{CSF}}\nonumber \\{} & {} + (1-\sigma _{B_{ISF}})\cdot Q_{B_{ECF}}\cdot C_{B_{I}}-(L_T+L_B)\cdot C_L \end{aligned}$$

  (27)

• 14. FcRn concentration in tissue endosome ($C_{T_{FcRn,U}}$)

  $$\begin{aligned} V_{T_{E}}\cdot \frac{C_{T_{FcRn,U}}}{dt}= & {} -V_{T_{E}}\cdot (kon_{FcRn}\cdot C_{T_{E,U}} \cdot C_{T_{FcRn,U}}-koff_{FcRn}\cdot C_{T_{E,B}})\nonumber \\{} & {} +CLUP_T\cdot C_{T_{E,B}} \end{aligned}$$

  (28)

• 15. FcRn BBB endosome ($C_{B_{BBBFcRn,U}}$)

  $$\begin{aligned} V_{B_{EBBB}}\cdot \frac{C_{B_{BBBFcRn,U}}}{dt}= & {} V_{B_{EBBB}}\cdot (-kon_{FcRn}\cdot C_{B_{EBBB,U}}\cdot C_{B_{BBBFcRn,U}}\nonumber \\{} & {} +koff_{FcRn}\cdot C_{B_{EBBB,B}})\nonumber \\{} & {} +CLUP_{BBB}\cdot C_{B_{EBBB,B}} \end{aligned}$$

  (29)

• 16. FcRn BCSFB endosome ($C_{B_{BCSFBFcRn,U}}$)

  $$\begin{aligned} V_{B_{EBCSFB}}\cdot \frac{C_{B_{BCSFBFcRn,U}}}{dt}= & {} V_{B_{EBCSFB}}\cdot (-kon_{FcRn}\cdot C_{B_{EBCSFB,U}}\cdot \nonumber \\{} & {} C_{B_{BCSFBFcRn,U}}+ koff_{FcRn}\cdot C_{B_{EBCSFB,B}}) \nonumber \\{} & {} +CLUP_{BCSFB}\cdot C_{B_{EBCSFB,B}} \end{aligned}$$

  (30)

This system of equations is augmented with initial conditions. The first concentration is prescribed an initial value $\frac{Dose_{0}}{V_P}$, where $Dose_{0}=\frac{Body_{weight} \times Dose_{amount}}{Molecular_{weight}} \times 1000$ with $Body_{weight}=70 kg$, $Molecular_{weight}=150kDa$, $Dose_{amount}=10 mg/kg$. The subsequent 12 concentrations are prescribed initial values of zero, and the remaining three concentrations ($C_{T_{FcRn,U}}$, $C_{B_{BBBFcRn,U}}$, $C_{B_{BCSFBFcRn,U}}$) are all prescribed a nonzero initial value of $0.4982\times 10^{-4}.$ In this study, a 10 mg/kg dosage was given over 1000 h to a 70 kg individual using a 1-hour step size.