Modeling Syphilis and HIV Coinfection: A Case Study in the USA

Abstract

Syphilis and HIV infections form a dangerous combination. In this paper, we propose an epidemic model of HIV-syphilis coinfection. The model always has a unique disease-free equilibrium, which is stable when both reproduction numbers of syphilis and HIV are less than 1. If the reproduction number of syphilis (HIV) is greater than 1, there exists a unique boundary equilibrium of syphilis (HIV), which is locally stable if the invasion number of HIV (syphilis) is less than 1. Coexistence equilibrium exists and is stable when all reproduction numbers and invasion numbers are greater than 1. Using data of syphilis cases and HIV cases from the US, we estimated that both reproduction numbers for syphilis and HIV are slightly greater than 1, and the boundary equilibrium of syphilis is stable. In addition, we observed competition between the two diseases. Treatment for primary syphilis is more important in mitigating the transmission of syphilis. However, it might lead to increase of HIV cases. The results derived here could be adapted to other multi-disease scenarios in other regions.

1 Introduction

Syphilis and HIV form a dangerous combination. Syphilis and HIV affect similar patient groups and coinfection is common (Lynn and Lightman 2004). Both syphilis and HIV are sexually transmitted. Therefore, it is no surprise that a substantial number of people is infected with both agents. HIV has several effects on the presentation, diagnosis, disease progression, and therapy of syphilis (Golden et al. 2003). Syphilis significantly increases the risk of contracting HIV infection, and HIV can alter the natural course of syphilis (Pialoux et al. 2008). Most patients coinfected with HIV and syphilis are affected by larger, deeper, and more numerous chancres that take longer to heal (Pialoux et al. 2008). All patients presenting with syphilis should be offered HIV testing and all HIV-positive patients should be regularly screened for syphilis.

Syphilis is a multistage disease with diverse and wide-ranging manifestations. The distinct stages of syphilis were first described in detail by Philippe Ricord in the mid-1800s (LaFond and Lukehart 2006). Typically syphilis occurs in three phases, namely, primary, secondary, and tertiary disease. Syphilis is a chronic disease, and T. pallidum’s only known natural host is human. Infection is initiated when T. pallidum penetrates dermal microabrasions or intact mucous membranes, typically resulting in a single chancre at the site of inoculation. The chancre usually becomes indurated and will progress to ulceration but typically is not purulent (Lynn and Lightman 2004). Syphilis is one of the leading causes of infant mortality worldwide, with 6.3 million new cases in 2016 and approximately 200,000 stillbirths and neonatal deaths (World Health Organization 2022a). The human immunodeficiency virus (HIV) targets the immune system and weakens people’s defense against many infections and some types of cancer that people with healthy immune systems can fight off. As the virus destroys and impairs the function of immune cells, in the first few weeks after initial infection people may experience no symptoms or an influenza-like illness including fever, headache, rash or sore throat, as the infection progressively weakens the immune system, they can develop other signs and symptoms, such as swollen lymph nodes, weight loss, fever, diarrhoea and cough (World Health Organization 2022b). Without treatment, they could also develop severe illnesses such as tuberculosis (TB), cryptococcal meningitis, severe bacterial infections, and cancers such as lymphomas and Kaposi’s sarcoma. The most advanced stage of HIV infection is acquired immunodeficiency syndrome (AIDS), which can take many years to develop if not treated, depending on the individual (World Health Organization 2022b). There were estimated 37.7 million [30.2–45.1 million] people living with HIV at the end of 2020, over two thirds of whom (25.4 million) are in the WHO African Region (World Health Organization 2022b). In 2020, 680 000 [480 000–1.0 million] people died from HIV-related causes, 1.5 million [1.0–2.0 million] people acquired HIV, and 7.7 million people will die from HIV-related diseases in the next 10 years (World Health Organization 2022b).

Some deterministic mathematical models of syphilis have been formulated and analyzed. E. Iboi and D. Okuonghae studied a multistage syphilis model with early latent and late latent stages. They found that high treatment rates for individuals in the primary and secondary stages can significantly reduce the number of infected individuals in the remaining stages of infection (Iboi and Okuonghae 2016). Saad-Roy et al. (2016) formulated a mathematical model of syphilis transmission in an MSM population with multiple stages and all treated males were divided into four classes. E. Iboi and D. Okuonghae introduced three deterministic models for syphilis, mainly analyzing the conditions for the occurrence of the backward bifurcation of the model (Milner and Zhao 2010).

There are many deterministic mathematical models studying coinfection of two diseases, such as HIV/TB (Roeger et al. 2009; Mtisi et al. 2009), HIV/gonorrhea (Mushayabasa et al. 2011), malaria/meningitis (Maseno 2011) and HIV/heroin (Duan et al. 2020). For example, Roeger et al. (2009) found that as the progression rates from HIV to AIDS increase, the prevalence of HIV increases while TB decreases. Using the invasion reproduction numbers, Duan et al. (2020) showed that HIV and heroin infection in the US are in a coexistence regime. Similar strategy was used in another mathematical model with coinfection (Li et al. 2021). Gao et al. studied a general coinfection model with bilinear incidence. They obtained richer dynamic behavior such as backward bifurcation and Hopf bifurcation through simulations (Gao et al. 2016).

There are few mathematical models investigating HIV and syphilis coinfection. Nwankwo and Okuonghae studied a complicated HIV/syphilis coinfection model. They analyzed syphilis sub-model and HIV sub-model completely. But for the full model, they only have local stability for the DFE (Nwankwo and Okuonghae 2018). In this paper, we will formulate a relatively simple HIV/syphilis coinfection model and derive more analytic results for the full model. In addition, using data from the US, a case study will be given. The paper is organized as follows. In Sect. 2, we formulate an ODE model for syphilis and HIV coinfection, assuming that syphilis has only three stages. In Sect. 3, the local stability of the disease-free equilibrium and two boundary equilibria are strictly proved using the reproduction numbers and invasion numbers. The existence of the coexistence equilibrium of syphilis and HIV is analyzed in Sect. 4. In Sect. 5, we perform elasticity analysis of invasion numbers with respect to parameters related to control strategies. By fitting syphilis and HIV cases from the US to our model, we carry several numerical simulations to illustrate and extend the theoretical results in Sect. 6. Conclusions and discussions are given in Sect. 7.

2 Syphilis and HIV Coinfection Model

In this paper, we introduce a new mathematical model with syphilis and HIV coinfection. We divided the total population into seven compartments, namely, the number of susceptible individuals (S), the number of infected individuals only with primary syphilis (I), the number of infected individuals only with secondary syphilis (L), the number of infected individuals only with HIV (H), the number of infected individuals with primary syphilis and HIV ($H_{I}$), the number of infected individuals with secondary syphilis and HIV ($H_{L}$), the number of infected individuals with tertiary syphilis (X), regardless of HIV status. Including exposed class will only slightly affect the dynamic of the model. Therefore, for simplicity, exposed period for syphilis is not included in this work. Since patients in both latent syphilis period and tertiary period are not infectious and not active, we group them together and still call it tertiary period. We assume that individuals with tertiary syphilis are isolated and that the number of total active population is $N=S+I+L+H+H_{I}+H_{L}$.

Fig. 1

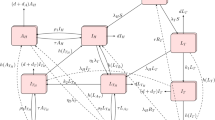
Flow diagram of the model (1) (Color figure online)

We assume that newborns are susceptible to both syphilis and HIV and enter the susceptible compartment S with a recruitment rate $\Lambda$. Susceptible individuals get infected by syphilis with the force of infection $\lambda _{I}$ related to effective contact rate $\beta _{1}$ and move to the compartment I. They can also get infected by HIV with force of infection $\lambda _{H}$ related to effective contact rate $\beta _{2}$ and move to the compartment H. Individuals from compartment H or I can be infected by the other disease and move to compartment $H_I$ with adjusted force of infection $q\lambda _{I}$ and $\theta \lambda _{H}$, respectively. Individuals with primary syphilis in compartment I or $H_I$ can progress to the secondary stage at a rate $\rho _1$ and move to compartments L and $H_L$, respectively. Individuals with secondary syphilis in compartment L or $H_L$ can progress to the tertiary stage at a rate $\rho _2$ and move to compartment X. Individuals in compartment I or L can receive treatment at rates $\alpha _1$ and $\alpha _2$ respectively and move to compartment S. Individuals in compartment $H_I$ or $H_L$ can also get treatment with adjusted rates $\sigma \alpha _1$ and $\sigma \alpha _2$ and move to HIV infection only compartment H. All individuals can leave their compartments by natural death with a rate $\mu$. In addition, individuals in compartments H, $H_I$, $H_L$ or X can die from disease with rates $\mu _1$, $\mu _2$, $\mu _3$ and $\mu _4$, respectively. Patients in the secondary syphilis period usually already have severe symptoms and hence are more cautious. Therefore, we assume that they are not infectious and will not contract HIV. In addition, it is less likely for an individual to contract both syphilis and HIV simultaneously. Therefore, transition from the susceptible class S to the class with two infections $H_I$ is not included here. A flow diagram of the model is shown in Fig. 1. The detailed descriptions of variables and parameters are given in Table 1. The model is described by the following deterministic nonlinear differential equations:

$$\begin{aligned} \begin{aligned} \frac{\textrm{d}S}{\textrm{d}t}&=\Lambda -\lambda _{I}S-\lambda _{H}S-\mu S+\alpha _{1}I+\alpha _{2}L,\,\,\\ \frac{\textrm{d}I}{\textrm{d}t}&=\lambda _{I}S-\rho _{1}I-\mu I-\alpha _{1}I-\theta \lambda _{H}I,\,\,\\ \frac{\textrm{d}L}{\textrm{d}t}&=\rho _{1}I-\rho _{2}L-\mu L-\alpha _{2}L,\,\,\\ \frac{\textrm{d}H}{\textrm{d}t}&=\lambda _{H}S-\mu H-\mu _{1}H-q\lambda _{I}H+\sigma \alpha _{1}H_{I}+\sigma \alpha _{2}H_{L},\,\,\\ \frac{\textrm{d}H_{I}}{\textrm{d}t}&=q\lambda _{I}H+\theta \lambda _{H}I-\mu H_{I}-\mu _{2}H_{I}-\sigma \alpha _{1}H_{I}-\rho _{1}H_{I},\,\,\\ \frac{\textrm{d}H_{L}}{\textrm{d}t}&=\rho _{1}H_{I}-\mu H_{L}-\mu _{3}H_{L}-\sigma \alpha _{2}H_{L}-\rho _{2}H_{L},\,\,\\ \frac{\textrm{d}X}{\textrm{d}t}&=\rho _{2}L+\rho _{2}H_{L}-\mu X-\mu _{4}X, \end{aligned} \end{aligned}$$

(1)

with the initial conditions:

$$\begin{aligned} \begin{aligned}&S(0)=S_{0},\ \ I(0)=I_{0},\ \ L(0)=L_{0},\ \ H(0)=H_{0},\\&H_{I}(0)=H_{I0} ,\ \ H_{L}(0)=H_{L0},\ \ X(0)=X_{0}. \end{aligned} \end{aligned}$$

(2)

Here the force of infections are given by

$$\begin{aligned}&\lambda _{I}=\beta _{1}(I+H_{I}),\ \ \lambda _{H}=\beta _{2}(H+H_{I}).&\end{aligned}$$

(3)

Table 1 Description of variables and parameters of the model (1)

Since the first six equations are independent of the last equation of system (1), we only need to consider the following system

$$\begin{aligned} \begin{aligned} \frac{\textrm{d}S}{\textrm{d}t}&=\Lambda -\lambda _{I}S-\lambda _{H}S-\mu S+\alpha _{1}I+\alpha _{2}L,\,\,\\ \frac{\textrm{d}I}{\textrm{d}t}&=\lambda _{I}S-\rho _{1}I-\mu I-\alpha _{1}I-\theta \lambda _{H}I,\,\,\\ \frac{\textrm{d}L}{\textrm{d}t}&=\rho _{1}I-\rho _{2}L-\mu L-\alpha _{2}L,\,\,\\ \frac{\textrm{d}H}{\textrm{d}t}&=\lambda _{H}S-\mu H-\mu _{1}H-q\lambda _{I}H+\sigma \alpha _{1}H_{I}+\sigma \alpha _{2}H_{L},\,\,\\ \frac{\textrm{d}H_{I}}{\textrm{d}t}&=q\lambda _{I}H+\theta \lambda _{H}I-\mu H_{I}-\mu _{2}H_{I}-\sigma \alpha _{1}H_{I}-\rho _{1}H_{I},\,\,\\ \frac{\textrm{d}H_{L}}{\textrm{d}t}&=\rho _{1}H_{I}-\mu H_{L}-\mu _{3}H_{L}-\sigma \alpha _{2}H_{L}-\rho _{2}H_{L}, \end{aligned} \end{aligned}$$

(4)

$$\begin{aligned}&S(0)=S_{0},\ I(0)=I_{0},\ L(0)=L_{0},\ H(0)=H_{0},\ H_{I}(0)=H_{I0} ,\ H_{L}(0)=H_{L0}.&\nonumber \\ \end{aligned}$$

(5)

Define the set

$$\begin{aligned} {\mathcal {D}}:=\left\{ (S,I,L,H,H_I,H_L)\in {\mathbb {R}}_{+}^{6}:N\le \frac{\Lambda }{\mu }\right\} . \end{aligned}$$

Define the solution semiflow $\Psi :{\mathbb {R}}_{+}^{6}\rightarrow {\mathbb {R}}_{+}^{6}$ of system (4)-(5) by

$$\begin{aligned} \Psi (t)\psi =(S(t),I(t),L(t),H(t),H_I(t),H_L(t)),\ \ \ \forall t\ge 0, \end{aligned}$$

where $\psi =(S_0,I_0,L_0,H_0,H_{I0},H_{L0})\in {\mathbb {R}}_{+}^{6}$. Then ${\mathcal {D}}$ is positively invariant for $\Psi (t)$ in the sense that

$$\begin{aligned} \Psi (t)\psi \in {\mathcal {D}},\ \ \ \forall t\ge 0,\ \ \ \psi \in {\mathcal {D}}. \end{aligned}$$

For the convenience of calculation, we use the following notations:

$$\begin{aligned}{} & {} g_1=\rho _1+\mu +\alpha _1,\ \ g_2=\rho _2+\mu +\alpha _2,\\ {}{} & {} g_3=\mu +\mu _1,\ \ g_4=\mu +\mu _2+\sigma \alpha _1+\rho _1,\\ {}{} & {} g_5=\mu +\mu _3+\sigma \alpha _2+\rho _2. \end{aligned}$$

3 Disease-Free and Boundary Equilibria and Their Stability

In this section, we will obtain the disease-free equilibrium and two boundary equilibria of system (4) and prove their local stability.

3.1 Disease-Free Equilibrium and Its Stability

System (4) always has a disease-free equilibrium $E_{0}^{*}=(S_{0}^{*},0,0,0,0,0)$ with $S_{0}^{*}=\Lambda /\mu$. To investigate the stability of $E_{0}^{*}$, we use the next-generation approach (Diekmann et al. 1990; Van den Driessche and Watmough 2002). Using the notion in Van den Driessche and Watmough (2002), the matrices F and V, for the new infection terms and the remaining transfer terms are, respectively, given by

$$\begin{aligned} F=\left( \begin{array}{lllll}\beta _1 S_{0}^{*}&{}\quad 0&{}\quad 0&{}\quad \beta _1 S_{0}^{*}&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad \beta _2 S_{0}^{*}&{}\quad \beta _2 S_{0}^{*}&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0 \end{array}\right) , V=\left( \begin{array}{lllll}g_1&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ rho_1&{}\quad g_2&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad g_3&{}\quad -\sigma \alpha _1&{}\quad -\sigma \alpha _2\\ 0&{}\quad 0&{}\quad 0&{}\quad g_4&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad -\rho _1&{}\quad g_5 \end{array}\right) . \end{aligned}$$

Hence, the reproduction number of model (4) is given by

$$\begin{aligned}&{\mathcal {R}}=\rho (F V^{-1})=\max \{{\mathcal {R}}_{I},{\mathcal {R}}_{H}\},&\end{aligned}$$

where

$$\begin{aligned} {\mathcal {R}}_I=\frac{\beta _1}{g_1}S_{0}^{*},\ \ {\mathcal {R}}_H=\frac{\beta _2}{g_3}S_{0}^{*} \end{aligned}$$

The result follows from Theorem 2 in Van den Driessche and Watmough (2002).

Lemma 3.1

The DFE, $E_{0}^{*}$, of system (4) is locally asymptotically stable if ${\mathcal {R}}<1$, and unstable if ${\mathcal {R}}>1$.

Furthermore, we have the global stability of the DFE under a certain condition as follows. The proof is given in “Appendix A.”

Theorem 3.2

When ${\mathcal {R}}<1$, if $\rho _1+\alpha _1+\rho _2+\alpha _2+\mu \le \mu _2$, the DFE $E_{0}^{*}$ is globally asymptotically stable.

The above result indicates that the disease may not die out only with the condition ${\mathcal {R}}<1$. In fact, we can show that there exists backward bifurcation under a certain condition, which is given in the following Proposition with the proof given in “Appendix B.”

Proposition 3.3

When ${\mathcal {R}}_I\ne {\mathcal {R}}_H$, system (4) has backward bifurcation.

3.2 Boundary Equilibria and Their Local Stability

In this subsection, we consider two boundary equilibria $E_{1}^{*}$ and $E_{2}^{*}$ corresponding to the syphilis and HIV infection only, respectively. We have the following result on their existence. The proof is given in “Appendix C.”

Theorem 3.4

System (4) has a unique boundary equilibrium $E_{1}^{*}$ of syphilis transmission if the reproduction number ${\mathcal {R}}_I>1$, and a unique boundary equilibrium $E_{2}^{*}$ of HIV transmission if the reproduction number ${\mathcal {R}}_H>1$, where $E_{1}^{*}=(S_{1}^{*}, I_{1}^{*}, L_{1}^{*}, 0, 0, 0)$ with

$$\begin{aligned} S_{1}^{*}=\frac{g_1}{\beta _1}, \qquad I_{1}^{*}=\frac{g_{1}g_{2}\mu ({\mathcal {R}}_{I}-1)}{\beta _1[\mu g_{2}+\rho _{1}(\rho _{2}+\mu )]},\qquad L_{1}^{*}=\frac{\rho _1}{g_2}I_{1}^{*}, \end{aligned}$$

(6)

and $E_{2}^{*}=(S_{2}^{*}, 0, 0, H_{2}^{*}, 0, 0)$ with

$$\begin{aligned} S_{2}^{*}=\frac{g_3}{\beta _2},\qquad H_{2}^{*}=\frac{\mu }{\beta _{2}}({\mathcal {R}}_{H}-1). \end{aligned}$$

(7)

To prove the stability of the boundary equilibria of system (4), we define two invasion reproductive numbers as follows:

$$\begin{aligned}{} & {} {\mathcal {R}}_{2}^{1}=\frac{\beta _{2}S_{1}^{*}g_4g_5+(g_3+q\beta _{1}I_{1}^{*})\theta \beta _{2}I_{1}^{*}g_5 +\theta \beta _{2}I_{1}^{*}\rho _1\sigma \alpha _2+g_5q\beta _{1}I_{1}^{*}\beta _{2}S_{1}^{*} +g_5\theta \beta _{2}I_{1}^{*}\sigma \alpha _1}{(g_3+q\beta _{1}I_{1}^{*})g_4g_5- (\rho _1\sigma \alpha _2+\sigma \alpha _1g_5)q\beta _{1}I_{1}^{*}},\nonumber \\ \end{aligned}$$

(8)

$$\begin{aligned}{} & {} {\mathcal {R}}_{1}^{2}=\frac{\theta \beta _2H_{2}^{*}\beta _1S_{2}^{*}+q\beta _1H_{2}^{*}(g_1 +\theta \beta _2H_{2}^{*})+\beta _1S_{2}^{*}g_4}{(g_1+\theta \beta _2H_{2}^{*})g_4}. \end{aligned}$$

(9)

Here ${\mathcal {R}}_{2}^{1}$ is the invasion number of HIV infection, which represents the reproduction of HIV infection at the equilibrium $E_{1}^{*}$. Similarly, ${\mathcal {R}}_{1}^{2}$ is the invasion number of syphilis infection representing the reproduction of syphilis infection at the equilibrium $E_{2}^{*}$.

The local stability for two boundary equilibria are stated in the following theorems with proofs are given in “Appendix D” and “Appendix E,” respectively.

Theorem 3.5

The unique boundary equilibrium $E_{1}^{*}$ is locally stable if ${\mathcal {R}}_{2}^{1}<1$, and it is unstable if ${\mathcal {R}}_{2}^{1}>1$.

Theorem 3.6

The unique boundary equilibrium $E_{2}^{*}$ is locally stable if ${\mathcal {R}}_{1}^{2}<1$, and it is unstable if ${\mathcal {R}}_{1}^{2}>1$.

4 Coexistence Equilibrium of Syphilis and HIV Transmission

To study the coexistence equilibrium $E^{*}=(S^{*}, I^{*}, L^{*}, H^{*}, H_{I}^{*}, H_{L}^{*})$, we set the right-hand side of system (4) to zero:

$$\begin{aligned} \begin{aligned} 0&=\Lambda -\lambda _{I}S^*-\lambda _{H}S^*-\mu S^*+\alpha _{1}I^*+\alpha _{2}L^*,\,\,\\ 0&=\lambda _{I}S^*-\rho _{1}I^*-\mu I^*-\alpha _{1}I^*-\theta \lambda _{H}I^*,\,\,\\ 0&=\rho _{1}I^*-\rho _{2}L^*-\mu L^*-\alpha _{2}L^*,\,\,\\ 0&=\lambda _{H}S^*-\mu H^*-\mu _{1}H^*-q\lambda _{I}H^*+\sigma \alpha _{1}H_{I}^{*} +\sigma \alpha _{2}H_{L}^{*},\,\,\\ 0&=q\lambda _{I}H^*+\theta \lambda _{H}I^*-\mu H_{I}^{*}-\mu _{2}H_{I}^{*} -\sigma \alpha _{1}H_{I}^{*}-\rho _{1}H_{I}^{*},\,\,\\ 0&=\rho _{1}H_{I}^{*}-\mu H_{L}^{*}-\mu _{3}H_{L}^{*}-\sigma \alpha _{2}H_{L}^{*}-\rho _{2}H_{L}^{*},\,\,\\ \end{aligned} \end{aligned}$$

(10)

with

$$\begin{aligned} \lambda _I=\beta _1(I^*+H_{I}^{*}),\ \ \ \lambda _H=\beta _2(H^*+H_{I}^{*}). \end{aligned}$$

(11)

From the first three equations of (10), we have

$$\begin{aligned} S^*\,\,= & {} \,\,\frac{\Lambda g_2(g_1+\theta \lambda _H)}{g_2(g_1+\theta \lambda _H) (\lambda _I+\lambda _H+\mu )-(\alpha _1g_2+\alpha _2\rho _1)\lambda _I},\,\,\\ I^*\,\,= & {} \,\,\frac{\lambda _I}{g_1+\theta \lambda _H}S^*,\,\,\\ L^*\,\,= & {} \,\,\frac{\rho _1}{g_2}I^*, \end{aligned}$$

where

$$\begin{aligned} g_1g_2-(\alpha _1g_2+\alpha _2\rho _1)=\rho _1(\rho _2+\mu )+\mu g_2>0. \end{aligned}$$

From the last three equations of (10), we have

$$\begin{aligned} H^*\,\,= & {} \,\,\frac{g_4g_5(g_1+\theta \lambda _H)\lambda _H+(\sigma \alpha _1g_5+\sigma \alpha _2\rho _1)\theta \lambda _H\lambda _I}{[(g_3+q\lambda _I)g_4g_5-(\sigma \alpha _1g_5+\sigma \alpha _2\rho _1)q\lambda _I](g_1+\theta \lambda _H)}S^*,\,\,\\ H_{I}^{*}\,\,= & {} \,\,\frac{q\lambda _I}{g_4}H^*+\frac{\theta \lambda _H}{g_4}I^*,\,\,\\ H_{L}^{*}\,\,= & {} \,\,\frac{\rho _1}{g_5}H_{I}^{*}. \end{aligned}$$

Substituting the expressions of $I^*$, $H^*$ and $H_{I}^{*}$ into (11), we get

$$\begin{aligned} \lambda _I\,\,= & {} \,\,\beta _1(I^*+H_{I}^{*})\,\,\\ \,\,= & {} \,\,\beta _1\frac{q\lambda _Ig_4g_5(g_1+\theta \lambda _H)\lambda _H+(\sigma \alpha _1g_5+\sigma \alpha _2\rho _1)\theta \lambda _Hq\lambda _I^2}{[(g_3+q\lambda _I)g_4g_5-(\sigma \alpha _1g_5+\sigma \alpha _2\rho _1)q\lambda _I](g_1+\theta \lambda _H)g_4}S^*\,\,\\{} & {} +\beta _1\frac{\theta \lambda _H\lambda _I}{g_4(g_1+\theta \lambda _H)}S^* +\beta _1\frac{\lambda _I}{g_1+\theta \lambda _H}S^*,\,\,\\ \lambda _H\,\,= & {} \,\,\beta _2(H^*+H_{I}^{*})\,\,\\ \,\,= & {} \,\,\beta _2\frac{g_4g_5(g_1+\theta \lambda _H)\lambda _H+(\sigma \alpha _1g_5+\sigma \alpha _2\rho _1)\theta \lambda _I\lambda _H}{[(g_3+q\lambda _I)g_4g_5-(\sigma \alpha _1g_5+\sigma \alpha _2\rho _1)q\lambda _I](g_1+\theta \lambda _H)}S^*\,\,\\{} & {} +\beta _2\frac{q\lambda _Ig_4g_5(g_1+\theta \lambda _H)\lambda _H+(\sigma \alpha _1g_5+\sigma \alpha _2\rho _1)\lambda _H\theta \lambda _Iq\lambda _I}{[(g_3+q\lambda _I)g_4g_5-(\sigma \alpha _1g_5+\sigma \alpha _2\rho _1)q\lambda _I](g_1+\theta \lambda _H)g_4}S^*\\{} & {} +\beta _2\frac{\theta \lambda _H\lambda _I}{(g_1+\theta \lambda _H)g_4}S^*. \end{aligned}$$

Dividing both sides of the above two equations by $\lambda _I$ and $\lambda _H$, we have

$$\begin{aligned} 1\,\,= & {} \,\,\beta _1\frac{qg_4g_5(g_1+\theta \lambda _H)\lambda _H+(\sigma \alpha _1g_5+\sigma \alpha _2\rho _1)\theta \lambda _Hq\lambda _I}{[(g_3+q\lambda _I)g_4g_5-(\sigma \alpha _1g_5+\sigma \alpha _2\rho _1)q\lambda _I](g_1+\theta \lambda _H)g_4}S^*\,\,\\{} & {} +\beta _1\frac{\theta \lambda _H}{g_4(g_1+\theta \lambda _H)}S^* +\beta _1\frac{1}{g_1+\theta \lambda _H}S^*\,\,\\ \,\,= & {} \,\,F_1(\lambda _I,\lambda _H),\,\,\\ 1\,\,= & {} \,\,\beta _2\frac{g_4g_5(g_1+\theta \lambda _H)+(\sigma \alpha _1g_5+\sigma \alpha _2\rho _1)\theta \lambda _I}{[(g_3+q\lambda _I)g_4g_5-(\sigma \alpha _1g_5+\sigma \alpha _2\rho _1)q\lambda _I](g_1+\theta \lambda _H)}S^*\,\,\\{} & {} +\beta _2\frac{q\lambda _Ig_4g_5(g_1+\theta \lambda _H)+(\sigma \alpha _1g_5+\sigma \alpha _2\rho _1)\theta \lambda _Iq\lambda _I}{[(g_3+q\lambda _I)g_4g_5-(\sigma \alpha _1g_5+\sigma \alpha _2\rho _1)q\lambda _I](g_1+\theta \lambda _H)g_4}S^* +\beta _2\frac{\theta \lambda _I}{(g_1+\theta \lambda _H)g_4}S^*\,\,\\ \,\,= & {} \,\,F_2(\lambda _I,\lambda _H). \end{aligned}$$

We want to use $F_2(\lambda _I,\lambda _H)=1$ to express $\lambda _H=h(\lambda _I)$. Since $F_2(\lambda _I,\lambda _H)=1$ is a decreasing function of $\lambda _H$, if there is a solution for $\lambda _H$, that solution is unique. There will be a solution if $F_2(\lambda _I,0)>1$ for arbitrary $\lambda _I$. We have

$$\begin{aligned} F_2(\lambda _I,0)\,\,= & {} \,\,\beta _2\frac{g_4g_5g_1+(\sigma \alpha _1g_5+\sigma \alpha _2\rho _1)\theta \lambda _I}{[(g_3+q\lambda _I)g_4g_5-(\sigma \alpha _1g_5+\sigma \alpha _2\rho _1)q\lambda _I]g_1}\\{} & {} \cdot \frac{\Lambda g_2g_1}{g_2g_1(\lambda _I+\mu )-(\alpha _1g_2+\alpha _2\rho _1)\lambda _I}\,\,\\{} & {} +\beta _2\frac{q\lambda _Ig_4g_5g_1+(\sigma \alpha _1g_5+\sigma \alpha _2\rho _1)\theta \lambda _Iq\lambda _I}{[(g_3+q\lambda _I)g_4g_5-(\sigma \alpha _1g_5+\sigma \alpha _2\rho _1)q\lambda _I]g_1g_4} \\{} & {} \cdot \frac{\Lambda g_2g_1}{g_2g_1(\lambda _I+\mu )-(\alpha _1g_2+\alpha _2\rho _1)\lambda _I}\,\,\\{} & {} +\beta _2\frac{\theta \lambda _I}{g_1g_4} \cdot \frac{\Lambda g_2g_1}{g_2g_1(\lambda _I+\mu )-(\alpha _1g_2+\alpha _2\rho _1)\lambda _I}. \end{aligned}$$

If $\lambda _I=0$, then $S^*=\frac{\Lambda }{\mu }$, $F_2(0,0)={\mathcal {R}}_H>1$. If $\lambda _I=\lambda _I^*=\beta _1I_{1}^{*}$, then $S^*=S_{1}^{*}=\frac{g_1}{\beta _1}$.

$$\begin{aligned} F_2(\lambda _I^*,0)\,\,= & {} \,\,\beta _2\frac{g_4g_5g_1+(\sigma \alpha _1g_5+\sigma \alpha _2\rho _1)\theta \lambda _{I}^{*}}{[(g_3+q\lambda _{I}^{*})g_4g_5-(\sigma \alpha _1g_5+\sigma \alpha _2\rho _1)q\lambda _{I}^{*}]g_1}\frac{g_1}{\beta _1}\,\,\\{} & {} +\beta _2\frac{q\lambda _{I}^{*}g_4g_5g_1+(\sigma \alpha _1g_5+\sigma \alpha _2\rho _1)\theta \lambda _{I}^{*}q\lambda _{I}^{*}}{[(g_3+q\lambda _I)g_4g_5-(\sigma \alpha _1g_5+\sigma \alpha _2\rho _1)q\lambda _{I}^{*}]g_1g_4}\frac{g_1}{\beta _1} +\beta _2\frac{\theta \lambda _{I}^{*}}{g_1g_4}\frac{g_1}{\beta _1}\,\,\\= & {} \frac{\beta _2S_{1}^{*}g_4g_5}{(g_3+q\lambda _{I}^{*})g_4g_5-(\sigma \alpha _1g_5+\sigma \alpha _2\rho _1)q\beta _1I_{1}^{*}}\\{} & {} \quad +\frac{(\sigma \alpha _1g_5+\sigma \alpha _2\rho _1)\theta \beta _2I_{1}^{*}}{(g_3+q\lambda _{I}^{*})g_4g_5-(\sigma \alpha _1g_5+\sigma \alpha _2\rho _1)q\beta _1I_{1}^{*}}\,\,\\{} & {} +\frac{g_5q\beta _1I_{1}^{*}\beta _2S_{1}^{*}}{(g_3+q\lambda _{I}^{*})g_4g_5-(\sigma \alpha _1g_5+\sigma \alpha _2\rho _1)q\beta _1I_{1}^{*}}\\{} & {} \,\, +\frac{(g_3+q\beta _1I_{1}^{*})\theta \beta _2I_{1}^{*}g_5}{(g_3+q\lambda _{I}^{*})g_4g_5-(\sigma \alpha _1g_5+\sigma \alpha _2\rho _1)q\beta _1I_{1}^{*}}\,\,\\ \,\,= & {} \,\,{\mathcal {R}}_{2}^{1}>1. \end{aligned}$$

Therefore, we only need to prove $F_2(\lambda _I,0)>1$. In other words, we only need

$$\begin{aligned} c_1\lambda _{I}^{2}+c_2\lambda _I+c_3>d_1\lambda _{I}^{2}+d_2\lambda _I+d_3, \end{aligned}$$

(12)

where

$$\begin{aligned} c_1\,\,= & {} \,\,\beta _2\theta q\Lambda g_1g_2g_4g_5+(\sigma \alpha _1g_5+\sigma \alpha _2\rho _1)qg_{1}^{2}g_2g_4+(\alpha _1g_2 +\alpha _2\rho _1)qg_{1}g_{4}^{2}g_5,\,\,\\ c_2\,\,= & {} \,\,\theta \beta _2\Lambda (\sigma \alpha _1g_5+\sigma \alpha _2\rho _1)g_1g_2g_4+\beta _2q\Lambda g_{1}^{2}g_2g_4g_5+\beta _2\theta \Lambda g_1g_2g_3g_4g_5\,\,\\{} & {} +(\alpha _1g_2+\alpha _2\rho _1)g_1g_3g_{4}^{2}g_5 +(\sigma \alpha _1g_5+\sigma \alpha _2\rho _1)q\mu g_{1}^{2}g_2g_4,\,\,\\ c_3\,\,= & {} \,\,\beta _2\Lambda g_{1}^{2}g_2g_{4}^{2}g_5,\,\,\\ d_1\,\,= & {} \,\,qg_{1}^{2}g_2g_{4}^{2}g_5+q(\alpha _1g_2+\alpha _2\rho _1)(\sigma \alpha _1g_5+\sigma \alpha _2\rho _1)g_1g_4,\,\,\\ d_2\,\,= & {} \,\,q\mu g_{1}^{2}g_2g_{4}^{2}g_5+g_{1}^{2}g_2g_3g_{4}^{2}g_5,\,\,\\ d_3\,\,= & {} \,\,\mu g_{1}^{2}g_2g_3g_{4}^{2}g_5. \end{aligned}$$

Assume $c_2>d_2$, if we want to get (12), we need to consider the following two cases.

Case 1 $c_1>d_1$

Since $c_1>d_1$, $c_2>d_2$, to get (12), we only need to prove $c_3>d_3$:

$$\begin{aligned} c_3-d_3=g_{1}^{2}g_2g_{4}^{2}g_5(\beta _2\Lambda -g_3\mu )=g_{1}^{2}g_2g_{4}^{2}g_5g_3\mu ({\mathcal {R}}_H-1). \end{aligned}$$

It is clear that $c_3>d_3$ if ${\mathcal {R}}_H>1$. Therefore, $F_2(\lambda _I,0)>1$ for any $\lambda _I$, there is a unique solution for all $\lambda _I$.

Case 2 $c_1<d_1$

We have

$$\begin{aligned} \lim _{\lambda _I \rightarrow \infty }F_2(\lambda _I,0)<1. \end{aligned}$$

Since $F_2(0,0)={\mathcal {R}}_H>1$, there exists a ${\bar{\lambda }}_{I}^{*}$ such that $F_{2}(\lambda _I,0)>1$ for any $\lambda _I<{\bar{\lambda }}_{I}^{*}$ and $F_{2}({\bar{\lambda }}_{I}^{*},0)=1$. It follows that there is a unique $\lambda _H$ for any $\lambda _I\in (0,{\bar{\lambda }}_{I}^{*})$ such that $\lambda _H=h(\lambda _I)$.

We define

$$\begin{aligned} f(\lambda _I)=F_1(\lambda _I,h(\lambda _I)). \end{aligned}$$

When $\lambda _I=0$, we get

$$\begin{aligned} F_2(0,\lambda _H)=\frac{\beta _2g_4g_5(g_1+\theta \lambda _H)}{(g_3+q\lambda _I)g_4g_5(g_1+\theta \lambda _H)}\cdot \frac{\Lambda g_2(g_1+\theta \lambda _H)}{g_2(g_1+\theta \lambda _H) (\lambda _H+\mu )-(\alpha _1g_2+\alpha _2\rho _1)\lambda _I}=1. \end{aligned}$$

Hence,

$$\begin{aligned} \lambda _H=\mu ({\mathcal {R}}_H-1)=\beta _2H_{2}^{*}=\lambda _{H}^{*}. \end{aligned}$$

Therefore, $h(0)=\mu ({\mathcal {R}}_H-1)=\beta _2H_{2}^{*}=\lambda _{H}^{*}$. It corresponds to the HIV boundary equilibrium. Hence,

$$\begin{aligned} f(0)\,\,= & {} \,\,F_1(0,\lambda _{H}^{*})\,\,\\ \,\,= & {} \,\,\beta _1\frac{qg_4g_5(g_1+\theta \lambda _{H}^{*})\lambda _{H}^{*}}{g_3g_4g_5(g_1+\theta \lambda _{H}^{*})g_4}\frac{g_3}{\beta _2} +\beta _1\frac{\theta \lambda _{H}^{*}}{g_4(g_1+\theta \lambda _{H}^{*})}\frac{g_3}{\beta _2} +\beta _1\frac{1}{g_1+\theta \lambda _{H}^{*}}\frac{g_3}{\beta _2}\,\,\\ \,\,= & {} \,\,\frac{q\beta _1H_{2}^{*}}{g_4}+\frac{\theta \beta _2H_{2}^{*}\beta _1S_{2}^{*}}{(g_1+\theta \beta _2H_{2}^{*})g_4} +\frac{\beta _1S_{2}^{*}g_4}{(g_1+\theta \beta _2H_{2}^{*})g_4}\,\,\\ \,\,= & {} \,\,{\mathcal {R}}_{1}^{2}>1. \end{aligned}$$

Let $\lambda _H=0=h({\bar{\lambda }}_{I}^{*})$. Then when ${\bar{S}}^{*}\le S_{1}^{*}$, we have

$$\begin{aligned} f({\bar{\lambda }}_{I}^{*})=F_1({\bar{\lambda }}_{I}^{*},0)=\beta _1\frac{{\bar{S}}^{*}}{g_1}\le \beta _1\frac{S_{1}^{*}}{g_1}=1. \end{aligned}$$

The above inequality is equivalent to $\lambda _{I}^{*}\le {\bar{\lambda }}_{I}^{*}$. We prove this by contradiction. Assuming $\lambda _{I}^{*}>{\bar{\lambda }}_{I}^{*}$, then at least two values satisfy $F_2(\lambda _I,0)=1$. On the other hand, we can rewrite $F_2(\lambda _I,0)=1$ as a quadratic equation about $\lambda _I$ as follows:

$$\begin{aligned} m_1\lambda _{I}^{2}+m_2\lambda _I+m_3=0, \end{aligned}$$

(13)

where

$$\begin{aligned}{} & {} m_1=c_1-d_1<0,\,\,\\{} & {} m_2=c_2-d_2, \,\,\\{} & {} m_3=c_3-d_3=g_{1}^{2}g_2g_{4}^{2}g_5g_3\mu ({\mathcal {R}}_H-1)>0. \end{aligned}$$

Therefore, Eq. (13) has only one positive root. This conclusion contradicts the hypothesis. Thus, we have $\lambda _{I}^{*}\le {\bar{\lambda }}_{I}^{*}$ and $f({\bar{\lambda }}_{I}^{*})=F_1({\bar{\lambda }}_{I}^{*},0)<1$. For any $\lambda _I\in (0,{\bar{\lambda }}_{I}^{*})$, there exists a unique $\lambda _H$ such that $F_1(\lambda _I,\lambda _H)=1,\ F_2(\lambda _I,\lambda _H)=1$. Therefore, we have the following result:

Theorem 4.1

Assume $c_2>d_2$, system (4) has a coexistence equilibrium when ${\mathcal {R}}_I>1$, ${\mathcal {R}}_H>1$, ${\mathcal {R}}_{2}^{1}>1$ and ${\mathcal {R}}_{1}^{2}>1$.

5 Elasticities of the Invasion Numbers

From Sects. 3 and 4, we know that invasion numbers serve as switches indicating which disease will persist. To estimate the impact of control strategies on this procedure, we consider elasticity analysis according to Martcheva (2015). Here we perform the elasticity analysis of ${\mathcal {R}}_2^1$ and ${\mathcal {R}}_1^2$ with respect to parameters related to treatment and education, i.e. $\alpha _1$, $\alpha _2$, q, $\theta$. For convenience, we denote

$$\begin{aligned} {\mathcal {R}}_{1}^{2}=\frac{A_1+A_2g_4}{A_3g_4}, \end{aligned}$$

(14)

and

$$\begin{aligned} {\mathcal {R}}_{2}^{1}=\frac{B_1+B_2g_4}{B_3+B_4g_4}, \end{aligned}$$

(15)

where

$$\begin{aligned}{} & {} A_1=\theta \beta _2H_{2}^{*}\beta _1S_{2}^{*}+q\beta _1H_{2}^{*}(g_1+\theta \beta _2H_{2}^{*}),\,\,\\{} & {} A_2=\beta _1S_{2}^{*},\,\,\\{} & {} A_3=g_1+\theta \beta _2H_{2}^{*}, \end{aligned}$$

and

$$\begin{aligned}{} & {} B_1=(g_3+q\beta _1I_{1}^{*})\theta \beta _2I_{1}^{*}g_5+\theta \beta _2I_{1}^{*}\rho _1\sigma \alpha _2 +g_5q\beta _1I_{1}^{*}\beta _2S_{1}^{*}+g_5\theta \beta _2I_{1}^{*}\sigma \alpha _1,\,\,\\{} & {} B_2=g_5\beta _2S_{1}^{*},\,\,\\{} & {} B_3=-(\rho _1\sigma \alpha _2+\sigma \alpha _1g_5)q\beta _1I_{1}^{*},\,\,\\{} & {} B_4=(g_3+q\beta _1I_{1}^{*})g_5. \end{aligned}$$

We start from investigating the elasticity index of ${\mathcal {R}}_{2}^{1}$ with respect to $\omega$, where $\omega \in \{\alpha _1,\ \alpha _2,\ q,\ \theta \}$. It follows that

$$\begin{aligned} \varepsilon _{{\mathcal {R}}_{2}^{1}}^{\omega }=\frac{\partial {\mathcal {R}}_{2}^{1}}{\partial \omega } \frac{\omega }{{\mathcal {R}}_{2}^{1}}, \end{aligned}$$

where

$$\begin{aligned} \frac{\partial {\mathcal {R}}_{2}^{1}}{\partial \omega }=\frac{\frac{\partial (B_1+B_2g_4)}{\partial \omega }(B_3+B_4g_4) -\frac{\partial (B_3+B_4g_4)}{\partial \omega }(B_1+B_2g_4)}{(B_3+B_4g_4)^2}. \end{aligned}$$

Case 1 $\omega =\alpha _1$

$$\begin{aligned} \frac{\partial (B_1+B_2g_4)}{\partial \alpha _1}\,\,= & {} \,\,q\beta _1\theta \beta _2I_{1}^{*}g_5\frac{\partial I_{1}^{*}}{\partial \alpha _1}+(g_3+q\beta _1I_{1}^{*})\theta \beta _2g_5\frac{\partial I_{1}^{*}}{\partial \alpha _1} +\theta \beta _2\rho _1\sigma \alpha _2\frac{\partial I_{1}^{*}}{\partial \alpha _1}\\{} & {} +g_5q\beta _1\beta _2S_{1}^{*}\frac{\partial I_{1}^{*}}{\partial \alpha _1}+g_5q\beta _1I_{1}^{*}\beta _2\frac{\partial S_{1}^{*}}{\partial \alpha _1} +g_5\theta \beta _2\sigma \alpha _1\frac{\partial I_{1}^{*}}{\partial \alpha _1} \\{} & {} +\beta _2g_4g_5\frac{\partial S_{1}^{*}}{\partial \alpha _1} +g_5\theta \beta _2I_{1}^{*}\sigma +g_5\beta _2S_{1}^{*}\sigma ,\,\,\\ \frac{\partial (B_3+B_4g_4)}{\partial \alpha _1}\,\,= & {} \,\,-\sigma g_5q\beta _1I_{1}^{*}-(\rho _1\sigma \alpha _2+\sigma \alpha _1g_5)q\beta _1\frac{\partial I_{1}^{*}}{\partial \alpha _1}\\{} & {} +q\beta _1g_4g_5\frac{\partial I_{1}^{*}}{\partial \alpha _1} +(g_3+q\beta _1I_{1}^{*})g_5\sigma , \end{aligned}$$

where

$$\begin{aligned} \frac{\partial S_{1}^{*}}{\partial \alpha _1}\,\,= & {} \,\,\frac{1}{\beta _1},\,\,\\ \frac{\partial I_{1}^{*}}{\partial \alpha _1}\,\,= & {} \,\,\frac{[g_2\mu ({\mathcal {R}}_I-1)-g_2\Lambda \frac{\beta _1}{g_1}] }{[\beta _1(\mu g_2+\rho _1(\rho _2+\mu ))]}. \end{aligned}$$

Case 2 $\omega =\alpha _2$

$$\begin{aligned} \frac{\partial (B_1+B_2g_4)}{\partial \alpha _2}\,\,= & {} \,\,q\beta _1\theta \beta _2I_{1}^{*}g_5\frac{\partial I_{1}^{*}}{\partial \alpha _2}+(g_3+q\beta _1I_{1}^{*})\theta \beta _2g_5\frac{\partial I_{1}^{*}}{\partial \alpha _2}+(g_3+q\beta _1I_{1}^{*})\theta \beta _2I_{1}^{*}\sigma \,\,\\{} & {} +\theta \beta _2\rho _1\sigma \alpha _2\frac{\partial I_{1}^{*}}{\partial \alpha _2} +\theta \beta _2I_{1}^{*}\rho _1\sigma +q\sigma \beta _1I_{1}^{*}\beta _2S_{1}^{*} +g_5q\beta _1\beta _2S_{1}^{*}\frac{\partial I_{1}^{*}}{\partial \alpha _2}\\{} & {} +g_5\theta \beta _2\sigma \alpha _1\frac{\partial I_{1}^{*}}{\partial \alpha _2}+\sigma \theta \beta _2I_{1}^{*}\sigma \alpha _1 +\beta _2S_{1}^{*}\sigma g_4,\,\,\\ \frac{\partial (B_3+B_4g_4)}{\partial \alpha _2}\,\,= & {} \,\, -\rho _1\sigma q\beta _1I_{1}^{*}-\sigma \alpha _1\sigma q\beta _1I_{1}^{*}-(\rho _1\sigma \alpha _2+\sigma \alpha _1g_5)q\beta _1\frac{\partial I_{1}^{*}}{\partial \alpha _2}\,\,\\{} & {} +q\beta _1g_4g_5\frac{\partial I_{1}^{*}}{\partial \alpha _2} +q\beta _1I_{1}^{*}g_5\sigma , \end{aligned}$$

where

$$\begin{aligned} \frac{\partial I_{1}^{*}}{\partial \alpha _2}\,\,= & {} \,\,\frac{g_1\mu ({\mathcal {R}}_I-1)\beta _1[\mu g_2+\rho _1(\rho _2+\mu )]-\beta _1\mu g_1g_2\mu ({\mathcal {R}}_I-1)}{[\beta _1(\mu g_2+\rho _1(\rho _2+\mu ))]^2}. \end{aligned}$$

Case 3 $\omega =q$

$$\begin{aligned} \frac{\partial (B_1+B_2g_4)}{\partial q}\,\,= & {} \,\,\beta _1I_{1}^{*}\theta \beta _2I_{1}^{*}g_5+g_5\beta _1I_{1}^{*}\beta _2S_{1}^{*},\,\,\\ \frac{\partial (B_3+B_4g_4)}{\partial q}\,\,= & {} \,\,-(\rho _1\sigma \alpha _2+\sigma \alpha _1g_5)\beta _1I_{1}^{*}+\beta _1I_{1}^{*}g_4g_5. \end{aligned}$$

Case 4 $\omega =\theta$

$$\begin{aligned} \frac{\partial (B_1+B_2g_4)}{\partial \theta }\,\,= & {} \,\,(g_3+q\beta _1I_{1}^{*})\beta _2I_{1}^{*}g_5+\beta _2I_{1}^{*}\rho _1\sigma \alpha _2 +g_5\beta _2I_{1}^{*}\sigma \alpha _1,\\ \frac{\partial (B_3+B_4g_4)}{\partial \theta }\,\,= & {} \,\,0. \end{aligned}$$

Similarly, we study the elasticity index of ${\mathcal {R}}_{1}^{2}$ with respect to $\omega$, where $\omega \in \{\alpha _1,\ \alpha _2,\ q,\ \theta \}$. It follows that

$$\begin{aligned} \varepsilon _{{\mathcal {R}}_{1}^{2}}^{\omega }=\frac{\partial {\mathcal {R}}_{1}^{2}}{\partial \omega } \frac{\omega }{{\mathcal {R}}_{1}^{2}}, \end{aligned}$$

where

$$\begin{aligned} \frac{\partial {\mathcal {R}}_{1}^{2}}{\partial \omega }=\frac{\frac{\partial (A_1+A_2g_4)}{\partial \omega }(A_3g_4)-\frac{\partial (A_3g_4)}{\partial \omega }(A_1+A_2g_4)}{(A_3g_4)^2}, \end{aligned}$$

Case 1 $\omega =\alpha _1$

$$\begin{aligned}{} & {} \frac{\partial (A_1+A_2g_4)}{\partial \alpha _1}\,\,=\,\,q\beta _1 H_2^* + A_2\sigma , \,\,\\{} & {} \frac{\partial (A_3 g_4)}{\partial \alpha _1}\,\,=\,\,g_4 + A_3 \sigma . \end{aligned}$$

Case 2 $\omega =\alpha _2$

$$\begin{aligned}{} & {} \frac{\partial (A_1+A_2g_4)}{\partial \alpha _2}\,\,=\,\,0, \,\,\\{} & {} \frac{\partial (A_3 g_4)}{\partial \alpha _2}\,\,=\,\, 0. \end{aligned}$$

Case 3 $\omega =q$

$$\begin{aligned}{} & {} \frac{\partial (A_1+A_2g_4)}{\partial q}=\beta _1H_{2}^{*}(g_1+\theta \beta _2H_{2}^{*}),\,\,\\{} & {} \frac{\partial (A_3g_4)}{\partial q}=0. \end{aligned}$$

Case 4 $\omega =\theta$

$$\begin{aligned}{} & {} \frac{\partial (A_1+A_2g_4)}{\partial \theta }=\beta _2H_{2}^{*}\beta _1S_{2}^{*}+q\beta _1H_{2}^{*}\beta _2H_{2}^{*},\,\,\\{} & {} \frac{\partial (A_3g_4)}{\partial q}=\beta _2H_{2}^{*}g_4. \end{aligned}$$

6 Numerical Simulation

6.1 Data and Fixed Parameter Values

We collected new cases of primary and secondary syphilis per year between 2000 and 2019 from the Centers for Disease Control and Prevention (CDC) (CDC 2022a). However, for the new cases of HIV, we only found data from 2006 to 2019, which were also collected from the US CDC (CDC 2022b). The data set for model calibration is listed in Table 2. Correspondingly, we collected the demographic data of the US from 2000 to 2019 from the website (Macrotrends 2022) to generate the recruitment rate and natural death rate during this period. More specifically, from the population size and birth rate (per 1000 individuals), we estimated the recruitment rate to be population * birth rate/1000. From the life expectancy, we estimated the natural death rate to be 1/life expectancy. For simplicity, in our model, the recruitment rate $\Lambda$ and natural death rate $\mu$ are constants. Therefore, we use the average of the recruitment rate and natural death rate per year from 2000 to 2019, i.e. $\Lambda =4039262$ and $\mu =0.013$ with units person/year and year$^{-1}$ respectively (see Table 3). According to Garnett et al. (1997), the mean durations for primary and secondary syphilis are 46 and 108 days, respectively. Hence, we set the progression rates $\rho _1=365/46$ and $\rho _2=365/108$ with unit year$^{-1}$. The above results are tabulated in Table 4.

Table 2 Data from the US CDC for model calibration (CDC 2022a, b)

Table 3 Data from the website to generate recruitment rate and natural death rate (Macrotrends 2022)

6.2 Model Calibration

We use weighted least-squares approach to minimize the mean squared errors (MSE) between the observed data and predicted results from the model. Reported data of yearly primary and secondary syphilis cases and HIV cases in the US are used in this paper.

First, to make two data sets and two sets of corresponding simulated values from the model have the same order of magnitude, we normalize them by dividing by the mean value of each data set. Then we minimize the following mean squared error (MSE):

$$\begin{aligned} \text {MSE}=\sum _{i=1}^{N_1}\frac{\left( x(t_i)/{\bar{X}}-X_i/{\bar{X}}\right) ^2}{N_1}+\sum _{j=1}^{N_2}\frac{\left( y(t_j)/{\bar{Y}}-Y_j/{\bar{Y}}\right) ^2}{N_2}, \end{aligned}$$

where the first and the second terms correspond to new syphilis cases and HIV cases, respectively. $X_i$, $Y_j$ are data values, and $N_1$, $N_2$ are the numbers of data points for syphilis and HIV, respectively. ${\bar{X}}$, ${\bar{Y}}$ are mean values of $\{X_i\}_{i=1}^{N_1}$ and $\{Y_j\}_{j=1}^{N_2}$, respectively. $x(t_i)$ and $y(t_j)$ are predicted values from the model at the same time points corresponding to the data. It follows that

$$\begin{aligned} x(t_i)=\beta _{1}\Big (I(t_i)+H_I(t_i)\Big )\Big (S(t_i)+q H(t_i)\Big )+\rho _1\Big (I(t_i)+H_I(t_i)\Big ) \end{aligned}$$

and

$$\begin{aligned} y(t_j)=\beta _{2}\Big (H(t_j)+H_I(t_j)\Big )\Big (S(t_j)+\theta I(t_j)\Big ). \end{aligned}$$

Here $\beta _{1}\Big (I(t_i)+H_I(t_i)\Big )S(t_i)$ and $\beta _{1}\Big (I(t_i)+H_I(t_i)\Big )q H(t_i)$ represent newly primary syphilis infections coming from susceptible individuals and individuals only infected with HIV at time $t_i$, respectively. While $\rho _1 I(t_i)$ and $\rho _1 H_I(t_i)$ represent newly secondary syphilis infections coming from individuals only infected with primary syphilis and individuals infected with HIV and primary syphilis at time $t_i$, respectively. Newly HIV infections coming from susceptible individuals and individuals only infected with syphilis at time $t_j$ are given by $\beta _{2}\Big (H(t_j)+H_I(t_j)\Big )S(t_j)$ and $\beta _{2}\Big (H(t_j)+H_I(t_j)\Big )\theta I(t_j)$, respectively.

The fitted parameter values are given in Table 4. We can see that syphilis is more transmissible than HIV since $\beta _1>\beta _2$. $\mu _1<\mu _2<\mu _3$ implies that having higher-stage syphilis will increase the risk of death for HIV-positive individuals. Since $q>1$, we can derive that HIV-positive individuals are more likely to be infected by syphilis compared with HIV-negative individuals. Similarly, $\theta >1$ shows that patients with syphilis have higher risk to be infected by HIV compared with those without syphilis. $\alpha _1>\alpha _2$ implies that the treatment is longer for secondary syphilis compared with primary syphilis. The corresponding reproduction numbers and invasion numbers are also computed and shown in Table 4. In addition, the comparison of observed data and model estimation using fitted parameter values from Table 4 is shown in Fig. 2. We also derived the 95% confidence intervals for syphilis new cases and HIV new cases, which are shown in shaded regions in Fig. 2.

Fig. 2

Model calibration by new primary and secondary syphilis cases and HIV cases in the US. The results for syphilis infection and HIV infection are shown in (a) and (b), respectively. The shaded regions are 95% confidence intervals. The data set used here is listed in Table 2 (Color figure online)

Table 4 Fixed and fitted parameter values and corresponding reproduction numbers and invasion numbers

Fig. 3

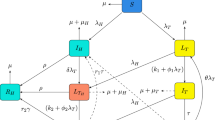
a The existence and stability of the equilibrium of model (4) with different values of ${\mathcal {R}}_{I}$, ${\mathcal {R}}_{H}$, ${\mathcal {R}}_{2}^1$ and ${\mathcal {R}}_{1}^2$. The circled equilibrium is stable in each region. The dashed circle indicates that it is only numerically verified. The arrows represent that the corresponding invasion number changes from less that 1 to greater that 1. b The prevalence when ${\mathcal {R}}_{I}=2.18$, ${\mathcal {R}}_{H}=2.02$, ${\mathcal {R}}_{2}^1=1.03$, ${\mathcal {R}}_{1}^2=1.15$. Here $c_2=7.33\times 10^5$ and $d_2=1.07\times 10^6$. It shows that the coexistence equilibrium exists and is stable when ${\mathcal {R}}_{I}>1$, ${\mathcal {R}}_{H}>1$, ${\mathcal {R}}_{2}^1>1$ and ${\mathcal {R}}_{1}^2>1$, even when $c_2<d_2$ (Color figure online)

6.3 Equilibria and Their Stability

In Sect. 3 we derived the existence and stability of the disease-free and boundary equilibria, which are summarized in Fig. 3a. The circled equilibrium is stable in each region. However, due to the complexity of the model, we only have the existence of the coexistence equilibrium when $c_2>d_2$ in Sect. 4. By running several simulations, we found that when $c_2<d_2$, the coexistence equilibrium also exists once ${\mathcal {R}}_I>1$, ${\mathcal {R}}_H>1$, ${\mathcal {R}}_2^1>1$ and ${\mathcal {R}}_1^2>1$. In either case, the coexistence equilibrium is stable. This result is also summarized in Fig. 3a. The dashed circle indicates that the stability of the coexistence equilibrium is only numerically verified. The arrows represent that the corresponding invasion number changes from less than 1 to greater than 1. An example of the stable coexistence equilibrium is given in Fig. 3b when $c_2<d_2$.

6.4 Elasticity Visualization

From Sects. 3, 4 and 6.3 we know that reproduction numbers (${\mathcal {R}}_I$, ${\mathcal {R}}_H$) and invasion numbers (${\mathcal {R}}_{2}^1$, ${\mathcal {R}}_{1}^2$) are thresholds for disease elimination and switches indicating which disease will persist. Therefore, we first visualize the elasticity of ${\mathcal {R}}_{2}^1$ and ${\mathcal {R}}_{1}^2$ using formulas from Sect. 5 and parameter values from Table 4. In Fig. 4a, the elasticity index of ${\mathcal {R}}_{2}^1$ with respect to $\alpha _1$ is 0.2129. This shows that $1\%$ increase of $\alpha _1$ leads to $0.2129\%$ increase of ${\mathcal {R}}_{2}^1$. The other terms in Fig. 4a, b have similar meanings. It shows that $\alpha _1$ has much more influence on ${\mathcal {R}}_{2}^1$ and ${\mathcal {R}}_{1}^2$ than other three parameters. More specifically, improving treatment for primary syphilis (increasing $\alpha _1$) will increase the invasion capability of HIV and decrease the invasion capability of syphilis. This sign difference of elasticities of ${\mathcal {R}}_{2}^1$ and ${\mathcal {R}}_{1}^2$ is also true for other three parameters. The above results indicate that ${\mathcal {R}}_{2}^1$ and ${\mathcal {R}}_{1}^2$ might be negatively correlated. To verify this,

we plotted ${\mathcal {R}}_{2}^1$ in terms of ${\mathcal {R}}_{1}^2$ in Fig. 4c. As we can see, ${\mathcal {R}}_{1}^2$ is a decreasing function of ${\mathcal {R}}_{2}^1$. It implies that increasing of invasion capability of one disease will weaken the invasion capability of the other disease. In other words, there exists some kind of competition between the two diseases.

Fig. 4

a, b Elasticity indices of ${\mathcal {R}}_{2}^1$ and ${\mathcal {R}}_{1}^2$ with respect to parameters related to treatment and education. Parameter values are from Table 4. c The relation between ${\mathcal {R}}_{2}^1$ and ${\mathcal {R}}_{1}^2$. Here we vary $\alpha _1$ and the other parameter values are from Table 4 (Color figure online)

Fig. 5

a Reproduction numbers and invasion numbers given different values of $\alpha _1$. b Zoomed-in invasion numbers from (a). c–e Total syphilis infections, total HIV infections and total infections of two diseases respectively given different values of $\alpha _1$. In all panels, the other parameter values are from Table 4 (Color figure online)

Fig. 6

Total syphilis infections and total HIV infections respectively given different values of $\alpha _2$ (a, b), q (c, d), and $\theta$ (e, f). In all panels, the other parameter values are from Table 4 (Color figure online)

6.5 Control Strategies

From above we know that $\alpha _1$ (treatment for primary syphilis) has great impact on both ${\mathcal {R}}_{2}^1$ and ${\mathcal {R}}_{1}^2$. We are also interested in its influence on reproduction numbers and prevalence. Therefore, in Fig. 5a we plotted all reproduction numbers and invasion numbers as functions of $\alpha _1$. We recall that ${\mathcal {R}}_{2}^1$ exists only when ${\mathcal {R}}_I>1$ and ${\mathcal {R}}_{1}^2$ exists only when ${\mathcal {R}}_H>1$. Based on parameter values from Table 4, when $\alpha _1\in [2.5, 3]$, ${\mathcal {R}}_H>1$ in the whole interval and ${\mathcal {R}}_I>1$ only when $\alpha _1\in [2.5, 2.91)$. In addition, we can see that as $\alpha _1$ increases, both ${\mathcal {R}}_I$ and ${\mathcal {R}}_1^2$ decrease, ${\mathcal {R}}_2^1$ increases and ${\mathcal {R}}_H$ stays the same. These results agree with Fig. 4. By zooming in, Fig. 5b shows that when $\alpha _1\in (2.802, 2.8203)$, both ${\mathcal {R}}_2^1>1$ and ${\mathcal {R}}_1^2>1$. In this case, we have coexistence equilibrium. Consequently, the prevalence of total syphilis infections ($I+L+H_I+H_L$) is diminished as $\alpha _1$ increases. More specifically, the peak of infection is lowered and postponed (see Fig. 5c). In contrast, the prevalence of total HIV infections ($H+H_I+H_L$) increases as $\alpha _1$ increases (see Fig. 5d). It is worth mentioning that improving treatment for primary syphilis (increasing $\alpha _1$) is still helpful to diminish the prevalence of total infections of two diseases (see Fig. 5e). On the other hand, $\alpha _2$ (treatment for secondary syphilis) only has minor influence on the prevalence of total syphilis infections and total HIV infections (see Fig. 6a, b). Similar results are shown for q and $\theta$ corresponding to education (see Fig. 6c–f). These results agree with Fig. 4a, b.

From above we can see that treatment in the primary stage of syphilis is more important than that in the secondary stage. Hence, we are interested in the impact of initiating years of treatment on the prevalence. For example, in Fig. 7a, b, we assume that the baseline corresponds to the current treatment ($\alpha _1=2.53$) and improving treatment corresponds to $\alpha _1=2.58$. Since $\alpha _1$ represents the treatment rate of primary syphilis, $1/\alpha _1$ represents the length of the treatment. It follows that increasing $\alpha _1$ corresponds to shortening the length of treatment. Figure 7 shows that improving treatment earlier can postpone the infection peak of syphilis but increase the prevalence of HIV. This further verifies the competition between the two diseases. Compared to the baseline scenario, improving treatment at any time leads to a lower and delayed peak. However, the relation between the peak size of total syphilis infections and the starting years of improvement is not linear. One possible reason is that here we only consider the treatment for primary syphilis infection. It might compensate the infections of HIV.

Fig. 7

Total syphilis infections (a) and total HIV infections (b) respectively given different starting years of the treatment improvement. In both panels, baseline corresponds to $\alpha _1=2.53$ and treatment improvement corresponds to $\alpha _1=2.58$. The other parameter values are from Table 4 (Color figure online)

7 Conclusion and Discussion

In this paper, we formulated a syphilis and HIV coinfection model to study the dynamics of syphilis and HIV transmission in Sect. 2. The explicit formulas of two reproduction numbers (${\mathcal {R}}_I$, ${\mathcal {R}}_H$) and invasion numbers (${\mathcal {R}}_2^1$, ${\mathcal {R}}_1^2$) were derived. We also interpreted their biological meanings. Rigorous analyses of the existence and stability of the disease-free equilibrium and two boundary equilibria are given in Sect. 3. Due to the complexity of the model, we only proved the existence of the coexistence equilibrium when $c_2>d_2$ in Sect. 4. But we numerically verified its existence when $c_2<d_2$ as well as its stability. The above results were summarized in Fig. 3. More specifically, the unique disease-free equilibrium always exists and is stable when both reproduction numbers are less than 1. The boundary equilibrium for syphilis infection $E_1^*$ exists when ${\mathcal {R}}_I>1$ and is stable when ${\mathcal {R}}_2^1<1$. Similarly, the boundary equilibrium for HIV infection $E_2^*$ exists when ${\mathcal {R}}_H>1$ and is stable when ${\mathcal {R}}_1^2<1$. If both invasion numbers ${\mathcal {R}}_2^1>1$ and ${\mathcal {R}}_1^2>1$, coexistence equilibrium exists, which might be stable.

We calibrated the model using yearly confirmed syphilis and HIV data from the US CDC. Based on the fitted parameter values as well as several fixed parameter values generated from website or previous literature, we obtained that both reproduction numbers for syphilis and HIV are slightly greater than 1. The invasion reproduction number for syphilis is slightly greater than 1 while this number for HIV is slightly less than 1 (see Table 4). In this case, the boundary equilibrium for syphilis infection will be stable. According to our model, the cases for syphilis will gradually increase while HIV cases will gradually decrease since all four values above are close to 1. This agrees with what we observed in real life (see data in Table 2). Additionally, the resurgence of syphilis infection in the US was also reported in Schmidt et al. (2019) and Bach and Heavey (2021). While the trends of HIV cases in the US was decreasing based on data from 1992 to 2013 (Williams et al. 2020).

Reproduction numbers and invasion numbers are thresholds for disease elimination and switches indicating which disease will persist. It is important to know the impact of key parameters on them. Therefore, we performed elasticity analysis of ${\mathcal {R}}_2^1$ and ${\mathcal {R}}_1^2$ with respect to parameters related to treatment and education. Based on parameter values from Table 4, we visualized the above elasticity values and found that increasing of invasion capability of one disease would weaken the invasion capability of the other disease. In addition, we found that treatment for primary syphilis is more important in mitigating the transmission of syphilis among considered control strategies. Similar results were shown in Saad-Roy et al. (2016) and Pialoux et al. (2008). However, it might lead to more HIV cases. Further, we showed that the infection peak of syphilis would be postponed by improving treatment for primary syphilis. The same effect is produced by implementing better syphilis treatment earlier. The importance of early initiating of control strategies was also discussed in He et al. (2021), Knock et al. (2021) and Shen et al. (2021) regarding COVID-19.

There are several limitations of this study. Firstly, standard incidence and mass action are two most common incidences used in epidemiology modeling. When the total population is a constant, standard incidence becomes mass action incidence. But we need to pay attention that the transmission parameters in two incidences have different meanings and units. For sexually transmitted diseases, standard incidence is more proper (Martcheva 2015). However, it will bring challenges for model analysis. The population size is stable in the US for the period of the data. Therefore, for simplicity, we adopted mass action in this paper, which is also used in other papers about syphilis or HIV (Saad-Roy et al. 2016; Milner and Zhao 2010; Iboi and Okuonghae 2016; Cai et al. 2009). Secondly, it is more realistic for multi-disease models to include co-transmission (Gao et al. 2016; Teixeira et al. 2021). However, the possibility for individuals to be infected by two diseases simultaneously is quite small. In most cases, a person will contract one disease firstly. For simplicity, transmission from susceptible class to the class infected with two diseases is not included in our model, which is also not considered in some other multi-disease or multi-strain models (Nwankwo and Okuonghae 2018; Poolman et al. 2008). Thirdly, patients in the secondary syphilis period are infectious. However, since most of them have severe symptoms and hence are more cautious, we simply assume that secondary syphilis patients are not infectious and will not contract HIV. Fourthly, we didn’t include vertical transmission for both syphilis and HIV infection. Another limitation of this paper is the reliability of data set for calibration. Here we use newly confirmed syphilis cases and HIV cases, which are reported cases instead of true cases. However, it is hard to get true cases, which might be higher than reported cases and affect fitted parameter values.

In summary, we adopted a deterministic model to investigate the coinfection of syphilis and HIV. Even though we considered two specific diseases, and data are from the US, the results derived here could be adapted to other multi-diseases scenarios in other regions.

Appendices

Appendix A: Proof of Theorem 3.2

We define the following Lyapunov function

$$\begin{aligned} {\mathcal {L}}=I+H+H_I+\frac{\sigma \alpha _2}{g_5}H_L. \end{aligned}$$

It is clear that ${\mathcal {L}}$ is radially unbounded and positive definite in the entire space ${\mathcal {D}}$. The derivative of ${\mathcal {L}}$ along the trajectories of System (4) yields

$$\begin{aligned} \dot{{\mathcal {L}}}=&(\lambda _IS-g_1I-\theta \lambda _HI) + (\lambda _HS-g_3H-q\lambda _IH+\sigma \alpha _1H_I+\sigma \alpha _2H_L)\\&+ (q\lambda _IH+\theta \lambda _HI-g_4H_I) +\frac{\sigma \alpha _2}{g_5}(\rho _1H_I-g_5H_L)\\ \le&\big [\beta _1(I+H_I)S_0^*-g_1I\big ] + \big [\beta _2(H+H_I)S_0^*-g_3H+\sigma \alpha _1H_I+\sigma \alpha _2H_L\big ]\\&-g_4H_I + \frac{\sigma \alpha _2}{g_5} (\rho _1H_I-g_5H_L)\\ =&(\beta _1S_0^*-g_1)I + (\beta _2S_0^*-g_3)H + \bigg (\beta _1S_0^*+\beta _2S_0^*+\sigma \alpha _1-g_4+\frac{\sigma \alpha _2}{g_5}\rho _1\bigg )H_I. \end{aligned}$$

When ${\mathcal {R}}<1$, we have $\beta _1S_0^*<g_1$ and $\beta _2S_0^*<g_3$. In addition, if $\rho _1+\alpha _1+\rho _2+\alpha _2+\mu \le \mu _2$, we can verify that

$$\begin{aligned} \beta _1S_0^*+\beta _2S_0^*+\sigma \alpha _1-g_4+\frac{\sigma \alpha _2}{g_5}\rho _1< g_1+g_3+\sigma \alpha _1-g_4+\rho _1\le 0. \end{aligned}$$

It follows that $\dot{{\mathcal {L}}}\le 0$ and it is equal to zero only at the DFE. Therefore, by Krasovkii-LaSalle Theorem (Martcheva 2015), the DFE $E_0^*$ is globally asymptotically stable when ${\mathcal {R}}<1$ and $\rho _1+\alpha _1+\rho _2+\alpha _2+\mu \le \mu _2$.

Appendix B: Proof of Proposition 3.3

We use a theorem introduced by Castillo-Chavez and Song Castillo-Chavez and Song (2004) to prove this Proposition. Without loss of generality, we assume ${\mathcal {R}}_I>{\mathcal {R}}_H$. Then we choose $\beta _1$ as the bifurcation parameter and let $\beta _1^*$ be the critical value such that ${\mathcal {R}}={\mathcal {R}}_I=1$ (If ${\mathcal {R}}_I<{\mathcal {R}}_H$, we can choose $\beta _2$ as the bifurcation parameter). Reordering variables as $x=(I, L, H, H_I, H_L, S)^T$, the Jacobian matrix of system (4) evaluated at the DFE and $\beta _1^*$ is

$$\begin{aligned} {\mathcal {A}}=\begin{pmatrix} 0 &{} 0 &{} 0 &{} \beta _1^*S_0^* &{} 0 &{} 0\\ \rho _1 &{} -g_2 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} \beta _2S_0^*-g_3 &{} \beta _2S_0^*+\sigma \alpha _1 &{} \sigma \alpha _2 &{} 0\\ 0 &{} 0 &{} 0 &{} -g_4 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} \rho _1 &{} -g_5 &{} 0\\ -\beta _1^*S_0^*+\alpha _1 &{} \alpha _2 &{} -\beta _2S_0^* &{} -\beta _1^*S_0^*-\beta _2S_0^* &{} 0 &{} -\mu \\ \end{pmatrix}. \end{aligned}$$

The eigenvalues of ${\mathcal {A}}$ are $-\mu , -g_2, -g_4, -g_5, 0$ and $\beta _2S_0^*-g_3$. Since at $\beta _1=\beta _1^*$, ${\mathcal {R}}_H<{\mathcal {R}}_I=1$, then $\beta _2S_0^*<g_3$. Hence, zero is a simple eigenvalue of ${\mathcal {A}}$ and the other eigenvalues have negative real parts. Moreover, ${\mathcal {A}}$ has a right eigenvector (corresponding to the zero eigenvalue), given by $w=(w_1, w_2, 0, 0, 0, w_6)^T$, where

$$\begin{aligned} w_1=g_2,\qquad w_2=\rho _1,\qquad w_6=\frac{ (-\beta _1^*S_0^*+\alpha _1)g_2+\alpha _2\rho _1}{\mu }. \end{aligned}$$

Since $S>0$ at the DFE, then $w_6$ does not need to be nonnegative. In addition, ${\mathcal {A}}$ has a left eigenvector (corresponding to the zero eigenvalue), given by $v=(v_1, 0, 0, v_4, 0, 0)^T$, where

$$\begin{aligned} v_1=g_4,\qquad v_4=\beta _1^*S_0^*. \end{aligned}$$

We denote the right-hand side functions of system (4) as $f_i$, $i=1,\ldots ,6$. Because the nonnegative components of v are $v_1$ and $v_4$, we only need the derivatives of $f_1$ and $f_4$. At the DFE and $\beta _1=\beta _1^*$, the associated non-zero secondary partial derivatives are

$$\begin{aligned} \frac{\partial ^2f_1}{\partial I\partial S}=\beta _1^*,\qquad \frac{\partial ^2f_1}{\partial \beta _1\partial I}=S_0^*. \end{aligned}$$

Therefore,

$$\begin{aligned} a=v_1w_1w_6\frac{\partial ^2f_1}{\partial I\partial S}=g_4g_2\rho _1\beta _1^*>0, \qquad b=v_1w_1\frac{\partial ^2f_1}{\partial \beta _1\partial I}=g_4g_2S_0^*>0. \end{aligned}$$

According to the theorem by Castillo-Chavez and Song (Castillo-Chavez and Song 2004), system (4) has backward bifurcation.

Appendix C: Proof of Theorem 3.4

To obtain the equilibrium $E_{1}^{*}$, we let $H=H_I=H_L=0$. From system (4), we have that the equilibrium $E_{1}^{*}=(S_{1}^{*}, I_{1}^{*}, L_{1}^{*}, 0, 0, 0)$ satisfies

$$\begin{aligned} \begin{aligned} 0&=\Lambda -\lambda _{I}S_{1}^{*}-\mu S_{1}^{*}+\alpha _{1}I_{1}^{*}+\alpha _{2}L_{1}^{*},\\ 0&=\lambda _{I}S_{1}^{*}-\rho _{1}I_{1}^{*}-\mu I_{1}^{*}-\alpha _{1}I_{1}^{*},\\ 0&=\rho _{1}I_{1}^{*}-\rho _{2}L_{1}^{*}-\mu L_{1}^{*}-\alpha _{2}L_{1}^{*}.\\ \end{aligned} \end{aligned}$$

(16)

From the second equation of (16), we have

$$\begin{aligned} S_{1}^{*}=\frac{g_1}{\beta _1}. \end{aligned}$$

(17)

Substituting (17) into the first and third equation of (16), we have

$$\begin{aligned} I_{1}^{*}=\frac{g_{1}g_{2}\mu ({\mathcal {R}}_{I}-1)}{\beta _1[\mu g_{2}+\rho _{1}(\rho _{2}+\mu )]},\ \ \ L_{1}^{*}=\frac{\rho _1}{g_2}I_{1}^{*}. \end{aligned}$$

(18)

Similarly, we denote by $E_{2}^{*}=(S_{2}^{*}, 0, 0, H_{2}^{*}, 0, 0)$ the boundary equilibrium corresponding to HIV infection. To obtain equilibrium $E_{2}^{*}$, we let $I=L=H_{I}=H_{L}=0$. From system (4), we have that the equilibrium $E_{2}^{*}=(S_{2}^{*}, 0, 0, H_{2}^{*}, 0, 0)$ satisfies

$$\begin{aligned} \begin{aligned} 0&=\Lambda -\lambda _{H}S_{2}^{*}-\mu S_{2}^{*},\,\,\\ 0&=\lambda _{H}S_{2}^{*}-\mu H_{2}^{*}-\mu _{1}H_{2}^{*}. \end{aligned} \end{aligned}$$

(19)

Following similar steps as for $E_{1}^{*}$, we get

$$\begin{aligned} S_{2}^{*}=\frac{g_3}{\beta _2}, \end{aligned}$$

$$\begin{aligned} H_{2}^{*}=\frac{\mu }{\beta _{2}}({\mathcal {R}}_{H}-1). \end{aligned}$$

(20)

From (18) and (20), we can clearly see that $I_{1}^{*}>0$ and $L_{1}^{*}>0$ if and only if ${\mathcal {R}}_I>1$; $H_{2}^{*}>0$ if and only if ${\mathcal {R}}_H>1$.

Appendix D: Proof of Theorem 3.5

By linearizing system (4) at the boundary equilibrium $E_{1}^{*}$ , we have the Jacobian matrix

$$\begin{aligned} {\mathcal {J}}(E_{1}^{*})=\left( \begin{array}{cc}A&{}C\\ 0&{}B \end{array}\right) \end{aligned}$$

with

$$\begin{aligned} A=\left( \begin{array}{ccc}-\beta _{1}I_{1}^{*}-\mu &{}-\beta _{1}S_{1}^{*}+\alpha _1&{}\alpha _2\\ \beta _{1}I_{1}^{*}&{}\beta _{1}S_{1}^{*}-g_1&{}0\\ 0&{}\rho _1&{}-g_2 \end{array}\right) , \end{aligned}$$

$$\begin{aligned} B=\left( \begin{array}{ccc}\beta _{2}S_{1}^{*}-g_3-q\beta _{1}I_{1}^{*}&{}\beta _{2}S_{1}^{*}+\sigma \alpha _1&{}\sigma \alpha _2\\ q\beta _{1}I_{1}^{*} +\theta \beta _{2}I_{1}^{*}&{}\theta \beta _{2}I_{1}^{*}-g_4&{}0\\ 0&{}\rho _1&{}-g_5 \end{array}\right) , \end{aligned}$$

$$\begin{aligned} C=\left( \begin{array}{ccc}-\beta _{2}S_{1}^{*}&{}-\beta _{1}S_{1}^{*}-\beta _{2}S_{1}^{*}&{}0\\ theta\beta _{2}I_{1}^{*}&{}\beta _{1}S_{1}^{*} -\theta \beta _{2}I_{1}^{*}&{}0\\ 0&{}0&{}0 \end{array}\right) . \end{aligned}$$

The stability of matrix ${\mathcal {J}}(E_{1}^{*})$ is determined by matrix A and matrix B.

Eigenvalues of A satisfy the following characteristic equation:

$$\begin{aligned} \lambda ^{3}+a_{1}\lambda ^{2}+a_{2}\lambda +a_{3}=0, \end{aligned}$$

(21)

where

$$\begin{aligned} \left\{ \begin{array}{lll} a_1=\beta _{1}I_{1}^{*}+\mu +g_1-\beta _{1}S_{1}^{*}+g_2,\,\,\\ a_2=(\beta _{1}I_{1}^{*}+\mu )(g_1-\beta _{1}S_{1}^{*})+(\beta _{1}I_{1}^{*}+\mu )g_2 +(g_1-\beta _{1}S_{1}^{*})g_2+(\beta _{1}S_{1}^{*}-\alpha _1)\beta _{1}I_{1}^{*},\,\,\\ a_3=(\beta _{1}I_{1}^{*}+\mu )(g_1-\beta _{1}S_{1}^{*})g_2-\beta _{1}I_{1}^{*}\rho _1\alpha _2 +g_{2}(\beta _{1}S_{1}^{*}-\alpha _1)\beta _{1}I_{1}^{*}=g_1g_2\mu ({\mathcal {R}}_I-1). \end{array}\right. \end{aligned}$$

(22)

Note that $g_1=\beta _{1}S_{1}^{*}.$ Obviously, we have

$$\begin{aligned} \left\{ \begin{array}{ll} a_1>0, a_2>0, a_3>0,\,\,\\ a_{1}a_{2}>a_3. \end{array}\right. \end{aligned}$$

According to Routh-Hurwitz criterion, we get that all roots of the characteristic equation (21) have negative real parts. Thus, all eigenvalues of A have negative real parts.

Eigenvalues of B satisfy the following characteristic equation:

$$\begin{aligned} \lambda ^{3}+b_{1}\lambda ^{2}+b_{2}\lambda +b_{3}=0, \end{aligned}$$

(23)

where

$$\begin{aligned} \left\{ \begin{array}{lll} b_1=g_3+q\beta _{1}I_{1}^{*}-\beta _{2}S_{1}^{*}+g_4-\theta \beta _{2}I_{1}^{*}+g_5,\,\,\\ b_2=(g_3+q\beta _{1}I_{1}^{*}-\beta _{2}S_{1}^{*})(g_4-\theta \beta _{2}I_{1}^{*}) \qquad +(g_3+q\beta _{1}I_{1}^{*}-\beta _{2}S_{1}^{*})g_5\,\,\\ \qquad +(g_4-\theta \beta _{2}I_{1}^{*})g_5 -(\beta _{2}S_{1}^{*}+\sigma \alpha _1)(q\beta _{1}I_{1}^{*}+\theta \beta _{2}I_{1}^{*}),\,\,\\ b_3=(g_3+q\beta _{1}I_{1}^{*}-\beta _{2}S_{1}^{*})(g_4-\theta \beta _{2}I_{1}^{*})g_5 -(q\beta _{1}I_{1}^{*}+\theta \beta _{2}I_{1}^{*})\rho _1\sigma \alpha _2\,\,\\ \qquad -(\beta _{2}S_{1}^{*}+\sigma \alpha _1)(q\beta _{1}I_{1}^{*}+\theta \beta _{2}I_{1}^{*})g_5. \end{array}\right. \end{aligned}$$

(24)

We define the invasion number of HIV infection as follows:

$$\begin{aligned} {\mathcal {R}}_{2}^{1}=\frac{\beta _{2}S_{1}^{*}g_4g_5+(g_3+q\beta _{1}I_{1}^{*})\theta \beta _{2}I_{1}^{*}g_5 +\theta \beta _{2}I_{1}^{*}\rho _1\sigma \alpha _2+g_5q\beta _{1}I_{1}^{*}\beta _{2}S_{1}^{*} +g_5\theta \beta _{2}I_{1}^{*}\sigma \alpha _1}{(g_3+q\beta _{1}I_{1}^{*})g_4g_5- (\rho _1\sigma \alpha _2+\sigma \alpha _1g_5)q\beta _{1}I_{1}^{*}},\nonumber \\ \end{aligned}$$

(25)

where

$$\begin{aligned} g_4g_5-(\rho _1\sigma \alpha _2+\sigma \alpha _1g_5)=(\mu +\mu _2)g_5+\rho _1(\mu +\mu _3+\rho _2)>0. \end{aligned}$$

If ${\mathcal {R}}_{2}^{1}<1$, we have

$$\begin{aligned} \left\{ \begin{array}{ll} g_3+q\beta _{1}I_{1}^{*}>\beta _{2}S_{1}^{*},\ \ g_4>\theta \beta _{2}I_{1}^{*},\,\,\\ (g_3+q\beta _{1}I_{1}^{*})g_4>\beta _{2}S_{1}^{*}g_4 +(g_3+q\beta _{1}I_{1}^{*})\theta \beta _{2}I_{1}^{*}\,\,\\ +q\beta _{1}I_{1}^{*}\beta _{2}S_{1}^{*}+\sigma \alpha _1\theta \beta _{2}I_{1}^{*} +\sigma \alpha _1q\beta _{1}I_{1}^{*}. \end{array}\right. \end{aligned}$$

It follows that

$$\begin{aligned} \left\{ \begin{array}{ll} b_1>0, b_2>0, b_3>0,\,\,\\ b_{1}b_{2}>b_3. \end{array}\right. \end{aligned}$$

According to Routh-Hurwitz criterion, we get that all roots of the characteristic equation (23) have negative real parts. Thus, all eigenvalues of A and B have negative real parts. Hence, all eigenvalues of ${\mathcal {J}}(E_{1}^{*})$ have negative real parts. When ${\mathcal {R}}_2^1>1$, $b_3<0$. It indicates that there is at least one positive eigenvalue of ${\mathcal {J}}(E_{1}^{*})$. Therefore, $E_{1}^{*}$ is locally stable if ${\mathcal {R}}_{2}^{1}<1$, and unstable if ${\mathcal {R}}_{2}^{1}>1$. This completes the proof of stability of $E_{1}^{*}$.

Appendix E: Proof of Theorem 3.6

By linearizing system (4) at the boundary equilibrium $E_{2}^{*}$ , we have the Jacobian matrix ${\mathcal {J}}(E_{2}^{*})=(a_{ij})_{6\times 6}$ as follows:

$$\begin{aligned} {\mathcal {J}}(E_{2}^{*})\,=\,\,\left( \begin{array}{cccccc} -\beta _2H_{2}^{*}-\mu &{}\quad -\beta _1S_{2}^{*}+\alpha _1&{}\quad \alpha _2&{}\quad -\beta _2S_{2}^{*} &{}\quad -\beta _1S_{2}^{*}-\beta _2S_{2}^{*}&{}\quad 0\,\,\\ 0&{}\beta _1S_{2}^{*}-g_1-\theta \beta _2H_{2}^{*}&{}0&{}0&{}\beta _1S_{2}^{*}&{}0\,\,\\ 0&{}\rho _1&{}-g_2&{}0&{}0&{}0\,\,\\ \beta _2H_{2}^{*}&{}\quad -q\beta _1H_{2}^{*}&{}\quad 0&{}\quad \beta _2S_{2}^{*}-g_3&{}\quad \beta _2S_{2}^{*}-q\beta _1H_{2}^{*}+\sigma \alpha _1 &{}\quad \sigma \alpha _2\,\,\\ 0&{}\quad q\beta _1H_{2}^{*}+\theta \beta _2H_{2}^{*}&{}\quad 0&{}\quad 0&{}\quad q\beta _1H_{2}^{*}-g_4&{}\quad 0\,\,\\ 0&{}0&{}0&{}0&{}\rho _1&{}-g_5 \end{array}\right) , \end{aligned}$$

with eigenvalues satisfying the following characteristic equation:

$$\begin{aligned} |\lambda E-{\mathcal {J}}(E_{2}^{*})|=0, \end{aligned}$$

(26)

where E is the identity matrix. For convenience, we denote $\lambda E-{\mathcal {J}}(E_{2}^{*})=(b_{ij})_{6\times 6}$. Here $b_{ij}=-a_{ij}$ if $i\ne j$; $b_{ii}=\lambda -a_{ii}$. We notice that $\beta _2S_{2}^{*}=g_3$. Expanding Eq. (26) along the last column, we have

$$\begin{aligned} |\lambda E-{\mathcal {J}}(E_{2}^{*})|=b_{66}\left| \begin{array}{lllll} b_{11} &{}\quad b_{12} &{}\quad b_{13} &{}\quad b_{14} &{}\quad b_{15} \\ 0 &{}\quad b_{22} &{}\quad 0 &{}\quad 0 &{}\quad b_{25} \\ 0 &{}\quad b_{32} &{}\quad b_{33} &{}\quad 0 &{}\quad 0 \\ b_{41} &{}\quad b_{42} &{}\quad 0 &{}\quad b_{44} &{}\quad b_{45} \\ 0 &{}\quad b_{52} &{}\quad 0 &{}\quad 0 &{}\quad b_{55} \\ \end{array}\right| . \end{aligned}$$

Expanding along the first column, we get

$$\begin{aligned} \left| \lambda E-{\mathcal {J}}(E_{2}^{*})\right|&=b_{66}\left[ b_{11}b_{33}b_{44} \left| \begin{array}{cc} b_{22} &{} b_{25} \\ b_{52} &{} b_{55} \\ \end{array}\right| - b_{41}b_{33}b_{14}\left| \begin{array}{cc} b_{22} &{} b_{25} \\ b_{52} &{} b_{55} \\ \end{array} \right| \right] \\&=b_{66}b_{33}\left| \begin{array}{cc} b_{11} &{} b_{14} \\ b_{41} &{} b_{44} \\ \end{array}\right| \left| \begin{array}{cc} b_{22} &{} b_{25} \\ b_{52} &{} b_{55} \\ \end{array} \right| \\&=(\lambda +g_2)(\lambda +g_5)|\lambda E-D_1||\lambda E-D_2|, \end{aligned}$$

where

$$\begin{aligned}&D_1=\left( \begin{array}{cc} -\beta _{2}H_{2}^{*}-\mu &{}-\beta _{2}S_{2}^{*}\\ \beta _{2}H_{2}^{*}&{}0 \end{array}\right) , \\&D_2=\left( \begin{array}{cc} \beta _{1}S_{2}^{*}-g_{1}-\theta \beta _{2}H_{2}^{*}&{}\beta _{1}S_{2}^{*}\\ q\beta _{1}H_{2}^{*}+\theta \beta _{2}H_{2}^{*}&{}q\beta _{1}H_{2}^{*}-g_{4} \end{array}\right) . \end{aligned}$$

Obviously, some roots of the above equation are $\lambda _1=-g_2$, $\lambda _2=-g_5$. The stability of matrix ${\mathcal {J}}(E_{2}^{*})$ is determined by matrix $D_1$ and matrix $D_2$. We can see that $Tr(D_1)<0$, Det$(D_1)>0$, all eigenvalues of $D_1$ have negative real parts.

We define the invasion number of HIV infections as follows:

$$\begin{aligned} {\mathcal {R}}_{1}^{2}=\frac{\theta \beta _2H_{2}^{*}\beta _1S_{2}^{*}+q\beta _1H_{2}^{*}(g_1 +\theta \beta _2H_{2}^{*})+\beta _1S_{2}^{*}g_4}{(g_1+\theta \beta _2H_{2}^{*})g_4}. \end{aligned}$$

When ${\mathcal {R}}_{1}^{2}<1$, $Tr(D_2)<0$, Det$(D_2)>0$, all eigenvalues of $D_2$ have negative real parts. Hence, all eigenvalues of ${\mathcal {J}}(E_{2}^{*})$ have negative real parts. When ${\mathcal {R}}_1^2>1$, Det$(D_2)<0$. It indicates that there is at least one positive eigenvalue of ${\mathcal {J}}(E_{2}^{*})$. Therefore, $E_{2}^{*}$ is locally asymptotically stable when ${\mathcal {R}}_{1}^{2}<1$, and unstable when ${\mathcal {R}}_{1}^{2}>1$. This completes the proof of stability of $E_{2}^{*}$.