A Fractional Order Recovery SIR Model from a Stochastic Process

Abstract

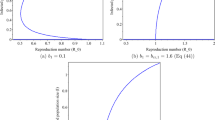
Over the past several decades, there has been a proliferation of epidemiological models with ordinary derivatives replaced by fractional derivatives in an ad hoc manner. These models may be mathematically interesting, but their relevance is uncertain. Here we develop an SIR model for an epidemic, including vital dynamics, from an underlying stochastic process. We show how fractional differential operators arise naturally in these models whenever the recovery time from the disease is power-law distributed. This can provide a model for a chronic disease process where individuals who are infected for a long time are unlikely to recover. The fractional order recovery model is shown to be consistent with the Kermack–McKendrick age-structured SIR model, and it reduces to the Hethcote–Tudor integral equation SIR model. The derivation from a stochastic process is extended to discrete time, providing a stable numerical method for solving the model equations. We have carried out simulations of the fractional order recovery model showing convergence to equilibrium states. The number of infecteds in the endemic equilibrium state increases as the fractional order of the derivative tends to zero.

Appendices

Appendix 1: Derivation of the Kermack–McKendrick Model for Infecteds in a Age-Structured System

Let i(a, t) denote the number of individuals who are infected at time t and who have been infected for time a. The total number of infected individuals at time t is given by

$$\begin{aligned} \int _0^t i(a,t)\, \hbox {d}a=\int _0^t \varPhi (t,t')i(0,t')\, \hbox {d}t' \end{aligned}$$

(127)

where

$$\begin{aligned} \varPhi (t,t')=\phi (t-t')\theta (t,t') \end{aligned}$$

(128)

is the product of the probability of surviving death, $\theta (t,t')$, and of ‘surviving’ the transition out of the next stage, $\phi (t-t')$. If we differentiate Eq. (127) with respect to t using Leibniz rule, we have

$$\begin{aligned} \int _0^t\frac{\partial i}{\partial t}\, \hbox {d}a+i(t,t)=\int _0^t\frac{\partial \varPhi (t,t')}{\partial t}i(0,t')\, \hbox {d}t' +\varPhi (t,t)i(0,t) \end{aligned}$$

(129)

We also have

$$\begin{aligned} \int _0^t\frac{\partial i}{\partial a}\, \hbox {d}a=i(t,t)-i(0,t). \end{aligned}$$

(130)

But

$$\begin{aligned} \varPhi (t,t)=1 \end{aligned}$$

(131)

so that if we add Eqs. (129) and (130) then we obtain

$$\begin{aligned} \int _0^t\left( \frac{\partial i}{\partial t}+\, \frac{\partial i}{\partial a}\right) \, \hbox {d}a=\int _0^t\frac{\partial \varPhi (t,t')}{\partial t}i(0,t')\, \hbox {d}t' \end{aligned}$$

(132)

We can expand the partial derivative of $\varPhi (t,t')$ using the product rule in Eq. (128) with

$$\begin{aligned} \frac{\partial \theta (t,t')}{\partial t}=-\gamma (t)\theta (t,t') \end{aligned}$$

(133)

and

$$\begin{aligned} \frac{\partial \phi (t-t')}{\partial t}=-\psi (t-t'), \end{aligned}$$

(134)

to obtain

$$\begin{aligned}&\int _0^t\left( \frac{\partial i}{\partial t}+\, \frac{\partial i}{\partial a}\right) \, \hbox {d}a=-\int _0^t\psi (t-t')\theta (t,t')i(0,t')\, \hbox {d}t'\nonumber \\&\quad -\int _0^t\gamma (t)\theta (t,t')\phi (t-t')i(0,t')\, \hbox {d}t'. \end{aligned}$$

(135)

Using Eq. (128) and then Eq. (127) in the second term on the RHS of Eq. (135), we now have

$$\begin{aligned} \int _0^t\left( \frac{\partial i}{\partial t}+\, \frac{\partial i}{\partial a}\right) \, \hbox {d}a=-\int _0^t\psi (t-t')\theta (t,t')i(0,t')\, \hbox {d}t' -\gamma (t)\int _0^t i(a,t)\, \hbox {d}a. \end{aligned}$$

(136)

We now define

$$\begin{aligned} \beta (t-t')=\frac{\psi (t-t')}{\phi (t-t')} \end{aligned}$$

(137)

and use Eq. (128) in the first term on the RHS of Eq. (136) to obtain

$$\begin{aligned} \int _0^t\left( \frac{\partial i}{\partial t}+\, \frac{\partial i}{\partial a}\right) \, \hbox {d}a=-\int _0^t\beta (t-t')\varPhi (t,t')i(0,t')\, \hbox {d}t' -\gamma (t)\int _0^t i(a,t)\, \hbox {d}a. \end{aligned}$$

(138)

In the first integral on the RHS of Eq. (138), it is convenient to make a change in variables $t'=t-a$ with $\hbox {d}t'=-\hbox {d}a$; then, we have

$$\begin{aligned} \int _0^t\left( \frac{\partial i}{\partial t}+\, \frac{\partial i}{\partial a}\right) \, \hbox {d}a=-\int _0^t\beta (a)\varPhi (t,t-a)i(0,t-a)\, \hbox {d}a -\gamma (t)\int _0^t i(a,t)\, \hbox {d}a. \end{aligned}$$

(139)

Finally, we note that

$$\begin{aligned} i(a,t)=\varPhi (t,t-a)i(0,t-a) \end{aligned}$$

(140)

so that Eq. (139) can be written as

$$\begin{aligned} \int _0^t\left( \frac{\partial i}{\partial t}+\, \frac{\partial i}{\partial a}\right) \, \hbox {d}a=-\int _0^t\beta (a)i(a,t)\, \hbox {d}a -\gamma (t)\int _0^t i(a,t)\, \hbox {d}a. \end{aligned}$$

(141)

This is consistent with Eq. (27) for the change in infectives in the age-structured Kermack McKendrick model.

Appendix 2: Limits to Continuous Time

The discrete time fractional recovery SIR model can be shown to limit to the frSIR model by identifying $t=n\Delta t$ and taking the limit $\Delta t \rightarrow 0$ with $r/\Delta t^{\alpha }$ finite. The continuous time equations can be obtained from the discrete time equations using Z star transform methods. The Z star transform of Y(n) is given by

$$\begin{aligned} Z^*[Y(n)|s,\Delta t]=\sum _{n=0}^\infty Y(n) e^{-ns\Delta t} \end{aligned}$$

(142)

It follows that

$$\begin{aligned} \Delta t Z^*[Y(n)|s,\Delta t]= & {} \sum _{n=0}^\infty Y(n) e^{-ns\Delta t}\Delta t \end{aligned}$$

(143)

$$\begin{aligned}= & {} \sum _{n=0}^\infty \tilde{Y}(n\Delta t) e^{-ns\Delta t}\Delta t \end{aligned}$$

(144)

where we have introduced $\tilde{Y}(t)$ as a function defined over a continuous variable t. We can now take the inverse Laplace transform from s to t

$$\begin{aligned} \mathcal {L}^{-1}_s\left[ \Delta t Z^*[Y(n)|s,\Delta t]\Bigg \vert t\right] =\sum _{n=0}^\infty \tilde{Y}(n\Delta t) \delta (t-n\Delta t)\Delta t \end{aligned}$$

(145)

where $\delta (t)$ is the Dirac delta function. Here, and in the following, we use the notation $\mathcal {L}^{-1}_s\left[ Y(s)\Bigg \vert t\right]$ to denote the inverse Laplace transform from s to t and we use the notation $\mathcal {L}_t\left[ Y(t)\Bigg \vert s\right]$ to denote the Laplace transform from t to s.

It is useful to define the function

$$\begin{aligned} \tilde{Y}(t|\Delta t)=\sum _{n=0}^\infty \tilde{Y}(n\Delta t) \delta (t-n\Delta t)\Delta t. \end{aligned}$$

(146)

In a similar fashion, we have

$$\begin{aligned} \mathcal {L}^{-1}_s\left[ \Delta t Z^*[Y(n-1)|s,\Delta t] \Bigg \vert t \right]= & {} \sum _{n=0}^\infty \tilde{Y}(n\Delta t) \delta (t-(n+1)\Delta t)\Delta t \end{aligned}$$

(147)

$$\begin{aligned}= & {} \sum _{n=0}^\infty \tilde{Y}((n-1)\Delta t)\delta (t-n\Delta t)\Delta t \end{aligned}$$

(148)

$$\begin{aligned}= & {} \tilde{Y}(t-\Delta t|\Delta t). \end{aligned}$$

(149)

Note that, with $t'=n\Delta t$, in Eq. (146), we have

$$\begin{aligned} \lim _{\Delta t\rightarrow 0}\tilde{Y}(t|\Delta t)= & {} \lim _{\Delta t\rightarrow 0}\sum _{n=0}^\infty \tilde{Y}(n\Delta t) \delta (t-n\Delta t)\Delta t \end{aligned}$$

(150)

$$\begin{aligned}= & {} \int _0^\infty \tilde{Y}(t')\delta (t-t')\, \hbox {d}t' \end{aligned}$$

(151)

$$\begin{aligned}= & {} \tilde{Y}(t). \end{aligned}$$

(152)

This formally identifies

$$\begin{aligned} \tilde{Y}(t)=\lim _{\Delta t\rightarrow 0} \mathcal {L}^{-1}_s\left[ \Delta t Z^*[Y(n)|s,\Delta t] \Bigg \vert t\right] , \end{aligned}$$

(153)

provided that the limit exists.

We further note the product rule

$$\begin{aligned}&\lim _{\Delta t\rightarrow 0}\sum _{n=0}^\infty \tilde{X}(n\Delta t)\tilde{Y}(n\Delta t)\delta (t-n\Delta t)\Delta t\nonumber \\&=\left( \lim _{\Delta t\rightarrow 0}\sum _{n=0}^\infty \tilde{X}(n\Delta t)\delta (t-n\Delta t)\Delta t\right) \left( \lim _{\Delta t\rightarrow 0}\sum _{n=0}^\infty \tilde{Y}(n\Delta t)\delta (t-n\Delta t)\Delta t\right) ,\nonumber \\ \end{aligned}$$

(154)

which equates to $\tilde{X}(t)\tilde{Y}(t)$ in each case, with $t'=n\Delta t$, provided that both $\tilde{X}(t)$ and $\tilde{Y}(t)$ exist.

We now take the inverse Laplace transform of the Z star transform of Eq. (105) and multiply by $\frac{\Delta t}{\Delta t}$ to write

$$\begin{aligned} \begin{aligned} \sum _{n=0}^\infty&\frac{\tilde{I}(n\Delta t)-\tilde{I}((n-1)\Delta t)}{\Delta t}\delta (t-n\Delta t)\Delta t\\&=\sum _{n=0}^\infty \frac{\tilde{\omega }(n\Delta t)}{\Delta t} \tilde{S}((n-1)\Delta t)\tilde{I}((n-1)\Delta t)\delta (t-n\Delta t)\Delta t\\&-\frac{r}{\Delta t}\sum _{n=0}^\infty \tilde{\theta }(n\Delta t,0)\left( \sum _{k=0}^{n-1}\tilde{\kappa }((n-k)\Delta t)\frac{\tilde{I}(k\Delta t)-\tilde{I}_0(k\delta t)}{\tilde{\theta }(k\Delta t,0)}\right) \delta (t-n\Delta t)\Delta t\\&-\sum _{n=0}^\infty \frac{\tilde{\gamma }(n\Delta t)}{\Delta t} \left( \tilde{I}((n-1)\Delta t)-\tilde{I}_0((n-1)\delta t)\right) \delta (t-n\Delta t)\Delta t\\&+\sum _{n=0}^\infty \frac{\tilde{I}_0(n\Delta t)-\tilde{I}_0((n-1)\Delta t)}{\Delta t}\delta (t-n\Delta t)\Delta t \end{aligned} \end{aligned}$$

(155)

We now take the continuous time limit of Eq. (155) using $t'=n\Delta t$ and the product rule in Eq. (154) to obtain

$$\begin{aligned} \begin{aligned} \int _0^\infty&\left( \lim _{\Delta t\rightarrow 0}\frac{\tilde{I}(t')-\tilde{I}(t'-\Delta t)}{\Delta t}\right) \delta (t-t')\, \hbox {d}t'\\&\quad =\int _0^\infty \hat{\omega }(t') \tilde{S}(t')\tilde{I}(t')\delta (t-t')\, \hbox {d}t'\\&\qquad -\left( \int _0^\infty \tilde{\theta }(t',0)\delta (t-t')\, \hbox {d}t'\right) \\&\qquad \times \left( \lim _{\Delta t\rightarrow 0}\frac{r}{\Delta t}\sum _{n=0}^\infty \left( \sum _{k=0}^{n-1}\tilde{\kappa }((n-k)\Delta t)\frac{\tilde{I}(k\Delta t)-\tilde{I}_0(k\Delta t)}{\tilde{\theta }(k\Delta t,0)}\right) \delta (t-n\Delta t)\Delta t\right) \\&\qquad -\int _0^\infty \hat{\gamma }(t')\left( \tilde{I}(t')-\tilde{I}_0(t')\right) \delta (t-t')\, \hbox {d}t'\\&\qquad +\int _0^\infty \left( \lim _{\Delta t\rightarrow 0}\frac{\tilde{I}_0(t')-\tilde{I}_0(t'-\Delta t)}{\Delta t}\right) \delta (t-t')\, \hbox {d}t' \end{aligned} \end{aligned}$$

(156)

where we have defined continuous time rate parameters

$$\begin{aligned} \hat{\omega }(t')=\lim _{\Delta t\rightarrow 0}\frac{\tilde{\omega }(n\Delta t)}{\Delta t} \end{aligned}$$

(157)

and

$$\begin{aligned} \hat{\gamma }(t')=\lim _{\Delta t\rightarrow 0}\frac{\tilde{\gamma }(n\Delta t)}{\Delta t}. \end{aligned}$$

(158)

Equation (156) simplifies further to

$$\begin{aligned} \begin{aligned}&\frac{\hbox {d}\tilde{I}(t)}{\hbox {d}t}= \hat{\omega }(t)\tilde{S}(t)\tilde{I}(t)-\hat{\gamma }(t)\left( \tilde{I}(t)-\tilde{I}_0(t)\right) +\frac{\hbox {d}\tilde{I}_0(t)}{\hbox {d}t}\\&\quad -\tilde{\theta }(t,0)\left( \lim _{\Delta t\rightarrow 0} \frac{r}{\Delta t}\sum _{n=0}^\infty \left( \sum _{k=0}^{n-1}\tilde{\kappa }((n-k)\Delta t)\frac{\tilde{I}(k\Delta t)-\tilde{I}_0(k\Delta t)}{\tilde{\theta }(k\Delta t,0)}\right) \delta (t-n\Delta t)\Delta t\right) \end{aligned} \end{aligned}$$

(159)

The further reduction in this equation depends on the specific form of the memory kernel $\kappa (n)$. In the case of a jump at each time step, the memory kernel is

$$\begin{aligned} \kappa (n)=\delta _{n,1}. \end{aligned}$$

(160)

In this case, we can perform the sum over k explicitly in Eq. (159) to arrive at

$$\begin{aligned} \frac{\hbox {d}\tilde{I}(t)}{\hbox {d}t}&= \hat{\omega }(t)\tilde{S}(t)\tilde{I}(t)-\hat{\gamma }(t)\left( \tilde{I}(t)-\tilde{I}_0(t)\right) +\frac{\hbox {d}\tilde{I}_0(t)}{\hbox {d}t}\nonumber \\&\quad -\,\tilde{\theta }(t,0)\left( \lim _{\Delta t\rightarrow 0} \frac{r}{\Delta t}\sum _{n=0}^\infty \frac{\tilde{I}((n-1)\Delta t)-\tilde{I}_0((n-1)\Delta t)}{\tilde{\theta }((n-1)\Delta t,0)}\delta (t-n\Delta t)\Delta t\right) \nonumber \\ \end{aligned}$$

(161)

In order for the continuous time limit of the above equation to exist, we define

$$\begin{aligned} \mu =\lim _{\Delta t\rightarrow 0}\frac{r}{\Delta t}. \end{aligned}$$

(162)

Note that r is a free parameter in the range [0, 1], and hence, $\mu$ is only well defined in this limit if we take r to be a function of $\Delta t$. With this definition of $\mu$, we can now perform the limit $\delta t\rightarrow 0$ to obtain the continuous time equation

$$\begin{aligned} \frac{\hbox {d}\tilde{I}(t)}{\hbox {d}t} =\hat{\omega }(t) \tilde{S}(t)\tilde{I}(t) -\mu (\tilde{I}(t)-\tilde{I}_0(t))-\hat{\gamma }(t)(\tilde{I}(t)-\tilde{I}_0(t))+\frac{\hbox {d}\tilde{I}_0(t)}{\hbox {d}t}. \end{aligned}$$

(163)

This further simplifies to

$$\begin{aligned} \frac{\hbox {d}\tilde{I}}{\hbox {d}t} =\hat{\omega }(t) \tilde{S}(t)\tilde{I}(t) -\mu \tilde{I}(t)-\hat{\gamma }(t)\tilde{I}(t) \end{aligned}$$

(164)

Equation (164) recovers the corresponding equation in the classic SIR model.

We now consider the continuous time limit of Eq. (159) with the Sibuya memory kernel, given by Eq. (104). First, we simplify the double sum in Eq. (159) using Laplace transforms and Z star transforms as follows:

$$\begin{aligned}&\lim _{\Delta t\rightarrow 0}\frac{r}{\Delta t}\sum _{n=0}^\infty \left( \sum _{k=0}^{n-1}\tilde{\kappa }((n-k)\Delta t)\frac{\tilde{I}(k\Delta t)-\tilde{I}_0(k\Delta t)}{\tilde{\theta }(k\Delta t,0)}\right) \delta (t-n\Delta t)\Delta t\nonumber \\&= \mathcal {L}_s^{-1}\left[ \mathcal {L}_t\left[ \lim _{\Delta t\rightarrow 0}\frac{r}{\Delta t} \sum _{n=0}^\infty \left( \sum _{k=0}^{n-1}\tilde{\kappa }((n-k)\Delta t)\frac{\tilde{I}(k\Delta t)-\tilde{I}_0(k\Delta t)}{\tilde{\theta }(k\Delta t,0)}\right) \delta (t-n\Delta t)\Delta t\Bigg \vert s\right] \Bigg \vert t\right] \nonumber \\&=\mathcal {L}_s^{-1}\left[ \lim _{\Delta t\rightarrow 0}\frac{r}{\Delta t} \sum _{n=0}^\infty \left( \sum _{k=0}^{n-1}\tilde{\kappa }((n-k)\Delta t)\frac{\tilde{I}(k\Delta t)-\tilde{I}_0(k\Delta t)}{\tilde{\theta }(k\Delta t,0)}\right) e^{-sn\Delta t}\Delta t\Bigg \vert t\right] \nonumber \\&=\mathcal {L}_s^{-1}\left[ \lim _{\Delta t\rightarrow 0}\frac{r}{\Delta t} Z^*\left[ \sum _{k=0}^{n-1}\kappa (n-k)\frac{I(k)-I_0(k)}{\theta (k,0)}| s,\Delta t \right] \Delta t\Bigg \vert t\right] \nonumber \\&= \mathcal {L}_s^{-1}\left[ \lim _{\Delta t\rightarrow 0}\frac{r}{\Delta t}Z^*[\kappa (n)| s,\Delta t] Z^{*}\left[ \frac{I(n)-I_0(k)}{\theta (n,0)}| s,\Delta t \right] \Delta t\Bigg \vert t\right] . \end{aligned}$$

(165)

The last line in the above follows from the convolution theorem for Z star transforms.

To proceed further, we use the Z transform of the Sibuya memory kernel in Eq. (114) to write

$$\begin{aligned} Z^*[\kappa (n)| s,\Delta t]= & {} \left[ ((1-e^{-s\Delta t})^{1-\alpha }-(1-e^{-s\Delta t}))\right] \end{aligned}$$

(166)

$$\begin{aligned}\approx & {} (s\Delta t)^{1-\alpha }+o(s\Delta t). \end{aligned}$$

(167)

The result in Eq. (165) can now be written as

$$\begin{aligned}&\lim _{\Delta t\rightarrow 0}\frac{r}{\Delta t}\sum _{n=0}^\infty \left( \sum _{k=0}^{n-1}\tilde{\kappa }((n-k)\Delta t)\frac{\tilde{I}(k\Delta t)-\tilde{I}_0(k\Delta t)}{\tilde{\theta }(k\Delta t,0)}\right) \delta (t-n\Delta t)\Delta t\nonumber \\&\quad = \mathcal {L}_s^{-1}\left[ \lim _{\Delta t\rightarrow 0}\frac{r}{\Delta t^\alpha } s^{1-\alpha } \sum _{n=0}^\infty \frac{\tilde{I}(n\Delta t)-\tilde{I}_0(n\Delta t)}{\tilde{\theta }(n\Delta t,0)}e^{-sn\Delta t}\Delta t\Bigg \vert t\right] \nonumber \\&\quad = \mu \mathcal {L}_s^{-1}\left[ s^{1-\alpha }\int _0^\infty \frac{\tilde{I}(t)-\tilde{I}_0(t)}{\tilde{\theta }(t,0)}e^{-st}\, \hbox {d}t\Bigg \vert t\right] \nonumber \\&\quad = \mu \mathcal {L}_s^{-1}\left[ s^{1-\alpha } \mathcal {L}_t \left[ \frac{\tilde{I}(t)-\tilde{I}_0(t)}{\tilde{\theta }(t,0)}\Bigg \vert s\right] \Bigg \vert t\right] , \end{aligned}$$

(168)

where

$$\begin{aligned} \mu =\lim _{\Delta t\rightarrow 0}\frac{r}{\Delta t^\alpha }. \end{aligned}$$

(169)

Finally, we substitute the result of Eq. (168) into Eq. (159) and use the known result (Podlubny 1999)

$$\begin{aligned} \mathcal {L}_t\left[ \, _0D_t^{1-\alpha } Y(t)\Bigg \vert s\right] = s^{1-\alpha } \mathcal {L}_t\left[ Y(t)\Bigg \vert s\right] \end{aligned}$$

(170)

to invert the Laplace transform and obtain

$$\begin{aligned} \frac{\hbox {d}\tilde{I}(t)}{\hbox {d}t} =\hat{\tilde{\omega }}(t) \tilde{S}(t)\tilde{I}(t) - \mu \hat{\tilde{\theta }}(t,0) \, _0D_t^{1-\alpha }\left( \frac{\tilde{I}(t)-\tilde{I}_0(t)}{\hat{\tilde{\theta }}(t,0)}\right) - \hat{\tilde{\gamma }}(t)\left( \tilde{I}(t)-\tilde{I}_0(t)\right) +\frac{\hbox {d}\tilde{I}_0(t)}{\hbox {d}t} \end{aligned}$$

(171)

Equation (171) recovers the continuous time frSIR model equation.

Note that in order for the continuous time limit of the frSIR model equation to exist, we defined

$$\begin{aligned} \mu =\lim _{\Delta t\rightarrow 0}\frac{r}{\Delta t^\alpha } \end{aligned}$$

(172)

which requires $r\in [0,1]$ to be a function of $\Delta t$. This is important for numerical simulations based on this DTRW method where we take $r=\mu \Delta t^\alpha$ and then the requirement that $r\in [0,1]$ places restrictions on $\Delta t$ for given $\alpha$ and $\mu$.