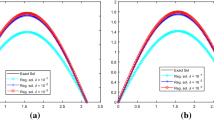
Abstract
It is well known that the Cauchy problem for Laplace equations is an ill-posed problem in Hadamard’s sense. Small deviations in Cauchy data may lead to large errors in the solutions. It is observed that if a bound is imposed on the solution, there exists a conditional stability estimate. This gives a reasonable way to construct stable algorithms. However, it is impossible to have good results at all points in the domain. Although numerical methods for Cauchy problems for Laplace equations have been widely studied for quite a long time, there are still some unclear points, for example, how to evaluate the numerical solutions, which means whether they can approximate the Cauchy data well and keep the bound of the solution, and at which points the numerical results are reliable? In this paper, the authors will prove the conditional stability estimate which is quantitatively related to harmonic measures. The harmonic measure can be used as an indicate function to pointwisely evaluate the numerical result, which further enables us to find a reliable subdomain where the local convergence rate is higher than a certain order.
Similar content being viewed by others
References
Adams, R. A. and Fournier, J. J. F., Sobolev Spaces, Elsevier, Amsterdam, 2003.
Alessandrini, G., Rondi, L., Rosset, E. and Vessella, S., The stability for the Cauchy problem for elliptic equations, Inverse Problems, 25, 2009, 123004.
Burman, E., Hansbo, P. and Larson, M., Solving ill-posed control problems by stabilized finite element methods: An alternative to Tikhonov regularization, Inverse Problems, 34(3), 2018, 035004.
Chakib, A. and Nachaoui, A., Convergence analysis for finite element approximation to an inverse Cauchy problem, Inverse Problems, 22, 2006, 1191–1206.
Cheng, J., Hon, Y. C., Wei, T. and Yamamoto, M., Numerical computation of a Cauchy problem for Laplace’s equation, Z. Angew. Math. Mech., 81, 2001, 665–674.
Cheng, J. and Yamamoto, M., Unique continuation on a line for harmonic functions, Inverse Probl., 14(4), 1998, 869–882.
Cheng, J. and Yamamoto, M., One new strategy for a priori choice of regularizing parameters in Tikhonov’s regularization, Inverse Problems, 16(4), 2000, L31–L38.
Friedman, A. and Vogelius, M., Determining cracks by boundary measurements, Indiana University Mathematics Journal, 38(3), 1989, 527–556.
Gilbarg, D. and Trudinger, N. S., Elliptic Partial Differential Equations of Second Order, Springer-Verlag, Berlin, 1983.
Hadamard, J., Sur les problèmes aux dérivées partielles et leur signification physique, Princeton University Bulletin, 13, 1902, 49–52.
Hadamard, J., Lectures on Cauchy’s Problem in Linear Partial Differential Equations, Yale University Press, New Haven, 1923.
Hrycak, T. and Isakov, V., Increased stability in the continuation of solutions to the Helmholtz equation, Inverse Problems, 20(3), 2004, 697–712.
Isakov, V., Inverse Problems for Partial Differential Equations, Springer-Verlag, Berlin, 2006.
Johansson, T., An iterative procedure for solving a Cauchy problem for second order elliptic equations, Mathematische Nachrichten, 272(1), 2004, 46–54.
Ke, Y. and Chen, Y., Unique continuation on quadratic curves for harmonic functions, Chinese Annals of Mathematics, Series B, 43, 2022, 17–32.
Kellogg, O. D., Foundations of Potential Theory, Dover Publications, Inc., New York, 1953.
Kozlov, V. A. and Maz’ya, V. G., On iterative procedures for solving ill-posed boundary value problems that preserve differential equations, Algebra i Analiz, 1, 1989, 144–170. English transl.: Leningrad Math. J., 1, 1990, 1207–1228.
Larsson, S. and Thomé, V., Partial Differential Equations with Numerical Methods, Springer-Verlag, Berlin, 2003.
Lattès, R. and Lions, J.-L., The Method of Quasi-Reversibility, Applications to Partial Differential Equations, American Elsevier Publishing Co., New York, 1969.
Lax, P. D., A stability theorem for solutions of abstract differential equations, and its application to the study of the local behavior of solutions of elliptic equations, Comm. Pure Appl. Math., 9(4), 1956, 747–766.
Natterer, F., The finite element method for ill-posed problems, R.A.I.R.O., Analyse Numérique, 11(1), 1977, 271–278.
Payne, L. E., Bounds in the Cauchy problem for the Laplace equation, Archive for Rational Mechanics and Analysis, 5(1), 1960, 35–45.
Rüland, A. and Salo, M., Quantitative runge approximation and inverse problems, International Mathematics Research Notices, 20, 2019, 6216–6234.
Yang, X., Choulli, M. and Cheng, J., An iterative method for the inverse problem of detecting corrosion in a pipe, Numerical Mathematics-A Journal of Chinese Universities (English Series), 14(3), 2005, 252–266.
Acknowledgement
The authors thank the anonymous referee for helpful comments.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflicts of interest The authors declare no conflicts of interest.
Additional information
This work was suported by the National Natural Science Foundation of China (Nos. 11971121, 12201386, 12241103) and Grant-in-Aid for Scientific Research (A) 20H00117 of Japan Society for the Promotion of Science.
Rights and permissions
About this article
Cite this article
Chen, Y., Cheng, J., Lu, S. et al. Harmonic Measures and Numerical Computation of Cauchy Problems for Laplace Equations. Chin. Ann. Math. Ser. B 44, 913–928 (2023). https://doi.org/10.1007/s11401-023-0051-8
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11401-023-0051-8