Introduction

Nowadays, the widespread use of metals and alloys as the main material in various applications have led to greater demands for the understanding of material characteristics including plastic behavior, damage and failure. Sheet metals and alloys are subjected to biaxial stresses and changing strain paths, especially during forming processes. Under biaxial stress conditions, the mechanical properties can differ from those obtained under uniaxial loading. In order to get the accurate information regarding the states of stress which enable plastic deformation, the required yield surfaces are often determined with the help of biaxial loading. This method is increasingly becoming the favoured material testing method in contrast to other multiaxial tests such as the Erichsen cupping test, the Marciniak test, the Nakajima test or the hydraulic bulge test as it can achieve frictionless, in-plane, multiaxial stress states with a single sample geometry [1,2,3,4].

In order to standardize biaxial tensile testing methods, the International Organization for Standardization (ISO) has published in 2014 the standard ISO 16842 [5], 101 years after the publication of the first biaxial tensile test [6]. The ISO 16842 specifies the testing method for measuring biaxial stress-strain curves of sheet metals subject to biaxial tension at an arbitrary stress ratio. From the measured biaxial stress-strain curves, the yield surfaces which are also known as the contours of plastic work are determined. The cruciform shaped test pieces are of uniform thickness with parallel slits cut into each arm. The ISO standard is based on the research work of Kuwabara et al. [7] and the proposed geometry has been used in several studies [8, 9] to perform non-proportional strain path changes and to determine the yield surface evolution. However, the standard cruciform design has a few drawbacks which includes the development of large stress concentrations at the slit ends during uniaxial or biaxial loading. Consequently, only low strain levels can be achieved in the gauge area.

Significant efforts have been made in terms of optimizing the cruciform geometry in order to increase the gauge area strains. An efficient and simple method is to reduce the thickness of the gauge area without introducing slits into the arms. Even after publication of the ISO standard, this type of cruciform test specimen is still in use and continuously optimized, see for instance, Baptista et al. [10, 11], Creuziger et al. [12], Seymen et al. [13], Tomicevic et al. [14], Van Petegem et al. [15] and Xiao et al. [16, 17]. Goal of the proposed designs is to measure the initiation and evolution of cracks. However, the determination of yield surfaces is difficult since stresses cannot be obtained directly from the applied forces due to the inhomogeneous stress field.

More sophisticated cruciform test geometries make use of both arms with slits and a reduced gauge area thickness. The idea of combining these two main design features goes back to the work of Hayhurst [18] and Kelly [19] in the seventies of the last century. Many different design variants have been developed since then, usually by means of finite element simulations. For example, Zidane et al. introduced a cruciform test specimen with four 2 mm wide slits per arm and a two-step thickness reduction on both sides [20, 21]. The cruciform specimen used by Merklein and Biasutti has seven slits per arm [22]. The slits are only 0.2 mm wide and the specimen is thinned only at one side. The release of the ISO standard has not stopped the development of new cruciform designs of the Hayhurst-Kelly type. Liu et al. proposed a design with slits of different lengths, circular notches at the corners and a steep transition to the gauge area [3, 23]. Shao et al. developed a cruciform specimen with three slits and a circular gauge region to measure forming limit diagrams (FLD) under elevated temperatures [24, 25]. Deng et al. used a modified slit design similar to the ISO standard specifications which consists of eleven equispaced slits that stretch along each arm and a gauge section with 40% of the arm thickness. With these optimizations, not only the level of plastic deformation can be increased, the failure can even be induced in the gauge section instead of the arm section [26].

The majority of cruciform test specimens has been optimized from a fracture mechanics point of view. For the determination of yield surfaces, however, these designs are inappropriate since the gauge areas are very small and the stress fields are inhomogeneous. At first glance, the specimen proposed by Merklein and Biasutti [22] is a suitable candidate for the measurement of yield surfaces. Unfortunately, the stress distribution is quite heterogenous since the slit width has not been adapted to the thickness reduction. Another candidate for the determination of yield surfaces is the specimen developed by Deng et al. [26]. However, the achievable strain levels are limited by stress concentrations at the abrupt transition to the gauge area.

In this paper, a cruciform test specimen design is introduced which is optimized especially with respect to the measurement of yield surfaces. It can be seen as an assembly of spring elements arranged both in series and in parallel. Thanks to the specimen’s well-balanced proportions, this system of springs is in equilibrium, or rather, the stress distribution is homogenous. The achievable plastic strain levels are significantly higher than those obtained by means of the standard ISO 16842 cruciform test piece. In order to maintain a homogeneous stress field within a large gauge area, it is accepted that the crack initiation takes place at the slit ends. Standard and optimized biaxial test specimens are compared numerically and experimentally for the example of an aluminium 5754 alloy.

Determination of Yield Surfaces According To ISO 16842

Since metals and alloys can undergo large plastic deformations, the ISO 16842 makes use of the finite strain theory. The nominal strain components ex and ey, which represent the change in length per reference length in x and y direction, have to be converted into true strain components:

$$ \begin{array}{@{}rcl@{}} \varepsilon_{x} &=& \ln(1+e_{x}) \end{array} $$
(1)
$$ \begin{array}{@{}rcl@{}} \varepsilon_{y} &=& \ln(1+e_{y}) \end{array} $$
(2)

Note that in case of small deformations, the true strains which are also known as logarithmic strains and as Hencky strains converge to the nominal strains.

Assuming plastic incompressibility and that the recoverable elastic strains are small, the true stress components can be calculated by means of the following formulas:

$$ \begin{array}{@{}rcl@{}} \sigma_{x} &=& \frac{F_{x}}{A} (1+e_{x}) \end{array} $$
(3)
$$ \begin{array}{@{}rcl@{}} \sigma_{y} &=& \frac{F_{y}}{A} (1+e_{y}) \end{array} $$
(4)

The adjective “true” indicates that the forces Fx and Fy refer to the actual cross-sectional areas \(A_{x}=\frac {A}{1+e_{x}}\) and \(A_{y}=\frac {A}{1+e_{y}}\), in contrast to nominal stress components where the force is divided by the reference cross-sectional area A.

Hooke’s law for plane stress with σz = 0 reads

$$ \begin{array}{@{}rcl@{}} \varepsilon_{x}^{\mathrm{e}} &=& \frac{1}{E} [\sigma_{x}-\nu \sigma_{y}] \end{array} $$
(5)
$$ \begin{array}{@{}rcl@{}} \varepsilon_{y}^{\mathrm{e}} &=& \frac{1}{E} [\sigma_{y}-\nu \sigma_{x}] \end{array} $$
(6)

where the superscript e indicates that the strains are elastic. Since \(\varepsilon _{x}^{\mathrm {e}}\) and \(\varepsilon _{y}^{\mathrm {e}}\) are small, the force ratio equals the stress ratio:

$$ \alpha = \frac{F_{x}}{F_{y}} = \frac{\sigma_{x}}{\sigma_{y}} $$
(7)

When the stress ratio α is held constant, Hooke’s law can be written as

$$ \begin{array}{@{}rcl@{}} \sigma_{x} &=& \underbrace{E\frac{\alpha}{\alpha-\nu}}_{\text{$=C_{x}$}} \varepsilon_{x}^{\mathrm{e}} \end{array} $$
(8)
$$ \begin{array}{@{}rcl@{}} \sigma_{y} &=& \underbrace{E\frac{1}{1-\alpha\nu}}_{\text{$=C_{y}$}} \varepsilon_{y}^{\mathrm{e}} \end{array} $$
(9)

where the constants Cx and Cy can be interpreted as stiffnesses. Note that negative values are possible: Cx < 0 for α ∈ (0;ν) and Cy < 0 for \(\alpha >\frac {1}{\nu }\). If Young’s modulus E and Poisson’s ratio ν are known, Cx and Cy can be calculated directly. Otherwise, Cx and Cy can be taken as initial slopes from the measured stress-strain curves σx-εx and σy-εy.

Subtracting the elastic part from the total strains gives the (true) plastic strain components:

$$ \begin{array}{@{}rcl@{}} \varepsilon_{x}^{\mathrm{p}} &=& \varepsilon_{x} - \varepsilon_{x}^{\mathrm{e}} = \varepsilon_{x} - \frac{\sigma_{x}}{C_{x}} \end{array} $$
(10)
$$ \begin{array}{@{}rcl@{}} \varepsilon_{y}^{\mathrm{p}} &=& \varepsilon_{y} - \varepsilon_{y}^{\mathrm{e}} = \varepsilon_{y} - \frac{\sigma_{y}}{C_{y}} \end{array} $$
(11)

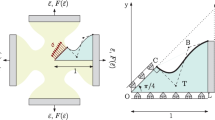
According to ISO 16842, anisotropic yield surfaces are determined based on the principle of equivalent plastic work. As illustrated in Fig. 1, this includes two types of equivalence: Each plastic work value W0 (per unit volume) can be assigned a unique plastic strain value \(\varepsilon _{0}^{\mathrm {p}}\). Furthermore, the plastic work is used to compare the different biaxial stress states. The uniaxial tensile test in rolling direction is taken as reference (0) for the biaxial tests. For selected true plastic strain values \(\varepsilon ^{\mathrm {p}}_{0}\), e.g. 0.2, 0.5, 1, 2, 3, 4 and 5%, the corresponding true stress values σ0 together with the specific plastic work W0 are taken from the uniaxial true stress-true plastic strain curve. Since true (logarithmic) strains are work compatible with true stresses (work conjugate relation), W0 is the area under the curve.

Fig. 1
figure 1

Method of measuring anisotropic yield surfaces according to ISO 16842 [5]

Full size image

Afterwards, biaxial tensile tests at different loading ratios as well as the uniaxial tensile test in transverse direction are carried out. In case of biaxial tension, plastic work has to be considered for both directions. The sum of both parts,

$$ W_{x} = \int \sigma_{x} d\varepsilon_{x}^{\mathrm{p}} $$
(12)

and

$$ W_{y} = \int \sigma_{y} d\varepsilon_{y}^{\mathrm{p}} , $$
(13)

is set equal to the plastic work W0 of the uniaxial reference test:

$$ W_{0} = W_{x} + W_{y} $$
(14)

To form the yield surface associated with \(\varepsilon ^{\mathrm {p}}_{0}\), stress points (σx,σy) for which the same amount of plastic work W0 is required are plotted in the principal stress plane and connected by a polyline or rather by means of splines. It is suggested to use the following stress ratios: α = 1:0, 4:1, 2:1, 4:3, 1:1, 3:4, 1:2, 1:4 and 0:1. This results in a total of nine stress points for each yield surface: seven biaxial and two uniaxial stress states.

For the biaxial tensile tests presented in “Experimental Results from Standard Test Pieces”, cruciform test pieces according to ISO 16842 are used which feature uniform thickness and seven equidistant parallel slits per arm made by laser cutting. The selected dimensions are listed in Table 1 with B, C, L, ws and R denoting the arm width, clamping length, slit length, slit width and corner radius, respectively. For comparison purposes, aluminium alloy sheets (AA5754, AlMg3) from various manufacturers have been acquired with the sheet thickness a varying between 0.5 and 2 mm. For the uniaxial tensile tests in rolling and transverse direction, standard uniaxial test pieces according to DIN 50125, type H are applied [27].

Table 1 Selected dimensions for standard test specimen according to ISO 16842
Full size table

The recommended strain rate is between 0.0001 and 0.1\(\frac {1}{\mathrm {s}}\). For force-controlled experiments where the loading rate is held constant, the strain rate increases significantly at the elastic-plastic transition. Therefore, a relatively low initial strain rate (during elastic deformation) of

$$ \dot{\varepsilon_{0}} = 0.0002\frac{1}{\mathrm{s}} $$
(15)

is chosen and converted into an equivalent loading rate

$$ \dot{F} = \dot{\varepsilon_{0}} \cdot E B a $$
(16)

where E = 70000 MPa is the Young’s modulus. Under consideration of the stress ratio α, the loading rate can then be decomposed into its components:

$$ \begin{array}{@{}rcl@{}} \dot{F}_{x} &=& \dot{F} \frac{\alpha}{\sqrt{\alpha^{2}+1}} \end{array} $$
(17)
$$ \begin{array}{@{}rcl@{}} \dot{F}_{y} &=& \dot{F} \frac{1}{\sqrt{\alpha^{2}+1}} \end{array} $$
(18)

For the limit case \(\alpha =1:0 = \infty \), the application of Hospital’s rule gives uniaxial tension in x-direction: \(\dot {F}_{x} =\dot {F}\) and \(\dot {F}_{y}=0\).

Optimization of Cruciform Test Specimen

Design Goals and Variables

The design of cruciform test specimens has to be viewed as a multi-objective optimization problem. To be applicable for the determination of yield surfaces, the specimen must meet the following requirements:

  1. 1.

    The stress field has to be homogeneous to be obtainable from the ratio of applied force to the cross-sectional area.

    This is realized by the introduction of slits to the arms.

  2. 2.

    The achievable stresses in the gauge area should be as high as possible, ideally they reach the ultimate tensile strength.

    Therefore, the specimen has to be reduced in thickness at the gauge area. Together with the first requirement, this leads to a specimen design of the Hayhurst-Kelly type.

  3. 3.

    The size of the gauge area should be as large as possible to increase the quality of strain measurement by video extensometer.

    As the strain is determined from the displacements of two selected points which are identified by means of image recognition, the thickness of the gauge area has to be constant.

  4. 4.

    The manufacturing costs should be moderate.

    Hence, only milling tools with standard dimensions are accepted.

Note that most other specimen geometries are the result of a single-objective optimization. For example, the design proposed by Deng et al. [26] is optimized with respect to an utmost homogeneous stress distribution in a large gauge area. This is achieved by an abrupt transition between gauge area and arms. As shown in “Comparison with Other Hayhurst-Kelly Type Specimens”, this transition leads to a premature specimen failure due to high stress concentrations which makes the design useless for the determination of yield surfaces. Other geometries maximize the achievable stresses, but have a heterogenous stress distribution, etc.

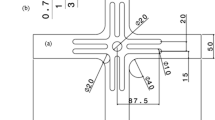
Figure 2 shows some of the introduced variables which are classified as follows:

  • Design variables

    Design variables are the most important variables. They are regarded as independent parameters for the optimization process. Examples include the slit width wS, the corner radius R and the gauge area thickness a.

  • Predetermined variables

    To reduce the numerical effort, some dimensions are introduced as predetermined or fixed variables such as the slit length L = 40 mm, the arm width B = 35 mm, the clamping length C = 20 mm, the number of slits per arm, namely 7, and the size of the gauge area, c × c = 25 mm × 25 mm. These values are adapted from the standard specimen given in Table 1.

    It should be remarked, that the classification in design and predetermined parameters itself has been the result of an optimization process — even though not an automated one.

  • Dependent variables

    Dependent or auxiliary variables such as the slit radius RS or the overall length are required for the model setup. They are defined as a function of the design variables, e.g. \(R_{\mathrm {S}} = \frac {w_{\mathrm {S}}}{2}\).

Fig. 2
figure 2

Introduction of geometric dimensions as variables: slit length L, slit width wS, arm width B, finger widths dS, dS1, dS2 and dS3, radii R, RC, RG and RS, sheet thickness t, gauge area thickness a, size of the reduced thickness area b and the gauge area size c

Full size image

The dimensions of the test specimen are optimized using the commercial finite element software Abaqus in combination with an in-house parameter identification tool called MatFit. It minimizes the objective function by means of the SLSQP method (Sequential Least Squares Programming) implemented in Python/SciPy. For this purpose, MatFit automatically creates the Abaqus input files, starts the analyses and evaluates the result files. The objective function includes, among other terms, the relative error

$$ E_{\text{rel}} = \frac{q_{\max}-q_{\min}}{q_{\min}} $$
(19)

of the gauge area (measurement area) where

$$ q = \sqrt{\frac{3}{2} \mathbf{S}:\mathbf{S}} $$
(20)

is the Mises equivalent stress and

$$ \mathbf{S}:\mathbf{S} = S_{11}S_{11}+S_{12}S_{12}+\ldots+S_{33}S_{33} $$
(21)

is the scalar product of the deviatoric stress tensor S.

Figure 3 illustrates that a cruciform test piece can be seen as an assembly of spring elements arranged in series and in parallel. The quarter model of a specimen with 7 slits per arm consists of a total number of 12 spring elements for each direction, as shown on the left-hand side. Only when this system of springs is in equilibrium, the load Fy introduced on the right-hand side leads to a homogenous deformation. To be precise, only spring elements which belong to the same section (arranged in parallel) undergo the same amount of straining: springs between slits (S, S1, S2 and S3), corner springs (C, C1, C2 and C3) and gauge section springs (G, G1, G2 and G3).

Fig. 3
figure 3

Idealization of biaxial test piece as assembly of spring elements arranged both in series and in parallel

Full size image

Consider, for instance, the corner spring C. Its stiffness value kC not only depends on the gauge area thickness a but also on the three radii R, RC and RG (see Fig. 2). Hence, an alteration of one of these variables would lead to a stiffness kC that is either too high or too low. As shown in Fig. 4, the deformation would be heterogeneous, as would be the strain and stress distribution.

Fig. 4
figure 4

Heterogeneous deformation as a result of a too low or too high corner spring stiffness kC

Full size image

Achieving an optimal stiffness value \(k_{\mathrm {C}}^{\text {opt}}\), or rather, maintaining it during the optimization process, is not an easy task due to manufacturing issues. For example, a slight reduction of the gauge area thickness a by 2% cannot be compensated by changing the radii RC and RG since only certain values and combinations (corner radius end mills) are available. Only R can be adjusted freely because the specimen outline can be manufactured by means of laser or water-jet cutting.

There is no need to set up a mathematical model for the correlation between dimensions (design variables) and spring stiffnesses. The spring model shall only help to gain a better understanding of how the load is distributed within the cruciform test piece. Thus, it helps to reduce the number of independent parameters: Since a is constant, the corresponding stiffnesses must be identical: kG1 = kG2 = kG3. It follows that kC1 = kC2 = kC3 and kS1 = kS2 = kS3. Finally, it can be concluded that the slit distances must be identical: dS1 = dS2 = dS3. Note that dS has to be larger than dS1 due to the relatively stiff transition zone (represented by kG).

Stress Distribution and Material Model

For a two-dimensional stress state, the Mises equivalent stress is given as:

$$ q= \sqrt{{\sigma_{x}^{2}}+{\sigma_{y}^{2}}-\sigma_{x}\sigma_{y}+3\sigma_{xy}^{2}} $$
(22)

For example, σx = 160 MPa, σy = 120 MPa and σxy = 0 yields q = 144.2 MPa.

Figure 5 shows the maximum and minimum Mises stresses, \(q_{\max \limits }=145.7\) MPa and \(q_{\min \limits }=144.1\) MPa, obtained from the gauge area for the optimum specimen geometry. The average Mises stress value, 144.9 MPa, is slightly higher than the analytical solution, 144.2 MPa, since a geometric nonlinear analysis is performed which uses true stresses. The stress field can be regarded as homogeneous as the error is only Erel = 1.1%.

Fig. 5
figure 5

Homogeneous stress distribution in 25 mm × 25 mm gauge area of optimized cruciform test specimen

Full size image

As illustrated in Fig. 6, there is no interaction between the applied forces Fx and Fy if the specimen has well-balanced proportions. The stresses σx and σy are decoupled and the gauge area can be regarded as being shear-free, since the rotation of the spring elements which represent the specimen arms is relatively small. For other materials such as rubber which experience larger deformations than metals, cruciform test pieces with longer arms (and longer slits) are required.

Fig. 6
figure 6

Homogeneous strain and stress distribution, even under biaxial loading

Full size image

The simulation can be considered elastic, at least for the gauge area. A classical metal plasticity model with Mises yield surface and associated plastic flow has been used. The material parameters have been adapted to the uniaxial tensile test of the 0.5 mm aluminium sheet given in Fig. 16: a yield strength of 180 MPa, tensile strength of 272 MPa and a fracture strain of 10.1%. Simulations using the Hill yield surface which allows for anisotropic yield had little influence on the optimization procedure or rather on the identified geometric parameters which define the shape of the optimized cruciform test specimen.

While the Mises stresses in the gauge area are below the yield strength, this is not the case for the slit ends. As explained in greater detail in “Comparison with Standard Test Specimen”, the Mises stresses at the slit ends have exceeded 180 MPa, leading to small, but irreversible plastic deformations.

Abaqus offers the opportunity to extend the elasto-plastic model by a continuum damage approach which is applicable for ductile metals. Since this extension significantly increases the computational cost, it is not used during the parameter optimization process which requires hundreds or even thousands of simulation runs. However, this option has been proven to be very useful when it comes to getting an impression of the failure mode. For the failure analyses, the shear criterion has been chosen which uses the equivalent plastic strain at damage as material parameter: εf = 0.1 = 10% (from the 0.5 mm aluminium sheet given in Fig. 16). The damage evolution part of the model uses the fracture energy as material parameter, thus ensuring that the results are independent from the mesh refinement. Instead of providing the fracture energy directly, it can also be given by means of the total displacement at failure (1mm), measured from the time of damage initiation.

Adaption to Manufacturing Issues and Sensitivity Analysis

The dimensions of the optimized cruciform test piece design can be taken from Fig. 7. While the outer shape matches the standard sample, the slits are wider, the gauge area thickness is reduced, and the corner radius R is increased from 1 to 2 mm. The slits of the optimized specimen are manufactured by water-jet cutting, without rounding of the edges (to avoid additional costs).

Fig. 7
figure 7

Optimized cruciform test piece design for determining yield surfaces

Full size image

A corner radius end mill of 8 mm diameter and 2 mm corner radius is used for milling both sides of the specimen. Thus, in contrast to cylindrical end mills used e.g. by Deng et al. [26], a rather smooth transition can be achieved. The cutting depth is 1.25 mm which gives a transition angle of

$$ \alpha = \arccos\left( \frac{0.75}{2}\right) = 1.1864 = 67.98^{\circ} . $$
(23)

The cross-sectional area is smallest between two opposing slit ends:

$$ \begin{array}{@{}rcl@{}} A &=& 35 \cdot 5 -2\cdot \underbrace{31 \cdot 1.25}_{=A_{1}} -4\cdot \underbrace{\left[\frac{1}{2}\alpha\cdot 2^{2} -\frac{1}{2}\cdot 2\sin(\alpha) \cdot 2\cos(\alpha)\right]}_{=A_{2}} \end{array} $$
(24)
$$ \begin{array}{@{}rcl@{}} &=& 90.79~\text{mm}^{2} \end{array} $$
(25)

The effective cross-sectional area is slightly higher and identified by means of inverse parameter identification, i.e., by adapting the finite element results to the analytical stress-strain curve (Hooke’s law):

$$ A_{\text{eff}} = 94.15\text{mm}^{2} $$
(26)

Division by the arm width provides an average gauge section thickness of

$$ t_{\text{eff}} = \frac{A_{\text{eff}}}{35\text{mm}} = 2.69~\text{mm} . $$
(27)

Not only the dimensions that define the end mill (a corner radius end mill — to be more specific) have been rounded, but also the other dimensions. Examples include the corner radius R = 2 mm, the slit width wS = 2 mm and the reduced sheet thickness a = 2.5 mm. For the sensitivity analysis presented in Tables 2, 3 and 4, the specimen is subject to nominal stresses of σx,nom = 160 MPa and σy,nom = 120 MPa. As expected, the reference dimensions minimize the relative error.

Table 2 Influence of corner radius R on homogeneity of stress distribution in gauge area
Full size table
Table 3 Influence of slit width ws on homogeneity of stress distribution
Full size table
Table 4 Influence of gauge area thickness a on homogeneity of stress distribution
Full size table

Comparison with Standard Test Specimen

While the applied stresses, 160 and 120 MPa, lead to an elastic deformation of the gauge area, the maximum Mises stresses at the slit ends have exceeded the yield strength, causing local plastic deformations. For the standard specimen which features a slit width of 0.1 mm and a sheet thickness of 0.5 mm, the stresses correspond to tensile forces of 2.1 and 2.8 kN. A finite element simulation using adaptive remeshing yields a maximum Mises stress of q = 253 MPa, see Fig. 8.

Fig. 8
figure 8

Mises stress concentration at slit ends of 0.5 mm thick standard cruciform test piece obtained by adaptive remeshing

Full size image

To obtain the same stress field in the gauge area, the optimized test specimen is subject to tensile loading of 120 MPa ⋅ 2.69 mm ⋅ 35 mm = 11.298 kN and 15.064 kN. As can be seen from Fig. 9, the maximum Mises stress at the slit ends is only 194 MPa, thanks to the wider slits and the thinner gauge area.

Fig. 9
figure 9

Optimized cruciform test specimen showing lower maximum stresses due to wider slits and thinner gauge area

Full size image

The differences between the standard and the optimized specimen become even more apparent when comparing the equivalent plastic strain

$$ \tilde{\varepsilon}_{\text{pl}} = {{\int}_{0}^{t}} \sqrt{\frac{2}{3}\dot{{\varepsilon}}_{\text{pl}} : \dot{{\varepsilon}}_{\text{pl}}} dt $$
(28)

listed in Table 5. The stresses given in the first two columns correspond to a constant force ratio of \(\frac {F_{x}}{F_{y}}=\frac {4}{3}\) and refer to the gauge area (center).

Table 5 Equivalent plastic strains of standard and optimized test specimen at gauge area (center) and maximum values (slits) obtained for a force ratio of \(\frac {F_{x}}{F_{y}}=\frac {4}{3}\)
Full size table

For the standard cruciform test specimen, yielding at the slit ends starts at quite low nominal stresses, (σx,σy) = (25.6 MPa,19.2 MPa). At the fourfold loading, (100.5 MPa, 75.4 MPa), the optimized test specimen is still in the elastic regime. When yielding starts in the gauge area, the maximum plastic strains are 20.1% for the standard specimen and only 0.6% for the optimized specimen. When the equivalent plastic strain reaches a value of 1% at the gauge area, the slits ends have to endure 45.0% for the standard specimen and only 3.9% for the optimized specimen, etc.

Neither of the two designs is capable of measuring the fracture strain of 10.1%. However, the optimized specimen can achieve a much higher maximum strain. Using the elasto-plastic damage mechanics approach yields a maximum gauge area strain of 3.2% for the standard specimen and 7.5% for the optimized specimen. Figure 10 shows the destroyed optimized test specimen.

Fig. 10
figure 10

Failure of optimized test specimen at maximum equivalent plastic strain \(\tilde {\varepsilon }_{\text {pl}}^{\text {center}}=7.5\%\) simulated by means of damage mechanics

Full size image

Comparison with Other Hayhurst-Kelly Type Specimens

As already pointed out in “Design Goals and Variables”, developing a cruciform sample design is a challenging task as contradictory objectives have to be balanced against each other. The proposed design has been optimized with respect to the measurement of yield surfaces in accordance with the standard ISO 16842. At first glance, several other cruciform test specimen design seem to meet the requirements, too, of which the most important is a homogeneous stress distribution. To the authors’ experience, however, almost all specimen designs found in the literature lead to a quite heterogeneous stress distribution, even those of the Hayhurst-Kelly type.

For demonstration purposes, Fig. 11 shows the Mises stress distributions of 8 different specimen designs, using a rather tight range: stresses below 144.2 MPa are given in blue, stresses above 145.6 MPa in red. The standard cruciform specimen (a) is subjected to normal stresses of σx = 160 MPa and σy = 120 MPa. For the other specimen designs, the load has been adapted to a target Mises stress value of 144.9 MPa at the center point (in green), while the stress ratio is kept constant: α = 4 : 3.

Fig. 11
figure 11

Mises stress distribution of different test specimen designs at a stress ratio of α = 4 : 3 (reference value of 144.9 MPa is given in green, stresses below 144.2 MPa in blue, stresses above 145.6 MPa in red) [28]

Full size image

Only three specimen designs yield a homogenous stress distribution: standard (a), optimized (b) and the design developed by Deng et al. (f). While “yellow and dark green stresses” (as well as orange and turquoise) can be found in the gauge area (error still below 1 percent) of standard and optimized specimen designs, the Deng specimen provides immaculate “green stresses”. The designs proposed by Merklein and Biasutti (e) and Liu et al. (g) use a one-sided thickness reduction. This reduces the manufacturing costs, but also introduces a bending moment to the gauge area which is responsible for the circular stress distribution. The specimen designs proposed by Kelly (c), Shao et al. (d) and Tiernan and Hannon (h) lead to asymmetric Mises stress distributions which reveal that the stresses in x-direction (160 MPa) are higher than those in y-direction (120 MPa).

While a heterogeneous stress distribution is inevitable when the cruciform test specimen is optimized from a fracture mechanics point of view, a homogeneous stress distribution does not guarantee that the specimen design is applicable for yield surface measurements. In the case of the specimen proposed by Deng et al., there are no fillets to smooth the thickness reduction. On the one hand, this leads to a perfect stress distribution in the gauge area, on the other hand, the stress singularities at the transition zone cause premature failure of the specimen.

Figure 12 shows the corresponding equivalent plastic strains of the specimen designs with homogeneous stress distribution. The maximum values are \(\tilde {\varepsilon }_{\text {pl}}^{\text {slits}} = 5.7\%\) for the standard test specimen and only \(\tilde {\varepsilon }_{\text {pl}}^{\text {slits}} = 0.2\%\) for the optimized test specimen (see also Table 5), thanks to the thickness reduction and wider slits. For the specimen design proposed by Deng et al. [26], no mesh convergence can be obtained due to stress singularities at the 90-degree angles. Nevertheless, the trend is clear: the maximum equivalent plastic strain value is considerably higher than that of the standard design and also much higher than the value obtained by the authors who use a relatively coarse mesh.

Fig. 12
figure 12

Equivalent plastic strains of specimen designs with homogeneous stress distribution

Full size image

Influence of Stress Ratio

It is reported that the force-stress relationship can depend on the imposed stress ratio [4]. For the optimized specimen, fortunately, the average gauge section thickness teff = 2.69 mm given in (27) is independent from the stress ratio. For demonstration purposes, Fig. 13 shows the normal stress distributions σx = σxx and σy = σyy, obtained for the stress ratios a) α = 1 : 0 (uniaxial tension), b) α = 2 : 1 and c) α = 1 : 1 (equi-biaxial tension). Since there are three symmetry planes, a reduced FE model has been used where the force in x-direction is given as

$$ F_{x} = \frac{1}{4} \cdot 160\text{MPa} \cdot 2.69~\text{mm} \cdot 35~\text{mm} = 3.766\text{kN} . $$
(29)

The resulting stress distribution is homogeneous with σx = 160MPa at the gauge area not only for α = 4 : 3 (see previous Sections) but for all stress ratios. In y-direction, the normal stresses are σy = 0MPa for α = 1 : 0, σy = 40MPa for α = 2 : 1 and σy = 80MPa for α = 1 : 1.

Fig. 13
figure 13

Normal stresses of the optimized cruciform test design (reduced FE model, three symmetry planes), obtained for different stress ratios

Full size image

Figure 14 demonstrates that the shear stresses are minimized by the new specimen geometry. The legend is chosen to range only from − 3 to + 3 MPa to demonstrate that there are no shear stresses within the whole gauge area. At the corner and the slit ends, however, shear stresses are inevitable. More interesting than the values, which exceed 3 MPa, is the sign. While the shear stresses at the corner are positive for all stress ratios, the sign at the slit ends depends on the loading. For example, consider the point next to the yz-symmetry plane: The equi-biaxial stress state leads to negative shear (c) whereas positive shear is observed for a stress ratio of α = 2 : 1 (b). This change of sign can be seen as proof that the specimen’s proportions are in good balance. Even under uniaxial loading, shear stresses cannot be avoided (a). For this reason, the standard ISO 16842 recommends the use of uniaxial test specimens for α = 1 : 0 and 0 : 1.

Fig. 14
figure 14

Shear stresses of the optimized cruciform test design, obtained for different stress ratios

Full size image

Experimental Results

Biaxial tensile testing machine

To verify the simulation results and to demonstrate the advantages of the proposed specimen design, a biaxial testing machine from Walter + Bai AG, type LFM BIAX is used. It is equipped with the video extensometer hardware MercuryRT from Sobriety S.R.O. for the purpose of measuring the strain. The image recognition is improved by additional markers as shown in Figure 15 for the example of an optimized sample. The forces are applied using four digital controllers of the PCS8000 series and the DION7 testing software.

Fig. 15
figure 15

Performing a biaxial tensile test using the optimized cruciform test specimen

Full size image

The testing machine is programmed to stop when the force difference between two opposing arms is too large or when the load suddenly drops in order to avoid lateral forces. Lateral forces would destroy the load cells and deform the testing cylinders by bending. Hence, it is possible to measure the initiation of cracks but not the crack evolution.

Standard and optimized specimen are compared by their ability to measure yield surfaces. The 0.5, 1 and 2 mm aluminium alloy sheets (AA5754, AlMg3) are fabricated into standard test pieces, while a 5 mm sheet of the same material is used for the preparation of the optimized cruciform test piece as presented in Figure 7. All tests are performed at room temperature.

Experimental Results from Standard Test Pieces

At least three uniaxial tests have been performed for each sheet thickness in rolling direction. As the stress-strain curves are very similar, only one result is selected from each series. The true stress-true plastic strain curves shown in Fig. 16 reveal relatively large discrepancies in terms of yield strength and fracture strain. The 1 mm sheet has the highest yield strength of approximately 215 MPa, followed by the 0.5 mm sheet with 175 MPa and the 2 mm sheet with only 142 MPa. The higher the yield strength, the lower the fracture strain: approximately 6% for the 1 mm sheet, 10% for the 0.5 mm sheet and 14% for the 2 mm sheet.

Fig. 16
figure 16

Uniaxial true stress-true plastic strain curves for 0.5, 1 and 2 mm alloy 5754 sheets

Full size image

The different behavior cannot be attributed to the sheet thickness but is due to the heat treatment. For instance, when the temperature of the medium used for quenching (water, oil or air) increases or the quenchant is renewed, this directly affects the mechanical properties. As long as yield and tensile strength are within a certain range (see standard DIN EN 485-2), process parameters are allowed to change. For this reason, it is crucial that all test specimens required to obtain yield surfaces are manufactured from the same alloy sheet.

As far as the comparability of cruciform test geometries is concerned, two things can be concluded. First, it is almost impossible to measure the influence of sheet thickness because of the interaction with heat treatment. Second, it makes no sense to compare maximum strains. Instead, the ratio of maximum strain to fracture strain has to be used. Another noticeable characteristic that is observed from the yield curves is the serrated flow behavior. It is referred to as Portevin-Le Chatelier (PLC) effect and typical for AA5754. The PLC effect is caused by dynamic strain aging or rather dynamic interaction of solute atoms with mobile dislocations within the material [29].

Figures 17, 18 and 19 illustrate yield surfaces which are obtained by means of standard cruciform test pieces. Only complete curves are shown. For the 0.5 mm sheet, the largest equivalent plastic strain achieved for all stress ratios is 2%, see Fig. 17. For the 1 mm sheet, the outermost yield surface corresponds to a plastic strain of only 1%, i.e. the 2% curve is incomplete. The maximum equivalent strain is about 1.5% (Fig. 18). With the 2 mm standard samples, a maximum plastic strain value of 3% is recorded (Fig. 19).

Fig. 17
figure 17

Experimental yield surfaces for 0.5 mm sheet obtained using standard test pieces

Full size image
Fig. 18
figure 18

Experimental yield surfaces for 1 mm sheet obtained using standard test pieces

Full size image
Fig. 19
figure 19

Experimental yield surfaces for 2 mm sheet obtained using standard test pieces

Full size image

Note that, independent from the sheet thickness, the ratio of maximum equivalent strain to fracture strain is approximately 25 percent: \(\frac {2+0.5}{10}=0.25\) for the 0.5 mm sheet, \(\frac {1+0.5}{6} =0.25\) for the 1 mm sheet and \(\frac {3+0.5}{14}=0.25\) for the 2 mm sheet. The premature failure of the arms due to high stress concentrations at the slit ends prevents the measurement of further yield surfaces.

Experimental Results from Optimized Test Pieces

Figure 20 shows the yield curve of the 5 mm aluminium sheet obtained from uniaxial loading in rolling direction. The yield strength is about 170 MPa and the fracture strain is approximately 6.8%.

Fig. 20
figure 20

True stress-true plastic strain curve obtained from uniaxial loading in rolling direction

Full size image

The yield surfaces measured using the optimized cruciform test pieces are depicted in Fig. 21. The yield surface can be expanded up to the equivalent true plastic strain value of 4%. The ratio of maximum equivalent strain to fracture strain is approximately \(\frac {4.5}{6.8}=66\) percent which is about 2.5 times higher compared to the standard ISO 16842 design. For other materials, this ratio may be slightly different as the maximum equivalent plastic strain applicable to the gauge area depends on the hardening behavior. For more information on that subject, it is referred to the standard ISO 16842, Section B.2 “Effect on work hardening exponent (n-value)”.

Fig. 21
figure 21

Experimental yield surfaces for alloy 5754 sheet using optimized cruciform test piece

Full size image

Figure 22 shows the evolution of nominal strains in x-direction, ex, within the optimized cruciform test specimen for the stress ratio α = 4 : 3. In order to improve the full-field strain measurement, the specimen was first primed white to reduce light reflection and then covered with a random pattern of black dots. The digital image correlation (DIC) was performed using the software package GOM Correlate. The applied true stresses σx (3) and σy (4) as well as the equivalent plastic strains \(\varepsilon _{0}^{\text {pl}}\) can be taken from the subfigure captions.

Fig. 22
figure 22

Evolution of nominal strains ex, obtained from DIC for biaxial tensile test with stress ratio α = 4 : 3 (optimized cruciform test specimen)

Full size image

The stress state σx = 209MPa and σy = 156MPa leads to nominal strains of ex = 1.0% and ey = 0.3% (obtained from MercuryRT and confirmed by GOM Correlate). As explained in “Determination of Yield Surfaces According To ISO 16842”, the plastic works Wx (12) and Wy (13) calculated from yield curves are summed up which gives \(W_{0}=1818\frac {\text {kJ}}{\mathrm {m}^{3}}\) (14). A comparison with the plastic work from the uniaxial reference test (Fig. 20) results in the plastic strain value \(\varepsilon _{0}^{\text {pl}}=1.0\%\) (a).

Note that there is a difference between ex and \(\varepsilon _{0}^{\text {pl}}\). The second strain field (b) is the result of σx = 241MPa and σy = 179MPa. The nominal strains are measured to be ex = 3.0% and ey = 0.5%. The plastic work is \(W_{0}=6481\frac {\text {kJ}}{\mathrm {m}^{3}}\) which corresponds to \(\varepsilon _{0}^{\text {pl}}=3.2\)%.

While the strain distribution is homogeneous in the gauge area, increased strain values are observed at the transition zone where the sheet thickness changes from 2.5 to 5 mm, and at the slits ends. Subfigures (c) and (d) show the strain fields at the maximum stress level, σx = 250MPa and σy = 185MPa, just before and after specimen failure due to necking. At the localization zone which forms between the first vertical slits, strain values reach up to 8% (white spots just mean that the DIC evaluation has failed). As already mentioned, the biaxial testing machine is programmed to stop at this point to protect the load cells from being destroyed by lateral forces.

Conclusion

Both finite element simulations and experiments indicate that the cruciform test specimen proposed by ISO 16842 is not very suitable for the determination of yield surfaces. For the example of AA5754 sheets, it is found that the maximum equivalent plastic strain under biaxial loading is only 25 percent of the maximum strain. This limitation has been shown to be independent from the sheet thickness and is attributed to the stress singularities at the slit ends.

The new cruciform test piece design is the result of an elaborate multi-objective parameter optimization. The optimized specimen allows the determination of yield surfaces at significantly higher stress levels. The maximum plastic strain is increased to more than 60 percent of the fracture strain. The stress field at the gauge area can be considered homogeneous. In the elastic regime, the relative error is only about 1 percent.

A more extreme thickness reduction would increase the obtainable maximum plastic strain. Even the fracture strain could be reached, if the crack initiation were shifted from the slit ends to the gauge area. However, a further thickness reduction would also lead to a heterogeneous stress field or rather would reduce the size of the gauge area.

Thanks to the well-balanced proportions, the new specimen geometry is better suited for the determination of yield surfaces than any other geometry proposed so far, which are the result of single-objective optimization or deal with other materials. Although the new specimen geometry is optimized with respect to metals, it can easily be adapted to materials which experience larger deformations such as rubber. To avoid an interaction of the two loading directions even at very large strains, the arms and slits would have to be elongated accordingly.