Abstract
The ply elastic constants needed for classical lamination theory analysis of multi-directional laminates may differ from those obtained from unidirectional laminates because of three dimensional effects. In addition, the unidirectional laminates may not be available for testing. In such cases, full-field displacement measurements offer the potential of identifying several material properties simultaneously. For that, it is desirable to create complex displacement fields that are strongly influenced by all the elastic constants. In this work, we explore the potential of using a laminated plate with an open-hole under traction loading to achieve that and identify all four ply elastic constants (E 1 , E 2 , ν 12 , G 12 ) at once. However, the accuracy of the identified properties may not be as good as properties measured from individual tests due to the complexity of the experiment, the relative insensitivity of the measured quantities to some of the properties and the various possible sources of uncertainty. It is thus important to quantify the uncertainty (or confidence) with which these properties are identified. Here, Bayesian identification is used for this purpose, because it can readily model all the uncertainties in the analysis and measurements, and because it provides the full coupled probability distribution of the identified material properties. In addition, it offers the potential to combine properties identified based on substantially different experiments. The full-field measurement is obtained by moiré interferometry. For computational efficiency the Bayesian approach was applied to a proper orthogonal decomposition (POD) of the displacement fields. The analysis showed that the four orthotropic elastic constants are determined with quite different confidence levels as well as with significant correlation. Comparison with manufacturing specifications showed substantial difference in one constant, and this conclusion agreed with earlier measurement of that constant by a traditional four-point bending test. It is possible that the POD approach did not take full advantage of the copious data provided by the full field measurements, and for that reason that data is provided for others to use (as on line material attached to the article).





Similar content being viewed by others
References
Molimard J, Le Riche R, Vautrin A, Lee JR (2005) Identification of the four orthotropic plate stiffnesses using a single open-hole tensile test. Exp Mech 45:404–411
Lecompte D, Sol H, Vantomme J, Habraken AM (2007) Mixed numerical-experimental technique for orthotropic parameter identification using biaxial tensile tests on cruciform specimens. Int J Solids Struct 44:1643–1656
Avril S, Bonnet M, Bretelle AS, Grédiac M, Hild F, Ienny P, Latourte F, Lemosse D, Pagano S, Pagnacco E (2008) Overview of identification methods of mechanical parameters based on full-field measurements. Exp Mech 48(4):381–402
Kaipio JP, Somersalo E (2005) Statistical and computational inverse problems. Springer, New York
Gogu C, Haftka RT, Le Riche R, Molimard J, Vautrin A (2010) An introduction to the Bayesian approach applied to elastic constants identification. AIAA J 48(5):893–903
Isenberg J (1979) Progressing from least squares to Bayesian estimation. Proc., ASME Winter Annual Meeting, New York, NY, Paper 79-A/DSC-16
Sol H (1986) Identification of anisotropic plate rigidities, PhD dissertation (Vrije Universiteit Brussel)
Lai TC, Ip KH (1996) Parameter estimation of orthotropic plates by Bayesian sensitivity analysis. Compos Struct 34(1):29–42
Lecompte D, Sol H, Vantomme J, Habraken AM (2005) Identification of elastic orthotropic material parameters based on ESPI measurements.Proc, SEM Annual Conf Expo Exp Appl Mech
Silva G, Le Riche R, Molimard J, Vautrin A, Galerne C (2007) Identification of material properties using FEMU: application to the open hole tensile test. Appl Mech Mater 7–8:73–78
Noh WJ (2004) Mixed mode interfacial fracture toughness of sandwich composites at cryogenic temperatures, Master’s Thesis, University of Florida.
Post D, Han B, Ifju P (1997) High sensitivity moiré: Experimental analysis for mechanics and materials. Springer, New York
Walker CA (1994) A historical review of moiré interferometry. Exp Mech 34(4):281–299
Wood JD, Wang R, Weiner S, Pashley DH (2003) Mapping of tooth deformation caused by moisture change using moire interferometry. Dent Mater 19(3):159–166
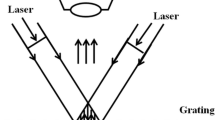
Lee JR, Molimard J, Vautrin A, Surrel Y (2006) Diffraction grating interferometers for mechanical characterisations of advanced fabric laminates. Opt Laser Technol 38(1):51–66
Yin W (2009) Automated strain analysis system: Development and applications. PhD dissertation, University of Florida.
Gogu C (2009) Facilitating Bayesian identification of elastic constants through dimensionality reduction and response surface methodology, PhD dissertation, University of Florida and Ecole des Mines de Saint Etienne.
Myers RH, Montgomery DC (2002) Response surface methodology: Process and product in optimization using designed experiments. Wiley, New York
Gogu C, Haftka RT, Le Riche R, Molimard J, Vautrin A, Sankar BV (2009) Bayesian statistical identification of orthotropic elastic constants accounting for measurement and modeling errors, AIAA paper 2009–2258, 11th AIAA Non-Deterministic Approaches Conference, Palm Springs, CA, May 2009
Smarslok BP, Haftka RT, Ifju P (2008) A correlation model for graphite/epoxy properties for propagating uncertainty to strain response, 23rd Annual Technical Conference of the American Society for Composites, Memphis, Tenn.
Jolliffe IT (2002) Principal component analysis, 2nd edn. Springer, New York
Allen DM (1971) Mean square error of prediction as a criterion for selecting variables. Technometrics 13:469–475
Gogu C, Haftka RT, Le Riche R, Molimard J (2010) Effect of approximation fidelity on vibration based elastic constants identification. Struct Multidiscip Optim 42(2):293–304
Acknowledgements
This work was supported in part by the NASA grant NNX08AB40A. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Aeronautics and Space Administration.
Author information
Authors and Affiliations
Corresponding author
Additional information
A. Vautrin deceased.
Appendices
Appendix 1: Proper Orthogonal Decomposition
The objective of this appendix is to provide an overview of the proper orthogonal decomposition method that is used for the dimensionality reduction of the full-fields. First the theoretical foundations of the method are presented followed by some results of its application to the plate with a hole problem.
Let us consider U i ∈ ℝn, which is the vector representation of a field (e.g. displacement field). Note that n is usually several thousands. We seek, based on N sample vectors {U i}i = 1..N, a reduced dimensional representation of the fields’ variations with some input parameters.
The aim of the proper orthogonal decomposition (POD) method is to construct an optimal, reduced dimensional basis for the representation of the sample vectors (also called snapshots). In the POD approach the snapshots need to have zero mean, if this is not the case the mean value needs to be subtracted.
We denote \( {\left\{ {{\Phi_k}} \right\}_{{_{{k = 1..K}}}}} \) the vectors of the orthogonal basis of the reduced dimensional representation of the snapshots. The POD method seeks to find the basis vectors Φ k that minimize the representation error:
Because \( {\left\{ {{\Phi_k}} \right\}_{{_{{k = 1..K}}}}} \) is an orthogonal basis, the coefficients α i,k are given by the orthogonal projection of the snapshots onto the basis vectors. As a result we have the following reduced dimensional representation \( {\widetilde{U}^i} \) of the vectors of the snapshot set:
The reduction in dimension is from N to K. The truncation order K needs to be selected such as to maintain a reasonably small error in the approximate representations \( {\widetilde{U}^i} \) of U i. Selecting such a K is always problem specific and an error criterion is given further down.
The main advantage of the POD method is that it provides a simple procedure for constructing the basis from the samples {U i}i = 1..N. The procedure guarantees that for a given truncation order we cannot find any other basis that better approximates the snapshots subspace.
The basis \( {\left\{ {{\Phi_k}} \right\}_{{_{{k = 1..K}}}}} \) is constructed using the following matrix:
The vectors \( {\left\{ {{\Phi_k}} \right\}_{{_{{k = 1..K}}}}} \) are then obtained by the singular values decomposition of X, or equivalently by calculating the eigenvectors of the matrix XX T. The singular values decomposition allows writing that:
where Φ is the matrix of the column vectors Φ k . The svd() function in Matlab was used here for the singular value decomposition.
A truncation error criterion ε is then defined by the sum of the error norms as shown in equation 10.
where \( \varepsilon = 1 - \left( {{{{\sum\limits_{{j = 1}}^K {\sigma_j^2} }} \left/ {{\sum\limits_{{j = 1}}^N {\sigma_j^2} }} \right.}} \right) \), and σ j are the diagonal terms of the diagonal matrix Σ. For a derivation of this criterion and further details on POD the reader can refer to [21]. The variation of this criterion with the truncation order for the plate with a hole problem is provided in Table 3 of the main section.
The error norm truncation criterion ε, while being a global error criterion, is relatively hard to interpret physically. Furthermore the criterion is based only on the convergence of the snapshots that served for the POD basis construction. However in most cases we will want to decompose a field that is not among the snapshots, so we also want to know the convergence of the truncation error in such cases.
Accordingly we chose to construct a different error measure based on cross validation. The basic idea of cross validation is the following: if we have N snapshots, instead of using them all for the POD basis construction we can use only N-1 snapshots and compute the error between the actual fields of the snapshot that was left out and its truncated POD decomposition. By successively changing the snapshot that is left out we can thus obtain N errors. The root mean square of these N errors, which we denote by CVRMS, is then a global error criterion that can be used to assess the truncation inaccuracy.
In order to use the cross validation technique we need to define how to measure the error between two strain fields (the actual strain field and its truncated POD decomposition). We chose the maximum absolute difference between two fields. This maximum error is computed at each of the N (N = 200 here) cross validation steps and the root mean square leads to the global error criterion CVRMS. Table 8 provides these values for different truncation orders. The relative CVRMS error with respect to the value of the field where the maximum error occurs is also given in Table 8.
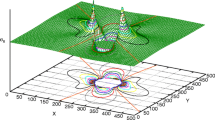
Next we provide a graphical representation of POD results in order to have a more intuitive understanding of the modal decomposition. First an illustration of the fields obtained for a particular snapshot (snapshot 1) is shown in Fig. 6, which provides an idea of the spatial variations and order of magnitude of the displacement fields. These fields were obtained with the following parameters: E 1 = 202.2 GPa, E 2 = 10.84 GPa, ν 12 = 0.2142, G 12 = 4.989 GPa, t = 0.1312 mm.
The first four POD modes that we obtained are represented graphically in Figs. 7 and 8. We note that the first modes are relatively close (but not identical even though the differences cannot be seen by naked eye) to the typical U and V displacement fields (see Fig. 6). Furthermore we see that the modes have a more complicated shape with increasing mode number, as expected for a modal decomposition basis.
Appendix 2: Error Measures of the Response Surface Approximations
The error measures used to assess the quality of the response surface approximations (RSA) constructed in “Identification Results and Discussion” are given in Table 9 for the first four POD coefficients of the U fields and in Table 10 for those of the V fields. The second row gives the mean value of the POD coefficient across the design of experiments (DoE). The third row provides the standard deviation of the coefficients across the DoE, which gives an idea of the magnitude of variation in the coefficients. Row four provides R2, the correlation coefficient obtained for the fit, while row five gives the root mean square error among the DoE points. The final column gives the cross validation PRESS error [22].
Comparing the error measures for each coefficient to their range of variation (i.e. standard deviations) we considered that the RSA are accurate enough to be used in the identification process, with the approximation error being negligible compared to the other sources of uncertainty.
Appendix 3: Bayesian Numerical Implementation
A Bayesian identification numerical procedure able to account for measurement uncertainty, modeling uncertainty as well as uncertainty in other model parameters was previously developed by the authors in [23] and will also be used here.
The numerical procedure uses Monte Carlo simulations for uncertainty propagation. While the use of Monte Carlo simulation has the advantage of propagating uncertainties represented by arbitrary probability distribution functions it has the drawback of being computationally expensive. The POD method and response surface methodology are thus used for reducing the cost associated with the construction of the likelihood function. A flowchart overview of the utilized procedures is presented in Fig. 9.
The likelihood function is computed point by point within the prior distribution’s support (truncation bounds) at a grid in the four-dimensional space of the material properties E = {E 1 , E 2 , ν 12 , G 12 }. We chose a 174 grid, which is a compromise between convergence and computational cost considerations.
At each of the grid points, E is fixed and we need to evaluate the probability density function (PDF) of the POD coefficients, \( {f_{{{{\alpha } \left/ {{E = {E^{{fixed}}}}} \right.}}}}(\alpha ) \), at the point α = α measure. The PDF of the POD coefficients is determined by propagating through Monte Carlo with 4,000 simulations the uncertainties in the other model parameters (plate thickness here) and adding a sampled value of the normally distributed uncertainty in the POD coefficients resulting from measurement and modeling uncertainty, as described in the previous subsection.
Physical considerations showed that the resulting samples must be close to Gaussian so the samples were replaced by the normal distribution, having the sample mean and variance-covariance matrix. This Gaussian nature is due to the fact that the uncertainty resulting from the measurement noise is Gaussian and the uncertainty due to thickness is proportional to 1/h, which can in this case be well approximated by a normal distribution. The distribution \( {f_{{{{\alpha } \left/ {{E = {E^{{fixed}}}}} \right.}}}}(\alpha ) \) was then evaluated at the point α = α measure, leading to \( {f_{{{{\alpha } \left/ {{E = {E^{{fixed}}}}} \right.}}}}({\alpha^{{measure}}}) \). In this way we obtain a discretized likelihood function, which multiplied by the prior distribution gives us the posterior distribution of the elastic constants that we seek to identify.
At this point we want to make the following note. We found that the overall uncertainty on the POD coefficients is close to normal, which means that the Bayesian identification could have been treated within a purely analytical framework, thus avoiding the need for expensive Monte Carlo simulations. The analytical treatment would however have no longer been possible if uncertainties on more complex input parameters would have been considered leading to a clearly non-Gaussian distribution on the POD coefficients. In such a case the Monte Carlo simulations based approach would still work and this is the purpose why we developed this more general approach in [23]. For convenience we reused our already developed approach here, even though with several days of computational cost this approach is clearly not numerically the most efficient. More efficient numerical implementation are certainly possible and we provide the data files of the experimental results together with this paper such as to allow interested persons (including possibly ourselves at a future point) to test other implementations on the same experimental data.
Appendix 4: Data Structure of the Provided Measurements
The authors also provide attached to the online version of the paper the experimental displacement fields obtained. These are the displacement fields obtained based on the moiré interferometry images and the automated phase extraction procedure described in “Experiment”. The data is provided in matrix form as .txt files which can be opened with any text editor. The X.txt file provides the X coordinate (in millimeters) of each point where a displacement value is provided. Similarly the Y.txt file provides the Y coordinate. The U.txt file provides the displacements in micrometers at each point in the loading direction (Y direction). The V.txt file provides the displacements in the orthogonal direction (X direction). Note that the X and Y direction are related to the actual experiment axes (Fig. 2) not to the 1 and 2-driections provided in Fig. 1.
Rights and permissions
About this article
Cite this article
Gogu, C., Yin, W., Haftka, R. et al. Bayesian Identification of Elastic Constants in Multi-Directional Laminate from Moiré Interferometry Displacement Fields. Exp Mech 53, 635–648 (2013). https://doi.org/10.1007/s11340-012-9671-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11340-012-9671-8