1 Introduction

WSANs are composed of sensors and actuators distributed in a geographic area of interest. Sensors are devices of low processing capacity, very low power consumption, and low cost, responsible for monitoring the physical environment, while the actuators perform a task according to the collected data and reported by sensors during an event [1]. In WSANs, knowing the position of the sensor nodes is very important, since it enables determining the geographic localization of an event, and a timely response to this, apart from facilitating the routing through the network and reduce the node power consumption [2]. Therefore, the precise localization of sensors is a critical requirement for the deployment of WSANs in a wide variety of applications such as animal tracking, logistics, health care, monitoring spatial evolution of an extraordinary phenomenon, among others.

In WSANs, the localization is described according to a reference coordinate system defined by RNs with known positions [3]. In reconfigurable networks, such as ad-hoc and WSAN, connectivity is not always direct between two nodes, and the access points are connected through multiple hops to the node of interest (NOI), [3, 4]. In a multi-hop scenario [5], neighboring nodes provide information of the NOI, which is necessary and required to find its localization. Currently, there is a wide range of localization algorithms used in WSANs for determining the localization of a sensor node. Some algorithms are based on GPS systems, which are useful outdoors, while their performance is severely decreased in indoor scenarios [3, 6].

In the literature, localization algorithms are classified in range and range-free based algorithms (or connectivity-based). The former assumes that the signal strength decreases with distance, thus, signal strength readings can be used to estimate distance, which are then used to infer the position of the NOI. These techniques present very accurate results. However, they require specialized hardware, which makes them expensive in large networks [7]. When estimating the distance between nodes is unfeasible (or prone to errors), distance free algorithms are recommended as they use information about connectivity. These algorithms assume that the transmission rate is constant, or that the distribution of nodes across the network is uniform it is known. This means that the performance depends on the difference between expected and actual values of the transmission range and distribution of nodes (COM-LOC) [8]. In terms of accuracy, these techniques are not as good as those based on range but its implementation is relatively simple and low cost. Due to the limitations of hardware in WSANs and restrictions on power consumption, this article focuses on investigating range-free algorithms localization in WSANs.

This article presents two contributions to the problem of localization in WSANs. First, this work evaluates the performance of range-free multi-hop localization algorithms, such as DV-Hop [9], IDV-Hop [10] and WDV-Hop [11]. Second, in this work a new range-free localization algorithm is proposed, which improves accuracy and precision, merging the WDV-Hop [11] and Weighted Hyperbolic (WH) algorithms. WDV-Hop is responsible for estimating the distance between the NOI to the RNs, and WH computes the position of NOI and reduces localization error by including weights to the correlation matrix of the estimated distances between the NOI and the RNs. As performance metrics, accuracy is evaluated in terms of Mean Squared Error (MSE) of the actual position and the estimated position of the NOI; precision, as the distribution of errors and localization, and computational complexity based on the average time it takes a computer algorithm to estimate the position of a node.

The rest of the paper is organized as follows: Sect. 2 describes formally the problem. Section 3 presents some localization techniques used in multi-hop networks. In Sect. 4, the performance localization techniques presented in Sect. 2 are discussed. The main contribution of this work is presented in Sect. 5, where an improved localization algorithm is presented. The performance analysis of algorithms evaluated and compared with the proposed algorithm is presented in Sect. 6 in terms of the Mean Squared Error and computational complexity under different densities of nodes. Finally, The Conclusions are presented.

2 Problem Statement

This section provides a formal description of the range-free localization problem. In this work, a set of randomly distributed sensor nodes in a two dimensional plane is considered to determine the position of an unknown NOI node. Also, in this work, we assume that there is a set of N RNs \(A_i\) with known coordinates \(p_i=(x_i,y_i), \quad i=1,2,\ldots ,N\), which may be inside or outside the transmission range of the NOI.

Free-range localization algorithms use connectivity information between two nodes to estimate the distance between the NOI to the RNs. For the purpose of this work, there is connectivity between two nodes when they are within the coverage range of each other. The radio coverage is obtained by the Received Signal Strength Indicator (RSSI). In this work, the Log-Normal Shadowing Model (LNSM) is used to estimate the signal strength in the distances distribution [COM-LOC-1] [11], because both theoretical and experimental studies support this model in indoor and exterior scenarios. The Log-Normal model propagation is used to estimate the power received, which is inversely proportional to the distance \(d^{-\eta }\) where \({\eta }\) is the path loss exponent. This model is expressed by:

$$\begin{aligned} P_{RX}(dBm)=A-10{\eta }\log \frac{d}{d_0}+X_{\sigma }, \end{aligned}$$
(1)

where A is the average power received at a reference distance \(d_{0}, X_{\sigma }\) is a Gaussian random variable with zero mean and standard deviation \(\sigma\) in dB. Typical values for the path loss exponent are in the range of 1.5 through 5 and for \(\sigma\) in the ranges of values from 4 to 12 dB [3, 12, 13]. Multilateration is used in order to estimate the position of the NOI.

3 Related Work: Localization Techniques

Localization techniques in WSNs are mainly classified into three categories: The first class are distance estimation techniques such as Angle of Arrival (AoA), Time of Arrival (ToA), Time Difference of Arrival (TDoA), and Received Signal Strength (RSS), used to estimate the distance between two sensor nodes. ToA computes physical distance by speed and time of signal propagation, which requires a perfect synchronization of the nodes. AoA estimates the distance of the NOI using the direction of the neighboring nodes signal through an array of antennas and multiple receivers, which involves costly hardware. TDoA computes the time difference of arrival of the received signals to avoid dependency of the synchronization nodes and performs the multilateration combining measurements from multiple nodes. For the RSSI, the received power is used to calculate propagation losses to estimate the distance, and uses this to infer the position of the NOI [14], using an empirical or theoretical path loss model. The second class involves algorithms for estimating the position of the NOI. The localization techniques in the third class are classified into three groups: range-based, range-free, and proximity-based and Hybrid. Range-based techniques estimate distance between a group of nodes using an estimation range technique. Some of these techniques are least squares multilateration [4]; multidimensional scaling (MDS) [15], Ad-hoc Positioning Systems (APS) [16], and ranking Circular and Hyperbolic algorithms [17]. The range-free techniques estimate the position of the NOI by RSS, so estimating the distance between nodes is not required, but decreases accuracy with respect to the former techniques. These techniques include DV-Hop [4, 18, 19], APIT method (Approximate Point in Triangle) [4, 20], centroid [4], rectangular intersection [21], circular intersection [21], and hexagonal intersection [21], among others. Finally, hybrid techniques merge range-free and range-based techniques for a more precise localization of the NOI.

We next describe some of the range-free multi-hop algorithms used for the evaluation performance in this work: DV-Hop, IDV-Hop and WDV-Hop.

3.1 DV-Hop Localization Algorithm

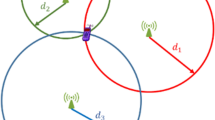
DV-Hop (Distance Vector Hop) uses the hop-based propagation model [22], which exchange information about the distances among all nodes of the network, both RNs and nodes with unknown localization (hereinafter referred to as unknown nodes), so that each unknown node belonging to the network stores the distance in hops to all RNs \(A_i\). Each unknown node maintains a table with information: \({x_i, y_i, H_i}\), where \((x_i, y_i)\) is the coordinate of the RN and \(A_i\) and \(H_i\) is the number of hops from the unknown node to the RN. This table is updated only with information provided by the neighboring nodes of the unknown node. Figure 1 shows the DV-Hop localization scheme. For each RN \(A_i\), the average distance of a simple hop known as correction factor \(c_i\) is estimated using Eq. (2).

$$\begin{aligned} c_i=\frac{\sum d_{ij}}{\sum h_{ij}}=\frac{\sum \sqrt{(x_i-x_j)^2+(y_i-y_j)^2}}{\sum h_{ij}},\quad i\ne j, \end{aligned}$$
(2)

where \(d_{ij}\) is the euclidean distance between the RNs \(A_i\) and \(A_j\), and \(h_{ij}\) is the smallest number of hops between RNs \(A_i\) and \(A_j\).

Fig. 1
figure 1

DV-Hop localization scheme

Full size image

The estimated distance between an unknown node to the RN \(A_i\) is represented by Eq. (3):

$$\begin{aligned} \hat{d}_{pi}=c_i*h_{pi}, \end{aligned}$$
(3)

where \(h_{pi}\) is the smallest number of hops between the RN \(A_i\) and the unknown node P, \(c_i\) is the average distance per hop of the \(A_i\) RN closest to the unknown node P, and \(\hat{d}_{pi}\) is the estimated distance of the unknown node to the reference node \(A_i\).

3.2 Improved DV-Hop Localization Algorithm

One of the problems with the DV-Hop is that as the number of nodes in the network increases, the number of hops between RNs and unknown nodes also increases, causing a cumulative error. An increase in the average distance error of hops also increases the localization error of an unknown node. To address this, in [23, 24], they proposed the IDV-Hop, wherein they use a mean correction factor in the network, which is defined by Eq. (4):

$$\begin{aligned} \bar{c}=\frac{\sum c_i}{N}, \end{aligned}$$
(4)

where N is the number of RNs, and \(\bar{c}\) is the average correction factor of the network. In this way, the mean distance in each hop is neither too big nor too small compared to the mean length of the other hops. The estimated distance between an unknown node to the RN \(A_i\) is computed using the Eq. (5).

$$\begin{aligned} \hat{d}_{pi}=\bar{c}*h_{pi}. \end{aligned}$$
(5)

3.3 Weighted DV-Hop Localization Algorithm

WDV-Hop reduces the localization error by adding a correction parameter in the network [11]. For this, it first computes the mean correction factor of the network \(\hat{c}\). Then, it obtains the mean hop distance error in the network, modifying the mean hop distance in the network, aiming at improving the accuracy of the unknown node positioning, and, finally, it computes the mean hop distance error in the network with Eq. (6):

$$\begin{aligned} \delta =\frac{\Sigma |d_{ij}-\hat{d}_{ij}|/h_{ij}}{\sum h_{ij}},\quad i\ne j, \end{aligned}$$
(6)

where \(\hat{d}_{ij}=\bar{c}*h_{ij}\) represents the estimated distance between RNs \(A_j\) and \(A_i\). Afterwards, parameter \(\delta\) is sent to every node in the network. Finally, the mean hop length in the network is computed using (7)

$$\begin{aligned} \hat{c}=\bar{c}+k\delta , \end{aligned}$$
(7)

where \(k\in [-1,1]\) is a parameter used to balance the mean hop distance in the network, which highly depends on the network simulation environment. To estimate the distance between an unknown node P and a RN \(A_i\), the Eq. (8) is used.

$$\begin{aligned} \hat{d}_{pi}=\hat{c}*h_{pi}. \end{aligned}$$
(8)

3.4 Hyperbolic Positioning Algorithm

The DV-Hop, IDV-Hop, and WDV-Hop algorithms make use of the hyperbolic positioning algorithm to find the position of the NOI. The idea behind this algorithm is to find the position (x, y) which minimizes the sum of squared error from all the set of estimated distances. If \((x_i, y_i)\) represents the position of RN \(A_i\) where \((i = 1,2, ..., N\), where N is the number of RNs) and \(\hat{d}_i\) is the estimated distance from the RN \(A_i\) to the NOI, then the error is provided by:

$$\begin{aligned} \varepsilon =\sum _{i=1}^{N}\left( \sqrt{(x-x_i)^2+(y-y_i)^2}-\hat{d}_i\right) ^2. \end{aligned}$$
(9)

The Eq. (9) shows a nonlinear optimization problem. The Hyperbolic positioning algorithm [17] transforms the nonlinear problem in a linear problem that can be solved with a least squares estimator. The distance between a mobile node and a RN \(A_i\), is expressed by Eq. (10).

$$\begin{aligned} d_{i}^2=(x-x_i)^2+(y-y_i)^2. \end{aligned}$$
(10)

Expanding Eq. (10) and redefining in matrix form, the following expression is obtained:

$$\begin{aligned} \begin{bmatrix} 2x_2&2y_2 \\ \vdots&\vdots \\ 2x_N&2y_N \\ \end{bmatrix} \begin{bmatrix} x \\ \\ y \\ \end{bmatrix}= \begin{bmatrix} x_2^2+y_2^2-d_2^2+d_1^2 \\ \vdots \\ x_N^2+y_N^2-d_N^2+d_1^2\\ \end{bmatrix}. \end{aligned}$$
(11)

Then, this problem can be formulated as

$$\begin{aligned} H\hat{p}=\tilde{b}, \end{aligned}$$
(12)

where

$$\begin{aligned} H=\begin{bmatrix} 2x_2&2y_2 \\ \vdots&\vdots \\ 2x_N&2y_N \\ \end{bmatrix},\qquad \hat{p}=\begin{bmatrix} x \\ \\ y \\ \end{bmatrix},\qquad \tilde{b}=\begin{bmatrix} x_2^2+y_2^2-d_2^2+d_1^2 \\ \vdots \\ x_N^2+y_N^2-d_N^2+d_1^2\\ \end{bmatrix}. \end{aligned}$$
(13)

Therefore, the estimated position \(\hat{p}\) of the NOI can be calculated by expression (14).

$$\begin{aligned} \hat{p}=(H^TH)^{-1}H^T\tilde{b}. \end{aligned}$$
(14)

The hyperbolic algorithm does not directly minimize the localization error given by (9). The algorithm minimizes the sum of distances to the hyperbolas defined by the subtraction of two estimated distances.

4 Performance Evaluation of State-of-the-Art Algorithms for Multi-hop Localization

Figure 2 shows the localization error for the WDV-Hop algorithm, varying the value of k, where k is the balancing parameter of the average length hop in the network, considering a network of 200 randomly distributed nodes, where each node transmits at a maximum distance of 30 m. Figure 2 shows the localization error for a network of AN = 10, 20, 30 RNs, where AN (Anchor Nodes) represents the number of RNs. Following Fig. 2, it can be seen that as the number of RNs increases, the localization error decreases. The purpose of this test is to obtain the value of k that minimizes the localization error of the NOI. In Fig. 2, with \(k=1.2\), the smallest localization error is obtained. In the analysis of accuracy and precision a value of \(k=0.6\) was selected, since this value is within the range \([-1,1]\), which enables that the mean hop length is not as far from the actual mean hop length.

Fig. 2
figure 2

MSE normalized versus k of [0.4, 1.6]

Full size image

In Fig. 3, the performance of localization error of the DV-Hop, IDV-Hop, and WDV-Hop algorithms are observed, considering a 100-node network where the number of RNs increases from 5 to 30. In this particular scenario, IDV-Hop resulted in a smaller localization error than that of DV-Hop and WDV-Hop for a 5–15 RNs variation. However, as seen, the error is smaller for the WDV-Hop when the number of RNs is larger than 20. This means that there is a 25 % decrease of the MSE when comparing the 5 and 30 RNs.

Fig. 3
figure 3

Normalized MSE versus Reference nodes for a 100-node network

Full size image

Similarly, Fig. 4 shows the performance in a (randomly distributed) 150-node network for a set of 5, 10, 15, 20, 25 and 30 RNs. As seen, there is around 25 % decrease in the localization error, where WDV-Hop performs better than DV-Hop and IDV-Hop. However, as expected, the improvement of the WDV-Hop algorithms is due to the increase in density of the nodes. Thus, it can be argued that as the density of RNs increases, WDV-Hop will result in smaller a localization error than DV-Hop and IDV-Hop.

Fig. 4
figure 4

Normalized MSE versus reference nodes for a 150-node network

Full size image

Figure 5 shows the cumulative distribution function (CDF) for the DV-Hop, IDV-Hop and WDV-Hop algorithms considering a 150-node network with 10 RNs and a transmission ratio of 20 m for each node. In this scenario, the WDV-Hop algorithm resulted in a higher precision due to the size of the network (150 nodes). This was not noticeable in a 100 node network. Following Fig. 4, the WDV-Hop results in a smaller error from 10 RNs onward, which is consistent with Fig. 5.

Fig. 5
figure 5

Localization error [R] for a 10 reference node network

Full size image

5 Our Proposal: Weighted Hyperbolic DV-Hop Algorithm (WHDV-Hop)

In this section, we present our proposed localization algorithm for multihop networks. This proposal involves using a weighted DV-Hop algorithm [11] merged with the weighted hyperbolic localization algorithm [25], which computes the localization of the NOI. the hyperbolic localization and weighted hyperbolic algorithms require a priori knowledge about the estimated distance between the RNs and the NOI, as well as the position of the RNs. The difference relies in the manner in which these algorithms solve the linear problem: the former uses a least squares estimator proposed in [17], while the latter algorithm uses a weighted least squares estimator proposed in [25]. The weighted hyperbolic algorithm achieves higher accuracy than the hyperbolic algorithm, but requires a greater number of arithmetic operations during implementation since it runs in time \(\mathcal {O}(n^3)\) [25].

5.1 Weighted Hyperbolic Positioning Algorithm

The traditional hyperbolic positioning algorithm computes the position of the mobile node using Eq. (14). This algorithm solves the linear problem using a weighted least squares estimator proposed in [25]. In this case, the position of the mobile node is computed by the Eq. (15).

$$\begin{aligned} \hat{p}=(H^TS^{-1}H)^{-1}H^TS^{-1}\tilde{b}, \end{aligned}$$
(15)

where S is the covariance matrix of the vector \(\tilde{b}\). It is important to note that the noise affects the vector \(\tilde{b}\) measurements whose mean is not zero, so the estimator (16) is a biased estimator. Assuming the estimated distances \(\hat{d}_i\) are independent and the coordinates of the RNs are constant, the covariance matrix S can be computed using Eq. (15). The development of the covariance matrix shown in [25].

$$\begin{aligned} S= \begin{bmatrix} 1+\left( \frac{d_2}{d_1}\right) ^4&1&\ldots&1 \\ 1&1+\left( \frac{d_3}{d_1}\right) ^4&\ldots&1 \\ \vdots&\vdots&\ddots&\vdots \\ 1&1&\ldots&1+\left( \frac{d_n}{d_1}\right) ^4 \\ \end{bmatrix} \end{aligned}$$
(16)

The elements of the covariance matrix S depends on the actual distance \(d_i\) between the NOI and the RN \(A_i\). Therefore, for an implementation in a real environment estimator in (15), it is necessary to approximate the actual distance \(d_i\) by the estimated distance \(\hat{d}_i\).

In [14], it was shown that the weighted hyperbolic positioning algorithm achieves higher accuracy than the classic algorithm of hyperbolic positioning under the same evaluation scenario, since this algorithm includes a covariance matrix, which contains information relating the behavior of the estimated distances affected by noise, but implies more computational complexity.

Our proposed technique is described as follows: first the WDV-Hop algorithm is used, which should correct the error of the mean hop length \(\delta\) in the network. The parameter \(\delta\) is sent to all nodes in the network. After the unknown and reference nodes receive the information of parameter \(\delta\), Eq. (7) is used to compute the mean hop length of the entire network \(\hat{c}\) and Eq. (8) is used to estimate the distance P between an unknown and a RN \(A_i\). Finally, the NOI position is estimated by weighted hyperbolic positioning algorithm presented in this section using the Eq. 15. It it important to note that the weighted hyperbolic positioning algorithm and the classic hyperbolic positioning algorithm requires only to know the coordinates of the reference nodes and estimated distances by weighted DV-Hop to the NOI to find its position.

6 WHDV-Hop Versus State-of-the-Art Algorithms: A Performance Comparison

In this section, the performance of the DV-Hop algorithm and its variants discussed in previous sections is compared with our proposal, the WHDV-Hop algorithm, in terms of three performance metrics: (1) accuracy (i.e., mean square error - MSE), (2) precision (i.e., cumulative probability distribution - CDF), and (3) computational complexity.

6.1 Evaluation Scenario

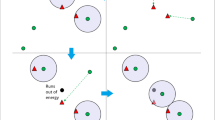
The localization techniques were evaluated with MATLAB version 2011 B in a scenario with 100 sensor nodes formed with RNs or anchor nodes (blue triangles) and unknown nodes (gray circle), are randomly distributed in a 100 m\(\times\)100 m area as shown in Fig. 6. Each node has a broadcast range of 20 m, where 20 nodes are considered as RNs (or anchor nodes). A total of \(M=1000\) runs were evaluated. The Table 1 shows the parameters used in for this scenario. For each scenario, the position of all unknown nodes is calculated. Figure 6 shows that the cross-shaped node represents a node to locate (i.e, the NOI) among the set of unknown nodes.

Table 1 Parameters used for the simulations
Full size table
Fig. 6
figure 6

Distribution of the sensor nodes in a 100 m\(\times\)100 m area

Full size image

6.2 Performance Metrics

1. Accuracy This parameter is defined as the mean square error (MSE) of the actual and the estimated NOI position, across several iterations. If (x, y) is the actual position of the NOI and \((\hat{x}_k, \hat{y}_k)\) is the estimated position in the \(k=1,2,..., M\) iterations, then the metrics are given by:

$$\begin{aligned} MSE=\frac{1}{M}\sum _{k=1}^{M}(x-x_k)^2+(y-y_k)^2. \end{aligned}$$
(17)

2. Precision These metrics consider the distance error distribution while the accuracy considers the mean value of those errors. When two techniques are compared, technique with concentrated distance errors on small values is preferred.

3. Computational complexity It refers to the number of mathematical operations performed by an algorithm in run time. In this paper, this parameter is measured by computing the mean time it takes for an algorithm to estimate the position of a node for each density of nodes. It also considers the complexity of the algorithm.

6.3 Accuracy Analysis

Figure 7 shows the behavior of the analyzed algorithms, considering a randomly distributed 100-node network varying the number of RNs by 5, 10, 15, 20, 25, 30. Analyzing the localization error obtained shows that the proposed algorithm has a smaller error than the other localization analyzed algorithms. This analysis shows that WDV-Hop with weighted hyperbolic positioning yields higher accuracy. The improvement is due to the weighted hyperbolic positioning algorithm, which is more accurate in locating the NOI in scenarios where the RN is one hop distance from the NOI. Similarly, Fig. 8 shows an analysis considering a randomly distributed 150-node network. This configuration shows that by increasing the number of nodes in the network, the localization error decreases, which is observed in the analyzed algorithms. The weighted hyperbolic WDV-Hop positioning algorithms, reaches a localization error below \(20\,\%\) for a 30 RN network, which is an improvement compared with the results shown in Fig. 3, where the proposed algorithm reaches a localization error of approximately \(25\,\%\). Figure 9 shows the results of localization error for a network of 10 RNs, where the number of nodes in the network varies from 100 to 350 nodes nodes. In Fig. 10, the weighted hyperbolic WDV-Hop positioning algorithm shows the best performance in terms of accuracy, reaching a localization error of approximately \(28\,\%\) for a network of 350 randomly distributed nodes, while DV-Hop and IDV-Hop show a very similar pattern, reaching a localization error of about \(30\,\%\) for a network with 350 randomly distributed nodes. The analysis shown in Fig. 10 is similar to Fig. 9. This analysis considers a network with 20 RNs, where the number of nodes in the network varies. The results show that increasing the number of RNs causes the the localization error to decrease. Performance graphs of accuracy of the analyzed algorithms show that the WDV-Hop with weighted hyperbolic positioning algorithm yields better performance. In this analysis, the WDV-Hop with weighted hyperbolic positioning algorithm, localization error reaches about \(20\,\%\). The localization error for a randomly distributed 150-node network with 10 RNs is observed in Fig. 11. In this analysis, the radio of communication nodes in the network is increased from 15 to 40 m. The results show that increasing the radio of communication of any node in the network, reduces the localization error analyzed algorithms, since an increased radio of communication implies that there is greater connectivity in the network. In Fig. 12, a randomly distributed 150-node network with 20 RNs is considered. The results show that increasing the number of RNs in the network yields a higher localization accuracy of the NOI. Following Fig. 12, we can observe that the weighted hyperbolic WDV-Hop positioning algorithm has the smallest localization error for any radio of communication node in the network. The algorithm WDV-Hop with weighted hyperbolic positioning provides a localization error of about \(20\,\%\) whereas in Fig. 11 this algorithm yields a localization error of approximately \(25\,\%\).

Fig. 7
figure 7

Normalized MSE versus RNs for a 100-node network

Full size image
Fig. 8
figure 8

Normalized MSE versus RNs for a 150-node network

Full size image
Fig. 9
figure 9

Normalized MSE versus 10-RN network

Full size image
Fig. 10
figure 10

Normalized MSE versus 20-RN network

Full size image
Fig. 11
figure 11

Normalized MSE versus radio communication for a 10-RN network

Full size image
Fig. 12
figure 12

Normalized MSE versus radio communication for a 20-RN network

Full size image

6.4 Analysis of Precision

For the evaluation of the precision the cumulative probability was calculated. In Fig. 13 shows the cumulative distribution function (CDF) for the analyzed algorithms. The results show that the algorithm weighted hyperbolic WDV-Hop positioning has a better precision in the localization of the NOI than the other analyzed algorithms in this evaluation scenario, that is, considering a randomly distributed 150-node network with 10 RNs. Analyzing the behavior of the CDF from the weighted hyperbolic WDV-Hop positioning algorithm, it can be seen that for a localization error of \(30\,\%\) there is a probability of about \(45\,\%\) of any node in the network is located with an localization error less than \(30\,\%\) error, while an localization error for a \(33\,\%\) the probability of finding any node with an error of less than \(33\,\%\) localization is about \(80\,\%\). The improvement in precision of the analyzed algorithms with the proposed algorithm of weighted hyperbolic positioning is considerable. The results show that the precision of localization the NOI will be between \([25\,\%, 40\,\%]\) of the localization error while for the precision of the localization for the DV-Hop algorithms and WDV-Hop is between \([30\,\%, 50\,\%]\) of the localization error. Figure 14 shows the CDF of the algorithms analyzed for a 150-node network with 20 RNs. The results show an improvement in the precision of the localization by increasing the number of RNs. Analyzing the CDF of algorithm with weighted hyperbolic WDV-Hop positioning, it can be seen that for a localization error of \(25\,\%\), the probability of finding an unknown node in the network with an error of less \(25\,\%\) is about \(87\,\%\). The probability to find an unknown node with an error of smaller than \(30\,\%\) is \(100\,\%\) probability, which is a significant improvement compared with the analysis made for a network with 10 RNs. Figure 15 shows the CDF of analyzed algorithms for a 200-node network with 10 RNs. Comparing the CDF of the WDV-Hop with weighted hyperbolic positioning algorithm and the CDF shown in Fig. 13, we can observe that, in this scenario, the precision is improved in locating the unknown node, for a localization error of \(30\,\%\) the probability of finding the node of interest is approximately \(65\,\%\), whereas the results shown in Fig. 13, the probability of finding the node of interest with an error less than \(30\,\%\) is approximately \(45\,\%\). Figure 16 shows the behavior of the CDF of the analyzed algorithms for a 200-node network with 20 RNs. The results prove that increasing the amount of RNs in the network, yields an increase in the precision of the localization of the NOI. Comparing the CDF between WDV-Hop with weighted hyperbolic positioning and the CDF of the algorithm shown in Fig. 14, it shows that for this analysis the precision can be improved, since for a localization error of \(22\,\%\) the probability of finding the NOI is about \(78\,\%\) while those shown in Fig. 14, the CDF is about \(40\,\%\) for a localization error approximately \(22\,\%\), then there is an improvement of \(38\,\%\) of precision in locating the node of interest.

Fig. 13
figure 13

Localization error [R] for a 150-node network and 10 RNs

Full size image
Fig. 14
figure 14

Localization error [R] for a 150-node network and 20 RNs

Full size image
Fig. 15
figure 15

Localization error [R] for a 200-node network and 10 RNs

Full size image
Fig. 16
figure 16

Localization error [R] for a 200-node network and 20 RNs

Full size image

6.5 Analysis of Complexity

Table 2 shows the execution time in seconds of the algorithms described in previous sections for different node densities. The results of Table 2 were obtained as an average of 750 iterations for each node density. According to the results, it is observed that the weighted hyperbolic WDV-Hop positioning algorithm has higher execution time, but the difference is not significant. In Fig. 17, the runtime of the analyzed algorithms for different densities of nodes is observed. Basically, all the analyzed algorithms describe a similar behavior with low density of nodes. However, as the number of nodes increases it can be seen a small variation between them, so that WDV-Hop requires more processing time to find the position of the NOI.

Table 2 Run-time of the analyzed algorithms for different densities of nodes
Full size table
Fig. 17
figure 17

Number of nodes in the network versus runtime [s] for a 200-node network with 20 RNs

Full size image

6.6 Results Discussion

In Table 3, the performance of localization techniques analyzed using performance metrics as RMS error, accuracy, and complexity is shown. The indicators used to measure the quality of performance of each algorithm are analyzed: very bad, bad, fair, good and very good. Table 3 shows that DV-Hop, IDV-Hop, and WDV-Hop have a very good accuracy and precision, but according to the results WDV-Hop yields higher accuracy and precision in locating the NOI due to the average-distance correction factor per hop included in the algorithm.

Table 3 Quality performance metrics
Full size table

The complexity of these algorithms is bad since they use the weighted hyperbolic positioning algorithm, its order of complexity is \(O(n^3)\), where n is the number of RNs within the coverage area of NOI, but no all RNs. Instead the DV-Hop, IDV-Hop, and WDV-Hop with classic hyperbolic positioning algorithms, provide regular complexity, since this algorithm is asymptotic cost of O(n), because it only involves matrix multiplication operations. In a sensor network, a regular node requires considerable processing time for range-based localization algorithms, instead, it is recommended to have the information processed in a data fusion center or a central computer to which sensor nodes would send it since nodes would be of low power consumption and need to be energy efficient. Besides, the efficiency of these algorithms can be improved employing parallelization techniques for matrix operations. Range-free algorithms would be a better implementation choice for WSNs. WHDW-Hop algorithm shows a better performance in accuracy and precision during the NOI localization in comparison with other mentioned algorithms. It requires, however, a higher number of computing operations in order to estimate the NOI position.

WHDW-Hop algorithm could be used on WSN applications such as health, energy quality, remote monitoring, object tracking, home automation, fire detection, among others, since the precision of this algorithm guarantees a more accurate object localization or event detection.

7 Conclusions

In WSN, the connectivity information from neighboring nodes to access points is used to estimate the position of an unknown node. Analyzing evaluated algorithms, range-free algorithms are computationally more efficient than the algorithms range-based as DV-Distance, since this algorithm requires knowing the distance between two nodes, using some distance estimation technique. On the other side, range-free algorithms such as DV-Hop only estimate the number of intermediate nodes between two access points. In this manuscript, we proposed a fusion of WDV-Hop with the weighted hyperbolic positioning algorithm, which yields higher precision and accuracy than the other analyzed algorithms, albeit more computationally complex. As a future work, we will reduce the computing complexity related to the designed algorithm, and improve accuracy and precision in localization using alternate algorithms. Finally, we will analyze the impact of localization algorithms described in this article on a real environment and extend the localization of nodes in WSN applications.