Performance analysis of multiple RISs aided multi-user mmWave MIMO systems

Abstract

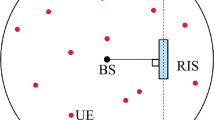
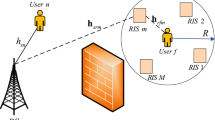
Reconfigurable intelligent surface (RIS) is envisioned to be a promising solution to enhance coverage and capacity of future wireless networks. With the deployment of multiple RISs, the optimal placement and topology are crucial issues that need to be addressed, which are significantly different from that of active BSs/relays. This paper considers a mmWave MIMO system aided by multiple RISs in a circular layout to observe the effect of RIS placement and power scaling law. The active and passive beamforming are configured to combine the signals coherently to improve the spectral efficiency (SE). To this end, we investigate the effect of quantization error on the SE and derive an upper bound. It indicates that the SE loss is only affected by the number of quantization bits and numerical results show that 5-bit quantizer is sufficient to ensure an acceptable SE degradation. Furthermore, we evaluate the performance of the system by formulating the tight upper bounds on the average ergodic spectral efficiency and propose three effective schemes for RIS selection. Our simulation results verify the derivations and validate that the performance of deploying the RISs close to BS is significantly better than that of deploying the RISs randomly in the cell.

Appendices

Appendix A

We denote the quantization error on the phase of each n-th element as ${\delta _{i,n}}$ which satisfies $- \frac{{2\pi }}{{{2^B} + 1}} \le {\delta _{i,n}} \le \frac{{2\pi }}{{{2^B} + 1}}$. Define

$$\begin{aligned} {z_1}= {{\tilde{\varvec{w}}}}_k^H{\varvec{a}}\left( {\phi _{{\text{r}},2,k,{q_k}}^{{\bar{l}}},\varphi _{{\text{r}},2,k,{q_k}}^{\bar{l}}} \right) = \frac{1}{{{N_{\mathrm{{r}}}}}}\sum \limits _{n = 1}^{{N_{\mathrm{{r}}}}} {{e^{j{\delta _{1,n}}}}}, \end{aligned}$$

(30)

$$\begin{aligned} {z_2}&= {{\varvec{a}}^H}\left( {\phi _{{\text{t,}}2,k,{q_k}}^{\bar{l}},\varphi _{{\text{t}},,2,k,{q_k}}^{{\bar{l}}}} \right) {\tilde{{\varTheta }} _{{q_k}}}{\varvec{a}}\left( {\phi _{{\text{r}},{\text{1}},{q_k}}^{{\bar{c}}},\varphi _{{\text{r}},{\text{1}},{q_k}}^{{\bar{c}}}} \right) \nonumber \\ &= \frac{1}{N}\sum \limits _{n = 1}^N {{e^{j{\delta _{2,n}}}}}, \end{aligned}$$

(31)

$$\begin{aligned} {z_3} &= {{\varvec{a}}^H}\left( {\phi _{{\text{t}},{\text{1}},{q_k}}^{\bar{c}},\varphi _{{\text{t}},{\text{1}},{q_k}}^{{\bar{c}}}} \right) {\varvec{\tilde{f}}}_{{\text{RF}}}^k = \frac{1}{{{N_{\mathrm{{t}}}}}}\sum \limits _{n = 1}^{{N_{\mathrm{{t}}}}} {{e^{j{\delta _{3,n}}}}}. \end{aligned}$$

(32)

The baseband equivalent channel of the UE k can be written as

$$\begin{aligned} {{{{\tilde{\varvec{H}}}}}_{{\text{eq}}}} &= {{\tilde{\varvec{w}}}}_k^H{{{\varvec{\tilde{H}}}}_k}{\varvec{{\tilde{f}}}}_{{\text{RF}}}^k\nonumber \\ &= \sqrt{\frac{{{\beta _{k,{q_k}}}{N_{\mathrm{{t}}}}{N_{\mathrm{{r}}}}{N^2}}}{{{L_{1,{q_k}}}{L_{2,k,{q_k}}}}}} \alpha _{{\text{1,}}{q_k}}^{{\bar{c}}}\alpha _{2,k,{q_k}}^{\bar{l}}{z_1}{z_2}{z_3}. \end{aligned}$$

(33)

Since $B \ge 1$, we have

$$\begin{aligned} \left| {{z_i}} \right| \ge \left| {\frac{{{e^{- j\frac{{2\pi }}{{{2^{B + 1}}}}}} + {e^{j\frac{{2\pi }}{{{2^{B + 1}}}}}}}}{2}} \right| = \cos \left( {\frac{\pi }{{{2^B}}}} \right) , i = 1,2,3. \end{aligned}$$

(34)

Then the SE of the UE k in (3) achieved by using finite-resolution beamforming can be rewritten as

$$\begin{aligned} {\tilde{{\mathcal {R}}}_k} = {\log _2}\left( {1 + {\gamma _k}{{\left| {{z_1}} \right| }^2}{{\left| {{z_2}} \right| }^2}{{\left| {{z_3}} \right| }^2}} \right) , \end{aligned}$$

(35)

where

$$\begin{aligned} {\gamma _k} = \frac{{P{\beta _{k,{q_k}}}{N_{\mathrm{{t}}}}{N_{\mathrm{{r}}}}{N^2}{{\left| {\alpha _{{\text{1,}}{q_k}}^{{\bar{c}}}} \right| }^2}{{\left| {\alpha _{2,k,{q_k}}^{{\bar{l}}}} \right| }^2}}}{{K{\sigma ^2}{L_{1,{q_k}}}{L_{2,k,{q_k}}}}}. \end{aligned}$$

(36)

Then the SE loss can be calculated as

$$\begin{aligned} \varDelta {{{\mathcal {R}}}_k}= & {} {\log _2}\left( {\frac{{1 + {\gamma _k}}}{{1 + {\gamma _k}{{\left| {{z_1}} \right| }^2}{{\left| {{z_2}} \right| }^2}{{\left| {{z_3}} \right| }^2}}}} \right) \nonumber \\{} & {} \mathop \le \limits ^{\left( a \right) } {\log _2}\left( {\frac{1}{{{{\left| {{z_1}} \right| }^2}{{\left| {{z_2}} \right| }^2}{{\left| {{z_3}} \right| }^2}}}} \right) \nonumber \\{} & {} \mathop \le \limits {\log _2}\left( {{{\cos }^{ - 6}}\left( {\frac{\pi }{{{2^B}}}} \right) } \right) , \end{aligned}$$

(37)

where $\left( a \right)$ is from the fact that $\log \left( {\frac{{1 + a}}{{1 + b}}} \right) \le \log \left( {\frac{a}{b}} \right)$ for any positive numbers a and b.

Consequently, we can get the upper bound in (13).

Appendix B

By using (19), we have

$$\begin{aligned}{} & {} {\mathbb {E}} \left\{ {{{\left| {\alpha _{{\text{1,}}{q}}^{{\bar{c}}}} \right| }^2}} \right\} \nonumber \\{} & {} \quad = \int \limits _0^\infty {{L_{1,{q}}}{{\left( {1 - {e^{ - x}}} \right) }^{{L_{1,{q}}} - 1}}{e^{ - x}}xdx} \nonumber \\{} & {} \quad \mathop = \limits ^{\left( a \right) } \int \limits _0^\infty {{L_{1,{q}}}\sum \limits _{t = 0}^{{L_{1,{q}}} - 1} {\left( {\begin{matrix} {{L_{1,{q}}} - 1}\\ t \\ \end{matrix}} \right) } {{\left( { - {e^{ - x}}} \right) }^t}{e^{ - x}}xdx} \nonumber \\{} & {} \quad = \sum \limits _{t = 1}^{{L_{1,{q}}}} {\left( {\begin{matrix} {{L_{1,{q}}}}\\ t \\ \end{matrix}} \right) } {\left( { - 1} \right) ^{t - 1}}t\int \limits _0^\infty {{e^{ - tx}}xdx} \nonumber \\{} & {} \quad \mathop = \limits ^{\left( b \right) } \sum \limits _{t = 1}^{{L_{1,{q}}}} {\left( {\begin{matrix} {{L_{1,{q}}}}\\ t \\ \end{matrix}} \right) } {\left( { - 1} \right) ^{t - 1}}{t^{ - 1}}, \end{aligned}$$

(38)

where (a) makes use of the binomial theorem ${\left( {a + b} \right) ^n} = \sum \limits _{k = 0}^n {{\text{C}}_n^k{a^{n - k}}{b^k}}$ where the coefficient ${\text{C}}_n^k = \left( {\begin{matrix} n\\ k \end{matrix}} \right) = \frac{{n!}}{{k!\left( {n - k} \right) !}}$, and (b) results from $\int \limits _0^\infty {{e^{ - tx}}xdx = {t^{ - 2}}}$. In the same way, we can deduce that ${\mathbb {E}} \left\{ {{{\left| {\alpha _{2,k,{q}}^{{\bar{l}}}} \right| }^2}} \right\} = \sum \limits _{t = 1}^{{L_{2,k,{q}}}} {\left( {\begin{matrix} {{L_{2,k,{q}}}}\\ t\\ \end{matrix}} \right) } {\left( { - 1} \right) ^{t - 1}}{t^{ - 1}}$.

We introduce the new variables defined as

$$\begin{aligned} {\xi _\varDelta } = \frac{1}{{{L_\varDelta }}}\sum \limits _{t = 1}^{{L_\varDelta }} {\left( {\begin{array}{*{20}{c}} {{L_\varDelta }}\\ t \end{array}} \right) } {\left( { - 1} \right) ^{t - 1}}{t^{ - 1}}, \end{aligned}$$

(39)

where $\varDelta$ is used to replace subscripts in ${{L_{1,{q}}}}$ and ${{L_{2,k,{q}}}}$.

When $5 \le L \le 10$, the variables ${\xi _\varDelta }$ can be approximated by ${\xi _\varDelta } \approx 0.0106L_\varDelta ^2 - 0.185{L_\varDelta } + 1.116$. With ${L_\varDelta } \sim DU\left[ {1,L} \right]$, $L_\varDelta$ has the maximum value when ${L_\varDelta }=1$, i.e., ${{\xi _\varDelta }} \le 0.9416$.

With the assumption $\theta _{{\mathop {\text{inter}}} }^{{q}} \sim U\left[ {{\vartheta _a},{\vartheta _b}} \right]$ and $0 \le {\vartheta _a} \le {\vartheta _b} \le \pi$, we have

$$\begin{aligned} {\mathbb {E}} \left\{ {{{\cos }^2}\left( {\theta _{{\mathop {\text{inter}}} }^{{q}}} \right) } \right\} =\frac{1}{2} + \frac{{\sin 2{\vartheta _b} - \sin 2{\vartheta _a}}}{{4\left( {{\vartheta _b} - {\vartheta _a}} \right) }} \le 1. \end{aligned}$$

(40)

By using (14), we have

$$\begin{aligned}{} & {} {\mathbb {E}} \left\{ {\frac{1}{{{{\left( {{U_k} - r} \right) }^2}}}} \right\} \nonumber \\{} & {} \quad = \frac{1}{{R - 3{d_0} }}\int \limits _\varGamma {\frac{1}{{{{\left( {x - r} \right) }^2}}}} dx\nonumber \\{} & {} \quad = \frac{1}{{R - 3{d_0} }}\left( {\int \limits _{{d_0}}^{r - {d_0}} {\frac{1}{{{{\left( {x - r} \right) }^2}}}dx} + \int \limits _{r + {d_0}}^R {\frac{1}{{{{\left( {x - r} \right) }^2}}}dx} } \right) \nonumber \\{} & {} \quad = \frac{1}{{R - 3{d_0} }}\left( {\frac{1}{{r - R}} + \frac{2}{{{d_0}}} - \frac{1}{{r - {d_0}}}} \right) . \end{aligned}$$

(41)

In addition, according to ${\mathbb {E}}\left( {AB} \right) ={\mathbb {E}} \left( A \right) {\mathbb {E}}\left( B \right)$ and $\sum \limits _{q = 1}^Q {{m_{k,q}}} = 1$, we have

$$\begin{aligned} {\mathbb {E}} \left\{ {\sum \limits _{q = 1}^Q {{m_{k,q}}{{\hat{\gamma }}_{k,q}}} } \right\}= & {} {\mathbb {E}} \left\{ {{{{\hat{\gamma }} }_{k,{q_k}}}} \right\} \nonumber \\\le & {} \frac{{0.8866}}{{R - 3{d_0}}}\left( {\frac{1}{{r - R}} + \frac{2}{{{d_0}}} - \frac{1}{{r - {d_0}}}} \right) \end{aligned}$$

(42)

Substituting (42) into (18), the upper bound expression on the average ESE of the cell can be calculated as (20).

Appendix C

According to the definite integral formula

$$\begin{aligned}{} & {} \int \limits _n^m {\ln \left( {1 + \frac{a}{{{{\left( {x - b} \right) }^2}}}} \right) } dx = b\ln \left( {\frac{{\left( {{{\left( {b - n} \right) }^2} + a} \right) {{\left( {b - m} \right) }^2}}}{{\left( {{{\left( {b - m} \right) }^2} + a} \right) {{\left( {b - n} \right) }^2}}}} \right) \nonumber \\{} & {} \quad + m\ln \left( {\frac{{{{\left( {b - m} \right) }^2} + a}}{{{{\left( {b - m} \right) }^2}}}} \right) - n\ln \left( {\frac{{{{\left( {b - n} \right) }^2} + a}}{{{{\left( {b - n} \right) }^2}}}} \right) \nonumber \\{} & {} \quad + 2\sqrt{a} \left( {\arctan \left( {\frac{{b - n}}{{\sqrt{a} }}} \right) - \arctan \left( {\frac{{b - m}}{{\sqrt{a} }}} \right) } \right) , \end{aligned}$$

(43)

we can obtain

$$\begin{aligned}{} & {} \int \limits _{{d_0}}^{r - {d_0}} {\ln \left( {1 + \frac{A}{{{{\left( {x - r} \right) }^2}}}} \right) dx} = r\ln \left( {\frac{{\left( {{{\left( {r - {d_0}} \right) }^2} + A} \right) d_0^2}}{{\left( {d_0^2 + A} \right) {{\left( {r - {d_0}} \right) }^2}}}} \right) \nonumber \\{} & {} \quad + \left( {r - {d_0}} \right) \ln \left( {\frac{{d_0^2 + A}}{{d_0^2}}} \right) - {d_0}\ln \left( {\frac{{{{\left( {r - {d_0}} \right) }^2} + A}}{{{{\left( {r - {d_0}} \right) }^2}}}} \right) \nonumber \\{} & {} \quad + 2\sqrt{A} \left( {\arctan \left( {\frac{{r - {d_0}}}{{\sqrt{A} }}} \right) - \arctan \left( {\frac{{{d_0}}}{{\sqrt{A} }}} \right) } \right) , \end{aligned}$$

(44)

$$\begin{aligned}{} & {} \int \limits _{r + {d_0}}^R {\ln \left( {1 + \frac{A}{{{{\left( {x - r} \right) }^2}}}} \right) dx} = r\ln \left( {\frac{{\left( {d_0^2 + A} \right) {{\left( {r - R} \right) }^2}}}{{\left( {{{\left( {r - R} \right) }^2} + A} \right) d_0^2}}} \right) \nonumber \\{} & {} \quad + R\ln \left( {\frac{{{{\left( {r - R} \right) }^2} + A}}{{{{\left( {r - R} \right) }^2}}}} \right) - \left( {r + {d_0}} \right) \ln \left( {\frac{{d_0^2 + A}}{{d_0^2}}} \right) \nonumber \\{} & {} \quad + 2\sqrt{A} \left( {\arctan \left( {\frac{{ - {d_0}}}{{\sqrt{A} }}} \right) - \arctan \left( {\frac{{r - R}}{{\sqrt{A} }}} \right) } \right) . \end{aligned}$$

(45)

Substituting (44) and (45) into (23), the upper bound in (24) can be obtained.