Game theoretic approach for multi-tier 5G heterogeneous network optimization based on joint power control and spectrum trading

Abstract

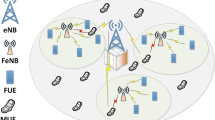
Multi-tier heterogeneous network (MHN) has recently emerged as a main technology in 5G network. Dense deployment of heterogeneous nodes in 5G MHN will have more density than single-tier networks. In 5G MHN, by increasing the number of small cells, network capacity, spectral efficiency, and data rate will increase. But reducing the dimension of the cell will cause inter/intra-tier interference in both uplink and downlink channels of MHN. High transmit power of Macro Base Station (MBS) downlink channel causes interference to Small cell User Equipment (SUE). Also, neighbor macrocell and small cell users suffer from interference created in both uplink and downlink channels of small cell. Thus interference management and mitigation is the important challenge for 5G MHN. In this paper, in order to mitigate both types of inter/intra-tier interferences, spectrum trading issue and power control are presented based on non-cooperative Stackelberg game under some sub-games through a pricing-based algorithm and convex optimization method. Finally, simulation results show that the performance of our system model such as average utility function of the small cell, SBS, energy efficiency and so on, will be improved through the proposed algorithm.

Appendix

1.1 Appendix(1)

According to Eq. (6), the second derivation of ${U}_{sbs(i)}$ on ${W_{i}}$ is computed:

$$\begin{aligned} \frac{{{\partial }^{2}}{{U}_{sbs(i)}}}{{{\partial }^{2}}{{W}_{i}}}=\frac{-D\times K}{W_{i}^{2}}\le 0\ \end{aligned}$$

(38)

As the second derivation is less than zero, it is concluded that ${U}_{sbs(i)}$ is a concave function. Therefore ${W_{i}}^{*}$ is obtained by:

$$\begin{aligned} \frac{\partial {{U}_{sbs(i)}}}{\partial ({{W}_{i}})}=\frac{D\times K}{{{W}_{i}}}-(1-\lambda )\times p=0 \end{aligned}$$

(39)

According to Eq. (8), the second derivation of ${U}_{mbs}$ on ${\lambda }$ is computed:

$$\begin{aligned} \frac{{{\partial }^{2}}{{U}_{mbs}}}{{{\partial }^{2}}\lambda } &= \frac{-{{D}_{m}}\times {{K}_{m}}}{{{(1-\lambda )}^{2}}}- \frac{D_{m}^{'}\times K_{m}^{'}}{{{\lambda }^{2}}} \nonumber \\&\quad -\frac{D_{m}^{'}\times K_{m}^{'}}{{{(1-\lambda )}^{2}}}\le 0 \end{aligned}$$

(40)

As the second derivation is less than zero, it is concluded that ${U}_{mbs}$ is a concave function. Therefore ${\lambda }^{*}$ is obtained by:

$$\begin{aligned} \frac{-{{D}_{m}}\times {{K}_{m}}}{1-\lambda }+\frac{{{{{D}'}}_{m}}\times {{{{K}'}}_{m}}}{\lambda }+\frac{{{{{D}'}}_{m}}\times {{{{K}'}}_{m}}}{1-\lambda }=0 \end{aligned}$$

(41)

1.2 Appendix(2)

1.3 Appendix(2-1)

${U}_{sbs(i)}$ is a concave function, due to the maximization of concave function is a convex problem so it can be solved by Lagrangian method as:

$$\begin{aligned}&L({{P}_{sbs(i)}},{{P}_{sue({{k}_{s}})}},\mu ,\beta )= {{U}_{smallcell(i)}}\nonumber \\&\quad +\mu (P_{\max }^{sbs}-{{P}_{sbs}})+\beta (P_{\max }^{sue}-{{P}_{sue}}) \end{aligned}$$

(42)

From (42) it can be written:

$$\begin{aligned}&\frac{\partial L({{P}_{sbs(i)}},{{P}_{sue({{k}_{s}})}},\mu ,\beta )}{\partial {{P}_{sbs(i)}}}= \nonumber \\&\quad \frac{1}{ln2}\times \left( \frac{A}{1+{{P}_{sbs(i)}}\times A}\right) -pric{{e}_{sbs(i)}}\times C1-{{\mu }}=0 \nonumber \\&\quad A=\frac{{{h}_{s,s}}(i,{{k}_{s}})}{{I}_{sbs(i)}} \end{aligned}$$

(43)

From above, ${{P}_{sbs(i)}^{*}}$ can be obtained according to Eq. (19). According to the Lagrangian method, we have:

$$\begin{aligned}&\frac{\partial L({{P}_{sbs(i)}},{{P}_{sue({{k}_{s}})}},\mu ,\beta )}{\partial \mu }=0 \Rightarrow P_{\max }^{sbs}={{P}_{sbs(i)}} \end{aligned}$$

(44)

Therefore, when SBS transmit at ${{P}_{max}^{sbs}}$, interference price will be minimum at this point so:

$$\begin{aligned} pric{{e}_{sbs(i)}}\approx 0 \end{aligned}$$

(45)

Then from (19) ${{\mu }}$ can be derived according to (21).

By solving sub-game(2), ${{Price}_{sbs(i)}^{*}}$ is calculated. Therefore, after replacing ${{P}_{sbs(i)}^{*}}$ in (16), sub-game(2) is written as:

$$\begin{aligned}&sub-game(2):\underset{Pric{{e}_{sbs(i)}}}{\mathop {Max}}\, \sum \limits _{i=1}^{I}Pric{{e}_{sbs(i)}}\nonumber \\&\times \left[ \left( \frac{1}{ln2\times [Pric{{e}_{sbs(i)}}+\frac{{{\mu }}}{C1}]}\right) - \frac{{{I}_{sbs(i)}}\times C1}{{{h}_{s,s}}(i,{{k}_{s}})}\right] _{0}^{\max } \nonumber \\&\quad s.t\sum \limits _{i=1}^{I}\left[ \left( \frac{1}{ln2\times [Pric{{e}_{sbs(i)}}+\frac{{{\mu }}}{C1}]}\right) -\frac{{{I}_{sbs(i)}}\times C1}{{{h}_{s,s}}(i,{{k}_{s}})}\right] _{0}^{\max }\nonumber \\&\quad \le {{I}_{\max }} \end{aligned}$$

(46)

But, due to the maximization of convex function is difficult [22], (46) is converted to the minimization problem as:

$$\begin{aligned}&sub-game(2): \nonumber \\&\quad \underset{Pric{{e}_{sbs(i)}}}{\mathop {Min}}\,\sum \limits _{i=1}^{I}{\frac{Pric{{e}_{sbs(i)}}\times {{I}_{sbs(i)}}\times C1}{{{h}_{s,s}}(i,{{k}_{s}})}} \nonumber \\&\quad s.t\sum \limits _{i=1}^{I}{(\frac{1}{ln2\times [Pric{{e}_{sbs(i)}}+\frac{{{\mu }}}{C1}]}})\nonumber \\&\quad \le {{I}_{\max }}+\sum \limits _{i=1}^{I}{\frac{{{I}_{sbs(i)}}\times C1}{{{h}_{s,s}}(i,{{k}_{s}})}} \end{aligned}$$

(47)

As problem (47) is a convex optimization, so ${{Price}_{sbs(i)}^{*}}$ can be obtained by the Lagrangian method as:

$$\begin{aligned} L(Pric{{e}_{sbs(i)}},\alpha ) &= \sum \limits _{i=1}^{I}{\frac{Pric{{e}_{sbs(i)}}\times {{I}_{sbs(i)}}\times C1}{{{h}_{s,s}}(i,{{k}_{s}})}}+ \nonumber \\&\quad \alpha \times \left[ \sum \limits _{i=1}^{I}\left( \frac{1}{ln2\times [Pric{{e}_{sbs(i)}}+\frac{{{\mu }}}{C1}]}\right) \right. \nonumber \\&\quad \left. -{{I}_{\max }}-\sum \limits _{i=1}^{I}{\frac{{{I}_{sbs(i)}}\times C1}{{{h}_{s,s}}(i,{{k}_{s}})}}\right] \end{aligned}$$

(48)

From (48) it can be written:

$$\begin{aligned} \frac{\partial L}{\partial Pric{{e}_{sbs(i)}}} &= \frac{{{I}_{sbs(i)}}\times C1}{{{h}_{s,s}}(i,{{k}_{s}})}\nonumber \\&-\frac{\alpha }{ln2\times {{[Pric{{e}_{sbs(i)}}+\frac{{{\mu }}}{C1}]}^{2}}}=0 \end{aligned}$$

(49)

From above, ${{Price}_{sbs(i)}^{*}}$ can be obtained as:

$$\begin{aligned} \left[ Price_{sbs(i)}^{*}=\sqrt{\frac{\alpha \times {{h}_{s,s}}(i,{{k}_{s}})}{ln2\times {{I}_{sbs(i)}}\times C1}}-\frac{{{\mu }}}{C1}\right] \end{aligned}$$

(50)

Due to, ${{Price}_{sbs(i)}^{*}}$ must be positive, we have:

$$\begin{aligned}&Pric{{e}_{sbs(i)}}\ge 0\Rightarrow \frac{1}{ln2\times [Pric{{e}_{sbs(i)}}+\frac{{{\mu }}}{C1}]}-{{I}_{\max }}\nonumber \\&\quad -\frac{{{I}_{sbs(i)}}\times C1}{{{h}_{s,s}}(i,{{k}_{s}})}=0 \end{aligned}$$

(51)

After replacing ${{Price}_{sbs(i)}^{*}}$ in (51), ${\alpha }$ can be calculated as:

$$\begin{aligned} \alpha =\left[ {{(\frac{\sum \limits _{i=1}^{I}{\sqrt{\frac{ln2\times {{I}_{sbs(i)}}\times C1}{{{h}_{s,s}}(i,{{k}_{s}})}}}}{ln2\times \left[ {{I}_{\max }}+\sum \limits _{i=1}^{I}\frac{{{I}_{sbs(i)}}\times C1}{{{h}_{s,s}}(iF,{{k}_{s}})}\right] })}}\right] ^{2} \end{aligned}$$

(52)

Also, (23) can be obtained by replacing ${{P}_{sbs(i)}^{*}}$ in (53):

$$\begin{aligned} P_{sbs(i)}^{*}\ge 0 \end{aligned}$$

(53)

1.4 Appendix(2-2)

${{U}_{sue({{k}_{s}})}}$ is a concave function, due to the maximization of concave function is a convex problem, so it can be solved by the Lagrangian method as:

$$\begin{aligned}&\frac{\partial L({{P}_{sbs(i)}},{{P}_{sue({{k}_{s}})}},\mu ,\beta )}{\partial {{P}_{sue({{k}_{s}})}}}= \frac{1}{ln2} \times \left( \frac{B}{1+{{P}_{sue({{k}_{s}})}}\times B}\right) \nonumber \\&\quad -price{_{sbs(i)}}\times {{h}_{s,s}}({{k}_{s}},k)-\beta =0 \nonumber \\&\quad B=\frac{{{h}_{s,s}}({{k}_{s}},i)}{{I}_{sue({k}_{s})}} \end{aligned}$$

(54)

From above, ${{P}_{sue({{k}_{s}})}^{*}}$ can be obtained according to Eq. (24).

According to the Lagrangian method, we have:

$$\begin{aligned} \frac{\partial L({{P}_{sbs(i)}},{{P}_{sue({{k}_{s}})}},\mu ,\beta )}{\partial \beta }=0 \Rightarrow P_{\max }^{sue}={{P}_{sue({{k}_{s}})}} \end{aligned}$$

(55)

Therefore, when SUE transmit at ${{P}_{max}^{sue}}$, interference price will be minimum at this point:

$$\begin{aligned} pric{{e}_{sue({k}_{s})}}\approx 0 \end{aligned}$$

(56)

Then from (24), ${\beta }$ can be driven according to (26). By solving sub-game(3), ${{Price}_{sue({k}_{s})}^{*}}$ is calculated. Therefore, after replacing ${{P}_{sue({k}_{s})}^{*}}$ in (18), sub-game(3) is written as:

$$\begin{aligned}&sub-game(3): \underset{Pric{{e}_{sue({{k}_{s}})}}}{\mathop {Max}}\,\nonumber \\&\sum \limits _{{{k}_{s}}=1}^{K}Pric{{e}_{sue({{k}_{s}})}}\times \left[ \left( \frac{1}{ln2\times [Pric{{e}_{sue({{k}_{s}})}}+\frac{\beta }{{{h}_{s,m}}({{k}_{s}},k)}]}\right) \right. \nonumber \\&\left. \quad \quad -\frac{{{I}_{sue({{k}_{s}})}}\times {{h}_{s,m}}({{k}_{s}},k)}{{{h}_{s,s}}({{k}_{s}},i)}\right] _{0}^{\max }\nonumber \\&\quad \quad s.t\sum \limits _{{{k}_{s}}=1}^{K}\left( \frac{1}{ln2\times [Pric{{e}_{sue({{k}_{s}})}}+\frac{\beta }{{{h}_{s,m}}({{k}_{s}},k)}]}\right) \le {{I}_{\max }}\nonumber \\&\quad \quad +\sum \limits _{{{k}_{s}}=1}^{K}{\frac{{{I}_{sue}}({{k}_{s}})\times {{h}_{s,m}}({{k}_{s}},k)}{{{h}_{s,s}}({{k}_{s}},i)}} \end{aligned}$$

(57)

But, due to the maximization of convex function is difficult [22], (57) is converted to the minimization problem as:

$$\begin{aligned}&sub-game(3): \nonumber \\&\quad \quad \underset{Pric{{e}_{sue({{k}_{s}})}}}{\mathop {Min}}\,\sum \limits _{{{k}_{s}}=1}^{K}{\frac{Pric{{e}_{sue({{k}_{s}})}}\times {{I}_{sue({{k}_{s}})}}\times {{h}_{s,m}}({{k}_{s}},k)}{{{h}_{s,s}}({{k}_{s}},i)}} \nonumber \\&\quad s.t\sum \limits _{{{k}_{s}}=1}^{K}\left( \frac{1}{ln2\times [Pric{{e}_{sue({{k}_{s}})}}+\frac{\beta }{{{h}_{s,m}}({{k}_{s}},k)}]}\right) \le {{I}_{\max }}+ \nonumber \\&\qquad \quad \quad \sum \limits _{{{k}_{s}}=1}^{K}{\frac{{{I}_{sue({{k}_{s}})}}\times {{h}_{s,m}}({{k}_{s}},k)}{{{h}_{s,s}}({{k}_{s}},i)}} \end{aligned}$$

(58)

As problem (58) is a convex optimization, so ${{Price}_{sue({k}_{s})}^{*}}$ can be obtained by the Lagrangian method as:

$$\begin{aligned}&\left[ L(Pric{{e}_{sue({{k}_{s}})}},{{\alpha }^{'}})= \right. \nonumber \\&\quad \quad \left. \sum \limits _{{{k}_{s}}=1}^{K}{\frac{Pric{{e}_{sue({{k}_{s}})}}\times {{I}_{sue({{k}_{s}})}}\times {{h}_{s,m}}({{k}_{s}},k)}{{{h}_{s,s}}({{k}_{s}},i)}}\right] + \nonumber \\&\quad \quad {{\alpha }^{'}}\times \left[ \sum \limits _{{{k}_{s}}=1}^{K}(\frac{1}{ln2\times [Pric{{e}_{sbs(i)}}+\frac{\beta }{{{h}_{s,m}}({{k}_{s}},k)}]}) \right. \nonumber \\&\left. \quad \quad -{{I}_{\max }}-\sum \limits _{{{k}_{s}}=1}^{K}{\frac{{{I}_{sue({{k}_{s}})}}\times {{h}_{s,m}}({{k}_{s}},k)}{{{h}_{s,s}}({{k}_{s}},i)}}\right] \end{aligned}$$

(59)

From (59) it can be written:

$$\begin{aligned}&\frac{\partial L}{\partial Pric{{e}_{sue({{k}_{s}})}}}=\frac{{{I}_{sue({{k}_{s}})}}\times {{h}_{s,m}}({{k}_{s}},k)}{{{h}_{s,s}}({{k}_{s}},i)} \nonumber \\&\quad -\frac{{{\alpha }^{'}}}{ln2\times {{[Pric{{e}_{sbs(i)}}+\frac{\beta }{{{h}_{s,m}}({{k}_{s}},k)}]}^{2}}}=0 \end{aligned}$$

(60)

From above, ${{Price}_{sue({k}_{s})}^{*}}$ can be obtained according as:

$$\begin{aligned} Price_{sue({{k}_{s}})}^{*} &= \sqrt{\frac{{{\alpha }^{'}}\times {{h}_{s,s}}({{k}_{s}},i)}{ln2\times {{I}_{sue({{k}_{s}})}}\times {{h}_{s,m}}({{k}_{s}},k)}}- \nonumber \\&\quad \frac{\beta }{{{h}_{s,m}}({{k}_{s}},k)}] \end{aligned}$$

(61)

Due to, ${{Price}_{sue({k}_{s})}^{*}}$ must be positive, we have:

$$\begin{aligned}&Pric{{e}_{sue({{k}_{s}})}}\ge 0\Rightarrow \nonumber \\&\quad \sum \limits _{{{k}_{s}}=1}^{K}\left( \frac{1}{ln2\times [Pric{{e}_{sue({{k}_{s}})}}+\frac{\beta }{{{h}_{s,m}}({{k}_{s}},k)}]}\right) -{{I}_{\max }} \nonumber \\&\quad -\sum \limits _{{{k}_{s}}=1}^{K}{\frac{{{I}_{sue({{k}_{s}})}}\times {{h}_{s,m}}({{k}_{s}},k)}{{{h}_{s,s}}({{k}_{s}},i)}}=0 \end{aligned}$$

(62)

After replacing ${{Price}_{sue({k}_{s})}^{*}}$ in (62), ${{\alpha }^{'}}$ can be calculated as:

$$\begin{aligned} {{\alpha }^{'}}=\left[ {{(\frac{\sum \limits _{{{k}_{s}}=1}^{K}{\sqrt{\frac{ln2 \times {{I}_{sue({{k}_{s}})}}\times {{h}_{s,m}}({{k}_{s}},k)}{{{h}_{s,s}} ({{k}_{s}},i)}}}}{ln2\times \left[ {{I}_{\max }}+\sum \limits _{{{k}_{s}}=1}^{K}{ \frac{{{I}_{sue({{k}_{s}})}}\times {{h}_{s,m}}({{k}_{s}},k)}{{{h}_{s,s}} ({{k}_{s}},i)}}\right] })}}\right] ^{2} \end{aligned}$$

(63)

Also, (28) can be obtained by replacing ${{P}_{sue({k}_{s})}^{*}}$ in (64):

$$\begin{aligned} P_{sue({k}_{s})}^{*}\ge 0 \end{aligned}$$

(64)

1.5 Appendix(3)

${{U}_{mbs(n)}}$ is a concave function, due to the maximization of concave function is a convex problem, so it can be solved by the Lagrangian method as:

$$\begin{aligned}{}[L({{P}_{mbs(n)}},\nu )={{U}_{mbs(n)}}+\nu (P_{\max }^{mbs}-{{P}_{mbs}})] \end{aligned}$$

(65)

From (65) it can be written:

$$\begin{aligned} \frac{\partial L({{P}_{mbs(n)}},\nu )}{\partial {{P}_{mbs(n)}}} &= \frac{1}{ln2}\times \left( \frac{C}{1+{{P}_{mbs(n)}}\times C}\right) \nonumber \\ &\quad-pric{{e}_{mbs(n)}}\times C2-\nu =0 \nonumber \\&\quad C=\frac{{{h}_{m,m}}(n,k)}{{{I}_{mbs(n)}}} \end{aligned}$$

(66)

From above, ${{P}_{mbs(n)}^{*}}$ can be obtained to Eq. (33).

According to the Lagrangian method, we have:

$$\begin{aligned} \frac{\partial L({{P}_{mbs(n)}},\nu )}{\partial \nu }=0 \Rightarrow P_{\max }^{mbs}={{P}_{mbs(n)}} \end{aligned}$$

(67)

Therefore, when MBS transmit at ${{P}_{mbs(n)}^{*}}$, interference price will be minimum at this point so:

$$\begin{aligned} pric{{e}_{mbs(n)}}\approx 0 \end{aligned}$$

(68)

Then, from (33) ${\nu }$ can be derived according to (35).

By solving sub-game(2), ${{Price}_{mbs(n)}^{*}}$ is calculated. Therefore, after replacing ${{P}_{mbs(n)}^{*}}$ in (31), sub-game(2) is written as:

$$\begin{aligned}&sub-game(2): \underset{Pric{{e}_{mbs(n)}}}{\mathop {Max}}\,{{U}_{sbs}}= Pric{{e}_{mbs(n)}} \nonumber \\&\quad \times \left[ (\frac{1}{ln2\times [Pric{{e}_{mbs(n)}}+\frac{\nu }{C2}]}-\frac{{{I}_{mbs(i)}}\times C2}{{h}_{m,m}}(n,k)\right] _{0}^{\max } \nonumber \\&\quad s.t\sum \limits _{i=1}^{I}\left[ \left( \frac{1}{ln2\times [Pric{{e}_{mbs(n)}}+\frac{\nu }{C2}]}\right) - \right. \nonumber \\&\left. \quad \frac{{{I}_{mbs(n)}}\times C2}{{h}_{m,m}}(n,k)\right] _{0}^{\max } \le {{I}_{\max }} \end{aligned}$$

(69)

But, due to the maximization of convex function is difficult [22], (69) is converted to the minimization problem as:

$$\begin{aligned}&sub-game(2): \underset{Pric{{e}_{mbs(n)}}}{\mathop {Min}}\,\frac{Pric{{e}_{mbs(n)}}\times {{I}_{mbs(n)}}\times C2}{{{h}_{m,m}}(n,k)} \nonumber \\&\quad s.t\left( \frac{1}{ln2\times [Pric{{e}_{mbs(n)}}+\frac{\nu }{C2}]}\right) \le {{I}_{\max }}\nonumber \\&\quad +\frac{{{I}_{mbs(n)}}\times C2}{{{h}_{m,m}}(n,k)} \end{aligned}$$

(70)

As problem (70) is a convex optimization, so ${{Price}_{mbs(n)}^{*}}$ can be obtained by the Lagrangian method as:

$$\begin{aligned}&L(Pric{{e}_{mbs(n)}},\gamma )=\frac{Pric{{e}_{mbs(n)}}\times {{I}_{mbs(n)}}\times C2}{{{h}_{m,m}}(n,k)}+ \nonumber \\&\quad \gamma \times \left[ \frac{1}{ln2\times [Pric{{e}_{mbs(n)}}+\frac{\nu }{C2}]} -{{I}_{\max }}\right. \nonumber \\&\left. \quad -\frac{{{I}_{mbs(n)}}\times C2}{{{h}_{m,m}}(n,k)}\right] \end{aligned}$$

(71)

From (71) it can be written as:

$$\begin{aligned}&\frac{\partial L}{\partial Pric{{e}_{mbs(n)}}}= \nonumber \\&\quad \frac{{{I}_{mbs(n)}}\times C2}{{{h}_{m,m}}(n,k)}-\frac{\nu }{ln2\times {{[Pric{{e}_{mbs(n)}}+\frac{\nu }{C2}]}^{2}}}=0 \end{aligned}$$

(72)

From above, ${{Price}_{mbs(n)}^{*}}$ can be obtained as:

$$\begin{aligned} Price_{mbs(n)}^{*}=\sqrt{\frac{\gamma \times {{h}_{m,m}}(n,k)}{ln2\times {{I}_{mbs(n)}}\times C2}}-\frac{\nu }{C2} \end{aligned}$$

(73)

Due to, ${{Price}_{mbs(n)}^{*}}$ must be positive, we have:

$$\begin{aligned} Pric{{e}_{mbs(n)}} &\ge 0\Rightarrow \frac{1}{ln2\times [Pric{{e}_{mbs(n)}} +\frac{\nu }{C2}]} -{{I}_{\max }}\nonumber \\&\quad -\frac{{{I}_{mbs(n)}}\times C2}{{{h}_{m,m}}(n,k)}=0 \end{aligned}$$

(74)

After replacing ${{Price}_{mbs(n)}^{*}}$ in (74), ${\gamma }$ can be calculated as:

$$\begin{aligned} \gamma ={{(\frac{\sqrt{\frac{ln2\times {{I}_{mbs(n)}}\times C2}{{{h}_{m,m}}(n,k)}}}{ln2\times [{{I}_{\max }}+\frac{{{I}_{mbs(n)}}\times C2}{{{h}_{m,m}}(n,k)}]})^{2}}} \end{aligned}$$

(75)

Also, (37) can be obtained by replacing ${{P}_{mbs(n)}^{*}}$ in (76):

$$\begin{aligned} P_{mbs(n)}^{*}\ge 0 \end{aligned}$$

(76)