Skip to main content
SpringerLink
Log in

Superintegrable and Scale-Invariant Quantum Systems with Position-Dependent Mass

  • Published:
Ukrainian Mathematical Journal Aims and scope

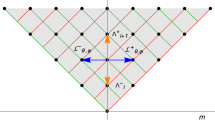
We present a classification of the scale-invariant Schrödinger equations with position-dependent mass admitting second-order integrals of motion.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. V. I. Fushchich and A. G. Nikitin, Symmetries of Equations of Quantum Mechanics, Allerton Press, New York (1994).

    MATH  Google Scholar 

  2. A. G. Nikitin, “The maximal ‘kinematical’ invariance group for an arbitrary potential revised,” J. Math. Phys., Analysis, Geometry 14, 519–531 (2018).

  3. A. G. Nikitin, “Symmetries of Schrödinger equation with scalar and vector potentials,” J. Phys. A, 53, 455202 (2020).

    Article  MathSciNet  Google Scholar 

  4. A. G. Nikitin, “Symmetries of the Schrödinger–Pauli equation for neutral particles,” J. Math. Phys., 62, 083509 (2021).

  5. A. G. Nikitin, “Symmetries of the Schrödinger–Pauli equations for charged particles and quasirelativistic Schrödinger equations,” J. Phys. A, 55, 115202 (2022).

  6. U. Niederer, “The maximal kinematical invariance group of the free Schrödinger equations,” Helv. Phys. Acta, 45, 802–810 (1972).

    MathSciNet  Google Scholar 

  7. R. L. Anderson, S. Kumei, and C. E. Wulfman, “Invariants of the equations of wave mechanics. I,” Rev. Mex. Fis., 21, 1–33 (1972).

    MathSciNet  Google Scholar 

  8. C. P. Boyer, “The maximal kinematical invariance group for an arbitrary potential,” Helv. Phys. Acta, 47, 450–605 (1974).

    MathSciNet  Google Scholar 

  9. P. Winternitz, J. Smorodinsky, M. Uhliř, and I. Friš, “Symmetry groups in classical and quantum mechanics,” Sov. J. Nucl. Phys., 4, 444–450 (1967).

    MathSciNet  Google Scholar 

  10. A. Makarov, J. Smorodinsky, Kh. Valiev, and P.Winternitz, “A systematic search for non-relativistic systems with dynamical symmetries,” Nuovo Cim. A, 52, 1061–1084 (1967).

    Article  Google Scholar 

  11. I. Marquette and P.Winternitz, “Higher order quantum superintegrability: a new Painleve conjecture. Integrability,” in: Supersymmetry and Coherent States, Springer, Cham (2019), pp. 103–131.

  12. A. G. Nikitin, “Higher-order symmetry operators for Schrödinger equation,” in: CRM Proceedings and Lecture Notes (AMS), 37 (2004), pp. 137–144.

  13. O. von Roos, “Position-dependent effective masses in semiconductor theory,” Phys. Rev. B, 27, 7547 (1983).

    Article  Google Scholar 

  14. A. de Saavedra, F. Boronat, A. Polls, and A. Fabrocini, “Effective mass of one He 4 atom in liquid He 3,” Phys. Rev. B, 50, 4248 (1994).

    Article  Google Scholar 

  15. P. Harrison, Quantum Wells, Wires,s and Dots, Wiley, New York (2000).

  16. R. Heinonen, E. G. Kalnins, W. Miller Jr., and E. Subag, “Structure relations and Darboux contractions for 2D 2nd order superintegrable systems,” SIGMA, 11, 043 (2015).

    MathSciNet  MATH  Google Scholar 

  17. B. K. Berntson, E. G. Kalnins, and W. Miller Jr., “Toward classification of 2nd order superintegrable systems in 3-dimensional conformally flat spaces with functionally linearly dependent symmetry operators,” SIGMA: Symmetry, Integrability and Geometry: Methods and Applications, 16, 135 (2020).

  18. A. Ballesteros, A. Enciso, F. J. Herranz, O. Ragnisco, and D. Riglioni, “Superintegrable oscillator and Kepler systems on spaces of nonconstant curvature via the Stäckel transform,” SIGMA, 7, 048 (2011).

    MATH  Google Scholar 

  19. O. Ragnisco and D. Riglioni, “A family of exactly solvable radial quantum systems on space of nonconstant curvature with accidental degeneracy in the spectrum,” SIGMA, 6, 097 (2010).

    MATH  Google Scholar 

  20. A. G. Nikitin, “Superintegrable and shape invariant systems with position dependent mass,” J. Phys. A: Math. Theor., 48, 335201 (2015).

    Article  MathSciNet  MATH  Google Scholar 

  21. A. G. Nikitin and T. M. Zasadko, “Superintegrable systems with position dependent mass,” J. Math. Phys., 56, 042101 (2015).

    Article  MathSciNet  MATH  Google Scholar 

  22. A. G. Nikitin, “Kinematical invariance groups of the 3d Schrödinger equations with position dependent masses,” J. Math. Phys., 58, No. 8, 083508 (2017).

  23. A. G. Nikitin, “Group classification of systems of nonlinear reaction-diffusion equations with triangular diffusion matrix,” Ukr. Mat. Zh., 59, No. 3, 395–411 (2007)); English translation: Ukr. Math. J., 59, No. 3, 439–458 (2007).

  24. A. G. Nikitin and V. I. Fushchich, “Equations of motion for particles with arbitrary spin invariant under the Galileo group,” Theor. Math. Phys., 44, 584–592 (1980)

    Article  Google Scholar 

  25. O. O. Vaneeva, R. O. Popovych, and C. Sophocleous, “Equivalence transformations in the study of integrability,” Physica Scripta, 89, 038003 (2014).

    Article  Google Scholar 

  26. A. G. Nikitin, “Generalized Killing tensors of arbitrary rank and order,” Ukr. Mat. Zh., 43, No. 6, 786–795 (1991); English translation: Ukr. Math. J., 43, No. 6, 734–743 (1991).

  27. A. G. Nikitin, “Exact solvability of PDM systems with extended Lie symmetries,” Proc. Inst. Math. Nat. Acad. Sci. Ukr., 16, No. 1, 1–18 (2019).

    MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Institute of Mathematics, National Academy of Sciences of Ukraine, Kyiv, Ukraine

    A. G. Nikitin

Authors
  1. A. G. Nikitin
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to A. G. Nikitin.

Additional information

Translated from Ukrains’kyi Matematychnyi Zhurnal, Vol. 74, No. 3, pp. 360–372, March, 2022. Ukrainian DOI: https://doi.org/10.37863/umzh.v74i3.7162.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Nikitin, A.G. Superintegrable and Scale-Invariant Quantum Systems with Position-Dependent Mass. Ukr Math J 74, 405–419 (2022). https://doi.org/10.1007/s11253-022-02072-8

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11253-022-02072-8

Search

Navigation