Comments on the Theory of Fluid Flow Between Solids with Anisotropic Roughness

Abstract

I consider fluid flow at the interface between solids with random roughness. For anisotropic roughness, obtained by stretching isotropic roughness in the x-direction by a factor of $\gamma ^{1/2}$ and in the y-direction with a factor of $\gamma ^{-1/2}$, I give an argument for why the flow conductivity in the critical junction theory should be proportional to $\gamma$ in the x-direction and proportional to $1/\gamma$ in the y-direction.

The influence of the surface roughness on the fluid flow dynamics is a complex topic. However, if there is a separation of length scales the problem can be simplified: if $R>> \lambda _0$, where R is the (smallest) length characterizing the macroscopic shape of the bodies and $\lambda _0$ is the longest (relevant) surface roughness component, then it is possible to eliminate (integrate out) the surface roughness and obtain effective fluid flow equations involving solid bodies with smooth surfaces (no roughness). The effective fluid flow equations depend on two quantities determined by the surface roughness, usually denoted fluid flow factors. These factors depend on the average surface separation ${\bar{u}}$, which will vary throughout the nominal contact region; ${\bar{u}}$ is the local interfacial surface separation u(x, y) averaged over the surface roughness.

The aim of this short communication is to add some new results for fluid flow between surfaces with anisotropic roughness. In particular, I will argue that the most narrow constrictions in the critical junction theory of fluid flow can be treated as square-like pores even for surfaces with anisotropic roughness. Only if this is the case will the effective flow conductivity (in the critical junction theory) scale as $\gamma$ and $1/\gamma$ along the two principal fluid flow directions, as also found in the effective medium theory [1], and in exact numerical calculations [2], close to the percolation threshold.

We consider the simplest fluid flow problems, which include the leakage of static seals [3, 4] and the squeeze-out of fluids between elastic solids. For these applications, the roughness enter only via one function, namely, the pressure flow factor $\phi _{\text{p}} ({\bar{u}})$ (in general a $2\times 2$ tensor) or, equivalently, the (effective) fluid flow conductivity $\sigma _\text{eff}$ defined by the equation

$$\begin{aligned} \bar{\mathbf{J}} = -\,\sigma _{\text{eff}} \nabla {\bar{p}} \end{aligned}$$

(1)

where ${\bar{p}}=\langle p(x,y)\rangle$ is the fluid pressure and $\bar{\mathbf{J}}=\langle \mathbf{J}(x,y)\rangle$ is the two-dimensional (2D) fluid flow current, both averaged over the surface roughness (ensemble averaging). The flow conductivity $\sigma _{\text{eff}}$ is a $2\times 2$ matrix (tensor). From the fluid flow conductivity, one can calculate the pressure flow factor using

$$\begin{aligned} \sigma _{\text{eff}} = {{\bar{u}}^3\over 12 \eta }\phi _{\text{p}} \end{aligned}$$

(2)

where $\eta$ is the fluid viscosity.

For randomly rough surfaces, the flow conductivity $\sigma _{\text{eff}}$ can be calculated approximately using the Bruggeman effective medium [1, 4] or the simpler critical junction theory [3]. These theories were originally developed for isotropic roughness but have been generalized to surfaces with anisotropic roughness, where the roughness is characterized by the Peklenik number [5, 6] $\gamma$. Here, it is assumed that a surface with anisotropic roughness can be obtained from a surface with isotropic roughness by stretching the surface along the x-direction by a factor of $\gamma$.

The 2D Bruggeman effective medium theory predicts that the contact area percolates for $A/A_0 = 0.5$ independent of $\gamma$. Numerical contact mechanics calculations for randomly rough surfaces predict that the contact area percolates for $A/A_0 \approx 0.42$ for $\gamma =1$ (see Ref. [7]), and for $A/A_0 >0.42$ when $\gamma <1$ and $A/A_0<0.42$ when $\gamma >1$ (see Ref. [8, 9]). However, the latest study of Wang and Müser [2] indicates that even for systems with anisotropic surface roughness, if the roll-off region in the surface roughness power spectra is large enough, the contact area percolates for $A/A_0 \approx 0.42$ independent of $\gamma$. The Bruggeman effective medium theory can be generalized to give percolation at $A/A_0 \approx 0.42$ .

According to the 2D Bruggeman effective medium theory, in the coordinate system where $\sigma _{\text{eff}}$ is diagonal,

$$\begin{aligned} \sigma _{\text{eff}}= \left[ {\begin{array}{cc} \sigma _x &{}\quad 0 \\ 0 &{}\quad \sigma _y \\ \end{array} } \right] , \end{aligned}$$

we have

$$\begin{aligned} {1\over \sigma _x} = \left\langle {1+\gamma ^*\over \sigma +\gamma ^* \sigma _x}\right\rangle \end{aligned}$$

(3)

$$\begin{aligned} {1\over \sigma _y} = \left\langle {1+(1/\gamma ^*)\over \sigma +(1/\gamma ^*) \sigma _y}\right\rangle \end{aligned}$$

(4)

where $\gamma ^*=(\sigma _y/\sigma _x)^{1/2} \gamma$, and where $\langle .. \rangle$ stands for ensemble averaging or averaging over the probability distribution P(u) of interfacial separations. The microscopic flow conductivity $\sigma = u^3/(12 \eta )$. From these equations, one can show that close to the percolation threshold (see Ref. [1]) $\sigma _x \approx \gamma ^2 \sigma _y$ so that in spite of the fact that percolation occurs in the x- and y-directions at the same time, the flow current before percolation can be very different in the two directions. We will now show that the relation $\sigma _x \approx \gamma ^2 \sigma _y$ can be easily understood using the critical junction theory.

Fig. 1

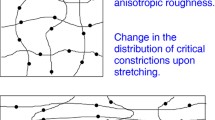
a Percolating fluid flow channels (lines) and critical constrictions (black dots) for a $L\times L$ square unit system with isotropic roughness. b The percolating fluid flow channels and critical constrictions for a system obtained by stretching by a factor of 2 in the x-direction and 1/2 in the y-direction (Pekeling number $\gamma = 4$). After this mapping, the concentration of flow channels is increased by a factor of 2 in the x-direction and reduced by a factor of 1/2 in the y-direction. For a square unit $L\times L$ (not shown), the number of critical constrictions along each percolating flow channel is reduced by a factor of 1/2 in the x-direction and increased by a factor of 2 in the y-direction. The net result is that the fluid flow conductivity is increased by a factor of 4 in the x-direction and reduced by a factor of 1/4 in the y-direction, i.e., $\sigma _x = \gamma \sigma _0$ and $\sigma _y = \sigma _0/\gamma$, where $\sigma _0$ is the flow conductivity for the system with isotropic roughness in (a). Adapted from [1]

Fig. 2

The contact region (black) at different magnifications (schematic). Note that at the point where the non-contact area (white area) percolates $A(\zeta _{\text{c}}) \approx 0.4 A_0$, while there appears to be complete contact between the surfaces at the lowest magnification $\zeta = 1$: $A(1)=A_0$. Adapted from [3]

Fig. 3

Fluid pressure flow factor $\phi _{\text{p}} =12 \eta \sigma _x/{\bar{u}}^3$ as a function of the average surface separation ${\bar{u}}$ (log–log scale). In the calculation, we have used the surface roughness power spectra shown in Fig. 7 in Ref. [1] and the Young’s elastic modulus $E=10 \ \text{MPa}$. Results were obtained using the effective medium (em) theory for $\gamma =1/4$ (red curve) and $\gamma =4$ (blue curve). Also shown is the result for $\gamma =1/4$ scaled by a factor of $\gamma ^2=16$ (green curve)

Let us study the contact between the two solids as we increase the magnification $\zeta$. We define $\zeta =L/\lambda$, where $\lambda$ is the resolution. We study how the apparent contact area (projected on the xy-plane), $A(\zeta )$, between the two solids depends on the magnification $\zeta$. At the lowest magnification, we cannot observe any surface roughness, and the contact between the solids appears to be completed, i.e., $A(1)=A_0$. As we increase the magnification, we will observe some interfacial roughness, and the (apparent) contact area will decrease. At high enough magnification, say $\zeta =\zeta _{\text{c}}$, a percolating path of non-contact area will be observed for the first time. We denote the most narrow constriction along this percolation path as the critical constriction. The critical constriction will have the lateral size $\lambda _{\text{c}} = L/\zeta _{\text{c}}$ and the surface separation at this point is denoted by $u_{\text{c}}$.

If the nominal contact pressure is high enough, an accurate estimate of the leak rate is obtained by assuming that all the leakage occurs through the critical percolation channels and that the whole pressure drop $\Delta P=P_{\text{a}}-P_{\text{b}}$ (where $P_{\text{a}}$ and $P_{\text{b}}$ is the pressure to the left and right of the seal) occurs over the critical constrictions (of width and length $\lambda _{\text{c}}\approx L/\zeta _{\text{c}}$ and height $u_{\text{c}}$). If we approximate the critical constriction as a pore with rectangular cross-section (width and length $\lambda _{\text{c}}$ and height $u_\text{c}<< \lambda _{\text{c}}$), and if we assume an incompressible Newtonian fluid, the volume flow per unit time through the critical constrictions will be given by (Poiseuille flow)

$$\begin{aligned} \dot{Q}={u_{\text{c}}^3 \over 12 \eta }\Delta P \end{aligned}$$

(5)

The flow conductivity $\sigma _{\text{eff}}$ can be obtained from $\dot{Q}$ using $\dot{Q}=J_x L = \sigma _{\text{eff}} (\Delta P/L) L$ giving

$$\begin{aligned} \sigma _{\text{eff}} = {u_{\text{c}}^3 \over 12 \eta } \end{aligned}$$

(6)

At the critical magnification, several fluid conducting channels may appear and each of them may have several critical constrictions as indicated in Fig. 1a. Let us now stretch the contact in the x-direction with a factor of $\gamma ^{1/2}$ and contract it by a factor of $\gamma ^{-1/2}$ in the y-direction. This will increase the number of flow channels per unit area in the x-direction by a factor of $\gamma ^{1/2}$, and on each flow channel, it will reduce the number of critical junctions per unit length by a factor of $\gamma ^{-1/2}$. Hence, the fluid conductivity $\sigma _x = \gamma \sigma _0$, where $\sigma _0$ is the flow conductivity for isotropic roughness. In a similar way, one can show that $\sigma _y = \sigma _0/\gamma$ which implies that $\sigma _x = \gamma ^2 \sigma _y$.

The argument for why $\sigma _x = \gamma ^2 \sigma _y$ only holds if the fluid pressure drop over a critical constriction is not modified by the stretching–contraction of the system. This assumption can be made plausible using the following argument:

Consider the contact between two solids as we increase the magnification. When we change the magnification, we change the resolution and hence the size of the smallest unit (pixel) which can be resolved. A pixel may be in contact (black) or out of contact (white). The size of a pixel depends on the magnification. Note the pixels are squares because the resolution is the same in the x and y-direction (as when the contact is observed using, e.g., an optical microscope). Now, when we increase the magnification, the contact area decreases and simultaneously the size of the pixel decreases but in a continuous way (see Fig. 2). However, I will assume we increase the magnification in discrete (but small) steps. Now in the step just before the non-contact area percolation, there will be some narrow contact regions which will open up when we increase the magnification. If the discretion step is small, most likely this opening-up is due to removal of just one contact pixel in this most narrow contact region. Thus, the critical constriction is square-like in this picture even for anisotropic roughness.

In the effective medium theory, the relation $\sigma _x = \gamma ^2 \sigma _y$ holds only close to the percolation threshold. This is illustrated in Fig. 3 which shows the fluid pressure flow factor $\phi _{\text{p}} =12 \eta \sigma _x/{\bar{u}}^3$ as a function of the average surface separation ${\bar{u}}$ (log-log scale). In the calculation, we have used the surface roughness power spectra shown in Fig. 7 in Ref. [1]. Results were obtained using the effective medium (em) theory for $\gamma =1/4$ (red curve) and $\gamma =4$ (blue curve). Also shown is the result for $\gamma =1/4$ scaled by a factor of $\gamma ^2=16$ (green curve). As expected, close to the percolation threshold, the relation $\sigma _x = \gamma ^2 \sigma _y$ is accurately obeyed.

Fig. 4

Fluid pressure flow factor $\phi _{\text{p}} =12 \eta \sigma _x/{\bar{u}}^3$ as a function of the average surface separation ${\bar{u}}$ (log–log scale). In the calculation, we have used the surface roughness power spectra shown in Fig. 7 in [1] and the Young’s elastic modulus $E=10 \ \text{MPa}$. Results are shown for $\gamma =1/4$ (red curves), $\gamma =1$ (green curves), and $\gamma =4$ (blue curves) using the effective medium theory (solid lines) and the critical junction (cj) theory (dashed curves)

In Ref. [7], it was suggested how to modify the Bruggeman effective medium theory for systems with isotropic roughness so that it correctly reproduce the percolation for $A_{\text{p}}/A_0 \approx 0.42$. The resulting theory was found to be in good agreement with exact numerical results for the flow conductivity.

In a similar way as for isotropic roughness, one can generalize the Bruggeman effective medium theory for anisotropic roughness so that it gives the correct percolation threshold. This was attempted in Ref. [1] but unfortunately, a factor was placed in the wrong place as described in Ref. [2]. This resulted in expressions for $\sigma _x$ and $\sigma _y$ which did not have the solution $\sigma _x=\sigma _y=\sigma$ which corresponds to a homogeneous system (no surface roughness and uniform surface separation). (In the numerical calculations, another expression for the flow conductivity was used which correctly describes the homogeneous system solution.) The correct equations for $\sigma _x$ and $\sigma _y$ were given by Wang et al. and can be obtained as follows [2].

For systems with anisotropic roughness, first consider a system in n dimension (in the study above, $n=2$). In this case in the coordinate system where $\sigma _{\text{eff}}$ is diagonal:

$$\begin{aligned} {1\over \sigma _x} = \left\langle {1+(n-1)\gamma ^*\over \sigma +\gamma ^* (n-1) \sigma _x}\right\rangle \end{aligned}$$

(7)

$$\begin{aligned} {1\over \sigma _y} = \left\langle {1+(n-1)(1/\gamma ^*)\over \sigma +(1/\gamma ^*) (n-1)\sigma _y}\right\rangle \end{aligned}$$

(8)

where $\gamma ^*=(\sigma _y/\sigma _x)^{1/2} \gamma$. From these equations, one can show that at percolation [1]

$$\begin{aligned} {A_{\text{p}} \over A_0} = {n-1\over n} \end{aligned}$$

Thus, given $A_{\text{p}}/A_0$ obtained from (exact) numerical simulations, if we choose

$$\begin{aligned} n={1\over 1-A_{\text{p}}/A_0} \end{aligned}$$

then the (modified) effective medium theory will result in a flow conductivity which vanishes when the (normalized) contact area reaches the value $A_{\text{p}}/A_0$ where the contact area percolates.

The equations above (with $A_{\text{p}}/A_0=0.42$) were used in producing the results in Fig. 3. The results of another calculation for the same system are shown in Fig. 4. Here, I show the fluid pressure flow factor as a function of the average surface separation ${\bar{u}}$ (log–log scale) for $\gamma =1/4$ (red curves), $\gamma =1$ (green curves) and $\gamma =4$ (blue curves) using the effective medium theory (solid lines) and the critical junction theory (dashed curves). As expected, the critical junction theory is accurate when the average surface separation is small enough but is inaccurate for very small contact pressures where the average surface separation is large; this is expected as for large average surface separation, a nearly uniformly thick fluid film separates the surfaces and the fluid pressure drop will not occur over a small number of narrow constrictions, but will occur in nearly uniformly over the whole nominal contact area. However, this limiting case is not of interest in sealing applications.