1 Introduction

The historical development of the problem of thermal convection in a porous layer under a local thermal non-equilibrium (LTNE) environment is lucidly described by Bidin and Rees (2020). This topic involves thermal convection in a single porosity porous medium where the solid skeleton is allowed to have a different temperature to that of the fluid occupying the pore space. As Bidin and Rees (2020) point out, “the very first publications presented some strongly nonlinear computations without the benefit of knowing the context provided by a linearized theory”, e.g. Combarnous (1972). The first accurate and rigorous linearized instability analysis of LTNE thermal convection in a porous material is due to Banu and Rees (2002). In a seminal paper, Rees et al. (2008) showed that the local thermal non-equilibrium theory leads to very different results to the case where there is only one temperature. Further revealing analyses are those of Rees and Bassom (2010), Rees and Pop (2010), and Rees (2003), where the different pore fluid and solid temperatures are shown to lead to significant changes with respect to the single temperature theory. Recent experimental work on LTNE effects on heat transport in porous materials, see Gossler et al. (2019), Baek et al. (2022), strongly justifies the need for the fundamental analyses of Rees and his co-workers. Since the instability analysis of Banu and Rees (2002), there has been a huge interest in this field and many writers have worked on problems of instability, global stability, even including second sound effects in the solid, exemplified by the recent articles of Bidin and Rees (2020), Capone et al. (2021), Freitas et al. (2022), Nandal et al. (2023), and the many references therein, and the work of Rees (2009, 2010, 2011), these identifying important parameters and how one may calculate them. Interest in this field is driven by the many real life applications such as extracting water from an aquifer, (Böttcher et al. 2019; Gossler et al. 2019; Baek et al. 2022), designing hydrogen fuel cells, (Damm and Fedorov 2006), producing tube refrigerators for space applications, (Ashwin et al. 2010), in renewable engineering such as electricity creation from a solar pond, (Mahfoudh et al. 2019), in nuclear engineering design, the behaviour of internal combustion engines or producing fibre-reinforced materials, as is described in Nandal et al. (2023) and many more examples can be found in the book by (Straughan (2015),  pages 4,5).

Another area which is attracting huge interest is in thermal convection in a bidisperse, or double porosity, material, see, e.g. Capone et al. (2020), Franchi et al. (2017), Gentile and Straughan (2020), Straughan (2019) and the references therein. A bidisperse medium is one where there are normal pores known as macropores, but additionally there are cracks or fissures leading to micropores. Thermal convection in a bidisperse porous medium was introduced by Nield and Kuznetsov (2006) and these writers had separate fields of velocity, temperature and pressure in both the macro- and the micropores cases. Gentile and Straughan (2017) argued that for many problems a single temperature in the macro- and micropores proved to be adequate for most problems, and many writers have since followed suit. Finally, we draw attention to the fact that flow in bidisperse porous media can also involve flows with different grain sizes. Kostynick et al. (2022) studied fast flows in dangerous slurries of soil and water and they noted that there are typically two different grain sizes, or even three. Bidisperse porous media is another sector which is of great interest in applications such as to electricity production via a solar pond in renewable energies, (Wang et al. 2018; Dineshkumar and Raja 2022), heat extraction from underground, (Duan et al. 2023), convection in volcanoes, (Di Renzo et al. 2016; Toy et al. 2019; Vieira et al. 2021; Allocca et al. 2022), materials for root canals in dentistry, (Stanusi et al. 2023), the way cement dries out, (Zhou et al. 2019a), (Zhou et al. 2019b), although interfacial stresses in the fluids themselves may also be important, (Straughan 2023). Various other practical applications for thermal convection in a bidisperse porous material are discussed in Straughan (2019).

A general theory to describe thermal problems in a bidisperse porous body where the LTNE assumption becomes relevant was developed by Franchi et al. (2017). These writers allowed a temperature \(T^s\) in the solid skeleton, independent actual velocity, temperature and pressure fields in the macropores, \(V_i^f\), \(T^f\), \(p^f\), and further independent actual velocity, temperature and pressure fields in the micropores, \(V_i^p\), \(T^p\), \(p^p\). They developed a model for thermal convection, but no explicit results were given for stability or instability. The object of this work is to thoroughly analyse the stability of the thermal convection problem in an LTNE setting; however, we believe there are many problems in which the temperature in the macropores and in the micropores may be assumed to be the same, i.e. \(T^f = T^p = T\).

The outline of the paper is as follows. The Bénard convection problem is introduced in Sect. 2: more precisely, in the first subsection we present the new mathematical model governing a bidisperse Darcy type porous medium, under an LTNE assumption which allows for a temperature \(T^s\) in the solid skeleton and another temperature T, in the fluid, both in the macro- and in the micropores. Then, in the second subsection, after determining the basic steady conduction solution in whose stability we are interested, we address standard perturbation theory, performing a suitable dimensionless process, to arrive at the boundary value problem for the non-dimensionalized perturbation system. In Sect. 3, we introduce the symmetry arguments, with the aim of proving the equivalence of the linear instability and nonlinear stability thresholds, by also furnishing some energy type details towards the global nonlinear stability. Interestingly, these results remain valid also in the presence of Brinkman effects, where one may demonstrate the symmetry of the operator characterizing the linearities of the associated perturbations system. The result of symmetry holds even in the case where we argue at the microlevel the boundaries of a porous medium are rough boundaries; in this case, we adapt the work of Celli and Kuznetsov (2018) which derives novel Saffman-type boundary conditions for the vertical gradients of the horizontal components of the perturbation velocities. In Sect. 4, we sketch the linear stability analysis, which determines the critical Rayleigh number. Numerical results are presented employing some realistic values for the many parameters which appear in the theory, before ending with concluding remarks.

2 Mathematical Formulation for Bidisperse Convection Under an LTNE Scheme

2.1 General Governing Equations

Starting from the general model proposed in Franchi et al. (2017), we now present the thermal convection problem for an LTNE theory in a Darcy double porosity medium, assuming the same temperature field T for the fluid in the macro- and micropores, but with a different temperature \(T^s\) for the stationary solid skeleton. The macro- and microporosities are denoted by \(\phi\) and \(\epsilon\), so that the expressions \(\epsilon (1 - \phi )\) and \(\epsilon _1=(1-\epsilon )(1-\phi )\) stand for the fractions of the volume occupied by the micropores and the solid matrix, respectively.

The fluid velocities involved in the macro- and micropores are interpreted as the pore-averaged velocities, herein denoted by \(U_i^f\) and \(U_i^p\), which are related to the actual velocities \(V_i^f\) and \(V_i^p\), through the relations \(U_i^f = \phi V_i^f\) and \(U_i^p = \epsilon (1 - \phi ) V_i^p\). The continuity equations reduce to solenoidal constraints for \(U_i^f\) and \(U_i^p\); the momentum equations, which involve Darcy terms, employ a Boussinesq approximation in their buoyancy terms and include typical interaction terms to express the momentum transfer between the macro- and micropores. The energy balance for the fluid temperature T includes an interaction term, which is supposed proportional to the difference temperature \(T^s-T\). The same thermal interaction, with a different sign, appears in the energy equation for the solid temperature \(T^s\). Thus, preserving the notations given in Franchi et al. (2017), the relevant system of equations reads as follows

$$\begin{aligned} \begin{aligned}&- \frac{\mu }{K_f}U_i^f - \zeta (U_i^f - U_i^p) - p^f_{ ,i} + g k_i \rho _0 \alpha T = 0 \, ,\\&U^f_{i,i} = 0 \, ,\\&- \frac{\mu }{K_p}U_i^p - \zeta (U_i^p - U_i^f) - p^p_{ ,i} + g k_i \rho _0 \alpha T = 0 \, ,\\&U^p_{i,i} = 0 \, ,\\&(\rho c)_m T_{, \, t} + (\rho c)_f \Big [U_i^f + \frac{(\rho c)_p}{(\rho c)_f} U_i^p \Big ] T_{, \, i} = \kappa _m \Delta T + (s_1 + s_2) (T^s - T) \, ,\\&\epsilon _1(\rho c)_s T^s_{, \, t} = \epsilon _1\kappa _s \Delta T^s + (s_1 + s_2) (T - T^s) \, , \end{aligned} \end{aligned}$$
(1)

where \(\mu\) is the dynamic viscosity of the fluid, \(K_f\), \(K_p\), \(p^f\), \(p^p\) are the permeability and the pressure in the macro- and micropores, respectively, the interaction coefficient \(\zeta\) is a transfer of momentum coefficient, first measured by Hooman et al. (2015), g is the gravity constant, \({\textbf{k}= (0, 0, 1)}\), \(\rho _0\) and \(\alpha\) are the reference density and the coefficient of thermal expansion in the fluid, arising from the Boussinesq approximation see Franchi et al. (2017); Barletta (2022). Additionally, \((\rho c)_s\) is the product of the density and the specific heat at constant pressure of the solid and \((\rho c)_m = [\phi (\rho c)_f +\epsilon (1 - \phi ) (\rho c)_p]\), \((\rho c)_f\) and \((\rho c)_p\) denoting the products of the density and the specific heat at constant pressure of the fluid in the macro- and micropores, respectively, \(\rho\) being the constant reference density \(\rho _0\). The term \(\kappa _s\) is the thermal conductivity of the solid, whereas \(\kappa _m = [\phi \kappa _f + \epsilon (1 - \phi ) \kappa _p]\), \(\kappa _f\) and \(\kappa _p\) being the thermal conductivities of the fluid in the macro- and micropores, respectively. The coefficients \(s_1\) and \(s_2\) are heat transfer coefficients which have been addressed by Rees (2010): these thermal interactions are herein assumed linear in the temperature differences. Finally, standard indicial notation is used throughout, in conjunction with the Einstein summation convention, with the subscript \(\,, i\) denoting \(\partial / \partial x_i\) and \(\Delta\) being the 3D Laplacian operator.

Since we are interested in investing the thermal convection problem, equations (1) are supposed to hold in the horizontal layer \(\{(x,y) \in \mathbb {R}^2\} \times \{0< z < d\}\), with \(t > 0\), i.e. the saturated porous medium is contained between the planes \(z = 0\) and \(z = d\). We append to this system the following boundary conditions

$$\begin{aligned} \begin{aligned}&U_i^f k_i = 0 \, , \, U_i^p k_i = 0\, , \qquad \qquad \hbox {on} \quad z = 0 \, , d\\&T^s = T = T_L \, , \qquad \quad \qquad \qquad \hbox {on} \quad z = 0 \, ,\\&T^s = T = T_U \, , \qquad \quad \qquad \qquad \hbox {on} \quad z = d \, , \end{aligned} \end{aligned}$$
(2)

where \(T_L\) and \(T_U\) are constants with \(T_L > T_U\).

It is pertinent to observe that the original set of equations for bidisperse convection of Nield and Kuznetsov (2006) is also an LTNE system. These writers employ a Brinkman theory as opposed to a Darcy one. However, they have equations not unlike (1)\(_{1-4}\), but they do not have (1)\(_6\), and instead they replace (1)\(_5\) by two equations for the macro- and microtemperatures \(T^f\) and \(T^p\). The original system of Franchi et al. (2017) has seven equations instead of those of (1) since they have equations for \(T^f\) and \(T^p\) rather than a single equation for T. In the context of our model, this is very important and we return to this in our discussion of the linear instability and nonlinear stability boundaries.

2.2 Basic Steady Solution and Perturbation Equations

The steady conduction solution of system (1)-(2) in whose stability we are interested in is one with

$$\begin{aligned} \tilde{U}_i^f = \tilde{U}_i^p = 0 \,, \quad \tilde{T}^s(z) = \tilde{T} = - \beta z + T_L \,, \ \end{aligned}$$

where

$$\begin{aligned} \beta = \frac{(T_L - T_U)}{d} > 0 \end{aligned}$$

is the adverse temperature gradient. As a consequence, from (1)\(_1\) and (1)\(_3\), the steady pressures \(\tilde{p}^f\) and \(\tilde{p}^p\) have form

$$\begin{aligned} \tilde{p}^f(z) = \tilde{p}^p(z) = - \rho _0 g \alpha \beta \frac{z^2}{2} + \rho _0 g \alpha T_L z \, , \end{aligned}$$

selecting both pressure scales to vanish at \(z= 0\).

In order to analyse the stability of the above equilibrium solution, we introduce perturbations \(u_i^f, u_i^p, \theta , \theta ^s, \pi ^f\) and \(\pi ^p\) such that

$$\begin{aligned} U_i^f = u_i^f \, , \; U_i^p = u_i^p \, , \; T = \tilde{T} + \theta \, , \quad T^s = \tilde{T}^s + \theta ^s \, , \quad p^f = \tilde{p}^f + \pi ^f \, , \; p^p = \tilde{p}^p + \pi ^p \, . \end{aligned}$$

So far, following Franchi et al. (2017), Nield and Kuznetsov (2006), we have allowed \((\rho c)_f\) and \((\rho c)_p\) to be different and likewise for \(\kappa _f\) and \(\kappa _p\). However, in the present study we have supposed \(T^f = T^p\) and hence we expect that \((\rho c)_f\) and \((\rho c)_p\) will be the same (as the macro- and micropores are composed of the same fluid) and for the same reason we suppose \(\kappa _f = \kappa _p\). In this way, in what follows \((\rho c)_m = D(\rho c)_f\) and \(\kappa _m = D \kappa _f\), with \(D = \phi + \epsilon (1-\phi )\). Then, the governing system for perturbations becomes

$$\begin{aligned} \begin{aligned}&\frac{\mu }{K_f} u_i^f + \zeta (u_i^f - u_i^p) = - \pi ^f_{, \, i} + g \rho _0 \alpha k_i \theta \, , \\&u^f_{i,i} = 0 \, , \\&\frac{\mu }{K_p} u_i^p + \zeta (u_i^p - u_i^f) = - \pi ^p_{, \, i}+ g \rho _0 \alpha k_i \theta \, , \\&u^p_{i,i} = 0 \, , \\&D(\rho c)_f \theta _{, \, t} = - (\rho c)_f (u_i^f + u_i^p) \theta _{, \, i} + \beta (\rho c)_f (w^f + w^p) \\&\qquad \qquad \quad + D \kappa _f \Delta \theta + (s_1 + s_2) (\theta ^s - \theta ) \, , \\&\epsilon _1(\rho c)_s \theta ^s_{, \, t} = \epsilon _1 \kappa _s \Delta \theta ^s + (s_1 + s_2) (\theta - \theta ^s) \, , \end{aligned} \end{aligned}$$
(3)

where \(w^f = u_3^f\) and \(w^p = u_3^p\). The boundary conditions we impose for (3) are

$$\begin{aligned} w^f = w^p = 0 \, , \qquad \theta = \theta ^s = 0 \, , \qquad \hbox {on} \quad z = 0 \, , \, d \end{aligned}$$
(4)

and \((u_i^f, u_i^p, \theta , \theta ^s, \pi ^f, \pi ^p)\) are assumed to have an (x, y)-dependence consistent with one that has a regular repetitive shape which tiles the plane. The planforms which are regular are composed of rolls, rectangles, hexagons and the triangles which make them, or tessellations of these; this topic including the typical hexagonal convection cell forms found in real life is described in full detail by (Chandrasekhar (1981), pages 43–52, ).

System (3) is now non-dimensionalized according to the scalings

$$\begin{aligned}&x = x^* \, d \, , \quad t = t^*\mathcal {T} \, , \quad \mathcal {T} = \frac{(\rho c)_f \, d^2}{\kappa _f} \, ,\quad u_i^f = u_i^{f*} \, U \, , \quad u_i^p = u_i^{p*} \, U \, , \\&U = \frac{D \kappa _f}{(\rho c)_f \, d} \, ,\quad \pi ^f = \pi ^{f *} \, P \, , \quad \pi ^p = \pi ^{p *} \, P \, , \quad P = \frac{\mu d U}{K_f} \, ,\\&\theta = \theta ^* \, T^\# \, , \quad \theta ^s = \theta ^{s *} \, T^\# \, , \quad T^\# = U\displaystyle \sqrt{\frac{(\rho c)_f \beta d^2 \mu }{D \kappa _f \, \rho _0 g \alpha K_f}} \, , \end{aligned}$$

and the new dimensionless parameters

$$\begin{aligned} \xi = \frac{\zeta K_f}{\mu } \, , \; K_r = \frac{K_f}{K_p} \, , \quad S = \frac{(s_1 + s_2) d^2}{D \kappa _f} \, . \end{aligned}$$
(5)

These parameters are essentially a non-dimensional version of \(\zeta\), the permeability ratio, and a non-dimensional version of the heat transfer coefficient between the fluid and solid, respectively. The Rayleigh number \(R_a = R^2\) is defined by

$$\begin{aligned} R = \displaystyle \sqrt{\frac{\rho _0 g \alpha K_f (\rho c)_f \beta d^2}{D \mu \kappa _f}} \, . \end{aligned}$$

With this scaling and dropping all *-superscripts, the dimensionless form of the perturbations system becomes

$$\begin{aligned} \begin{aligned}&u_i^f + \xi (u_i^f - u_i^p) = - \pi ^f_{, \, i} + R k_i \theta \, , \\&u^f_{i,i} = 0 \, , \\&K_r u_i^p + \xi (u_i^p - u_i^f) = - \pi ^p_{, \, i}+ R k_i \theta \, , \\&u^p_{i,i} = 0 \, , \\&\theta _{, \, t} + (u_i^f + u_i^p) \theta _{, \, i} = R (w^f + w^p) + \Delta \theta + S (\theta ^s - \theta ) \, , \\&a_1 \theta ^s_{, \, t} = b \Delta \theta ^s + S (\theta - \theta ^s) \, , \end{aligned} \end{aligned}$$
(6)

where

$$\begin{aligned} a_1 = \displaystyle \frac{\epsilon _1 (\rho c)_s}{D (\rho c)_f} \, , \qquad b = \displaystyle \frac{\epsilon _1 \kappa _s}{D \kappa _f} \, =\frac{(1-\epsilon )(1-\phi )}{\phi +\epsilon (1-\phi )}\,\frac{\kappa _s}{\kappa _f}\,. \end{aligned}$$
(7)

The parameter \(a_1\) represents the non-dimensional thermal inertia coefficient which does not appear directly in the stability threshold analysis, while b is the ratio between the thermal conductivity coefficients weighted due to the porosities. The domain of definition is now the horizontal layer \(\mathbb {R}^2\ \times \{0< z < 1\}\), with \(t > 0\). The boundary conditions are

$$\begin{aligned} w^f = w^p = 0 \, , \qquad \theta = \theta ^s = 0 \, , \qquad \hbox {on} \quad z = 0 \, , \, 1 \; \end{aligned}$$
(8)

together with the requirement that the perturbations field satisfies a plane tiling periodicity in x and y. Due to the periodicity requirement, we may work with the period cell \(V= \displaystyle \left[ 0, \frac{2\pi }{a_x}\right] \times \left[ 0, \frac{2\pi }{a_y}\right] \times (0,1)\), \(t>0\), where the wavenumber a is such that \(a^2 = a^2_x + a^2_y\). For example, for a hexagon, see Chandrasekhar (1981), we may take the \(x-\) and \(y-\) domains to be \(x\in [0,\sqrt{3}L],\) \(y\in [0,2L],\) where L is the side length of the triangles which make the hexagon.

3 Symmetry and (Global) Nonlinear Stability

Equations (6) may be rewritten in the abstract form

$$\begin{aligned} AU_t + LU + N(U) = 0 \end{aligned}$$

where the new vectorial variable U is equal to \((u_1^f, u_2^f, w^f, u_1^p, u_2^p, w^p, \theta , \theta ^s)\), A is the operator \(\hbox {diag}[0,0,0,0,0,0,1,a_1]\), L represents the linear operator characterizing the linearities, whereas the nonlinear vectorial field N(U) consists of the nonlinear terms \((u_i^f + u_i^p) \theta _{, \, i}\).

In view of our homogeneous boundary conditions, we may easily show that

$$\begin{aligned} \Big (U, N(U) \Big ) = 0 \end{aligned}$$

where \(\Big (\cdot , \cdot \Big )\) is now the inner product on \([L^2(V)]^8\), V being the periodicity cell with zero cross-flow through its boundary. Again, thanks to the boundary conditions (8), one may easily check that the condition

$$\begin{aligned} \Big (V_1, LU_1\Big ) = \Big (LV_1, U_1\Big ) \end{aligned}$$

holds for any \(U_1 \,, \,V_1\) in the space of admissible solutions to the above boundary value problem. Thus, L is a symmetric linear operator and hence, by the results in Galdi and Straughan (1985), one may show that the linear instability boundary is exactly the same as the nonlinear stability boundary. Therefore, sub-critical instabilities do not exist; this means that we need only calculate the linear instability critical Rayleigh number threshold and we are guaranteed also global nonlinear stability. This is a very important result. To appreciate the significance, we note that since the linear operator is symmetric, exchange of stabilities holds, in the sense that the growth rate \(\sigma\) is real. For the original bidisperse thermal convection problem of Nield and Kuznetsov (2006) where the solid temperature is not taken into account, but there are still potentially different macropore and micropore temperatures, \(T^f\) and \(T^p\), (Straughan 2009) was not able to show exchange of stabilities. He found that in all the cases he analysed numerically the growth rate was real at the onset of instability. However, this does not establish exchange of stabilities. The nonlinear energy stability results of Straughan (2009) were reasonably close to linear instability theory, but there still remains the possibility of sub-critical instability, see also (Straughan (2015),  pages 185–193). When Darcy bidisperse theory with \(T^f\) and \(T^p\) is studied (see (Straughan (2015),  pages 193–202)), again exchange of stabilities has not been proved and the numerical results of Straughan (2015) are not close to those of linear instability theory, suggesting the possible occurrence of sub-critical instabilities. Additionally when one considers the full local thermal non-equilibrium theory of Franchi et al. (2017), where one has solid temperature \(T^s\), macropore fluid temperature \(T^f\) and micropore fluid temperature \(T^p\), we are unaware of any proof of exchange of stabilities. We stress that in the case under analysis here where we study the full local thermal non-equilibrium bidisperse convection problem but with \(T^f=T^p\) the equivalence of the linear instability and nonlinear stability thresholds is a very strong result. It certainly shows that in this problem the linear instability theory captures fully the key physics of the onset of thermal convection.

For completeness, let us give some details on the nonlinear stability topic: one multiplies (6)\(_1\) by \(u_i^f\), (6)\(_3\) by \(u_i^p\), (6)\(_5\) by \(\theta\) and (6)\(_6\) by \(\theta ^s\), integrates over the period cell V and then adds the resulting equations. Thus, after some integration by parts and use of the boundary conditions, it is an easy matter to derive an energy equation of form

$$\begin{aligned} \frac{d}{d \, t} \left( \displaystyle \frac{1}{2} \Vert \theta \Vert ^2 + \frac{a_1}{2} \Vert \theta ^s\Vert ^2\right) = RI - \mathcal {D} \, , \end{aligned}$$
(9)

where

$$\begin{aligned} I = 2(\theta , w^f) + 2 (\theta , w^p) \end{aligned}$$

and the dissipation term \(\mathcal {D}\) is expressed as

$$\begin{aligned} \mathcal {D} = \Vert u^f\Vert ^2 + K_r \Vert u^p\Vert ^2 + \Vert \nabla \theta \Vert ^2 + b \Vert \nabla \theta ^s\Vert ^2 + \xi \Vert u^f - u^p\Vert ^2 + S \Vert \theta -\theta ^s\Vert ^2 \, , \end{aligned}$$

with \(\Vert \cdot \Vert\) and \((\cdot , \cdot )\) being the norm and the inner product on the real Hilbert space \(L^2(V)\).

Define now the threshold \(R_E\) such that

$$\begin{aligned} \displaystyle \frac{1}{R_E} = \underset{{\mathcal H}}{max} \frac{I}{D} \, , \end{aligned}$$
(10)

where \({\mathcal H}\) is the space of admissible perturbations, i.e. consisting of \(L^2(V)\)-functions divergence-free \(u_i^f\) and \(u_i^p\) and \(H^1(V)\)-functions \(\theta\) and \(\theta ^s\), satisfying homogeneous boundary conditions on \(z =0 \,, 1\).

Therefore, the energy equation is written

$$\begin{aligned} \frac{\text {d}}{\text {d} \, t} \left( \displaystyle \frac{1}{2} \Vert \theta \Vert ^2 + \frac{a_1}{2} \Vert \theta ^s\Vert ^2\right) \le - D \left( 1- \frac{R}{R_E} \right) \, . \end{aligned}$$
(11)

Now, employing arguments similar to those of Rionero (1968) one may prove that the maximizing solution to (9) exists. Then, for \(R < R_E\), say \(\displaystyle 1 - \frac{R}{R_E} = c > 0\), by using Poincaré inequality in (11), we deduce the energy inequality

$$\begin{aligned} \displaystyle \frac{\text {d} \, E}{\text {d}\,t} \le - c \kappa E \, , \end{aligned}$$

where

$$\begin{aligned} E = \displaystyle \frac{1}{2} \Vert \theta \Vert ^2 + \frac{a_1}{2} \Vert \theta ^s\Vert ^2 \end{aligned}$$

and \(\displaystyle \kappa = \frac{\pi ^2}{2} \min \left\{ 1, \frac{b}{a_1}\right\} > 0\), \(\pi ^2\) denoting the Poincaré constant.

Hence, we see that

$$\begin{aligned} E(t) \le E(0) \exp {\{- c \kappa t\}} \quad \forall t > 0 \, ; \end{aligned}$$

thus \(E(t) \rightarrow 0\) at least exponentially in t, provided \(R < R_E\). Consequently, both \(\Vert \theta \Vert\) and \(\Vert \theta ^s\Vert\) decay to zero exponentially in t.

For completeness, see Franchi et al. (2017), one applies the energy method only to the momentum perturbation equations (6)\(_1\) and (6)\(_3\) and then adds the resulting equations. With the final aid of the arithmetic–geometric mean inequality, it is a simple matter to find the estimate

$$\begin{aligned} \Vert u^f\Vert ^2 + K_r \Vert u^p\Vert ^2 \le R^2 \left( 1 + \frac{1}{K_r} \right) \Vert \theta \Vert ^2 \, . \end{aligned}$$

This bound guarantees the exponential decay of both \(\Vert u^f\Vert\) and \(\Vert u^p\Vert\).

We may conclude that the condition \(R < R_E\) assures the global (i.e. for all initial data) nonlinear stability of the steady conduction solutions under study.

Remark 1

We have only dealt with Darcy theory in equations (6). We could equally deal with Brinkman theory. In particular, motivated by the work of Fried and Gurtin (2006) on length scale effects on flow in geometry with small dimensions, we allow for the possibility of different Brinkman viscosities in the macro- and micropores, \(\tilde{\mu }^f\) and \(\tilde{\mu }^p\). In that case the non-dimensional equations (6)\(_1\) and (6)\(_3\) should have terms \(B^f_r \Delta u_i^f\) and \(B^p_r \Delta u_i^p\) added to their right hand sides, where \(B^f_r\), \(B^p_r\), play the role of Brinkman numbers. Of course, one would then have to prescribe boundary conditions on \(u_i^f\) and \(u_i^p\), \(i = 1,2,3\). Nevertheless, the linear operator L attached to the Darcy–Brinkman theory continues to be symmetric. Hence, the key result that the linear instability boundary is equivalent to the global nonlinear stability boundary remains true.

Remark 2

In the case of the Brinkman theory, one could argue that at the boundaries \(z = 0, \, 1\), at the microscopic level, the presence of solid, of fluid in the macropores, and of fluid in the micropores should be more accurately described by treating the planes \(z = 0, \, 1\) as rough boundaries. In this case, we can adapt the prescription of new boundary conditions suggested by Celli and Kuznetsov (2018). Celli and Kuznetsov (2018) suggested using Saffman-type boundary conditions for a fluid touching rough boundaries and we here argue that their method carries over naturally to a Brinkman porous medium. In this case, the boundary conditions on the perturbation velocities become

$$\begin{aligned} \begin{aligned} w^f = 0 \, , \quad \qquad \qquad&w^p = 0 \, , \qquad \qquad \qquad \hbox {on} \; z = 0 \, , 1 \, , \\ \displaystyle \frac{\partial u_j^f}{\partial z} = - \frac{\alpha }{\sqrt{K_f}} u_j^f \, , \quad&\frac{\partial u_j^p}{\partial z} = - \frac{\alpha }{\sqrt{K_p}} u_j^p \qquad \hbox {on} \; z = 0 \, ,\quad j= 1,2 \, , \\ \displaystyle \frac{\partial u_j^f}{\partial z} = \frac{\alpha }{\sqrt{K_f} } u_j^f \, , \quad \;&\frac{\partial u_j^p}{\partial z} = \frac{\alpha }{\sqrt{K_p} }u_j^p \qquad \quad \hbox {on} \; z = 1 \, , \quad j= 1,2 \, . \end{aligned} \end{aligned}$$

One may now demonstrate, even in this case with rough boundaries, that the result of equivalence of the linear instability and global nonlinear stability thresholds continues to hold.

4 Stability Thresholds: Calculation of the critical Rayleigh and Wave Numbers

To complete our analysis, we find the linear instability boundary, working with the linearized version of the perturbation system (6), i.e. we omit the nonlinear term in (6)\(_4\). Then, we seek a solution in which \(u_i^f, u_i^p, \theta , \theta ^s, \pi ^f, \pi ^p\) exhibit a separate time dependence like \(e^{\sigma t}\), where the growth rate parameter \(\sigma\), due to the symmetry of the linear operator L, is necessarily real. This shows that the transition threshold to the onset of the convective instabilities occurs when \(\sigma = 0\), and hence we address the steady convection problem, i.e. \(\sigma = 0\).

To proceed, from the stationary form of the linearized version of (6), after removing the pressures by applying the double curl operator to (6)\(_1\) and (6)\(_3\), one focusses on the third component of the resulting equations. This leaves us with solving the following system

$$\begin{aligned} \begin{aligned}&- (1 + \xi ) \Delta w^f + \xi \Delta w^p + R \Delta ^* \theta = 0 \, , \\&- (K_r + \xi ) \Delta w^p + \xi \Delta w^f + R \Delta ^* \theta = 0 \, , \\&- R (w^f + w^p) - \Delta \theta + S (\theta - \theta ^s) = 0 \, , \\&- b \Delta \theta ^s - S (\theta - \theta ^s) = 0 \, , \end{aligned} \end{aligned}$$
(12)

where \(\Delta ^*\) is the horizontal Laplacian, i.e. \(\Delta ^* = \displaystyle \frac{\partial ^2}{\partial x^2} + \frac{\partial ^2}{\partial y^2}\).

The boundary conditions are

$$\begin{aligned} w^f = w^p = 0 \, , \qquad \theta = \theta ^s = 0 \, , \qquad \hbox {on} \quad z = 0 \, , \, 1 \, , \end{aligned}$$

and we assume periodicity in x, y, with periods \(\displaystyle \frac{2\pi }{a_x}\) and \(\displaystyle \frac{2\pi }{a_y}\), respectively.

We perform the Fourier normal modes procedure and seek solutions of form \(w^f= W^f(z) h(x,y)\), with a similar representation for \(w^p\), \(\theta\) and \(\theta ^s\), where h(x, y) just denotes a planform which tiles the plane and satisfies the condition \(\Delta ^*h = - a^2\,h\), for a given horizontal wavenumber a, see Chandrasekhar (1981), pages 43–52.

From equations (12), one may show that the further boundary conditions hold

$$\begin{aligned} \displaystyle \frac{d^{2n} W^f(z)}{dz^{2n}} = \frac{d^{2n} W^p(z)}{dz^{2n}} = 0 \, , \qquad n\in \mathbb {N},\qquad \hbox {on} \quad z = 0 \, , \, 1 \, . \end{aligned}$$

In this way, we may select \(W^f(z)= \sum _{n=1}^{\infty }\hat{W}_n^f \sin (n \pi z)\), where \(\hat{W}_n^f\) are the Fourier coefficients, with analogous forms for \(W^p(z)\), \(\Theta (z)\) and \(\Theta ^s(z)\), \(\hat{W}^p\), \(\hat{\Theta }\) and \(\hat{\Theta }^s\). The normal mode procedure is beautifully explained by Barletta (2021), see also Barletta (2019).

In this way, we arrive at an expression for the eigenvalue R, as a function of \(a^2\) and \(n^2\). The result reads

$$\begin{aligned} R^2(n^2, a^2) = \displaystyle \frac{\Lambda _n^2}{a^2} \left[ \frac{b(\Lambda _n + S) + S}{b \Lambda _n + S} \right] \left[ \frac{K_r + K_r \xi + \xi }{1+ 4 \xi + K_r}\right] \, , \end{aligned}$$

where \(\Lambda _n = a^2 + n^2 \pi ^2\). Fixing \(a^2\), it can be shown that its minimum value with respect to \(n^2\), is attained at \(n=1\); so, we take \(n=1\) in the previous formula.

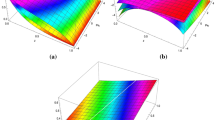
In order to calculate the critical Rayleigh number \(R_s\), we must minimize

$$\begin{aligned} R^2(a^2) = \displaystyle \frac{\Lambda ^2}{a^2} \left[ \frac{b(\Lambda + S) + S}{b \Lambda + S} \right] \left[ \frac{K_r + K_r \xi + \xi }{1+ 4 \xi + K_r}\right] \end{aligned}$$
(13)

in \(a^2\), with \(\Lambda = a^2 + \pi ^2\).

A comparison of (13) with earlier published results is possible.

Following the notations \(\gamma\) and H in Banu and Rees (2002), let \(b=1/\gamma\) and \(S \equiv H\). For the case of one porosity, besides \(\xi = 0\), we take \(K_p=0\) and hence the permeability ratio \(K_r=K_f/K_p\) tends to infinity. Now take the limit \(K_r\rightarrow \infty\) in (13), to see that

$$\begin{aligned} R^2=\frac{\Lambda ^2}{a^2}\Bigl [\frac{b(\Lambda +S)+S}{b\Lambda +S}\Bigr ] \equiv \frac{\Lambda ^2}{a^2}\Bigl [\frac{\Lambda +H(1+\gamma )}{\Lambda +\gamma H}\Bigr ]\,. \end{aligned}$$
(14)

Equation (14) is exactly the stability threshold found by Banu and Rees (2002) in their original analysis of the LTNE single porosity problem.

If instead we take \(S=0\) in (13), we are in the bidisperse case where the temperature in the solid is assumed to be the same as that in the macropores and micropores, as analysed in Gentile and Straughan (2017). Then, (13) yields

$$\begin{aligned} R^2=\frac{\Lambda ^2}{a^2}\Bigl (\frac{K_r+K_r\xi +\xi }{1+4\xi +K_r}\Bigr )\,. \end{aligned}$$
(15)

This expression is just the same as that derived by Gentile and Straughan (2017).

The original bidisperse work of Nield and Kuznetsov (2006) employs Brinkman theory in the macropore and micropore equations. The analogous problem for Darcy theory, but again for different macropore and micropore temperatures, is developed in (Straughan (2015), pages 196–202), where stationary and oscillatory convection Rayleigh number thresholds are obtained (see equations (13.39), (13.41)). Since there is the possibility of oscillatory convection, it is difficult to make a direct comparison with the threshold (13).

5 Numerical Results

In this section, we present numerical results for the minimization of (13) as a function of \(a^2\) for realistic values of \(b, K_r\) and \(\xi\), for S varying.

Typical \(K_r\) and \(\xi\) values for a variety of solids and fluids are reported by Gentile and Straughan (2020). Based on the values given there we estimate typical values to be in the range, \(\xi =0.01, 0.1, 1\) and \(K_r=10,100\). If we work with water as the fluid and glass beads as the porous structure, then the thermal conductivities are for water, \(\kappa _f=0.5918\) \(W/m^{\circ }K\) and for glass \(\kappa _s=0.8\) \(W/m^{\circ }K\). The values of b may be then found from

$$\begin{aligned} b=1.3518\frac{(1-\epsilon )(1-\phi )}{\phi +\epsilon (1-\phi )}\,. \end{aligned}$$

This yields the following values for b, when \(\phi =0.2,\epsilon =0.2\), \(b=1.78\), when \(\phi =0.3,\epsilon =0.3\), \(b=0.96\), when \(\phi =0.2,\epsilon =0.5\), \(b=0.67\), when \(\phi =0.8,\epsilon =0.2\), \(b=0.19\). We work with some of these values below.

We also select another example of a solid with a high thermal conductivity, copper. For copper, \(\kappa _s=398\) \(W/m^{\circ }K\). We employ as fluid a typical oil, as an oil copper system may have use in a heat exchanger. Elam et al. (1989) measured thermal conductivity values for binary mixtures of aromatic and paraffinic components in the range \(\kappa _f=0.120\), \(W/m^{\circ }K\), \(\kappa _f=0.130\), \(W/m^{\circ }K\). Turgut et al. (2009) measured the thermal conductivity of sunflower oil, corn oil and olive oil. The values they obtain are all close and a typical value at \(25^{\circ }C\) is \(\kappa _f=0.168\), \(W/m^{\circ }K\). If we take \(\phi =0.9,\epsilon =0.6,\) \(\kappa _f=0.120\), \(W/m^{\circ }K\), then from (7) we obtain \(b=138.2.\)

Values for the heat transfer coefficient S prove to be more elusive. Buonomo et al. (2019) report such values for LTNE with a high porosity aluminium foam when the saturating fluid is air. The work of Rees (2009, 2010) may be shown to yield the result that \(S=1.23C\) where C is a geometrical shape factor. Depending on the geometry Rees (2009, 2010) shows that C may take values of 12 or \(3N^2\) for \(N\ge 2\). Hence, we here allow H to vary in the range \(0\le H\le 100\).

From the energy equation (9), we observe that as b and S are increased then the strength of dissipation increases and so we expect that both parameters will have a stabilizing effect on thermal convection. Numerical results do, indeed, confirm this. We have fixed S and varied b and we find the critical Rayleigh number and wave numbers increase as b increases. In practice we determine b from the materials we are using and so we mainly investigate the effect of increasing S with b fixed.

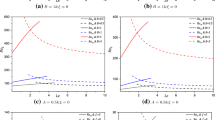
In Figs. 1, 2 and 3, we display the variation of the critical Rayleigh number Ra against S keeping \(K_r,\xi\) and b fixed. Figure 1 is for \(\xi =0.01\) whereas Figs. 2 and 3 have \(\xi =1\). It is seen that the effect of increasing S is to stabilize the conduction solution, although as S continues to increase this effect lessens. We observe higher values of Ra as \(K_r\) is increased, but the effect is less than increasing b. Since b is in general given by

$$\begin{aligned} b=\frac{\kappa _s}{\kappa _f}\,\frac{(1-\phi )(1-\epsilon )}{[\phi +\epsilon (1-\phi )]}\,, \end{aligned}$$

one may increase stabilization by increasing \(\kappa _s/\kappa _f\) or by increasing the function \(f(\phi ,\epsilon )=(1-\phi )(1-\epsilon )/[\phi +\epsilon (1-\phi )]\). Thus, for a fixed bidisperse geometry, a combination of solid and fluid with greater solid thermal conductivity to fluid thermal conductivity will yield a larger critical Rayleigh number and larger stabilizing effect. Alternatively, for a fixed combination of fluid and solid the stabilization may be controlled by varying the macro- and micropermeabilities through \(f(\phi ,\epsilon )\). If both porosities are high then f will be small, whereas when both porosities are low f will be larger, consider, e.g. \(\phi =\epsilon =0.9\) then \(f=1/99\) whereas when \(\phi =\epsilon =0.1\), then \(f=81/19\). In principle this yields a way to control whether one wishes the layer to convect or not.

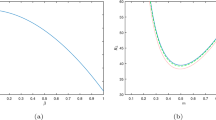
The wavenumber behaviour is interesting as shown in Fig. 4. We find numerically that the critical wave number as displayed in Fig. 4 is relatively insensitive to changes in \(K_r\) and \(\xi\). As S increases the wave number increases to a maximum and then decreases; it eventually appears to tend to an asymptotic value. The rate of increase in \(a^2\) is very dependent on the value of b. Thus, the thermal interaction parameter S being increased has the effect of initially making the convection cells narrower and convect more vigorously. However, there is a critical value of S and once S exceeds this the cells become wider again. The parameter S is essentially the non-dimensional interaction coefficient for the transfer of heat from the solid to fluid, or vice versa. Banu and Rees (2002) call the analogous coefficient in the one porosity situation the interphase heat transfer coefficient. They note that large values of this parameter correspond to rapid transfer of heat between the solid and fluid phases. We point out that this maximum effect is also witnessed in the one porosity problem by (Banu and Rees (2002), figure 4) and by (Bidin and Rees (2020),  figure 2). They used k rather than a and H rather than S. It thus appears that there is an optimum value of S which will yield the narrowest convection cells, and this should be useful in heat transfer applications. Banu and Rees (2002) report that for the one porosity case these tall thin cells should be observed readily by suitable experiments.

In Figs. 5 and 6, we report critical Rayleigh number and wave number values against S for the copper-oil porous system. Here, the parameter b has a much higher value, and consequently, the Ra and \(a^2\) values are considerably different. We do, however, obtain similar qualitative agreement with what we witnessed for the glass-water case. The critical Rayleigh number is strongly increasing in S. Again, we find \(a^2\) reaches a maximum as S is increased, but the value of S is much higher for the larger value of b.

6 Conclusions

We have produced a model for thermal convection in a bidisperse porous material when the temperature in the solid skeleton is allowed to differ from the temperature of the fluid in the macro- and micropores. We have shown the key result that the linear instability threshold is the same as the global nonlinear stability one. This means that linear instability theory fully captures the physics of the onset of thermal convection and sub-critical instabilities do not arise. We have further shown that the parameters b and S which represent the bidisperse geometry and thermal conductivity ratio, and the heat transfer coefficient, play an important role in determining when thermal convective motion may occur.

It is important to note that the bidisperse system of Nield and Kuznetsov (2006) is also an LTNE one. There, however, the fluid in the macro- and micropores may have different temperatures \(T^f\) and \(T^p\). The solid temperature is not specifically taken into account. This model has recently been extensively analysed from a linear instability and from a weakly nonlinear perspective by Siddabasappa et al. (2023). It is not known whether exchange of stabilities holds for the Nield and Kuznetsov (2006) model, and so sub-critical bifurcation cannot be ruled out. A similar statement may be made for the full bidisperse theory of Franchi et al. (2017), where the fluid macropore and micropore temperatures may be different, and different from the solid skeleton temperature. We believe that the single temperature theory presented here should be useful for many applications, and the fact that the linear instability threshold is the same as the global nonlinear stability one is particularly noteworthy.

Fig. 1
figure 1

Graph of Ra versus S, \(\xi =0.01\). Kr and b values shown on the figure. When \(S=0,\) \(Ra=36.15\), for \(K_r=10\); when \(S=0,\) \(Ra=39.83\), for \(K_r=1000\)

Full size image
Fig. 2
figure 2

Graph of Ra versus S, \(\xi =1\). Kr and b values shown on the figure

Full size image
Fig. 3
figure 3

Graph of Ra versus S, \(\xi =1\), \(b=0.19\). \(K_r=10,1000\), as shown on the figure

Full size image
Fig. 4
figure 4

Graph of \(a^2\) versus S. The maximum values of \(a^2\) are \(a^2=10.32,b=0.19,S=4\), \(a^2=11.84,b=0.96,S=15\), \(a^2=13.16,b=1.78,S=24\). \(K_r=1000,\xi =0.01\)

Full size image
Fig. 5
figure 5

Graph of Ra versus S. Values of \(K_r,b,\xi\) shown on the figure

Full size image
Fig. 6
figure 6

Graph of \(a^2\) versus S. The maximum value of \(a^2\) is \(a^2=63.16,S=855.0\)

Full size image