1 Introduction

A fluid flow driven by buoyancy and gravitational forces in fluid-saturated porous media is a physical phenomenon commonly observed under natural or laboratory conditions. Buoyancy-driven flow arises due to significant fluid density changes induced by thermal or concentration gradients. When a denser fluid layer is placed onto a less dense one in the porous medium with sufficient permeability, the denser fluid can flow downwards to displace the lighter fluid, which in turn flows upwards to replace the denser fluid, and the convective circulation ensues.

Using mathematical modelling techniques, buoyancy-driven flow in porous media was studied in many publications (for reviews, see e.g. Holzbecher (1998); Phillips (2009) ). One of the first laboratory and numerical experiments describing this type of fluid flow was performed by Elder (1967a, b). In Elder (1967a), he investigated steady convection in a horizontal slab of a homogeneous porous material saturated with a viscous fluid where buoyant instabilities were created by sudden heating a portion of the lower boundary of the slab. Some attention was also paid to the role of end effects and mass discharge in the system. Extending his original model, Elder (1967b) numerically computed a time-dependent solution featuring a single plume. The other solutions to the Elder problem were later found using advanced numerical procedures (Frolkovič and De Schepper 2000; Johannsen 2003; van Reeuwijk et al. 2009).

To eliminate truncation errors associated with spatial discretization (Arakawa 1966), van Reeuwijk et al. (2009) implemented the pseudospectral method to solve a saline analogue of the Elder problem. Unlike the original thermal Elder problem, the convective circulation pattern in the saline Elder problem is initiated by a saline concentration gradient, where the salt is dissolved by freshwater at a portion of the upper boundary of the system. In van Reeuwijk et al. (2009), all the known stable steady-state solutions to the saline Elder problem were reproduced, and a bifurcation diagram for the steady states up to the saline Rayleigh number of 400 was determined. The bifurcation diagram confirmed the existence of three stable steady-state solutions reported previously using numerical continuation methods (Johannsen 2003). Moreover, van Reeuwijk et al. (2009) recommended the Elder problem at the Rayleigh number of 60, where only one steady-state solution exists, as a benchmark test case for density-dependent groundwater flow and mass transport models. For the purely diffusive case, corresponding to zero Rayleigh number, the analytical solution was derived and tested against the numerical pseudospectral solution with excellent agreement.

Buoyancy-driven flow plays a crucial role in a wide range of hydrogeological processes such as saline contamination (Bear et al. 1999; Gilman and Bear 1996; Zimmermann et al. 2006; Lin et al. 2009), carbon dioxide sequestration (Riaz et al. 2006; Ranganathan et al. 2012; Huppert and Neufeld 2014; Celia et al. 2015) and heat transfer in geothermal systems (Horne and O’Sullivan 1974; Cheng 1979; Oldenburg and Pruess 1998). Such flows through porous media are often accompanied by local chemical reactions between the liquid phase and a solid structure of the porous matrix. Adopting a system configuration similar to that of the saline Elder problem, Post and Prommer (2007) considered a reactive multicomponent transport with complex chemical reactions based on ion exchange and calcite dissolution and precipitation. They investigated the feedback mechanisms between geochemical reactions and buoyancy-driven flow in the system. The main result of their work was that the flow patterns developed during saltwater intrusion into freshwater were significantly different in comparison to the non-reactive saline Elder case for relatively small density contrasts between saltwater and freshwater. However, the importance of this feedback was shown to decrease with the increasing density contrast.

Although Post and Prommer (2007) did not take into account any porosity and permeability changes of the porous medium due to calcite dissolution or precipitation, these changes may affect the development of the flow and mass transport in a system. This was shown for calcite dissolution during seawater intrusion in a coastal carbonate-rock aquifer using the Henry problem geometry by Laabidi and Bouhlila (2016). Specifically, a reactive solute flowing through a porous medium tends to follow relatively narrow and high-permeability zones and dissolve them further, thereby increasing the permeability even more. This local reactive-infiltration instability is generally caused by an unstable dissolution front. The local stability of dissolution fronts moving through porous media has been addressed in a number of studies (e.g. Chadam et al. 1986, 2001; Sherwood 1987; Hinch and Bhatt 1990; Szymczak and Ladd 2013)).

More recently, Ritchie and Pritchard (2011) carried out a theoretical study of geochemical convection in a fluid-saturated porous medium with evolving porosity and permeability. Kinetics of the dissolution reactions was very similar to that introduced by Chadam et al. (1986, 2001). The convective motion was evoked by imposing a vertically varying equilibrium solubility. Linear stability analysis of the full problem was employed to describe the onset of convection, and numerical simulations were used to investigate the long-term behaviour of the system. In the strongly buoyantly-unstable regime at high Rayleigh numbers, it was shown that the reaction process stabilised the system by removing the destabilising reactive solute. Over very long-time scales, horizontally-layered porosity structures, penetrated by narrow vertical channels of enhanced porosity, were developed.

In this paper, we present a model of buoyancy-driven flow and reactive solute transport in a fluid-saturated porous medium (Sect. 2). Adopting the Elder problem geometry, we consider the simplest model in which local chemical interactions between a solute and a mineral structure of the solid can occur, with the reactive solute and dissoluble minerals consumed and reaction products generated in the liquid. A second-order reaction rate for solid mineral dissolution is assumed following Lund and Fogler (1976) and Hinch and Bhatt (1990), and any dissolution effects on porosity and permeability are neglected as in Post and Prommer (2007). In Sect. 3, we describe a pseudospectral numerical approach to tackle the considered problem. In Sect. 4, for a weakly reactive case without buoyancy-driven flow and for a reactive case with solute-driven flow, we analyse and explain effects of the geochemical processes on the flow and mass transport. Furthermore, we investigate the effects occurring when the flow is driven not only by a concentration gradient of the solute but also by a concentration gradient of the products.

2 Mathematical Formulation

In a two-dimensional Cartesian coordinate system \({\varvec{x}}^{*} = (x^{*},z^{*})^{T}\), we consider a homogeneous and isotropic porous medium, originally saturated with freshwater, in the region \(-2\,H^{*} \le x^{*} \le 2\,H^{*}\) and \(0 \le z^{*} \le H^{*}\) \([\textrm{m}]\) over time \(t^{*} \ge 0\) \([\textrm{s}]\). We consider a solute (e.g. salt) in the pore liquid with the concentration \(c^{*}({\varvec{x}}^{*},t^{*})\) \([\textrm{mol} \, \textrm{m}^{-3}]\), which reacts with a solid structure of the porous medium and in turn dissolves it. The porous matrix consists of dissoluble minerals (e.g. calcite) with the concentration \(m^{*}({\varvec{x}}^{*},t^{*})\) \([\textrm{mol} \, \textrm{m}^{-3}]\). For simplicity, there is a bimolecular reaction between a solute molecule in the liquid phase and a mineral molecule in the solid phase, which generates reaction products in the liquid phase represented by a single concentration quantity \(n^{*}({\varvec{x}}^{*},t^{*})\) \([\textrm{mol} \, \textrm{m}^{-3}]\). The solute and the products are perfectly mixed in the liquid phase and do not interact themselves. The liquid motion through the porous medium is governed by Darcy’s law for the volume flux \({\varvec{u}}^{*}({\varvec{x}}^{*},t^{*})\) \([\textrm{m} \, \textrm{s}^{-1}]\). The pressure field in the liquid phase is described by \(p^{*}({\varvec{x}}^{*},t^{*})\) \([\textrm{kg} \, \textrm{m}^{-1} \, \textrm{s}^{-2}]\). All dimensional variables and operators are denoted by the asterisk.

Fig. 1
figure 1

Schematic diagram of a the dimensional and b non-dimensional geometry of the model for buoyancy-driven flow and mass transport in the considered porous medium in the 2D vertical cross-section

Full size image

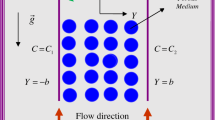
Boundary conditions for the concentrations of the solute and products are as follows. At the top, we impose that the solute concentration has a fixed profile: for \(\vert x^{*} \vert > H^{*}\), we have \(c^{*}(x^{*},H^{*}, t^{*}) = c_{0}^{*}\) and for \(\vert x^{*} \vert \le H^{*}\), we have \(c^{*}(x^{*},H^{*}, t^{*}) = c_{1}^{*} > c_{0}^{*}\) (see Fig. 1a). Here, \(c_{0}^{*}\) and \(c_{1}^{*}\) represent the reference concentrations of the solute in the liquid. The above boundary conditions, applied to the system with the initial solute concentration \(c_{0}^{*}\), yield a vertical concentration gradient. In case of the concentration-dependent fluid density, it can result in a sudden emergence of buoyant instabilities. Along the whole upper boundary, we consider the concentration of the products \(n_{0}^{*}\). At the bottom, the solute concentration \(c_{0}^{*}\) and the concentration of the products \(n_{0}^{*}\) are prescribed. While these conditions entail removing the solute and products from the bottom of the system, there is no mass loss across the vertical boundaries, which is guaranteed by zero Neumann conditions for the solute and products. In addition, all the boundaries are impermeable to the liquid, so there is no advective flux across any boundary.

Taking into account advection and diffusion of the solute, and the chemical interactions between the solute and the dissoluble minerals, the local mass conservation law for the solute is governed by

$$\begin{aligned} \phi \frac{\partial c^{*}}{\partial t^{*}} + { \varvec{\nabla }^{*} \varvec{\cdot } ({\varvec{u}}^{*}c^{*})} - \varvec{\nabla }^{*}\varvec{\cdot }(\phi D_{c}^{*}\varvec{\nabla }^{*}c^{*}) = - k^{*}c^{*}m^{*}, \end{aligned}$$
(1)

where \(\phi\) is the porosity (liquid fraction) of the porous medium, \(D_{c}^{*}\) \([\textrm{m}^{2} \, \textrm{s}^{-1}]\) is the molecular diffusion coefficient for the solute of the liquid phase and \(k^{*}\) \([\textrm{m}^{3} \, \textrm{mol}^{-1} \, \textrm{s}^{-1}]\) is the rate constant for the reaction. The left-hand side of Eq. (1) follows from the transport equation for a component moving with a fluid (Holzbecher 1998). Dispersion and its effects on the flow and mass transport are fully omitted. However, under high-density differences and high dispersivity, Jamshidzadeh et al. (2013) demonstrated that the dispersive fluid flux considered in the non-reactive saline Elder problem could noticeably influence the shape and number of developed plumes. The strongly nonlinear reaction term on the right side is incorporated to capture collision between the solute and mineral molecule, which leads to the chemical reaction related to consuming the solute and minerals. Since we assume that the surface area for the mineral dissolution is proportional to the volume of the dissoluble minerals (Hinch and Bhatt 1990), the nonlinear term is proportional to the product of the concentrations of the solute and the minerals according to Guldberg and Waage’s law (Davis and Davis 2003).

From the mass conservation law for the dissoluble minerals in the solid phase, we have

$$\begin{aligned} (1- \phi )\frac{\partial m^{*}}{\partial t^{*}} = - k^{*}c^{*}m^{*}. \end{aligned}$$
(2)

The conservation equation for the reaction products in the liquid phase is given by

$$\begin{aligned} \phi \frac{\partial n^{*}}{\partial t^{*}} + {\varvec{\nabla }^{*} \varvec{\cdot } ({\varvec{u}}^{*}n^{*})} - \varvec{\nabla }^{*}\varvec{\cdot }(\phi D_{n}^{*}\varvec{\nabla }^{*}n^{*}) = k^{*}c^{*}m^{*}, \end{aligned}$$
(3)

where \(D_{n}^{*}\) \([\textrm{m}^{2} \, \textrm{s}^{-1}]\) is the molecular diffusion coefficient for the products in the liquid phase. Note that we do not take into account any effects of different types of intermediates that commonly appear in reaction networks (Davis and Davis 2003).

Darcy’s law for porous media flow can be expressed as follows:

$$\begin{aligned} {\varvec{u}}^{*} = -\frac{\kappa ^{*}}{\mu ^{*}}[ \varvec{\nabla }^{*}p^{*} - (\rho ^{*}-\rho _{0}^{*}){\varvec{g}}^{*}], \end{aligned}$$
(4)

where \(\kappa ^{*}\) \([\textrm{m}^{2}]\) is the intrinsic permeability, \(\mu ^{*}\) \([\textrm{kg} \, \textrm{m}^{-1} \, \textrm{s}^{-1}]\) is the dynamic viscosity, \({\varvec{g}}^{*} = (0,-g^{*})^{T}\) is the gravitational field and \(g^{*}\) \([\textrm{m} \, \textrm{s}^{-2}]\) is the gravitational acceleration. The fluid density \(\rho ^{*}\) \([\textrm{kg} \, \textrm{m}^{-3}]\) is taken to vary with the concentrations of solute and products, \(\rho ^{*} = \rho ^{*}(c^{*},n^{*})\), which provides a two-way coupling between the mass transport Eqs. (1), (3) and Darcy’s Eq. (4). The linear approximation of the state equation for the density \(\rho ^{*}\) is

$$\begin{aligned} \rho ^{*}(c^{*},n^{*}) = \rho _{0}^{*}[1+\beta _{c}^{*}(c^{*} - c_{0}^{*}) + \beta _{n}^{*}(n^{*} - n_{0}^{*})], \end{aligned}$$

where \(\beta _{c}^{*}\) and \(\beta _{n}^{*}\) \([\textrm{m}^{3} \, \textrm{mol}^{-1}]\) are the concentration expansion coefficients for the solute and the products, respectively, and \(\rho _{0}^{*} \equiv \rho ^{*}(c_{0}^{*},n_{0}^{*})\) is the reference liquid-phase density at the reference concentrations of the solute and products.

Conservation of fluid mass requires

$$\begin{aligned} \varvec{\nabla }^{*} \varvec{\cdot } {\varvec{u}}^{*} = 0. \end{aligned}$$
(5)

In deriving (1)–(5), we have applied the Oberbeck–Boussinesq approximation, which amounts to taking the liquid density as constant everywhere in the equations except for the buoyancy term. The validity of the Oberbeck–Boussinesq approximation in the non-reactive case was discussed by Johannsen (2003).

2.1 Non-dimensionalisation and Streamfunction Formulation

In order to transform Eqs. (1) –(5) to the dimensionless form, we rescale the dimensional spatial and temporal variables as

$$\begin{aligned}{} & {} \varvec{x} = \frac{\varvec{x}^{*}}{H^{*}}, \end{aligned}$$
(6a)
$$\begin{aligned}{} & {} t = \frac{t^{*}}{(H^{*})^2/D_{c}^{*}}, \end{aligned}$$
(6b)

the dimensional concentration fields as

$$\begin{aligned}{} & {} c = \frac{c^{*}}{ \Delta c^{*}}, \end{aligned}$$
(6c)
$$\begin{aligned}{} & {} m = \frac{m^{*}}{ m{_{0}}^{*}}, \end{aligned}$$
(6d)
$$\begin{aligned}{} & {} n = \frac{n^{*}}{ \Delta n^{*}}, \end{aligned}$$
(6e)

and the dimensional velocity and pressure as

$$\begin{aligned}{} & {} \varvec{u} = \frac{\varvec{u}^{*}}{\phi D_{c}^{*}/H^{*}}, \end{aligned}$$
(6f)
$$\begin{aligned}{} & {} p = \frac{p^{*}}{\mu ^{*}\phi D_{c}^{*}/\kappa ^{*}}, \end{aligned}$$
(6g)

where \(\Delta c^{*} = c_{1}^{*} - c_{0}^{*}\), \(m_{0}^{*}\) is the uniform concentration of the minerals in the solid and \(\Delta n^{*} = n_{1}^{*} - n_{0}^{*}\), where \(n_{1}^{*}\) is the reference concentration of the products such that \(n_{0}^{*} < n_{1}^{*}\). We then obtain a system of dimensionless equations in the form

$$\begin{aligned}{} & {} \frac{\partial c}{\partial t} + {\varvec{\nabla \cdot }(\varvec{u} c)} - \nabla ^{2}c = - \text {Da} \, cm, \end{aligned}$$
(7a)
$$\begin{aligned}{} & {} \frac{\partial m}{\partial t} = -\alpha ^{}_{m} \text {Da} \, cm, \end{aligned}$$
(7b)
$$\begin{aligned}{} & {} \frac{\partial n}{\partial t} + {\varvec{\nabla \cdot }(\varvec{u} n)} - \frac{1}{\delta } \nabla ^{2}n = \alpha ^{}_{n} \text {Da} \, cm, \end{aligned}$$
(7c)
$$\begin{aligned}{} & {} \varvec{u} = - \varvec{\nabla }p_{R} - (\text {Ra}_{c} \, c + \text {Ra}_{n} \, n)\hat{\varvec{z}}, \end{aligned}$$
(7d)
$$\begin{aligned}{} & {} \varvec{\nabla \cdot u} = 0, \end{aligned}$$
(7e)

where \(\alpha ^{}_{m} = \phi \Delta c^{*}/[(1-\phi ) m{_{0}}^{*}]\) and \(\alpha ^{}_{n} = \Delta c^{*}/ \Delta n^{*}\) are concentration ratios of the solute in the liquid to the minerals in the solid and to the products in the liquid, respectively; the Damköhler number, measuring the solute reaction rate relative to the solute diffusion rate, is defined as

$$\begin{aligned} \text {Da} = \frac{k^{*} m{_{0}}^{*}(H^{*})^2}{\phi D_{c}^{*}}; \end{aligned}$$

\(\delta = D_{c}^{*}/D_{n}^{*}\) is a molecular diffusion ratio of the solute to the products; \(p_{R} = p - ( \text {Ra}_{c}c_{0}^{*}/ \Delta c^{*} + \text {Ra}_{n}n_{0}^{*}/ \Delta n^{*})\,z\) is the reduced pressure; the concentration Rayleigh numbers for the solute and the products, respectively, are

$$\begin{aligned} \text {Ra}_{c} = \frac{\kappa ^{*} \rho _{0}^{*} \beta _{c}^{*} \Delta c^{*} H^{*} g^{*}}{\mu ^{*}\phi D_{c}^{*}}, \\ \text {Ra}_{n} = \frac{\kappa ^{*} \rho _{0}^{*} \beta _{n}^{*} \Delta n^{*} H^{*} g^{*}}{\mu ^{*}\phi D_{c}^{*}}, \end{aligned}$$

and \(\hat{{\varvec{z}}}\) is the upward unit vector.

To describe the flow field, for which the continuity Eq. (7e) holds, a streamfunction \(\psi = \psi ({\varvec{x}},t)\) with \({\varvec{u}} = [-\partial \psi /\partial z, \partial \psi /\partial x]^{T}\) can be used in place of the velocity variable \({\varvec{u}}\) (Holzbecher 1998). Introducing \(\psi\), we can rewrite the governing equations as

$$\begin{aligned}{} & {} \frac{\partial c}{\partial t} - \frac{\partial \psi }{\partial z}\frac{\partial c}{\partial x} + \frac{\partial \psi }{\partial x}\frac{\partial c}{\partial z} - \frac{\partial ^2 c}{\partial x^2} - \frac{\partial ^2 c}{\partial z^2} = - \text {Da} \, cm, \end{aligned}$$
(8a)
$$\begin{aligned}{} & {} \frac{\partial m}{\partial t} = - \alpha ^{}_{m} \text {Da} \, cm, \end{aligned}$$
(8b)
$$\begin{aligned} \frac{\partial n}{\partial t} - \frac{\partial \psi }{\partial z}\frac{\partial n}{\partial x} + \frac{\partial \psi }{\partial x}\frac{\partial n}{\partial z} - \frac{1}{\delta }\left( \frac{\partial ^2 n}{\partial x^2} + \frac{\partial ^2 n}{\partial z^2}\right) \end{aligned}\begin{aligned}{} {} = \alpha ^{}_{n} \text {Da} \, cm, \end{aligned}$$
(8c)
$$\begin{aligned}{} & {} \frac{\partial ^2 \psi }{\partial x^2} + \frac{\partial ^2 \psi }{\partial z^2} = - \text {Ra}_{c}\frac{\partial c}{\partial x} - \text {Ra}_{n}\frac{\partial n}{\partial x} \end{aligned}$$
(8d)

with boundary conditions

$$\begin{aligned}{} & {} c(x,0,t) = c_{0}, \end{aligned}$$
(9a)
$$\begin{aligned}{} & {} c(x,1,t) = {\left\{ \begin{array}{ll} c_{1}, &{} \vert x \vert \le 1,\\ c_{0}, &{} \vert x \vert > 1,\\ \end{array}\right. } \end{aligned}$$
(9b)
$$\begin{aligned}{} & {} \frac{\partial c}{\partial x}\bigg \vert _{x = -2} = 0, \end{aligned}$$
(9c)
$$\begin{aligned}{} & {} \frac{\partial c}{\partial x}\bigg \vert _{x = 2} = 0, \end{aligned}$$
(9d)
$$\begin{aligned}{} & {} n(x,0,t) = n_{0}, \end{aligned}$$
(9e)
$$\begin{aligned}{} & {} n(x,1,t) = n_{0}, \end{aligned}$$
(9f)
$$\begin{aligned}{} & {} \frac{\partial n}{\partial x}\bigg \vert _{x = -2} = 0, \end{aligned}$$
(9g)
$$\begin{aligned}{} & {} \frac{\partial n}{\partial x}\bigg \vert _{x = 2} = 0, \end{aligned}$$
(9h)
$$\begin{aligned}{} & {} \psi (x,0,t) = 0, \end{aligned}$$
(9i)
$$\begin{aligned}{} & {} \psi (x,1,t) = 0, \end{aligned}$$
(9j)
$$\begin{aligned}{} & {} \psi (-2,z,t) = 0, \end{aligned}$$
(9k)
$$\begin{aligned}{} & {} \psi (2,z,t) = 0, \end{aligned}$$
(9l)

for \(x \in [-2,2]\), \(z \in [0, 1]\) and \(t > 0\), where \(c_{0} = c_{0}^{*}/ \Delta c^{*}\), \(c_{1} = 1+c_{0}\) and \(n_{0} = n_{0}^{*}/ \Delta n^{*}\) (see Fig. 1b). In this work, we set \(c_{0} = 0\), \(c_{1} = 1\) and \(n_{0} = 0\), which corresponds to zero reference concentrations of the solute and products.

The initial conditions for c, n and \(\psi\) are taken to be zero throughout the entire domain, unless stated otherwise. The initial condition for m is identically equal to unity. Note that the zero initial concentrations of the solute and products, ensuring an ideal initial situation for mass transport in the system, can be commonly fulfilled in a laboratory experiment but seldom in a field site.

3 Numerical Method

Because of the symmetry of the governing Eqs. (8) and the boundary conditions (9), we consider only the right half of the model region, i.e. \(0 \le x \le 2\) and \(0 \le z \le 1\), with corresponding boundary conditions

$$\begin{aligned}{} & {} c(x,0,t) = 0, \end{aligned}$$
(10a)
$$c(x,1,t) = \left\{ {\begin{array}{*{20}l} {1,} \hfill & {0 \le x \le 1,} \hfill \\ {0,} \hfill & {1 < x \le 2,} \hfill \\ \end{array} } \right.$$
(10b)
$$\begin{aligned}{} & {} \frac{\partial c}{\partial x}\bigg \vert _{x = 0} = 0, \end{aligned}$$
(10c)
$$\begin{aligned}{} & {} \frac{\partial c}{\partial x}\bigg \vert _{x = 2} = 0, \end{aligned}$$
(10d)
$$\begin{aligned}{} & {} n(x,0,t) = 0, \end{aligned}$$
(10e)
$$\begin{aligned}{} & {} n(x,1,t) = 0, \end{aligned}$$
(10f)
$$\begin{aligned}{} & {} \frac{\partial n}{\partial x}\bigg \vert _{x = 0} = 0, \end{aligned}$$
(10g)
$$\begin{aligned}{} & {} \frac{\partial n}{\partial x}\bigg \vert _{x = 2} = 0, \end{aligned}$$
(10h)
$$\begin{aligned}{} & {} \psi (x,0,t) = 0, \end{aligned}$$
(10i)
$$\begin{aligned}{} & {} \psi (x,1,t) = 0, \end{aligned}$$
(10j)
$$\begin{aligned}{} & {} \psi (0,z,t) = 0, \end{aligned}$$
(10k)
$$\begin{aligned}{} & {} \psi (2,z,t) = 0. \end{aligned}$$
(10l)

3.1 Pseudospectral Discretization

For spatial discretization, we use a pseudospectral method based on sine and cosine series expansions in the horizontal direction and a Chebyshev expansion in the vertical direction. Expansions for c, m, n and \(\psi\) in the x direction are

$$\begin{aligned}{} & {} c(x,z,t) = \sum _{k=0}^{K} {\hat{c}}_{k}(z,t) \cos (g_{k}x), \end{aligned}$$
(11a)
$$\begin{aligned}{} & {} m(x,z,t) = \sum _{k=0}^{K} {\hat{m}}_{k}(z,t) \cos (g_{k}x), \end{aligned}$$
(11b)
$$\begin{aligned}{} & {} n(x,z,t) = \sum _{k=0}^{K} {\hat{n}}_{k}(z,t) \cos (g_{k}x), \end{aligned}$$
(11c)
$$\begin{aligned}{} & {} \psi (x,z,t) = \sum _{k=1}^{K} {\hat{\psi }}_{k}(z,t) \sin (g_{k}x), \end{aligned}$$
(11d)

where \(g_{k} = k\pi /2\) is a wave number of a horizontal mode k. The sine and cosine basis functions for c, n and \(\psi\) are chosen such that the expansions for c, n and \(\psi\) satisfy the horizontal boundary conditions (10c, d), (10g, h) and (10k, l), respectively. For m, we choose the cosine basis functions, so that each of Eqs. (8a–c) has a definite parity and a problem of parity mixing is avoided (Vasil et al. 2008).

Using a set of new nonlinear variables, the governing Eqs. (8a–c) can be rearranged as follows:

$$\begin{aligned}{} & {} \frac{\partial c}{\partial t} + \frac{\partial uc}{\partial x} + \frac{\partial wc}{\partial z} - \frac{\partial ^{2} c}{\partial x^{2}} - \frac{\partial ^{2} c}{\partial z^{2}} = - \text {Da} \, r, \end{aligned}$$
(12a)
$$\begin{aligned}{} & {} \frac{\partial m}{\partial t} = - \alpha _{m} \text {Da} \, r, \end{aligned}$$
(12b)
$$\begin{aligned}{} & {} \frac{\partial n}{\partial t} + \frac{\partial un}{\partial x} + \frac{\partial wn}{\partial z} - \frac{1}{\delta } \left( \frac{\partial ^{2} n}{\partial x^{2}} + \frac{\partial ^{2} n}{\partial z^{2}}\right) = \alpha _{n} \text {Da} \, r, \end{aligned} \qquad $$
(12c)

where

$$uc(x,z,t) = - \frac{\partial \psi }{\partial z}c, $$
(13a)
$$\begin{aligned}{} & {} wc(x,z,t) = \frac{\partial \psi }{\partial x}c \end{aligned}$$
(13b)

represent the local fluxes of the solute in the horizontal and vertical directions, respectively;

$$\begin{aligned}{} & {} un(x,z,t) = - \frac{\partial \psi }{\partial z}n, \end{aligned}$$
(14a)
$$\begin{aligned}{} & {} wn(x,z,t) = \frac{\partial \psi }{\partial x}n \end{aligned}$$
(14b)

represent the local fluxes of the products in the horizontal and vertical directions, respectively, and

$$\begin{aligned} r(x,z,t) = cm \end{aligned}$$
(15)

is the second-order reaction rate. It follows from (13), (14) and (15) that uc and un are odd in the x direction, and wc, wn and r are even. As a result, we expand these variables in the form

$$\begin{aligned}{} & {} uc(x,z,t) = \sum _{k=1}^{K} {\widehat{uc}}_{k}(z,t) \sin (g_{k}x), \end{aligned}$$
(16a)
$$\begin{aligned}{} & {} wc(x,z,t) = \sum _{k=0}^{K} {\widehat{wc}}_{k}(z,t) \cos (g_{k}x), \end{aligned}$$
(16b)
$$\begin{aligned}{} & {} un(x,z,t) = \sum _{k=1}^{K} {\widehat{un}}_{k}(z,t) \sin (g_{k}x), \end{aligned}$$
(16c)
$$\begin{aligned}{} & {} wn(x,z,t) = \sum _{k=0}^{K} {\widehat{wn}}_{k}(z,t) \cos (g_{k}x), \end{aligned}$$
(16d)
$$\begin{aligned}{} & {} r(x,z,t) = \sum _{k=0}^{K} {\widehat{r}}_{k}(z,t) \cos (g_{k}x). \end{aligned}$$
(16e)

The sine and cosine series can be constructed using discrete sine and cosine transforms. For example, the coefficients \({\hat{c}}_{k}\) and \({\hat{\psi }}_{k}\) can be numerically calculated using the type-II discrete cosine transform (DCT-II) and the type-II discrete sine transform (DST-II), respectively:

$$\begin{aligned}{} & {} {\hat{c}}_{k}(z,t) = \text {DCT-II}\{ c(x_{k},z,t) \}, \end{aligned}$$
(17a)
$$\begin{aligned}{} & {} {\hat{\psi }}_{k}(z,t) = \text {DST-II}\{ \psi (x_{k},z,t) \}, \end{aligned}$$
(17b)

where

$$\begin{aligned} x_{k} = \frac{2k}{K}, \qquad k = 0, 1, \ldots , K, \end{aligned}$$

are equally spaced collocation points on the interval [0, 2].

Further, we expand these coefficients in the z direction using Chebyshev polynomials (Boyd 2001). For example, Chebyshev expansions for \({\hat{c}}_{k}\) are defined as

$$\begin{aligned} {\hat{c}}_{k}(z,t) = \sum _{l=0}^{L} {\tilde{c}}_{k,l}(t)\, T_{l}(\zeta (z)) \end{aligned}$$
(18)

for each k, where \(T_{l}\) is the l-th Chebyshev polynomial on \([-1,1]\) and \(\zeta (z) = 2z-1\). The other coefficients \({\hat{m}}_{k}\), \({\hat{n}}_{k}\), \({\hat{\psi }}_{k}\), \({\widehat{uc}}_{k}\), \({\widehat{wc}}_{k}\), \({\widehat{un}}_{k}\), \({\widehat{wn}}_{k}\) and \({\hat{r}}_{k}\) can be expanded similarly. The Chebyshev coefficients \({\tilde{c}}_{k,l}\) can then be calculated using DCT-II:

$$\begin{aligned} {\tilde{c}}_{k,l}(t) = \text {DCT-II}\{ {\hat{c}}_{k}(z_{l},t) \} \end{aligned}$$
(19)

for each k, where

$$\begin{aligned} z_{l} = \frac{ \cos (l\pi /L) + 1}{2}, \qquad l = 0, 1, \ldots , L, \end{aligned}$$

are Chebyshev points transformed onto the interval [0, 1]. The application of the Chebyshev points, which cluster near the ends of the interval, can result in a better approximation of the concentration field c, which is affected by relatively large gradients in the vertical direction near the boundaries of the domain.

We also need to expand partial derivatives of the coefficients \({\hat{c}}_{k}\), \({\hat{n}}_{k}\), \({\hat{\psi }}_{k}\), \({\widehat{wc}}_{k}\) and \({\widehat{wn}}_{k}\) in the z direction. For example, Chebyshev expansions for \(\partial ^{2} {\hat{c}}_{k}/ \partial z^{2}\) are given by

$$\begin{aligned} \frac{\partial ^{2} {\hat{c}}_{k}}{\partial z^{2}} = \sum _{l=0}^{L} {\bar{c}}_{k,l}(t)\, T_{l}(\zeta (z)) \end{aligned}$$
(20)

for each k. Then the Chebyshev coefficients \({\bar{c}}_{k,l}\) can be expressed as a linear combination of the coefficients \({\tilde{c}}_{k,l}\):

$$\begin{aligned} \bar{{\varvec{c}}}_{k} = {\varvec{D}}_{zz} \tilde{{\varvec{c}}}_{k}, \end{aligned}$$
(21)

where \(\tilde{{\varvec{c}}}_{k} = ({\tilde{c}}_{k,0}, \ldots , {\tilde{c}}_{k,L})^{T}\) and \(\bar{{\varvec{c}}}_{k} = ({\bar{c}}_{k,0}, \ldots , {\bar{c}}_{k,L})^{T}\) are \((L+1) \times 1\) vectors of coefficients and \({\varvec{D}}_{zz}\) is a \((L+1)\times (L+1)\) second-order differentiation matrix. The matrix \({\varvec{D}}_{zz}\) can be constructed using relations \({\varvec{D}}_{zz} = {\varvec{D}}_{z}^{2}\) and \({\varvec{D}}_{z} = 2 {\varvec{D}}_{\zeta }\), where

$$\begin{aligned} {\varvec{D}}_{\zeta } = \begin{pmatrix} 0 &{} 1 &{} 0 &{} 3 &{} 0 &{} 5 &{} \cdots &{} L\\ 0 &{} 0 &{} 4 &{} 0 &{} 8 &{} 0 &{} \cdots &{} 0\\ \vdots &{} &{} \ddots &{} 6 &{} 0 &{} 10 &{} \cdots &{} 2L\\ \vdots &{} &{} &{} \ddots &{} \ddots &{} \ddots &{} \ddots &{} \\ \vdots &{} &{} &{} &{} \ddots &{} \ddots &{} \ddots &{} 2L\\ \vdots &{} &{} &{} &{} &{} \ddots &{} \ddots &{} 0\\ \vdots &{} &{} &{} &{} &{} &{} \ddots &{} 2L\\ 0 &{} \cdots &{} \cdots &{} \cdots &{} \cdots &{} \cdots &{} \cdots &{} 0 \end{pmatrix} \end{aligned}$$
(22)

is the \((L+1)\times (L+1)\) upper triangular differentiation matrix (Johnson 1996).


Using orthogonal properties of the basis functions, we obtain a system of ordinary differential equations for the time-dependent coefficients in the form

$$\begin{aligned} \frac{\textrm{d}\tilde{{\varvec{c}}}_{k}}{\textrm{d}t} + g_{k}\widetilde{\varvec{uc}}_{k} + {\varvec{D}}_{z}\widetilde{\varvec{wc}}_{k} - \left( {\varvec{D}}_{zz} - g_{k}^{2}{\varvec{I}}\right) \tilde{{\varvec{c}}}_{k} = - \text {Da} \, \tilde{{\varvec{r}}}_{k}, \end{aligned}$$
$$\begin{aligned}{} & {} k = 0, 1, \ldots , K, \end{aligned}$$
(23a)
$$\begin{aligned}{} & {} \frac{\textrm{d}\tilde{{\varvec{m}}}_{k}}{\textrm{d}t} = - \alpha _{m} \text {Da} \, \tilde{{\varvec{r}}}_{k}, \qquad k = 0, 1, \ldots , K, \end{aligned}$$
(23b)
$$\begin{aligned} \frac{\textrm{d}\tilde{{\varvec{n}}}_{k}}{\textrm{d}t} + g_{k}\widetilde{\varvec{un}}_{k} + {\varvec{D}}_{z}\widetilde{\varvec{wn}}_{k} - \frac{1}{\delta } \left( {\varvec{D}}_{zz} - g_{k}^{2}{\varvec{I}}\right) \tilde{{\varvec{n}}}_{k} \end{aligned}$$
$$\begin{aligned} = \alpha _{n} \text {Da} \, \tilde{{\varvec{r}}}_{k}, \qquad k = 0, 1, \ldots , K, \end{aligned}$$
(23c)
$$\begin{aligned} \left( {\varvec{D}}_{zz} - g_{k}^{2}{\varvec{I}}\right) \tilde{\varvec{\psi }}_{k} = \text {Ra}_{c} \, g_{k}\tilde{{\varvec{c}}}_{k} + \text {Ra}_{n} \, g_{k}\tilde{{\varvec{n}}}_{k}, \end{aligned}$$
$$\begin{aligned} k = 1, 2, \ldots , K, \end{aligned}$$
(23d)

where \(\tilde{{\varvec{m}}}_{k} = ({\tilde{m}}_{k,0}, \ldots , {\tilde{m}}_{k,L})^{T}\), \(\tilde{{\varvec{n}}}_{k} = ({\tilde{n}}_{k,0}, \ldots , {\tilde{n}}_{k,L})^{T}\), \(\tilde{\varvec{\psi }}_{k} = ({\tilde{\psi }}_{k,0}, \ldots , {\tilde{\psi }}_{k,L})^{T}\), \(\widetilde{\varvec{uc}}_{k} = ({\widetilde{uc}}_{k,0}, \ldots , {\widetilde{uc}}_{k,L})^{T}\), \(\widetilde{\varvec{wc}}_{k} = ({\widetilde{wc}}_{k,0},\ldots, {\widetilde{wc}}_{k,L})^{T}\), \(\% This \,expression \,has \,been \,merged \,to \,the \,expression\, from \,the \,previous \,equation \,environment.\) \(\widetilde{\varvec{un}}_{k} = ({\widetilde{un}}_{k,0}, \ldots , {\widetilde{un}}_{k,L})^{T}\), \(\widetilde{\varvec{wn}}_{k} = ({\widetilde{wn}}_{k,0}, \ldots , {\widetilde{wn}}_{k,L})^{T}\) and \(\tilde{{\varvec{r}}}_{k} = ({\tilde{r}}_{k,0}, \ldots , {\tilde{r}}_{k,L})^{T}\) are \((L+1) \times 1\) vectors of coefficients, and \({\varvec{I}}\) is the \((L+1)\times (L+1)\) identity matrix. It should be noted that the unknown coefficients \({\tilde{c}}_{k,l}\), \({\tilde{m}}_{k,l}\), \({\tilde{n}}_{k,l}\), \({\tilde{\psi }}_{k,l}\), \({\widetilde{uc}}_{k,l}\), \({\widetilde{wc}}_{k,l}\), \({\widetilde{un}}_{k,l}\), \({\widetilde{wn}}_{k,l}\) and \({\tilde{r}}_{k,l}\) are coupled with each other in the vertical direction whereas in the horizontal direction they can be calculated for each mode k independently.

3.2 Time-Stepping

The dynamical system (23), consisting of nonlinear equations for \(\tilde{{\varvec{c}}}_{k}\), \(\tilde{{\varvec{m}}}_{k}\) and \(\tilde{{\varvec{n}}}_{k}\), and of linear equations for \(\tilde{\varvec{\psi }}_{k}\), can be solved numerically by applying a one-step implicit–explicit Runge–Kutta method. To achieve appropriate convergence behaviour, explicit discretization is used for advection terms and implicit discretization for diffusion terms (Ascher et al. 1997). So, we have

$$\begin{aligned} \widetilde{\user2{c}}_{k}^{{(i + 1)}} =& ~ \widetilde{\user2{c}}_{k}^{{(i)}} + h\Big[ - g_{k} \widetilde{{\user2{uc}}}_{k}^{{(i)}} - \user2{D}_{z} \widetilde{{\user2{wc}}}_{k}^{{(i)}} \\ & + \left( {\user2{D}_{{{zz}}} - g_{k}^{2} \user2{I}} \right)\widetilde{\user2{c}}_{k}^{{(i + 1)}} - {\text{Da}}{\mkern 1mu} \widetilde{\user2{r}}_{k}^{{(i)}}\Big], \nonumber\\ \end{aligned}$$
$$\begin{aligned}{} & {} k = 0, 1, \ldots , K, \end{aligned}$$
(24a)
$$\begin{aligned}{} & {} \tilde{{\varvec{m}}}_{k}^{(i+1)} = \tilde{{\varvec{m}}}_{k}^{(i)} - h \, \alpha _{m} \text {Da} \, \tilde{{\varvec{r}}}_{k}^{(i)}, \quad k = 0, 1, \ldots , K, \end{aligned}$$
(24b)
$$\begin{aligned} \widetilde{\user2{n}}_{k}^{{(i + 1)}} =~ & \widetilde{\user2{n}}_{k}^{{(i)}} + h\Big[ - g_{k} \widetilde{{\user2{un}}}_{k}^{{(i)}} - \user2{D}_{z} \widetilde{{\user2{wn}}}_{k}^{{(i)}} \\ & + \frac{1}{\delta }\left( {\user2{D}_{{{zz}}} - g_{k}^{2} \user2{I}} \right)\widetilde{\user2{n}}_{k}^{{(i + 1)}} + \alpha _{n} {\text{Da}}{\mkern 1mu} \widetilde{\user2{r}}_{k}^{{(i)}} \Big], \\ \end{aligned}$$
$$\begin{aligned} k = 0, 1, \ldots , K, \end{aligned}$$
(24c)
$$\begin{aligned} \left( {\varvec{D}}_{zz} - g_{k}^{2}{\varvec{I}}\right) \tilde{\varvec{\psi }}_{k}^{(i)} = \text {Ra}_{c} \, g_{k}\tilde{{\varvec{c}}}_{k}^{(i)} + \text {Ra}_{n} \, g_{k}\tilde{{\varvec{n}}}_{k}^{(i)}, \end{aligned}$$
$$\begin{aligned} k = 1, 2, \ldots , K, \end{aligned}$$
(24d)

with initial values \(\tilde{{\varvec{c}}}_{k}^{(0)}\), \(\tilde{{\varvec{m}}}_{k}^{(0)}\) and \(\tilde{{\varvec{n}}}_{k}^{(0)}\), where h is the time step and \(t_{i} = ih\) is the time discretization for \(i = 0, 1, \ldots , I\).

The boundary conditions in the z direction are imposed by incorporating them into the last two rows of differential operators, since the last two rows of \({\varvec{D}}_{zz}\) contain only zeros. Note that Eqs. (24a, c) give solutions for \(\tilde{{\varvec{c}}}_{k}^{(i+1)}\) and \(\tilde{{\varvec{n}}}_{k}^{(i+1)}\) at time \(t_{i+1}>0\), which are subsequently used for computing a solution for \(\tilde{\varvec{\psi }}_{k}^{(i+1)}\) in (24d). At each time step, the coefficients \({\widetilde{uc}}_{k,l}\), \({\widetilde{wc}}_{k,l}\), \({\widetilde{un}}_{k,l}\), \({\widetilde{wc}}_{k,l}\) and \({\tilde{r}}_{k,l}\) are recalculated using the discrete sine and cosine transforms and their inverse analogues.

We perform all numerical computations implementing the above approach in Dedalus (Burns et al. 2020). To ensure pointwise convergence of the pseudospectral method, the discontinuity in the step-wise boundary condition (10b) is avoided by approximating c with a smooth function in the form

$$\begin{aligned} {f(x) = \frac{1}{2} \left[ 1 - \text {tanh}{\left( \frac{x-1}{d}\right) } \right] , \qquad x \in [0,2],} \end{aligned}$$

where d is a transition length (van Reeuwijk et al. 2009). As \(d \rightarrow 0\), f(x) tends to the original boundary condition. In this study, we set a value for d to 0.005, which has been shown to be sufficiently small to capture the main characteristics of the classical Elder problem. Although this value of d is too low to achieve pointwise convergence very close to the upper boundary at \(x = \pm 1\), the solution converges globally (see van Reeuwijk et al. (2009) for further details). Verification of the numerical code has been done for a non-reactive, purely diffusive case (\(\text {Da} = 0\), \(\text {Ra}_{c} = 0\) and \(\text {Ra}_{n} = 0\)) that can be solved analytically (van Reeuwijk et al. 2009). The agreement between the analytical and pseudospectral steady-state solution on the grid with \(256\times 64\) collocation points for \(h = 10^{-4}\) has been achieved at the level of \(O(10^{-5})\).

4 Results and Discussion

4.1 Weakly Reactive Case without Buoyancy-Driven Convection (\(\text {Ra}_{c} = 0\) and \(\text {Ra}_{n} = 0\))

When the Rayleigh numbers \(\text {Ra}_c\) and \(\text {Ra}_n\) are set to zero, Eq. (8d) reduces to Laplace’s equation with a trivial solution for the streamfunction (no flow). The remaining quantities c, m and n satisfy

$$\begin{aligned}{} & {} \frac{\partial c}{\partial t} - \frac{\partial ^2 c}{\partial x^2} - \frac{\partial ^2 c}{\partial z^2} = - \text {Da} \, cm, \end{aligned}$$
(25a)
$$\begin{aligned}{} & {} \frac{\partial m}{\partial t} = - \alpha ^{}_{m} \text {Da} \, cm, \end{aligned}$$
(25b)
$$\begin{aligned}{} & {} \frac{\partial n}{\partial t} - \frac{1}{\delta }\left( \frac{\partial ^2 n}{\partial x^2} + \frac{\partial ^2 n}{\partial z^2}\right) = \alpha _{n} \text {Da} \, cm \end{aligned}$$
(25c)

subject to (10a–h). Note the one-way coupling of c and m to n in Eq. (25c).

We will seek solution to this nonlinear reactive system in the limit of small \(\text {Da}\) and expand the concentration quantities as

$$\begin{aligned}{} & {} c = c^{0}(x,z,t) + \text {Da} \, c^{1}(x,z,t) + \ldots \end{aligned}$$
(26a)
$$\begin{aligned}{} & {} m = m^{0}(x,z) + \text {Da} \, m^{1}(x,z,t) + \ldots \end{aligned}$$
(26b)
$$\begin{aligned}{} & {} n = n^{0}(x,z,t) + \text {Da} \, n^{1}(x,z,t) + \ldots \end{aligned}$$
(26c)

Note that the leading-order solution \(m^0\) does not change with time, which can be clearly seen by setting \(\text {Da}=0\) in Eq. (25b). Moreover, expressing the series (26b) at \(t=0\) and using the fact that the initial value of m is independent of \(\text {Da}\), we have that \(m^0(x,z) \equiv 1\) and \(m^1(x,z,0) \equiv 0\).

Fig. 2
figure 2

Concentration fields \(c^{0}\), \(c^{1}\) and \(m^{1}\) at time \(t = 0.5\). Parameter values are \(\alpha _{m} = 1\) and \(N = 500\). Concentration contours are depicted by black solid lines

Full size image

Substituting the series (26) into Eqs. (25) and comparing coefficients of equal powers of \(\text {Da}\) at \(O(\text {Da}^{0})\) and \(O(\text {Da}^{1})\), we obtain a system of linear differential equations for \(c^{0}\), \(m^{0}\), \(n^{0}\) and \(c^{1}\), \(m^{1}\), \(n^{1}\). We then apply the Fourier transform in the x direction and the Laplace transform in the time domain and solve the resulting algebraic equations to yield

$$\begin{aligned} {\bar{c}}^{\,0}(x,z,s) = \frac{\textrm{sinh}{\left( \!\sqrt{s} z \right) }}{2s \, \textrm{sinh}{\left( \!\sqrt{s} \right) }} \end{aligned}\begin{aligned} + \sum _{k = 1}^{\infty } \frac{\textrm{sin}{(g_{k})} \, \textrm{sinh}{\left( \lambda _{k} z \right) } \, \textrm{cos}{(g_{k}x)}}{s g_{k} \, \textrm{sinh}{\left( \lambda _{k}\right) }}, \end{aligned}$$
(27a)
$$\begin{aligned} {\bar{c}}^{\,1}(x,z,s) = \frac{z \, \textrm{cosh}{\left( \!\sqrt{s}z\right) } - \textrm{sinh}{\left( \!\sqrt{s}z\right) } \, \textrm{coth}{\left( \!\sqrt{s}\right) }}{4 \sqrt{s^{3}} \, \textrm{sinh}{\left( \!\sqrt{s}\right) }} \\ + \sum _{k = 1}^{\infty } \frac{z \, \textrm{sin}{(g_{k})} \, \textrm{cosh}{\left( \lambda _{k} z \right) } \, \textrm{cos}{(g_{k}x)}}{2 s g_{k}\lambda _{k} \, \textrm{sinh}{\left( \lambda _{k}\right) }} \end{aligned}$$
$$\begin{aligned} - \sum _{k = 1}^{\infty } \frac{\textrm{sin}{(g_{k})} \, \textrm{sinh}{\left( \lambda _{k}z\right) } \, \textrm{coth}{\left( \lambda _{k}\right) } \, \textrm{cos}{(g_{k}x)}}{2 s g_{k}\lambda _{k} \, \textrm{sinh}{\left( \lambda _{k}\right) }} \end{aligned}$$
(27b)

and

$$\begin{aligned} {\bar{m}}^{1}(x,z,s) = -\frac{\alpha _{m} \, \textrm{sinh}{\left( \!\sqrt{s} z \right) }}{2s^{2} \, \textrm{sinh}{\left( \!\sqrt{s} \right) }} \end{aligned}\begin{aligned} - \sum _{k = 1}^{\infty } \frac{\alpha _{m} \, \textrm{sin}{(g_{k})} \, \textrm{sinh}{\left( \lambda _{k} z \right) } \, \textrm{cos}{(g_{k}x)}}{s^{2} g_{k} \, \textrm{sinh}{\left( \lambda _{k}\right) }}, \end{aligned}$$
(27c)

where \(g_{k} = k\pi /2\) and \(\lambda _{k}^{2} = g_{k}^{2} + s\). The function \({\bar{c}}^{\, 0}\)represents the Laplace transform of the function \(c^{0}\), i.e. \({\bar{c}}^{\,0}(x,z,s) = \int _{0}^{\infty }c^{0}(x,z,t)\textrm{e}^{-st}\, \textrm{d}t\). The other functions \({\bar{c}}^{\, 1}\) and \({\bar{m}}^{\, 1}\) are defined similarly.

Taking into account the first \(N + 1\) terms in the series (27), we numerically invert the Laplace transform using the Stehfest method (Johansson 2023). The concentration fields \(c^{0}\), \(c^{1}\) and \(m^{1}\) at time \(t = 0.5\) are shown in Fig.  2. The solution \(c^{0}\) corresponds to the non-reactive, purely diffusive case. The structure of \(c^1\) indicates that the largest decrease in the solute concentration as compared to the non-reactive case occurs near the point (0, 0.6), arising as a result of solute consumption caused by chemical interactions with the solid minerals. The solution \(m^{0}\) is equal to unity throughout the domain, corresponding to the non-reactive case with the prescribed initial concentration field m. The correction \(m^{1}\) is negative throughout and represents a decrease in the concentration of the minerals located mainly in the region where the concentration field c is highest. The solution \(n^{0}\) is equal to zero throughout the domain, which corresponds to the non-reactive case with no products generated in the porous medium. Although we do not present the general solution of \(n^{1}\) due to its complexity, we note from the form of Eqs. (25a,c) that \(n^{1}(x,z,t) = -c^{1}(x,z,t)\) for \(\alpha _{n} = 1\) and \(\delta = 1\). It implies that the decrease in the solute concentration of the weakly reactive case leads to an increase in the concentration field n of a comparable magnitude.

4.2 Reactive Case with Solute-Driven Convection (\(\text {Ra}_{c} = 400\) and \(\text {Ra}_{n} = 0\))

4.2.1 Solute Plume Development

For the non-reactive saline Elder problem, the onset of convection occurs at any positive \(\text {Ra}_{c}\) (van Reeuwijk et al. 2009). Based on the numerical bifurcation analysis with the appropriate selection of initial conditions (Johannsen 2003; van Reeuwijk et al. 2009), three distinct steady-state solutions have been identified in different ranges of \(\text {Ra}_{c}\). In particular, the solution featuring one plume exists for \(0 < \text {Ra}_{c} \le 400\), two plumes for \(76 \le \text {Ra}_{c} \le 400\) and three plumes for \(172 \le \text {Ra}_{c} \le 400\).

Fig. 3
figure 3

a, c, e Concentration fields c at time \(t = 0.5\) for parameters \(\alpha _{m} = 1\), \(\alpha _{n} = 1\), \(\delta = 1\), \(\text {Da} = 1\), \(\text {Ra}_{c} = 400\) and \(\text {Ra}_{n} = 0\), calculated with three different initial solute concentrations. b, d, f Comparison between the reactive and non-reactive solute concentration fields, respectively. The quantity \(c_{NR}\) represents the corresponding solute concentration for the non-reactive simulation with \(\text {Da} = 0\). Concentration contours of c are depicted by black solid lines in all figures

Full size image

Figure 3a, c and e show three qualitatively different solute concentration fields at \(t=0.5\) for \(\text {Da} = 1\), \(\text {Ra}_{c} = 400\) and \(\text {Ra}_{n} = 0\). Values of the other parameters are \(\alpha _{m} = 1\), \(\alpha _{n} = 1\) and \(\delta = 1\). Numerical simulations were carried out using the pseudospectral method with \(256 \times 64\) nodes for \(h = 10^{-4}\). The results differ by the number of vertical solute plumes that have developed as a result of convective solute transport. To obtain them, we used three different initial conditions for the solute concentration, as described in the bifurcation analyses of Johannsen (2003) and van Reeuwijk et al. (2009). As an initial condition for the solution featuring one plume (shown in Fig. 3a and denoted as \(R_1\)), we took the solution for \(\text {Da} = 0\), \(\text {Ra}_{c} = 60\) and \(\text {Ra}_{n} = 0\) featuring a single plume. The solution featuring two plumes (shown in Fig. 3c, denoted as \(R_{2}\)) was calculated using the zero initial condition, and the solution with three plumes (shown in Fig. 3e, denoted as \(R_{3}\)) using \(c(x, z, 0) = [\cos (\pi z) + 1 ] / 2\) over the entire domain.

Figure 3b, d and f show a concentration difference \(c - c_{NR}\), where \(c_{NR}\) corresponds to the non-reactive case, for all solutions \(R_1, R_2\) and \(R_3\), respectively. In all cases, most of the domains are coloured by blue shades, indicating less solute in these regions at \(t = 0.5\) relative to the non-reactive case. The average decrease for \(R_{1}\) is \(1.9\%\), for \(R_2\) is \(1.6\%\) and for \(R_3\) is \(1.3\%\). For solutions \(R_2\) and \(R_3\), there is a slight symmetrical displacement of the individual plumes compared to the non-reactive case: for \(R_{2}\), the roots of the plumes are closer to each other with the maximum absolute difference in the concentration of \(7.4\%\) (Fig. 3d); for \(R_3\), we can observe similar behaviour for the roots of the two outer plumes with the maximum absolute difference of \(7.9\%\) (Fig. 3f). In addition, the lower parts of the outer plumes near \(x = \pm 0.5\) are extended slightly towards the inner plume so that the inner plume is correspondingly narrower. As a result, there are regions with higher concentration (red shades) compared to the non-reactive case. The occurrence of these regions is due to advective mass transport present in the convective system. Note that no regions of increased c appear in Fig. 2b, because the weakly reactive case is purely diffusive and features no fluid flow.

One of the characteristics describing the system behaviour is the vertical solute flux at the top of the domain. Formally, this quantity is defined by

$$\begin{aligned} \text {Sh}_{c}(x, t) = \frac{\partial c}{\partial z} \bigg \vert _{z = 1} \end{aligned}$$
(28)

and is referred to as the local Sherwood number. The average value of \(\text{Sh}_{c}\) can be expressed as

$$\begin{aligned} {\overline{\text{Sh}}}_{c}(t) = \frac{1}{2} \int _{0}^{2} \text {Sh}_{c}(x, t) \, \textrm{d} x \end{aligned}$$
(29)

and is referred to as the average Sherwood number. Since the upper boundary is considered impermeable to the liquid, \({\overline{\text{Sh}}}_{c}\) measures the average diffusive solute flux across the upper boundary. In Prasad and Simmons (2003), in contrast, the Nusselt rather than Sherwood number is used to quantify the total (advective plus diffusive) solute transport rate relative to the diffusive solute transport rate since the imposed pressure boundary conditions at the top allow for solute advection across the boundary.

Fig. 4
figure 4

Temporal evolution of the average vertical diffusive solute flux \({\overline{\text{Sh}}}_{c}\) at the top of the domain for the non-reactive simulation with \(\text {Da} = 0\) (blue) and reactive simulations with \(\text {Da} = 0.1\) (black), 1 (red) and 10 (green). Values of the other parameters are \(\alpha _{m} = 1\), \(\alpha _{n} = 1\), \(\delta = 1\), \(\text {Ra}_{c} = 400\) and \(\text {Ra}_{n} = 0\). Phases of the flow development and solute transport in the considered medium are denoted by letters from A to E. Between points A and B, a boundary layer is formed through diffusion near the solute source at the top. From point B, the onset of instability is exhibited by the formation of vertical solute plumes, which touch the bottom first at point C. During the phase between C and D, the denser part of the generated plumes reaches the bottom. Finally, between D and E, mass transport in the system is dominated by diffusion

Full size image

Figure 4 compares temporal evolution of \({\overline{\text{Sh}}}_{c}\) in the time range from 0 to 0.2 for different \(\text {Da}\). The average vertical diffusive solute flux at the top for the non-reactive simulation coincides with the results by Prasad and Simmons (2003). They performed calculations up to dimensional time \(t^{*} = 20\) years, which approximately corresponds to dimensionless time \(t = 0.1\) for typical material transport properties. From Fig. 4, we can see that values of \({\overline{\text{Sh}}}_{c}\) begin to differ from the non-reactive case with increasing \(\text {Da}\). The curves for \(\text {Da} = 0\) and 0.1 virtually overlap, while those for \(\text {Da} = 1\) and 10 vary significantly from the others. The average flux of the solute for \(\text {Da} = 1\) decreases more slowly from point D compared to the non-reactive case. The values of \({\overline{\text{Sh}}}_{c}\) for \(\text{Da} = 10\) are larger in the phase A–B and C–E relative to those for the other values of \(\text {Da}\), and this difference becomes more pronounced behind point D. The explanation for this is the decrease in the solute concentration and increase in the solute transport rate from the source boundary into the domain interior as the chemical reaction rate increases. It occurs only in the diffusive regime D–E because advection is more effective in slowing down the reaction process than diffusion. In the long term, we might expect the concentration of the minerals to be zero throughout the entire domain since the minerals are gradually being dissolved. At the same time, the system tends towards the non-reactive state (the consumption of the reactive solute is being reduced), thereby effectively reaching a steady state. Therefore, all values of \({\overline{\text{Sh}}}_{c}\) shown in Fig. 4 are expected to tend to the value of 4 in the long term. This value approximately corresponds to the average diffusive solute flux at the top for the non-reactive steady state (\(\text {Da} = 0\), \(\text {Ra}_{c} = 400\) and \(\text {Ra}_{n} = 0\)) featuring two plumes, as reported by van Reeuwijk et al. (2009).

4.2.2 Redistribution of Reaction Products

Fig. 5
figure 5

a, b, c Concentration fields n at time \(t = 0.5\) for the solutions \(R_{1}\), \(R_{2}\) and \(R_{3}\), respectively. Parameter values are \(\alpha _{m} = 1\), \(\alpha _{n} = 1\), \(\delta = 1\), \(\text {Da} = 1\), \(\text {Ra}_{c} = 400\) and \(\text {Ra}_{n} = 0\). Streamlines of the velocity field \({\varvec{u}}\) are depicted by blue solid lines

Full size image
Fig. 6
figure 6

Vertical diffusive fluxes of the solute, \(\text{Sh}_{c}\) (a, c, e), and the products, \(\text{Sh}_{n}\) (b, d, f), at the top (black) and bottom (blue) of the domain at time \(t = 0.5\) for the solutions \(R_{1}\), \(R_{2}\) and \(R_{3}\), respectively. Parameter values are \(\alpha _{m} = 1\), \(\alpha _{n} = 1\), \(\delta = 1\), \(\text{Da} = 1\), \(\text{Ra}_{c} = 400\) and \(\text{Ra}_{n} = 0\)

Full size image

The choice of the initial condition for c affects not only the development of the solute concentration field but also the concentration field of the products. Since these products result from the chemical reaction between the solute and the minerals, we will assume that at \(t = 0\) they are absent in the liquid phase.

Besides the solutions \(R_{1}\), \(R_{2}\) and \(R_{3}\) discussed above, we also obtain the corresponding concentration fields for the products, which are shown together with the streamlines of the flow in Fig. 5. All three solutions for the products are affected by the number of the vertical solute plumes in the system. The concentrations of the products are rather low because the mass is absorbed at the upper and lower boundaries. For \(R_1\), the maximum concentration of the products is \(3.9\%\), for \(R_2\) is \(3.3\%\) and for \(R_3\) is just \(2.9\%\). The remaining portion of the products in the system is largely concentrated in the two outer convection eddies.

For a better understanding of the mass discharge in the system, in Fig. 6, we show the local vertical diffusive fluxes of the solute, \(\text {Sh}_{c}\), and the products, \(\text {Sh}_{n}\), at the top and bottom of the domain at \(t = 0.5\). The quantity \(\text {Sh}_{n}\) is defined analogously to \(\text {Sh}_{c}\). At the top, the products are absorbed most in the regions where \(\text {Sh}_{n}\) approaches the smallest (negative) values (Fig. 6b, d and f). In all cases, this occurs at the edges of the solute source near \(x = \pm 1\), and for \(R_2\) and \(R_3\) also in the regions between the roots of two adjacent solute plumes. In these regions, there is a higher supply of the solute from the source to the system, especially near \(x = \pm 1\) (Fig. 6a, c and e), where it is invoked by the discontinuous transition of c in the boundary condition. However, both local fluxes at the top, where the plume roots are located, are relatively small in magnitude. This local phenomenon can be explained by the presence of the convective circulation accompanied by vertical solute transport from the source boundary into the domain interior, as shown by the streamlines in Fig. 5. Thus, at the top along the source, the local diffusive flux of the products \(\text {Sh}_{n}\) is inverse to the local diffusive flux of the solute \(\text {Sh}_{c}\).

At the bottom, the solute and products are discharged in the regions below the individual solute plumes, where the downward flow from the top is strongest. Along the lower boundary towards the vertical edges of the domain and in the regions between two adjacent solute plumes, values of \(\text {Sh}_{c}\) and \(\text {Sh}_{n}\) tend to zero. The reason for this is the upward flow of fluid with a lower solute concentration from the bottom. To sum up, at the bottom, the local diffusive flux of the products \(\text {Sh}_{n}\) is proportional to the local diffusive flux of the solute \(\text {Sh}_{c}\). The same behaviour also holds for \(\text {Sh}_{n}\) at the upper boundary outside the solute source.

Fig. 7
figure 7

Temporal evolution of the average amount of the solute, \(\text {SP}_{c}\) (a), the minerals, \(\text {SP}_{m}\) (b), and the products, \(\text {SP}_{n}\) (c), for the non-reactive simulation with \(\text {Da} = 0\) (blue solid) and reactive simulations with \(\text {Da} = 0.1\) (orange dashed), 1 (green dash-dotted) and 10 (red dotted). Values of the other parameters are \(\alpha _{m} = 1\), \(\alpha _{n} = 1\), \(\delta = 1\), \(\text {Ra}_{c} = 400\) and \(\text {Ra}_{n} = 0\)

Full size image

Following Prasad and Simmons (2003) and Post and Prommer (2007), we define the additional indicator variables

$$\begin{aligned}{} & {} \text {SP}_{c}(t) = \frac{1}{2} \int _{0}^{2} \int _{0}^{1} c(x,z,t) \, \textrm{d}x \, \textrm{d}z, \end{aligned}$$
(30a)
$$\begin{aligned}{} & {} \text {SP}_{m}(t) = \frac{1}{2} \int _{0}^{2} \int _{0}^{1} m(x,z,t) \, \textrm{d}x \, \textrm{d}z, \end{aligned}$$
(30b)
$$\begin{aligned}{} & {} \text {SP}_{n}(t) = \frac{1}{2} \int _{0}^{2} \int _{0}^{1} n(x,z,t) \, \textrm{d}x \, \textrm{d}z. \end{aligned}$$
(30c)

The quantity \(\text {SP}_{c}\) measures the average amount of the reactive solute present in the liquid at a particular time, \(\text {SP}_{m}\) represents the dissoluble minerals in the solid and \(\text {SP}_{n}\) represents the reaction products in the liquid.

Figure 7a illustrates how \(\text {SP}_{c}\) varies with time for different \(\text {Da}\). In all cases, there is a sharp break in the slope of the individual curves at \(t \approx 0.05\) indicating a change in the growth rate of the solute saturation. For \(\text {Da} = 0\), when \(\text {SP}_{c}\) reaches about \(25\%\), the solute saturation slows down until it stabilizes at \(36.3\%\). For \(\text {Da} = 10\), we can see the largest decrease in the saturation rate. This decrease occurs since the diffusive mass transport rate begins to increase (Fig. 4). Values of \(\text {SP}_{c}\) for \(\text {Da} = 1\) and 10 reach about \(35\%\) at \(t = 1\) and tend to the value of the non-reactive case with increasing time. For the reactive simulations, \(\text {SP}_{m}\) decreases with time until all minerals are consumed, and the rate of the decrease is influenced by \(\text {Da}\) (see Fig. 7b). By \(t = 1\), this decrease in the average mineral content for \(\text {Da} = 0.1\) is relatively small—just about \(3\%\), for \(\text {Da} = 1\) is about \(27\%\), and for \(\text {Da} = 10\) reaches about \(81\%\). Although the products are not initially present in the liquid, they quickly generate as time proceeds. The average amount of the products at a particular time strongly depends on \(\text {Da}\) (see Fig. 7c). For \(\text {Da} = 1\), \(\text {SP}_{n}\) increases with time until it reaches the maximum value of \(1.7\%\) at \(t = 0.33\), then it begins to decline slightly. The quantity \(\text {SP}_{n}\) for \(\text {Da} = 10\) behaves in a similar way, but it grows faster to reach its maximum of \(8.7\%\) at \(t = 0.18\). Subsequently, the products are being removed from the system, and at \(t = 1\) the value of \(\text {SP}_{n}\) for \(\text {Da} = 10\) is nearly identical to that for \(\text {Da} = 1\).

4.3 Impact of Reaction Products on Convection (\(\text {Ra}_{c} = 400\) and \(\text {Ra}_{n} \ge 0\))

So far, we have considered that the concentration of the products does not affect fluid density in the system (\(\text {Ra}_{n} = 0\)). However, in general, the fluid density can be affected by the reaction products. An example of this is the chemical reaction between solid calcium carbonate (\(\textrm{CaCO}_{3}\)) and aqueous solution of sodium chloride (NaCl) generating sodium carbonate (\(\textrm{Na}_{2}\textrm{CO}_{3}\)) and calcium chloride (\(\textrm{CaCl}_{2}\)) in the liquid phase. This is a typical reaction network that occurs under some natural conditions (Harvey 2000). Such reaction network is nowadays used for industrial production of the sodium carbonate by Solvay process.

In this section, we will analyse buoyancy-driven flow in the porous medium using the streamfunction \(\psi\) calculated for reactive simulations (\(\text {Da}=1\) and \(\text {Ra}_{c}=400\)) in dependence on \(\text {Ra}_{n}\). The temporal development of a maximum value of \(\psi\) can be used to characterise the flow regime (Holzbecher 1998). The streamfunction reaches extreme values in the centre of the convection eddies and zero values at the edges of the domain. Therefore, an increase or decrease in the maximum values of \(\psi\) at a particular time can be associated with the emergence or disappearance of an eddy in the solution.

Fig. 8
figure 8

Temporal development of the streamfunction maximum for \(\text {Ra}_{n} = 0\) (blue), 40 (black), 400 (red) and 4000 (green). Values of the other parameters are \(\alpha _{m} = 1\), \(\alpha _{n} = 1\), \(\delta = 1\), \(\text {Da} = 1\) and \(\text {Ra}_{c} = 400\)

Full size image

Figure 8 illustrates how the maximum values of \(\psi\) change with time for different \(\text {Ra}_{n}\) in the range from 0 to 4000. The curves for \(\text {Ra}_{n} = 0\), 40 and 400 are almost identical—just the curve for \(\text {Ra}_{n} = 400\) is slightly below the others from \(t \approx 0.1\). For \(\text {Ra}_{n} = 4000\), the maximum values of \(\psi\) are initially greater than those for the other values of \(\text {Ra}_{n}\) until \(t \approx 0.1\), when they become moderately smaller. At \(t \approx 0.2\), there is a sharp increase leading to damped periodic oscillations about a nonzero mean. The oscillation period is approximately 0.014 and the frequency is 71 (in dimensionless units). This behaviour is essentially a consequence of a secondary instability in the flow regime due to the gradual decrease in the concentration of the products, as shown in Fig. 7c. The oscillatory convection makes its first appearance at a value of \(\text{Ra}_n = 2370\).

Fig. 9
figure 9

a, c, e Solute concentration fields c at time \(t = 0.5\) for parameters \(\text {Da} = 1\), \(\text {Ra}_{c} = 400\) and \(\text {Ra}_{n} = 4000\), calculated with three different initial solute concentrations. Values of the other parameters are \(\alpha _{m} = 1\), \(\alpha _{n} = 1\) and \(\delta = 1\). Concentration contours of c are depicted by black solid lines. Product concentration fields n (b, d, f) correspond to the solute concentration fields (a, c, e), respectively. Streamlines of the velocity field \({\varvec{u}}\) are depicted by blue solid lines

Full size image

Figure 9a, c and e show the solute concentration fields for \(\text {Da} = 1\), \(\text {Ra}_{c} = 400\) and \(\text {Ra}_{n} = 4000\) at \(t = 0.5\), where the three stable steady states, discussed above, were used as initial conditions for c, respectively. Compared to Fig. 3a, c and e, we observe tongue-like structures in the lower parts of the domains. The associated change in distribution of the products is noticeable in Fig. 9b, d and f. Furthermore, in Fig. 9b and d, we can clearly see how the localized streamlines are deformed by the periodically generated solute tongues. The formation of similar fluid tongues was previously reported in Hele–Shaw cell experiments by Horne and O’Sullivan (1974), who investigated oscillatory convection in a non-reactive porous medium heated from below.

5 Conclusion

In this paper, we have formulated the two-dimensional porous-medium model including the local chemical interactions between the solute in the pore liquid and the solid space of the porous medium as an extension of the classical Elder problem. For the model in the non-dimensional and streamfunction formulation, we have derived the asymptotic solution to the weakly reactive, purely diffusive case by applying the Fourier and Laplace transforms. Solutions to the reactive case with fully developed convection have been calculated numerically by applying the pseudospectral method for spatial discretization and the implicit–explicit Runge–Kutta method for time-stepping.

Our attention has been further focused on analysing mass distribution in the reactive porous medium in dependence on the Damköhler number \(\text {Da}\). For the strongly reactive case with \(\text {Da} = 1\), we have made direct comparisons to the corresponding non-reactive problem (van Reeuwijk et al. 2009) in terms of the solute concentration fields with the different number of vertical plumes. In the regime dominated by the diffusive mass transport, we have found a decrease in the net solute concentration as compared to the non-reactive case. This decrease is more pronounced at higher values of \(\text {Da}\). Interestingly, the associated reaction products are largely concentrated in the convection eddies at the side boundaries with the maximum concentration of about \(4\%\).

We have also investigated the impact of the chemical reaction on the flow regimes quantified by the concentration Rayleigh numbers \(\text {Ra}_{c}\) for the solute and \(\text {Ra}_{n}\) for the products. The flow structure in the reactive convective case with \(\text {Da} = 1\) and \(\text {Ra}_{c} = 400\) is affected by the reaction products when \(\text {Ra}_{n}\) is sufficiently high. Numerical simulations with \(\text {Ra}_{n} = 4000\) showed the formation of diluted fluid tongues that exhibited damped periodic oscillations about a nonzero mean.