Fixed priority scheduling with pre-emption thresholds and cache-related pre-emption delays: integrated analysis and evaluation

Abstract

Commercial off-the-shelf programmable platforms for real-time systems typically contain a cache to bridge the gap between the processor speed and main memory speed. Because cache-related pre-emption delays (CRPD) can have a significant influence on the computation times of tasks, CRPD have been integrated in the response time analysis for fixed-priority pre-emptive scheduling (FPPS). This paper presents CRPD aware response-time analysis of sporadic tasks with arbitrary deadlines for fixed-priority pre-emption threshold scheduling (FPTS), generalizing earlier work. The analysis is complemented by an optimal (pre-emption) threshold assignment algorithm, assuming the priorities of tasks are given. We further improve upon these results by presenting an algorithm that searches for a layout of tasks in memory that makes a task set schedulable. The paper includes an extensive comparative evaluation of the schedulability ratios of FPPS and FPTS, taking CRPD into account. The practical relevance of our work stems from FPTS support in AUTOSAR, a standardized development model for the automotive industry. [(This paper forms an extended version of Bril et al. (in Proceedings of 35th IEEE real-time systems symposium (RTSS), 2014). The main extensions are described in Sect. 1.2.]

1 Introduction

1.1 Background and motivation

For cost-effectiveness reasons, it is preferred to use commercial off-the-shelf (COTS) programmable platforms for real-time embedded systems rather than dedicated, application-domain specific platforms. These COTS platforms typically contain a cache to bridge the gap between the processor speed and main memory speed and to reduce the number of conflicts with other devices on the system bus. Unfortunately, caches give rise to additional delays upon pre-emptions, because pre-emptions may lead to cache flushes and reloads of blocks that are replaced. These cache-related pre-emption delays (CRPDs) can significantly increase the computation times of tasks, i.e., literature has reported inflated computation times of up to 50% (Pellizzoni and Caccamo 2007. In order to account for the impact of the CRPD on the timeliness of a task system, CRPD has therefore been integrated into the schedulability analysis of tasks (Busquets-Mataix et al. 1996; Lee et al. 1998; Staschulat et al. 2005; Ramaprasad and Mueller 2006; Altmeyer et al. 2012).

In real-time embedded systems, such as embedded vehicle control, fixed-priority pre-emptive scheduling (FPPS) is widely used. The majority of the commercial real-time operating systems (RTOSes) supports FPPS and makes use of corresponding timing-analysis tools. FPPS is inherently fully pre-emptive, which causes at least two types of pre-emption costs when using COTS hardware: spatial costs for saving and restoring the context of all tasks in memory and contention delays such as CRPD when cache blocks need to be reloaded. With FPPS these run-time overheads cannot be resolved analytically. An important disadvantage of FPPS therefore remains that arbitrary pre-emptions during execution may lead to inefficient memory use and high run-time overheads (Gai et al. 2001; Ghattas and Dean 2007).

In order to overcome these inefficiencies, some RTOS manufacturers were inclined to use two static priorities per task (Carbone 2013; Wang and Saksena 1999): one base priority is applied at task dispatching (sometimes also referred to as a task’s dispatching priority) and a second priority is applied once a task is selected for execution until its completion (referred to as a task’s pre-emption threshold). This scheme of fixed-priority scheduling with pre-emptions thresholds (FPTS) has been shown to greatly reduce the memory footprint of concurrent task systems (Gai et al. 2001) and reduce the average case response times of tasks (Ghattas and Dean 2007). Currently, FPTS is therefore already adopted by industry.

An important reason for the success of FPTS in industry is that pre-emption thresholds can be applied to task systems even without making any changes to the tasks’ code. Pre-emption thresholds can be easily assigned to tasks at integration time. Such support is specified by both the OSEK (OSE 2005) and AUTOSAR (AUT 2010) operating-system standards in the form of internal resources. Strictly speaking, the restriction in OSEK and AUTOSAR to assign at most one internal resource to each task must be lifted in order to fully implement and deploy FPTS. Many standards-compliant RTOSes therefore go beyond the standard by implementing internal resources more liberally than prescribed by their standard.

To the best of our knowledge, however, the integration of CRPD in the schedulability analysis of FPTS has not been considered. The limited pre-emptive nature of FPTS gives rise to specific challenges when integrating CRPD in the analysis, in particular to prevent over-estimations of CRPD. For example, not all tasks contributing to the worst-case response time of a task can actually pre-empt the execution of a job of that task, unlike with FPPS, as illustrated by a non-pre-emptive task. Next, there is no optimal (pre-emption) threshold assignment (OTA) algorithm available for FPTS taking CRPD into account, not to mention an algorithm that minimizes CRPD. Finally, existing comparisons between FPPS and FPTS, e.g. Buttazzo et al. (2013), do not consider CRPD.

1.2 Contributions

This paper presents four main contributions. Firstly, it provides worst-case response-time analysis of sporadic tasks with arbitrary deadlines for FPTS with CRPD, generalizing the work in Altmeyer et al. (2012) from FPPS to FPTS and from constrained deadlines to arbitrary deadlines. Secondly, it provides and proves an OTA algorithm for FPTS with CRPD. Thirdly, it presents a schedulable task-layout search (STLS) algorithm that searches for a layout of tasks in memory that makes a task set schedulable. The algorithm generalizes the one in Lunniss et al. (2012) from FPPS to FPTS by exploring memory layouts and applying the OTA algorithm to them. In this way, reloads of memory blocks into the cache result in minimal CRPD for the considered memory layout. Finally, this paper presents an extensive comparative evaluation of the schedulability ratios of FPPS and FPTS with and without CRPD. The evaluation is based on three orthogonal dimensions, i.e. (i) the CRPD approach applied in the analysis, (ii) the deadline type, being constrained, implicit, and arbitrary deadlines, and (iii) the memory layout, and seven main experiments in which task-set parameters and cache related parameters are varied. In addition, the effectiveness of the STLS algorithm is evaluated.

1.2.1 Extended version

Compared to Bril et al. (2014), this extended version has the following two major contributions. Firstly, it presents a generalized algorithm to improve the layout of tasks in memory (Sect. 10). Secondly, it presents a major extension of the comparative evaluation (Sect. 11). In particular, we added two orthogonal dimensions, i.e. the CRPD approach and the deadline type, and two experiments, i.e. the evaluation of the STLS algorithm (Sect. 11.2.2) and cache reuse (Sect. 11.4.3).

1.3 Outline

The remainder of this paper is organized as follows. Section 2 presents related work. Section 3 presents our scheduling model for FPTS and CRPD. Section 4 recapitulates analysis for FPTS without CRPD and analysis for FPPS with CRPD. Sections 5–8 present our response-time analysis for FPTS with CRPD [which revisits our analysis in Bril et al. (2014)]. The analysis is split into the following sections: Sect. 5 addresses the main challenges, Sect. 6 focusses on pre-empting tasks, Sect. 7 on the pre-empted tasks and Sect. 8 combines pre-empting and pre-empted tasks.

Next, Sect. 9 presents our Optimal Threshold Assignment (OTA) algorithm. Section 10 presents our STLS algorithm which aims at further decreasing the CRPD by improving the layout of the memory blocks of tasks. Section 11 evaluates the performance of FPPS and FPTS in the presence of CRPD. Finally, Sect. 12 concludes this paper. A complementary appendix contains all graphs of the comparative evaluation.

2 Related work

In this section, we first present an overview of scheduling schemes (including FPTS) that may reduce the number of pre-emptions and their related costs in concurrent real-time task systems. Secondly, we look at related works that investigated techniques for dealing with CRPDs in pre-emptive systems.

2.1 Limited pre-emptive scheduling

Limited pre-emptive scheduling schemes received a lot of attention from academia in the last decade. In particular, fixed-priority scheduling with deferred pre-emption (FPDS) (Burns 1994; Bril et al. 2009; Davis and Bertogna 2012), also called co-operative scheduling, and fixed-priority scheduling with pre-emption thresholds (FPTS) (Wang and Saksena 1999; Saksena and Wang 2000; Regehr 2002; Keskin et al. 2010) are considered viable alternatives between the extremes of fully pre-emptive and non-pre-emptive scheduling. Compared to fully pre-emptive scheduling, limited pre-emptive schemes can (i) reduce memory requirements (Saksena and Wang 2000; Gai et al. 2001; Davis et al. 2000) and (ii) reduce the cost of arbitrary pre-emptions (Burns 1994; Bril et al. 2009; Bertogna et al. 2011b). In addition, compared to both FPPS and non-pre-emptive scheduling, these schemes may significantly improve the schedulability of a task set (Bril et al. 2009; Saksena and Wang 2000; Bertogna et al. 2011a; Davis and Bertogna 2012).

Assuming strictly periodic tasks with known phasing, a single non-pre-emptive region (NPR) can significantly reduce the pre-emptions that can feasibly occur (Ramaprasad and Mueller 2008). NPRs may be placed statically in the code of a task (as they are with FPDS) or they may be floating. Baruah (2005) proposed the use of sporadic tasks with floating NPRs. Floating NPRs were designed for earliest-deadline-first (EDF) scheduling of tasks in order to retain schedulability with limited pre-emptions. However, floating NPRs require specific operating-system support, as investigated by Baldovin et al. (2013), and they could lead to pre-emptions by all higher priority tasks at arbitrary points in the code (Yao et al. 2009). These pre-emptions may incur highly fluctuating CRPDs, which are non-monotonic in the length of the NPR (Marinho et al. 2012), and CRPDs are therefore hard to analyze. With fixed-priority scheduling, FPDS shows more schedulability improvements with its statically placed NPRs compared to task models with floating NPRs, even when pre-emption costs are ignored (Buttazzo et al. 2013).

Although FPDS also outperforms FPTS from a theoretical perspective (Buttazzo et al. 2013), applying FPDS in practice is still a challenge, because pre-emption points have to be explicitly added in the code. Bertogna et al. (2011b) presented a model based on constant pre-emption costs in order to place pre-emption points in the tasks’ code appropriately. Recently, Cavicchio et al. (2015) have further extended this work by placing pre-emption points after computing and optimizing the CRPDs of a task. However, these works assume a linear flow of the code blocks of tasks. In our current work on FPTS we refrain from any assumption on the structure of the tasks’ code.

2.2 Cache-related pre-emption delays (CRPDs)

There are different techniques to deal with CRPDs. If the total number of memory blocks of the tasks in a system exceeds the cache size, then this may obviously lead to CRPDs due to reloads of blocks from memory to the cache. However, even if all memory blocks fit in the cache simultaneously, there are scenarios in which some memory blocks that are occupied by the tasks may be mapped to the same cache block. Since the mapping of memory to cache is often statically prescribed by the hardware (Patterson and Hennessy 2014), a proper memory layout of the tasks is important even when the total number of occupied memory blocks fits into the cache. Gebhard and Altmeyer (2007) and Lunniss et al. (2012) therefore tried to optimize the CRPDs by changing the layout of tasks in memory, subject to a static mapping of memory blocks to cache blocks. In our paper, we build upon the earlier work for FPPS by Lunniss et al. (2012) and we generalize their approach to FPTS.

The resulting optimization procedures have complex underlying models for the mapping of memory to cache and their usage by the tasks. These models are unnecessary if one could avoid the eviction of cache blocks by other tasks. For this purpose, cache locking and cache partitioning techniques have been devised. Using cache locking, the eviction of cache blocks is restricted once a cache block has been loaded. This restriction can either be for the duration of the system, resulting in a static locking scheme (Campoy et al. 2001, 2005; Puaut and Decotigny 2002; Liu et al. 2012), or for specific intervals of time, such as the duration of a code-fragment or until a pre-emption occurs, resulting in a dynamic locking scheme (Campoy et al. 2002; Arnaud and Puaut 2006; Liu et al. 2012). Moreover, cache-locking can either be global, where each task “owns” a specific part of the cache, or local, where each task can use the entire cache, but the cache is reloaded each time a pre-emption occurs. Although static and dynamic cache locking schemes are incomparable in general, the dynamic scheme typically performs better than the static scheme, in particular when the cache is relatively small compared to the size of the code (Campoy et al. 2003; Liu et al. 2012). The reloading costs for dynamic schemes give rise to pessimistic results, however. Using cache partitioning, each tasks “owns” a specific part of the cache, like global cache-locking. Unlike cache locking, self-evictions of cache blocks by tasks are not restricted or prevented. Cache partitioning (or cache locking) may be implemented by means of hardware support (Kirk 1989) or by means of software support (Puaut and Decotigny 2002). Altmeyer et al. (2014) showed that cache partitioning may slightly improve the performance of simple, short control tasks of which the pre-emption costs are relatively high compared to the computation times. However, they observed that the advantage of cache partitioning is often negligible when the memory layout of tasks is improved, so that memory blocks are loaded in the cache with less overlap. Moreover, cache partitioning is not very suitable for tasks with lower locality of memory accesses and higher amounts of computation, i.e. when the pre-emption costs are small compared to the computation times.

Wang et al. (2015) extended the applicability of cache partitioning to larger task sets with the help of FPTS. They created mutual non-pre-emptive task groups, so that tasks of the same group can together use a larger cache partition. However, we expect that the scalability of their approach is limited, because for large task sets, with lower locality of memory accesses and higher amounts of computation, FPTS will suffer from the same drawbacks as FPPS. The elimination of CRPDs between tasks may then not compensate for the performance degradation in the computation times of tasks. In the current paper, we therefore follow the line of reasoning by Altmeyer et al. (2014) and we complement our assignment of pre-emption thresholds with an algorithm for improving the memory layout of tasks.

The CRPDs of tasks can be analysed based on the concepts of evicting cache blocks (ECBs) and useful cache blocks (UCBs) (Lee et al. 1998; Altmeyer and Maiza 2011). A cache block that may be accessed by a task is termed an ECB, as it may overwrite the content of that cache block. A cache block that may be (re-) used at multiple program points without being evicted by the task itself is termed a UCB. The set of UCBs and ECBs of tasks can be analyzed with, for example, a prototype version of AbsInt’s aiT Timing Analyzer for ARM (Ferdinand and Heckmann 2004). This type of analysis using ECBs and UCBs applies to direct-mapped caches with a write-through policy and to set-associative caches with a least-recently used (LRU) replacement policy and a write-through policy (Altmeyer et al. 2012). The concepts of ECBs and UCBs cannot be applied to set-associative caches with a first-in-first-out (FIFO) or a pseudo-LRU (PLRU) replacement policy, as shown in Burguière et al. (2009).

The integration of CRPD in the schedulability analysis of tasks has been addressed for FPPS with a focus on the pre-empting tasks (Busquets-Mataix et al. 1996; Tomiyama and Dutt 2000), the pre-empted tasks (Lee et al. 1998), and by considering both the pre-empting and pre-empted tasks (Staschulat et al. 2005; Tan and Mooney 2007; Altmeyer et al. 2012). Figure 1 gives an overview of the various approaches and their relation. When focussing on the pre-empting tasks, only the ECBs of a task $\tau _j$ pre-empting another task $\tau _i$ are used to bound the CRPD of task $\tau _i$, as exemplified by the ECB-Only approach (Busquets-Mataix et al. 1996). When focussing on the pre-empted tasks, only the UCBs of the tasks pre-empted by task $\tau _j$ that can affect the response time of task $\tau _i$ are used to bound the CRPD of task $\tau _i$, as exemplified by the UCB-Only approach (Lee et al. 1998) and the UCB-Only Multiset approach (Bril et al. 2014). Finally, when considering both the pre-empting and pre-empted tasks both the ECBs of the pre-empting tasks as well as the UCBs of the pre-empted tasks are used. Following the work of Staschulat et al. (2005), other approaches that further tighten the CRPDs by combining the analysis of pre-empted and pre-empting tasks are the UCB-Union approach by Tan and Mooney (2007) and the ECB-Union approach, the UCB-Union Multiset and the ECB-Union Multiset approaches by Altmeyer et al. (2012). In the current paper we extend the most effective approaches to FPTS, i.e., the UCB/ECB-Union Multiset approaches.

Fig. 1

Venn diagram showing the relationship between the different approaches for computing CRPDs (as presented by Altmeyer et al. 2012)

3 Models and notation

This section presents the models and notation that we use throughout this paper. We start with a basic, continuous scheduling model for FPPS, i.e., we assume time to be taken from the real domain ($\mathbb {R}$), similar to, e.g., Koymans (1990), Bril et al. (2009) and Bertogna et al. (2011a). We subsequently refine this basic model for FPTS (Wang and Saksena 1999). Next, we introduce a basic memory model and a model for cache-related pre-emption costs. The section is concluded with remarks.

3.1 Basic model for FPPS

We assume a single processor and a set $\mathcal{T}$ of n independent sporadic tasks $\tau _1, \tau _2, \ldots , \tau _n$, with unique priorities ${\pi }_1,{\pi }_2,\ldots ,{\pi }_n$. At any moment in time, the processor is used to execute the highest priority task that has work pending. For notational convenience, we assume that (i) tasks are given in order of decreasing priorities, i.e. $\tau _1$ has the highest and $\tau _n$ the lowest priority, and (ii) a higher priority is represented by a higher value, i.e. ${\pi }_1> {\pi }_2> \ldots > {\pi }_n$. We use ${\text{ hp }}({\pi })$ (and ${\text{ lp }}({\pi })$) to denote the set of tasks with priorities higher than (lower than) ${\pi }$. Similarly, we use ${\text{ hep }}({\pi })$ (and ${\text{ lep }}({\pi })$) to denote the set of tasks with priorities higher (lower) than or equal to ${\pi }$.

Each task $\tau _i$ is characterized by a minimum inter-activation time $T_i~{\in }~\mathbb {R}^+$, a worst-case computation time $C_i~{\in }~\mathbb {R}^+$, and a (relative) deadline $D_i~{\in }~\mathbb {R}^+$. We assume that the constant pre-emption costs, such as context switches and pipeline flushes, are subsumed into the worst-case computation times. We feature arbitrary deadlines, i.e. the deadline $D_i$ may be smaller than, equal to, or larger than the period $T_i$. The utilization $U_i$ of task $\tau _i$ is given by $C_i / T_i$, and the utilization U of the set of tasks $\mathcal{T}$ by $\sum _{1 \le i \le n} U_i$. An activation of a task is also termed a job. The first job arrives at an arbitrary time.

We also adopt standard basic assumptions (Liu and Layland 1973), i.e. tasks do not suspend themselves and a job of a task does not start before its previous job is completed.

For notational convenience, we introduce $E_j(t) = \left\lceil t/T_j \right\rceil$ and $E_j^\mathrm{*}(t) = \left( 1 + \left\lfloor t/T_j \right\rfloor \right)$ to represent the maximum number of activations of $\tau _j$ in an interval $[x, x+t)$ and $[x, x+t]$, respectively, where both intervals have a length t.

3.2 Refined model for FPTS

In FPTS, each task $\tau _i$ has a pre-emption threshold ${\theta }_i$, where ${\pi }_1 \ge {\theta }_i \ge {\pi }_i$. When $\tau _i$ is executing, it can only be pre-empted by tasks with a priority higher than ${\theta }_i$. Note that we have FPPS and FPNS as special cases when $\forall _{1 \le i \le n} {\theta }_i = {\pi }_i$ and $\forall _{1 \le i \le n} {\theta }_i = {\pi }_1$, respectively.

We use ${\text{ het }}({\pi })$ (and ${\mathrm{lt}}({\pi })$) to denote the set of tasks with thresholds higher than or equal to (lower than) ${\pi }$. Finally, we use b(i) to denote the set of tasks that may block $\tau _i$ due to their pre-emption threshold assignment. An overview of notations for sets of tasks is given in Table 1. Note that for FPPS ${\text{ hep }}({\pi }) = {\text{ het }}({\pi }),{\text{ lp }}({\pi }) = {\mathrm{lt}}({\pi })$, and $\mathrm{b}(i) = \emptyset$.

Table 1 Notations for various sets of indices of tasks

3.3 A memory model

We consider two types of memory, (main) memory and cache (memory). Memory and cache are assumed to contain (memory) blocks of a fixed size, where memory contains $N^\mathrm{M}$ blocks and cache $N^\mathrm{C}$ blocks, and typically $N^\mathrm{M} \gg N^\mathrm{C}$. Memory blocks and cache blocks are numbered from 0 until $N^\mathrm{M}-1$ and from 0 to $N^\mathrm{C}-1$, respectively. Similar to Altmeyer et al. (2012), we assume direct-mapped caches (Patterson and Hennessy 2014), i.e. a memory block is mapped to exactly one cache block, with a write-through policy. A typical mapping scheme ${ MapM2C}$ for direct-mapped caches and systems without virtual memory is that memory block m is mapped to cache block

$$\begin{aligned} { MapM2C}(m) = m \bmod N^\mathrm{C}. \end{aligned}$$

(1)

The worst-case block-reload time (${\text{ BRT }}$) is assumed to be a constant that upper bounds the time to load a block from main memory to cache. The set of memory blocks of task $\tau _i$ is denoted by ${\text{ MB }}_i$. This set contains natural numbers and each number refers to a certain memory block.

The cache utilization of a task $\tau _i$ is given by $U_i^\mathrm{C} = \vert {\text{ MB }}_i \vert /N^\mathrm{C}$, where $\vert {\text{ MB }}_i \vert$ denotes the cardinality of the set ${\text{ MB }}_i$. The cache utilization of an individual task can therefore be larger than one, i.e. when $\vert {\text{ MB }}_i \vert > N^\mathrm{C}$. The cache utilization $U^\mathrm{C}$ of the set of tasks $\mathcal T$ is given by $U^\mathrm{C} = \sum _{1 \le i \le n} U_i^\mathrm{C}$.

The set of cache blocks of task $\tau _i$ is determined by ${\text{ MB }}_i$ and ${ MapM2C}$.

3.4 A model for cache-related pre-emption costs

Similar to Altmeyer et al. (2012), we use also the concepts of evicting cache blocks (ECBs) and useful cache blocks (UCBs) in order to analyze CRPDs. The ECBs of a task $\tau _i$ are denoted by the set ${\text{ ECB }}_i$; the UCBs of a task $\tau _i$ are denoted by the set ${\text{ UCB }}_i$. Just like ${\text{ MB }}_i$, these sets are also represented as sets of natural numbers. By definition, the set ${\text{ UCB }}_i$ is a subset of the set ${\text{ ECB }}_i$, i.e. ${\text{ UCB }}_i \subseteq {\text{ ECB }}_i$. The set ${\text{ ECB }}_i$ is determined by

$$\begin{aligned} {\text{ ECB }}_i = \mathop {\bigcup }\limits _{m \in {\mathrm{MB}}_i} { MapM2C}(m). \end{aligned}$$

(2)

Example 1 shows the relation between the ECBs of a task (${\text{ ECB }}_i$), the UCBs of a task (${\text{ UCB }}_i$) and the BRT.

Example 1

We assume a direct-mapped cache with 4 cache blocks and two tasks $\tau _1$ and $\tau _2$. The memory blocks of $\tau _1$ map to cache blocks 0, 1 and 2. Only $\tau _1$’s memory block mapping to cache block 1 is useful, i.e. ${\text{ ECB }}_1 = \{0,1,2\} \text{ and } {\text{ UCB }}_1 = \{1\}$. The memory blocks of $\tau _2$ map to cache blocks 1, 2, and 3 and all three are useful, i.e. ${\text{ ECB }}_2 = \{1,2,3\} \text{ and } {\text{ UCB }}_2 = \{1,2,3\}$. The cache-related pre-emption cost of task $\tau _1$ pre-empting task $\tau _2$ is thus given as follows:

$$\begin{aligned} \vert {\text{ ECB }}_1 \cap {\text{ UCB }}_2 \vert \cdot {\text{ BRT }}= \vert \{1,2\} \vert \cdot {\text{ BRT }}= 2\cdot {\text{ BRT }}. \end{aligned}$$

Whether or not all memory blocks of a task $\tau _i$ can be mapped on different cache blocks depends on the memory size $\vert {\text{ MB }}_i \vert$ of $\tau _i$ and the size $N^\mathrm{C}$ of the cache. As described in Altmeyer et al. (2014) and Wang et al. (2015), the worst-case computation time of a task depends on the size of the cache. Whereas the worst-case computation $C_i$ of task $\tau _i$ is fixed when $\vert {\text{ MB }}_i \vert \le N^\mathrm{C}$, it may increase when $\vert {\text{ MB }}_i \vert$ becomes larger than $N^\mathrm{C}$ due to self-eviction, i.e. $\tau _i$ may evict some of its own cache blocks. In the remainder, we will assume that the costs of self-evictions, which are also referred to as intra-task CRPDs, are subsumed into the worst-case computation times.

3.5 Concluding remarks

The schedulability analyses presented in this paper (Sect. 5–8) assumes direct-mapped caches with a write-through policy and applies to instruction, data, and unified caches. The analysis only operate on the sets of UCBs and ECBs and are thus (i) independent of the mapping ${ MapM2C}$ from memory blocks to cache blocks and (ii) applicable for every cache size. Primarily for ease of evaluation, we will make simplifying assumptions for ${ MapM2C}$, e.g. assume the typical mapping scheme as given by (1).

4 Recap of response time analysis for FPPS and FPTS

This section starts with a recapitulation of the exact schedulability analysis for FPTS, as presented in Keskin et al. (2010). Next, that analysis is specialized for FPPS with constrained deadlines, i.e. for cases with $D_i \le T_i$, and extended with CRPD (Altmeyer et al. 2012).

4.1 FPTS with arbitrary deadlines (without CRPD)

A set $\mathcal{T}$ of tasks is schedulable if and only if for every task $\tau _i \in \mathcal{T}$ its worst-case response time $R_i$ is at most equal to its deadline $D_i$, i.e. $\forall _{1 \le i \le n} R_i \le D_i$. To determine $R_i$, we need to consider the worst-case response times of all jobs in a so-called level-i active period (Bril et al. 2009). The worst-case length $L_i$ of that period is given by the smallest positive solution of

$$\begin{aligned} L_i = B_i + \sum _{\forall j \in {\mathrm{hep}}({\pi }_i)} E_j(L_i) \cdot C_j, \end{aligned}$$

(3)

where $B_i$ denotes the worst-case blocking of task $\tau _i$, given by

$$\begin{aligned} B_i = \max \left( 0,\max _{\forall b \in \mathrm{b}(i)}C_b \right) . \end{aligned}$$

(4)

$L_i$ can be found by fixed point iteration that is guaranteed to terminate for all i when $U < 1$ (Bril et al. 2009).

As mentioned above, when a task $\tau _i$ is executing, it can only be pre-empted by tasks $\tau _j$ with $j \in {\text{ hp }}({\theta }_i)$. In the worst-case response time analysis, we therefore consider both the start-time and the finishing time of a job of a task. For a job k of $\tau _i$, with $0 \le k < E_i(L_i)$, the worst-case start time $S_{i,k}$ and worst-case finalization time $F_{i,k}$ are given by

$$\begin{aligned} S_{i,k} = \left\{ \begin{array}{ll} B_i + kC_i + \mathop {\sum }\limits _{\forall j \in {\mathrm{hp}}({\pi }_i)} E_j(S_{i,k}) \cdot C_j &{} \text{ if } B_i > 0 \\ kC_i + \mathop {\sum }\limits _{\forall j \in {\mathrm{hp}}({\pi }_i)} E^\mathrm{*}_j(S_{i,k}) \cdot C_j &{} \text{ if } B_i = 0 \end{array} \right. \end{aligned}$$

(5)

and

$$\begin{aligned} F_{i,k} = S_{i,k} + C_i + \left\{ \begin{array}{ll} \mathop {\sum }\limits _{\forall j \in {\mathrm{hp}}({\theta }_i)} \left( E_j(F_{i,k}) - E_j(S_{i,k}) \right) \cdot C_j &{} \text{ if } B_i > 0 \\ \mathop {\sum }\limits _{\forall j \in {\mathrm{hp}}({\theta }_i)} \left( E_j(F_{i,k}) - E^\mathrm{*}_j(S_{i,k})\right) \cdot C_j &{} \text{ if } B_i = 0 \end{array} \right. . \end{aligned}$$

(6)

Later in this paper we prove that (6) can be simplified by removing the case distinction, because $E_j(S_{i,k}) = E^*_j(S_{i,k})$ (see Corollary 1). Similar to $L_i$, the values for $S_{i,k}$ and $F_{i,k}$ can be found by means of an iterative procedure.

The worst-case response time $R_i$ of task $\tau _i$ is now given by

$$\begin{aligned} R_i = \max _{0 \le k < E_i(L_i)} \left( F_{i,k} - k \cdot T_i\right) . \end{aligned}$$

(7)

4.2 FPPS with constrained deadlines and CRPD

FPPS is a special case of FPTS, and the analysis of FPTS can therefore be simplified for FPPS. For FPPS with constrained deadlines without CRPD, the worst-case response time $R_i$ of task $\tau _i$ is given by the smallest positive solution (Joseph and Pandya 1986; Audsley et al. 1991) of

$$\begin{aligned} R_i = C_i + \sum _{\forall j \in {\mathrm{hp}}({\pi }_i)} E_j(R_i) \cdot C_j. \end{aligned}$$

(8)

An upper bound for $R_i$ with CRPD (Staschulat et al. 2005; Altmeyer et al. 2012) can be found using

$$\begin{aligned} R_i = C_i + \sum _{\forall j \in {\mathrm{hp}}({\pi }_i)} \left( E_j(R_i) \cdot C_j + \gamma _{i,j}(R_i)\right) , \end{aligned}$$

(9)

where $\gamma _{i,j}(R_i)$ represents the cache-related pre-emption cost due to all jobs of a higher priority pre-empting task $\tau _j$ executing within the worst-case response time of task $\tau _i$. The definition of $\gamma _{i,j}(t)$ depends on the specific approach chosen for determining these costs (Altmeyer et al. 2012).

As we observed before (see Sect. 2), the integration of CRPD in the schedulability analysis of tasks has been addressed for FPPS with a focus on the pre-empting tasks (Busquets-Mataix et al. 1996; 2000, the pre-empted tasks (Lee et al. 1998), and by considering both the pre-empting and pre-empted tasks (Staschulat et al. 2005; 2007; Altmeyer et al. 2012). These techniques use different ways to bound the contribution of the CRPD, $\gamma _{i,j}(R_i)$, in the response-time analysis of a task $\tau _i$. Below, we briefly recapitulate representative approaches that we will use to illustrate our analysis for FPTS including CRPD in subsequent chapters; see Altmeyer et al. (2012) for further explanations of these approaches.

4.2.1 Pre-empting tasks

The ECB-Only approach focusses on the pre-empting tasks, i.e. only the ECBs of a task $\tau _j$ pre-empting task $\tau _i$ are used to bound the CRPD of task $\tau _i$. For each pre-emption of $\tau _j$, a cost ${\text{ BRT }}\cdot \vert {\text{ ECB }}_j \vert$ is accounted. For this case, $\gamma _{i,j}(t)$ is given by¹

$$\begin{aligned} \gamma ^{{\mathrm{ecb}\hbox {-}\mathrm{o}}}_{i,j}(t) = \left\{ \begin{array}{ll} {\text{ BRT }}\cdot E_j(t) \cdot \left| {\text{ ECB }}_j \right| &{} \quad \text{ if }\; {\text{ aff }}({\pi }_i,{\pi }_j) \ne \emptyset \\ 0 &{}\quad \text{ otherwise } \end{array} \right. , \end{aligned}$$

(10)

where ${\text{ aff }}({\pi }_i,{\pi }_j)$ denote the set of tasks that have a priority (i) higher than or equal to ${\pi }_i$, i.e. can affect the response time of $\tau _i$, and (ii) lower than ${\pi }_j$, i.e. can be pre-empted by $\tau _j$. For FPPS with constrained deadlines, the set of tasks ${\text{ aff }}({\pi }_i,{\pi }_j)$ affecting task $\tau _i$ and affected by $\tau _j$ is defined as

$$\begin{aligned} {\text{ aff }}({\pi }_i,{\pi }_j) \mathop {=}\limits ^{\mathrm {def}}{\text{ hep }}({\pi }_i) \cap {\text{ lp }}({\pi }_j). \end{aligned}$$

(11)

Applying the ECB-Only approach to Example 1 would yield a CRPD of ${\text{ BRT }}\cdot \vert {\text{ ECB }}_1 \vert = {\text{ BRT }}\cdot 3$ rather than ${\text{ BRT }}\cdot 2$ for a pre-emption of task $\tau _2$ by task $\tau _1$, i.e. a pessimistic result.

4.2.2 Pre-empted tasks

The UCB-Only Multiset approach focusses on the pre-empted tasks, i.e. only the UCBs of the tasks pre-empted by task $\tau _j$ that can affect the response time of task $\tau _i$ are used to bound the CRPD of task $\tau _i$. Although the maximum number of UCBs over all tasks from ${\text{ aff }}({\pi }_i,{\pi }_j)$ can be used for every pre-emption of $\tau _j$ to account for nested pre-emptions (Lee et al. 1998), this may give rise to pessimism. This is due to the fact that the task with the maximum number of UCBs cannot necessarily be pre-empted up to $E_j(t)$ times. In particular, a task $\tau _h$, with $h \in {\text{ aff }}({\pi }_i,{\pi }_j)$, affecting task $\tau _i$ and affected by task $\tau _j$ is activated at most $E_h(t)$ in an interval of length t, and each of those activations is pre-empted at most $E_j(R_h)$ times by task $\tau _j$. An upper bound for the number of times task $\tau _j$ can pre-empt $\tau _h$ in an interval of length t is therefore given by $E_j(R_h) \cdot E_h(t)$, which may be considerably smaller than $E_j(t)$. Therefore, a multiset $M^{{\mathrm{ucb}\hbox {-}\mathrm{o}}}_{i,j}(t)$ is created containing $E_j(R_h) \cdot E_h(t)$ copies of the size of ${\text{ UCB }}_h$ of each task $\tau _h$, with $h \in {\text{ aff }}({\pi }_i,{\pi }_j)$, i.e.

$$\begin{aligned} M^{{\text {ucb-o}}}_{i,j}(t)\mathop {=}\limits ^{\mathrm {def}}\bigcup _{h \in {\mathrm{aff}}({\pi }_i,{\pi }_j)} \left( \bigcup _{E_j(R_h) \cdot E_h(t)} \bigl \vert {\text{ UCB }}_h \bigr \vert \right) . \end{aligned}$$

(12)

For this approach, $\gamma _{i,j}(t)$ is subsequently defined as²

$$\begin{aligned} \begin{aligned} \gamma ^{{\text {ucb-o}}}_{i,j}(t) \mathop {=}\limits ^{\mathrm {def}}{\text { BRT }}\cdot \sum _{\ell =1}^{E_j(t)} \mathtt {sort}\left( M^{{\text {ucb-o}}}_{i,j}(t)\right) [\ell ], \end{aligned} \end{aligned}$$

(13)

where the function $\mathtt{sort}()$ sorts the values in the multiset $M^{{\text {ucb-o}}}_{i,j}(t)$ in non-increasing order. Hence, the sum of the $E_j(t)$ largest sizes in the multiset $M^{{\text {ucb-o}}}_{i,j}(t)$ is taken and multiplied by ${\text{ BRT }}$.³

Applying the UCB-Only Multiset approach to Example 1 would yield a CRPD of ${\text{ BRT }}\cdot \vert {\text{ UCB }}_2 \vert = {\text{ BRT }}\cdot 3$ rather than ${\text{ BRT }}\cdot 2$ for a pre-emption of task $\tau _2$ by task $\tau _1$, i.e. a pessimistic result.

4.2.3 Pre-empting and pre-empted tasks

The ECB-Union Multiset approach focusses on both the pre-empting and pre-empted tasks. To account for nested pre-emptions, the union of all ECBs that may affect a pre-empted task is computed, i.e. $\bigcup _{g \in {\mathrm{hep}}({\pi }_j) } {\text{ ECB }}_g$. Although the maximum number over all tasks from ${\text{ aff }}({\pi }_i,{\pi }_j)$ of the intersection of the UCBs and that union of ECBs can be used for every pre-emption of $\tau _j$ (Altmeyer et al. 2012), this may give rise to pessimism for the same reason as for the UCB-Only Multiset approach. Therefore, for each task $\tau _h$ with $h \in {\text{ aff }}({\pi }_i,{\pi }_j)$ the multiset $M^{{\text {ecb-u}}}_{i,j}(t)$ contains $E_j(R_h) \cdot E_h(t)$ copies of the size of the intersection of ${\text{ UCB }}_h$ and the ${\text{ ECB }}$s of all tasks in ${\text{ hep }}({\pi }_j)$, i.e.

$$\begin{aligned} M^{{\text {ecb-u}}}_{i,j}(t) \mathop {=}\limits ^{\mathrm {def}}\bigcup _{h \in {\mathrm{aff}}({\pi }_i,{\pi }_j)} \left( \bigcup _{E_j(R_h) \cdot E_h(t)} \left| {\text{ UCB }}_h \cap \left( \bigcup _{g \in {\mathrm{hep}}({\pi }_j) } {\text{ ECB }}_g \right) \right| \right) . \end{aligned}$$

(14)

Note that (14) extends (12) by intersecting every ${\text{ UCB }}_h$ with $\left( \bigcup _{g \in {\mathrm{hep}}({\pi }_j) } {\text{ ECB }}_g \right)$. The definition of $\gamma _{i,j}(t)$ for the ECB-Union Multiset approach is identical to the definition in (13) for the UCB-Only Multiset approach, except that it uses $M^{{\text {ecb-u}}}_{i,j}(t)$ instead of $M^{{\text {ucb-o}}}_{i,j}(t)$.

Applying the ECB-Union Multiset approach to Example 1 would yield a CRPD of ${\text{ BRT }}\cdot \vert {\text{ UCB }}_2 \cap {\text{ ECB }}_1 \vert = {\text{ BRT }}\cdot 2$ for every pre-emption of task $\tau _2$ by task $\tau _1$.

The UCB-Union Multiset approach also focusses on both the pre-empting and pre-empted tasks. To account for nested pre-emptions, the union of UCBs of all tasks from ${\text{ aff }}({\pi }_i,{\pi }_j)$ can be computed and combined with the ECBs of the pre-empting task $\tau _j$ (Tan and Mooney 2007), i.e. $\left( \bigcup _{h \in {\mathrm{aff}}({\pi }_i,{\pi }_j)}\right) {\text{ UCB }}_h \cap {\text{ ECB }}_j$. Because task $\tau _j$ cannot necessarily pre-empt any task $\tau _h$ ($h \in {\text{ aff }}({\pi }_i,{\pi }_j)$) up to $E_j(t)$ times, dedicated multisets are constructed for the affected tasks and the pre-empting task to reduce pessimism. To this end, a multiset $M^{{\text {ucb}}}_{i,j}(t)$ is formed containing $E_j(R_h) \cdot E_h(t)$ copies of the ${\text{ UCB }}_h$ of each task $\tau _h$ with $h \in {\text{ aff }}({\pi }_i,{\pi }_j)$, i.e.

$$\begin{aligned} M^{{\text {ucb}}}_{i,j}(t) \mathop {=}\limits ^{\mathrm {def}}\bigcup _{h \in {\mathrm{aff}}({\pi }_i,{\pi }_j)} \left( \bigcup _{E_j(R_h) \cdot E_h(t)} {\text{ UCB}}_h \right) . \end{aligned}$$

(15)

Apart from the cardinality operator in (12), the Eqs. (12) and (15) are identical. Next a multi-set $M_j^{{\mathrm{ecb}}}(t)$ is formed containing $E_j(t)$ copies of the ${\text{ ECB }}_j$ of task $\tau _j$, i.e.

$$\begin{aligned} M^{{\mathrm{ecb}}}_{j}(t) \mathop {=}\limits ^{\mathrm {def}}\bigcup _{E_j(t)} {\text{ ECB}}_j. \end{aligned}$$

(16)

The CRPD $\gamma _{i,j}^{{\text {ucb-u}}}(t)$ is then given by the size of the multi-set intersection of $M_j^{{\mathrm{ecb}}}(t)$ and $M^{{\mathrm{ucb}}}_{i,j}(t)$ multiplied by ${\text{ BRT }}$, i.e.

$$\begin{aligned} \begin{aligned} \gamma _{i,j}^{{\text {ucb-u}}}(t) \mathop {=}\limits ^{\mathrm {def}}{\text { BRT }}\cdot \left| M_j^{{\text { ecb}}}(t) \cap M^{{\text {ucb}}}_{i,j}(t) \right| . \end{aligned} \end{aligned}$$

(17)

Similar to the ECB-Union Multiset approach, applying the UCB-Union Multiset approach to Example 1 also yields a CRPD of ${\text{ BRT }}\cdot 2$ for a pre-emption of task $\tau _2$ by task $\tau _1$.

In the remainder of this paper, we follow a similar structure for extending FPTS with CRPD. Before looking at specific approaches, we consider challenges for FPTS with CRPD (Sect. 5). We subsequently focus on pre-empting tasks (Sect. 6), pre-empted tasks (Sect. 7), and the combination of pre-empting and pre-empted tasks (Sect. 8).

5 FPTS with CRPD: Preliminaries and challenges

To extend the schedulability analysis of FPTS with CRPD, we must extend the corresponding formulas. For this purpose, we extend the worst-case length $L_i$ of the level-i active period in (3), the worst-case start-time $S_{i,k}$ in (5) and the worst-case finalization time $F_{i,k}$ in (6) of job k of task $\tau _i$ with a new term $\gamma _{i,j}(t)$ in a similar way as the worst-case response time $R_i$ in (9) has been extended for FPPS with constrained deadlines. However, due to (i) the generalization towards arbitrary deadlines and (ii) the limited-pre-emptive nature of FPTS, it is not possible to simply extend these equations for FPTS with a term $\gamma _{i,j}(t)$ by reusing the existing approaches to determine CRPD. This section addresses preliminaries and challenges for FPTS with CRPD.

5.1 Distinguishing executing and affected tasks

The extension for FPPS is based on the tasks that can execute and affect the execution of a task $\tau _i$ in the interval under consideration.

Table 2 Overview of tasks that can execute and affect the execution of task $\tau _i$ in a level-i active period starting at time $t = 0$ for both FPPS with constrained deadlines and FPTS with arbitrary deadlines, assuming a task $\tau _b$ that blocks $\tau _i$ for FPTS, i.e. $b \in \mathrm{b}(i)$

An overview of these tasks for the response interval $[0, R_i)$ is given in Table 2, i.e. the table shows

• Interval: A description of an interval under consideration, being $[0, R_i)$;

• Execute: The tasks that can execute jobs in the interval, being tasks with a priority higher than or equal to the priority of $\tau _i$, i.e. ${\text{ hep }}({\pi }_i)$;

• Affected by $\tau _j$: The set of tasks that (i) can execute jobs in the interval and (ii) can be pre-empted by task $\tau _j$, i.e. ${\text{ hep }}({\pi }_i) \cap {\text{ lp }}({\pi }_j)$;

• $\#$-jobs: The number of job activations of a task that can execute in the interval, i.e. $E_h(R_i)$ for each task $\tau _h \in {\text{ hep }}({\pi }_i)$.

The “ $\#$-jobs” in the interval $[0, R_i)$ can be immediately derived from $R_i$, see (8). If $R_i \le D_i \le T_i$, then $E_i(R_i) = 1$ and, as a result, task $\tau _i$ can be treated as any other task.

When we focus only on the pre-empting tasks, e.g. when using the ECB-Only approach, we only need the information of the row affected by $\tau _j$ in Table 2; see (10). When we consider the pre-empted tasks, e.g. when using the UCB-Only Multiset approach, the $\#$-jobs also play a role. To be more specific, the multiset $M^{{\text {ucb-o}}}_{i,j}(t)$ in (12) contains $E_j(R_h)$ copies of the size of ${\text{ UCB }}_h$ for each of the $E_h(t)$ jobs of task $\tau _h$, with $h \in {\text{ aff }}({\pi }_i,{\pi }_j)$, affecting $\tau _i$ and affected by $\tau _j$.

In the remainder of this section, we first show how the number of pre-emptions $E_j(R_h)$ of a job of a task $\tau _h$ by a task $\tau _j$ can be tightened for FPTS. Next, we determine the information in Table 2 for FPTS. We subsequently address specific topics related to FPTS, such as blocking and termination of the iterative procedure for $L_i$. We conclude with a brief description of how the information presented in this section can be applied to the extensions for FPTS with CRPD, which is addressed in the next sections.

5.2 Bounding the number of pre-emptions using hold times

For FPPS with constrained deadlines, all pre-emptions during the response time of a job of a task may actually evict ${\text{ UCB }}$s of that job. For FPTS, however, some pre-emptions can only take place between the activation and the start of a job, and therefore do not evict ${\text{ UCB }}$s of that job. An obvious example is a non-pre-emptive task, where no pre-emption can take place during the actual execution of its jobs.

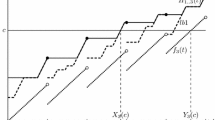
To prevent pessimism in the analysis when focussing on pre-empted tasks, we consider so-called hold times. To that end, we distinguish the (absolute) activation time $a_{i,k}$, (absolute) start-time $s_{i,k}$ and (absolute) finishing time $f_{i,k}$ of a job k of task $\tau _i$; see Fig. 2. The lengths of the intervals $[a_{i,k}, f_{i,k})$ and $[s_{i,k}, f_{i,k})$ are termed the response time $R_{i,k}$ and the hold time ⁴ $H_{i,k}$ of job k of task $\tau _i$, respectively.

Fig. 2

The response time and hold time of job k of task $\tau _i$

Under FPPS, the worst-case hold time $H_i$ of a task $\tau _i$ can be calculated by means of (8), i.e. by using the equation to determine the worst-case response time $R_i$ for FPPS with constrained deadlines; see Bril (2004) and Bril et al. (2008). Under FPTS, only tasks with a priority higher than the pre-emption threshold ${\theta }_i$ can pre-empt task $\tau _i$. Hence, the worst-case hold time $H_i$ (without CRPD) is given by

$$\begin{aligned} H_i = C_i + \sum _{\forall j \in {\mathrm{hp}}({\theta }_i)} E_j(H_i) \cdot C_j. \end{aligned}$$

(18)

We will now show that the worst-case hold time is both a proper value to determine an upper bound for the number of pre-emptions of a job of task $\tau _i$ as well as a potential improvement over using the worst-case response time $R_i$. This allows us to tighten the number of pre-emptions $E_j(R_h)$ by $E_j(H_h)$ in the construction of the multisets for the approaches considering pre-empted tasks.

Being the worst-case hold time $H_i$ of a task $\tau _i,H_i$ is an upper bound for the hold time for every job of $\tau _i$ in general and for every job in the level-i active period with a worst-case length $L_i$ in particular. The former is an immediate consequence of the fact that the tasks that can influence the hold time of an individual job k of $\tau _i$ are identical to those that can influence $H_i$, i.e. ${\text{ hp }}({\theta }_i)$. The latter follows from the observation that a critical instant to determine the worst-case response time $R_i$ is not necessarily a critical instant for the worst-case hold time $H_i$, hence $\forall _{0 \le k < E_i(L_i)} H_{i,k} \le H_i$. The worst-case hold time $H_i$ is therefore a proper value to determine an upper bound on the number of pre-emptions of a job of task $\tau _i$.

The worst-case hold time $H_i$ of a task $\tau _i$ is at most equal to the worst-case response time $R_i$ of $\tau _i$, i.e. $H_i \le R_i$. This result immediately follows from the fact that the set of tasks that influences the worst-case hold time $H_i$ of task $\tau _i$ is a subset of the set of tasks that influences the worst-case response time $R_i$ of $\tau _i$. The worst-case hold time $H_i$ of a task $\tau _i$ may be smaller than the worst-case response time $R_i$. This is because (i) the potential delay of the execution of a job by a previous job (Bril et al. 2008), (ii) the blocking by a task $\tau _b$ with $b \in \mathrm{b}(i)$, and (iii) the interference of tasks $\tau _j$ with $j \in {\text{ hp }}({\pi }_i) \cap {\text{ lep }}({\theta }_i)$ are included in $R_i$ but not in $H_i$. Example 2 below illustrates (i) and Example 3 illustrates (ii) and (iii).

Example 2

The characteristics of a set $\mathcal{T}_2$ of periodic tasks is given in Table 3. The timeline shown in Fig. 3 illustrates both the worst-case hold time $H_2 = 8.2$ and the worst-case response time $R_2 = 8.6$ for the job activated at time $t = 14$. $R_2$ is larger than $H_2$, because $R_2$ includes a delay of 0.4 of the job activated at time $t = 7$. This illustrates (i).

Table 3 Task characteristics of $\mathcal{T}_2$ and worst-case response times and hold times of periodic tasks with non-constrained deadlines under FPPS without CRPD

Fig. 3

Timeline for $\mathcal{T}_2$ for an entire hyper period (i.e. $\mathrm{lcm}(T_1, T_2) = 35$) with a simultaneous release of $\tau _1$ and $\tau _2$ at time $t = 0$. The numbers to the top right corner of the boxes denote the response times of the respective job activations

Table 4 Task characteristics of $\mathcal{T}_2$ and worst-case response times and hold times of periodic tasks under FPTS without CRPD

Example 3

The characteristics of a set $\mathcal{T}_3$ of periodic tasks are given in Table 4. The worst-case hold times of all tasks are smaller than their worst-case response times. Task $\tau _1$ is an example of (ii), task $\tau _4$ is an example of (iii), and tasks $\tau _2$ and $\tau _3$ are examples of both (ii) and (iii).

Tasks $\tau _3$ and $\tau _4$ of Example 3 are particularly interesting when FPTS is extended with CRPD, because task $\tau _1$ can be activated twice during their worst-case response time but only once during their worst-case hold time; see Fig. 4.

Fig. 4

Task $\tau _1$ is activated twice during the worst-case response time of task $\tau _4$ but only once during the worst-case hold time of $\tau _4$

5.3 Determining the tasks that can execute and are affected by $\tau _j$

Having introduced the worst-case hold time $H_i$ of task $\tau _i$, we now determine for each of the intervals $[0, H_i),[0, L_i)$, $[0, S_{i,k})$, and $[0, F_{i,k})$ the tasks that can execute in the interval (“execute”) and from these tasks those that are affected by task $\tau _j$ (“affected by $\tau _i$”) for FPTS in Table 2.

The tasks that can execute in $[0, H_i)$ can immediately be derived from (18), i.e. task $\tau _i$ and all tasks with a priority higher than the pre-emption threshold ${\theta }_i$ of task $\tau _i$. This set of tasks is therefore characterized by the set of indices $\{i\} \cup {\text{ hp }}({\theta }_i)$. Similarly, the set of tasks that can execute in $[0, L_i),[0, S_{i,k})$, and $[0, F_{i,k})$ can immediately be derived from (3), (5), and (6), respectively. Assuming a task $\tau _b$ that blocks $\tau _i$, i.e. $b {\in \mathrm b}(i)$, all these three sets are characterized by the set of indices $\{b\} \cup {\text{ hep }}({\pi }_i)$.

To determine the “affected by $\tau _j$” for each of these intervals, we simply take the intersection of the set of indices for “execute” with ${\mathrm{lt}}({\pi }_j)$, similar to FPPS.

5.4 Determining the number of job activations “ $\#$-jobs”

We now show that we can derive the “ $\#$-jobs” for FPTS in Table 2 from the equations corresponding to the intervals, similar to FPPS. We start with the interval $[0, H_i)$. The intervals $[0, L_i),[0, S_{i,k})$ and $[0,F_{i,k})$ are subsequently addressed for $B_i \ne 0$ and $B_i = 0$.

5.4.1 $\#$-jobs for $[0,H_i)$

The “ $\#$-jobs” for the interval $[0, H_i)$ follows immediately from (18). Exactly 1 activation of $\tau _i$ is taken into account. To prevent pessimism when $T_i$ is smaller than $H_i$, Table 2 contains a dedicated clause for identifying the appropriate number of job activations of task $\tau _i$ itself.

Example 4

We reconsider $\mathcal{T}_2$ of Example 2. For that example, $E_2(H_2) = 2$ rather than 1. To prevent this pessimism, we take exactly one activation of $\tau _i$ into account.

5.4.2 $\#$-jobs for $[0,L_i),[0,S_{i,k})$, and $[0,F_{i,k})$ when $B_i \ne 0$

Given a task $\tau _b$ that blocks $\tau _i$ under FPTS, i.e. $b \in \mathrm{b}(i)$, the number of activations $\#$-jobs in the intervals $[0, L_i),[0, S_{i,k})$ and $[0, F_{i,k})$ in Table 2 can be immediately derived from (3) for $L_i$, (5) for $S_{i,k}$ and (6) for $F_{i,k}$. To prevent pessimism, exactly one activation of $\tau _b$ is taken into account. Similarly, exactly k and $k+1$ jobs of $\tau _i$ are taken into account when determining $S_{i,k}$ and $F_{i,k}$, respectively.

Example 5

We reconsider $\mathcal{T}_2$ of Example 2. The worst-case finalization time $F_{2,0}$ of the first job of $\tau _2$ is equal to 8.2. Because $E_2(8.2) = 2$, (12) would include 2 jobs of $\tau _2$ in $M_{2,1}^{{\text {ucb-o}}}(8.2)$ rather than 1. To prevent this pessimism, we explicitly take the number of jobs of $\tau _i$ into account.

5.4.3 $\#$-jobs for $[0,L_i),[0,S_{i,k})$, and $[0,F_{i,k})$ when $B_i = 0$

Lemma  shows that $E_j^\mathrm{*}(S_{i,k})$ can be replaced by $E_j(S_{i,k})$ for the case $B_i = 0$ in (6) for $F_{i,k}$.

Lemma 1

Let $j \in {\text{ hp }}({\pi }_i)$ and assume a level-i active period starting at time $t = 0$ with a simultaneous release of $\tau _i$ and $\tau _j$. Let $S_{i,k}$ denote the worst-case start time of job k of $\tau _i$ in that level-i active period and be derived by (5). Now the following equality holds:

$$\begin{aligned} \forall _{j \in {\mathrm{hp}}({\pi }_i)} E^\mathrm{*}_j(S_{i,k}) = E_j(S_{i,k}). \end{aligned}$$

(19)

Proof

The term $E^\mathrm{*}_j(S_{i,k})$ represents the maximum number of activations of $\tau _j$ in the interval $[0, S_{i,k}]$. When $\exists _{m \in \mathbb {N}} S_{i,k} = m \cdot T_j$, task $\tau _j$ is activated at time $S_{i,k}$. This would imply that $\tau _i$ cannot start at $S_{i,k}$, which contradicts the definition of $S_{i,k}$. We therefore conclude that $\not \exists _{m \in \mathbb {N}} S_{i,k} = m \cdot T_j$. As a result, $E^\mathrm{*}_j(S_{i,k}) = E_j(S_{i,k})$, which proves the lemma. $\square$

Corollary 1

We may simplify (6) by replacing $E^\mathrm{*}_j(S_{i,k})$ by $E_j(S_{i,k})$ and ignoring the case distinction, i.e.

$$\begin{aligned} F_{i,k} = S_{i,k} + C_i + \mathop {\sum }\limits _{\forall j \in {\mathrm{hp}}({\theta }_i)} \left( E_j(F_{i,k}) - E_j(S_{i,k}) \right) \cdot C_j. \end{aligned}$$

(20)

Similarly, Lemma 2 shows that $\gamma _{i,j}(t)$ can be defined in terms of $E_j(S_{i,k})$ rather than $E_j^*(S_{i,k})$ for the case $B_i = 0$ in (5) when determining $S_{i,k}$.

Lemma 2

When $S_{i,k}$ is extended with a term $\gamma _{i,k}(t)$ for the case $B_i = 0,\gamma _{i,k}(t)$ can be based on $E_j(t)$ rather than $E^\mathrm{*}_j(t)$.

Proof

A solution for the recurrent relation for $S_{i,k}$ is found when $S_{i,k}^{(\ell )} = S_{i,k}^{(\ell +1)}$ for two subsequent iterations. For $S_{i,k}^{(\ell )}$ there are two cases, either $E_j(S_{i,k}^{(\ell )}) = E^\mathrm{*}_j(S_{i,k}^{(\ell )})$ or $E_j(S_{i,k}^{(\ell )}) \ne E^\mathrm{*}_j(S_{i,k}^{(\ell )})$.

Let $E_j(S_{i,k}^{(\ell )}) = E^\mathrm{*}_j(S_{i,k}^{(\ell )})$, i.e. $\not \exists _{m \in \mathbb {N}} S_{i,k}^{(\ell )} = m \cdot T_j$. As a result, it doesn’t matter whether $E_j(t)$ or $E^\mathrm{*}_j(t)$ is used in $\gamma _{i,k}(t)$.

Now let $E_j(S_{i,k}^{(\ell )}) \ne E^\mathrm{*}_j(S_{i,k}^{(\ell )})$, i.e. $\exists _{m \in \mathbb {N}} S_{i,k}^{(\ell )} = m \cdot T_j$. As a result, an additional activation of $\tau _j$ will be taken into account when determining $S_{i,k}^{(\ell +1)}$, irrespective of using either $E_j(t)$ or $E^\mathrm{*}_j(t)$ in $\gamma _{i,k}(t)$. Together, these two cases prove the lemma. $\square$

We therefore conclude that, apart from the number of job activations of $\tau _b$, the information in Table 2 also holds for $\tau _i$ when $B_i = 0$.

5.5 Identifying the task causing the largest blocking delay

A nice property of FPTS is that just one job of lower priority is able to cause blocking delays. In the presence of CRPD, however, the largest computation time among the blocking tasks does not necessarily result in the largest worst-case response time.

Example 6

We reconsider $\mathcal{T}_3$ of Example 3. Without CRPD, the blocking of $\tau _2$ due to $\tau _3$ and $\tau _4$ is the same because $C_3 = C_4$, i.e. $B_2 = \max (0, \max \{C_3, C_4\}) = 1$. The blocking including CRPD may be different, however, due to different UCBs of $\tau _3$ and $\tau _4$ and the ECBs of $\tau _1$. Even a smaller computation time of a blocking task may result in a larger overall blocking effect when CRPD is included.

For the case with blocking ($B_i \ne 0$), we therefore need a more complex procedure to compute response times. Our new procedure determines the values for $L_i,S_{i,k},F_{i,k}$, and $R_i$ with CRPD by taking the maximum value over all tasks that may block $\tau _i$.

5.6 Termination of the iterative procedure for $L_i$

Termination of the iterative procedure to determine $L_i$ is no longer guaranteed when $U < 1$, because the CRPD is not taken into account in the utilization U. To address this problem, we first observe that by definition every level-i active period, with $1 \le i < n$, is contained in a level-n active period (Bril et al. 2009). Hence, termination of the iterative procedure to determine $L_n$ guarantees termination for $L_i$ for all $1 \le i < n$. Next, the lowest priority task $\tau _n$ cannot be blocked. As a result, when $L_n$ exceeds the least common multiple (LCM) of the periods of the task set $\mathcal{T}$, the iterative procedure will not terminate. This is because at the LCM the activation pattern is repeated and if the iterative procedure for $L_n$ did not terminate at the LCM then there is pending load pushed across the LCM boundary. By integrating CRPD into the analysis, the effective utilization with CRPD is apparently larger than 1. The set is therefore considered unschedulable when $L_n$ exceeds the LCM.

5.7 Applying the results

In this section, we studied various preliminaries for the integration of CRPD in the analysis for FPTS. In the following sections, we apply the achieved results. In particular, we

• apply the notion of worst-case hold time by using $E_j(H_h)$ rather than $E_j(R_h)$ to tighten the number of times that $\tau _j$ may pre-empt a job of $\tau _h$ for approaches considering pre-empted tasks. This influences the definition of the multiset $M_{i,j}$ for the UCB-Only Multiset approach, the ECB-Union Multiset approach, and the UCB-Union Multiset approach.

• apply the derived “affected by $\tau _j$” information in the definitions of $\gamma _{i,j}$ and $M_{i,j}$ for the various approaches. This requires an extension of the subscripts of $S_{i,k}$, $F_{i,k},\gamma _{i,j}$ and $M_{i,j}$ with b for those cases where a task $\tau _b$ may block a task $\tau _i$.

• apply the derived “$\#$-jobs” information for approaches considering pre-empted tasks. This requires a case distinction following the information in Table 2 in the definition of the multiset $M_{i,j}$. Moreover, it requires a further extension of the subscripts of $\gamma _{i,j}$ and $M_{i,j}$ with k, and the introduction of an additional parameter for both $\gamma _{i,j}$ and $M_{i,j}$ to cater for the pre-emptions in the intervals corresponding to the worst-case start-time and the worst-case finalization time.

• take the maximum value over all tasks that may block $\tau _i$ to determine $L_i$ and $F_{i,k}$, when $\tau _i$ can be blocked.

6 FPTS with CRPD: pre-empting tasks

In this section, we consider the ECB-Only approach, i.e. focus only on the pre-empting tasks. Because the worst-case hold time $H_i$ and the row $\#$-jobs in Table 2 only play a role for pre-empted tasks, we ignore $H_i$ and $\#$-jobs in this section. In order to extend the equations for $L_i,S_{i,k}$ and $F_{i,k}$ for FPTS with a term $\gamma _{i,j}(t)$, we must adapt $\gamma ^{{\text {ecb-o}}}_{i,j}(t)$ by considering the tasks affected by task $\tau _j$ (see the row affected by $\tau _j$ in Table 2). As shown in Table 2, the tasks being affected by pre-emptions are the same for the intervals $[0, L_i),[0, S_{i,k})$, and $[0, F_{i,k})$, but differ from the tasks being affected under FPPS with constrained deadlines. We therefore generalize, i.e. redefine, the set of tasks ${\text{ aff }}({\pi }_i,{\pi }_j)$ for FPTS to

$$\begin{aligned} {\text{ aff }}({\pi }_i,{\pi }_j) \mathop {=}\limits ^{\mathrm {def}}{\text{ hep }}({\pi }_i) \cap {\mathrm{lt}}({\pi }_j). \end{aligned}$$

(21)

Because a task may but need not be blocked, we excluded “$\{b\}$” from (21) and will use dedicated clauses to treat blocking tasks in the sequel. Equation (21) for FPTS specializes to (11) for FPPS because ${\text{ lp }}({\pi }_j) = {\mathrm{lt}}({\pi }_j)$ for FPPS.

To determine the worst-case response time $R_i$ of task $\tau _i$, we can then reuse (7). In the subsections below, we consider the cases for tasks without and with blocking separately.

6.1 Worst-case length $L_i$

For a task $\tau _i$ without blocking ($B_i = 0$), we can find an upper bound for $L_i$ with CRPD by extending (3) with $\gamma _{i,j}(t)$, similar to the extension of $R_i$ in (9), i.e.

$$\begin{aligned} L_i = \sum _{\forall j \in {\mathrm{hep}}({\pi }_i)} \left( E_j(L_i) \cdot C_j + \gamma _{i,j}(L_i) \right) . \end{aligned}$$

(22)

For the ECB-Only approach, we can subsequently reuse (10) for $\gamma _{i,j}(t)$ with ${\text{ aff }}({\pi }_i,{\pi }_j)$ as defined in (21).

For the case $B_i \ne 0$, we rewrite (3) for $L_i$ by distributing addition over the inner-$\max$ operation in equation (4) for $B_i$ and subsequently extending the equation for CRPD as explained in Sect. 5.5, i.e.

$$\begin{aligned} L_i = \mathop {\max }\limits _{\forall b \in \mathrm{b}(i)} \left( C_b + \mathop {\sum }\limits _{\forall j \in {\mathrm{hep}}({\pi }_i)} \left( E_j(L_i) \cdot C_j + \gamma _{i,j,b}(L_i) \right) \right) . \end{aligned}$$

(23)

A subscript “b” has been introduced in $\gamma _{i,j,b}(t)$ to capture the CRPD related to the blocking task $\tau _b$. For the ECB-Only approach, $\gamma _{i,j,b}(t)$ is defined as

$$\begin{aligned} \gamma ^{{\text {ecb-o}}}_{i,j,b}(t) = \left\{ \begin{array}{ll} {\text{ BRT }}\cdot E_j(t) \cdot \left| {\text{ ECB }}_j \right| &{}\quad \text{ if } {\text{ aff }}({\pi }_i,{\pi }_j) \ne \emptyset \vee b \in {\mathrm{lt}}({\pi }_j) \\ 0 &{}\quad \text{ otherwise } \end{array} \right. . \end{aligned}$$

(24)

Compared to (10) for FPPS, the first clause for $\gamma ^{{\text {ecb-o}}}_{i,j,b}(t)$ in (24) for FPTS has been extended with $b \in {\mathrm{lt}}({\pi }_j)$, because $\tau _j$ may in that case also pre-empt task $\tau _b$. Note that $(\{b\} \cup {\text{ hep }}({\pi }_i)) \cap {\mathrm{lt}}({\pi }_j)$ in Table 2 is equal to ${\text{ aff }}({\pi }_i, {\pi }_j) \cup (\{b\} \cap {\mathrm{lt}}({\pi }_j))$ in (24).

6.2 Worst-case start time $S_{i,k}$

Similar to $L_i$, we extend Eq. (5) for $S_{i,k}$ with a term $\gamma _{i,k}(t)$ to include CRPD for tasks without blocking, i.e.

$$\begin{aligned} S_{i,k} = kC_i + \sum _{\forall j \in {\mathrm{hp}}({\pi }_i)} \left( E^\mathrm{*}_j(S_{i,k}) \cdot C_j + \gamma _{i,j}(S_{i,k}) \right) . \end{aligned}$$

(25)

Based on Lemma 2, we conclude that we can define $\gamma _{i,j}(t)$ in terms of $E_j(t)$ rather than $E^\mathrm{*}_j(t)$. Hence, we can also reuse $\gamma ^{{\text {ecb-o}}}_{i,j}(t)$ from (10) for the ECB-Only approach, i.e. we use ${\text{ aff }}({\pi }_i,{\pi }_j)$ as defined in (21), similar to $L_i$.

For tasks with blocking, we extend $S_{i,k}$ with an additional subscript “b” and a term $\gamma _{i,j,b}(t)$, i.e.

$$\begin{aligned} S_{i,k,b} = C_b + kC_i + \sum _{\forall j \in {\mathrm{hp}}({\pi }_i)} \left( E_j(S_{i,k,b}) \cdot C_j + \gamma _{i,j,b}(S_{i,k,b}) \right) . \end{aligned}$$

(26)

For the ECB-Only approach, we can reuse $\gamma ^{{\text {ecb-o}}}_{i,j,b}(t)$ from (24) for $\gamma _{i,j,b}(t)$, similar to $L_i$.

6.3 Worst-case finalization time $F_{i,k}$

For tasks without blocking, we can extend (20) with $\gamma _{i,j}(t)$ terms complementing $E_j(F_{i,k}) \cdot C_j$ and $E_j(S_{i,k}) \cdot C_j$, i.e.

$$\begin{aligned} F_{i,k}= & {} S_{i,k} + C_i + \sum _{\forall j \in {\mathrm{hp}}({\theta }_i)} \left( E_j(F_{i,k}) - E_j(S_{i,k}) \right) \cdot C_j \nonumber \\&+ \sum _{\forall j \in {\mathrm{hp}}({\theta }_i)} \left( \gamma _{i,j}(F_{i,k}) - \gamma _{i,j}(S_{i,k}) \right) . \end{aligned}$$

(27)

Similar to $L_i$ and $S_{i,k}$ we use (10) for $\gamma _{i,k}(t)$, with ${\text{ aff }}({\pi }_i,{\pi }_j)$ as defined in (21).

Similar to $S_{i,k}$, we add a subscript “b” to $F_{i,k}$ for tasks with blocking. Similar to the case $B_i = 0$, we expand the formula with terms for CRPD, i.e.

$$\begin{aligned} F_{i,k,b}= & {} S_{i,k,b} + C_i + \sum _{\forall j \in {\mathrm{hp}}({\theta }_i)} \left( E_j(F_{i,k,b}) - E_j(S_{i,k,b}) \right) \cdot C_j \nonumber \\&+ \sum _{\forall j \in {\mathrm{hp}}({\theta }_i)} \left( \gamma _{i,j,b}(F_{i,k,b}) - \gamma _{i,j,b}(S_{i,k,b}) \right) . \end{aligned}$$

(28)

The subtracted term $\gamma _{i,j,b}(S_{i,k,b})$ in (28) prevents the cache-related pre-emption costs already covered in (26) for $S_{i,k,b}$ being accounted for twice. Similar to $L_i$ and $S_{i,k}$, we apply (24) for $\gamma _{i,j,b}(t)$. To compute $F_{i,k}$, we take the maximum value over all tasks that may block $\tau _i$, similar to $L_i$ and as explained in Sect. 5.5, i.e.

$$\begin{aligned} F_{i,k} = \max _{\forall b \in \mathrm{b}(i)} F_{i,k,b}. \end{aligned}$$

(29)

7 FPTS with CRPD: pre-empted tasks

In this section, we consider the UCB-Only Multiset approach, i.e. we focus on the pre-empted tasks. In this case, the worst-case hold time $H_i$ and the row $\#$-jobs in Table 2 also play a role. As shown in Table 2, a case distinction is needed to capture the tasks that are being pre-empted, and these cases differ for $[0,H_i),[0, L_i),[0, S_{i,k})$ and $[0, F_{i,k})$. As a consequence, this section presents dedicated adaptations of $\gamma ^{{\text {ucb-o}}}_{i,j}(t)$ and $M^{{\text {ucb-o}}}_{i,j}(t)$, for each interval. For ease of presentation, we only consider the case where tasks may experience blocking. The other case is similar.

7.1 Worst-case hold time $H_i$

We can find an upper bound for $H_i$ with CRPD by extending (18) with $\gamma _{i,j}(t)$, similar to the extension of $R_i$ with $\gamma _{i,j}(t)$, i.e.

$$\begin{aligned} H_i = C_i + \sum _{j \in {\mathrm{hp}}({\theta }_i)} \left( E_j(H_i) \cdot C_j + \gamma _{i,j}(H_i) \right) . \end{aligned}$$

(30)

Although we can apply $\gamma ^{{\text {ucb-o}}}_{i,j}(t)$ in (13) for $\gamma _{i,j}(t)$ in (30) for the UCB-Only Multiset approach, we need to adapt the definition of $M^{{\text {ucb-o}}}_{i,j}(t)$ in (12) to prevent pessimism and use the proper set of affected tasks, as discussed in Sects. 5.2, 5.3 and 5.4. Firstly, worst-case hold times are to be considered for pre-empted tasks, rather than worst-case response times. Secondly, the set of affected tasks is to be adapted to $(\{i\} \cup {\text{ hp }}({\theta }_i)) \cap {\mathrm{lt}}({\pi }_i)$; see Table 2. Finally, exactly one job of task $\tau _i$ needs to be considered rather than $E_i(t)$ jobs, requiring a dedicated clause. These three adaptations of (12) result in

$$\begin{aligned} M^{{\text {ucb-o}}}_{i,j}(t) = \bigcup _{h \in {\mathrm{hp}}({\theta }_i) \cap {\mathrm{lt}}({\pi }_j)} \left( \bigcup _{E_j(H_h) \cdot E_h(t)} \bigl \vert {\text{ UCB }}_h \bigr \vert \right) \cup \left\{ \begin{array}{ll} \left( \mathop {\bigcup }\limits _{E_j(H_i)} \bigl \vert {\text{ UCB }}_i \bigr \vert \right) &{}\quad \text{ if }\; i \in {\mathrm{lt}}({\pi }_j)\\ \emptyset &{}\quad \text{ otherwise } \\ \end{array} \right. . \end{aligned}$$

(31)

7.2 Worst-case length $L_i$

Similar to the ECB-Only approach, we can use (23) to find an upper bound for $L_i$ by extending (13) for $\gamma ^{{\text {ucb-o}}}_{i,j}(t)$ with a subscript b for the blocking task $\tau _b$, with $b \in \mathrm{b}(i)$:

$$\begin{aligned} \begin{aligned} \gamma ^{{\text {ucb-o}}}_{i,j,b}(t) = {\text { BRT }}\cdot \sum _{\ell =1}^{E_j(t)} \mathtt {sort}\left( M^{{\text {ucb-o}}}_{i,j,b}(t) \right) [\ell ]. \end{aligned} \end{aligned}$$

(32)

The definition of $M^{{\text {ucb-o}}}_{i,j}(t)$ in (12) also needs to be extended with a subscript b, to consider exactly one blocking job of $\tau _b$ rather than $E_b(t)$ jobs; see Table 2.

$$\begin{aligned} M^{{\text {ucb-o}}}_{i,j,b}(t) = \bigcup _{h \in {\mathrm{aff}}({\pi }_i,{\pi }_j)} \left( \bigcup _{E_j(H_h) \cdot E_h(t)} \bigl \vert {\text{ UCB }}_h \bigr \vert \right) \cup \left\{ \begin{array}{ll} \left( \mathop {\bigcup }\limits _{E_j(H_b)} \bigl \vert {\text{ UCB }}_b \bigr \vert \right) &{} \quad \text{ if }\; b \in {\mathrm{lt}}({\pi }_j)\\ \emptyset &{}\quad \text{ otherwise } \\ \end{array} \right. . \end{aligned}$$

(33)

The pre-condition $b \in \mathrm{b}(i)$ for $M^{{\text {ucb-o}}}_{i,j,b}(t)$ is taken into account by the $\max$ in (23). The definition of $M^{{\text {ucb-o}}}_{i,j,b}(t)$ contains the worst-case hold times of $\tau _h$ and $\tau _b$ rather than their worst-case response times to avoid pessimism.

7.3 Worst-case start time $S_{i,k}$

As well as considering exactly one job of task $\tau _b$, the definitions of $\gamma ^{{\text {ucb-o}}}_{i,j,b}(t)$ and $M^{{\text {ucb-o}}}_{i,j,b}(t)$ are further extended for $S_{i,k}$ to consider exactly k jobs of $\tau _i$ (see Table 2), i.e.

$$\begin{aligned} \begin{aligned} \gamma ^{{\text {ucb-o}}}_{i,j,k,b}(t) = {\text { BRT }}\cdot \sum _{\ell =1}^{E_j(t)} \mathtt {sort}\left( M^{{\text {ucb-o}}}_{i,j,k,b}(t) \right) [\ell ] \end{aligned} \end{aligned}$$

(34)

and

$$\begin{aligned} M^{{\text {ucb-o}}}_{i,j,k,b}(t)= & {} \bigcup _{h \in {\mathrm{aff}}({\pi }_i,{\pi }_j) \setminus \{i\}} \left( \bigcup _{E_j(H_h) \cdot E_h(t)} \bigl \vert {\text{ UCB }}_h \bigr \vert \right) \cup \left\{ \begin{array}{ll} \left( \mathop {\bigcup }\limits _{E_j(H_i) \cdot k} \bigl \vert {\text{ UCB }}_i \bigr \vert \right) &{} \quad \text{ if }\; i \in {\mathrm{lt}}({\pi }_j)\\ \emptyset &{} \quad \text{ otherwise }\\ \end{array}\right. \nonumber \\&\cup \left\{ \begin{array}{ll} \left( \mathop {\bigcup }\limits _{E_j(H_b)} \bigl \vert {\text{ UCB }}_b \bigr \vert \right) &{} \quad \text{ if }\; b \in {\mathrm{lt}}({\pi }_j)\\ \emptyset &{} \quad \text{ otherwise } \\ \end{array} \right. . \end{aligned}$$

(35)

Similar to $H_i$, task $\tau _i$ is again treated by a separate clause, which makes it necessary to use ${\text{ aff }}({\pi }_i,{\pi }_j) \setminus \{i\}$ rather than ${\text{ aff }}({\pi }_i,{\pi }_j)$. Moreover, $M^{{\text {ucb-o}}}_{i,j,k,b}(t)$ is based on the worst-case hold times of the tasks $\tau _h,\tau _i$, and $\tau _b$ rather than their worst-case response times.

Similar to the ECB-Only approach, a subscript “b” is added to $S_{i,k}$, and the equation of $S_{i,k}$ in (5) is extended with $\gamma _{i,j,k,b}(t)$ as follows:

$$\begin{aligned} S_{i,k,b} = C_b + kC_i + \sum _{\forall j \in {\mathrm{hp}}({\pi }_i)} \left( E_j(S_{i,k,b}) \cdot C_j + \gamma _{i,j,k,b}(S_{i,k,b}) \right) . \end{aligned}$$

(36)

7.4 Worst-case finishing time $F_{i,k}$

As indicated in Table 2, exactly $k+1$ jobs of $\tau _i$ need to be considered for $F_{i,k}$. Moreover, we need to split the set of tasks ${\text{ hp }}({\pi }_i)$ into two subsets for $F_{i,k}$, i.e. the set ${\text{ hp }}({\pi }_i) \setminus {\text{ hp }}({\theta }_i)$ of tasks that can be blocked by $\tau _i$ and the set ${\text{ hp }}({\theta }_i)$ that cannot be blocked by $\tau _i$. The former set can execute and experience pre-emptions in $[0,S_{i,k})$, whereas the latter set can execute and experience pre-emptions in $[0,F_{i,k})$. To take the proper number of activations of tasks in these two sets into account, we use two parameters $t_s$ and $t_f$ for $\gamma ^{{\text {ucb-o}}}_{i,j,k,b}$ and $M^{{\text {ucb-o}}}_{i,j,k,b}$, i.e.

$$\begin{aligned} \gamma ^{{\text {ucb-o}}}_{i,j,k,b}(t_s, t_f) = {\text { BRT }}\cdot \sum _{\ell =1}^{E_j(t_f)} \mathtt {sort}\left( M^{{\text {ucb-o}}}_{i,j,k,b}(t_s, t_f) \right) [\ell ], \end{aligned}$$

(37)

and

$$\begin{aligned} \displaystyle M^{{\text {ucb-o}}}_{i,j,k,b}(t_s, t_f)=&{} \bigcup \limits _{h \in (({\text {aff }}({\pi }_i,{\pi }_j) \setminus \{i\}) \cap {\text { hp }}({\theta }_i))} \left( \bigcup \limits _{E_j(H_h) \cdot E_h(t_f)} \bigl \vert {\text { UCB}}_h \bigr \vert \right) \nonumber \\ {}&\cup \bigcup \limits _{h \in (({\text {aff }}({\pi }_i,{\pi }_j) \setminus \{i\}) \setminus {\text { hp }}({\theta }_i))} \left( \bigcup \limits _{E_j(H_h) \cdot E_h(t_s)} \bigl \vert {\text { UCB}}_h \bigr \vert \right) \nonumber \\ {}&\cup \left\{ \begin{array}{ll} \left( \mathop {\bigcup }\limits _{E_j(H_i) \cdot (k+1)} \bigl \vert {\text { UCB}}_i \bigr \vert \right) &{}\quad \text { if } i \in {\text { lt }}({\pi }_j) \\ \emptyset &{}\quad \text { otherwise } \\ \end{array} \right. \nonumber \\ {}&\cup \left\{ \begin{array}{ll} \left( \mathop {\bigcup }\limits _{E_j(H_b)} \bigl \vert {\text { UCB}}_b \bigr \vert \right) &{}\quad \text {if } b \in {\text { lt }}({\pi }_j) \\ \emptyset &{}\quad \text {otherwise } \\ \end{array} \right. . \end{aligned}$$

(38)

Similar to the ECB-Only approach, $F_{i,k}$ is extended with a subscript “b” and $\gamma _{i,j,k,b}$ terms, i.e.

$$\begin{aligned} F_{i,k,b}= & {} S_{i,k,b} + C_i \nonumber \\&+ \sum _{\forall j \in {\mathrm{hp}}({\theta }_i)} \left( E_j(F_{i,k,b}) - E_j(S_{i,k,b}) \right) \cdot C_j ~\nonumber \\&+ \sum _{\forall j \in {\mathrm{hp}}({\theta }_i)} \left( \gamma _{i,j,k,b}(S_{i,k,b}, F_{i,k,b}) - \gamma _{i,j,k,b}(S_{i,k,b}) \right) . \end{aligned}$$

(39)

The term $\gamma _{i,j,k,b}(S_{i,k,b})$ in (39) prevents the cache-related pre-emption costs already covered in (36) for $S_{i,k,b}$ being accounted for twice.

We may subsequently determine $F_{i,k}$ by (29) and can derive $R_i$ through (7) as before.

8 FPTS with CRPD: pre-empting and pre-empted tasks

In this section, we consider the ECB-Union and UCB-Union Multiset approaches, i.e. we consider both the pre-empting and the pre-empted tasks. As described in Sect. 4.2 for FPPS with CRPD, the definitions of the multisets for the ECB-Union and UCB-Union Multiset approaches can be derived from the definition of the multiset for the UCB-Only Multiset approach. A similar derivation applies for FPTS with CRPD. We therefore only consider the definition of the multisets $M^{{\text {ecb-u}}}_{i,j,k,b}(t_s,t_f)$ and $M^{{\text {ucb-u}}}_{i,j,k,b}(t_s,t_f)$ for the worst-case finalization time $F_{i,k}$ for the case with blocking. The derivation of the definitions for the case without blocking and for the worst-case hold time $H_i$, worst-case length $L_i$ and worst-case start time $S_{i,k}$ are similar.

8.1 ECB-Union Multiset approach

The ECB-Union Multiset approach considers the pre-emption cost of pre-empting tasks for every pre-empted task individually. Similar to FPPS with CRPD, the definition of the multiset of the UCB-Only Multiset approach is extended by intersecting the UCBs of every affected task with $\left( \bigcup _{g \in {\mathrm{hep}}({\pi }_j) } {\text{ ECB }}_g \right)$, e.g. from (38) for $M^{{\text {ucb-o}}}_{i,j,k,b}(t_s, t_f)$ we derive

$$\begin{aligned}&M^{{\text {ecb-u}}}_{i,j,k,b}(t_s, t_f)\nonumber \\&\quad = {} \bigcup \limits _{h \in (({\text {aff }}({\pi }_i,{\pi }_j) \setminus \{i\}) \cap {\text { hp }}({\theta }_i))} \left( \bigcup \limits _{E_j(H_h) \cdot E_h(t_f)} \left| {\text { UCB}}_h \cap \left( \bigcup \limits _{g \in {\text { hep}}({\pi }_j)} {\text { ECB}}_g \right) \right| \right) \nonumber \\&\qquad \cup \bigcup \limits _{h \in (({\text {aff }}({\pi }_i,{\pi }_j) \setminus \{i\}) \setminus {\text { hp }}({\theta }_i))} \left( \bigcup \limits _{E_j(H_h) \cdot E_h(t_s)} \left| {\text { UCB}}_h \cap \left( \bigcup \limits _{g \in {\text { hep}}({\pi }_j)} {\text { ECB}}_g \right) \right| \right) \nonumber \\&\qquad \qquad \qquad \cup \left\{ \begin{array}{ll} \left( \mathop {\bigcup }\limits _{E_j(H_i) \cdot (k+1)} \left| {\text { UCB}}_i \cap \left( \mathop {\bigcup }\limits _{g \in {\text { hep}}({\pi }_j)} {\text { ECB}}_g \right) \right| \right) &{}\quad \text {if } i \in {\text { lt }}({\pi }_j) \\ \emptyset &{}\quad \text {otherwise } \\ \end{array} \right. \nonumber \\&\qquad \qquad \qquad \cup \left\{ \begin{array}{ll} \left( \mathop {\bigcup }\limits _{E_j(H_b)} \left| {\text { UCB}}_b \cap \left( \mathop {\bigcup }\limits _{g \in {\text { hep}}({\pi }_j)} {\text { ECB}}_g \right) \right| \right) &{}\quad \text {if } b \in {\text { lt }}({\pi }_j) \\ \emptyset &{}\quad \text {otherwise } \\ \end{array} \right. . \end{aligned}$$

(40)

The equation for $\gamma ^{{\text {ecb-u}}}_{i,j,k,b}(t_s, t_f)$ for the ECB-Union Multiset approach is identical to (37) for the UCB-Only Multiset approach, except that it uses $M^{{\text {ecb-u}}}_{i,j,k,b}(t)$ instead of $M^{{\text {ucb-o}}}_{i,j,k,b}(t)$. The equations for $F_{i,k,b}$ in (39) and $F_{i,k}$ in (29) can be reused for the ECB-Union Multiset approach.

8.2 UCB-Union Multiset approach

For the UCB-Union Multiset approach, first a multiset $M^{{\text {ucb}}}_{i,j,k,b}(t_s, t_f)$ is formed. Similar to FPPS with CRPD, the definition for $M^{{\text {ucb}}}_{i,j,k,b}(t_s, t_f)$ can be derived from (38) for $M^{{\text {ucb-o}}}_{i,j,k,b}(t_s, t_f)$ by removing all cardinality operators, i.e.

$$\begin{aligned} M^{{\text {ucb}}}_{i,j,k,b}(t_s, t_f)=&{} \bigcup \limits _{h \in (({\text {aff }}({\pi }_i,{\pi }_j) \setminus \{i\}) \cap {\text { hp }}({\theta }_i))} \left( \bigcup \limits _{E_j(H_h) \cdot E_h(t_f)} {\text { UCB}}_h \right) \nonumber \\ {}&\cup \bigcup \limits _{h \in (({\text {aff }}({\pi }_i,{\pi }_j) \setminus \{i\}) \setminus {\text { hp }}({\theta }_i))} \left( \bigcup \limits _{E_j(H_h) \cdot E_h(t_s)} {\text { UCB}}_h \right) \nonumber \\&\cup \left\{ \begin{array}{ll} \left( \mathop {\bigcup }\limits _{E_j(H_i) \cdot (k+1)} {\text { UCB}}_i \right) &{}\quad \text { if } i \in {\text { lt }}({\pi }_j) \\ \emptyset &{}\quad \text { otherwise } \\ \end{array} \right. \nonumber \\ {}&\cup \left\{ \begin{array}{ll} \left( \mathop {\bigcup }\limits _{E_j(H_b)} {\text { UCB}}_b \right) &{}\quad \text { if } b \in {\text { lt }}({\pi }_j) \\ \emptyset &{}\quad \text { otherwise } \\ \end{array} \right. . \end{aligned}$$

(41)

Similar to FPPS with CRPD, the definition of $\gamma ^{{\text {ucb-u}}}_{i,j,k,b}$ is given in terms of the size of the multi-set intersection of $M_j^{{\mathrm{ecb}}}(t)$ and $M^{{\text {ucb}}}_{i,j,k,b}(t_s, t_f)$, i.e.

$$\begin{aligned} \begin{aligned} \gamma ^{{\text {ucb-u}}}_{i,j,k,b}(t_s,t_f) = {\text { BRT }}\cdot \left| M_j^{{\text { ecb }}}(t_f) \cap M^{{\text {ucb}}}_{i,j,k,b}(t_s,t_f) \right| , \end{aligned} \end{aligned}$$

(42)

where $M^{{\mathrm{ecb}}}_j(t)$ is defined in (16). The equations for the worst-case finalization time $F_{i,k,b}$ in (39) and $F_{i,k}$ in (29) also apply for the UCB-Union Multiset approach.

8.3 Composite approach

The ECB-Union Multiset and UCB-Union Multiset approaches can be combined into a simple composite approach that dominates both (Altmeyer et al. 2012). For FPPS, this composite approach uses

$$\begin{aligned} \begin{aligned} R_i = \min (R_i^{{\text {ecb-u}}}, R_i^{{\text {ucb-u}}}), \end{aligned} \end{aligned}$$

(43)

where $R_i^{{\mathrm{ecb}\hbox {-}\mathrm{u}}}$ and $R_i^{{\mathrm{ucb}\hbox {-}\mathrm{u}}}$ are the worst-case response times of task $\tau _i$ using the ECB-Union Multiset approach and the UCB-Union Multiset approach, respectively. As (43) is applied on a task by task basis, some task-sets are deemed schedulable by the combined approach, but not by any of the other approaches in isolation.

For FPTS, this simple composite approach is refined by first applying the composition to the worst-case hold times of the tasks. Thus we first use the ECB-Union Multiset and UCB-Union Multiset approaches to compute the worst-case hold times ($H_i^\mathrm{ecb}$ and $H_i^\mathrm{ucb}$, respectively) for each task $\tau _i$. Then for each task we take the minimum value, i.e.

$$\begin{aligned} H_i = \min (H_i^\mathrm{ecb}, H_i^\mathrm{ucb}). \end{aligned}$$

(44)

The minimum worst-case hold times given by (44) are then used in the calculation of response times using the ECB-Union Multiset and UCB-Union Multiset approaches. Finally, the minimum worst-case response time computed by either approach is used as output from the composite approach, as given by (43). Since this composite approach is the most effective analysis for FPTS with CRPD, we use it in our evaluation.⁵

9 An optimal threshold assignment algorithm

In Wang and Saksena (1999) an OTA for a set $\mathcal{T}$ scheduled under FPTS without CRPD is described, which assumes that priorities of tasks are given, i.e. it finds pre-emption thresholds achieving schedulability of $\mathcal{T}$ under FPTS, if such an assignment exists. When the OTA finds pre-emption thresholds for a set $\mathcal{T}$, those thresholds will be minimal. The algorithm traverses the tasks in ascending priority order, exploiting the property that the schedulability test for task $\tau _i$ is independent of the pre-emption thresholds of tasks with a priority higher than $\tau _i$. For FPTS with CRPD this property does not hold. As an example, a task $\tau _j$ may affect a task $\tau _h$, with $j, h \in {\text{ hp }}({\pi }_i)$, when the pre-emption threshold ${\theta }_h$ of $\tau _h$ is lower than the priority ${\pi }_j$ of $\tau _j$. The algorithm subsequently presented in Saksena and Wang (2000) can determine the maximum pre-emption thresholds of tasks, taking a threshold assignment for which the set is schedulable as input.

This section presents an OTA algorithm for FPTS with CRPD, yielding the maximum pre-emption thresholds of tasks when the set is schedulable. The algorithm also assumes that priorities of tasks are given and traverses the tasks in descending priority order. It exploits the property that once a task $\tau _i$ is schedulable, it remains schedulable when the pre-emption threshold ${\theta }_\ell$ of a task $\tau _\ell$ with a priority lower than task $\tau _i$ is reduced and the pre-emption threshold ${\theta }_\ell$ either was or becomes lower than priority ${\pi }_i$.

9.1 Algorithm description

Our OTA algorithm (see Algorithm 1) uses an auxiliary set $\widehat{\Theta } = \{\widehat{{\theta }_1}, \widehat{{\theta }_2}, \ldots , \widehat{{\theta }_n}\}$ of maximum pre-emption thresholds next to a set $\Theta = \{{\theta }_1, {\theta }_2, \ldots , {\theta }_n\}$ of assigned pre-emption thresholds. Upon initialization, all values in $\widehat{\Theta }$ are set to the highest priority ${\pi }_1$ (line 2), i.e. tasks are non-pre-emptive and therefore experience minimal CRPD. The algorithm traverses the tasks in descending priority order (lines 5–23). When it considers a task $\tau _i$, it first assigns its maximum pre-emption threshold $\widehat{{\theta }_i}$ to ${\theta }_i$ (line 7). Next, it tests schedulability of $\tau _i$ without any blocking and returns unschedulable when the test fails (line 9). Otherwise, it tests schedulability of $\tau _i$ with blocking by considering each lower priority task $\tau _\ell$ in isolation (lines 11–22). It decreases the maximum pre-emption threshold $\widehat{{\theta }_\ell }$ of $\tau _\ell$ if-and-only-if $\tau _i$ is unschedulable due to blocking by task $\tau _\ell$ (lines 17–19). In that case, $\widehat{{\theta }_\ell }$ is decreased to the highest priority of all tasks with a priority lower than $\tau _i$, i.e. ${\pi }_{i+1}$ of $\tau _{i+1}$. This may increase the CRPD of tasks with a priority lower than $\tau _i$ but does not affect the schedulability of tasks with a priority higher than ${\pi }_i$. Hence, when the algorithm returns schedulable, i.e. the task set is schedulable, it has assigned the maximum pre-emption threshold to each task. A proof of correctness and detailed explanation of our OTA algorithm using invariants are given in the next subsection.

9.2 Correctness and proof of OTA algorithm

Our algorithm is based on two invariants, which use $\Pi = \{{\pi }_1, {\pi }_2, \ldots , {\pi }_n\}$ to denote the set of priorities and $\mathcal{T}^\mathrm{H}_m$ to denote the subset of m highest priority tasks with $0 \le m \le n$, i.e. $\mathcal{T}^\mathrm{H}_0 = \emptyset$, $\mathcal{T}^\mathrm{H}_i = \{\tau _h \vert h \in {\text{ hep }}({\pi }_i)\}$ for $1 \le i \le n$, and $\mathcal{T}^\mathrm{H}_n = \mathcal{T}$.

If the following main invariant holds for $\mathcal{T}$, then $\Theta$ contains the maximum pre-emption thresholds for which all tasks in $\mathcal{T}$ are schedulable, where $\Theta = \widehat{\Theta } \subseteq \Pi$.

Invariant 1

Given a subset $\mathcal{T}^\mathrm{H}_m$ of m highest priority tasks

• 1. the set $\widehat{\Theta }$ contains the maximum pre-emption threshold of each task such that all tasks in $\mathcal{T}^\mathrm{H}_m$ meet their deadlines, i.e. $\forall _{\tau _i \in \mathcal{T}^\mathrm{H}_m} R_i \le D_i$, where $\widehat{\Theta } \subseteq \Pi$.

• 2. the set $\Theta$ contains the assigned pre-emption threshold of $\tau _j$ if $\tau _j \in \mathcal{T}^\mathrm{H}_m$, i.e. ${\theta }_j = \widehat{{\theta }_j}$, and it contains the priority of $\tau _j$ if $\tau _j \notin \mathcal{T}^\mathrm{H}_m$, i.e. ${\theta }_j = {\pi }_j$.

The variables in $\widehat{\Theta }$ and $\Theta$ are initialized to the highest (non-pre-emptive) priority ${\pi }_1$ (line 2) and the (fully pre-emptive) priority of the corresponding task (line 3), respectively. As a result, Invariant 1 holds for the empty set $\mathcal{T}^\mathrm{H}_0$.

Next, the algorithm traverses the tasks in descending priority order (lines 5–23). When a task $\tau _i$ is considered (line 5), Invariant 1 holds for $\mathcal{T}^\mathrm{H}_{i-1}$. First the pre-emption threshold of $\tau _i$ is assigned its maximum value, i.e. ${\theta }_i$ is set to $\widehat{{\theta }_i}$ (line 7), and the schedulability of $\tau _i$ without blocking is determined. If $\tau _i$ is not schedulable, then the algorithm returns unschedulable (line 9), i.e. there does not exist a pre-emption threshold assignment making the set of tasks $\mathcal{T}^\mathrm{H}_i$ schedulable. Otherwise 2) has been established for $\mathcal{T}^\mathrm{H}_i$ and the inner-loop is entered.

The inner-loop (lines 11–22) considers each task $\tau _\ell$ with a priority lower than $\tau _i$ separately. The aim is to establish 1) for $\mathcal{T}^\mathrm{H}_i$, based on the following invariant.

Invariant 2

Given a task $\tau _i$ and a subset $\mathcal{T}^\mathrm{H}_{\ell }$ with $\ell \in {\text{ lep }}({\pi }_i)$, the set $\widehat{\Theta }$ contains the maximum pre-emption threshold for each task, where $\widehat{\Theta } \subseteq \Pi$, such that

• 1. all tasks in $\mathcal{T}^\mathrm{H}_{i-1}$ are schedulable, and

• 2. $\tau _i$ is schedulable when only the set $\mathcal{T}^\mathrm{H}_{\ell }$ is considered, i.e. when all tasks in $\mathcal{T} \setminus \mathcal{T}^\mathrm{H}_{\ell }$ are ignored.

If this invariant holds for $\tau _i$ and $\mathcal{T}$ then $\widehat{\Theta }$ contains the maximum pre-emption thresholds for which all tasks in $\mathcal{T}^\mathrm{H}_i$ are schedulable, where $\widehat{\Theta } \subseteq \Pi$, i.e. Invariant 1 holds for $\mathcal{T}^\mathrm{H}_i$.

Before the inner-loop, Invariant 2 holds for $\tau _i$ and $\mathcal{T}^\mathrm{H}_i$, and when a task $\tau _\ell$ is considered (line 11), it holds for $\tau _i$ and $\mathcal{T}^\mathrm{H}_{\ell -1}$. When $\tau _i$ remains schedulable when blocked by $\tau _\ell ,\widehat{{\theta }_\ell }$ remains unchanged. Otherwise $\widehat{{\theta }_\ell }$ is set to the priority ${\pi }_{i+1}$ of task $\tau _{i+1}$, i.e. the highest priority in $\Pi$ for which $\tau _i$ is not blocked by $\tau _\ell$. This may increase the CRPD of tasks with a priority lower than $\tau _i$, but does not affect the schedulability of tasks with a priority higher than $\tau _i$. Note that it doesn’t make sense to decrease the threshold of $\tau _\ell$ to a priority higher than or equal to the priority of $\tau _i$, because the CRPD experienced by $\tau _i$ remains at best the same and may even increase due to additional pre-emptions during the execution of a job of $\tau _\ell$. Invariant 2 has therefore been established for $\mathcal{T}^\mathrm{H}_{\ell }$.

Theorem 1

Given a set of tasks $\mathcal{T}$ and a priority assignment $\Pi$, the OTA algorithm (Algorithm 1) assigns the maximum pre-emption thresholds $\Theta \subseteq \Pi$ to tasks achieving schedulability, if such an assignment exists.

Proof

At each iteration of the outer-loop, the set $\mathcal{T}^\mathrm{H}_m$ of Invariant 1 is increased by one task. Similarly, at each iteration of the inner-loop, the set $\mathcal{T}^\mathrm{H}_\ell$ of Invariant 2 is increased by one task. Hence, the algorithm terminates with either schedulable and a set of maximum pre-emption thresholds that deem the task set schedulable with the least possible CRPD or unschedulable, in which case no assignment of pre-emption thresholds achieving schedulability exists under the given priority assignment. $\square$

9.3 Algorithmic complexity

Algorithm 1 traverses the set of tasks (of size n) in descending priority order and it may then consider any lower-priority task (at most $n-1$ tasks). Hence, just like the algorithm in Wang and Saksena (1999), our algorithm has $\mathcal{O}(n^2)$ iterations. In each iteration, the response time analysis is applied, which has a pseudo-polynomial time complexity.

10 Layout of tasks in memory

The analysis presented in the previous sections integrates CRPD into the analysis of FPTS based on ECBs and UCBs of tasks, i.e. the analysis is independent of the memory blocks of tasks and the mapping from memory blocks to cache blocks. In this section, we take a closer look at how the layout of tasks in memory influences the schedulability of task sets.

10.1 Influence of task layout on CRPD

Given a mapping ${ MapM2C}$ from memory blocks to cache blocks, the layout of a task $\tau _i$ in memory, as described by ${\text{ MB }}_i$, determines $\tau _i$’s set of evicting cache blocks ${\text{ ECB }}_i$, see (2). The layout of tasks in memory therefore impacts the pre-emption delays, as illustrated by the following example.

Example 7

Figure 5 illustrates the impact of a task layout for FPTS. The cache contains 8 cache blocks. The task set contains 4 tasks, each with 4 ECBs and 4 UCBs. Task $\tau _1$ and $\tau _2$ as well as $\tau _3$ and $\tau _4$ are mutually non-pre-emptive due to pre-emption thresholds. An initial task layout resulting in ${\text{ ECB }}_1 = {\text{ ECB }}_3$ and ${\text{ ECB }}_2 = {\text{ ECB }}_4$ produces pre-emption related cache eviction in all cache blocks, whereas an optimal layout resulting in ${\text{ ECB }}_1 = {\text{ ECB }}_2$ and ${\text{ ECB }}_3 = {\text{ ECB }}_4$ eliminates CRPD completely under FPTS. Unlike FPTS, both layouts produce CRPD in all cache blocks under FPPS for this task set.

Fig. 5

Impact of the task layout on the pre-emption overhead. a The initial task layout produces pre-emption related cache eviction in all cache blocks, because $\tau _1$ may pre-empt $\tau _3$ and $\tau _2$ may pre-empt $\tau _4$. b An optimal task layout, which eliminates CRPD completely for FPTS, because tasks $\tau _1$ and $\tau _2$ as well as tasks $\tau _3$ and $\tau _4$ are mutually non-pre-emptive. FPPS still produces CRPD in all cache blocks, however

The pre-emption costs can thus be reduced and the schedulability improved by determining an appropriate memory layout. An intuitive task layout positions the memory blocks of all tasks consecutively in memory without leaving gaps, i.e. without leaving unused memory blocks between tasks’ blocks. This means that the memory blocks of the first task $\tau _1$ are positioned at initial memory block $M_{\text {init}}$, the blocks of the second task $\tau _2$ at $M_{\text {init}} + \vert {\text{ MB }}_1 \vert$, and of task $\tau _i$ at $M_{\text {init}} + \sum _{j < i} \vert {\text{ MB }}_j \vert$. Lunniss et al. (2012) have observed that gaps within a task layout, i.e. memory blocks that are left empty between the tasks, only improves the schedulability slightly for FPPS, at the cost of wasting memory. We therefore focus on sequential layouts in this paper and only vary the order in which tasks are positioned in memory.

10.2 Determining ECBs and UCBs for a given task layout

As illustrated above, the ECBs and UCBs of tasks may change when the task layout changes. We describe a task layout by means of a permutation $\mathfrak {P}$, i.e. an ordered n-tuple that contains each task index 1 to n exactly once. In this paper, we assume an initial task permutation $\mathfrak {P}_\mathrm{init}$ defined by the tasks’ priorities

$$\begin{aligned} \mathfrak {P}_\mathrm{init} = (1,2,3,\ldots , n). \end{aligned}$$

(45)

To determine the ECBs and UCBs of tasks for a given task layout, we assume that they are initially given in normalized form, i.e. as if the first evicting cache blocks of every task start at cache block 0. We denote the normalized form of the ECBs and UCBs of task $\tau _i$ as ${\text{ ECB }}_i^\mathrm{N}$ and ${\text{ UCB }}_i^\mathrm{N}$, respectively. Given this normalized form, we can determine the sets ${\text{ ECB }}_i$ and ${\text{ UCB }}_i$ of $\tau _i$ for a given permutation $\mathfrak {P}$ and a cache size $N^\mathrm{C}$ using (1), i.e. simply by means of shifting. The set ${\text{ UCB }}_i$ of task $\tau _i$ for a permutation $\mathfrak {P}$ and cache size $N^\mathrm{C}$ is given by

$$\begin{aligned} {\text{ UCB }}_i = \bigcup _{c \in {\text{ UCB }}_i^\mathrm{N}} \left( M_\mathrm{init} + \sum _{1 \le j < p_i} \vert {\text{ MB }}_{\mathfrak {P}[j]} \vert + c\right) \bmod N^\mathrm{C}, \end{aligned}$$

(46)

where $\mathfrak {P}[j]$ denotes the index of the task at position j in $\mathfrak {P}$, and $p_i$ denotes the position of task $\tau _i$ in $\mathfrak {P}$, i.e. $\mathfrak {P}[p_i] = i$. The set ${\text{ ECB }}_i$ of task $\tau _i$ is defined analogously, i.e.

$$\begin{aligned} {\text{ ECB }}_i = \bigcup _{c \in {\text{ ECB }}_i^\mathrm{N}} \left( M_\mathrm{init} + \sum _{1 \le j < p_i} \vert {\text{ MB }}_{\mathfrak {P}[j]} \vert + c\right) \bmod N^\mathrm{C}. \end{aligned}$$

(47)

We note that the normalization of the sets of UCBs and ECBs does not impact the relative order of a task’s memory blocks. Instead, normalization corresponds to shifting the complete task in memory without any modifications to the task itself.

In the following, we will use $\mathcal{T}^\mathrm{N}$ to denote a task set with ECBs and UCBs in normalized form. Moreover, we assume a function ${ ShiftCBs}(\mathcal{T}^\mathrm{N},\mathfrak {P}, N^\mathrm{C})$ which takes a task set $\mathcal{T}^\mathrm{N}$ with ECBs and UCBs in normalized form and yields the same task set but with ECBs and UCBs determined for permutation $\mathfrak {P}$ and cache size $N^\mathrm{C}$.

10.3 An algorithm to search for a schedulable task layout

For a task set consisting of n tasks, there exists n! permutations. Given the size of this space, we search for a schedulable task layout using simulated annealing (SA), similar to Lunniss et al. (2012). When we encounter a schedulable task layout, we stop immediately. In order to compare an unschedulable task layout with a new, unschedulable, candidate layout, we need a metric. For this purpose, we use the breakdown utilization $U^*$ (Lehoczky et al. 1989) based on scaling the computation times of tasks with a factor $\Delta$. For an unschedulable task layout of a task set $\mathcal{T}$, the breakdown utilization $U^*$ is smaller than the utilization U of $\mathcal{T}$, i.e. the largest possible scaling factor $\Delta ^*$ for which $\mathcal{T}$ is schedulable for that layout will satisfy $0< \Delta ^* < 1$.

In contrast to hill-climbing, which never selects the candidate if the breakdown utilization becomes worse, simulated annealing allows to select worse candidates to escape local optima. To this end, simulated annealing maintains a temperature ($\mathfrak {T}$) indicating the likelihood to select a neighboring candidate worse than the current candidate. A candidate is selected with a probability P given by

$$\begin{aligned} P = \min (1, e^{\frac{U^*_\mathrm{new} - U^*}{\mathfrak {T}}}), \end{aligned}$$

(48)

where $U^*$ is the breakdown utilization of the current permutation and $U^*_\mathrm{new}$ the breakdown utilization of the new candidate. Similar to hill-climbing, better candidates are always selected because $U^*_\mathrm{new} \ge U^* \Rightarrow P = 1$, i.e. the candidate layout is selected when the breakdown utilization improves.

The STLS algorithm (Algorithm 2) starts with an initial task permutation $\mathfrak {P}_\mathrm{init}$ (line 1). Next, it tests schedulability of the task set for the initial permutation and returns schedulable when the test succeeds (line 4). When the test fails, the initializations required for simulated annealing are performed (lines 7–8). The algorithm subsequently repeatedly selects new layout candidates until either a schedulable layout is found (line 19) or the bound on the maximum number of permutations considered is reached (line 9). This bound can be expressed in terms of an initial temperature $\mathfrak {T}_\mathrm{init}$ (line 7) with $0 < \mathfrak {T}_\mathrm{init}$, a target temperature $\mathfrak {T}_\mathrm{target}$ (line 9) with $0 < \mathfrak {T}_\mathrm{target} \le \mathfrak {T}_\mathrm{init}$, and a cooling factor $f_\mathrm{cooling}$ (line 27) with $0< f_\mathrm{cooling} < 1$. A candidate layout is randomly chosen by swapping the position of two tasks in the current permutation (lines 11–15). With equal probability, the algorithm swaps two neighboring tasks, or two tasks at random irrespective of the position in the current layout. When the candidate is schedulable, we are done (lines 17–19). Otherwise, we determine whether or not to select the new candidate (lines 22–26).

Although the SA algorithm will not always find a schedulable layout whenever one exists, i.e. Algorithm 2 is not an optimal algorithm, it performs close to a brute-force algorithm (Lunniss et al. 2012) in terms of precision when appropriate parameters are used.

10.4 Algorithmic complexity

The STLS algorithm (Algorithm 2) tries at most $\left\lceil \frac{\log \mathfrak {T}_\mathrm{target} - \log \mathfrak {T}_\mathrm{init}}{\log f_\mathrm{cooling}} + 1 \right\rceil$ out of n! permutations of a task set $\mathcal{T}$ of size n. For each permutation $\mathfrak {P}$, the response time analysis is applied to determine schedulability of $\mathcal{T}$ using $\textit{IsSchedulable}(\mathcal{T})$, which has a pseudo-polynomial time complexity. The algorithm BreakdownUtil $(\mathcal{T})$ determines the breakdown utilization of an unschedulable task layout. The breakdown utilization can be approximated with a binary search on the scaling factor $0< \Delta < 1$ and the schedulability test. With a fixed number of m steps, an approximation $\Delta '$ on the scaling factor $\Delta$ is derived with a precision of $\frac{1}{2^{m+1}}$, i.e. $\Delta ' - \frac{1}{2^{m+1}} \le \Delta < \Delta ' + \frac{1}{2^{m+1}}$.

10.5 Instantiating the algorithm

Algorithm 2 is applicable to both FPPS and FPTS, i.e. the specific schedulability tests to be executed are invoked within the functions IsSchedulable $(\mathcal{T})$ and BreakdownUtil $(\mathcal{T})$. Our optimal threshold assignment algorithm (Algorithm 1) is executed as part of the schedulability test for FPTS.

11 Evaluation

We perform similar simulation studies as in Altmeyer et al. (2012) to compare the relative inter-task CRPD costs under FPTS, FPPS and FPNS. The results are compared with those of the scheduling analysis ignoring inter-task CRPD. In all cases, we assume intra-task CRPD is subsumed into the worst-case computation times of tasks; see also Sect. 3.4. We have therefore generated system configurations so that (i) the results for FPTS ignoring inter-task CRPD match those in Bertogna et al. (2011b, 2012) and (ii) the results for FPPS with CRPD match

• those in Altmeyer et al. (2012) for an initial layout of tasks in memory, i.e. conform the initial task permutation $\mathfrak {P}_\mathrm{init}$ (45) and

• those in Lunniss et al. (2012) using the algorithm searching for a schedulable layout of tasks in memory.

Our evaluation is based on three orthogonal dimensions:

• 1. CRPD approach: To compute the schedulability of a task set under CRPD, we compare the most effective approaches, i.e. the composite approach combining the UCB-Union Multiset and the ECB-Union Multiset, both for FPPS (see Altmeyer et al. 2012) and FPTS (developed in this paper). In addition, we compare the various approaches presented in this paper, i.e. the composite approach, the UCB-Union Multiset, the ECB-Union Multiset, the UCB-Only Multiset, and the ECB-Only approach.

• 2. Deadline type: We consider constrained deadlines, where tasks’ relative deadlines are at most equal to their periods (i.e. $D_i \le T_i$), implicit deadlines, where relative deadlines are equal to periods (i.e. $D_i =T_i$), and arbitrary deadlines, where no relationship exists between relative deadlines and periods of tasks.

• 3. Memory layout: Next to the initial (sequential) layout of tasks in memory we also consider permutations of the sequential layout using our schedulable task-layout search (STLS) algorithm (Algorithm 2). These evaluations are only performed for the composite approach, however.

In our evaluation, we compute the schedulability of a task set under FPTS and FPPS with CRPD as well as under FPTS and FPPS ignoring inter-task CRPD. As described in Sect. 3.4, intra-task CRPDs have been incorporated in the worst-case computation times of tasks. Ignoring inter-task CRPD provides an upper bound on schedulability that cannot be exceeded even with perfect analysis of CRPD, i.e. with no pessimism. Hence, it gives a useful indicator of the maximum amount of pessimism that could be present in the derived approaches.

In the remainder of this section, we first present our basic system configuration. Next, we present the results of a series of experiments. In the first series of experiments, we show the ratio of schedulable task sets as a function of task-set utilization and evaluate our STLS algorithm for the composite approach. In the next two series of experiments we vary task-set parameters and cache-related parameters.

In many experiments, we use the so-called weighted schedulability ratio (Bastoni et al. 2010) as a metric. This metric takes a weighted average of the schedulability ratio over the entire utilization range $U \in [0,~1]$ using the utilization (U) as a weight. It is defined as follows (Bastoni et al. 2010). Let $S_y(\mathcal{T}, p)$ be the binary result (1 if schedulable, 0 otherwise) of schedulability test y for a task set $\mathcal{T}$ and parameter value p. Then:

$$\begin{aligned} W_y(p) = \frac{\sum _{\forall \mathcal{T}} U \cdot S_y(\mathcal{T}, p)}{ \sum _{\forall \mathcal{T}} U}, \end{aligned}$$

(49)

where U is the utilization of task set $\mathcal{T}$. This weighted schedulability ratio reduces what would otherwise be a 3-dimensional plot to 2 dimensions (Bastoni et al. 2010). Weighting the individual schedulability results by task-set utilization reflects the higher value placed on being able to schedule higher utilization task sets.

11.1 Experimental setup

As described in Sect. 3.5, we assume the typical mapping scheme from memory blocks to cache blocks as given in (1).

In our basic system configuration, we assume a cache with $N^\mathrm{C} = 512$ cache blocks and a total cache utilization of $U^\mathrm{C} = 4$, i.e. the total number of ECBs of all tasks is $N^\mathrm{C} \times U^\mathrm{C} = 2048$. We then select the cache utilization $U_i^\mathrm{C}$ of each task (the number of MBs of a task, $\vert {\text{ MB }}_i \vert$) using UUnifast (Bini and Buttazzo 2005), and derive the number of ECBs of a task, $\vert {\text{ ECB }}_i \vert$ using (2). $40\%$ of a task’s ECBs are also UCBs, i.e. $\vert {\text{ UCB }}_i \vert = 0.4 \cdot \vert {\text{ ECB }}_i\vert$. We assume a block reload time (${\text{ BRT }}$) of 8 $\upmu$s. For each experiment and for each parameter configuration, we generate a new set of 1000 systems.

For each system, we generate $n = 10$ tasks which are assigned deadline monotonic priorities. For constrained deadlines and arbitrary deadlines, the deadlines $D_i$ are selected from $[(C_i+T_i)/2, T_i]$ and $[(C_i + T_i)/2, 4 T_i]$, respectively. The task periods $T_i$ are randomly drawn from the interval [10, 1000] ms. The individual task utilizations $U_i$ (with $C_i = U_i\times T_i$) are generated using the UUnifast algorithm (Bini and Buttazzo 2005). The pre-emption thresholds of tasks are selected by our OTA algorithm (see Sect. 9).

The parameters used for simulated annealing in the algorithm searching for a schedulable layout of tasks in memory (see Sect. 10) match those in Lunniss et al. (2012). The breakdown utilization is calculated in $m = 10$ steps, yielding a scaling factor $\Delta$ with a precision of $\frac{1}{2^{m+1}} \approx 0.5 \times 10^{-3}$. The initial temperature is set to $\mathfrak {T}_\mathrm{init} = 1$, the cooling factor is given by $f_\mathrm{cooling} = 0.98$, and the target temperature by $\mathfrak {T}_\mathrm{target} = 0.05$. Hence, the task-layout search algorithm tries at most $\left\lceil \frac{\log \mathfrak {T}_\mathrm{target} - \log \mathfrak {T}_\mathrm{init}}{\log f_\mathrm{cooling}} + 1 \right\rceil = 150$ out of $n! = 3,628,800$ permutations. The evaluation for FPPS in Lunniss et al. (2012) has shown that even though the number of evaluated layouts is only a fraction of the total number of layouts, the layout search is likely to find a schedulable layout, if one exists. We perform a similar evaluation for FPTS in the next section.

11.2 Task-sets’ utilization

In our first series of experiments, we vary the task-set utilization. We start with an evaluation of the CRPD approaches and deadline types and subsequently evaluate our STLS algorithm for FPTS.

Fig. 6

Ratio of schedulable task sets versus task set utilization for constrained (top), implicit (middle) and arbitrary (bottom) deadlines. The composite approach is used when CRPD is taken into account

Fig. 7

Ratio of schedulable task sets versus task set utilization for constrained (top), implicit (middle) and arbitrary (bottom) deadlines. The initial layout is used for the various CRPD approaches

Fig. 8

Weighted schedulability ratio for varying deadline factor and the composite approach for CRPD

11.2.1 CRPD approaches and deadline types

The CRPD approaches and deadline types are evaluated by varying the task-set utilization in four experiments. In the first three experiments, we evaluate the CRPD approaches for implicit deadlines, constrained deadlines, and arbitrary deadlines. The results of these experiments are presented by six graphs on two facing pages. The even pages show 3 graphs for the composite approach for constrained (top), implicit (middle), and arbitrary (bottom) deadlines using both the initial layout and the layout search. The odd pages show the 3 additional graphs for the various CRPD approaches presented in this paper for constrained (top), implicit (middle), and arbitrary (bottom) deadlines using the initial layout. The graphs have been aligned both vertically (on one page) as well as horizontally (on the even and odd page) to ease comparison. Furthermore, the lines on the graphs appear in the same order as they are described in the legend. The graphs are best viewed online in color. In the fourth experiment, we evaluate the CRPD approaches by varying the deadline factor, i.e. by determining the weighted schedulability ratio for different values of a deadline factor x, where the relative deadline of each task $\tau _i$ is given by $D_i = x \cdot T_i$.

Figure 6 (middle) shows the ratio of task sets deemed schedulable for implicit deadlines, where the composite approach is used when CRPD is taken into account. The relative performance improvement of FPTS compared to FPPS is strongly amplified when including the CRPD. In contrast, FPTS and FPPS ignoring inter-task CRPD, which is denoted by means of “without CRPD” in the figures, only differ in case of high task utilization (starting at $U=0.85$) and at most by $20\%$. In the presence of CRPD, however, FPPS is only able to schedule half of all generated task sets at a utilization of $U=0.8$ for the initial permutation, while FPTS is able to schedule more than $90\%$. FPTS only experiences a similar performance degradation at a considerably higher utilization, i.e. approximately at $U = 0.88$. With the task-layout search algorithm, the performance of FPPS with CRPD can be improved, but remains well below the performance of FPTS with CRPD for the initial permutation. The task-layout search algorithm allows to improve the performance of FPTS with CRPD even further, e.g. with approximately $20\%$ for a utilization $U = 0.9$. The evaluation indicates that even though FPTS with layout-search cannot completely hide the effects of CRPD, it can mitigate the impact significantly.

Figure 7 (middle) shows the ratio of task sets deemed schedulable for implicit deadlines and the initial memory layout using various approaches when CRPD is taken into account. We have put Figures 6 and 7 on facing pages to ease comparison. Note that the lines in Figures 6 and 7 for FPTS and FPPS without CRPD, and FPNS are the same. Moreover, the line for FPTS with CRPD (initial layout) in Fig. 6 is the same as the line for FPTS - Composite Approach in Fig. 7. For this experiment, the composite approach and the UCB-Union Multiset approach give comparable results, i.e. the ECB-Union Multiset approach provides hardly any advantage over the UCB-Union Multiset approach for the settings of this experiment. The UCB-Only Multiset and ECB-Only approach are outperformed by the UCB-Union Multiset and ECB-Union Multiset approaches, as expected. For FPTS with CRPD, the UCB-Only Multiset and ECB-Only approach (shown if Fig. 7) are even outperformed by FPPS with CRPD and the combined approach (shown in Fig. 6), clearly showing the superiority of the composite approach over other approaches.

Our second and third experiments consider the ratio of task sets deemed schedulable versus the task set utilization for constrained and arbitrary deadlines. From constrained towards arbitrary deadlines, the performance of all algorithms improve; see Fig. 6. The relative performance improvement of FPTS compared to FPPS when including CRPD is remarkable; FPPS with CRPD and layout search can hardly schedule any task sets for arbitrary deadlines and a utilization of 0.975, while FPTS can still schedule approximately 45% for the initial layout and almost 70% with layout search. Moreover, the advantage of layout search over the initial layout for FPTS only increases for increasing utilizations, whereas the advantage reduces again after an initial increase for FPPS.

Figure 7 also shows the results for constrained and arbitrary deadlines. Similar to implicit deadlines, the ECB-Union Multiset approach provides hardly any advantage over the UCB-Union Multiset approach, as shown by the overlapping lines of the UCB-Union Multiset approach and the composite approach. Whereas the UCB-Only Multiset approach outperforms the ECB-Only approach for both implicit deadlines and constrained deadlines, the ECB-Only approach outperforms the UCB-Only Multiset approach for arbitrary deadlines with utilizations higher than 0.85.

Fig. 9

Weighted schedulability ratio for varying deadline factor, the initial memory layout, and the various CRPD approaches

Our fourth experiment concerns the weighted schedulability ratio for a varying deadline factor, using the composite approach when CRPD is taken into account; see Fig. 8. For any deadline factor, a deadline monotonic priority assignment is identical to a rate monotonic priority assignment. For FPPS, the worst-case response times of tasks are therefore independent of the deadline factor. For FPTS, where pre-emption thresholds can still be selected, worst-case response times are not necessarily fixed, however. As an example, with an increasing deadline factor, a task can tolerate more blocking from lower priority tasks, potentially allowing more lower tasks to raise their preemption threshold. As a result, the ability to increase worst-case response times of higher priority tasks for an increasing deadline factor, allows lower priority tasks to reduce their worst-case response times, and therefore meet their deadlines at lower deadline factors. Although this potential advantage of FPTS over FPPS is hardly noticeable without CRPD, it explains (i) why FPTS with CRPD performs close to FPPS and FPTS without CRPD, in particular for larger deadline factors, and (ii) why FPPS with CRPD experiences a clear performance loss compared to FPTS with CRPD, in particular for larger deadline factors. As expected, the weighted schedulability ratio is increasing as a function of the deadline factor, although the lines for FPPS with CRPD converge to a value well below 1. Figure 9 complements Fig. 8 by also showing the weighted schedulability ratio for the various CRPD approaches for the initial memory layout. Similar to Fig. 8, the weighted schedulability ratio is increasing for an increasing deadline factor for all approaches. Although the UCB-Only Multiset and the ECB-Only approaches are considerably less effective in bounding the CRPD than the UCB-Union Multiset and the ECB-Union Multiset approaches, their performance remain increasing for FPTS whereas the combined approach converged for FPPS in Fig. 8. The relative performance improvement of FPTS compared to FPPS is highest around a deadline factor equal to one (i.e. for implicit deadlines) and gradually decreases for both a decreasing as well as an increasing deadline factor. For an increasing deadline factor, both FPTS and FPPS can achieve a weighted schedulability ratio of 1. In the presence of CRPD, however, FPPS is only able to achieve a weighted schedulability ratio of 80% of the task sets (with layout search), while FPTS is able to achieve close to 100% for an increasing deadline factor. The evaluation therefore indicates that FPTS can almost completely hide the effects of CRPD when the deadline factor is increased.

11.2.2 Schedulable task-layout search (STLS) algorithm

In this section, we first evaluate the effectiveness of the STLS algorithm (Algorithm 2) for FPTS. Next, we discuss the relative improvements that can be achieved using the STLS algorithm for FPPS and FPTS.

Fig. 10

Ratio of schedulable task sets for $n = 7$ tasks, constrained (top), implicit (middle) and arbitrary (bottom) deadlines, and the composite approach for CRPD. The ratios have been normalized based on the sequential layout

To evaluate the effectiveness of the STLS algorithm, we compare the ratio of schedulable task sets with $n = 7$ tasks of a brute force algorithm, with the STLS algorithm using different values for the cooling factor $f_{\textit{cooling}}$ and the initial (sequential) layout of tasks in memory. The brute-force algorithm, potentially trying every permutation of task ordering, determines the schedulability of at most $7! = 5040$ different layouts. Figure 10 (middle) shows the results for implicit deadlines for an initial temperature $\mathfrak {T}_\mathrm{init} = 100$ and cooling factors 0.98, 0.95, 0.9, and 0.8, resulting in at most 378, 150, 74, and 36 configurations to be examined, respectively.

Whereas the relative improvement of using the STLS algorithm for a cooling factor of 0.8 is significant compared to the initial layout, subsequent increases in the maximum number of layout configurations considered clearly show diminishing results. Similar to the SA-algorithm for FPPS (Lunniss et al. 2012), the STLS algorithm is able to find a schedulable layout for FPTS in many cases, but in significantly less time than the brute-force approach. The STLS algorithm for FPTS does not get as close to a brute-force algorithm as the SA algorithm for FPPS, however. This could be due to the fact that the STLS algorithm is agnostic of FPTS, i.e. it does not exploit that tasks could be mutually non-preemptive based on their preemption thresholds. Figure 10 also shows the results for constrained and arbitrary deadlines. The peak of the ratio shifts towards a higher utilization from constrained deadlines to implicit deadlines, and is gone for arbitrary deadlines, as also shown by the evaluation in Fig. 6.

Table 5 Weighted schedulability ratio for the various scheduling algorithms

We discuss the relative improvements that can be achieved using the STLS algorithm for FPPS and FPTS based on the single weighted schedulability values for the lines for FPTS and FPPS with CRPD in the baseline experiment, which are given in Table 5. We use five metrics that give the improvements achieved using

• 1. layout search with FPPS: $(W_{\mathrm{FPPS}_\mathrm{LS}} - W_{\mathrm{FPPS}_\mathrm{IL}})/W_{\mathrm{FPPS}_\mathrm{IL}}$;

• 2. layout search with FPTS: $(W_{\mathrm{FPTS}_\mathrm{LS}} - W_{\mathrm{FPTS}_\mathrm{IL}})/W_{\mathrm{FPTS}_\mathrm{IL}}$;

• 3. FPTS instead of FPPS with initial layout: $(W_{\mathrm{FPTS}_\mathrm{IL}} - W_{\mathrm{FPPS}_\mathrm{IL}})/W_{\mathrm{FPPS}_\mathrm{IL}}$;

• 4. FPTS instead of FPPS with layout search: $(W_{\mathrm{FPTS}_\mathrm{LS}} - W_{\mathrm{FPPS}_\mathrm{LS}})/W_{\mathrm{FPPS}_\mathrm{LS}}$;

• 5. both FPTS and layout search over FPPS: $(W_{\mathrm{FPTS}_\mathrm{LS}} - W_{\mathrm{FPPS}_\mathrm{IL}})/W_{\mathrm{FPPS}_\mathrm{IL}}$.

Table 6 Relative improvements achieved for the weighted schedulability ratio

Metrics 1 and 2 illustrate that the layout search for FPPS is more effective than for FPTS; whereas a 12% improvement can be achieved for FPPS with implicit deadlines, only 5% can be achieved for FPTS; see Table 6. The improvement that can be achieved by the layout search for FPTS decreases from constrained towards arbitrary deadlines. This is an immediate consequence of the improved performance for FPTS with CRPD, decreasing the relative advantage of the layout search over the initial layout; see Fig. 6. Metrics 3 and 4 show the amount of improvement we get employing pre-emption thresholds, e.g. 27% for the initial layout and implicit deadlines and 18% with the layout search and implicit deadlines. Because the improvement of FPTS compared to FPPS when CRPD is included increases from constrained towards arbitrary deadlines (see Fig. 6) both metric 3 and 4 increase from constrained towards arbitrary deadlines as well. Finally, metric 5 shows the merit of applying both FPTS and layout search, i.e. the recommended solution, over what might be considered the default option of FPPS and initial layout. The amount of improvement is almost 33% for implicit deadlines.

11.3 Varying task-set parameters

In this first series of experiments, we vary task-set parameters, i.e. the range of the task period and the number of tasks. For each of these experiments, we use the weighted schedulability ratio as metric.

11.3.1 Period range

In the first experiment in this series, we vary the range of the task periods in steps of increasing orders of magnitude. Figure 11 (middle) shows the weighted schedulability ratio for a varying period range and implicit deadlines, using the composite approach when CRPD is taken into account. Since we generate computation times depending on the task periods, a larger range of the periods results in a larger computation time for some tasks. The performance of FPNS quickly drops, because computation times of tasks with a large period may exceed the periods (and the implicit deadlines) of other tasks in the system. For the same reason, however, we may be unable to assign a pre-emption threshold to tasks with a large period and long computation time other than its regular priority. The performance of FPPS with CRPD therefore approaches the performance of FPTS with CRPD. At the other extreme, when the range of task periods is small, then FPTS with CRPD provides performance close to that of FPTS without CRPD. This is because with a small range of periods and deadlines, the OTA algorithm can set pre-emption thresholds such that most tasks cannot pre-empt each other, thus greatly reducing CRPD. Overall, FPTS provides consistently high performance irrespective of the range of task periods. The performance benefits of the task-layout search remain stable.

Fig. 11

Weighted schedulability ratio for varying period range and constrained (top), implicit (middle) and arbitrary (bottom) deadlines. The composite approach is used when CRPD is taken into account

Fig. 12

Weighted schedulability ratio for varying period range, constrained (top), implicit (middle) and arbitrary (bottom) deadlines. The initial layout is used for the various CRPD approaches

Fig. 13

Weighted schedulability ratio for varying number of tasks and constrained (top), implicit (middle) and arbitrary (bottom) deadlines. The composite approach is used when CRPD is taken into account

Figure 11 (top and bottom) also shows the results for constrained and arbitrary deadlines (respectively). The graphs clearly illustrate that the weighted schedulability ratio increases from constrained to arbitrary deadlines for all algorithms. The graphs also illustrate that the performance loss for FPTS due to CRPD gradually decreases from constrained to arbitrary deadlines, whereas the performance loss for FPPS due to CRPD remains roughly the same. As before, we attribute this relative strength of FPTS to its ability to increase the worst-case response time of higher priority tasks allowing a decrease of response times of lower priority tasks. This strength becomes amplified for increasing deadlines.

Figure 12 shows the results for the various approaches when CRPD is taken into account. Similar to the earlier experiments, the UCB-Union Multiset approach and the composite approach have overlapping lines in the graphs.

Fig. 14

Weighted schedulability ratio for varying number of tasks, constrained (top), implicit (middle) and arbitrary (bottom) deadlines. The initial layout is used for the various CRPD approaches

Fig. 15

Weighted schedulability ratio for varying block reload time, constrained (top), implicit (middle) and arbitrary (bottom) deadlines, and the composite approach for CRPD. The vertical black line indicates a change in the scale of the x-axis

Fig. 16

Weighted schedulability ratio for varying block reload time, the initial memory layout, constrained (top), implicit (middle) and arbitrary (bottom) deadlines, and various approaches for CRPD. The vertical black line indicates a change in the scale of the x-axis

11.3.2 Number of tasks

In the second experiment we vary the number of tasks from 2 to 20 in steps of 2. Figure 13 (middle) shows the results for implicit deadlines. An increasing number of tasks leads to an improved performance of FPTS with CRPD relative to FPPS with CRPD. There are two reasons for this: (i) as the cache utilization remains constant, the ECBs per task decrease and (ii) by increasing the number of tasks, the individual task utilizations and execution times decrease, thus decreasing the potential blocking times. This gives the OTA algorithm more freedom to set pre-emption thresholds such that most tasks cannot pre-empt each other, again greatly reducing CRPD. For a low number of tasks, the task-layout search algorithm has only a minor impact on the performance of FPPS and FPTS. The number of task layouts is limited, and thus also the potential gain. The difference between the initial and the improved layout becomes noticeable at a task-set size of 6, and has its peak at 10 and 12 tasks. Although the task-layout search remains effective in case of large task sets, the performance benefits drop slightly. The larger the task set, the more potential task permutations exist. Consequently, the search algorithm is only able to explore a smaller fraction of the complete search-space making it less likely to find an optimal or near-optimal task layout.

Figure 13 (top and bottom) also shows the results for constrained and arbitrary deadlines (respectively). The performance of FPTS with CRPD converges to FPTS without CRPD for an increasing number of tasks. For arbitrary deadlines, the performance of FPTS with CRPD and FPTS without CRPD are almost the same. For FPPS, however, a relative performance improvement of FPPS with CRPD compared to FPPS without CRPD is not noticeable from constrained deadlines towards arbitrary deadlines.

Figure 14 shows the results for the various CRPD approaches for constrained, implicit, and arbitrary deadlines. Similar to the earlier experiments, the UCB-Union Multiset approach and the composite approach have overlapping lines in the graphs. For an increasing number of tasks, the performance of the UCB-Only Multiset approach degrades faster than that of the ECB-Only approach. The rationale for this behavior is that as the number of tasks gets larger, so the affected sets tend to become bigger and hence the change that the number of UCBs of the tasks affected by a task $\tau _j$ is larger than the ECBs of task $\tau _j$ increases.

11.4 Varying cache-related parameters

In the second series of experiments, we vary cache-related parameters, i.e. the block-reload time, the cache utilization, the cache reuse, and the number of cache blocks. For each of these experiments, we use the weighted schedulability ratio as a metric. Because we assume that intra-task CRPD is subsumed in the worst-case response times of tasks and we generate a new set of 1000 systems for each parameter configuration the weighted schedulability ratios for FPTS and FPPS without CRPD as well as FPNS are independent of the parameter configuration. Stated differently, FPTS and FPPS without CRPD as well as FPNS are represented in the graphs by means of horizontal lines.

11.4.1 Block reload time

In the first experiment, we vary the block reload time (BRT) from 0 to 640 $\upmu$s. Figure 15 (middle) shows the results for implicit deadlines. By increasing the BRT, we increase the CRPD and therefore penalise pre-emption. Consequently, the number of task sets deemed schedulable with FPPS with CRPD quickly drops to zero, while the performance of FPTS with CRPD converges to the performance of FPNS (as expected). The impact of the task-layout is naturally limited on the two extremes, i.e. when the overall impact of the pre-emption delay is either negligible or dominating. Consequently, the layout-search is most efficient in the middle range. Nevertheless, the absolute difference between the initial layout and the improved layout remains largely constant for most values of the BRT and hence, the relative benefits of the task-layout search increase with the pre-emption overhead.

It is interesting to see that FPTS with CRPD is able to deem more task sets schedulable than FPNS, even for an infinite BRT. The reason is as follows. If the sets of UCBs and ECBs of two tasks are completely disjoint (which may happen for randomly generated UCBs and ECBs of tasks), the CRPD of these two tasks pre-empting each other will remain zero. It is therefore possible that FPTS with CRPD outperforms FPNS, because not every pre-emption will be penalised.

Figure 16 (middle) shows the results for various CRPD approaches and implicit deadlines. Similar to the earlier experiments, the UCB-Union Multiset approach and the composite approach have overlapping lines in the graphs.

Figures 15 and 16 also show the results for constrained and arbitrary deadlines. Again, FPTS with CRPD can take advantage of increasing deadlines, as illustrated by (i) the reducing performance gap between FPTS without CRPD and FPTS with CRPD and (ii) the increasing performance gap between FPTS with CRPD and FPPS with CRPD from constrained deadlines to arbitrary deadlines.

11.4.2 Cache utilization

In the second experiment, we vary the total cache utilization ($U^\mathrm{C}$) from 0 to 160 and we reset the BRT to 8 $\upmu$s. Since the number of cache blocks ($N^\mathrm{C}$) remains the same, increasing $U^\mathrm{C}$ means increasing the number of ECBs of tasks. Figure 17 (middle) shows again a weighted schedulability ratio for implicit deadlines. FPPS and FPTS with CRPD are both able to schedule considerably more task sets than FPNS. This is due to the fixed number of cache blocks, which restricts the maximum possible pre-emption cost. At a total cache utilization of 40, each pre-emption evicts most of the cache contents which then need to be reloaded, hence further increases in cache utilization have little effect on schedulability. The performance of the task-layout search follows the same scheme as in Fig. 15: The task layout has no impact when there is no CRPD at all, and also, when each task evicts the complete cache content on pre-emption.

Figure 18 (middle) shows the results for various CRPD approaches and implicit deadlines. Unlike the earlier experiments, the line of the UCB-Union Multiset approach no longer coincides with the composite approach in Fig. 18. As the cache utilization becomes very large, then nearly all tasks have ECBs that fill the cache; however the UCBs are only 40% of the ECBs. This means that the ECB-Union Multiset approach, which uses the UCBs of affected tasks (intersected with ECBs - which then makes very little reduction) reduces to the performance of the UCB-Only Multiset approach. The UCB-Union Multiset approach combines UCBs for affected tasks into larger sets before intersection with ECBs (which again makes very little reduction). As the cache utilization becomes large, fewer tasks have less than the maximum amount of UCBs (e.g. 40% of the cache size, since the number of ECBs tend towards the size of the cache), thus the union of UCBs becomes increasingly larger than one task’s UCBs (as used in the ECB-Union Multiset approach). Hence, the performance of the UCB Union Multiset deteriorates faster than the ECB-Union Multiset approach. Note that is does not reduce to the same performance as the ECB-Only approach, since the union of UCBs still does not equate to the whole cache for many of the considered tasks, whereas with the ECB-Only approach, the ECBs nearly always do.

Fig. 17

Weighted schedulability ratio for varying total cache utilization, constrained (top), implicit (middle) and arbitrary (bottom) deadlines, and the composite approach. The vertical black line indicates a change in the scale of the x-axis

Fig. 18

Weighted schedulability ratio for varying total cache utilization, the initial memory layout, constrained (top), implicit (middle) and arbitrary (bottom) deadlines, and various approaches for CRPD. The vertical black line indicates a change in the scale of the x-axis

Because our earlier experiments assume a relatively low cache utilization, i.e. $U^\mathrm{C} = 4$, the lines in the graphs for the UCB-Union Multi-set approach and the composite approach coincide. From Fig. 10 in Altmeyer et al. (2012) and Fig. 18 we observe that the point at which the lines for the UCB-Union Multi-set approach and the ECB-Union Multiset approach cross differ. In the case of FPPS, they cross at $U^\mathrm{C} = 9$, while for FPTS they cross at $U^\mathrm{C} = 20$.

Figures 17 and 18 also show the results for constrained and arbitrary deadlines. The trends of the graphs for constrained and arbitrary deadlines are the same as for implicit deadlines.

Fig. 19

Weighted schedulability ratio for varying reuse factors (percentage of UCBs), constrained (top), implicit (middle) and arbitrary (bottom) deadlines, and the composite approach for CRPD.

Fig. 20

Weighted schedulability ratio for varying reuse factors (percentage of UCBs), the initial memory layout, constrained (top), implicit (middle) and arbitrary (bottom) deadlines, and various approaches for CRPD

Fig. 21

Weighted schedulability ratio for varying cache size (number of cache blocks), constrained (top), implicit (middle) and arbitrary (bottom) deadlines, and the composite approach for CRPD

Fig. 22

Weighted schedulability ratio for varying cache size (number of cache blocks), the initial memory layout, constrained (top), implicit (middle) and arbitrary (bottom) deadlines, and various approaches for CRPD

11.4.3 Cache reuse

In the third experiment, we vary the cache reuse, i.e. the percentage of ECBs that are also UCBs. Figure 19 (middle) shows the weighted schedulability ratio for implicit deadlines. As the UCB percentage increases, the performance of FPTS and FPPS with CRPD decreases. Figure 19 also shows the results for constrained and arbitrary deadlines. Similar to earlier experiments, e.g. where the block reload time is varied, FPTS with CRPD can take more advantage of increasing deadlines than FPPS with CRPD. Considering the graphs from constrained deadlines to arbitrary deadlines, this is illustrated by (i) the reducing performance gap between FPTS without CRPD and FPTS with CRPD and (ii) the increasing performance gap between FPTS with CRPD and FPPS with CRPD.

Figure 20 shows the results for constrained (top), implicit (middle) and arbitrary (bottom) deadlines. In general, the graphs have the same trends as those of earlier experiments, with the exception of the ECB-Only approach. Because the number of ECBs remains the same, Fig. 20 contains horizontal lines for the ECB-Only approach. This figure nicely illustrates the difference between the ECB-Only approach and the UCB-Only Multiset approach. When including a contribution for a task $\tau _j$, the ECB-Only approach includes the ECBs of task $\tau _j$ itself, whereas the UCB-Union Multiset approach uses the ECBs of the tasks affected by task $\tau _j$. Which method performs best depends on the comparison between these two factors. When the UCB percentage is high, the number of UCBs of affected tasks is larger than the number of ECBs of task $\tau _j$, and the ECB-Only approach outperforms the UCB-Only Multiset approach. In contrast, when the UCB percentage is small, the opposite is true and the UCB-Only Multiset approach outperforms the ECB-Only approach.

11.4.4 Number of cache blocks

In the last experiment of this series, we vary the number of cache blocks ($N^\mathrm{C}$). Figure 21 (middle) shows the weighted schedulability ratio for implicit deadlines. As $N^\mathrm{C}$ increases, the total number of ECBs being used by tasks also increases and, contrary to the second experiment, more of these ECBs fit into the cache. Hence, the pre-emption costs increase when more blocks need to be reloaded. The schedulability ratios of FPPS and FPTS with CRPD therefore decrease. FPPS will eventually be unable to schedule any tasks. The performance of FPTS, however, converges to the performance of FPNS, i.e. with FPNS task sets are unaffected by the increased pre-emption costs. We recall that FPTS with CRPD still outperforms FPNS, because, after assigning the highest possible pre-emption thresholds to tasks using our OTA, some of the remaining pre-emptions in the system may effectively come for free due to the limited overlap between the UCBs of some tasks and the ECBs of others. While the schedulability ratios for FPPS and FPTS decrease with the number of cache blocks, the impact of the task-layout search increases. More cache blocks means that the difference between different layouts increases. Nevertheless, the overall trend remains: increasing the cache size decreases the schedulability ratios.

Figure 21 again shows that FPTS with CRPD can take more advantage of increasing deadlines than FPPS with CRPD.

Figure 22 shows the results for various CRPD approaches for constrained (top), implicit (middle), and arbitrary (bottom) deadlines. These figures have the same trends as those of earlier experiments.

12 Conclusions

In this paper, we integrated analysis of CRPD into response time analysis for fixed priority scheduling of tasks with pre-emption thresholds (FPTS) and arbitrary deadlines. Moreover, we introduced an OTA algorithm that minimizes the effects of CRPD given an initial set of task priorities. The analysis we provided generalizes existing analysis for FPPS with constrained deadlines and CRPD described in Altmeyer et al. (2012), and covers the most effective approaches presented in that paper, in particular the ECB-Union and UCB-Union Multiset approaches. Finally, building on the work in Lunniss et al. (2012), we presented a Schedulable Task-Layout Search (STLS) algorithm to improve the layout of tasks in memory in order to make the task set schedulable.

We presented an extensive comparative evaluation of the performance of the schedulability tests for FPTS and FPPS with and without CRPD based on 3 orthogonal dimensions and seven main experiments. Interestingly, we found that the theoretical performance advantage that FPTS has over FPPS when there are no CRPDs is magnified when CRPDs are taken into account. Further, even when the overheads (block reload times) affecting CRPD are increased to very high levels, FPTS still retains a performance advantage over FPNS (which it also dominates). This is due to the limited overlap between the UCBs of some tasks and the ECBs of others, meaning that some pre-emptions effectively come for free (i.e. no CRPD).

Regarding the three orthogonal dimensions on which the comparative evaluation is based, i.e. CRPD approach, deadline type, and task layout, we can draw the following conclusions. In most of our experiments, the UCB-Union Multiset approach outperforms the ECB-Union Multiset approach for FPTS with CRPD. In particular, the UCB-Union Multiset approach has the same performance as the composite approach that combines the UCB-Union Multiset and ECB-Union Multiset approaches. This differs from the results in Altmeyer et al. (2012) for FPPS and CRPD. The reason for this can be found in the experiment in which the cache utilization is varied, which shows that the UCB-Union Multiset approach out performs the ECB-Union Multiset approach until a cache utilization of 20 is reached (compared to 9 for a similar transition with FPPS), showing that the two methods are incomparable. In our evaluation, we considered constrained, implicit, and arbitrary deadlines. We observed that in all major experiments the performance of FPTS with CRPD improved significantly from constrained towards arbitrary deadlines, unlike FPPS with CRPD, which showed only marginal improvements. We attribute this strength of FPTS to its ability to decrease the worst-case response time of lower priority tasks by means of preemption thresholds at the expense of an increase of the worst-case response time of higher priority tasks whenever higher priority tasks tolerate the additional blocking incurred. Finally, our evaluation shows the merit of applying both FPTS and layout search, i.e. the recommended solution, over what might be considered the default option of FPPS and initial layout. The amount of improvement in the weighted schedulability range is 33% for implicit deadlines.

Our results indicate that FPTS can rightly be viewed as a potential successor to FPPS as a defacto standard in industry, where it is already supported by both OSEK (2005) and AUTOSAR (AUT 2010) compliant operating systems.

There are a number of ways in which this work can be extended. Firstly, our STLS-algorithm is based on simulated annealing and considers sequential layouts of tasks in memory. A more comprehensive search based on genetic algorithms, including variations in layout including gaps between tasks, is a direction for future work. Secondly, OSEK and AUTOSAR only specify/require a restricted version of FPTS. Although the consequences of this restriction on the schedulability ratio of task sets without CRPD is shown to be limited (Hatvani and Bril 2015), the consequences with CRPD are to be investigated. Thirdly, our OTA algorithm assumes that task priorities are provided. The problem of optimally assigning both priorities and thresholds using a computationally tractable method remains open.