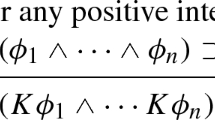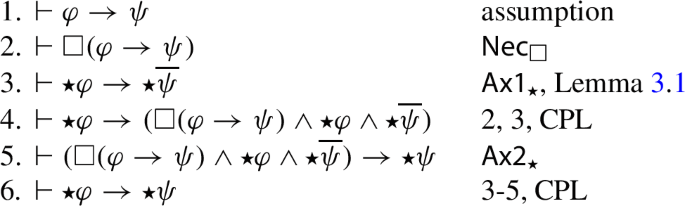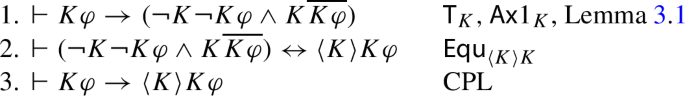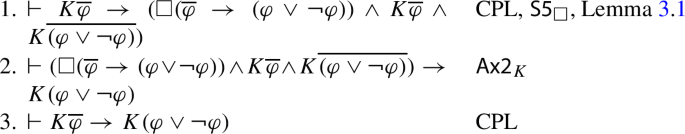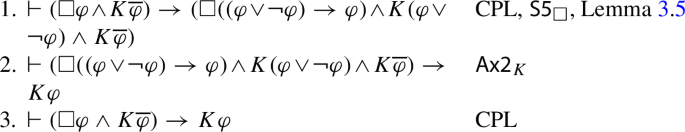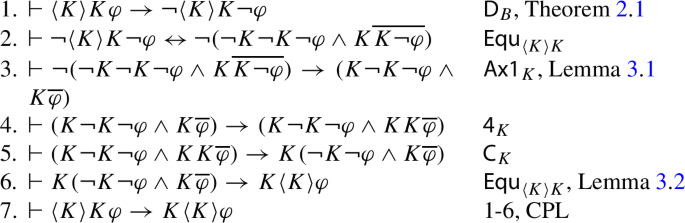A hyperintensional approach to positive epistemic possibility

Abstract

The received view says that possibility is the dual of necessity: a proposition is (metaphysically, logically, epistemically etc.) possible iff it is not the case that its negation is (metaphysically, logically, epistemically etc., respectively) necessary. This reading is usually taken for granted by modal logicians and indeed seems plausible when dealing with logical or metaphysical possibility. But what about epistemic possibility? We argue that the dual definition of epistemic possibility in terms of epistemic necessity generates tension when reasoning about non-idealized agents and is a problem of concern for most hyperintensional epistemic logics that alleviate the problem of logical omniscience. The tension is particularly evident when knowledge is taken as a primitive to define other epistemic concepts, such as justification and belief, as done in the knowledge-first tradition. We propose a non-dual interpretation of epistemic possibility, employing a hyperintensionality filter similar to the one that makes the corresponding epistemic necessity operator hyperintensional. We employ the proposed semantics to model Stalnaker’s belief as epistemic possibility of knowledge and provide a sound and complete axiomatization for a hyperintensional version of his bimodal logic of knowledge and belief.

1 Epistemic possibility and hyperintensional logics

Possibility is usually considered to be the dual of necessity: a proposition $\varphi$ is (metaphysically, logically, epistemically etc.) possible iff not-$\varphi$ is not (metaphysically, logically, epistemically etc.) necessary.¹ One can reason analogously about knowledge (Hintikka, 1962), as knowledge is often taken as epistemic necessity and epistemic possibility is defined as its dual. This yields the definition of epistemic possibility as the dual of knowledge, that will be the target of our criticism in this paper:

EP:=DK: A proposition $\varphi$ is an epistemic possibility for an agent S iff S does not know not-$\varphi$.

As Egan and Weatherson (2011b, p. 1) point out, EP:=DK is a “very simple analysis of epistemic possibility”   but it is also “problematic for a few reasons”.² Epistemologists have widely scrutinized this definition of epistemic possibility and have come up with more articulated definitions in order to overcome its problems (see, e.g., (Carey, 2020; DeRose, 1991; Hacking, 1967, 1975; Huemer, 2007; Teller, 1972), among others). Nonetheless, given its simplicity, EP:=DK is usually taken for granted in the field of epistemic logic.³

Following Hintikka (1962), standard epistemic logic formalizes knowledge intensionally as a normal modal operator interpreted on relational possible worlds models. That is, knowledge is modelled as truth in a set of possible worlds determined by an accessibility relation R:

As is well known, the notion of knowledge this approach implements is too strong, leading to the problem of logical omniscience.⁴ It is therefore usually taken to model what an ideal agent with unlimited cognitive, computational, and conceptual capacities knows or to model derivative epistemic notions, such as logical commitment given what one knows or what one ought to know given what one knows. Possible-worlds models for ideal epistemic agents (or a relevant derivative attitude) which interpret the epistemic modality in question as truth in a specific set of possible worlds can also take different forms, such as Scott–Montague style neighbourhood models (Chellas, 1980; Montague, 1970; Pacuit, 2017; Scott, 1970),⁵ topological models (McKinsey, 1941; McKinsey & Tarski, 1944; Baltag et al., 2019), plausibility models (for belief) (Baltag & Smets, 2008; Grove, 1988; van Benthem, 2007, 2011), and subset space models (Bjorndahl & Özgün, 2020; Bjorndahl, 2018; Moss & Parikh, 1992; Özgün, 2017; van Ditmarsch et al., 2019). Abstracting away from their detailed features and conceptual underpinnings, all these models interpret epistemic necessity in a structurally similar manner, which can be schematically represented as follows:

where $\textsf{MOD}$ stands for a model-theoretic condition formalized as truth in a set of possible worlds, and $\textsf{KNOW}$ and $\textsf{MOD}$ are total functions defined from the object language of the underlying logic to the set $\{0, 1\}$. (Mapping to 1 means that the condition is satisfied and mapping to 0 means that it is not.)

EP:=DK might not be problematic per se when applied to Know, that is, when epistemic possibility is given by:

Crucially, however, it generates tension between the epistemic necessity and possibility operators of several influential hyperintensional epistemic logics that have been developed to reason about non-idealized agents. Among such approaches and of particular importance for us in this paper, are the logics that attack certain forms of logical omniscience by imposing additional constraints on the possible worlds semantics for knowledge. These additional constraints intend to represent an agent’s cognitive, computational, or conceptual limitations that are constitutive of their epistemic reach. Examples of such approaches are topic-sensitive epistemic logics (Berto, 2019, 2022; Berto & Hawke, 2021; Hawke et al., 2019; Özgün & Berto, 2021), awareness logics (Fagin & Halpern, 1988; Fagin et al., 1995; Fernández-Fernández, 2021; Grossi & Velázquez-Quesada, 2015), and logics based on impossible worlds semantics (Berto & Jago, 2019; Hintikka, 1975; Jago, 2014; Rantala, 1982; Solaki, 2021), among others.

Again, abstracting away from their individual characteristics, all these approaches interpret knowledge in a structurally analogous way, namely as a conjunction of two conditions. The first is the model-theoretic condition—the same encountered in Know—and the second is the hyperintensionality condition that restricts the epistemic reach of the agent, shrinking the set of propositions they can know due to their epistemic limitations, be they cognitive, conceptual, or computational. This condition deserves the label hyperintensional as it helps to distinguish propositions with the same intension (i.e. the logically or necessarily equivalent propositions). According to this general structure, an agent knows $\varphi$ iff both the model-theoretic and hyperintensionality conditions are satisfied, schematically written as:

where $\textsf{KNOW}$ and $\textsf{MOD}$ are as before, and $\textsf{HYPE}$ stands for the hyperintensionality condition and is a total function defined from the object language of the underlying logic to the set $\{0, 1\}$. In the aforementioned approaches, $\textsf{MOD}$ can be the reader’s favourite possible worlds semantics and $\textsf{HYPE}$ denotes ‘grasping $\varphi$’s topic’ in topic-sensitive logics, ‘being aware of $\varphi$’ in awareness logics, and ‘truth of $\varphi$ in all epistemically accessible impossible worlds’ in impossible worlds semantics.⁶

When EP:=DK is applied to this schema, not satisfying the hyperintensionality condition for $\lnot \varphi$, i.e., $\textsf{HYPE}(\lnot \varphi )=0$, becomes a sufficient condition for an agent to consider $\varphi$ epistemically possible. Put differently, we run into the problem of trivial epistemic possibility, concisely described by Huemer in his criticism of EP:=DK:

TEP: [I]f a person does not actually believe $\lnot p$, perhaps due to his having failed to consider it or lacking the concepts required to entertain it, then p is thereby guaranteed to be epistemically possible (Huemer, 2007, p. 125).

As illustrated by the following two examples put forward by Huemer (2007) and Carey (2023), respectively, this leads to intuitively incorrect ascriptions of epistemic possibility. These examples, in turn, also motivate our fix to the problem.

Rigel 7 is the seventh planet in the Rigel star system. Sam, however, knows nothing of Rigel and consequently has no thoughts about Rigel or any of its planets. Sam looks at his couch in normal conditions and sees nothing on it. Mary (who happens to know of Rigel 7) says: ‘For all Sam knows, Rigel 7 might be on the couch.’ (Huemer, 2007, p. 122)

As Huemer argues, EP:=DK mishandles the above case: as Sam has no concept of Rigel 7, he does not know that Rigel 7 is not on the couch. However, EP:=DK entails that it is epistemically possible for Sam that Rigel 7 is on the couch, leading to an intuitively wrong epistemic possibility assertion by Mary. The following example by Carey (2023) provides further support against EP:=DK:

Suppose, for example, that Holmes knows that Adler has stolen his pipe. Holmes is perfectly capable of deducing from this that someone stole his pipe, but he has not bothered to do so (our emphasis). So, Holmes has not formed the belief that someone stole his pipe. As a result, he does not know that someone stole the pipe. According to [EP:=DK], then, it is still epistemically possible for Holmes that no one stole the pipe (that is, that it is not the case that someone stole the pipe), even though it is not epistemically possible for Holmes that Adler did not steal the pipe. (Carey, 2023, Sect. 3.a)

While the condition for acquiring knowledge is made stronger with a deduction constraint (to know that someone stole his pipe Holmes needs to explicitly deduce this from the fact that Adler stole his pipe), EP:=DK leaves too much open as epistemic possibility (e.g., that no one stole the pipe), which leads to an intuitive tension between what one explicitly knows and what is epistemically possible for them.⁷

Huemer’s and Carey’s examples are excellent candidates to be modelled in a topic-sensitive and in an awareness framework, respectively. In fact, topic-sensitive logics have been often used to model mastery of concepts or lack thereof and awareness logics to model resource-bounded agents, by distinguishing between their explicit knowledge and what they can come to know by competent deduction, i.e. their implicit knowledge.⁸ Some versions of awareness logics (such as the ones where awareness is propositionally generated (Halpern, 2001)) and, to the best of our knowledge, all topic-sensitive logics satisfy the property $\textsf{HYPE}(\lnot \varphi )=\textsf{HYPE}(\varphi )$.⁹ Under this condition, EP:=DK and Hyper-Know yield:

and $\textsf{HYPE}(\varphi )=0$ becomes a sufficient condition for an agent to consider $\varphi$ epistemically possible.

Possibly more strikingly, according to Possibility-II, whenever the hyperintensionality constraint fails for a blatant contradiction such as $\varphi \wedge \lnot \varphi$, i.e., whenever $\textsf{HYPE}(\varphi \wedge \lnot \varphi )=0$, the agent considers $\varphi \wedge \lnot \varphi$ epistemically possible. We think that this is a crucial instance where the epistemic possibility operator becomes too weak, making too many propositions epistemically possible for the agent in question.

To summarize, the main reason for the tension seems to be that as Hyper-Know makes the notion of epistemic necessity stronger, compared to the one given by Know, applying EP:=DK to Hyper-Know renders the corresponding possibility operator too weak. To put it differently, while the hyperintensionality constraints imposed on the epistemic necessity operator model an agent who knows less, respecting their epistemic limitations, many more propositions become epistemically possible for the same agent.

To address this type of problem, we propose to conceive epistemic possibility as subject to the same hyperintensionality restrictions as its necessity counterpart (Sect. 2). We then argue (in Sect. 3) that the issue described above becomes particularly pressing when knowledge is taken as a primitive that can be used to define other epistemic concepts, as done in the knowledge-first tradition (Williamson, 2000). An eminent example is Stalnakerian belief defined as epistemic possibility of knowledge (Stalnaker, 2006). A more recent example is Rosenkranz’s notion of propositional justification as the epistemic possibility of being in a position to know.¹⁰ Finally, we apply our proposal to extant proposals in knowledge-first epistemology and devise a sound and complete axiomatization for a hyperintensional version of Stalnakerian logic of knowledge and belief (Sect. 3.2). To ease readability, proofs are collected in appendices.

2 A non-dual definition of epistemic possibility

Before we present our fix to the problem, a few explanatory notes on the notion of epistemic possibility we are after—the notion of positive epistemic possibility—seem to be warranted. EP:=DK provides a negative definition of epistemic possibility: the epistemic possibility of $\varphi$ is equated with not knowing its negation. Nonetheless, there is also a positive sense of epistemic possibility of $\varphi$ for which the agent needs to bear some relation to $\varphi$, where the kind of relation in question may vary depending on one’s epistemological stance. The proposition must be in some way accessible to the agent.

One may understand the standard relational possible worlds semantics as implicitly endorsing this positive conception of epistemic possibility. Due to the classical interpretation of negation and the duality between the existential and universal quantifiers, applying EP:=DK to the Hintikkian clause H, we obtain that:

$$\begin{aligned} \begin{array}{lcl} \langle K \rangle \varphi \text{ is } \text{ true } \text{ in } w&\text{ iff }&\varphi \text{ is } \text{ true } \text{ in } \text{ a } \text{ world } w' \text{ such } \text{ that } Rww' \end{array} \end{aligned}$$

That is, $\varphi$ is an epistemic possibility for S in w iff for S there is at least one world $w'$ accessible from w such that $\varphi$ is true in $w'$. In other words, a $\varphi$-world must be S-accessible. The dual of knowledge loses its positive flavour in a hyperintensional context though. Even if a $\varphi$-world is S-accessible, if $\varphi$ is out of S’s epistemic reach, then S cannot stand in any relation with $\varphi$, since the boundaries of S’s epistemic reach are determined by their cognitive, computational, or conceptual limitations. A finer-grained distinction between a positive and a negative reading of epistemic possibility is required, and the literature provides ample evidence for that.

Chalmers (2002, pp. 149–150) proposes a similar distinction between negative and positive conceivability. A proposition $\varphi$ is negatively conceivable when $\varphi$ “is not ruled out a priori”   and is positively conceivable when “one can form some sort of positive conception of a situation in which [$\varphi$] is the case”. Moreover, a positive reading of epistemic possibility is particularly needed when dealing with assertions involving epistemic modals. Von Fintel and Gillies (2008, p. 83) say that a “might-claim is (pragmatically) more than just a profession of ignorance”. In other words, asserting the epistemic possibility of $\varphi$ is more than admitting not to know not-$\varphi$, which corresponds to the negative definition of epistemic possibility. There is also a positive side: “the speaker is highlighting that possibility as one that should not be ignored”, and “there is often a reliance on positive evidence that makes that possibility seem to be a serious possibility”  (our emphasis).

But the relevance of a positive reading of epistemic possibility is not limited to pragmatics: it is also at play when we take epistemic possibility as a propositional attitude, i.e. a mental state held toward a proposition. This kind of epistemic possibility (albeit with respect to belief, not knowledge) seems to be what Yalcin (2011, p. 306) investigates as corresponding to “believing that something might be so, or that something is possibly so”. In his formal modelling of believing what an epistemic modal claim says, he differentiates between “a proposition’s merely being compatible with a state of mind and its being epistemically possible [...] in the thicker sense connoted by epistemic possibility modals” (Yalcin, 2011, p. 314), and defends that in order for a proposition $\varphi$ to be epistemically possible for an agent S, $\varphi$ must be compatible with S’s state of mind (which corresponds to the negative definition of epistemic possibility provided by EP:=DK) and moreover needs to be an answer to a question to which S is sensitive or to be about a subject matter S is sensitive to (where the latter constraint gives the positive reading, playing the role of a hyperintensionality condition).¹¹¹²

In the next subsection, we treat the notion of positive epistemic possibility from a technical perspective within a hyperintensional framework, solving the problem of TEP.

2.1 Epistemic possibility revisited

We propose a positive definition of epistemic possibility that is able to escape TEP:

PEP: A proposition $\varphi$ is an epistemic possibility for an agent S iff not-$\varphi$ is not knowable in principle for S and $\varphi$ is within S’s epistemic reach.

There is a lot to unpack here. We use ‘knowable in principle’ and ‘within S’s epistemic reach’ as technical expressions. A proposition $\varphi$ is knowable in principle for an agent S iff S would know it if no cognitive, computational, or conceptual limitations stood in S’s way of getting to know $\varphi$ (i.e. if the hyperintensionality condition was satisfied). In other words, $\varphi$ is knowable in principle for agent S iff S has sufficient information or evidence to rule out all the non-$\varphi$ worlds, but they may fail to know $\varphi$ because of some other epistemic limitation. Technically, this corresponds to satisfying the model-theoretic condition we spelt out in Sect. 1.

The concept of epistemic reach has already been introduced in Sect. 1. We do it here in more detail for the sake of clarity. A proposition $\varphi$ is within S’s epistemic reach iff S would know $\varphi$ if they had sufficient information to rule out non-$\varphi$ worlds (i.e. if the model-theoretic condition was satisfied). In other words, $\varphi$ is within S’s epistemic reach iff no cognitive, computational, or conceptual limitations stand in one’s way of getting to know $\varphi$. Technically, this means that the hyperintensionality condition is satisfied for S with respect to $\varphi$. In a topic-sensitive framework, this clause corresponds to having grasped the topic of $\varphi$. In an awareness logic, it means being aware of $\varphi$. Accordingly, we formalize positive epistemic possibility as follows:

Hyper-Possibility escapes the problem of TEP since failing to know $\lnot \varphi$ because of the failure of a hyperintensionality condition, such as having failed to consider it or lacking the concepts required to entertain it, is no longer a sufficient condition for $\varphi$ to be considered an epistemic possibility. This is in line with the analysis of the problematic examples presented in Sect. 1. According to Hyper-Possibility, since Holmes did not bother performing the trivial deduction to conclude that somebody stole the pipe, and Sam has no concept of Rigel 7 (i.e. the hyperintensionality constraint is satisfied in neither case), it is not an epistemic possibility for Holmes that nobody stole the pipe and it is not an epistemic possibility for Sam that Rigel 7 is on the couch. Moreover, since positive epistemic possibility (henceforth denoted by ${\langle K \rangle }$) is defined as a strengthening of negative epistemic possibility (henceforth denoted by $\lnot K\lnot$) by imposing a hyperintensionality constraint, unsurprisingly, the former always implies the latter, that is ${\langle K \rangle }\varphi \rightarrow \lnot K \lnot \varphi$ holds, but not the other way around.¹³

Losing the duality between epistemic necessity and possibility allows us to differentiate among a wider plurality of epistemic states. What can be seen as a malus in terms of technical simplicity, we take to be a bonus in terms of explanatory power. This applies, for example, to the concept of epistemic impossibility.

2.2 Epistemic impossibility

In normal modal logic, the epistemic impossibility of $\varphi$ can be defined either as the negation of the epistemic possibility of $\varphi$ or equivalently as the knowledge of the negation of $\varphi$:

EI:=NEP: A proposition $\varphi$ is an epistemic impossibility for an agent S iff $\varphi$ is not an epistemic possibility for S.

EI:=KN: A proposition $\varphi$ is an epistemic impossibility for an agent S iff not-$\varphi$ is known by S.

The two definitions above diverge though, when we refer to the hyperintensional versions of epistemic possibility and knowledge as defined in Hyper-Possibility and Hyper-Know respectively.

It is not difficult to observe that, when applied to Hyper-Possibility, EI:=NEP generates the following schematic semantic clause for epistemic impossibility:

$$\begin{aligned} \textsf{POSS} (\varphi ) =0 \, \text {iff} \, \textsf{MOD}(\lnot \varphi )=1 \, \text {or} \, \textsf{HYPE}(\varphi )=0 \end{aligned}$$

which yields the principle of trivial epistemic impossibility, analogous to TEP: every proposition which is not in an agent’s epistemic reach is epistemically impossible. Nonetheless, we may not want to say that for Sam it is epistemically impossible that Rigel 7 is on the couch and that for Holmes it is epistemically impossible that nobody stole the pipe. In fact, there is a stronger sense of epistemic impossibility which requires the agent to be able to dismiss or rule out the truth of a certain proposition in order for that proposition to be considered epistemically impossible.¹⁴ In order to rule out a proposition, the agent must stand in some relation with it. Nonetheless, no such relationship can be in place if the proposition is out of the agent’s epistemic reach. The kind of epistemic impossibility that requires the agent to rule out the proposition in question is exactly the one described by EI:=KN. By knowing not-$\varphi$, the agent is able to properly rule out $\varphi$. Consider the following semantic clause for epistemic impossibility generated by EI:=KN:

$$\begin{aligned} \textsf{KNOW} (\lnot \varphi ) =1 \, \text {iff} \, \textsf{MOD}(\lnot \varphi )=1 \, \text {and} \, \textsf{HYPE}(\lnot \varphi )=1 \end{aligned}$$

Given EI:=KN, in order for a proposition $\varphi$ to be an epistemic impossibility for an agent S, not-$\varphi$ must be within S’s epistemic reach: trivial epistemic impossibility is avoided.

We have shown how our approach avoids some intuitively incorrect ascriptions of epistemic possibility and impossibility, and makes it possible to distinguish among epistemic states that are indistinguishable in epistemic systems based on normal modal logics. Let us see now how the new approach can be fruitfully applied in the context of knowledge-first epistemology.

3 Epistemic possibility for knowledge-firsters

In contrast to a long tradition in epistemology—which defines knowledge in terms of other epistemic concepts, e.g., in terms of justified true belief or strengthening of justified true belief¹⁵—Williamson (2000) proposed a knowledge-first epistemology, which takes knowledge as a non-decomposable epistemic state and defines other epistemic states in terms of knowledge. This has started a new line of research in epistemology (McGlynn, 2014). The Stalnakerian conception of belief, which is of particular interest in this work, can be seen as following this line.

Stalnaker (2006) puts forward a bimodal logic for knowledge and belief, focusing on the relationship between these two notions. The notion of belief he considers is a specific kind, that of so-called ‘full belief’, which corresponds to “subjective certainty [for which] believing implies believing that one knows”: $B\varphi \rightarrow BK\varphi$ (Stalnaker, 2006, p. 179).¹⁶ Given further assumptions he makes (see Table 1 for Stalnaker’s system), the following equivalence holds:¹⁷

$$\begin{aligned} B\varphi \leftrightarrow \lnot K \lnot K\varphi . \end{aligned}$$

Therefore, according to Stalnaker’s system, one believes $\varphi$ iff one doesn’t know that one doesn’t know $\varphi$. This “permits a more economical formulation of the combined belief-knowledge logic in which the belief operator is defined in terms of the knowledge operator”  (Stalnaker, 2006, p. 179). As recently noticed by Stalnaker (2019, p. 3) himself, this reduction is “appropriate to the ‘knowledge first’ ideology”, that he admits endorsing.¹⁸

Stalnaker adopts a particular kind knowledge-first approach that is gaining growing attention in the recent literature. The core idea consists in defining other epistemic concepts as $\lnot K \lnot K$. Carter and Goldstein (2021, p. 2510) call such an identity ‘Reduction’ and Littlejohn and Dutant (2020, 1607) call it ‘Ignorance is strength’. Stalnaker (2006)—following Lenzen (1978) and followed by Halpern et al. (2009)—defines belief as $\lnot K \lnot K$. More recently (Rosenkranz, 2018, 2021) has defined propositional justification as $\lnot K \lnot K$ (where K stands for being in position to know).¹⁹ In the following we will refer to Stalnakerian belief, but our aim is more general: our approach will be beneficial for any knowledge-firster who endorses such a reduction and wants to work within a hyperintensional framework.²⁰ We must stress at this point that we are not criticizing Stalnaker’s original proposal. Stalnaker models idealized, logically omniscient agents (Stalnaker, 2006, 179). For these special agents, the dual definition is not problematic since the hyperintensionality constraint is not in place.²¹ We are enlarging the set of agents, allowing us to consider also subjects with epistemic limitations.

Let us now return to the problem. When we derive the semantic clause for Stalnakerian belief from the identity $B\varphi \leftrightarrow \lnot K \lnot K\varphi$ and Hyper-Know, we obtain the following:

where $\textsf{BEL}_\textsf{Stal}$ denotes Stalnakerian full belief. Unsurprisingly, Hyper-Bel suffers from the problems of EP:=DK presented in previous sections and, in particular, TEP strikes back in stronger form: if $\lnot K \varphi$ is not within the agent’s epistemic reach, they believe $\varphi$.

The problem becomes worse if the following simple closure condition on $\textsf{HYPE}$ holds:

With K-Closure in place, Hyper-Bel yields that one believes every sentence that is not within one’s epistemic reach.²² If one is not inclined to accept K-Closure, but still inclined to accept closure under negation for $\textsf{HYPE}$, the following is still in place: if $K\varphi$ is not within one’s epistemic reach, then one believes $\varphi$.²³ In any case, the result is highly problematic.

Stalnakerian full belief is an interesting target for our proposal not only because of the problems just mentioned but also because it can be defined as the epistemic possibility of knowledge: $B\varphi \leftrightarrow {\langle K \rangle }K \varphi$. Within his intensional framework, Stalnaker endorses $B\varphi \leftrightarrow {\langle K \rangle }K \varphi$ as well since it is equivalent to $B \varphi \leftrightarrow \lnot K \lnot K \varphi$, given EP:=DK.²⁴ Since our proposal abandons EP:=DK, $\lnot K \lnot K \varphi$ does not coincide with ${\langle K \rangle }K \varphi$. Let us consider the schematic semantic clause for the latter definition of belief we obtain via Hyper-Possibility:

Now, to believe $\varphi$, $K\varphi$ must be within one’s epistemic reach. One might prefer to relax the hyperintensionality condition and simply impose $\textsf{HYPE}(\varphi )=1$, rather than $\textsf{HYPE}(K\varphi )=1$. In fact, believing $\varphi$ seems to require having the proposition $\varphi$—rather than the more complex proposition $K\varphi$—within one’s epistemic reach. When dealing with full belief, however, also the more strict requirement makes sense. In fact, full belief is subjective certainty: when one believes $\varphi$, one believes to know $\varphi$. Therefore, whenever one believes $\varphi$, not only $\varphi$ must be within one’s epistemic reach, but also $K \varphi$ must be.

Having seen how our approach can help obtain hyperintensional semantics for a modality defined in terms of $\lnot K\lnot K$ when K itself is interpreted by the schema Hyper-Know, in the next section we explore the sound and complete logic of the hyperintensional version of Stalnaker’s system. We do so by interpreting belief as in Hyper-Bel* and using topic-sensitive semantics.²⁵

3.1 Stalnaker’s system

We first introduce Stalnaker’s original logic of knowledge and belief. Stalnaker works with the bimodal language $\mathcal {L}_{KB}$ recursively generated by the following grammar:

$$\begin{aligned} \varphi := p_i \; | \; \lnot \varphi \; | \; (\varphi \wedge \varphi ) \ | \ K\varphi \ | \ B\varphi \end{aligned}$$

where $p_i\in \textsf{Prop}$, a countable set of propositional variables. We often use $p, q, r,\ldots$ for propositional variables and employ the usual abbreviations for propositional connectives $\vee , \rightarrow , \leftrightarrow$ as $\varphi \vee \psi :=\lnot (\lnot \varphi \wedge \lnot \psi )$, $\varphi \rightarrow \psi := \lnot \varphi \vee \psi$, and $\varphi \leftrightarrow \psi := (\varphi \rightarrow \psi ) \wedge (\psi \rightarrow \varphi )$. We will follow the usual rules for the elimination of the parentheses. Finally, we read $K\varphi$ as “the agent knows that $\varphi$” and $B\varphi$ as “the agent believes that $\varphi$”.

Stalnaker interprets this language on Kripke models in which the accessibility relation is a directed preorder.²⁶ We call Stalnaker’s epistemic-doxastic system, given in Table 1, $\textsf{Stal}$.

Table 1 Stalnaker’s axoims $\textsf{Stal}$

The first three axioms in Table 1 are the axioms of the modal system $\textsf{S4}$ for knowledge. $\textsf{D}_B$ guarantees consistency of belief: one cannot believe a proposition and its negation at the same time. $\textsf{sPI}$ and $\textsf{sNI}$ describe strong belief as fully introspective. $\textsf{KB}$ is a standard bridge principle governing the relation between knowledge and belief. $\textsf{FB}$ is the core axiom that defines belief as subjective certainty (the other direction of the axiom is derivable in $\textsf{Stal}$). Deriving $B\varphi \leftrightarrow \lnot K \lnot K \varphi$ from these axioms makes belief reducible to knowledge and allows us to translate every formula in $\mathcal {L}_{KB}$ into a provably equivalent one in $\mathcal {L}_{K}$, by replacing B with $\lnot K \lnot K$. Stalnaker also shows that even if the system $\textsf{S4}_K$ is assumed for knowledge, the stronger system $\mathsf {S4.2}_K$ can be derived from $\textsf{Stal}$. In fact replacing B with $\lnot K \lnot K$ in $\textsf{D}_B$, axiom $.2_K$ ($\lnot K \lnot K\varphi \rightarrow K\lnot K\lnot \varphi$) is obtained. Moreover, $\textsf{Stal}$ also yields the unimodal system $\textsf{KD45}_B$ as the logic of belief.²⁷ The plausibility of each principle in Stalnaker’s system may be debatable; their defence is out of the scope of this paper. However, the resulting normal modal logics for knowledge ($\mathsf {S4.2}_K$) and belief ($\textsf{KD45}_B$) have been studied by several authors as logics for idealized, logically omniscient reasoners, e.g., Lenzen (1978) defends $\mathsf {S4.2}_K$ as a logic of knowledge, and van Ditmarsch et al. (2007), Baltag et al. (2008), Baltag and Smets (2008) take $\textsf{KD45}_B$ as the logic of belief.²⁸

In the next section, we propose a sound and complete axiomatization for a hyperintensional version of Stalnaker’s logic.

3.2 Stalnaker’s system revised: a hyperintensional version

In this section, we propose our revised, hyperintensional semantics for Stalnaker’s system. To do so, we choose to work with topic-sensitive semantics. The logic so defined, labelled HyperStal, is hyperintensional and embraces our concept of positive epistemic possibility.

We work with the language $\mathcal {L}_{K B {\langle K \rangle }\Box }$, recursively defined as follows as an extension of $\mathcal {L}_{K B}$:

$$\begin{aligned} \varphi := p_i \; | \; \lnot \varphi \; | \; (\varphi \wedge \varphi ) \ | \ K\varphi \ | \ {\langle K \rangle }\varphi \ | \ B\varphi \ | \ \Box \varphi \end{aligned}$$

$K\varphi$ and $B\varphi$ are read as before. We read ${\langle K \rangle }\varphi$ as ‘the agent considers $\varphi$ epistemically possible’. $\Box$ is a normal epistemic modality, standing for analyticity or an a priori modality.²⁹ The epistemic possibility operator ${\langle K \rangle }\varphi$ is a primitive component of the language and, in particular, not defined as $\lnot K \lnot \varphi$. Going further, the following notation will be useful: for any $\varphi \in \mathcal {L}_{K B {\langle K \rangle }\Box }$, $Var(\varphi )$ denotes the set of propositional variables occurring in $\varphi$. We will use ‘$\overline{\varphi }$’ to denote the tautology $\bigwedge _{p\in Var(\varphi )}(p\vee \lnot p)$, following a similar idea in Giordani (2019).

Next, we briefly introduce a simple topic-sensitive logic (following the presentation in (Özgün & Berto, 2021)).³⁰

Definition 1

(Topic model) A topic model is a tuple $\mathcal T=( T, \oplus , t, \mathfrak K)$ where

• T is a non-empty set of possible topics;

• $\oplus$: $T\times T\mapsto T$ is an idempotent, commutative, associative topic-fusion operator;

• $\mathfrak K\in T$ is a designated topic representing the totality of topics grasped by the agent; and

• $t: \textsf{Prop}\mapsto T$ is a topic function assigning a topic to each element in $\textsf{Prop}$.

Definition 2

(Topic-sensitive model) A topic-sensitive model is a tuple $\mathcal {M}=(W, R, V, \mathcal T)$ where W is a non-empty set of possible worlds, $R\subseteq W\times W$ is a binary accessibility relation between worlds, $V: \textsf{Prop}\mapsto \mathcal {P}(W)$ is a standardly defined valuation function that assigns to each propositional variable in $\textsf{Prop}$ a set of possible worlds and $\mathcal T$ is a topic model as given in Definition 1.

The function t extends to the whole language $\mathcal {L}_{K B {\langle K \rangle }\Box }$ by taking the topic of $\varphi$ as the fusion of the topics of the elements in $Var(\varphi )$: $t(\varphi )=\bigoplus \{t(p): p\in Var(\varphi )\}$. This entails topic-transparency of operators, that is, $t(\varphi )=t(K\varphi )=t(B\varphi )=t({\langle K \rangle }\varphi )=t(\Box \varphi )=t(\lnot \varphi )$ and $t(\varphi \wedge \psi )=t(\varphi )\oplus t(\psi )$.³¹ Topic parthood $\sqsubseteq$ is defined in a standard way: $\forall a, b\in T: a\sqsubseteq b\, \text {iff} \, a\oplus b=b$. It follows that $(T, \oplus )$ is a join semilattice and $(T, \sqsubseteq )$ is a partially ordered set.

Definition 3

(Semantics for $\mathcal {L}_{K B {\langle K \rangle }\Box }$) Given a topic-sensitive model $\mathcal {M}=(W, R, V, \mathcal T)$ and a possible world $w\in W$, the semantics for $\mathcal {L}_{K B {\langle K \rangle }\Box }$ is given recursively as follows:

$$\begin{aligned} \begin{array}{lcl} \mathcal {M}, w \vDash p &{} \text{ iff } &{} w \in V(p)\\ \mathcal {M}, w \vDash \lnot \varphi &{} \text{ iff } &{} \text{ not } \mathcal {M}, w \vDash \varphi \\ \mathcal {M}, w \vDash \varphi \wedge \psi &{} \text{ iff } &{} \mathcal {M}, w \vDash \varphi \text{ and } \mathcal {M}, w \vDash \psi \\ \mathcal {M}, w \vDash K\varphi &{} \text{ iff } &{} (\text{ for } \text{ all } v\in W, Rwu \text{ implies } \mathcal {M}, u\vDash \varphi ) \text{ and } t(\varphi )\sqsubseteq \mathfrak K\\ \mathcal {M}, w \vDash B\varphi &{} \text{ iff } &{} (\text{ there } \text{ is } v\in W, Rwv \text{ and } \mathcal {M}, v\vDash K\varphi ) \text{ and } t(\varphi )\sqsubseteq \mathfrak K\\ \mathcal {M}, w \vDash {\langle K \rangle }\varphi &{} \text{ iff } &{} (\text{ there } \text{ is } \in W, Rwv \text{ and } \mathcal {M}, v\vDash \varphi ) \text{ and } t(\varphi )\sqsubseteq \mathfrak K \\ \mathcal {M}, w \vDash \Box \varphi &{} \text{ iff } &{} \text{ for } \text{ all } v\in W (\mathcal {M}, v\vDash \varphi ) \end{array} \end{aligned}$$

While $\Box$ is interpreted as the global modality, the semantic clauses for K, B and ${\langle K \rangle }$ are respectively obtained by the schemas Hyper-Know, Hyper-Bel*, and Hyper-Possibility, as motivated earlier. When it is not the case that $\mathcal {M}, w\vDash \varphi$, we simply write $\mathcal {M}, w\not \vDash \varphi$.

We call a formula $\varphi$ valid in a topic-sensitive model $\mathcal {M}=(W, R, V, \mathcal T)$, denoted by $\mathcal {M}\vDash \varphi$, if $\mathcal {M}, w\vDash \varphi$ for all $w\in W$. We call a formula $\varphi$ valid in a class of topic-sensitive models $\mathfrak {C}$ if $\mathcal {M}\vDash \varphi$ for all $\mathcal {M}\in \mathfrak {C}$. Soundness and completeness are defined standardly (see, e.g., (Blackburn et al., 2001, Chapter 4.1)).

It is easy to see that, as in (Özgün & Berto, 2021), we have

$$\begin{aligned} \mathcal {M}, w\vDash B\overline{\varphi } \text{ iff } t(\varphi )\sqsubseteq \mathfrak {K}. \end{aligned}$$

Similarly for $K\overline{\varphi }$ and ${\langle K \rangle }\overline{\varphi }$. Therefore, $B\overline{\varphi }$, as well as $K\overline{\varphi }$ and ${\langle K \rangle }\overline{\varphi }$, express that ‘the agent has grasped the topic of $\varphi$’. This reading will be helpful in interpreting the axioms of $\textsf{HyperStal}$.

Theorem 1

$\textsf{HyperStal}$ is sound and complete wrt the class of reflexive, transitive, and directed topic-sensitive models.

Proof

See Appendix C.$\square$

Table 2 Axiomatization of $\textsf{HyperStal}$

Axioms and rules for $\Box$ require no comments: this is the logic of the global modality. Group (I) explains the behaviour of our hyperintensional knowledge and belief operators. $\textsf{C}_\star$ says that both knowledge and belief are fully conjunctive. $\textsf{Ax1}_\star$ states that the agent cannot know/believe a proposition without grasping its topic. $\textsf{Ax2}_\star$ is a restricted closure principle: the agent knows/believes a priori consequences of what they know/believe as long as they grasp the topics of these consequences. This axiom obviously states an idealization of the agent’s bounded deductive/computational powers and, in turn, points to a limitation of topic-sensitive logics in dealing with computational sources of logical omniscience. As also stated in (Özgün & Berto, 2021), further tools — such as the ones employed in (Smets & Solaki, 2018; Solaki, 2021) — are needed to tackle this sources of logical omniscience.³²$\textsf{Ax3}_\star$ just says that topics are world independent. Groups II and III are as in Stalnaker’s original system. Axiom $\textsf{Equ}_{{\langle K \rangle }K}$ defines the intended notion of hyperintensional epistemic possibility as a positive notion, it is the syntactic counterpart of Hyper-Possibility. Axioms in Group V are the same as the characteristic axioms in Stalnaker’s original system, with one caveat on the Strong Negative Introspection principle: the agent has strong introspective access to only those propositions whose topics they grasp. Indeed, $\textsf{sNI}$ is not a validity in the topic-sensitive semantics (see below): if the agent does not believe $\varphi$ because they have not grasped the topic of $\varphi$, they do not know that they do not believe it. Group V shows that we stay close to Stalnaker’s original system as much as possible, eliminating only the typical principles that work for highly idealized, logically omniscient agents (more on this at the end of the section). In fact, as shown in Theorem 2, we can derive the following two important theorems that are also part of Stalnaker’s original system: the identity of belief as epistemic possibility of knowledge, that is, $B \varphi \leftrightarrow {\langle K \rangle }K\varphi$, and axiom $\mathsf {.2}_K$ for knowledge, ${\langle K \rangle }K\varphi \rightarrow K{\langle K \rangle }\varphi$.

Theorem 2

The following are provable in $\textsf{HyperStal}$:

• 1 $B \varphi \leftrightarrow {\langle K \rangle }K\varphi$ (Positive Stalnakerian Belief)

• 2 ${\langle K \rangle }K\varphi \rightarrow K{\langle K \rangle }\varphi$ (Positive $\mathsf {.2}_K$)

Proof

See Appendix B. $\square$

Unsurprisingly, the ‘negative’ counterpart of these two principles, viz. $B\varphi \leftrightarrow \lnot K\lnot K\varphi$ and $\lnot K \lnot K\varphi \rightarrow K\lnot K\lnot \varphi$, are not valid, due to the topicality component in the semantics. The former invalidity is especially welcome if we consider the definition of belief as epistemic possibility of knowledge. As we have argued, believing a proposition requires grasping its topic. While belief as ${\langle K \rangle }K\varphi$ requires grasping the topic of $\varphi$, belief as $\lnot K\lnot K\varphi$ does not.

The following principles, which are part of Stalnaker’s original system $\textsf{Stal}$ are invalidated in (reflexive, transitive, and directed) topic-sensitive models due to topicality (see Appendix D for counterexamples):

• 1 from $\vdash \varphi$ infer $\vdash \star \varphi$, where $\star \in \{K, B, {\langle K \rangle }\}$ (Necessitation rule)

• 2 from $\vdash \varphi \leftrightarrow \psi$ infer $\vdash \star \varphi \leftrightarrow \star \psi$, where $\star \in \{K, B, {\langle K \rangle }\}$ (Closure under logical equivalents)

• 3 from $\vdash \varphi \rightarrow \psi$ infer $\vdash \star \varphi \rightarrow \star \psi$, where $\star \in \{K, B, {\langle K \rangle }\}$ (Closure under logical entailment)

• 4 $\vdash \lnot B\varphi \rightarrow K\lnot B \varphi$ (Strong negative introspection of B)

• 5 $\vdash B\varphi \leftrightarrow \lnot K\lnot K \varphi$ (Negative Stalnakerian belief)

We have already commented on the invalidity of the last two principles, so we focus on the first three. Given the Necessitation rule, every theorem is known/believed/epistemically possible. Closure under logical equivalents guarantees that an agent knows/believes/considers epistemically possible every proposition that is logically equivalent to what they know/believe/consider epistemically possible. Finally, by Closure under logical entailment, an agent knows/believes/considers epistemically possible every proposition that is a logical consequence of what they know/believe/consider epistemically possible. These inference rules are part of every normal modal logic. They are usually taken to be highly problematic for any epistemic logic that aims to alleviate the problem of logical omniscience though. While the failure of these principles is standard for necessity-like operators in topic-sensitive frameworks (see e.g. (Özgün & Berto, 2021)), their failure with respect to possibility-like operators is new in these frameworks.³³ The epistemic possibility operator is now subject to the same hypertintensionality restrictions as its necessity counterpart.

4 Concluding remarks

We argued that the reading of epistemic possibility as the dual of epistemic necessity generates intuitively problematic examples when reasoning about non-idealized agents. The notion of epistemic possibility, therefore, requires a more careful formal treatment within hyperintensional epistemic logics that aims to alleviate the problem of logical omniscience. We moreover showed that some of these problems strike back in a stronger form in frameworks that have knowledge as a primitive and define other epistemic concepts, such as justification and belief, in terms of ‘epistemic possibility’ of knowledge. To solve these problems, we proposed a non-dual interpretation of epistemic possibility, employing a hyperintensionality filter similar to the one that makes the corresponding epistemic necessity operator hyperintensional. As an application, we focused on Stalnaker’s combined logic of knowledge and belief, in which belief can be defined as the epistemic possibility of knowledge. We proposed an axiomatization of a hyperintensional version of the logic and proved its soundness and completeness with respect to a special class of topic-senitive models.

We consider our approach to be an improvement on the dual approach to epistemic possibility. In fact, one direction of EP:=DK is intact: if $\varphi$ is an epistemic possibility for S, then S does not know not-$\varphi$. The other direction does not hold anymore though. Not knowing not-$\varphi$ is not sufficient for $\varphi$ to be an epistemic possibility. For $\varphi$ to be (positively) epistemically possible, $\varphi$ should also be within the agent’s epistemic reach.

Our proposal also has the formal advantage to be a slight variation of the dual approach. If we restrict our attention to those propositions that are within the agent’s epistemic reach, duality is restored. This makes the proposal easily applicable to extant theories that already find a formalization in modal logic and provide them with a simple way to go hyperintensional, as already shown here with Stalnakerian belief.

Another advantage of the account is that we can model a wider variety of epistemic states that collapse into one another in the dual approach, as the knowledge of not-$\varphi$ and the absence of the epistemic possibility of $\varphi$. Moreover, it is a general account which can be applied to a wide family of hyperintensional logics. In our examples, $\textsf{MOD}$ was the Kripkean truth condition for knowledge and $\textsf{HYPE}$ was either topic-grasping or awareness. But both $\textsf{MOD}$ and $\textsf{HYPE}$ can stand for various other conditions. $\textsf{MOD}$ can represent any possible worlds modal clause (we mentioned a few in Sect. 1) and each of these can be combined with a different $\textsf{HYPE}$ condition. One natural candidate could be a complexity-filter on the kind of propositions the agent can process. (See, e.g., (Solaki, 2021) for an example of a complexity filter.) One can also impose an additional introspection-filter: an agent may be able to reason about their own epistemic state only up to a certain degree of introspection: an agent might know that $K\varphi$ holds for them, without knowing that $K\ldots K\varphi$ (with n-many Ks) does, when n is sufficiently high.

Appendices

Appendix A: Auxiliary results for completeness

Lemma 3

The following are provable in $\textsf{HyperStal}$:

• 1 $\star \overline{\varphi }\rightarrow \star \overline{\psi }$ if $Var(\psi )\subseteq Var(\varphi )$ (where $\star \in \{K, B\}$)

• 2 from $\vdash \varphi \rightarrow \psi$ infer $\vdash \star \varphi \rightarrow \star \psi$, if $Var(\psi )\subseteq Var(\varphi )$ (where $\star \in \{K, B\}$)

• 3 from $\vdash \varphi \leftrightarrow \psi$ infer $\vdash \star \varphi \leftrightarrow \star \psi$, if $Var(\psi )=Var(\varphi )$ (where $\star \in \{K, B\}$)

• 4 $\Box \lnot \varphi \rightarrow \lnot K\varphi$

• 5 $K\overline{\varphi }\rightarrow K(\varphi \vee \lnot \varphi )$

• 6 $(\Box \varphi \wedge K\overline{\varphi })\rightarrow K\varphi$

Proof

• 1. $\star \overline{\varphi }\rightarrow \star \overline{\psi }$ if $Var(\psi )\subseteq Var(\varphi )$ (where $\star \in \{K, B\}$)

  Follows easily from CPL and $\textsf{C}_\star$.

• 2. from $\vdash \varphi \rightarrow \psi$ infer $\vdash \star \varphi \rightarrow \star \psi$, if $Var(\psi )\subseteq Var(\varphi )$ (where $\star \in \{K, B\}$)

  

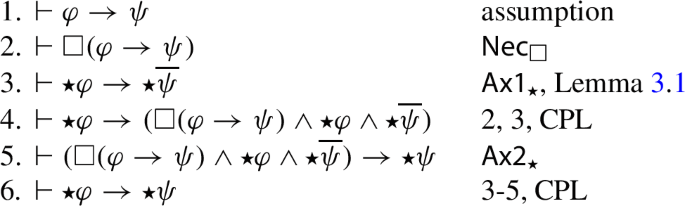
• 3. from $\vdash \varphi \leftrightarrow \psi$ infer $\vdash \star \varphi \leftrightarrow \star \psi$, if $Var(\psi )=Var(\varphi ).$ (where $\star \in \{K, B\}$)

  Similar to the proof of Lemma 3.2.

• 4. $K\varphi \rightarrow {\langle K \rangle }K\varphi$

  

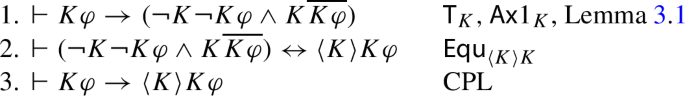
• 5. $\Box \lnot \varphi \rightarrow \lnot K\varphi$

  

• 6. $K\overline{\varphi }\rightarrow K(\varphi \vee \lnot \varphi )$

  

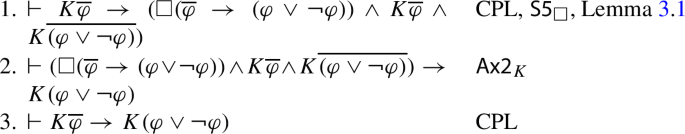
• 7. $(\Box \varphi \wedge K\overline{\varphi })\rightarrow K\varphi$

  

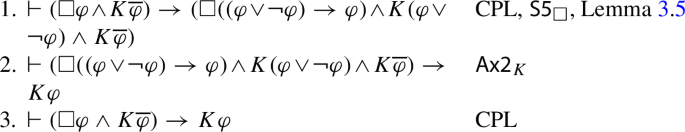
$\square$

Appendix B: Proof of Theorem 2

• 1. $B\varphi \leftrightarrow {\langle K \rangle }K\varphi$

  

• 2. ${\langle K \rangle }K\varphi \rightarrow K{\langle K \rangle }\varphi$

  

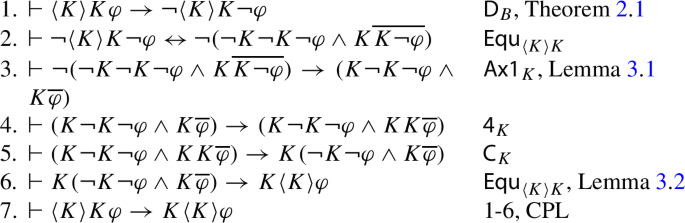
Appendix C: Proof of Theorem 1: Soundness and Completeness of $\textsf{HyperStal}$

The soundness proof is a matter of standard validity check so we skip the proof. In the remaining of this section, we prove the completeness of $\textsf{HyperStal}$. Our completeness proof is similar to the one presented in (Berto & Özgün, 2023). However, their completeness result is with respect to topic-sensitive subset spaces and we adapt it for reflexive, transitive, and directed relational models.

For any set of formulas $\Gamma \subseteq \mathcal {L}_{K B {\langle K \rangle }\Box }$ and any $\varphi \in \mathcal {L}_{K B {\langle K \rangle }\Box }$, we write $\Gamma \vdash \varphi$ if there exists a finitely many formulas $\varphi _1, \dots , \varphi _n\in \Gamma$ such that $\vdash (\varphi _1\wedge \dots \wedge \varphi _n)\vdash \varphi$. We say that $\Gamma$ is consistent if $\Gamma \not \vdash \bot$, and inconsistent otherwise. When $\Gamma$ is a singleton set of the form $\{\varphi \}$, we say $\varphi$ is consistent if $\{\varphi \}\not \vdash \bot$, and $\varphi$ is inconsistent otherwise. A sentence $\varphi$ is consistent with $\Gamma$ if $\Gamma \cup \{\varphi \}$ is consistent (or, equivalently, if $\Gamma \not \vdash \lnot \varphi$). Finally, a set of formulas $\Gamma$ is a maximally consistent set (or, in short, mcs) if it is consistent and any set of formulas properly containing $\Gamma$ is inconsistent (Blackburn et al., 2001).

Lemma 4

For every mcs $\Gamma$ of $\textsf{HyperStal}$ and $\varphi , \psi \in \mathcal {L}_{K B {\langle K \rangle }\Box }$, the following hold:

• 1 $\Gamma \vdash \varphi$ iff $\varphi \in \Gamma$,

• 2 if $\varphi \in \Gamma$ and $\varphi \rightarrow \psi \in \Gamma$, then $\psi \in \Gamma$,

• 3 if $\vdash \varphi$ then $\varphi \in \Gamma$,

• 4 $\varphi \in \Gamma$ and $\psi \in \Gamma$ iff $\varphi \wedge \psi \in \Gamma$,

• 5 $\varphi \in \Gamma$ iff $\lnot \varphi \not \in \Gamma$.

Proof

Standard. $\square$

In the following, we will use Lemma 4 in a standard way and often omit mention of it.

Lemma 5

(Lindenbaum’s Lemma) Every consistent set of $\textsf{HyperStal}$ can be extended to a maximally consistent one.

Proof

Standard. $\square$

Let $\mathcal {X}^c$ be the set of all $\textsf{HyperStal}$-maximally consistent sets. For each $\Gamma \in \mathcal {X}^c$, we define

• $\Gamma [\Box ]:=\{\varphi : \Box \varphi \in \Gamma \}$.

• $\Gamma [K]:=\{\varphi : K\psi \wedge \Box (\psi \rightarrow \varphi ) \in \Gamma \text{ for } \text{ some } \psi \in \mathcal {L}_{K B {\langle K \rangle }\Box }$}.

• $\Gamma [K, \Box ]:=\Gamma [K]\cup \Gamma [\Box ]$

Moreover, we define $\sim$ on $\mathcal {X}^c$ as

$$\begin{aligned} \Gamma \sim \Delta \ {}&\text{ iff } \ \Gamma [\Box ] \subseteq \Delta . \end{aligned}$$

Since $\Box$ is an $\textsf{S5}$ modality, it is easy to see that $\sim$ is an equivalence relation. For any maximally $\textsf{HyperStal}$-consistent set $\Gamma$, we denote by $\Gamma _\sim$ the equivalence class of $\Gamma$ induced by $\sim$, i.e., $\Gamma _{\sim }=\{\Delta \in \mathcal {X}^c : \Gamma \sim \Delta \}$.

Lemma 6

For any two maximally consistent sets $\Gamma$ and $\Delta$ such that $\Gamma \sim \Delta$, $\Gamma [\Box ]=\Delta [\Box ]$.

Proof

Follows from the axioms and rules of $\textsf{S5}_\Box$. $\square$

Definition 4

(Canonical Model for $\Gamma _0$) Given a mcs $\Gamma _0$ of $\textsf{HyperStal}$, the canonical model for $\Gamma _0$ is a tuple $\mathcal {M}^c=\{W^c, R^c, \mathcal {T}^c, V^c\}$, where

• $W^c= \{\Gamma \in \mathcal {X}^c : \Gamma _0\sim \Gamma \}$;

• $R^c\subseteq W^c\times W^c$ such that for all $\Gamma , \Delta \in W^c$:

  $$\begin{aligned} \Gamma R^c \Delta \text{ iff } \Gamma [K, \Box ] \subseteq \Delta \end{aligned}$$

• $\mathcal {T}^c$ is such that:

  • $T^c{=}\{a, b\}$ where $a{=}\{p \in \textsf{Prop}: \lnot K\bar{p}\in \Gamma _0 \}$ and $b{=}\{p\in \textsf{Prop}: K\bar{p}\in \Gamma _0\}$;

  • $\oplus ^c: T^c \times T^c\mapsto T^c$ such that $a\oplus ^c a=a$, $b\oplus ^c b=b$, $a\oplus ^c b=b\oplus ^c a=a$;

  • $\mathfrak K^c =b$;

  • $t^c: \textsf{Prop}\mapsto T^c$ such that for every $c\in T^c$ and $p\in \textsf {Prop}$: $t^c(p)=c$ iff $p\in c$, and $t^c$ extends to the whole language by $t^{c}(\varphi )=\bigoplus \limits ^{c} \{t^{c}(p): p\in Var(\varphi )\}$. The inclusion relation is defined as usual and it is such that $b \sqsubset ^c a$, i.e. b is strictly included in a;

• $V^c(p)=\{ \Gamma \in W^c: p \in \Gamma \}$.

Lemma 7

Given a mcs $\Gamma$, $\bigwedge _{i\le n} \varphi _i \in \Gamma [K, \Box ]$ for all finite $\{\varphi _1, \dots , \varphi _n\}\subseteq \Gamma [K, \Box ]$.

Proof

Let $\{\varphi _1, \dots , \varphi _n\}\subseteq \Gamma [K, \Box ]$, i.e., that $\{\varphi _1, \dots , \varphi _n\}\subseteq \Gamma [K]\cup \Gamma [\Box ]$. Without loss of generality, suppose that $\Phi \subseteq \Gamma [K]$ and $\Phi '\subseteq \Gamma [\Box ]$ for some $\Phi , \Phi '\subseteq \{\varphi _1, \dots , \varphi _n\}$ such that $\Phi \cup \Phi '= \{\varphi _1, \dots , \varphi _n\}$. Since $\Box$ is a normal modality, by following standard arguments, we know that $\bigwedge \Phi '\in \Gamma [\Box ]$. The assumption $\Phi \subseteq \Gamma [K]$ means that, for each $\varphi _i\in \Phi$ there is a $\psi _i \in \mathcal {L}_{K B {\langle K \rangle }\Box }$ such that $K\psi _i\wedge \Box (\psi _i\rightarrow \varphi _i)\in \Gamma$. Let $I_\Phi =\{i\in \mathbb {N} : \varphi _i\in \Phi \}$ (the set of indices of the elements in $\Phi$). Thus, $\bigwedge _{i\in I_\Phi } K\psi _i \wedge \bigwedge _{i\in I_\Phi } \Box (\psi _i\rightarrow \varphi _i)\in \Gamma$. Then, by $\textsf{C}_K$, we obtain that $K(\bigwedge _{i\in I_\Phi }\psi _i) \in \Gamma$. By $\textsf{S5}_\Box$, we also have $\Box (\bigwedge _{i\in I_\Phi }\psi _i \rightarrow \bigwedge _{i\le n} \varphi _i)\in \Gamma$. Moreover, by CPL (the theorem $\vdash ((\varphi \rightarrow \psi )\wedge \chi ) \rightarrow (\varphi \rightarrow (\psi \wedge \chi ))$), $\textsf{S5}_\Box$, and $\bigwedge \Phi '\in \Gamma [\Box ]$, this implies that $\Box (\bigwedge _{i\in I_\Phi }\psi _i \rightarrow (\bigwedge _{i\in I_\Phi } \varphi _i\wedge \bigwedge \Phi ') )\in \Gamma$, i.e., $\Box (\bigwedge _{i\in I_\Phi }\psi _i \rightarrow \bigwedge _{1\le i\le n} \varphi _i )\in \Gamma$. Therefore, $\bigwedge _{1\le i\le n} \varphi _i\in \Gamma [K]$, thus, $\bigwedge _{1\le i\le n} \varphi _i\in \Gamma [K,\Box ]$. $\square$

Lemma 8

For every mcs $\Gamma$, both $\Gamma [\Box ]$ and $\Gamma [K]$ are consistent. Moreover, $\Gamma [K,\Box ]$ is consistent.

Proof

Consistency of $\Gamma [\Box ]$ follows via a standard argument since $\Box$ is an $\textsf{S5}$ operator, in particular, since $\lnot \Box \bot$ is a theorem of $\textsf{HyperStal}$.

To show that $\Gamma [K]$ is consistent, assume, toward contradiction, that $\Gamma [K]$ is not consistent, i.e., $\Gamma [K]\vdash \bot$. This means that there is a finite subset $\Phi =\{\varphi _1, \dots , \varphi _n\}\subseteq \Gamma [K]$ such that $\vdash \bigwedge \Phi \rightarrow \lnot \varphi _j$ for some $j\le n$. By Lemma 7, we have that $\bigwedge \Phi \in \Gamma [K]$, thus, there is a $\psi \in \mathcal {L}_{K B {\langle K \rangle }\Box }$ such that $K\psi \in \Gamma$ and $\Box (\psi \rightarrow \bigwedge \Phi )\in \Gamma$. Since $\vdash \bigwedge \Phi \rightarrow \lnot \varphi _j$, by $\textsf{S5}_\Box$, we also have $\Box (\psi \rightarrow \lnot \varphi _j)\in \Gamma$. Hence, $\lnot \varphi _j\in \Gamma [K]$ too. As $\varphi _j\in \Gamma [K]$, we also have a $\psi '\in \mathcal {L}_{K B {\langle K \rangle }\Box }$ with $K\psi '\in \Gamma$ and $\Box (\psi '\rightarrow \varphi _j)\in \Gamma$. From $\Box (\psi \rightarrow \lnot \varphi _j)\in \Gamma$ and $\Box (\psi '\rightarrow \varphi _j)\in \Gamma$, by $\textsf{S5}_\Box$, we obtain that $\Box (\psi \rightarrow \lnot \psi ')\in \Gamma$. As $K\psi '\in \Gamma$, by $\textsf{Ax}1_{K}$ and Lemma 3.1, $K\overline{\lnot \psi '}\in \Gamma$. Therefore, $K\overline{\lnot \psi '}\in \Gamma$, $\Box (\psi \rightarrow \lnot \psi ')\in \Gamma$, $K\psi \in \Gamma$, by $\textsf{Ax}2_{K}$, imply that $K\lnot \psi '\in \Gamma$, contradicting the consistency of $\Gamma$: $K\psi '\in \Gamma$ and $K\lnot \psi '\in \Gamma$ imply, by $\textsf{T}_K$, that $\psi '\in \Gamma$ and $\lnot \psi '\in \Gamma$. Therefore, $\Gamma [K]$ is consistent.

Suppose now, toward contradiction, that $\Gamma [K,\Box ]$ is inconsistent, i.e., that $\Gamma [K]\cup \Gamma [\Box ]$ is inconsistent. Since both $\Gamma [\Box ]$ and $\Gamma [K]$ are consistent, inconsistency of $\Gamma [K,\Box ]$ implies (by Lemma 7) that there is $\psi \in \Gamma [K]$ and $\varphi \in \Gamma [\Box ]$ such that $\vdash (\varphi \wedge \psi ) \rightarrow \bot$, i.e., $\vdash \varphi \rightarrow \lnot \psi$, while both $\varphi$ and $\psi$ are consistent. Then, by $\textsf{S5}_\Box$ and since $\Box \varphi \in \Gamma$, we obtain that $\Box \lnot \psi \in \Gamma$. Moreover, $\psi \in \Gamma [K]$ implies that there is a $\chi \in \mathcal {L}_{K B {\langle K \rangle }\Box }$ such that $K\chi \wedge \Box (\chi \rightarrow \psi )\in \Gamma$. This implies that $\Box (\lnot \psi \rightarrow \lnot \chi )\in \Gamma$. Then, by $\textsf{K}_\Box$ (distributivity of $\Box$ over $\rightarrow$), we have that $\Box \lnot \psi \rightarrow \Box \lnot \chi \in \Gamma$. Thus, as $\Box \lnot \psi \in \Gamma$, we obtain that $\Box \lnot \chi \in \Gamma$. Moreover, by $K\chi \in \Gamma$, $\textsf{Ax}1_{K}$, and Lemma 3.1, we have $K\overline{\lnot \chi }\in \Gamma$. Then, as $\Box \lnot \chi \wedge K\overline{\lnot \chi }\in \Gamma$, by Lemma 3.6, we have $K\lnot \chi$, contradicting the consistency of $\Gamma$: $K\chi \in \Gamma$ and $K\lnot \chi \in \Gamma$ imply, by $\textsf{T}_K$, that $\chi \in \Gamma$ and $\lnot \chi \in \Gamma$. Therefore, $\Gamma [K, \Box ]$ is consistent. $\square$

For the Truth Lemma, we need the following auxiliary results.

Lemma 9

For any $\varphi \in \mathcal {L}_{K B {\langle K \rangle }\Box }$ and for any $\Gamma \in W^c$: $K \overline{\varphi }$ iff $\forall p\in Var(\varphi ): K\overline{p} \in \Gamma$.

Proof

($\Rightarrow$) Follows from Lemma 3.6.

($\Leftarrow$) Let $Var(\varphi )=\{p_1, \ldots , p_n\}$. It follows $\overline{\varphi }=\overline{p_1}\wedge \ldots \wedge \overline{p_n}$. If $K\bar{p_i}\in \Gamma$ for all $p_i\in \{p_1,\ldots , p_n\}$, then $\bigwedge _{i\le n}K\bar{p_i}\in \Gamma$ by Lemma 4.4 Then, by $\textsf{C}_K$ we obtain $K\bigwedge _{i\le n}\bar{p_i}\in \Gamma$, i.e. $K\bar{\varphi }$. $\square$

Corollary 10

Given a canonical topic-sensitive model $\mathcal {M}^c=\{W^c, R^c, \mathcal {T}^c, V^c\}$, for any $\Gamma \in W^c$, and $\varphi \in \mathcal {L}_{K B {\langle K \rangle }\Box }$, $K\overline{\varphi }\in \Gamma \text{ iff } t^c(\varphi )\sqsubseteq \mathfrak {K}^c$.

Proof

$\square$

Lemma 11

For every mcs $\Gamma$ and $\varphi \in \mathcal {L}_{K B {\langle K \rangle }\Box }$, if $\Gamma [K, \Box ]\vdash \varphi$ and $K\overline{\varphi }\in \Gamma$, then $K\varphi \in \Gamma$.

Proof

Suppose $\Gamma [K, \Box ]\vdash \varphi$ and $K\overline{\varphi }\in \Gamma$. Then, by Lemma 7, there is a $\chi \in \Gamma [K, \Box ]$ such that $\vdash \chi \rightarrow \varphi$. This means that $\Box (\chi \rightarrow \varphi )\in \Gamma$. We then have two cases:

• if $\chi \in \Gamma [K]$, there is a $\psi$ such that $K\psi \wedge \Box (\psi \rightarrow \chi )\in \Gamma$. Then, by $\textsf{S5}_\Box$ and the fact that $\Box (\chi \rightarrow \varphi )\in \Gamma$, we obtain that $\Box (\psi \rightarrow \varphi )\in \Gamma$. We also have $K\overline{\varphi }\in \Gamma$ and $K\psi \in \Gamma$. Therefore, by $\textsf{Ax}2_K$, we conclude that $K\varphi \in \Gamma$.

• if $\chi \in \Gamma [\Box ]$, then $\Box \chi \in \Gamma$. $\Box (\chi \rightarrow \varphi )\in \Gamma$ implies, by $\textsf{K}_\Box$, that $\Box \chi \rightarrow \Box \varphi \in \Gamma$. Therefore, $\Box \varphi \in \Gamma$. Since $K\overline{\varphi }\in \Gamma$ as well, by Lemma 3.6, we obtain that $K\varphi \in \Gamma$.

$\square$

Lemma 12

$\mathcal {M}^c=\{W^c, R^c, \mathcal {T}^c, V^c\}$ is a reflexive, transitive, and directed topic-sensitive model.

Proof

We need to prove that (1) $\mathcal {T}^c$ is topic model as described in Definition 1 and (2) $R^c$ is reflexive, transitive, and directed. For (1): it is easy to see that a and b are disjoint sets, thus $t^c$ is well-defined. Moreover, $\oplus ^c$ satisfies the desired properties by definition. In the remainder of the proof, we focus on (2):

$R^c$ is reflexive: let $\Gamma \in W^c$ and $\varphi \in \mathcal {L}_{K B {\langle K \rangle }\Box }$ such that $\varphi \in \Gamma [K, \Box ]$. This means, by the definition of $\Gamma [K, \Box ]$, that $\varphi \in \Gamma [K]$ or $\varphi \in \Gamma [\Box ]$. We then have two cases:

• If $\varphi \in \Gamma [K]$, there is $\psi \in \mathcal {L}_{K B {\langle K \rangle }\Box }$ such that $K\psi \wedge \Box (\psi \rightarrow \varphi )\in \Gamma$. Then, by axiom $\textsf{T}_K$ and $\textsf{T}_\Box$, we have that $\psi \in \Gamma$ and $\psi \rightarrow \varphi \in \Gamma$, respectively. Then, by Lemma 4.2, we obtain that $\varphi \in \Gamma$.

• If $\varphi \in \Gamma [\Box ]$, we have that $\Box \varphi \in \Gamma$. Thus, by axiom $\textsf{T}_\Box$ and Lemma 4.2, we have $\varphi \in \Gamma$.

As $\varphi$ has been chosen arbitrarily, we have $\Gamma [K, \Box ] \subseteq \Gamma$, i.e., $\Gamma R^c \Gamma$.

$R^c$ is transitive: let $\Gamma , \Delta ,$ and $\Sigma \in W^c$ such that $\Gamma R^c \Delta$ and $\Delta R^c \Sigma$, i.e., that $\Gamma [K, \Box ]\subseteq \Delta$ and $\Delta [K, \Box ]\subseteq \Sigma$. Let $\varphi \in \Gamma [K, \Box ]$, i.e., $\varphi \in \Gamma [K]$ or $\varphi \in \Gamma [\Box ]$. We again have two cases:

• If $\varphi \in \Gamma [K]$, there is $\psi \in \mathcal {L}_{K B {\langle K \rangle }\Box }$ such that $K\psi \wedge \Box (\psi \rightarrow \varphi )\in \Gamma$, i.e., that $K\psi \in \Gamma$ and $\Box (\psi \rightarrow \varphi )\in \Gamma$. The former together with $\textsf{4}_K$, CPL, and $\textsf{S5}_\Box$ implies that $KK\psi \wedge \Box (K\psi \rightarrow K\psi )\in \Gamma$. Therefore, $K\psi \in \Gamma [K, \Box ]$. Thus, by the assumption that $\Gamma [K, \Box ]\subseteq \Delta$, we obtain that $K\psi \in \Delta$. Moreover, $\Box (\psi \rightarrow \varphi )\in \Gamma$ and Lemma 6 imply that $\Box (\psi \rightarrow \varphi ) \in \Delta$. Therefore, $K\psi \wedge \Box (\psi \rightarrow \varphi ) \in \Delta$, i.e., $\varphi \in \Delta [K, \Box ]$. We then conclude, by our initial assumption $\Delta [K, \Box ]\subseteq \Sigma$, that $\varphi \in \Sigma$.

• If $\varphi \in \Gamma [\Box ]$, then, by Lemma 6, we have $\varphi \in \Delta [\Box ]$. Since $\Delta [\Box ] \subseteq \Delta [K, \Box ] \subseteq \Sigma$, we conclude that $\varphi \in \Sigma$.

As $\varphi$ has been chosen arbitrarily, we have $\Gamma [K, \Box ] \subseteq \Sigma$, i.e., $\Gamma R^c \Sigma$.

$R^c$ is directed: let $\Gamma _1, \Gamma _2, \Gamma _3\in W^c$ such that $\Gamma _1 R^c \Gamma _2$ and $\Gamma _1 R^c \Gamma _3$, i.e., that $\Gamma _1[K, \Box ]\subseteq \Gamma _2$ and $\Gamma _1[K, \Box ]\subseteq \Gamma _3$. To prove that $R^c$ is directed, we show that $\Gamma _2[K, \Box ]\cup \Gamma _3[K, \Box ]$ is consistent. Suppose otherwise, i.e., that $\Gamma _2[K, \Box ]\cup \Gamma _3[K, \Box ]$ is inconsistent. Then, by Lemma 7, there is $\varphi \in \Gamma _2[K, \Box ]$ and $\psi \in \Gamma _3[K, \Box ]$ such that $\vdash (\varphi \wedge \psi ) \rightarrow \bot$, i.e., $\vdash \psi \rightarrow \lnot \varphi$, while both $\varphi$ and $\psi$ are consistent (since both $\Gamma _2[K, \Box ]$ and $\Gamma _3[K, \Box ]$ are consistent, by Lemma 8). Notice that, by Lemma 6 and the definition of $W^c$, $\Gamma _2[\Box ]=\Gamma _3[\Box ]$. We then have three cases:

• if $\varphi \in \Gamma _2[K]$ and $\psi \in \Gamma _3[K]$, there exist $\chi , \chi '\in \mathcal {L}_{K B {\langle K \rangle }\Box }$ such that (1) $K\chi \wedge \Box (\chi \rightarrow \varphi )\in \Gamma _2$ and (2) $K\chi '\wedge \Box (\chi ' \rightarrow \psi )\in \Gamma _3$. The fact that $\vdash \psi \rightarrow \lnot \varphi$ implies, by $\textsf{S5}_\Box$, that $\Box (\psi \rightarrow \lnot \varphi )\in \Gamma _3$. Therefore, by $\Box (\chi ' \rightarrow \psi )\in \Gamma _3$, $\Box (\psi \rightarrow \lnot \varphi )\in \Gamma _3$, $\Box (\lnot \varphi \rightarrow \lnot \chi )\in \Gamma _3$ (by Lemma 6 and $\Box (\lnot \varphi \rightarrow \lnot \chi )\in \Gamma _2$), and $\textsf{S5}_\Box$, we obtain that $\Box (\chi '\rightarrow \lnot \chi )\in \Gamma _3$. Moreover, since $K\chi \in \Gamma _2$ and $\Gamma _1[K, \Box ]\subseteq \Gamma _2$, we have that $\lnot K\lnot K\chi \in \Gamma _1$. Moreover, by $K\chi \in \Gamma _2$, $\textsf{4}_K$, and $\textsf{Ax1}_K$, we obtain $K\overline{K\chi }\in \Gamma _1$. Then, by $\mathsf {Equ_{{\langle K \rangle }K}}$, we have ${\langle K \rangle }K\chi \in \Gamma _1$. Thus, by Theorem 2.2, $K{\langle K \rangle }\psi \in \Gamma _1$. Since $\Gamma _1[K, \Box ]\subseteq \Gamma _3$, we obtain that ${\langle K \rangle }\chi \in \Gamma _3$. Again by axiom $\mathsf {Equ_{{\langle K \rangle }K}}$, we have $\lnot K\lnot \chi \in \Gamma _3$. But we also have that $K\overline{\chi }\in \Gamma _3$ (since ${\langle K \rangle }\chi \in \Gamma _3$ and by $\mathsf {Equ_{{\langle K \rangle }K}}$), thus $K\overline{\lnot \chi }\in \Gamma _3$ (by Lemma 3.1), $\Box (\chi '\rightarrow \lnot \chi )\in \Gamma _3$, and $K\chi '\in \Gamma _3$. Thus, by $\textsf{Ax}2_K$, $K\lnot \chi \in \Gamma _3$, contradicting the consistency of $\Gamma _3$.

• if $\varphi \in \Gamma _2[K]$ and $\psi \in \Gamma _3[\Box ]$, there exist $\chi \in \mathcal {L}_{K B {\langle K \rangle }\Box }$ such that $K\chi \wedge \Box (\chi \rightarrow \varphi )\in \Gamma _2$. Moreover, $\psi \in \Gamma _3[\Box ]$ means, since $\Gamma _2[\Box ]=\Gamma _3[\Box ]$, that $\Box \psi \in \Gamma _2$. Therefore, by $\textsf{S5}_\Box$, we have $\Box (\chi \rightarrow \psi )\in \Gamma _2$. Similar to the case above, we obtain that $\Box (\chi \rightarrow \lnot \varphi )\in \Gamma _2$. Then, by $\textsf{S5}_\Box$, $\Box (\chi \rightarrow (\varphi \wedge \lnot \varphi ))\in \Gamma _2$, i.e., $\Box \lnot \chi \in \Gamma _2$. Then, by Lemma 3.4, we have $\lnot K\chi$, contradicting the consistency of $\Gamma _2$.

• if $\varphi \in \Gamma _2[\Box ]$ and $\psi \in \Gamma _3[K]$: Similar to the above case.

We, therefore, obtain that $\Gamma _2[K, \Box ]\cup \Gamma _3[K, \Box ]$ is consistent, therefore, by Lemma 5 (Lindenbaum’s Lemma), can be extended to a mcs $\Delta$ such that $\Gamma _2[K, \Box ]\cup \Gamma _3[K, \Box ]\subseteq \Delta$, i.e., that $\Gamma _2 R^c\Delta$ and $\Gamma _3 R^c\Delta$. Hence, $R^c$ is directed. $\square$

Lemma 13

(Truth Lemma) Let $\Gamma _0$ be a mcs of $\textsf{HyperStal}$ and $\mathcal {M}^c=\{W^c, R^c, \mathcal {T}^c, V^c\}$ the canonical model for $\Gamma _0$. Then, for every $\varphi \in \mathcal {L}_{K B {\langle K \rangle }\Box }$ and $\Gamma \in W^c$, we have $\mathcal {M}^c, \Gamma \vDash \varphi$ iff $\varphi \in \Gamma$.

Proof

By induction on the complexity of $\varphi$. In the proof we will exploit the proprieties of mcs given in Lemma 4 in a standard way and omit to mention it. The cases for the propositional variables, Booleans, and $\varphi :=\Box \psi$ are standard. We prove the cases for $\varphi :=K\psi$, $\varphi :={\langle K \rangle }\psi$, and $\varphi :=B\psi$.

Case $\varphi :=K\psi$:

($\Rightarrow$) Assume $\mathcal {M}^c, \Gamma \vDash K \psi$. This means, by the semantics of K, that for any $\Gamma '$ such that $\Gamma R^c\Gamma '$, $\mathcal {M}^c, \Gamma '\vDash \psi$ and $t(\psi )\sqsubseteq \mathfrak K^c$. The former, by IH, entails that $\psi \in \Gamma '$ for all $\Gamma '$ with $\Gamma R^c\Gamma '$. Now consider the set $\Gamma [K,\Box ]\cup \{\lnot \psi \}$ and assume it is consistent for the sake of contradiction. Then, by Lindenbaum’s Lemma (Lemma 5), there is a mcs $\Delta$ such that $\Gamma [K,\Box ]\cup \{\lnot \psi \}\subseteq \Delta$. This implies, by the definition of $R^c$, that $\Gamma R^c\Delta$ (since $\Gamma [\Box ]\subseteq \Gamma [K,\Box ]$, we have that $\Delta \in W^c$). Therefore, $\lnot \psi \in \Delta$, contradicting our assumption that $\psi \in \Gamma '$ for all $\Gamma '$ with $\Gamma R^c\Gamma '$. The set $\Gamma [K,\Box ]\cup \{\lnot \psi \}$ is then inconsistent, meaning that $\Gamma [K,\Box ]\vdash \psi$. Moreover, $t(\psi )\sqsubseteq \mathfrak K^c$, by Corollary 10, implies that $K\overline{\psi }\in \mathfrak {K}^c$. Then, by Lemma 11, we obtain that $K\psi \in \Gamma$.

($\Leftarrow$) Assume $K\psi \in \Gamma$. By $\textsf{Ax1}_K$, it follows $K \overline{\psi }\in \Gamma$. By Corollary 10, we obtain $t^c(\psi )\sqsubseteq \mathfrak K^c$. Now consider $\Gamma '\in W^c$ such that $\Gamma R^c\Gamma '$. Since $K\psi \in \Gamma$ and by $\textsf{S5}_\Box$ we have $\Box (\psi \rightarrow \psi )\in \Gamma$, it follows that $\psi \in \Gamma '$. Then, by IH, we have $\mathcal {M}^c, \Gamma '\vDash \psi$. Joining this result with $t^c(\psi )\sqsubseteq \mathfrak K^c$, we conclude $\mathcal {M}, \Gamma \vDash K\psi$.

Case $\varphi :={\langle K \rangle }\psi$:

Case $\varphi :=B\psi$: Follows via similar steps as in the cases for $\varphi := K\psi$ and $\varphi :={\langle K \rangle }\psi$, and Theorem 2.1. $\square$

Corollary 14

$\textsf{HyperStal}$ is complete wrt the class of reflexive, transitive and directed topic-sensitive models.

Proof

Let $\varphi \in \mathcal {L}_{K B \langle K\rangle \Box }$ such that $\nvdash \varphi$. This means that $\{\lnot \varphi \}$ is consistent. Then by Lindembaum’s Lemma (Lemma 5), there exists a mcs $\Gamma _0$ such that $\varphi \not \in \Gamma _0$. Therefore by Truth Lemma (Lemma 13), we conclude that $\mathcal M^c, \Gamma _0\nvDash \varphi$, where $\mathcal M^c$ is the canonical model for $\Gamma _0$. $\square$

Appendix D: Invalidities 1–5

For the sake of simplicity, in the following, we write $w\vDash \varphi$ for $\mathcal {M}, w\vDash \varphi$ and $w\nvDash \varphi$ for $\mathcal {M}, w\nvDash \varphi$.

Countermodel. Let $\mathcal {M}=(W, R, T, \oplus , t, \mathfrak K, V)$ be such that $W=\{w\}$, $R=\{(w, w )\}$, $T=\{a, b\}$, $b\sqsubset a$, $t(p)=a, t(q)=b=\mathfrak K$, $V(p)=V(q)=\{w\}$. It is easy to check that R is reflexive, transitive and directed.

Since $p\vee \lnot p$ is a propositional tautology, we have $w\vDash \Box (p\vee \lnot p)$. Nonetheless, since $\mathfrak K \sqsubset t(p)=t(p\vee \lnot p)=a$, it follows $w\nvDash \star (p\vee \lnot p)$ for $\star \in \{K, B, {\langle K \rangle }\}$, viz. the Necessitation rule (1) fail for all $\star \in \{K, B, {\langle K \rangle }\}$. Moreover, since $(p\vee \lnot p)\leftrightarrow (q\vee \lnot q)$ is a propositional tautology, and $w\vDash \star (q\vee \lnot q)$, we also obtain that Closure under logical equivalents and Closure under logical entailment (2-3) fail for all $\star \in \{K, B, {\langle K \rangle }\}$. Moreover, it is easy to see that $w\vDash \lnot B(p\vee \lnot p)$ and $w\not \vDash K\lnot B (p\vee \lnot p)$ (since $\mathfrak K\sqsubset t(p) =t(B (p\vee \lnot p))$), thus, $\textsf{sNI}$ (4) fails. Similarly $w\vDash \lnot K \lnot K (p\vee \lnot p)$ but $w\nvDash B (p\vee \lnot p)$, thus Negative Stalnekarian belief (5) fails.

Fig. 1

Model $\mathcal {M}$