Firm size and productivity from occupational choices

Abstract

We model the distributions of firm sizes and of firms’ total factor productivity (TFP) as outcomes of a market equilibrium from the occupational decisions of individuals with different entrepreneurial skills, of working as employees, employers, or solo entrepreneurs. The model explains empirical regularities such as (i) the positive cross-section correlation between average size of firms and average labor productivity of countries, (ii) the positive association between size and TFP of firms in an economy, and (iii) the power law distribution of firm sizes. Two parameters of the model, one that measures the organizational size diseconomies and other related to the dispersion of the distribution of entrepreneurial skills in the population, appear as main determinants of the differences in firm sizes and in productivity, across economies and among firms within an economy. The results of the paper should be of interest for the design and evaluation of firm-size-dependent policies.

Appendices

Appendix 1. The market equilibrium solution

From the main text, in the market equilibrium:

• i. Each agent makes the occupational choice (employee, solo entrepreneur, or employer-manager) that results in a higher “rent.”

• ii. Aggregate labor demand equals aggregate labor supply (this condition determines the equilibrium wage).

Both conditions are interrelated. The occupational choice depends on the wage that is set in the labor market, and the labor supply and demand depend on the individual occupational choices.

For a given wage w, the occupational choice of an individual with entrepreneurial skills e may be written as

$$ \operatorname{Max}\left[w,R(e),\Pi (e)\right] $$

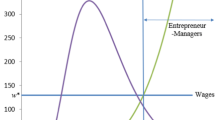
where Π(e) and R(e) are, respectively, the net revenues of the solo entrepreneur and the profits of employers, as functions of her respective level of skill, Eqs. (9) and (11) in the main text. There exist two levels of skill e₁ and e₂ (see Fig. 1), such that

$$ \operatorname{Max}\left[w,R(e),\Pi (e)\right]=\left\{\begin{array}{cc}w& \mathrm{for}\;\mathrm{e}\le {\mathrm{e}}_1\\ {}R(e)& \mathrm{for}\;{\mathrm{e}}_1\le \mathrm{e}\le {e}_2\\ {}\Pi (e)& \mathrm{for}\;\mathrm{e}\ge {\mathrm{e}}_2\end{array}\right. $$

(19)

and

$$ {\displaystyle \begin{array}{l}w=R\left({e}_1\right)\\ {}R\left({e}_2\right)=\Pi \left({e}_2\right)\end{array}} $$

(20)

Individuals with skills e < e₁ will choose to work as employees, individuals with skills e₁ < e < e₂ will prefer to be solo entrepreneurs, and individuals with skills e > e₂ will become employer-managers. The level of entrepreneurial skill of the (unique) individual who is indifferent between working as an employee and becoming a solo entrepreneur is e₁. Analogously, e₂ is the level of entrepreneurial skills of the (unique) individual who is indifferent between becoming a solo entrepreneur and working as an employer-manager.

The occupational choices determine the aggregate labor supply $S(w)=\underset{b}{\overset{e_1\left({w}^{\ast}\right)}{\int }}d\Gamma (e)$, and the aggregate labor demand $D(w)=\underset{e_2\left(w\ast \right)}{\overset{+\infty }{\int }}L\left(e;{w}^{\ast },c\right)d\Gamma (e)$. In equilibrium, the two must be equal, so the market equilibrium conditions are given by the three equations:

$$ {\displaystyle \begin{array}{l}w=R\left({e}_1\right)\\ {}R\left({e}_2\right)=\Pi \left({e}_2\right)\\ {}\underset{b}{\overset{e_1}{\int }}d\Gamma (e)=\underset{e_2}{\overset{+\infty }{\int }}L\left(e;w,c\right)d\Gamma (e)\end{array}} $$

where L(e, w, c), Π(e), and R(e) are given by Eqs. (9)–(11) in the main text, and Γ(e) is the Pareto-cumulative distribution function with parameters (a, b). After substituting these equations (demand for employees, profits of employers, and revenues of the solo self-employed), and doing some calculations, we obtain the following system of equations in (e₁, e₂, w) that characterize the equilibrium:

$$ w=\left({\left(\theta {e}_1\right)}^{\frac{\rho }{1+\rho }}{\left(\frac{c}{1-\mu}\right)}^{\frac{1}{1+\rho }}-c\right){\left(\frac{1}{\mu }{\left(\frac{\theta \left(1-\mu \right){e}_1}{c}\right)}^{\frac{\rho }{1+\rho }}-\frac{\left(1-\mu \right)}{\mu}\right)}^{\frac{1}{\rho }} $$

(21)

$$ \frac{\left({\left(\theta {e}_2\right)}^{\frac{\rho }{1+\rho }}{\left(\frac{c}{1-\mu}\right)}^{\frac{1}{1+\rho }}-c\right)}{{\left(\frac{1}{\mu }{\left(\frac{\theta \left(1-\mu \right){e}_2}{c}\right)}^{\frac{\rho }{1+\rho }}-\frac{\left(1-\mu \right)}{\mu}\right)}^{\frac{-1}{\rho }}}=\frac{{\beta \theta}^{\frac{1}{\beta }}{\left(1-\beta \right)}^{\frac{1-\beta }{\beta }}{e_2}^{\frac{\beta +1}{\beta }}}{{\left({\left(1-\mu \right)}^{\frac{1}{1+\rho }}{c}^{\frac{\rho }{1+\rho }}+{\mu}^{\frac{1}{1+\rho }}{w}^{\frac{\rho }{1+\rho }}\right)}^{\frac{\left(1-\beta \right)\left(1+\rho \right)}{\rho \beta}}} $$

(22)

$$ \frac{\beta {ab}^a}{\beta \left(a-1\right)-1}\frac{\theta^{\frac{1}{\beta }}{\left(1-\beta \right)}^{\frac{1}{\beta }}{\left(\frac{\mu }{w}\right)}^{\frac{1}{1+\rho }}}{{\left({\left(1-\mu \right)}^{\frac{1}{1+\rho }}{c}^{\frac{\rho }{1+\rho }}+{\mu}^{\frac{1}{1+\rho }}{w}^{\frac{\rho }{1+\rho }}\right)}^{\frac{\rho +1-\beta }{\rho \beta}}}{e_2}^{\frac{1-\beta \left(a-1\right)}{\beta }}=\left(1-{\left(\frac{b}{e_1}\right)}^a\right) $$

(23)

There is no closed-form solution to this non-linear system of equations. Although these equations are complex, we can prove existence and uniqueness⁸ of equilibrium, provided that the necessary condition β(a − 1) > 1 is satisfied, and we can solve them numerically, implicitly defining the equilibrium values of e₁, e₂, and w as functions of the seven exogenous parameters e₁^∗(θ, μ, c, ρ, β, a, b), e₂^∗(θ, μ, c, ρ, β, a, b),  and  w^∗(θ, μ, c, ρ, β, a, b).

Alternatively, we can express the equilibrium values of w and e₂ as functions of e₁, and then find the equilibrium value of e₁ by solving a single equation. Proceeding in this way, the equilibrium value of w (as a function of e₁) is directly given by (21) and the equilibrium value of e₂ is given by

$$ {e}_2={\left(\left(1-{\left(\frac{b}{e_1}\right)}^a\right)\frac{\left(\beta \left(a-1\right)-1\right){f}_1\left({e}_1\right)}{\theta^{\frac{1}{\beta }}{\left(1-\beta \right)}^{\frac{1}{\beta }}{\mu}^{\frac{1}{\rho }}\beta {ab}^a}{\left({\left(1-\mu \right)}^{\frac{1}{1+\rho }}{c}^{\frac{p}{1+\rho }}+{\left[{f}_1\left({e}_1\right)\right]}^{\rho}\right)}^{\frac{\rho +1-\beta }{\rho \beta}}\right)}^{\frac{\beta }{1-\beta \left(a-1\right)}} $$

(24)

where ${f}_1\left({e}_1\right)={\left({\left(\frac{c{\theta}^{\rho }{e}_1^{\rho }}{1-\mu}\right)}^{\frac{1}{1+\rho }}-c\right)}^{\frac{1}{1+\rho }}{\left({\left(\frac{\theta \left(1-\mu \right){e}_1}{c}\right)}^{\frac{\rho }{1+\rho }}-\left(1-\mu \right)\right)}^{\frac{1}{\rho \left(1+\rho \right)}}$.

Finally, the equilibrium value of e₁ is given by the unique⁹ solution to the following equation that satisfies conditions b ≤ e₁ ≤ e₂ and w ≥ 0:

$$ {\left({A}_4{\left(\frac{A_2\left(1-{\left(b/{e}_1\right)}^a\right){f}_1\left({e}_1\right)}{{\left({A}_3+{\left[{f}_1\left({e}_1\right)\right]}^{\rho}\right)}^{-{A}_6}}\right)}^{A_1}-1\right)}^{\frac{1+\rho }{\rho }}=\frac{{\beta \theta}^{\frac{1}{\beta }}{\left(1-\beta \right)}^{\frac{1-\beta }{\beta }}}{c{\left(1-\mu \right)}^{\frac{1}{\rho }}}\frac{{\left[{A}_2\left(1-{\left(b/{e}_1\right)}^a\right){f}_1\left({e}_1\right)\right]}^{A_5}}{{\left({A}_3+{\left[{f}_1\left({e}_1\right)\right]}^{\rho}\right)}^{A_6\left(1-{A}_5\right)-1}} $$

(25)

where,

$$ {\displaystyle \begin{array}{c}{A}_1=\frac{-\beta \rho}{\left(1+\rho \right)\left(\beta \left(a-1\right)-\tau \right)}<0,{A}_2=\frac{\left(\beta \left(a-1\right)-1\right)}{\theta^{\frac{1}{\beta }}{\left(1-\beta \right)}^{\frac{1}{\beta }}{\mu}^{\frac{1}{\rho }}\beta {ab}^a}>0,{A}_3={\left(1-\mu \right)}^{\frac{1}{1+\rho }}{c}^{\frac{\rho }{1+\rho }}>0,\\ {}{A}_4={\left(\frac{\theta^{\rho }}{c^{\rho}\left(1-\mu \right)}\right)}^{\frac{1}{1+\rho }}>0,{A}_5=\frac{-\left(\beta +1\right)}{\left(\beta \left(a-1\right)-1\right)}<0,{A}_6=\frac{1+\rho -\beta }{\rho \beta}>0,\mathrm{and}\\ {}{f}_1\left({e}_1\right)={\left({\left(\frac{c{\theta}^{\rho }{e}_1^{\rho }}{1-\mu}\right)}^{\frac{1}{1+\rho }}-c\right)}^{\frac{1}{1+\rho }}{\left({\left(\frac{\theta \left(1-\mu \right){e}_1}{c}\right)}^{\frac{\rho }{1+\rho }}-\left(1-\mu \right)\right)}^{\frac{1}{\rho \left(1+\rho \right)}}\end{array}} $$

This equation has no closed-form solution but can be solved numerically, implicitly defining the equilibrium value of e₁ as a function of the exogenous parameters ${e}_1^{\ast}\left(\theta, \mu, c,\rho, \beta, a,b\right)$

Once the equilibrium value of e₁ is found, it is straightforward to obtain the equilibrium wage, the equilibrium value of e₂, and any other endogenous variable (labor supply, equilibrium number of employees, and so on).

Appendix 2. Calibration of the parameters of the model

The exogenous parameters of the model are (θ, μ, c, ρ, β, a, b). In the main text, we justify the initial values for parameters c = 0.12, θ = 1, ρ = 0.5 (σ = 2/3), and μ = 0.75. Therefore, we have parameters a, b, and β remaining for calibration. For the calibration, we use information on the proportions of those employed as employees and as employers plus managers, together with information on the proportion of those occupied in firms with 250 employees or more, and the market equilibrium conditions of the model:

$$ {\displaystyle \begin{array}{c}\Gamma \left({e}_1\right)=1-{\left(\frac{b}{e_1}\right)}^a=0.79\\ {}1-\Gamma \left({e}_2\right)={\left(\frac{b}{e_2}\right)}^a=0.085\\ {}\frac{0.085{\left(\frac{L_{\mathrm{min}}}{250}\right)}^{\frac{a\beta}{1+\beta }}+0.79{\left(\frac{L_{\mathrm{min}}}{250}\right)}^{\frac{\beta \left(a-1\right)-1}{1+\beta }}}{0.875}=0.25\end{array}} $$

where L_min = L(w; e₂) is given in Result 1b, and w, e₁, and e₂ are given by the market equilibrium conditions, Eqs. (21)–(23) of Appendix 1. Substituting L_min, the complete system of equations is

$$ {\displaystyle \begin{array}{c}\begin{array}{l}1-{\left(\frac{b}{e_1}\right)}^a=0.79,\\ {}{\left(\frac{b}{e_2}\right)}^a=0.085,\end{array}\\ {}\begin{array}{l}0.875\times 0.25=0.08{\left(\frac{1}{250}{\theta}^{\frac{1}{\beta }}{\left(1-\beta \right)}^{\frac{1}{\beta }}{\left(\frac{\mu }{w}\right)}^{\frac{1}{1+\rho }}{\left({\left(1-\mu \right)}^{\frac{1}{1+\rho }}{c}^{\frac{\rho }{1+\rho }}+{\mu}^{\frac{1}{1+\rho }}{w}^{\frac{\rho }{1+\rho }}\right)}^{\frac{-\rho -1+\beta }{\rho \beta}}{e_2}^{\frac{\beta +1}{\beta }}\right)}^{\frac{a\beta}{1+\beta }}+\\ {}+0.79{\left(\frac{1}{250}{\theta}^{\frac{1}{\beta }}{\left(1-\beta \right)}^{\frac{1}{\beta }}{\left(\frac{\mu }{w}\right)}^{\frac{1}{1+\rho }}{\left({\left(1-\mu \right)}^{\frac{1}{1+\rho }}{c}^{\frac{\rho }{1+\rho }}+{\mu}^{\frac{1}{1+\rho }}{w}^{\frac{\rho }{1+\rho }}\right)}^{\frac{-\rho -1+\beta }{\rho \beta}}{e_2}^{\frac{\beta +1}{\beta }}\right)}^{\frac{\beta \left(a-1\right)-1}{1+\beta }},\end{array}\\ {}w=\left({\left(\theta {e}_1\right)}^{\frac{\rho }{1+\rho }}{\left(\frac{c}{1-\mu}\right)}^{\frac{1}{1+\rho }}-c\right){\left(\frac{1}{\mu }{\left(\frac{\theta \left(1-\mu \right){e}_1}{c}\right)}^{\frac{\rho }{1+\rho }}-\frac{\left(1-\mu \right)}{\mu}\right)}^{\frac{1}{\rho }},\\ {}\begin{array}{l}\frac{\left({\left({\theta e}_2\right)}^{\frac{\rho }{1+\rho }}{\left(\frac{c}{1-\mu}\right)}^{\frac{1}{1+\rho }}-c\right)}{{\left(\frac{1}{\mu }{\left(\frac{\theta \left(1-\mu \right){e}_2}{c}\right)}^{\frac{\rho }{1+\rho }}-\frac{\left(1-\mu \right)}{\mu}\right)}^{\frac{-1}{\rho }}}=\frac{{\beta \theta}^{\frac{1}{\beta }}{\left(1-\beta \right)}^{\frac{1-\beta }{\beta }}{e_2}^{\frac{\beta +1}{\beta }}}{{\left({\left(1-\mu \right)}^{\frac{1}{1+\rho }}{c}^{\frac{\rho }{1+\rho }}+{\mu}^{\frac{1}{1+\rho }}{w}^{\frac{\rho }{1+\rho }}\right)}^{\frac{\left(1-\beta \right)\left(1+\rho \right)}{\rho \beta}}},\\ {}\frac{\beta {a b}^a}{\beta \left(a-1\right)-1}\frac{\theta^{\frac{1}{\beta }}{\left(1-\beta \right)}^{\frac{1}{\beta }}{\left(\frac{\mu }{w}\right)}^{\frac{1}{1+\rho }}}{{\left({\left(1-\mu \right)}^{\frac{1}{1+\rho }}{c}^{\frac{\rho }{1+\rho }}+{\mu}^{\frac{1}{1+\rho }}{w}^{\frac{\rho }{1+\rho }}\right)}^{\frac{\rho +1-\beta }{\rho \beta}}}{e_2}^{\frac{1-\beta \left(a-1\right)}{\beta }}=\left(1-{\left(\frac{b}{e_1}\right)}^a\right).\end{array}\end{array}} $$

After substituting θ = 1, c = 0.12, μ = 0.75, and ρ = 0.5 into these equations, we obtain the following equations system on six unknowns: e₁, e₂, w, a, b, and β.

$$ {\displaystyle \begin{array}{c}\begin{array}{l}1-{\left(\frac{b}{e_1}\right)}^a=0.79,\\ {}{\left(\frac{b}{e_2}\right)}^a=0.085,\end{array}\\ {}\begin{array}{l}0.875\times 0.25=0.08{\left(\frac{1}{250}{\left(1-\beta \right)}^{\frac{1}{\beta }}{\left(\frac{0.75}{w}\right)}^{\frac{2}{3}}{\left({(0.25)}^{\frac{2}{3}}{0.12}^{\frac{1}{3}}+{0.75}^{\frac{2}{3}}{w}^{\frac{1}{3}}\right)}^{\frac{-1.5+\beta }{0.5\beta }}{e_2}^{\frac{\beta +1}{\beta }}\right)}^{\frac{a\beta}{1+\beta }}+\\ {}+0.79{\left(\frac{1}{250}{\left(1-\beta \right)}^{\frac{1}{\beta }}{\left(\frac{0.75}{w}\right)}^{\frac{2}{3}}{\left({(0.25)}^{\frac{2}{3}}{0.12}^{\frac{1}{3}}+{0.75}^{\frac{2}{3}}{w}^{\frac{1}{3}}\right)}^{\frac{-1.5+\beta }{0.5\beta }}{e_2}^{\frac{\beta +1}{\beta }}\right)}^{\frac{\beta \left(a-1\right)-1}{1+\beta }},\end{array}\\ {}\begin{array}{l}w=\left({e_1}^{\frac{1}{3}}{\left(\frac{0.12}{0.25}\right)}^{\frac{2}{3}}-0.12\right){\left(\frac{4}{3}{\left(\frac{0.75{e}_1}{0.12}\right)}^{\frac{2}{3}}-\frac{0.25}{0.75}\right)}^2\\ {}\frac{\left({e_2}^{\frac{1}{3}}{\left(\frac{0.12}{0.25}\right)}^{\frac{2}{3}}-0.12\right)}{{\left(\frac{1}{0.75}{\left(\frac{0.25{e}_2}{0.12}\right)}^{\frac{1}{3}}-\frac{0.25}{0.75}\right)}^{-2}}=\frac{\beta {\left(1-\beta \right)}^{\frac{1-\beta }{\beta }}{e_2}^{\frac{\beta +1}{\beta }}}{{\left({0.25}^{\frac{2}{3}}{0.12}^{\frac{1}{3}}+{0.75}^{\frac{2}{3}}{w}^{\frac{1}{3}}\right)}^{\frac{3\left(1-\beta \right)}{\beta }}},\end{array}\\ {}\frac{\beta {a b}^a}{\left[\beta \left(a-1\right)-1\right]}\frac{\left(1-\beta \right)\frac{1}{\beta }{\left(\frac{0.75}{w}\right)}^{\frac{2}{3}}}{{\left({0.25}^{\frac{2}{3}}{0.12}^{\frac{2}{3}}+{0.75}^{\frac{2}{3}}{w}^{\frac{1}{3}}\right)}^{\frac{3-2\beta }{\beta }}}{e_2}^{\frac{1-\beta \left(a-1\right)}{\beta }}=\left(1-{\left(\frac{b}{e_1}\right)}^a\right)\end{array}} $$

The numerical solution to this system of equations provides the calibrated values of the parameters of the model, as well as the values of the other endogenous variables: β = 0.36, a = 4.775, b = 3.269, w = 5.52, e₁ = 4.53, and e₂ = 5.48.