Abstract
In this paper, we analyze whether it is socially desirable that fines for exceeding pollution standards depend not only on the degree of non-compliance but also on technology investment efforts by the polluting firms. For that purpose, we consider a partial equilibrium framework where a representative firm chooses the investment effort and the pollution level in response to an environmental policy composed of a pollution standard, an inspection probability and a fine for non-compliance. We find that the fine should strictly decrease with the investment effort when (i) there are administrative costs of sanctioning; (ii) the optimal policy induces non-compliance; and (iii) either the fine is sufficiently convex in the degree of non-compliance or the investment effort decreases marginal abatement costs significantly.

Similar content being viewed by others
Notes
Incentives for Self-Policing: Discovery, Disclosure, Correction and Prevention of Violations—Final Policy Statement, 60 Fed. Reg. 66,706 (Dec. 22, 1995).
Incentives for those who meet the terms of the Audit Policy also include the determination not to recommend criminal prosecution of the disclosing entity, as well as not to request copies of regulated entities’ voluntary audit reports to trigger Federal enforcement investigations.
In particular, this assumption means that penalty reductions are announced in the laws (such as in the Laws on Residuals or Liquid Industrial Waste of the Autonomous Community of Madrid or in the EPA’s Audit Policy), and then they are applied accordingly by enforcers when firms are found out of compliance. We consider this assumption because our objective is to analyze whether announcing these incentives in advance is a socially desirable objective. Although the assumption of commitment can be criticized for being ex-post non-optimal in static settings such as ours, however it is crucial for ensuring credibility with regards to the application of the laws. In the concluding section we dicuss on several ways of relaxing this assumption.
We assume that choosing an investment effort z is equivalent to installing an environmental technology which reduces abatement costs. As Requate (2005) points out, For a polluting firm there are basically two strategies to reduce pollutants: one is to reduce gross emissions by reducing output, another one is to keep output constant and to reduce emissions by employing an abatement technology. In general, a mix of both will be optimal. Experts usually distinguish between two types of abatement technologies, end-of-pipe technologies, on the one hand, and process integrated technologies, on the other. The latter leads to a decline in gross emissions whereas, with the former, gross emissions remain unchanged and are subsequently decreased, for example by using a filter. In both cases a firm’s abatement cost is nothing else than its forgone profit incurred by reducing emissions.
For functions of one variable, we instead use the prime notation to denote full derivatives.
In the terminology of Maxwell and Decker (2006), this type of regulation is unresponsive, in the sense that the regulator does not subsequently respond to the firm’s investment decision. Here, the motivation for the firm to invest is given by the fact that abatement costs are reduced, but also because penalties for non-compliance may be lowered.
Although this is in principle a theoretical possibility, we show later on in Sect. 5 that it is never optimal for the regulator to set a very sensitive fine. Therefore, from now on, in the main text we concentrate on the intuitive case characterized in Lemma 2, while we discuss the alternative case in footnotes 11, 12, 13 and 16, below.
If, to the contrary, the fine were more sensitive to the investment effort than marginal abatement costs (i.e., if \( c_{ez}+pf_{e-s,z}<0\)), a smaller standard or a larger inspection probability could affect the pollution level and the investment effort in either way.
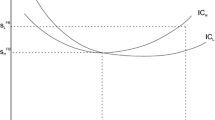
Note that \(s\) and \(p\) could be complementary policy variables \(\left( \left. \frac{dp}{ds}\right| _{e=s}<0\right) \) only in the event that \(\varepsilon _{c_{e},z}>\varepsilon _{f_{e-s},z}\). In that case, a decrease in the standard would increase investment effort \(z\), which would further increase the pollution level \(e\), by (4). Thus, the inspection probability should be increased to compensate for this effect. Policy \(C\) in Fig. 1 would represent this alternative policy: both monitoring and sanctioning costs would increase in \( C\) as compared to \(A\).
Another situation where the optimal policy would induce compliance is when \(\left. \frac{dp}{ds}\right| _{e=s}<0\), which is possible only if \(\varepsilon _{c_{e},z}>\varepsilon _{f_{e-s},z}\). In this case, the standard and the inspection probability would be complementary policy variables, see footnote 12 and Fig. 1. Here, a one unit reduction in the standard would not only causes sanctioning costs, but also additional monitoring costs, because the inspection probability should be increased to keep pollution constant.
This characterization directly follows from the first order conditions of problem (7) presented in the proof of Proposition 1, see the Appendix for details.
For example, penalty functions of the type \(\left( e-s\right) ^{n}\), with \( n\ge 2\), satisfy the condition \(1-\frac{f_{e-s}}{\left( e^{*}-s^{*}\right) f_{e-s,e-s}}\ge 0\) and, therefore, requirement (iii) in Proposition 3, but there are many other examples.
Also, it is never optimal to set a fine contingent on investment effort that leads to a complementarity relationship between the standard and the inspection probability, see footnote 12. This case can be possible only when the elasticity of the fine with respect to the investment effort is larger (in absolute terms) than the elasticity of marginal abatement costs with respect to the investment effort (\(\varepsilon _{f,z}<\varepsilon _{c_{e},z}\)). In that case, the optimal policy would induce compliance, see also Fig. 1. Therefore, the optimal fine would be maximum and independent of \(z\). But this contradicts the initial assumption that the fine is very sensitive to the investment effort.
See Baldwin and Black (2007) for an extensive analysis of different responsive regulatory practices at all the different tasks of the enforcement activity.
References
Andreoni, J. (1991). Reasonable doubt and the optimal magnitude of the fines: Should the penalty fit the crime? The RAND Journal of Economics, 22, 385–395.
Arguedas, C. (2005). Bargaining in environmental regulation revisited. Journal of Environmental Economics and Management, 50, 422–433.
Arguedas, C. (2008). To comply or not to comply? Pollution standard setting under costly monitoring and sanctioning. Environmental & Resource Economics, 41, 155–168.
Arguedas, C., Camacho, E., & Zofio, J. L. (2010). Environmental policy instruments: Technology adoption incentives with imperfect compliance. Environmental & Resource Economics, 47, 261–274.
Arguedas, C., & Hamoudi, H. (2004). Controlling pollution with relaxed regulations. Journal of Regulatory Economics, 26, 85–104.
Becker, G. S. (1968). Crime and punishment: An economic approach. Journal of Political Economy, 76, 169–217.
Baldwin, R., & Black, J. (2007). “Really Responsive Regulation”, LSE Law, Society and Economy Working Paper 15/ 2007. London School of Economics and Political Science, Law Department.
Cohen, M. A. (1999). Monitoring and enforcement of environmental policy. In H. Folmer & T. Tietemberg (Eds.), The international year-book of environmental resource economics 1999/2000. Cheltenham: Edward Elgar Publishing.
Decker, C. S. (2007). Flexible enforcement and fine adjustment. Regulation & Governance, 1, 312–328.
Friesen, L. (2003). Targeting enforcement to improve compliance with environmental regulations. Journal of Environmental Economics and Management, 46, 72–85.
Harrington, W. (1988). Enforcement leverage when penalties are restricted. Journal of Public Economics, 37, 29–53.
Heyes, A. G. (2000). Implementing environmental regulation: Enforcement and compliance. Journal of Regulatory Economics, 17, 107–129.
Innes, R. (1999). Remediation and self-reporting in optimal law enforcement. Journal of Public Economics, 72, 379–393.
Innes, R. (2000). Self reporting in optimal law enforcement when violators have heterogeneous probabilities of apprehension. Journal of Legal Studies, 29, 287–300.
Innes, R. (2001). Violator avoidance activities and self reporting in optimal law enforcement. Journal of Law, Economics and Organization, 17, 239–256.
Kambhu, J. (1989). Regulatory standards, noncompliance and enforcement. Journal of Regulatory Economics, 1, 103–114.
Kaplow, L., & Shavell, S. (1994). Optimal law enforcement with self-reporting of behavior. Journal of Political Economy, 102, 583–606.
Livernois, J., & Mckenna, C. J. (1999). Truth or consequences: Enforcing pollution standards with self-reporting. Journal of Public Economics, 71, 415–440.
Maxwell, J. W., & Decker, C. S. (2006). Voluntary environmental investment and responsive regulation. Environmental & Resource Economics, 33, 425–439.
Mishra, B. K., Newman, D. P., & Stinson, C. H. (1997). Environmental regulations and incentives for compliance audits. Journal of Accounting and Public Policy, 16, 187–214.
Pfaff, A., & Sanchirico, C. W. (2000). Environmental self-auditing: Setting the proper incentives for discovery and correction of environmental harm. Journal of Law, Economics and Organization, 16, 189–208.
Polinsky, A. M., & Shavell, S. (1992). Enforcement costs and the optimal magnitude and probability of fines. Journal of Law and Economics, 35, 133–148.
Polinsky, A. M., & Shavell, S. (2000). The economic theory of public enforcement of law. Journal of Economic Literature, 38, 45–76.
Raymond, M. (1999). Enforcement leverage when penalties are restricted: A reconsideration under asymmetric information. Journal of Public Economics, 73, 289–295.
Requate, T. (2005). Dynamic incentives by environmental policy instruments—A survey. Ecological Economics, 54, 175–195.
Requate, T., & Unold, W. (2001). On the incentives created by policy instruments to adopt advanced abatement technology if firms are asymmetric. Journal of Institutional and Theoretical Economics, 157, 536–554.
Requate, T., & Unold, W. (2003). Environmental policy incentives to adopt advanced abatement technology: Will the true ranking please stand up? European Economic Review, 47, 125–146.
Saha, A., & Poole, G. (2000). The economics of crime and punishment: An analysis of optimal penalty. Economics Letters, 68, 191–196.
Shavell, S. (1991). A note on marginal deterrence. International Review of Law and Economics, 12, 345–355.
Shavell, S. (1992). Specific versus general enforcement of law. Journal of Political Economy, 99, 1088–1108.
Stafford, S. (2005). Does self-policing help the environment? EPA’s audit policy and hazardous waste compliance. Vermont Journal of Environmental Law, 6, 1–22.
Stranlund, J. K. (2007). The regulatory choice of noncompliance in emission trading programs. Environmental & Resource Economics, 38, 99–117.
Villegas, C., & Coria, J. (2010). On the interaction between imperfect compliance and technology adoption: Taxes versus tradable emissions permits. Journal of Regulatory Economics, 38, 274–291.
Acknowledgments
I wish to thank an anonymous referee and the participants of the Spanish Economic Association, AERNA, EAERE and ASSET Meetings for useful comments and suggestions on an earlier draft. Financial support from the Spanish Government under research project number ECO2011-25349 is gratefully acknowledged.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
Proof of Lemma 1
First note that \(e<s\) is not an optimal decision, since the firm can save on abatement costs by infinitesimally increasing pollution without being penalized. This reduces the set of possible firm’s pollution choices to \(e\ge s\). Then, the problem to be solved is:
The optimality conditions of this problem are:
where \(\lambda \ge 0\) is the Kuhn–Tucker multiplier of the inequality restriction \(e\ge s\). From (9) and (10), \(\lambda \ge 0\) implies \(e=s\) and \(c_{e}\left( s,z\right) +pf_{e-s}\left( 0,z\right) \ge 0\). If conversely, \(\lambda =0\), we then have \(e>s\ \)and \(c_{e}\left( e,z\right) +pf_{e-s}\left( e-s,z\right) =0\). Combining both possibilities, we obtain the desired result.
Proof of Lemma 2
At the optimum, we have \( c_{e}+pf_{e-s}=0\), which can be rewritten as \(p=-\frac{c_{e}}{f_{e-s}}\). Thus, the expression \(c_{ez}+pf_{e-s,z}\) in the numerator of (4) can be written as \(c_{ez}-\frac{c_{e}}{ f_{e-s}}f_{e-s,z}\). Since \(c_{e}<0\), we have \(c_{ez}-\frac{c_{e}}{f_{e-s}} f_{e-s,z}>0\) if and only if \(\frac{c_{ez}}{c_{e}}-\frac{f_{e-s,z}}{f_{e-s}} <0 \). Multiplying both sides of this expression by \(z\), we have \(\frac{c_{ez} }{c_{e}}z-\frac{f_{e-s,z}}{f_{e-s}}z<0\), and applying the definitions \( \varepsilon _{c_{e},z}=c_{ez}\frac{z}{c_{e}}\) and \(\varepsilon _{f_{e-s},z}=f_{e-s,z}\frac{z}{f_{e-s}}\), we obtain the desired result.
Proof of Lemma 4
Fully differentiating expressions (3) and (6) with respect to \( \left( e,z,s,p\right) \), we obtain:
or put differently,
Let \(A=\left( \begin{array}{ll} c_{ee}+pf_{e-s,e-s} &{} c_{ez}+pf_{e-s,z} \\ c_{ez}+pf_{e-s,z} &{} c_{zz}+pf_{zz} \end{array} \right) . \) Note that \(\left| A\right| >0\) (this ensures that sufficient conditions for the firm’s optimal choices hold). Applying Cramer’s rule, we then have:
as desired.
Proof of Lemma 5
We consider expressions \(\frac{ \partial e}{\partial p}\) and \(\frac{\partial e}{\partial s}\) from Lemma 4 above to obtain:
Evaluating (11) at \(e\!=\!s\), we have \(\left. \frac{ dp}{ds}\right| _{e=s}\!=\!-\frac{p\left\{ f_{e-s,z}\left( c_{ez}+pf_{e-s,z}\right) -f_{e-s,e-s}\left( c_{zz}+pf_{zz}\right) \right\} }{ f_{e-s}\left( c_{zz}+pf_{zz}\right) }\), since \(f_{z}=0\) when \(e=s\). By Lemma 2, \(c_{ez}+pf_{e-s,z}\ge 0\) if and only if \(\varepsilon _{c_{e},z}\le \varepsilon _{f_{e-s},z}\). Therefore, \(\left. \frac{dp}{ds} \right| _{e=s}\ge 0\) if \(\varepsilon _{c_{e},z}\le \varepsilon _{f_{e-s},z}\), as desired.
Proof of Proposition 1
The first order conditions of problem (7) are the following:
where \(\left( \lambda , \gamma , \mu \right) \) are the respective Kuhn–Tucker multipliers associated with the constraints in problem (7).
Under compliance, we have \(e=s, \,\mu \le 0\) and \(c_{z}+1=0\), by (6). The optimality conditions reduce to:
from which we obtain \(\lambda =-\frac{m}{f_{e-s}}\) and \(\gamma =\frac{ m\left( c_{ez}+pf_{e-s,z}\right) }{f_{e-s}\left( c_{zz}+pf_{zz}\right) }\). Thus, \(\mu \le 0\) (or equivalently, \(e=s\)) if and only if
evaluated at \(e=s\).
Conversely, \(e>s\) if and only if:
evaluated at \(e=s\).
From expression (11), we have \(\left. \frac{dp}{ ds}\right| _{e}=-\frac{p\left\{ f_{e-s,z}\left( c_{ez}+pf_{e-s,z}\right) -f_{e-s,e-s}\left( c_{zz}+pf_{zz}\right) \right\} }{f_{e-s}\left( c_{zz}+pf_{zz}\right) }\) when \(e=s\). Therefore, (17) can be rewritten as:
as desired.
Proof of Proposition 3
Consider the solution of problem (7), \(\left( s^{*},p^{*}\right) \). Substituting this policy in the Lagrangian of problem (7), we have:
where \(\left( \lambda ^{*},\gamma ^{*},\mu ^{*}\right) \) are the respective Kuhn–Tucker multipliers associated with the constraints in problem (7). Since \(e^{*}\ge s^{*}\), we then have \(\mu ^{*}=0\).
From (13) and (15), the corresponding expressions for the Kuhn–Tucker multipliers \(\left( \lambda ^{*},\gamma ^{*}\right) \) evaluated at \(f_{z}=f_{e-s,z}=0\) reduce to:
since \(c_{z}+1=0\) under \(f_{z}=0\), see (6).
Now, consider the following polynomial approximation of the fine:
since we have assumed \(f\left( 0,0\right) =f_{z}\left( 0,0\right) =0\).
From (21), the corresponding expressions for \( f_{e-s}\left( e-s,z\right) \) and \(f_{z}\left( e-s,z\right) \) are the following:
We substitute (21), (22) and (23) in (18), and we now consider the effect on social costs of an infinitesimal change of the fine associated with the change in investment effort \(z\). Through (21), (22) and (23), we note that the fine has two components that measure the effect of \(z, \,f_{e-s,z}\left( 0,0\right) \) and \(f_{e-s,e-s,z}\left( 0,0\right) \). We then compute the partial derivatives of the Lagrangian expression (18) with respect to these two terms evaluated at \( f_{z}=f_{e-s,z}=0\):
where \(\left( \lambda ^{*},\gamma ^{*}\right) \) are given by (19) and (20), respectively.
Since \(f_{e-s,z}\left( 0,0\right) \le 0\) and \(f_{e-s,e-s,z}\left( 0,0\right) \le 0\), social costs decrease when the fine depends on the investment effort as long as (24) or (25) are strictly positive. Since \(tz^{*}+\gamma ^{*}>0\) (see 20), the requirement for (24) to be positive is weaker than that for (25), since \( tz^{*}+\gamma ^{*}>\frac{tz^{*}+\gamma ^{*}}{2}\). Therefore, substituting (19) and (20) in (24), we then have:
if and only if \(t>0, \,e^{*}>s^{*}\)and \(\left[ 1-\frac{f_{e-s}}{ \left( e^{*}-s^{*}\right) f_{e-s,e-s}}\right] z^{*}+\frac{f_{e-s} }{f_{e-s,e-s}}\frac{c_{ez}}{c_{zz}}>0\), as desired.
Rights and permissions
About this article
Cite this article
Arguedas, C. Pollution standards, technology investment and fines for non-compliance. J Regul Econ 44, 156–176 (2013). https://doi.org/10.1007/s11149-013-9217-8
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11149-013-9217-8