A global food–energy–water nexus with heterogeneity, non-stationarity and cross-sectional dependence

Abstract

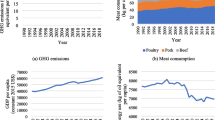
We estimate the Food–Energy–Water (FEW) nexus for 21 countries worldwide, with data available from year 1990–2000 in order to investigate the relationship between food production and two scarce resources: energy and water. Food production is proxied by four alternative variables: The index of agricultural production, the index of crops production, the index of livestock production and the value added from agriculture. Water and energy as independent variables are controlled by methane and nitrogen emissions, capital, labor and five versions of fertilizer proxy: pesticides, insecticides, fungicides, herbicide and other. For robust estimation, we have perused a number of standard and novel panel estimators such as the common correlated effects mean group estimator and the augmented mean group estimator (AMG). These estimators can account both for non-stationarity and the cross-dependence problems. Based on standard estimators such as the generalized least squares estimator or the Arellano-Bond generalized method of moments GMM, they reveal the existence of a significant FEW nexus while the mean group estimator, the group mean DOLS estimator, the common correlated effects and the augmented mean group estimator (AMG) do not yield significant coefficients for water and energy. In the latter models only labor and pesticides are significant at 5%. Also, the unobserved total factor productivity appears significant at 5% under the AMG estimation. When significant, energy and water elasticities ranged from − 0.001 to − 0.256 and from − 0.014 to − 0.084 respectively.

Appendix 1

This appendix contains the technical part and technical explanations of the six estimators used in this paper.

• i. The generalized least squares estimator

The perused model is a system of seemingly unrelated equations (SURE). The generalized least squares (GLS) approach is shown in matrix form shown as Eq. 12:

$$\left[ {\begin{array}{*{20}c} {y_{1} } \\ {y_{2} } \\ \vdots \\ {y_{M} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {X_{1} } & 0 & \ldots & 0 \\ 0 & {X_{2} } & \ldots & 0 \\ \vdots & \vdots & \ldots & \vdots \\ 0 & 0 & \ldots & {X_{M} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\beta_{1} } \\ {\beta_{2} } \\ \vdots \\ {\beta_{\rm M} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {\varepsilon_{1} } \\ {\varepsilon_{2} } \\ \vdots \\ {\varepsilon_{\rm M} } \\ \end{array} } \right]$$

(12)

namely it is y = Xβ + ε, where E(ε) = 0 and $E\left[ {\varepsilon \varepsilon^{{\prime }} } \right] = \varSigma \otimes I$. The GLS estimator is shown in Eq. 13

$$\hat{\beta } = \left[ {{\rm X}^{{\prime }} \left( {\varSigma^{ - 1} \otimes {\rm I}} \right){\rm X}} \right]^{ - 1} \left[ {{\rm X}^{{\prime }} \left( {\varSigma^{ - 1} \otimes {\rm I}} \right)y} \right]$$

(13)

The estimator allows for first order autocorrelation, namely ɛ_i,t = ρ_iɛ_i,t−1 + u_i,t. The Σ is a weighting matrix used for the estimation of the feasible GLS (FGLS). It is the estimate of the disturbance covariance matrix. Note that Σ = [E(1/n)E^′ E].

The autocorrelation coefficient is estimated using the OLS residuals and the Durbin-Watson statistic and estimated autocorrelation for the corrected GLS residuals:

$$\hat{u}_{i,t} = e_{i,t} - r_{i} e_{i,t - 1}$$

• ii. The Arellano-Bond dynamic model & the Generalized Method of Moments estimation (GMM)

The Arellano-Bond model (1991) is concerned with the estimation of a dynamic model for panel data and takes the form shown in Eq. 14 (Green 2007):

$$y_{it} = ay_{i,t - 1} + \beta^{{\prime }} x_{it} + \gamma^{{\prime }} f_{i} + \varepsilon_{it} + u_{i}$$

(14)

$$y_{it} = ay_{i,t - 1} + \beta^{{\prime }} x_{it} + \gamma^{{\prime }} f_{i} + v_{it}$$

Alpha is the autocorrelation parameter, the f_i are time invariant variables and γ captures the unobservable time constraints of i. To remedy the problem of endogeneity caused by the dependence of y_it and y_i,t−1 on γ_i, we use instrumental variables and the model is transformed into first differences. Instruments can be obtained with a GMM approach. The estimation criterion is shown in Eq. 15

$$M\left( \beta \right) = \varepsilon \left( \beta \right)^{{\prime }} {\rm Z}\left( {{\rm Z}^{\prime}\varOmega {\rm Z}} \right)^{ - 1} {\rm Z}^{{\prime }} \varepsilon \left( \beta \right)$$

(15)

Ζ is the matrix of instrumental variables, Ω is a weighting matrix, which for the random effects model takes the form Ω = σ ² _ɛ I + σ ² _u ii^′. The unrestricted (robust) estimation means that Ω = E[v_iv ^′ _i ].

The GMM process starts with a set of ℓ orthogonality conditions as shown in Eq. 16.

$$E\left[ {m_{il} \left( {\beta , x_{i} } \right)} \right] = 0$$

(16)

Β is a vector of parameters we estimate, xi are the variables in the information set that define the moment condition, m_il is one of the L expectations that the model specifies as above. The GMM estimator is provided by finding the beta that makes the empirical moment shown in Eq. 17 to imitate the population expectation as closely as possible.

$$\overline{m}_{l} = \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} m_{il} \left( {b,x_{i} } \right)$$

(17)

The GMM estimator is the minimum distance estimator which minimizes the quadratic form:

$$q = \overline{m}^{{\prime }} \varSigma \overline{m}$$

Also, according to Greene (2007), the optimal weighting matrix is given by $\varSigma^{*} = \left\{ {Var\left[ {\overline{m} } \right]} \right\}^{ - 1}$

Both the above two empirical specifications, which rely on pooled data, imply that there are common parameters across countries. However, we have stated some reasons why each or some countries may follow a different long-run FEW nexus pattern.

• iii. The Pesaran and Shin (1995) Mean Group Estimator (MGE)

The MGE is a recent advancement in panel data characterized by non-stationarity. Methods such as the fixed effects or random effects models, or the Arellano-Bond presume the pooling of individual groups together and allow only the intercepts to differ across groups. Pooling introduces data dependence in the residual terms if a series is integrated (Lee et al. 1997; Pedroni 2007) and this may cause a spurious regression (Kao 1999). The Pesaran and Smith estimator estimates N time-series regressions (one for each country) and averages the coefficients. Namely the MG estimates are the unweighted mean of N individual coefficients (Blackburne and Frank 2007). Given the endogeneity of the model set up, there is high probability that this estimator will be inconsistent (Kapetanios et al. 2006).

• iv. The Group mean DOLS estimator

Panel DOLS are an alternative to the fully modified OLS by Pedroni (1997). It has convenient properties when there are fixed effects in the cointegration equation (Kao and Chiang 2000). This estimator allows for individual country heterogeneity with country specific fixed effects and country specific time trends. Also, this estimator is more resilient to cross-sectional dependence. To construct a DOLS estimator, one begins by adding lead and lagged differences of the regressor to tackle endogeneity. The DOLS regression is written as in Eq. 18:

$$y_{it} = a_{i} + \beta_{i} p_{it} + \mathop \sum \limits_{{k = - K_{i} }}^{{K_{i} }} \gamma_{ik} \Delta p_{it - k} + \mu_{it}^{*}$$

(18)

And the group-mean panel DOLS estimator is written as in Eq. 19:

$$\hat{\beta }_{GD}^{*} = \left[ {N^{ - 1} \mathop \sum \limits_{i = 1}^{N} \left( {\mathop \sum \limits_{t = 1}^{T} z_{it} z_{it}^{{\prime }} } \right)^{ - 1} \left( {\mathop \sum \limits_{t = 1}^{T} z_{it} \tilde{s}_{it} } \right)} \right]$$

(19)

with z_it being the 2(K + 1) × 1 vector of regressors $z_{it} = \left( {p_{it} - \overline{\rho }_{i} , \Delta \rho_{it - K} , \ldots ,\Delta \rho_{it + K} } \right)$ and $\tilde{S}_{it} = S_{it} - \overline{S}_{i}$.

The associated t-statistic for the DOLS estimator can be constructed as in Eq. 20:

$$t_{{\hat{\beta }_{GD} }} = N^{{{\raise0.7ex\hbox{${ - 1}$} \!\mathord{\left/ {\vphantom {{ - 1} 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} \mathop \sum \limits_{i = 1}^{N} t_{{\hat{\beta }_{D,i}^{*} }} \quad {\text{with}}\quad t_{{\hat{\beta }_{D,i}^{*} }} = \left( {\hat{\beta }_{D,i}^{*} - \beta_{0} } \right)\left( {\hat{\sigma }_{i}^{ - 2} \mathop \sum \limits_{t = 1}^{T} \left( {p_{it} - \overline{p}_{i} } \right)^{2} } \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}}$$

(20)

If, we let $\sigma_{i}^{2} = \mathop {\lim }\limits_{T \to \infty } E\left[ {T^{ - 1} \left( {\mathop \sum \limits_{t = 1}^{T} \hat{m}_{it}^{*} } \right)^{2} } \right]$ to be the long-run variance of residuals from the DOLS regression.

• v. The Common correlated effects (CCE) mean group estimator

The CCE estimator was developed by Pesaran (2006) and accounts for unobserved heterogeneity. The regression equation is augmented with cross section averages of the dependent and independent variables to account for the unobserved common components across countries which have a heterogeneous impact. The estimator is written as on Eq. 21:

$$y_{it} = a_{i} + b_{i}^{{\prime }} x_{it} + c_{0i} \overline{y}_{t} + \mathop \sum \limits_{m = 1}^{k} c_{mi} \overline{x}_{mt} + e_{it}$$

(21)

The parameter estimates $\hat{b}_{i}$ are averaged across countries in a similar way as it is done in Pesaran and Shin (1995). This estimator yields consistent and efficient estimates of the technology parameters and are robust to structural breaks. According to Eberhardt and Teal (2011) are able to account for the presence of both global shocks and local spillover effects (termed as strong and weak factors respectively) and according to Kapetanios et al. (2006), this estimator does not require prior knowledge of the cointegration properties.

• vi. The augmented mean group (AMG) estimator

The AMG estimator was developed by Eberhardt and Teal (2010). The AMG is based on an initial pooled regression model, estimated with OLS, also containing the first differenced year dummies whose coefficients are collected to yield the common dynamic process (CDP) that refers to the unobservable TFP over time. The group-specific regression is then augmented with the CDP process that we have introduced as an explicit variable into the model (other model version are also possible). The group-specific parameters are averaged across the panel. The process from which the AMG estimator is derived, is described as in Eq. 22:

$$\Delta y_{it} = b^{{\prime }} \Delta x_{it} + \mathop \sum \limits_{t = 2}^{T} c_{t} \Delta D_{t} + e_{it} \to \hat{c}_{t} = \hat{\mu }_{t}^{.}$$

(22)

with $\hat{\mu }_{t}^{.}$ being the year dummy coefficients as in Eqs. 23, 24

$$y_{it} = a_{i} + b_{i}^{{\prime }} x_{it} + c_{it} + d_{i} \hat{\mu }_{t}^{.} + e_{it}$$

(23)

$$\hat{b}_{AMG} = N^{ - 1} \mathop \sum \limits_{i} \hat{b}_{i}$$

(24)