Abstract
This paper studies topological duals of locally convex function spaces that are natural generalizations of Fréchet and Banach function spaces. The dual is identified with the direct sum of another function space, a space of purely finitely additive measures and the annihilator of \(L^\infty \). This allows for quick proofs of various classical as well as new duality results e.g. in Lebesgue, Musielak–Orlicz, Orlicz–Lorentz space and spaces associated with convex risk measures. Beyond Banach and Fréchet spaces, we obtain completeness and duality results in general paired spaces of random variables.
Similar content being viewed by others
1 Introduction
Banach function spaces (BFS) provide a convenient set up for functional analysis in spaces of measurable functions. Many well known properties of e.g. Lebesgue spaces and Orlicz spaces extend to BFS with minor modifications; see e.g. [1, 20, 22, 38]. Extensions to Fréchet function spaces have been studied e.g. in [4]. This paper studies topological duals of more general locally convex function spaces where the topology is generated by an arbitrary collection of seminorms satisfying the usual BFS axioms.
Building on the classical result of Yosida and Hewitt [37, Section 2] on the dual of \(L^\infty \), we identify the topological dual as the direct sum of another space of random variables (Köthe dual), a space of purely finitely additive measures and the annihilator of \(L^\infty \). The last two components have a singularity property that has been found useful, e.g., in the analysis of convex integral functionals by Rockafellar [32] in the case of \(L^\infty \) and by Kozek [19] in the case of Orlicz spaces. In the case of \(L^\infty \), the last component in the dual vanishes while in other Orlicz spaces, the second one vanishes; see [28, Chapter IV]. Our result thus unifies the two seemingly complementary cases.
The main result is illustrated first by simple derivations of various existing as well as new duality results in Musielak–Orlicz, Marcinkiewicz, Lorentz and Orlicz–Lorentz spaces. We go beyond the existing BFS settings by identifying topological duals of the space of random variables with finite moments, generalized Musielak–Orlicz spaces as well as spaces of random variables associated with convex risk measures. The last instance has attracted attention in the recent literature of mathematical finance and insurance; see e.g. [21, 27] and [11].
Section 5 is concerned with dual pairs of linear spaces of random variables that play a central role e.g. in stochastic optimization and optimal control; see e.g. [36] and the examples in [33]. We show that the corresponding Mackey and strong topologies are generated by (uncountable) collections of seminorms satisfying the usual BFS axioms. We then obtain duality and completeness results as corollaries of the main results of the paper.
The rest of the paper is organized as follows. Section 2 reviews the duality theory for \(L^\infty \). Section 3 extends the notion of an integral with respect to a finitely additive measure to measurable not necessarily bounded random variables. Section 4 defines a general locally convex space of random variables and gives the main result of the paper by characterizing the topological dual of a space. Section 5 studies spaces of random variables in separating duality. Section 6 applies the main result to characterize the topological dual in various known and new settings.
2 Topological dual of \(L^\infty \)
Let \((\Omega ,{{\mathcal {F}}},P)\) be a probability space with a \(\sigma \)-algebra \({{\mathcal {F}}}\) and a countably additive probability measure P. This section reviews the topological dual of the Banach space \(L^\infty \) of equivalence classes of essentially bounded measurable functions on a probability space \((\Omega ,{{\mathcal {F}}},P)\). We consider \({\mathbb {R}}^n\)-valued functions and endow \(L^\infty \) with the norm
where \(|\cdot |\) is a norm on \({\mathbb {R}}^n\). The dual norm on \({\mathbb {R}}^n\) is denoted by \(|\cdot |^*\).
Let \({{\mathcal {M}}}\) be the set of P-absolutely continuous finitely additive \({\mathbb {R}}^n\)-valued measures on \((\Omega ,{{\mathcal {F}}})\) and let \({{\mathcal {M}}}_s\) be set of those \(m\in {{\mathcal {M}}}\) which are singular (“purely finitely additive” in the terminology of [37]; see [37, Theorem 1.22]) in the sense that there is a decreasing sequence \((A^\nu )_{\nu =1}^\infty \subset {{\mathcal {F}}}\) with  and \(|m|^*(\Omega \setminus A^\nu )=0\). Given \(m\in {{\mathcal {M}}}\), the set function \(|m|^*:{{\mathcal {F}}}\rightarrow {\mathbb {R}}\) is defined by
and \(|m|^*(\Omega \setminus A^\nu )=0\). Given \(m\in {{\mathcal {M}}}\), the set function \(|m|^*:{{\mathcal {F}}}\rightarrow {\mathbb {R}}\) is defined by
where ith components of \(m^+\in {{\mathcal {M}}}\) and \(m^-\in {{\mathcal {M}}}\) are the positive and negative parts, respectively, of the ith component \(m_i\) of m; see [37, Theorem 1.12].
Recall that the space \({{\mathcal {E}}}\) of \({\mathbb {R}}^n\)-valued simple random variables (i.e. piecewise constant with a finite range) is dense in \(L^\infty \). Given \(m\in {{\mathcal {M}}}\), the integral of a \(u\in {{\mathcal {E}}}\) is defined by
where \(A^j\in {{\mathcal {F}}}\) and \(\alpha ^j\in {\mathbb {R}}^n\), \(j=1,\ldots ,m\) are such that \(u=\sum _{j=1}^m \alpha ^j 1_{A^j}\) On \(L^\infty \), the integral is defined as the unique norm continuous linear extension from \({{\mathcal {E}}}\) to \(L^\infty \).
The following is from [37, Theorem 2.3] except that we do not assume that the underlying measure space is complete; see also [2, Sections 4.7 and 10.2]. The proof uses [9, Theorem 20.35] which does not rely on the completeness but identifies the dual of \(L^\infty \) with the space of finitely additive measures that are absolutely continuous with respect to P. Results of [37, Section 1] on decomposition of finitely additive measures then complete the proof. The above are concerned with real-valued random variables but the extension to the vector-valued case is straightforward; see [35, Lemma 1] for an extension to Banach space-valued random variables. Throughout this paper, the expectation of a random variable \(z\in L^1\) is denoted by E[z]. The inner product of two vectors \(\xi ,\eta \in {\mathbb {R}}^n\) is denoted by \(\xi \cdot \eta \).
Theorem 1
(Yosida–Hewitt) The topological dual \((L^\infty )^*\) of \(L^\infty \) can be identified with \({{\mathcal {M}}}\) in the sense that for every \(u^*\in (L^\infty )^*\) there exists a unique \(m\in {{\mathcal {M}}}\) such that
where the integral is defined componentwise. The dual norm is given by
Moreover, \({{\mathcal {M}}}=L^1\oplus {{\mathcal {M}}}_s\) in the sense that for every \(m\in {{\mathcal {M}}}\) there exist unique \(y\in L^1\) and \(m^s\in {{\mathcal {M}}}_s\) such that
We have \(m^s=0\) if and only if \(\langle u1_{A^\nu },u^*\rangle \rightarrow 0\) for every \(u\in L^\infty \) and every decreasing \((A^\nu )_{\nu =1}^\infty \subset {{\mathcal {F}}}\) such that  .
.
Proof
Assume first that \(n=1\). By [9, Theorem 20.35], the dual of \(L^\infty \) can be identified with the linear space of finitely additive P-absolutely continuous measures m in the sense that every \(u^*\in (L^\infty )^*\) can be expressed as
and, conversely, any such integral belongs to \((L^\infty )^*\). By [37, Theorem 1.24], there is a unique decomposition \(m=m^a+m^s\), where \(m^a\) is countably additive and \(m^s\) is purely finitely additive. The construction in [37] also shows that \(m^a\) and \(m^s\) are absolutely continuous with respect to m and thus, absolutely continuous with respect to P as well. By [37, Theorem 1.22], there is a decreasing sequence \((A^\nu )_{\nu =1}^\infty \subset {{\mathcal {F}}}\) such that \(P(A^\nu )\searrow 0\) and \(m^s(\Omega \setminus A^\nu )=0\). The functional \(y^s\in (L^\infty )^*\) given by
then has the property in the statement. By Radon-Nikodym, there exists a \(y\in L^1\) such that
To prove the last claim, it is clear that the given condition holds if \(m^s=0\). To prove the converse, let \(u^*\in (L^\infty )^*\) and consider the representation in terms of \(y\in L^1\) and \(m^s\in {{\mathcal {M}}}_s\) given by the second claim. Let \(A^\nu \) be the sets in the characterization of the singularity of \(m^s\). By [37, Theorems 1.12 and 1.17], \(m^s=m^{s+}-m^{s-}\) for nonnegative purely finitely additive \(m^{s+}\) and \(m^{s-}\). Given \(\epsilon >0\), [37, Theorem 1.21] gives the existence of \(A\in {{\mathcal {F}}}\) such that \(m^{s+}(\Omega \setminus A)<\epsilon \) and \(m^{s-}(A)<\epsilon \). We have
Under the given condition, the left side converges to zero. Since \(\epsilon >0\) was arbitrary, \(m^{s+}=0\). By symmetry, \(m^{s-}=0\) so \(m^s=0\).
By [37, Theorem 2.3], the dual norm of \(\Vert \cdot \Vert _{L^\infty }\) is given by \(\Vert m\Vert _{TV}:=m^+(\Omega )+m^-(\Omega )\). This completes the proof of the case \(n=1\). The general case follows from the fact that the dual of a Cartesian product of Banach spaces is the Cartesian product of the dual spaces with the norm
which completes the proof. \(\square \)
3 Extension of the integral
In [37] and in Sect. 2, integrals with respect to an \(m\in {{\mathcal {M}}}\) were defined only for elements of \(L^\infty \) as norm-continuous extensions of integrals of simple functions. Weakening the topology, it is possible to extend the definition of the integral to a larger space of measurable functions using Daniell’s construction much as in [3, Chapter II] which considered countably additive integrals of arbitrary (not necessarily \({{\mathcal {F}}}\)-measurable) functions.
Another approach to integration of unbounded functions with respect to finitely additive measures is that of Dunford; see Dunford and Schwartz [6] or Luxemburg [23]. A benefit of the Daniell extension adopted here is that it gives rise to a simpler definition of integrability that is easier to verify for larger classes of measurable functions.
Given \(m\in {{\mathcal {M}}}\), we define \(\rho _m:L^0\rightarrow \overline{{\mathbb {R}}}\) by
where
We denote
The extension of the one-dimensional integral in Theorem 29 gives the following.
Theorem 2
Given \(m\in {{\mathcal {M}}}\), the integral
has a unique linear extension from \(L^\infty \) to \(\mathop {\mathrm{dom}}\nolimits \rho _m\) such that
If m is purely finitely additive, there exists a decreasing \((A^\nu )_{\nu =1}^\infty \subset {{\mathcal {F}}}\) with \(P(A^\nu )\searrow 0\) and \(\int _\Omega u1_{\Omega \backslash A^\nu } dm =0\) for all \(u\in \mathop {\mathrm{dom}}\nolimits \rho _m\).
Proof
The extension is given by
where the integrals on the right are the extensions of the one-dimensional integrals given in Theorem 29. We get
where the second inequality comes from Theorem 29. The sets \(A^\nu \) can be taken as the unions of the componentwise sets given by Theorem 29. \(\square \)
We call the extension in Theorem 2 the m-integral of u and denote it by
The elements of \(\mathop {\mathrm{dom}}\nolimits \rho _m\) will be said to be m-integrable. If m is countably additive, then, by e.g. [34, Theorem 14.60],
where y is the density of m, and thus,
In this case, the integral is the Lebesgue integral.
4 Topological duals of spaces of random variables
This section contains the main result of the paper. The setup extends that of Banach function spaces by replacing the norm by an arbitrary collection of seminorms thus covering more general locally convex spaces of random variables. The main result identifies the topological dual of the space with the direct sum of a space of random variables and two spaces of singular functionals, the first of which is represented by finitely additive measures while the second is the orthogonal complement of \(L^\infty \).
Let \(L^0\) be the linear space of \({\mathbb {R}}^n\)-valued random variables. Let \({{\mathcal {P}}}\) be a collection of sublinear (i.e. convex and positively homogeneous) functions \(p:L^0\rightarrow \overline{{\mathbb {R}}}\) with \(p(u)=p(-u)\) for all \(u\in L^0\), define
and endow \(L_{{\mathcal {P}}}\) with the locally convex topology generated by \({{\mathcal {P}}}\). Recall that \(\mathop {\mathrm{dom}}\nolimits p:=\{u\in L^0\mid p(u)<\infty \}\). Our aim is to characterize the topological dual \(L_{{\mathcal {P}}}^*\) of \(L_{{\mathcal {P}}}\). To this end, we will assume that, for each \(p\in {{\mathcal {P}}}\),
-
(A1)
there exists a constant \(c>0\) such that \(p(u)\le c\Vert u\Vert _{L^\infty }\) for all \(u\in L^\infty \),
-
(A2)
\(p(u')\le p(u)\) for every \(u',u\in L^0\) with \(|u'_j|\le |u_j|\ \forall j=1,\ldots ,n\) almost surely.
Occasionally, we will also assume the following
-
(A3)
 for all \(u\in L^\infty \) and decreasing sequence \((A^\nu )_{\nu =1}^\infty \subset {{\mathcal {F}}}\) with
for all \(u\in L^\infty \) and decreasing sequence \((A^\nu )_{\nu =1}^\infty \subset {{\mathcal {F}}}\) with  .
. -
(A4)
 for all \(u\in L_{{\mathcal {P}}}\) and decreasing sequence \((A^\nu )_{\nu =1}^\infty \subset {{\mathcal {F}}}\) with
for all \(u\in L_{{\mathcal {P}}}\) and decreasing sequence \((A^\nu )_{\nu =1}^\infty \subset {{\mathcal {F}}}\) with  .
.
It is clear that (A3) and (A4) are implied by the following
-
 for all \((u^\nu )\in L^\infty \) such that
for all \((u^\nu )\in L^\infty \) such that  ,
, -
 for all \((u^\nu )\in L_{{\mathcal {P}}}\) such that
for all \((u^\nu )\in L_{{\mathcal {P}}}\) such that  ,
,
respectively. The case where \({{\mathcal {P}}}\) is a singleton has been extensively studied ever since the publication of [22]; see e.g. the monographs [1, 20, 38, 39]. When \({{\mathcal {P}}}\) is a singleton satisfying merely (A2), \(L^{{\mathcal {P}}}\) is usually called a Banach function space provided it is complete. A sufficient condition for completeness in the general case is given in Remark 9 below.
Our approach relies on (A1) which is assumed also e.g. in [1] but avoided in many other treatments of Banach function spaces. The assumption allows for simple proofs building on Theorem 1 and it provides more information on the structure of the topological dual; see Theorem 6 below. Under a mild condition, spaces satisfying (A2) alone are isomorphic to spaces satisfying both (A1) and (A2).
Remark 3
Let \({\tilde{{{\mathcal {P}}}}}\) be a collection of seminorms satisfying (A2) but not necessarily (A1). If there exists \({\bar{u}}\in L_{{\tilde{{{\mathcal {P}}}}}}\) such that \({\bar{u}}_j>0\) almost surely for all j, then \(L_{{\tilde{{{\mathcal {P}}}}}}\) is linearly isomorphic to a space \(L_{{\mathcal {P}}}\) satisfying (A1) and (A2). The elements of \(L_{{\tilde{{{\mathcal {P}}}}}}^*\) can thus be expressed as
where i is the isomorphism and \(u^*\in L_{{\mathcal {P}}}^*\).
Proof
Define \(i:L^0\rightarrow L^0\) by \(i(u)_j := u_j/{\bar{u}}_j\) and, for every \({\tilde{p}}\in {\tilde{{{\mathcal {P}}}}}\), let \(p(u):={\tilde{p}}(i^{-1}(u))\). By (A2),
so \({{\mathcal {P}}}:=\{{\tilde{p}}\circ i^{-1}\mid {\tilde{p}}\in {\tilde{{{\mathcal {P}}}}}\}\) satisfies (A1) and (A2). The restriction of A to \(L_{{\tilde{{{\mathcal {P}}}}}}\) is an isomorphism between \(L_{{\tilde{{{\mathcal {P}}}}}}\) and \(L_{{\mathcal {P}}}\). \(\square \)
A seminorm p is said to be rearrangement invariant (or symmetric) if \(p(u)=p({\tilde{u}})\) whenever u and \({\tilde{u}}\) have the same distribution in the sense that \(P(|u|>\tau )=P(|{\tilde{u}}|>\tau )\) for all \(\tau \ge 0\).
Remark 4
Consider the scalar case \(n=1\). Given \(p\in {{\mathcal {P}}}\), let
Under (A2), condition (A3) is equivalent to \(\lim _{t\searrow 0}{\hat{\phi }}_p(t)=0\). If \(\lim _{t\searrow 0}{\check{\phi }}_p(t)>0\), then \(\mathop {\mathrm{dom}}\nolimits p=L^\infty \). If p is rearrangement invariant, then, for any \(A\in {{\mathcal {F}}}\) with \(P(A)=t\),
where the common value is known as the fundamental function; see e.g. [1]. In this case, \(L_{{\mathcal {P}}}= L^\infty \) unless (A3) holds.
Proof
Assuming (A3), let \(t^\nu \searrow 0\). There exists \((A^\nu )_{\nu =1}^\infty \) such that \(P(A^\nu )\le t^\nu \) and \({\hat{\phi }}_p(t^\nu )\le p(1_{A^\nu })+1/\nu \). Passing to a subsequence if necessary, \(1_{A^\nu }\rightarrow 0\) almost surely. Defining \({\hat{A}}^\nu :=\bigcup _{\nu '\ge \nu } A^\nu \), \(({\hat{A}}^\nu )_{\nu =1}^\infty \) is decreasing with \(A^\nu \subset {\hat{A}}^\nu \) and \(P({\hat{A}}^\nu )\searrow 0\), so, by (A3)
For the converse, let \(u\in L^\infty \) and \((A^\nu )_{\nu =1}^\infty \subset {{\mathcal {F}}}\) with \(t^\nu :=P(A^\nu )\searrow 0\). By (A2),
If \(\inf _{t>0}{\check{\phi }}_p(t)>0\), then
unless \(u\in L^\infty \). \(\square \)
For each \(p\in {{\mathcal {P}}}\), we define a sublinear symmetric function \(p^\circ \) on the space \({{\mathcal {M}}}\) of P-absolutely continuous finitely additive measures by
The following shows, in particular, that every \(m\in \mathop {\mathrm{dom}}\nolimits p^\circ \) decomposes uniquely into the sum of countably additive and singular measures both in \(\mathop {\mathrm{dom}}\nolimits p^\circ \).
Lemma 5
Assume that \(p\in {{\mathcal {P}}}\) satisfies (A2) and let \(m\in \mathop {\mathrm{dom}}\nolimits p^\circ \). Every \(u\in \mathop {\mathrm{dom}}\nolimits p\) is m-integrable and
There exist unique \(y\in L^1\cap \mathop {\mathrm{dom}}\nolimits p^\circ \) and \(m^s\in {{\mathcal {M}}}_s\cap \mathop {\mathrm{dom}}\nolimits p^\circ \) such that
Given \(m^s\in {{\mathcal {M}}}_{s}\cap \mathop {\mathrm{dom}}\nolimits p^\circ \), there exists a decreasing \((A^\nu )_{\nu =1}^\infty \subset {{\mathcal {F}}}\) such that  and
and
Under (A3), \({{\mathcal {M}}}_{s}\cap \mathop {\mathrm{dom}}\nolimits p^\circ =\{0\}\).
Proof
By (A2),
so every \(u\in \mathop {\mathrm{dom}}\nolimits p\) is m-integrable. Theorem 2 now gives
and the existence of the sequence \((A^\nu )_{\nu =1}^\infty \) for very \(m^s\in {{\mathcal {M}}}_{s}\cap \mathop {\mathrm{dom}}\nolimits p^\circ \).
By Theorem 1, there exist unique \(y\in L^1\) and \(m^s\in (L^\infty )^s\) such that \(m=yP+m^s\). Let \(\alpha <p^\circ (y)\) and \(\alpha ^s<p^\circ (m^s)\) and \(u,u^s\in L^\infty \) such that \(p(u),p(u^s)\le 1\) and
Let \((A^\nu )_{\nu =1}^\infty \subset {{\mathcal {F}}}\) be decreasing with  and \(m^s(\Omega \setminus A^\nu )=0\) and let \(u^\nu =\lambda u1_{\Omega \setminus A^\nu }+(1-\lambda )u^s1_{A^\nu }\), where \(\lambda \in (0,1)\). By convexity and (A2),
and \(m^s(\Omega \setminus A^\nu )=0\) and let \(u^\nu =\lambda u1_{\Omega \setminus A^\nu }+(1-\lambda )u^s1_{A^\nu }\), where \(\lambda \in (0,1)\). By convexity and (A2),
while
Thus, \(p^\circ (m)\ge \lambda \alpha +(1-\lambda )\alpha ^s\). Since \(\alpha <p^\circ (y)\) and \(\alpha ^s<p^\circ (m^s)\) were arbitrary, \(p^\circ (m)\ge \lambda p^\circ (y)+(1-\lambda )p^\circ (m^s)\). Since \(\lambda \in (0,1)\) was arbitrary, we get \(p^\circ (y)\le p^\circ (m)\) and \(p^\circ (m^s)\le p^\circ (m)\). Thus, \(y\in \mathop {\mathrm{dom}}\nolimits p^\circ \) and \(m^s\in \mathop {\mathrm{dom}}\nolimits p^\circ \).
To prove the last claim, let \(m^s\in {{\mathcal {M}}}_{s}\cap \mathop {\mathrm{dom}}\nolimits p^\circ \). By the first claim,
so, by the last claim of Theorem 1, condition (A3) implies \(m^s=0\). \(\square \)
Let
the set of P-absolutely continuous finitely additive measures \(m\in {{\mathcal {M}}}\) such that \(p^\circ (m)<\infty \) for some \(p\in {{\mathcal {P}}}\). The set of purely finitely additive elements of \({{\mathcal {M}}}^{{{\mathcal {P}}}^\circ }\) will be denoted by \({{\mathcal {M}}}^{{{\mathcal {P}}}^\circ }_s\). The set of densities \(y=dm/dP\) of countably additive \(m\in {{\mathcal {M}}}^{{{\mathcal {P}}}^\circ }\) will be denoted by \(L^{{{\mathcal {P}}}^\circ }\). By Lemma 5, \({{\mathcal {M}}}^{{{\mathcal {P}}}^\circ }=L^{{{\mathcal {P}}}^\circ }\oplus {{\mathcal {M}}}^{{{\mathcal {P}}}^\circ }_s\). In the setting of Banach function spaces where \({{\mathcal {P}}}\) is a singleton, \(L^{{{\mathcal {P}}}^\circ }\) is often called the “associate space” or the Köthe dual of \(L_{{\mathcal {P}}}\); see e.g. [1, 8, 39] and Lemma 8 below.
The following is the main result of this section. It identifies the topological dual \(L_{{\mathcal {P}}}^*\) of \(L_{{\mathcal {P}}}\) with the direct sum of \({{\mathcal {M}}}^{{{\mathcal {P}}}^\circ }=L^{{{\mathcal {P}}}^\circ }\oplus {{\mathcal {M}}}^{{{\mathcal {P}}}^\circ }_s\) and the annihilator
of \(L^\infty \).
Theorem 6
We have
in the sense that for every \(u^*\in L_{{\mathcal {P}}}^*\) there exist unique \(y\in L^{{{\mathcal {P}}}^\circ }\), \(m^s\in {{\mathcal {M}}}^{{{\mathcal {P}}}^\circ }_s\) and \(w\in (L^\infty )^\perp \) such that
For every \(u\in L_{{\mathcal {P}}}\) and \(m\in {{\mathcal {M}}}^{{{\mathcal {P}}}^\circ }\),
In particular, restricted to \({{\mathcal {M}}}^{{{\mathcal {P}}}^\circ }\), \(p^\circ \) coincides with the polar seminorm of p, i.e.
Given \(w\in (L^\infty )^\perp \) and \(u\in L_{{\mathcal {P}}}\), there exists a decreasing sequence \((A^\nu )_{\nu =1}^\infty \subset {{\mathcal {F}}}\) with \(P(A^\nu )\searrow 0\) and
Under (A3), \({{\mathcal {M}}}^{{{\mathcal {P}}}^\circ }_s=\{0\}\) so
and under (A4), \({{\mathcal {M}}}^{{{\mathcal {P}}}^\circ }_s=\{0\}\) and \((L^\infty )^\perp =\{0\}\) so
Proof
By Lemma 5, \({{\mathcal {M}}}^{{{\mathcal {P}}}^\circ }\subset L_{{\mathcal {P}}}^*\), so \({{\mathcal {M}}}^{{{\mathcal {P}}}^\circ }\oplus (L^\infty )^\perp \subseteq L_{{\mathcal {P}}}^*\). To prove the opposite inclusion, let \(u^*\in L_{{\mathcal {P}}}^*\). There exists \(p\in {{\mathcal {P}}}\) and \(\gamma >0\) such that \(u^*\le \gamma p\). Assumption (A1) implies that \(u^*\) is continuous in \(L^\infty \). By Theorem 1, there exists a unique \(m\in {{\mathcal {M}}}\) such that \(\langle u,u^*\rangle = \int _\Omega udm\) for all \(u\in L^\infty \). Since \(u^*\le \gamma p\), we have \(m\in \mathop {\mathrm{dom}}\nolimits p^\circ \), so m is continuous on \(L_{{\mathcal {P}}}\) by Lemma 5. Now \(w := u^*-m\) belongs to \((L^\infty )^\perp \), so \(u^*\) has the required decomposition. Given another decomposition \(u^*={\tilde{m}} +{\tilde{w}}\) with \({\tilde{w}}\in (L^\infty )^\perp \) and \({\tilde{m}}\in {{\mathcal {M}}}^{{{\mathcal {P}}}^\circ }\), we have \((m-{\tilde{m}}) +(w-{\tilde{w}})=0\). Thus \(\int _\Omega ud(m-{\tilde{m}}) =0\) for all \(u\in L^\infty \), so \(m-{\tilde{m}}=0\) and hence also \(w-{\tilde{w}}=0\), so the decomposition is unique.
The inequality follows directly from that of Lemma 5. Let \(u\in L_{{\mathcal {P}}}\) and \(A^\nu :=\{|u|>\nu \}\). Clearly \(P(A^\nu )\searrow 0\) and \(u1_{\Omega \setminus A^\nu }\in L^\infty \), so \(\langle u1_{\Omega \setminus A^\nu },w\rangle =0\) and thus w is singular. That \({{\mathcal {M}}}^{{{\mathcal {P}}}^\circ }=L^{{{\mathcal {P}}}^\circ }\) under (A3) is the last claim of Lemma 5. Under (A4), the truncations \(u^\nu :=u1_{\{|u|\ge \nu \}}\) of any \(u\in L_{{\mathcal {P}}}\) converge to u so \(L^\infty \) is dense in \(L_{{\mathcal {P}}}\) and thus, \((L^\infty )^\perp =\{0\}\). \(\square \)
When \({{\mathcal {P}}}\) is a singleton, we are in the setting of [38, Theorem 15.70.2], where \(L_{{\mathcal {P}}}^*\) is decomposed into the direct sum of \(L^{{{\mathcal {P}}}^\circ }\) and "singular elements". Theorem 6 gives a more precise description of the singular elements as the direct sum of \({{\mathcal {M}}}^{{{\mathcal {P}}}^\circ }_s\) and \((L^\infty )^\perp \). Applications will be given in the following sections.
Let \(M_{{\mathcal {P}}}\) be the closure of \(L^\infty \) in \(L_{{\mathcal {P}}}\).
Corollary 7
We have
in the sense that for every \(u^*\in M_{{\mathcal {P}}}^*\) there exist unique \(y\in L^{{{\mathcal {P}}}^\circ }\) and \(m\in {{\mathcal {M}}}^{{{\mathcal {P}}}^\circ }_s\) such that
If (A3) holds, then \({{\mathcal {M}}}^{{{\mathcal {P}}}^\circ }_s=\{0\}\) and \(M_{{\mathcal {P}}}^*=L^{{{\mathcal {P}}}^\circ }\). If (A4) holds, then \(M_{{\mathcal {P}}}=L_{{\mathcal {P}}}\).
Proof
By Hahn-Banach, a continuous linear functional on \(M_{{\mathcal {P}}}\) is a restriction to \(M_{{\mathcal {P}}}\) of a continuous linear functional on \(L_{{\mathcal {P}}}\). The first two claims thus follow from Theorem 6. To prove the last claim, take any \(u\in L_{{\mathcal {P}}}\) and define \(u^\nu \in L^\infty \) as the pointwise projection of u on the Euclidean ball of radius \(\nu \). Under (A4),  for all \(p\in {{\mathcal {P}}}\), so \(L^\infty \) is dense in \(L_{{\mathcal {P}}}\). \(\square \)
for all \(p\in {{\mathcal {P}}}\), so \(L^\infty \) is dense in \(L_{{\mathcal {P}}}\). \(\square \)
The we end this section by giving some basic properties of \(L^{{{\mathcal {P}}}^\circ }\). The Köthe dual of \(L_{{\mathcal {P}}}\) is the linear space
By definition, \(L^{{{\mathcal {P}}}^\circ }\subseteq L_{{\mathcal {P}}}'\). Lemma 8 below gives sufficient conditions for the converse. Recall that a locally convex space is barreled if every closed convex absorbing set is a neighborhood of the origin. By the Baire category theorem, Banach and Fréchet spaces are barreled.
Lemma 8
For each \(p\in {{\mathcal {P}}}\),
-
1.
there is a constant \(c>0\) such that \(c\Vert y\Vert _{L^1}\le p^\circ (y)\) for all \(y\in L^1\),
-
2.
\(p^\circ (y')\le p^\circ (y)\) for every \(y',y\in L^1\) with \(|y'_j|\le |y_j|\) for \(j=1,\ldots ,n\),
-
3.
\(E[u\cdot y]\le p(u)p^\circ (y)\) for every \(u\in L^0\) and \(y\in L^1\) (Hölder’s inequality).
If the \({{\mathcal {P}}}\)-topology is barreled and stronger than that of \(L^0\), then \(L^{{{\mathcal {P}}}^\circ }=L_{{\mathcal {P}}}'\).
Proof
Assumption (A1) implies 1. Under (A2),
so 2 holds. The inequality in 3 follows from the inequality in Lemma 5.
To prove the last claim, let \(y\in L^0\) be such that \(E[u\cdot y]<\infty \) for all \(u\in L_{{\mathcal {P}}}\). Then \(p_y(u):=E[|u||y|]<\infty \) for all \(u\in L_{{\mathcal {P}}}\). By Fatou’s lemma, \(p_y\) is lsc in the \(L^0\)-topology. By assumption, \(p_y\) is lsc also in the \({{\mathcal {P}}}\)-topology. When the \({{\mathcal {P}}}\)-topology is barreled, \(p_y\) is continuous (see e.g. [33, Corollary 8B]), so \(y\mapsto E[u\cdot y]\) is continuous as well. By Theorem 6, \(y\in L^{{{\mathcal {P}}}^\circ }\). \(\square \)
In the setting of Banach function spaces where \({{\mathcal {P}}}\) is a singleton, the last claim of Lemma 8 recovers [1, Lemma 1.2.6]. The following gives sufficient conditions for the space \(L_{{\mathcal {P}}}\) to be complete and thus, barreled, when the topology is metrizable.
Remark 9
If the \({{\mathcal {P}}}\)-topology is stronger than that of \(L^0\) and \(p\in {{\mathcal {P}}}\) are lower semicontinuous on \(L^0\), then \(L_{{\mathcal {P}}}\) is complete. In this case, \(L_{{\mathcal {P}}}\) is a Banach/Fréchet (and, in particular, barreled) if \({{\mathcal {P}}}\) is a singleton/countable.
If \(p(u)=\rho (|u|)\) for an nondecreasing \(\rho :L^0\rightarrow \overline{{\mathbb {R}}}\), the function p is lsc in probability if and only if \(\rho \) has the Fatou property: for any sequence \((\eta ^\nu )_{\nu =1}^\infty \subset L^0_+\) with  , \(\lim \rho (\eta ^\nu )=\rho (\eta )\).
, \(\lim \rho (\eta ^\nu )=\rho (\eta )\).
Proof
If \((u^\nu )\) is a Cauchy net in \(L_{{\mathcal {P}}}\), it is Cauchy also in \(L^0\) so, by completeness of \(L^0\), it \(L^0\)-converges to an \(u\in L^0\). Being Cauchy in \(L_{{\mathcal {P}}}\) means that for every \(\epsilon >0\) and \(p\in {{\mathcal {P}}}\), there is a \({\bar{\nu }}\) such that
The lower semicontinuity then gives
so \(u\in L_{{\mathcal {P}}}\), by triangle inequality, and \((u^\nu )\) converges in \(L_{{\mathcal {P}}}\) to u. Thus \(L_{{\mathcal {P}}}\) is complete.
If p is lsc, \(\liminf \rho (\eta ^\nu )\ge \rho (\eta )\) while \(\rho (\eta ^\nu )\le \rho (\eta )\) since \(\rho \) is nondecreasing. If Fatou property holds and \(u^\nu \rightarrow u\) in probability, then, passing to a subsequence if necessary, \(u^\nu \rightarrow u\) almost surely. Then \(\eta ^\nu := \inf _{\nu '\ge \nu } |u^{\nu '}|\) increases pointwise to |u|, so \(p(u)=\liminf \rho (\eta ^\nu )\le \liminf p(u^\nu )\). \(\square \)
5 Solid spaces of random variables
Axiom (A1) implies that \(L_{{\mathcal {P}}}\) contains \(L^\infty \) while axiom (A2) implies that it is solid in the sense that it contains every \(u'\in L^0\) for which there exists \(u\in L_{{\mathcal {P}}}\) with \(|u'_j|\le |u_j|\) for all \(j=1,\ldots ,n\). By Lemma 8, \(L^{{{\mathcal {P}}}^\circ }\) is solid as well. This section starts with an arbitrary pair \(({{\mathcal {U}}},{{\mathcal {Y}}})\) of solid spaces of random variables in separating duality under the bilinear form
We assume that both \({{\mathcal {U}}}\) and \({{\mathcal {Y}}}\) contain \(L^\infty \) and show that the Mackey and the strong topologies arise from (uncountable) collections of seminorms on \(L^0\) satisfying the axioms of Sect. 4. We then obtain completeness and duality results as corollaries of the results there.
The weak topology generated by \({{\mathcal {Y}}}\) on \({{\mathcal {U}}}\) will be denoted by \(\sigma ({{\mathcal {U}}},{{\mathcal {Y}}})\). Similarly on \({{\mathcal {Y}}}\). The Mackey topology \(\tau ({{\mathcal {U}}},{{\mathcal {Y}}})\) on \({{\mathcal {U}}}\) is generated by the collection of seminorms defined as the support functions
of symmetric \(\sigma ({{\mathcal {Y}}},{{\mathcal {U}}})\)-compact sets \(C\subset {{\mathcal {Y}}}\). The strong topology on \({{\mathcal {U}}}\) is defined similarly by all the symmetric \(\sigma ({{\mathcal {Y}}},{{\mathcal {U}}})\)-bounded sets in \({{\mathcal {Y}}}\), i.e. symmetric sets \(C\subset {{\mathcal {Y}}}\) such that \(\sigma _C(u)<\infty \) for all \(u\in {{\mathcal {U}}}\). By the bipolar theorem, this is the topology generated by all \(\tau ({{\mathcal {U}}},{{\mathcal {Y}}})\)-lower semicontinuous seminorms on \({{\mathcal {U}}}\). By the Mackey–Arens theorem, the Mackey topology on \({{\mathcal {U}}}\) is the finest topology under which the topological dual of \({{\mathcal {U}}}\) coincides with \({{\mathcal {Y}}}\). Since compact sets are bounded, the strong topology is stronger than \(\tau ({{\mathcal {U}}},{{\mathcal {Y}}})\).
Lemma 11 below does not require solidity but merely decomposability in the sense that \(u1_A+{\bar{u}}1_{\Omega \setminus A}\in {{\mathcal {U}}}\) for every \(u\in {{\mathcal {U}}}\), \({\bar{u}}\in L^\infty \) and \(A\in {{\mathcal {F}}}\).
Example 10
Solid spaces containing \(L^\infty \) are decomposable but there are decomposable spaces that are not solid. Indeed, let \(\Omega =[0,1]\), \({{\mathcal {F}}}\) the Borel sigma algebra and P the Lebesgue measure. Let \(u(\omega ):=\omega ^{-\frac{1}{4}}+\omega ^{-\frac{1}{2}}\) and \({{\mathcal {U}}}:=L^\infty +L\), where L is the linear span of functions of the form \(u1_A\) with \(A\in {{\mathcal {F}}}\). Then \({{\mathcal {U}}}\) is decomposable, by construction, but not solid, since it does not contain \({\bar{u}}(\omega )=\omega ^{-\frac{1}{4}}\) while \(0<{\bar{u}}< u\).
The following is Lemma 6 from [26].
Lemma 11
If \({{\mathcal {U}}}\) and \({{\mathcal {Y}}}\) are decomposable, then \(L^\infty \subseteq {{\mathcal {U}}}\subseteq L^1\) and
Lemma 12
If \({{\mathcal {U}}}\) is solid, then, for every \(u\in {{\mathcal {U}}}\),
-
1.
\(y\mapsto u\cdot y\) is continuous from \(({{\mathcal {Y}}},\sigma ({{\mathcal {Y}}},{{\mathcal {U}}}))\) to \((L^1,\sigma (L^1,L^\infty ))\),
-
2.
\(\eta \mapsto \eta u\) is continuous from \((L^\infty ,\tau (L^\infty ,L^1))\) to \(({{\mathcal {U}}},\tau ({{\mathcal {U}}},{{\mathcal {Y}}}))\).
Proof
For any \(u\in {{\mathcal {U}}}\), \(y\in {{\mathcal {Y}}}\) and \(\eta \in L^\infty \),
Solidity implies that \(\eta u\in {{\mathcal {U}}}\) so 1 holds. Let \(K\subset {{\mathcal {Y}}}\) be \(\sigma ({{\mathcal {Y}}},{{\mathcal {U}}})\)-compact. We have
where \(D=\{u\cdot y\,|\, y\in K\}\) is \(\sigma (L^1,L^\infty )\)-compact since \(y\mapsto u\cdot y\) is continuous, by 1. \(\square \)
Lemma 12 implies, in particular, that axiom (A3) is necessary for the second claim of Corollary 7.
Corollary 13
In the setting of Corollary 7, (A3) holds if and only if \(M_{{\mathcal {P}}}^*=L^{{{\mathcal {P}}}^\circ }\).
Proof
By Corollary 7, (A3) implies \(M_{{\mathcal {P}}}^*=L^{{{\mathcal {P}}}^\circ }\). On the other hand, if \(M_{{\mathcal {P}}}^*=L^{{{\mathcal {P}}}^\circ }\), the topology of \(M_{{\mathcal {P}}}\) cannot be stronger than \(\tau (M_{{\mathcal {P}}},L^{{{\mathcal {P}}}^\circ })\). In that case, Lemma 12 implies that \(p(u\eta ^\nu )\rightarrow 0\) if \(\eta ^\nu \rightarrow 0\) in \(\tau (L^\infty ,L^1)\). Since \(1_{A^\nu }\rightarrow 0\) in \(\tau (L^\infty ,L^1)\) if \(P(A^\nu )\rightarrow 0\), assumption (A3) holds. \(\square \)
The following characterization of \(\sigma ({{\mathcal {U}}},{{\mathcal {Y}}})\)-compact sets will be useful. In the case of Orlicz spaces, a similar characterization of relative compactness can be found e.g. in [5, 28].
Lemma 14
Given \(C\subset {{\mathcal {U}}}\), the following are equivalent.
-
1.
C is \(\sigma ({{\mathcal {U}}},{{\mathcal {Y}}})\)-precompact,
-
2.
\(\{u\cdot y\mid u\in C\}\) is \(\sigma (L^1,L^\infty )\)-precompact for every \(y\in {{\mathcal {Y}}}\),
-
3.
\(\{u_j y_j\mid u\in C\}\) is \(\sigma (L^1,L^\infty )\)-precompact for every \(y\in {{\mathcal {Y}}}\) and \(j=1,\dots ,n\).
Proof
Since continuous images of precompact sets are precompact, 3 implies 2, and, by Lemma 12, 1 implies 3. Clearly, 2 implies 3, so it suffices to show that 2 and 3 imply 1. Let \((u^\nu )\) be a net in C. Since \({{\mathcal {Y}}}\) contains constants, the sets \(\{u_j\mid u\in C\}\) are \(\sigma (L^1,L^\infty )\)-precompact by 3. Thus there is a subnet and \(u\in C\) such that \(u^\nu \rightarrow u\) in \(\sigma (L^1,L^\infty )\). Let \(y\in {{\mathcal {Y}}}\) and \(\epsilon >0\). By the Dunford–Pettis theorem, 2 implies that \(\{u\cdot y\mid u\in C\}\) is uniformly integrable, so there exists n such that \(|E[(u^\nu -u)\cdot y 1_{|y|> n}]|<\epsilon \) for every \(\nu \). Since \(u^\nu \rightarrow u\) in \(\sigma (L^1,L^\infty )\), there exists \(\nu '\) such that \(|E[(u^\nu -u)\cdot y 1_{|y|\le n}]|<\epsilon \) for all \(\nu \ge \nu '\). Thus, for all \(\nu \ge \nu '\),
which proves that \(u^\nu \rightarrow u\) in \(\sigma ({{\mathcal {U}}},{{\mathcal {Y}}})\). \(\square \)
The solid hull s(C) of a set \(C\subseteq {{\mathcal {U}}}\) is the smallest solid set containing C. Clearly,
Corollary 15
The solid hull of a \(\sigma ({{\mathcal {U}}},{{\mathcal {Y}}})\)-bounded set is \(\sigma ({{\mathcal {U}}},{{\mathcal {Y}}})\)-bounded and the solid hull of a \(\sigma ({{\mathcal {U}}},{{\mathcal {Y}}})\)-precompact set is \(\sigma ({{\mathcal {U}}},{{\mathcal {Y}}})\)-precompact.
Proof
We have \(E[u\cdot y]<\infty \) if and only if \(E\sum _j |u_j||y_j|<\infty \), which implies the first claim. By Lemma 14 and the Dunford–Pettis theorem, a set \(C\subseteq {{\mathcal {U}}}\) is \(\sigma ({{\mathcal {U}}},{{\mathcal {Y}}})\)-precompact if and only if \(C_{y,j}:=\{u_j y_j\mid u\in C\}\) is uniformly integrable for every \(y\in {{\mathcal {Y}}}\) and \(j=1,\dots ,n\). Uniform integrability of \(C_{y,j}\) means that, for every \(\epsilon >0\), there exists \(M>0\) such that \(E|1_{|{\bar{u}}_j y_j|\ge M}{\bar{u}}_j y_j|<\epsilon \) for every \({\bar{u}}\in C\). Clearly, uniform integrability of \(C_{y,j}\) implies that of \(s(C)_{y,j}\). Thus, if C is precompact, then s(C) is precompact. \(\square \)
Let \({{\mathcal {C}}}_s\) be the collection of solid hulls of \(\sigma ({{\mathcal {Y}}},{{\mathcal {U}}})\)-bounded sets. We define \({{\mathcal {P}}}_s\) as the collection of functions \(p_C\) on \(L^0\) defined by
where \(C\in {{\mathcal {C}}}_s\) and the expectation is defined as \(+\infty \) unless the positive part of \(u\cdot y\) is integrable. Analogously, we define \({{\mathcal {C}}}_\tau \) as the collection of solid hulls of \(\sigma ({{\mathcal {Y}}},{{\mathcal {U}}})\)-compact sets and \({{\mathcal {P}}}_\tau \) as the collection of functions \(p_C\) with \(C\in {{\mathcal {C}}}_\tau \). By Corollary 15, the restrictions of \({{\mathcal {P}}}_s\) and \({{\mathcal {P}}}_\tau \) to \({{\mathcal {U}}}\) generate the strong and the Mackey topologies, respectively. Note that solid hulls of convex sets in \({{\mathcal {U}}}\) need not be convex. For subsets of \(L^0_+\), however, taking the solid hull and convex hull commute; see [18, Proposition 1.1].
Lemma 16
The members of \({{\mathcal {P}}}_s\) satisfy (A1) and (A2) while the members of \({{\mathcal {P}}}_\tau \) satisfy (A1)–(A4). Both \({{\mathcal {P}}}_s\) and \({{\mathcal {P}}}_\tau \) contain the \(L^1\)-norm and their members are \(L^0\)-lsc.
Proof
Since \(\sigma ({{\mathcal {Y}}},{{\mathcal {U}}})\)-bounded sets are \(L^1\)-bounded, the functions \(p_C\) are dominated by the \(L^\infty \)-norm. Thus, \({{\mathcal {P}}}_s\) satisfies (A1). Since the sets \(C\subset {{\mathcal {C}}}_s\) are solid, [34, Theorem 14.60] gives
so \(p_C\) satisfies (A2). By Fatou’s lemma, each supremand is \(L^0\)-lsc so \(p_C\) is \(L^0\)-lsc as well.
Since \({{\mathcal {P}}}_\tau \subset {{\mathcal {P}}}_s\), axioms (A1) and (A2) are again satisfied by \({{\mathcal {P}}}_\tau \) and its elements are \(L^0\)-lsc. Given \(C\in {{\mathcal {C}}}_\tau \) and \(u\in \mathop {\mathrm{dom}}\nolimits p_C\), Lemma 14 and the Dunford–Pettis theorem imply that the set \(\{u\cdot y\mid y\in C\}\) is uniformly integrable so  whenever \((A^\nu )_{\nu =1}^\infty \) is a decreasing sequence with
whenever \((A^\nu )_{\nu =1}^\infty \) is a decreasing sequence with  . Thus, \({{\mathcal {P}}}_\tau \) satisfies (A4).
. Thus, \({{\mathcal {P}}}_\tau \) satisfies (A4).
By Banach–Alaoglu, the unit ball B of \(L^\infty \) is \(\sigma (L^\infty ,L^1)\)-compact so, by Lemma 11, it is \(\sigma ({{\mathcal {Y}}},{{\mathcal {U}}})\)-compact as well. Thus, \(B\in {{\mathcal {C}}}_\tau \), so \({{\mathcal {P}}}_\tau \) contains the \(L^1\)-norm and thus \({{\mathcal {P}}}_s\) does as well. \(\square \)
Recall that the Köthe dual of a space \({{\mathcal {U}}}\) of measurable functions is the linear space
Our assumptions on \({{\mathcal {U}}}\) and \({{\mathcal {Y}}}\) imply that they are contained in each other’s Köthe duals. The following shows, in particular, that if \({{\mathcal {U}}}\) is equal to the Köthe dual of \({{\mathcal {Y}}}\), then \({{\mathcal {U}}}\) and \({{\mathcal {Y}}}\) arise from the construction of Sect. 4 with the Mackey-seminorms \({{\mathcal {P}}}_\tau \).
Theorem 17
We have \({{\mathcal {Y}}}=L^{{{\mathcal {P}}}_\tau ^\circ }\), \({{\mathcal {U}}}\subset L^{{{\mathcal {P}}}_\tau }\subset {{\mathcal {Y}}}'\) and the following are equivalent
-
1.
\({{\mathcal {U}}}={{\mathcal {Y}}}'\),
-
2.
\({{\mathcal {U}}}=L_{{{\mathcal {P}}}_\tau }\),
-
3.
\({{\mathcal {U}}}\) is \(\tau ({{\mathcal {U}}},{{\mathcal {Y}}})\)-complete,
-
4.
\({{\mathcal {U}}}\) is sequentially \(\sigma ({{\mathcal {U}}},{{\mathcal {Y}}})\)-complete.
Proof
Given \(C\in {{\mathcal {C}}}_\tau \), let \(D\subset {{\mathcal {Y}}}\) be its \(\sigma ({{\mathcal {Y}}},{{\mathcal {U}}})\)-closed convex hull. By definition, \(p_D=p_C\) on \({{\mathcal {U}}}\) and, in particular, on \(L^\infty \). The \(\sigma ({{\mathcal {Y}}},{{\mathcal {U}}})\)-precompactness of C implies that D is \(\sigma ({{\mathcal {Y}}},{{\mathcal {U}}})\)-compact. By Lemma 11, D is \(\sigma (L^1,L^\infty )\)-compact as well. An application of the bipolar theorem in the duality pairing \((L^1,L^\infty )\) thus gives
so \(\mathop {\mathrm{dom}}\nolimits p_C^\circ \subset {{\mathcal {Y}}}\). Thus, \(L^{{{\mathcal {P}}}_\tau ^\circ }\subseteq {{\mathcal {Y}}}\). Any \(y\in {{\mathcal {Y}}}\) belongs to some \(C\in {{\mathcal {C}}}_\tau \), so \(y\in \mathop {\mathrm{dom}}\nolimits p_C^\circ \). Thus, \({{\mathcal {Y}}}\subseteq L^{{{\mathcal {P}}}_\tau ^\circ }\).
Each \(p\in {{\mathcal {P}}}_\tau \) is finite on \({{\mathcal {U}}}\), so \({{\mathcal {U}}}\subset L_{{{\mathcal {P}}}_\tau }\). Let \(u\in L_{{{\mathcal {P}}}_\tau }\). For every \(y\in {{\mathcal {Y}}}\), there is a \(p\in {{\mathcal {P}}}_\tau \) such that \(p^\circ (y)<\infty \) so, by the Hölder’s inequality in Lemma 8,
This proves the second claim.
By the second claim, 1 implies 2. Lemma 16 and Remark 9 imply that \(L_{{{\mathcal {P}}}_\tau }\) is complete. Thus, 2 implies 3. On the other hand, by Lemma 16, \({{\mathcal {P}}}_\tau \) satisfies (A1)–(A4) so \(L^\infty \) is dense in \(L_{{{\mathcal {P}}}_\tau }\). Since \({{\mathcal {U}}}\) is decomposable, it contains \(L^\infty \). Thus, if \({{\mathcal {U}}}\) is complete in the relative topology of \({{\mathcal {P}}}_\tau \), it has to coincide with \(L_{{{\mathcal {P}}}_\tau }\). Thus, 3 implies 2.
We next show that 4 implies 1. Let \(u\in L^1\) be in the Köthe dual and let \(u^\nu \in L^\infty \) be the pointwise projection of u to the Euclidean ball with radius \(\nu \). By dominated convergence, \(E[u^\nu \cdot y]\rightarrow E[u\cdot y]\) for all \(y\in {{\mathcal {Y}}}\). Thus, \((u^\nu )_{\nu =1}^\infty \) is weakly Cauchy so 4 implies that it has a \(\sigma ({{\mathcal {U}}},{{\mathcal {Y}}})\)-limit \(u'\in {{\mathcal {U}}}\). It follows that \(E[u\cdot y]=E[u'\cdot y]\) for all \(y\in {{\mathcal {Y}}}\) so \(u=u'\).
It remains to show that 2 implies 4. Let \((u^\nu )_{\nu =1}^\infty \) be a \(\sigma ({{\mathcal {U}}},{{\mathcal {Y}}})\)-Cauchy sequence. Since \(\sigma ({{\mathcal {U}}},{{\mathcal {Y}}})\) is stronger than \(\sigma (L^1,L^\infty )\) which, by [6, Theorem IV.8.6], is sequentially complete, there exists \(u\in L^1\) such that \(u^\nu \rightarrow u\) in \(\sigma (L^1,L^\infty )\). Since \(\sigma ({{\mathcal {U}}},{{\mathcal {Y}}})\)-Cauchy sequences are bounded in any topology compatible with the pairing, the sequence is also bounded in the \({{\mathcal {P}}}_\tau \)-topology. Thus, for any \(p\in {{\mathcal {P}}}_\tau \), there exists \(\gamma \in {\mathbb {R}}\) such that \(p(u^\nu )\le \gamma \). Since level-sets of p are closed in \(L^1\) and \({{\mathcal {U}}}=L_{{{\mathcal {P}}}_\tau }\), we get \(u\in {{\mathcal {U}}}\). It suffices to show that \(u^\nu \rightarrow u\) in \(\sigma ({{\mathcal {U}}},{{\mathcal {Y}}})\).
Let \(y\in {{\mathcal {Y}}}\). By Lemma 12, \((u^\nu \cdot y)_{\nu =1}^\infty \) is Cauchy in \(\sigma (L^1,L^\infty )\), so by sequential completeness of \(L^1\) again, it converges in \(\sigma (L^1,L^\infty )\) to some \(\xi \in L^1\). By Mazur’s theorem, there is a subsequence of convex combinations \({\bar{u}}^\nu \) such that \({\bar{u}}^\nu \rightarrow u\) in \(L^1\)-norm, and thus \({\bar{u}}^\nu \cdot y\rightarrow u\cdot y\) in probability. Clearly, \({\bar{u}}^\nu \cdot y \rightarrow \xi \) in \(\sigma (L^1,L^\infty )\), so we must have \(\xi =u\cdot y\). Thus, \(E[u^\nu \cdot y]\rightarrow E[u\cdot y]\) which completes the proof. \(\square \)
The following shows, in particular, that if \({{\mathcal {U}}}\) and \({{\mathcal {Y}}}\) are Köthe duals of each other, then they arise from the construction of Sect. 4 with the strong seminorms \({{\mathcal {P}}}_s\). Theorem 6 then yields a characterization of the strong dual of \({{\mathcal {U}}}\).
Theorem 18
If \({{\mathcal {U}}}={{\mathcal {Y}}}'\), then \({{\mathcal {U}}}=L_{{{\mathcal {P}}}_s}\). If \({{\mathcal {Y}}}={{\mathcal {U}}}'\), then \({{\mathcal {Y}}}=L^{{{\mathcal {P}}}_s^\circ }\). If \({{\mathcal {U}}}=L_{{{\mathcal {P}}}_s}\) and \({{\mathcal {Y}}}=L^{{{\mathcal {P}}}_s^\circ }\), then the strong dual of \({{\mathcal {U}}}\) may be identified with \({{\mathcal {Y}}}\oplus {{\mathcal {M}}}^{{{\mathcal {P}}}_s^\circ }_s\oplus (L^\infty )^\perp \), in the sense that for every \(u^*\in {{\mathcal {U}}}^*\), there exist \(u\in {{\mathcal {Y}}}\), \(m^s\in {{\mathcal {M}}}^{{{\mathcal {P}}}_s^\circ }_s\) and \(w\in (L^\infty )^\perp \) such that
Proof
Since \({{\mathcal {U}}}\subset L_{{{\mathcal {P}}}_s}\subset L_{{{\mathcal {P}}}_\tau }\), the first claim follows from Theorem 17. Since \(L^{{{\mathcal {P}}}_\tau ^\circ }\subseteq L^{{{\mathcal {P}}}_s^\circ }\), Theorem 17 implies \({{\mathcal {Y}}}\subseteq L^{{{\mathcal {P}}}_s^\circ }\). On the other hand, since \({{\mathcal {U}}}\subseteq L_{{{\mathcal {P}}}_s}\), the Hölder’s inequality in Lemma 8 implies
so \(L^{{{\mathcal {P}}}_s^\circ }\subseteq {{\mathcal {U}}}'\). Thus, if \({{\mathcal {Y}}}={{\mathcal {U}}}'\), we have \(L^{{{\mathcal {P}}}_s^\circ }\subseteq {{\mathcal {Y}}}\). When \({{\mathcal {U}}}=L_{{{\mathcal {P}}}_s}\) and \({{\mathcal {Y}}}=L^{{{\mathcal {P}}}_s^\circ }\), we are in the setting of Sect. 4. By Lemma 16, \({{\mathcal {P}}}_s\) satisfies (A1) and (A2), so the last claim follows from Theorem 6. \(\square \)
In the setting of Theorem 6, one may wonder what is the strong topology generated by \(L^{{{\mathcal {P}}}^\circ }\) on \(L_{{\mathcal {P}}}\).
Theorem 19
If \(L_{{\mathcal {P}}}\) is barreled and \(p\in {{\mathcal {P}}}\) are \(\sigma (L_{{\mathcal {P}}},L^{{{\mathcal {P}}}^\circ })\)-lsc, then the strong topology generated by \(L^{{{\mathcal {P}}}^\circ }\) on \(L_{{\mathcal {P}}}\) coincides with the \({{\mathcal {P}}}\)-topology.
Proof
If p is \(\sigma (L_{{\mathcal {P}}},L^{{{\mathcal {P}}}^\circ })\)-lsc, Theorem 6 and the bipolar theorem imply that
It follows that the level sets of the functions \(p^\circ \) generate the \(L_{{\mathcal {P}}}\)-topology. Since the level sets are bounded, the \(L_{{\mathcal {P}}}\)-topology is weaker than the strong topology generated by \(L^{{{\mathcal {P}}}^\circ }\). On the other hand, if \(L_{{\mathcal {P}}}\) is barreled, then the elements of \({{\mathcal {P}}}_s\) are \(L_{{\mathcal {P}}}\)-continuous. \(\square \)
6 Applications
This section applies the results of the previous sections to more specific situations. We obtain quick proofs of many well known as well as new results.
6.1 Random variables with finite moments
Given an increasing sequence \(S\subset [1,\infty )\), let
If S contains its supremum \({\bar{p}}:=\sup S\), then \(L^S\) coincides with the classical Lebesgue space \(L^{{\bar{p}}}\). If \({\bar{p}}\notin S\), \(L^S\) is the space of random variables with finite pth moments \(m_p(u):=E[|u|^p]\) for p strictly less than \({\bar{p}}\). When S is unbounded, \(L^S\) is the space of random variables with finite moments. Let \(S'\) be the set of conjugate exponents of S, i.e.
and define
The \(L^p\)-norms with \(p<\infty \) satisfy (A1)–(A4). The following example is thus a direct consequence of Corollary 7.
Theorem 20
Equipped with the collection of seminorms \(\Vert \cdot \Vert _{L^p}\), \(s\in S\), the space \(L^S\) is Fréchet and its dual may be identified with \(L_{S'}\) under the bilinear form \(\langle u,y\rangle :=E[u\cdot y]\).
6.2 Marcinkiewicz and Lorentz spaces
Given a random variable \(u\in L^0\), we will denote the distribution function of |u| by \(n_u(\tau ):=P(|u|>\tau )\) and its quantile function by
In the terminology of Banach function spaces, the quantile function is usually called the “decreasing rearrangement of u; see e.g. [1]. Given a nonnegative concave increasing function \(\phi \) on [0, 1] with \(\phi (0)=0\), the associated Marcinkiewicz space is the set \(M_\phi \) of \(u\in L^0\) with
Recall that a probability space is resonant if it is atomless or completely atomic with all atoms having equal measure.
Theorem 21
Assume that \((\Omega ,{{\mathcal {F}}},P)\) is resonant. Endowed with the norm \(\Vert \cdot \Vert _\phi \), the space \(M_\phi \) is a Banach. If \(\lim _{t\searrow 0}t/\phi (t)>0\), we have \(M_\phi =L^\infty \). Assume now that \(\lim _{t\searrow 0}t/\phi (t)=0\). The topological dual of \(M_\phi \) is
where \(\Lambda _\Phi \) is the Lorentz space
where
The closure \(M^0_\phi \) of \(L^\infty \) in \(M_\phi \) can be expressed as
The topological dual of \(M^0_\phi \) is \(\Lambda _\Phi \) and the topological dual of \(\Lambda _\phi \) is \(M_\phi \).
Proof
We apply Theorem 6 with \({{\mathcal {P}}}=\{p\}\) where \(p(u)=\Vert u\Vert _\phi \). Since
we have \(M_\phi \subset L^1\) and its topology is stronger than the \(L^0\)-topology. By Lemma 30,
is the infimal projection of a sublinear function of s and u and thus, sublinear in u. It is also continuous in \(L^1\). It follows that \(\Vert \cdot \Vert _\phi \) is sublinear, symmetric and lsc in \(L^1\).
By Remark 9, \(M_\phi \) is Banach. Since \(q_u\le \Vert u\Vert _{L^\infty }\), we have
where \(\sup _{t\in (0,1]}\frac{t}{\phi (t)}<\infty \) since \(\phi \) is concave and strictly positive for \(t>0\). Thus, (A1) holds. Property (A2) is clear. Given \(A\in {{\mathcal {F}}}\),
since \(t\mapsto \frac{t}{\phi (t)}\) is increasing by concavity. Thus \({\hat{\phi }}_p(t):=\frac{t}{\phi (t)}\) is the fundamental function of \(M_\phi \). By Remark 4, \(M_\phi =L^\infty \) if \(\lim _{t\searrow 0}t/\phi (t)>0\) while (A3) holds if \(\lim _{t\searrow 0}t/\phi (t)=0\). We have
where the second equality follows from [1, Corollary 2.4.4] and the third from Hardy’s lemma [1, Proposition 2.3.6]. The representation of the topological dual of \(M_\phi \) now follows from Theorem 6.
If \(u\in L^\infty \), \(q_u\) is bounded, so
by assumption. Thus, \(L^\infty \subset M^0_\phi \). Let \(u\in M_\phi \) and \(M^0_\phi \). We have \(q_{u+{\tilde{u}}}(s^1+s^2)\le q_{u}(s^1)+q_{{\tilde{u}}}(s^2)\), so
where the second last inequality follows from concavity of \(\phi \). Thus, \(M^0_\phi \) is closed in \(M_\phi \) so \(M^0_\phi \) contains the closure of \(L^\infty \). To prove the converse, let \(u\in M^0_\phi \) and \(u^\nu =u1_{\{|u|\le \nu \}}\). We have \(q_{u-u^\nu }(t)=0\) for \(t\ge t^\nu :=P(|u|\ge \nu )\) while \(q_{u-u^\nu }(t)=q_u(t)\) for \(t<t^\nu \). Thus,
Since \(u\in M^0_\phi \), this converges to 0 as \(\nu \rightarrow \infty \). Thus, \(M^0_\phi \) is the closure of \(L^\infty \) in \(M_\phi \).
To prove the last claim, we apply Theorem 6 to \(p^\circ \). By Lemma 8, the Lorentz seminorm satisfies (A1) and (A2). If  with \(\Vert y^\nu \Vert _\phi ^*<\infty \), we have
with \(\Vert y^\nu \Vert _\phi ^*<\infty \), we have  , so by monotone convergence,
, so by monotone convergence,  . Thus, the Lorenz norm satisfies (A4) as well. The fact that the topological dual of \(\Lambda _\phi \) is \(M_\phi \) now follows from Theorem 6 and the fact that, by the bipolar theorem, p is the polar of \(p^\circ \). \(\square \)
. Thus, the Lorenz norm satisfies (A4) as well. The fact that the topological dual of \(\Lambda _\phi \) is \(M_\phi \) now follows from Theorem 6 and the fact that, by the bipolar theorem, p is the polar of \(p^\circ \). \(\square \)
Except for the the characterization of \(M_\phi ^*\), the statements of Theorem 21 can be found in Theorem 5.2, Theorem 5.4 and Lemma 5.4 of [20, Chapter II]; see also [13, Section 1] and the proof of [13, Theorem 1.5]. The general results of Sect. 4 simplifies the proofs and provide the additional characterization of \(M_\phi ^*\).
Much like in Theorem 20, one could also characterize topological duals of locally convex (resp. Fréchet) spaces obtained by intersecting Marcinkiewicz spaces associated with a (resp countable) collection of nonnegative concave increasing functions \(\phi \). One could also use the results of Sect. 4 to study the abstract Lorentz spaces recently introduced in [17].
6.3 Modular spaces and Luxemburg norms
This section studies a general class of Banach spaces that arise from a positive symmetric convex function (a convex modular in the terminology of [25]) on \(L^0\) much like Orlicz spaces arise from the Luxemburg norm associated with a given Young functional; see Sect. 6.4 below. Theorem 22 below allows for quick proofs and various extensions of existing results in the theory of Banach function spaces.
Given a set C in a linear space, we will use the notation
Let \(H:L^0\rightarrow \overline{{\mathbb {R}}}_+\) be a \(L^0\)-lsc symmetric convex function such that \(H(0)=0\) and
-
(H1)
\(L^\infty \subset \mathop {\mathrm{pos}}(\mathop {\mathrm{dom}}\nolimits H)\) and \(\{u\in L^0\mid H(u)\le 1\}\) is bounded in probability,
-
(H2)
\(H(u')\le H(u)\) whenever \(|u'_j|\le |u_j|\) for \(j=1,\ldots ,n\).
Consider the space
endowed with the Luxemburg norm
Define \(H^*:{{\mathcal {M}}}\rightarrow \overline{{\mathbb {R}}}\) by
and
The set of purely finitely additive elements of \({{\mathcal {M}}}^{H^*}\) is denoted by \({{\mathcal {M}}}^{H^*}_s\) and the set of densities of countably additive measures of \({{\mathcal {M}}}^{H^*}\) by \( L^{H^*}\). Note that
Theorem 22
Equipped with the norm \(\Vert \cdot \Vert _H\), the space \(L^H\) is Banach, its dual may be identified with
and \(L^{H^*}\) coincides with the Köthe dual of \(L^H\). For any \(m\in {{\mathcal {M}}}^{H^*}\), the dual norm can be expressed as
where the infimum is attained. Moreover,
where
The dual of the closure \(M^H\) of \(L^\infty \) in \(L^H\) can be identified with \(L^{H^*}\oplus {{\mathcal {M}}}^{H^*}_s\). If
-
(H3)
 whenever \((u^\nu )_{\nu =1}^\infty \subset L^\infty \) with
whenever \((u^\nu )_{\nu =1}^\infty \subset L^\infty \) with  almost surely,
almost surely,
then \({{\mathcal {M}}}^{H^*}_s=\{0\}\), \((L^H)^*=L^{H^*}\oplus (L^\infty )^\perp \) and \((M^H)^*=L^{H^*}\). If \(L^\infty \subseteq \mathop {\mathrm{dom}}\nolimits H\) and
-
(H4)
 whenever \((u^\nu )_{\nu =1}^\infty \subset \mathop {\mathrm{dom}}\nolimits H\) with
whenever \((u^\nu )_{\nu =1}^\infty \subset \mathop {\mathrm{dom}}\nolimits H\) with 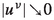 almost surely,
almost surely,
then \(M^H = (\mathop {\mathrm{dom}}\nolimits H)^\infty \) and, in particular, \(L^H=M^H\) if \(\mathop {\mathrm{dom}}\nolimits H\) is a cone.
Proof
We apply Theorem 6 in the case \({{\mathcal {P}}}=\{p\}\), where
By (H1), p is finite on \(L^\infty \). Since p is lsc on \(L^0\), it is lsc on \(L^\infty \). Thus, by [33, Corollary 8B], p is continuous in \(L^\infty \) and thus (A1) holds. Assumption (A2) is clear from (H2).
Let \(u^\nu \rightarrow u\) in \(L^0\) be such that \(p(u^\nu )\le \alpha \). This means that \(H(u^\nu /\alpha )\le 1\), so the \(L^0\)-lower semicontinuity of H implies that of p. Let O be an \(L^0\)-neighborhood of the origin. By the boundedness assumption in (H1), there exists \(\lambda >0\) such that \( \lambda O\supset \{u\in L^0\mid H(u)\le 1\} =\{u\in L^H \mid p(u)\le 1\}\). Thus \(O\cap L^H\) is a neighborhood in \(L^H\), so the topology of \(L^H\) is no weaker than the relative \(L^0\)-topology. By Remark 9, \(L^H\) is Banach. By Lemma 8, \(L^{H^*}\) is the Köthe dual of \(L^H\).
Let \(m\in {{\mathcal {M}}}\). Since the infimum in the definition of the p is attained,
Lagrangian duality (see e.g. [33, Example 1”]) gives
where the infimum is attained. It follows that \(\mathop {\mathrm{dom}}\nolimits p^\circ =\mathop {\mathrm{pos}}\mathop {\mathrm{dom}}\nolimits H^*\). The first claim thus follows from Theorem 6.
Clearly, \(p^\circ (m)=\Vert m\Vert _H^*\) for all \(m\in {{\mathcal {M}}}^{H^*}\) and
On the other hand, we have
where \(g(m)=H^*(m)+1\). Since \(H^*\ge 0\), we have \(g(m)\ge \Vert m\Vert _{H^*}\) when \(\Vert m\Vert _{H^*}\le 1\). When \(\Vert m\Vert _{H^*}>1\), convexity and the fact that \(H^*(0)=0\) give
By definition of \(\Vert m\Vert _{H^*}\), the left side equals 1 so \(\Vert m\Vert _{H^*}\le H^*(m)\le g(m)\). Thus,
The expression for the dual of \(M^H\) follows from Corollary 7. If (H3) holds and  almost surely in \(L^\infty \), then for all \(\beta >0\),
almost surely in \(L^\infty \), then for all \(\beta >0\),

so  . In particular, (A3) holds so, by Corollary 7, \({{\mathcal {M}}}^{H^*}_s=\{0\}\).
. In particular, (A3) holds so, by Corollary 7, \({{\mathcal {M}}}^{H^*}_s=\{0\}\).
To prove the last claim, let \(u\in (\mathop {\mathrm{dom}}\nolimits H)^\infty \), \(u^\nu := u\mathbb {1}_{|u|\le \nu }\) and \(\beta >0\). By (H2), \(u-u^\nu =u1_{\Omega \setminus \{|u|\le \nu \}}\in \beta \mathop {\mathrm{dom}}\nolimits H\) so (H4) implies

Since \(\beta >0\) was arbitrary, we get  so \((\mathop {\mathrm{dom}}\nolimits H)^\infty \subseteq M^H\). To prove the converse, note first that the assumption \(L^\infty \subset \mathop {\mathrm{dom}}\nolimits H\) implies \(L^\infty \subset (\mathop {\mathrm{dom}}\nolimits H)^\infty \). It thus suffices to show that \((\mathop {\mathrm{dom}}\nolimits H)^\infty \) is closed in \(L^H\). If \((u^\nu )\) is in \((\mathop {\mathrm{dom}}\nolimits H)^\infty \) and converges to \(u\in M^H\), we have for any \(\beta >0\),
so \((\mathop {\mathrm{dom}}\nolimits H)^\infty \subseteq M^H\). To prove the converse, note first that the assumption \(L^\infty \subset \mathop {\mathrm{dom}}\nolimits H\) implies \(L^\infty \subset (\mathop {\mathrm{dom}}\nolimits H)^\infty \). It thus suffices to show that \((\mathop {\mathrm{dom}}\nolimits H)^\infty \) is closed in \(L^H\). If \((u^\nu )\) is in \((\mathop {\mathrm{dom}}\nolimits H)^\infty \) and converges to \(u\in M^H\), we have for any \(\beta >0\),
for \(\nu \) large enough, so \(H(u/2\beta )<\infty \) and thus \(u\in (\mathop {\mathrm{dom}}\nolimits H)^\infty \). \(\square \)
6.4 Musielak–Orlicz spaces
Let \(\Phi :{\mathbb {R}}\times \Omega \rightarrow \overline{{\mathbb {R}}}\) be a random Young function in the sense that
is a measurable mapping (see [34, Chapter 14]) and for each \(\omega \in \Omega \) the function \(\Phi (\cdot ,\omega )\) is convex, symmetric, vanishes at the origin and, for P-almost every \(\omega \), \(\mathop {\mathrm{dom}}\nolimits \Phi (\cdot ,\omega )\ne \{0\}\) and \(\Phi (\cdot ,\omega )\) is nonconstant. If \(\Phi \) only takes finite real values, the measurability condition holds if and only if \(\Phi (\xi ,\cdot )\) is measurable for every \(\xi \in {\mathbb {R}}\); see [34, Example 14.29].
The associated Musielak–Orlicz space is the normed space
where
Theorem 22 gives a quick proof of the following characterization of the topological dual of \(L^\Phi \). The characterization involves the conjugate function
By [34, Theorem 14.50], \(\Phi ^*\) is a random Young function.
Theorem 23
Assume that \(\Phi (a,\cdot )\in L^1\) for some constant \(a>0\). The space \(L^\Phi \) is Banach and its dual \((L^\Phi )^*\) can be identified with
where \(L^{\Phi ^*}\) coincides with the Köthe dual of \(L^\Phi \) and
with \(\sigma _\Phi (m) :=\sup _{u\in L^\infty }\{ \int _\Omega udm \mid E\Phi (|u|)<\infty \}\). For any \(y+m^s \in L^{\Phi ^*}\oplus {{\mathcal {M}}}^{\Phi ^*}_s\), the dual norm can be expressed as
where the infimum is attained. Moreover,
where
The dual of the closure \(M^\Phi \) of \(L^\infty \) in \(L^\Phi \) is
If \(\Phi (a,\cdot )\in L^1\) for all \(a>0\), then \({{\mathcal {M}}}^{\Phi ^*}_s=\{0\}\) and
If \(\mathop {\mathrm{dom}}\nolimits E\Phi \) is a cone, then \(L^\Phi =M^\Phi \) and their dual is \(L^{\Phi ^*}\). The set \(\mathop {\mathrm{dom}}\nolimits E\Phi \) is a cone, in particular, if \(\Phi \) satisfies \(\Delta _2\)-condition: there exists \(x_0\in \mathop {\mathrm{dom}}\nolimits E\Phi \) and \(K>0\) such that \(\Phi (2x)\le K\Phi (x)\) for all \(x\ge x_0\).
Proof
We apply Theorem 22 to \(H(u):=E\Phi (|u|)\). The assumption \(\Phi (a)\in L^1\) implies that \(H(u)<\infty \) when \(\Vert u\Vert _{L^\infty }\le a\) so \(L^\infty \subseteq \mathop {\mathrm{pos}}(\mathop {\mathrm{dom}}\nolimits H)\). Defining
we have \(E\Phi ^*(\eta )\le 1\). Since \(\sup _a\Phi (a)>0\) almost surely, \(\eta >0\) almost surely. By Fenchel’s inequality,
so
Thus, the left is side is bounded in probability, since the right side is so. Thus, (H1) holds.
Condition (H2) holds since \(\Phi \) is increasing. By [32, Theorem 1] and [31, Theorem 15.3],
If \(\Phi (a)\in L^1\) for all \(a>0\), then \(L^\infty \subset \mathop {\mathrm{dom}}\nolimits H\) and (H3) and (H4) hold by monotone convergence theorem. If \(\mathop {\mathrm{dom}}\nolimits E\Phi \) is a cone, then \(\Phi (a,\cdot )\in L^1\) for all \(a>0\). All the claims except for the last one thus follow from Theorem 22. Assume the \(\Delta _2\)-condition and let \(x\in \mathop {\mathrm{dom}}\nolimits E\Phi \). We have \(E\Phi (2x)\le E\Phi (2(x\vee x_0))\le KE\Phi (x\vee x_0)=KE[\Phi (x)\vee \Phi (x_0)]<\infty \) so \(2x\in \mathop {\mathrm{dom}}\nolimits E\Phi \). Since \(\mathop {\mathrm{dom}}\nolimits E\Phi \) is a convex set, this implies that it is a cone. \(\square \)
If \(\Phi \) is nonrandom, we recover the classical Orlicz spaces and the last part of Theorem 23 implies that, if \(\Phi \) is finite, then \({{\mathcal {M}}}^{\Phi ^*}_s=\{0\}\), while otherwise, \(L^\Phi =L^\infty \) so \((L^\infty )^\perp =\{0\}\). Extensions to Banach space-valued functions have been studied in [12]. In [25], the assumption \(\Phi (a,\cdot )\in L^1\) for all \(a>0\) is called "local integrability". Thus we recover [25, Theorem 13.17] for probability spaces without assuming local integrability of \(\Phi ^*\); see also [24, Theorem 2.4.4]. Our characterization of the dual without local integrability seems new.
Proposition 24
Assume that the measure P is atomless. In the setting of Theorem 23, \({{\mathcal {M}}}^{\Phi ^*}_s=\{0\}\) if and only if \(\Phi (a,\cdot )\in L^1\) for all \(a>0\).
Proof
By Theorem 23, \(\Phi (a,\cdot )\in L^1\) for all \(a>0\) implies \({{\mathcal {M}}}^{\Phi ^*}_s=\{0\}\), where \({{\mathcal {M}}}^{\Phi ^*}_s=\mathop {\mathrm{dom}}\nolimits \sigma _\Phi \cap {{\mathcal {M}}}_s\ne \{0\}\). Assume now that \(\Phi (a,\cdot )\notin L^1\) for some \(a>0\). It suffices to show that \(\mathop {\mathrm{dom}}\nolimits \sigma _\Phi \cap {{\mathcal {M}}}_s\ne \{0\}\). There exists \(a'>a\) and \(\epsilon >0\) such that \(E\Phi (u)=+\infty \) for every \(u\in {\mathbb {B}}_\epsilon (a')\), so the \(L^\infty \)-strong closure of \(\mathop {\mathrm{dom}}\nolimits E\Phi \) is strictly smaller than \(L^\infty \). Since the strong closure is the domain of the \(\sigma (L^\infty ,{{\mathcal {M}}})\)-conjugate of \(\sigma _\Phi \), \(\mathop {\mathrm{dom}}\nolimits \sigma _\Phi \ne \{0\}\).
By Lemma 31, the \(\sigma (L^\infty ,L^1)\)-closure of \(\mathop {\mathrm{dom}}\nolimits E\Phi \) equals
where
If \(\rho =\infty \) almost surely, then \(\sigma (L^\infty ,L^1)\)-closure of \(\mathop {\mathrm{dom}}\nolimits E\Phi \) is the whole \(L^\infty \), so \(\sigma _{\Phi }(y)=+\infty \) for every nonzero \(y\in L^1\), and thus \(\mathop {\mathrm{dom}}\nolimits \sigma _\Phi \cap {{\mathcal {M}}}_s\ne \{0\}\).
If \(P(\rho < \infty )>0\), there exists a constant \({\bar{a}}>0\) such that \(P(A)>0\), where \(A:=\{\rho \le {\bar{a}}\}\). Since P is atomless, there exists \(A^\nu \subset A\) such that \(P(A^\nu )>0\) and \(P(A^\nu )\searrow 0\). There exists a nonzero \(m^s\in {{\mathcal {M}}}_s\) with \(m^s(\Omega \setminus A^\nu )=0\) for every \(\nu \) (e.g., take \(m^s\) as an accumulation point of the \(\sigma ({{\mathcal {M}}},L^\infty )\)-precompact net \((y^\nu )_{\nu =1}^\infty \subset L^1\), where \(y^\nu :=1_{A^\nu }/P(A^\nu )\)). Every \(u\in L^\infty \cap \mathop {\mathrm{dom}}\nolimits E\Phi \) satisfies \(|u|\le \rho \le {\bar{a}}\) almost surely on \(A^\nu \), so every such u satisfies \(\langle u,m^s\rangle \le {\bar{a}}|m^s|^*\). Thus \(\sigma _{\Phi }(m^s)<\infty \) and \(\mathop {\mathrm{dom}}\nolimits \sigma _\Phi \cap {{\mathcal {M}}}_s\ne \{0\}\). \(\square \)
General Musielak–Orlicz spaces are isomorphic to Musielak–Orlicz spaces whose Young function satisfies the the assumption in Theorem 23.
Remark 25
Given an arbitrary random Young function \({\tilde{\Phi }}\),
is measurable and takes values in \((0,\infty )\) almost surely. The space \(L^{{\tilde{\Phi }}}\) is isomorphic to \(L^{\Phi }\), where
satisfies the first assumption of Theorem 23. The dual of \(L^{{\tilde{\Phi }}}\) is thus isomorphic to that of \(L^\Phi \) characterized in Theorem 23. Indeed, the isomorphism is \((A {\tilde{u}})(\omega )={\tilde{u}}(\omega )/\rho (\omega )\) so the elements of \((L^{{\tilde{\Phi }}})^*\) can be expressed as
where \(u^*\in (L^\Phi )^*\).
6.5 Generalized Musielak–Orlicz spaces
Let r be an lsc norm on \(L^0\) satisfying (A1) and (A2) such that the r-topology is stronger than that of \(L^0\). By Remark 9, the space \(L_r\) is Banach. Let \(\Phi \) be as in Sect. 6.4 and define
where
Note that, if r is the \(L^1\)-norm, then \(L^{\Phi ,r}\) is the Musielak–Orlicz space studied in Sect. 6.4. If \(\Phi \) is nonrandom and r is the Lorentz-norm
associated with a concave function \(\phi \) (see Sect. 6.2), we get
so \(L^{\Phi ,r}\) becomes the Orlicz–Lorentz space; see e.g. [10] and its references.
Consider the positively homogeneous function
on \( L_r^*\times {{\mathcal {M}}}\) and let
Denote the absolutely continuous and singular elements of \({{\mathcal {M}}}^\Sigma \) by \(L^\Sigma \) and \({{\mathcal {M}}}^\Sigma _s\), respectively. Let
The second expression above comes from [31, Theorem 13.3]. It involves the recession function of the conjugate \(\Phi ^*\) defined as

Theorem 26
Assume that \(\Phi (|u|)\in L_r\) for all \(u\in L^\infty \) and that \(\{x\in L^0\mid r(x)\le 1\}\) is bounded in \(L^0\). Endowed with the norm \(\Vert u\Vert _{\Phi ,r}\), the space \(L^{\Phi ,r}\) is a Banach, its dual may be identified with
and \(L^\Sigma \) is the Köthe dual of \(L^{\Phi ,r}\). For any \(m\in {{\mathcal {M}}}^\Sigma \), the dual norm can be expressed as
where the infimum is attained. Moreover,
where
The dual of the closure \(M^{\Phi ,r}\) of \(L^\infty \) in \(L^{\Phi ,r}\) can be identified with \(L^\Sigma \oplus {{\mathcal {M}}}^\Sigma _s\).
If (a) r satisfies (A4) or (b) r satisfies (A3) and \(\Phi (u)\in L^\infty \) for every \(u\in L^\infty \), then \({{\mathcal {M}}}^\Sigma _s=\{0\}\),
and the dual of \(M^{\Phi ,r}\) is \(L^\Sigma \). If r satisfies (A4), then
and, \(M^{\Phi ,r}=L^{\Phi ,r}\) if there exists \(x_0\in L^0\) and \(K>0\) such that \(r(\Phi (x_0))<\infty \) and \(\Phi (2x)\le K\Phi (x)\) for all \(x\ge x_0\).
Proof
This fits Theorem 22 with
Given an \(L^0\)-converging sequence \(u^\nu \rightarrow u\), the pointwise lower semicontinuity of \(\Phi \) gives \(\liminf \Phi (u^\nu )\ge \Phi (u)\) so the lower semicontinuity and (A2) of r give
so H is \(L^0\)-lsc. As in the proof of Theorem 23, there exists an \(\eta \in L^0\) strictly positive such that \(\Phi (|u|)\ge |u|\eta -\Phi ^*(\eta )\) almost surely. We have
where the right side is \(L^0\)-bounded since \(\{\xi \in L^0\mid r(\xi )\le 1\}\) is \(L^0\)-bounded by assumption. Since \(\Phi (u)\in L_r\) for all \(u\in L^\infty \), we have \(L^\infty \subset \mathop {\mathrm{dom}}\nolimits H\). Thus, H satisfies (H1)–(H2).
We compute the conjugate H by employing conjugate duality; see [33]. The function
is convex and increasing in the partial order of \(L^0\) so the function \(F(x,u):=r_+(\Phi (|u|)+x)\) is convex on \( L_r\times L^\infty \). Clearly, \(F(0,u)=H(u)\). The conjugate \(F^*\) on \( L_r^*\times {{\mathcal {M}}}\) has the expression
where, by positive homogeneity of r,
where \(r^\circ (x^*):=\sup \{\langle x,x^*\rangle \mid r(x)\le 1\}\). For any \(u\in L^\infty \), the function \(F(\cdot ,u)\) is continuous on \( L_r\), so [33, Theorem 17] gives
where the infimum is attained. Thus, by Theorem 22 and positive homogeneity of \(\Sigma \),
The dual Luxemburg norm can be expressed as
Since \(\Sigma \) is positively homogeneous, we have
Thus, the claims concerning the dual space and its norm follow from Theorem 22.
By the first assumption, \(L^\infty \subset \mathop {\mathrm{dom}}\nolimits H\) so both (a) and (b) imply (H3) and then, \({{\mathcal {M}}}^\Sigma _s=\{0\}\), by Theorem 22. Let \(x^*\in L_r^*\) and \(y\in L^\Sigma \). By Theorem 6, (b) implies the existence \(v\in L^1\) and \(x^*_s\in (L^\infty )^\perp \) such that \(x^*=v+x^*_s\). Under (a), \(x^*_s=0\). We have \(\Sigma (x^*,y)=+\infty \) unless \(x^*\ge 0\). Otherwise, the supremum in the definition of \(\Sigma \) is attained with \(x=\Phi (|u|)\) which belongs to \(L^\infty \) under (b). We, thus have \(\Sigma (x^*,y)=\Sigma (v,y)\) for all \(x^*\ge 0\). By [34, Theorem 14.60],
If r satisfies (A4) then both (H3) and (H4) hold, so Theorem 22 gives
The set on the right can be written as \(\{u\in L^0\mid r(\Phi (|u|/\beta )<\infty \ \forall \beta >0\}\). Let \(x\in L^0_+\) be such that \(r(\Phi (x))<\infty \). Under the last condition,
so
and thus, \(r(\Phi (2x))<\infty \). Since \(\{u\in L^0\mid r(\Phi (|u|))<\infty \}\) is a convex set, it has to be a cone so \(L^{r,\Phi }=M^{r,\Phi }\). \(\square \)
The proof of Theorem 26 gives also the expression
where
and the infimum is attained. Under condition (b) in the theorem, we have \({{\mathcal {M}}}^\Sigma _s=\{0\}\) and
where
If r is the Lorentz-norm associated with a concave increasing function \(\phi \), then, by Theorem 21, \(r^\circ \) is the Marcinkiewicz-norm so
The above characterization of the Köthe dual thus extends that in [16, Corollary 4.12] and [15, Theorem 2.2] to random \(\Phi \) in the case of a finite underlying measure. The singular components of the dual have been analyzed in the recent article [14].
6.6 Risk measures
This section studies scalar-valued random variables so \(n=1\). A function \(\rho :L^0\rightarrow \overline{{\mathbb {R}}}\) is a convex risk measure if it is convex, nondecreasing, \(\rho (0)=0\) and \(\rho (\xi +r)=\rho (\xi )+r\) for all \(\xi \in L^0\) and \(r\in {\mathbb {R}}\); see e.g. [7]. As in [21], we consider the associated normed space
where
When \(\rho \) is positively homogeneous, we simply get \(\Vert u\Vert _\rho =\rho (|u|)\) as e.g. in [27].
Theorem 22 gives a quick proof of the following.
Theorem 27
Assume that \(\rho \) is \(L^0\)-lsc and that \(\{u\in L^0\mid \rho (|u|)\le 1\}\) is bounded in \(L^0\). The space \(L^\rho \) is a Banach and its dual can be identified with
where
with \(\alpha :{{\mathcal {M}}}\rightarrow \overline{{\mathbb {R}}}\) defined by
For any \(m\in {{\mathcal {M}}}^\alpha \), the dual norm can be expressed as
where the infimum is attained. Moreover,
where
If \(\rho \) has the Lebesgue property on \(L^\infty \):  for any decreasing sequence \((\xi ^\nu )\subset L^\infty \) with
for any decreasing sequence \((\xi ^\nu )\subset L^\infty \) with  almost surely, then the dual of the closure \(M^\rho \) of \(L^\infty \) in \(L^\rho \) can be identified with
almost surely, then the dual of the closure \(M^\rho \) of \(L^\infty \) in \(L^\rho \) can be identified with
and \((L^\rho )^*=L^\alpha \oplus (L^\infty )^\perp \). If \(\rho \) has the Lebesgue property on \(\mathop {\mathrm{dom}}\nolimits \rho \):  for any decreasing sequence \((\xi ^\nu )\subset \mathop {\mathrm{dom}}\nolimits \rho \) with
for any decreasing sequence \((\xi ^\nu )\subset \mathop {\mathrm{dom}}\nolimits \rho \) with  almost surely, then
almost surely, then
and, in particular, \(L^\rho =M^\rho \) if \(\mathop {\mathrm{dom}}\nolimits \rho \) is a cone.
Proof
We apply Theorem 22 to the function \(H(u):=\rho (|u|)\). By assumption, (H1) and (H2) hold. Indeed, by monotonicity and translation invariance, \(\rho (|u|)\le \rho (\Vert u\Vert _{L^\infty })=\Vert u\Vert _{L^\infty }\), so \(L^\infty \subset \mathop {\mathrm{dom}}\nolimits H\). Conditions (H3) and (H4) in Theorem 22 translate directly to 1 and 2. Thus the claims follow from Theorem 22, since here
where the second last equality follows from [37, Theorem 2.3] and the fact that \(\nu (A):=\int _A \xi dm\) is a finitely additive measure with \(|\nu |(A)= \int _A\xi d|m|\). \(\square \)
The fact that \((L^\rho )^*=L^\alpha \oplus (L^\infty )^\perp \) under the Lebesgue property sharpens [21, Theorem 4.12] which states that each \(u^*\in (L^\rho )^*\) can be expressed uniquely as \(u^*=y+u^s\) for some \(y\in L^1\) and \(u^s\in (L^\infty )^\perp \). The other statements seem new.
References
Bennett, C., Sharpley, R.: Interpolation of Operators. Pure and Applied Mathematics, vol. 129. Academic Press Inc, Boston, MA (1988)
Bhaskara Rao, K.P.S., Bhaskara Rao, M.: Theory of charges, volume 109 of Pure and Applied Mathematics. Academic Press, Inc. [Harcourt Brace Jovanovich, Publishers], New York,: A study of finitely additive measures. With a foreword by D. M, Stone (1983)
Bichteler, K.: Integration—A Functional Approach. Modern Birkhäuser Classics. Birkhäuser Verlag, Basel (2010) (reprint of the 1998 edition)
del Campo, R., Ricker, W.J.: Two Fatou completion of a Fréchet function space and applications. J. Aust. Math. Soc. 88(1), 49–60 (2010)
Delbaen, F., Owari, K.: Convex functions on dual Orlicz spaces. Positivity 23(5), 1051–1064 (2019)
Dunford, N., Schwartz, J.T.: Linear operators. Part I. Wiley Classics Library. Wiley, New York (1988). (general theory, with the assistance of William G. Bade and R. G. Bartle, Reprint of the 1958 original, a Wiley-Interscience Publication)
Föllmer, H., Schied, A.: Stochastic Finance, extended edn. Walter de Gruyter & Co., Berlin (2011) (an introduction in discrete time)
Harjulehto, P., Hästö, P.: Orlicz spaces and generalized Orlicz spaces. Lecture Notes in Mathematics, vol. 2236. Springer, Cham (2019)
Hewitt, E., Stromberg, K.: Real and abstract analysis. Springer, New York (1975) (a modern treatment of the theory of functions of a real variable, third printing, Graduate Texts in Mathematics, no. 25)
Hudzik, H., Kamińska, A., Mastyło, M.: On the dual of Orlicz–Lorentz space. Proc. Am. Math. Soc. 130(6), 1645–1654 (2002)
Kalmes, T., Pichler, A.: On Banach spaces of vector-valued random variables and their duals motivated by risk measures. Banach J. Math. Anal. 12(4), 773–807 (2018)
Kamińska, A.: Some convexity properties of Musielak–Orlicz spaces of Bochner type. In: Proceedings of the 13th Winter School on Abstract Analysis (Srní, 1985), number 10, pp. 63–73 (1986)
Kamińska, A., Lee, H.J.: \(M\)-ideal properties in Marcinkiewicz spaces. Comment. Math. (Prace Mat.), (Tomus specialis in Honorem Juliani Musielak):123–144 (2004)
Kamińska, A., Lee, H.J., Tag, H.-J.: \(M\)-ideal properties in Orlicz–Lorentz spaces. Houston J. Math. 45(1), 213–232 (2019)
Kamińska, A., Leśnik, K., Raynaud, Y.: Dual spaces to Orlicz–Lorentz spaces. Stud. Math. 222(3), 229–261 (2014)
Kamińska, A., Raynaud, Y.: New formulas for decreasing rearrangements and a class of Orlicz–Lorentz spaces. Rev. Mat. Complut. 27(2), 587–621 (2014)
Kamińska, A., Raynaud, Y.: Abstract Lorentz spaces and Köthe duality. Indag. Math. (N.S.) 30(4), 553–595 (2019)
Kardaras, C.: Uniform integrability and local convexity in \({\mathbb{L}}^0\). J. Funct. Anal. 266(4), 1913–1927 (2014)
Kozek, A.: Convex integral functionals on Orlicz spaces. Comment. Math. Prace Mat. 21(1), 109–135 (1980)
Kreĭn, S.G., Petunīn, Yu. V̄., Semënov, E.M.: Interpolation of linear operators, volume 54 of Translations of Mathematical Monographs. American Mathematical Society, Providence, R.I., (1982) (translated from the Russian by J. Szucs)
Liebrich, F.-B., Svindland, G.: Model spaces for risk measures. Insur. Math. Econom. 77, 150–165 (2017)
Luxemburg, W.A.J.: Banach function spaces. Thesis, Technische Hogeschool te Delft (1955)
Luxemburg, W.A.J.: Integration with respect to finitely additive measures. In: Positive Operators, Riesz Spaces, and Economics, pp. 109–150. Springer, Berlin (1991)
Méndez, O.: Analysis on Function Spaces of Musielak–Orlicz type, Monographs and Research Notes in Mathematics. CRC Press, Boca Raton, FL (2019)
Musielak, J.: Orlicz Spaces and Modular Spaces. Lecture Notes in Mathematics, vol. 1034. Springer, Berlin (1983)
Pennanen, T., Perkkiö, A.-P.: Stochastic programs without duality gaps. Math. Program. 136(1), 91–110 (2012)
Pichler, A.: The natural banach space for version independent risk measures. Insur. Math. Econ. 53(2), 405–415 (2013)
Rao, M.M., Ren, Z.D.: Theory of Orlicz Spaces. Monographs and Textbooks in Pure and Applied Mathematics, vol. 146. Marcel Dekker Inc, New York (1991)
Rockafellar, R.T.: Level sets and continuity of conjugate convex functions. Trans. Am. Math. Soc. 123, 46–63 (1966)
Rockafellar, R.T.: Integrals which are convex functionals. Pac. J. Math. 24, 525–539 (1968)
Rockafellar, R.T.: Convex Analysis. Princeton Mathematical Series, No. 28. Princeton University Press, Princeton, NJ (1970)
Rockafellar, R.T.: Integrals which are convex functionals. II. Pac. J. Math. 39, 439–469 (1971)
Rockafellar, R.T.: Conjugate Duality and Optimization. Society for Industrial and Applied Mathematics, Philadelphia (1974)
Rockafellar, R.T., Wets, R.J.-B.: Variational analysis. Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], vol. 317. Springer, Berlin (1998)
Sato, R.: On the range of a closed operator in an \(L_1\)-space of vector-valued functions. Comment. Math. Univ. Carolin. 46(2), 349–367 (2005)
Valadier, M.: Convex integrands on Souslin locally convex spaces. Pac. J. Math. 59(1), 267–276 (1975)
Yosida, K., Hewitt, E.: Finitely additive measures. Trans. Am. Math. Soc. 72, 46–66 (1952)
Zaanen, A.C.: Integration. North-Holland Publishing Co., Amsterdam; Interscience Publishers Wiley, New York (1967) (completely revised edition of an introduction to the theory of integration)
Zaanen, A.C.: Riesz spaces. II, volume 30 of North-Holland Mathematical Library. North-Holland Publishing Co., Amsterdam (1983)
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
The first part of this appendix studies integration of measurable not-necessarily bounded functions with respect to a real-valued finitely additive measure m. Define \(r_m:L^0_+\rightarrow \overline{{\mathbb {R}}}\) by
Lemma 28
Let m be a real-valued finitely additive measure.
-
1.
For any \(\eta \in L^\infty _+\),
$$\begin{aligned} r_m(\eta ) = \sup _{u'\in L^\infty } \left\{ \int _\Omega \eta (u' dm) \;\bigg |\;|u'|\le 1\right\} \le ||\eta ||_{L^\infty }||m||_{TV}. \end{aligned}$$In particular, \(r_m\) is \(L^\infty \)-norm continuous and sublinear relative to \(L^\infty _+\).
-
2.
For every \(\eta \in L^0_+\),
$$\begin{aligned} r_m(\eta )=\lim _{\nu \nearrow \infty } r_m(\eta \wedge \nu ) \end{aligned}$$ -
3.
\(r_m\) is subadditive in the sense that
$$\begin{aligned} r_m(\eta ^1+\eta ^2) \le r_m(\eta ^1)+r_m(\eta ^2)\quad \forall \eta ^1,\eta ^2\in \mathop {\mathrm{dom}}\nolimits r_m. \end{aligned}$$
Proof
The expression in 1 follows from the change of variables \({\tilde{u}}= \eta u'\). As to 2, the inequality \(r_m(\eta )\ge \lim _\nu r_m(\eta \wedge \nu )\) is clear. To prove the opposite inequality, let \(\alpha \in {\mathbb {R}}\) with \(r_m(\eta )>\alpha \). There exists \(u'\in L^\infty \) with \(|u'|\le \eta \) and \(r_m(|u'|)>\alpha \). Then \(|u'|\wedge \nu \rightarrow |u'|\) in \(L^\infty \)-norm, so monotonicity and 1 give
This proves 2. Given \(\eta ^1,\eta ^2\in \mathop {\mathrm{dom}}\nolimits p\) and \(\eta >0\), we have \((\eta ^1+\eta ^2)\wedge \nu \le \eta ^1\wedge \nu +\eta ^2\wedge \nu \). Indeed, a concave function vanishing at the origin is subadditive on the positive reals. Thus, by 2 and 1,
which completes the proof. \(\square \)
Define \(\rho _m:L^0\rightarrow \overline{{\mathbb {R}}}\) by
Theorem 29
For any real-valued finitely additive measure m,
-
1.
\(\rho _m\) is symmetric and sublinear, and \(\rho _m(u')\le \rho _m(u)\) whenever \(|u'|\le |u|\),
-
2.
for any \(u\in \mathop {\mathrm{dom}}\nolimits \rho _m\) and \(\epsilon >0\), there exists \(u'\in L^\infty \) with \(\rho _m(u-u')<\epsilon \),
-
3.
\(\int _\Omega u dm\) has a unique \(\rho _m\)-continuous linear extension from \(L^\infty \) to \(\mathop {\mathrm{dom}}\nolimits \rho _m\),
-
4.
if m is purely finite additive, there exists a decreasing \((A^\nu )_{\nu =1}^\infty \subset {{\mathcal {F}}}\) with \(P(A^\nu )\searrow 0\) and \(\int _\Omega u1_{\Omega \backslash A^\nu } dm =0\) for all \(u\in \mathop {\mathrm{dom}}\nolimits \rho _m\).
Proof
Properties in 1 are clear. To prove 2, assume first that m is nonnegative. Given \(u^i\in \mathop {\mathrm{dom}}\nolimits \rho _m\cap L^0_+\) and \(\epsilon >0\), let \({\tilde{u}}^i \in L^\infty \) be such that \(0\le {\tilde{u}}^i\le u^i\) and \(\rho _j(u^i)\le \langle {\tilde{u}}^i,m\rangle +\epsilon \). Then \({\tilde{u}}^1+{\tilde{u}}^2\le u^1+u^2\) and
Since \(\epsilon >0\) was arbitrary, \(\rho _m\) is superlinear on \(\mathop {\mathrm{dom}}\nolimits \rho _m\cap L^0_+\). Given \(u\in \mathop {\mathrm{dom}}\nolimits \rho _m\) and \(\epsilon >0\), Lemma 28 gives \(\rho _m(u^+)\le \rho _m(u^+\wedge \nu )+\epsilon \) for \(\nu \) large enough. By superlinearity,
Similarly, \(\rho _m(u^-- u^-\wedge \nu )\le \epsilon \), so \(\rho _m(u-\pi _{\nu {\mathbb {B}}} u)\le 2\epsilon \) by sublinearity of \(\rho _m\). By [37, Theorem 1.12], general \(m\in {{\mathcal {M}}}\) can be written as \(m=m^+-m^-\) for nonnegative \(m^+,m^-\in {{\mathcal {M}}}\), so
for \(\nu \) large enough.
We have \(\int _\Omega u dm\le \rho _m(u)\) on \(L^\infty \), so, by Hahn-Banach, there exists a \(\rho _m\)-continuous linear extension of m to \(\mathop {\mathrm{dom}}\nolimits \rho _m\). Since \(L^\infty \) is dense in \(\mathop {\mathrm{dom}}\nolimits \rho _m\), the extension is unique. If m is purely finitely additive, there exists \((A^\nu )_{\nu =1}^\infty \subset {{\mathcal {F}}}\) with \(P(A^\nu )\searrow 0\) and \(\int _\Omega u1_{\Omega \backslash A^\nu } dm =0\) for all \(u\in L^\infty \). Note that \(r_m\) inherits this property so that \(\rho _m\) and the integral does as well. \(\square \)
The following was used in the proof of Theorem 21. Its proof was given as an exercise on page 89 of [1].
Lemma 30
We have
Proof
By Theorems 23.5 and 24.2 of [31], the functions
and
are concave and conjugate to each other. By Fubini,
so
by the biconjugate theorem (see e.g. [31, Theorem 12.2]). \(\square \)
The following lemma was used in the proof of Proposition 24. Let \(\Phi :{\mathbb {R}}\times \Omega \rightarrow \overline{{\mathbb {R}}}\) be a convex normal integrand in the sense that
is a convex-valued measurable mapping (see [34, Chapter 14]). The associated integral functional \(E\Phi :L^0\rightarrow \overline{{\mathbb {R}}}\) is defined by
By [34, Theorem 14.50], \(\Phi ^*(y,\omega )=\sup _u\{u\cdot y-\Phi (u,\omega )\}\) is a normal integrand. The integral functional \(E\Phi ^*:L^0\rightarrow \overline{{\mathbb {R}}}\) is defined similarly.
Lemma 31
Assume that \({{\mathcal {U}}}\) and \({{\mathcal {Y}}}\) are decomposable spaces in separating duality under the bilinear form
If \(E\Phi :{{\mathcal {U}}}\rightarrow \overline{{\mathbb {R}}}\) and \(E\Phi ^*:{{\mathcal {Y}}}\rightarrow \overline{{\mathbb {R}}}\) are finite somewhere, then the \(\sigma ({{\mathcal {U}}},{{\mathcal {Y}}})\)-closure of \(\{u\in {{\mathcal {U}}}\mid u\in \mathop {\mathrm{dom}}\nolimits E\Phi \}\) is \(\{u\in {{\mathcal {U}}}\mid u\in \mathop {\mathrm{cl}}\nolimits \mathop {\mathrm{dom}}\nolimits \Phi \text { a.s.}\}\).
Proof
By [30, Theorem 2], \((E\Phi )^*(y)=E\Phi ^*(y)\). Thus, by [29, Corollary 3D], \(\sigma _{\mathop {\mathrm{cl}}\nolimits \mathop {\mathrm{dom}}\nolimits E\Phi }= (E\Phi ^*)^\infty \). By monotone convergence theorem, \((E\Phi ^*)^\infty =E(\Phi ^*)^\infty \), where, by [29, Corollary 3D] again, \((\Phi ^*)^\infty =\sigma _{\mathop {\mathrm{cl}}\nolimits \mathop {\mathrm{dom}}\nolimits \Phi }\). By [30, Theorem 2] again, \((E\sigma _{\mathop {\mathrm{cl}}\nolimits \mathop {\mathrm{dom}}\nolimits \Phi })^*=E\delta _{\mathop {\mathrm{cl}}\nolimits \mathop {\mathrm{dom}}\nolimits \Phi }\), so the claim follows from the biconjugate theorem. \(\square \)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Pennanen, T., Perkkiö, AP. Topological duals of locally convex function spaces. Positivity 26, 2 (2022). https://doi.org/10.1007/s11117-022-00867-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11117-022-00867-4




 for all
for all  .
. for all
for all  .
. for all
for all  ,
, for all
for all  ,
, whenever
whenever  almost surely,
almost surely, whenever
whenever 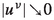 almost surely,
almost surely,