1 Introduction

Non-linear partial differential equations have extensive applications to deal with many physical problems. It is used to model many complicated dynamical systems. Mathematical modeling has a significant role in understanding the dynamics of such models and these are used in various fields of study such as engineering, science, and social sciences. Different models in neuroscience express the pulse behavior of neurons. The Fitz-Hugh Nagumo (FHN) model is one of the most important models in neuroscience and it was given by Huxle and Hodgkin in Wiese and Koppenhofer (1983). The FHN model has been studied many times in literature and various new results of the FHN model are presented in recent papers (Postnikov and Titkova 2016; Saha and Feudel 2017; Schmidt et al. 2017; Zemskov et al. 2017). There are different applications of the FHN equation such as flame propagation, branching Brownian motion process, autocatalytic chemical reaction, nuclear reactor theory, mobility in neurons, and population growth in the open environment as well as in liquid environment (Abbasbandy 2008; Abdusalam 2004; Zhang et al. 2023; Wang et al. 2022). The population growth can be described by the FHN equation in a wetter environment under the sea bed. So, it is directly connected with the ocean and engineering as well as where in the sea.

Most of the physical phenomena naturally carry the random phenomena in them, the continuous phenomena rarely exist. So Brownian motion or other processes play a fundamental role in the dynamics of the population which is governed by this model. For example certain stages you have sudden increases or decreases in the population growth. This type of sudden increase or decrease can not be expressed in the classical environment of the PDEs because in such a situation we have a certain random process, where derivatives of the function fail to exist and you have a jump situation, unbounded situation. In that situation, it is always better to consider a regular mathematical model under the influence of the Brownian motion. Of course, population growth can increase suddenly, can decrease suddenly or sometimes you have a very smooth phenomenon of growth for the decay of the population. So, all of these situations can be dealt with using this model. Since the Borel function is also multiplied with time noise. It is used to control noise phenomena in the solution.

In the last decade, the analytical solutions of stochastic PDEs have been an active area of research for scientists. Al-Askar et al. worked on the analytical solutions of the stochastic breaking soliton equation (SBSE) perturbed by the Wiener process. They obtained the various solutions, namely trigonometric, hyperbolic, and polynomial functions by using the tanh-coth method (Al-Askar et al. 2022). Abdel-Aty finds the soliton solutions of the Wick-type stochastic Schamel KdV equation. He used the modified Khater method to find the solutions (Abdel-Aty 2020). Pan et al. used the exp-function method to find the analytical solution stochastic Gardner equation(Pan et al. 2011). Yasin et al. obtained solitary wave solutions by using the Riccati equation mapping method for the nonlinear stochastic advection–diffusion equation under the influence of the time noise(Iqbal et al. 2023). Mohammed et al. worked on the solution of the stochastic fractional-space Kuramoto-Sivashinsky equation with the help of the Riccati equation method (Mohammed et al. 2022). Some more work on the solutions of PDEs (Akinyemi et al. 2022a, b).

The authors used the extended modified rational expansion method to gain the solitary wave solutions of Zakharov–Kuznetsov modified equal width equation (Iqbal et al. 2023). They gained the analytical solutions of the Kudryashov–Sinelshchikov equation with the modified mathematical method (Seadawy et al. 2019). The authors obtained a solution of the damped modified Korteweg–de Vries equation with reductive perturbation technique (Seadawy et al. 2020). The authors obtained the solitary wave solution of generalized Zakharov–Kuznetsov–Benjamin–Bona–Mahony and simplified modified form of Camassa–Holm equations with modified extended auxiliary equation mapping method (Lu et al. 2018). The authors used the analytical technique to obtain the solution of the nonlinear damped Korteweg–de Vries equation (Seadawy and Iqbal 2021). The authors considered the nonlinear evolution equation that describes the wave propagation in nonlinear low-pass electrical transmission lines by implementing the modification of mathematical method (Seadawy et al. 2020). The authors gained multiple optical soliton solutions for wave propagation in nonlinear low-pass electrical transmission lines (Iqbal et al. 2024). The authors gained the solution for the generalized breaking soliton system (Iqbal et al. 2022). The authors gained the multiple solitary wave solutions for the nonlinear Jaulent–Miodek hierarchy equation (Iqbal et al. 2024). The authors considered the coupled Drinfeld–Sokolov–Wilson equation and obtained a solution with the extension of the modified rational expansion approach (Iqbal et al. 2023). The solution of the nonlinear Nizhnik–Novikov–Vesselov dynamical equation was gained by the extended modified rational expansion method (Iqbal et al. 2020). The solution of coupled Whitham–Broer–Kaup, Broer–Kaup–Kupershmit, and Drinfel’d–Sokolow–Wilson equations was obtained (Lu et al. 2018). The Auxiliary equation mapping and direct algebraic method were used to investigate the families of solitary wave solutions of one-dimensional nonlinear longitudinal wave equation (Iqbal et al. 2019).

In recent years, the solitary wave solutions of nonlinear PDEs have their importance in the research area. Many techniques are used to get the soliton-solutions such as \(G'/G\)-expansion (Zhang et al. 2008; Younis and Rizvi 2015; Younis et al. 2021), new MEDA (Seadawy et al. 2021; Iqbal et al. 2023), Riccati equation mapping method (Iqbal et al. 2023; Younis et al. 2022) etc. In this research work, we use the \(\phi ^6\) -model expansion method (Zayed and Al-Nowehy 2018; Younis et al. 2022). The advantages of the under considered method is that it will provided us the jaccobi elliptic function solutions (JEFs). There are two types of the solutions are obtained by JEFs such as solitons and solitary wave solutions. There are different types of soliton solutions are obtained in the form of dark, bright, singular, combo and exact solitary wave solutions as well via \(\phi ^6\)-model expansion technique.

The organization of the manuscript is given in four sections. Section 2 contains the governing model. Section 3 is related to the analytical study of the given model. In Sect. 4, the description of the simulations is addressed. The last Sect. 5 contains the conclusion of the manuscript.

2 Governing model

The stochastic Fitz-Hugh Nagumo equation in Yasin et al. (2022) is given as

$$\begin{aligned} \phi _t= d\phi _{xx}+\phi (\phi -a)(1-\phi )+\sigma \phi \dot{W}(t), \end{aligned}$$
(1)

where \(\phi (x, t)\) is state variable. It represents the dynamical attitude of the transmission of the nerve impulses of a nervous system, population growth under the sea bed, \(0<a<1\) is a positive constant, W(t) is the Wiener process, \(\dot{W}(t)=\frac{dW}{dt}\) is a time noise and \(\sigma\) is the standard Borel function or control parameter for the time noise.

To get the solitary wave solution of Eq. (1), we are taking transformation as \(\phi (x,t)=U(\rho )e^{\sigma W-\frac{\sigma ^2}{2}}\) where \(\rho =rx+st\) and changes the Eq. (1) into an ordinary differential equation (ODE) as,

$$\begin{aligned} -sU^{'}+r^2d U^{''}+U\left( U e^{\sigma W-\frac{\sigma ^2}{2}}-a\right) \left( 1-U e^{\sigma W-\frac{\sigma ^2}{2}}\right) =0, \end{aligned}$$
(2)

by taking the expectation on both expressions such as

$$\begin{aligned} -sU^{'}+r^2d U^{''}+U\left( U e^{\sigma W(t)}e^{-\frac{\sigma ^2}{2}t}-a\right) \left( 1-U e^{\sigma W(t)}e^{-\frac{\sigma ^2}{2}t}\right) =0. \end{aligned}$$
(3)

Since \(\textbf{E}(e^{\sigma Z})\) for every real number \(\sigma\) and Z is the standard normal random variable, then identities are \(\textbf{E}(e^{\sigma W(t)})=e^{\frac{\sigma ^2}{2}t}\). So, the above equation takes the following form

$$\begin{aligned} -sU^{'}+r^2d U^{''}+U(U-a)(1-U)=0. \end{aligned}$$
(4)

3 Analytical study

Suppose that the solutions of Eq. (4) that can be expressed in the polynomial form as \(B^{k}(\rho )\). For further detail see, Bilal et al. (2021), Zayed and Al-Nowehy (2020), Bibi (2021), Shaikh et al. (2023), Younas et al. (2023).

$$\begin{aligned} U(\rho )=\sum _{k=0}^{2m}\delta _{k}B^{k}(\rho ), \quad \delta _{k}\ne 0, \end{aligned}$$
(5)

where \(\delta _{k} (0\le k \le 2m)\) are real constants and \(B(\rho )\) satisfies the Eq. (4). We are taking

$$\begin{aligned} (B^{'})^2(\rho )= & {} f_{0}+f_{2}B^2(\rho )+f_{4}B^{4}(\rho )+f_{6}B^6(\rho ), \end{aligned}$$
(6)
$$\begin{aligned} B^{''}(\rho )= & {} f_{2}B(\rho )+2f_{4}B^3(\rho )+3f_{6}B^5(\rho ), \end{aligned}$$
(7)

here, \(f_{k}(k=0,2,4,6)\) are real constants. So Eq. (5) has the solutions as,

$$\begin{aligned} B(\rho )=\frac{\Omega (\rho )}{\sqrt{g_{1}\Omega ^2(\rho )+g_{2}}}, \end{aligned}$$
(8)

where \((g_{1}\Omega ^2(\rho )+g_{2})\ge 0\) and the equation has the solution \(\Omega (\rho )\) as,

$$\begin{aligned} \Omega ^{'2}=k_{1}+k_{2}\Omega ^2(\rho )+k_{3}\Omega ^4(\rho ), \end{aligned}$$
(9)

where \(k_{i}\), \(i=1,2,3\) are constants, while \(g_{1}\) and \(g_{2}\) are given by,

$$\begin{aligned} g_{1}= & {} \frac{f_{4}(k_{2}-f_{2})}{(k_{2}-f_{2})^2+3k_{1}k_{3}-2k_{2}(k_{2}-f_{2})}, \end{aligned}$$
(10)
$$\begin{aligned} g_{2}= & {} \frac{3k_{1}f_{4}}{(k_{2}-f_{2})^2+3k_{1}k_{3}-2k_{2}(k_{2}-f_{2})}, \end{aligned}$$
(11)

under the constraint condition,

$$\begin{aligned} f_{4}^{2}(k_{2}-f_{2})\left[ 9k_{1}k_{3}-(k_{2}-f_{2})(2k_{2}+f_{2})\right] +3f_{6}\left[ 3k_{1}k_{3}-(k_{2}^2-f_{2}^2)\right] ^2=0. \end{aligned}$$
(12)

Here JEFs of \(\Omega (\rho )\) for the limits of N are taken as,

Table 1 Jacobi-Elliptic Functions and Trigonometric Conversions
Full size table

The above table provides the standard conversions of the Jacobi elliptic functions to the trigonometric ones and vice versa. This table helps the reader to understand the physical behaviors of the solutions dominant by the Jacobi elliptic functions (Table 1).

To find the value of N, we use the homogenous balancing principle (Jin-Liang et al. 2003), and obtain \(N=1\). So, by substituting the value of N in Eq. (4) takes the form,

$$\begin{aligned} U(\rho )= & {} \delta _{0}+\delta _{1}B(\rho )+\delta _{2}B^2(\rho ). \end{aligned}$$
(13)

Further, we substitute Eq. (13) and its derivatives in eq. (4) and equating the coefficients of the same power of \(B(\rho )\) equal to zero, then we get the system of algebraic equations. Further, solving this the system on Maple will lead to various families of solutions as follows,

Family 1: Here \(f_k\) and \(k_i\) are arbitrary constants along with

$$\begin{aligned} \delta _0=a,~~\delta _1=0,~~\delta _2=\frac{2 (a-1) a f_4}{(2 a-1) f_2},~~r=-\frac{\sqrt{a-1} \sqrt{a}}{\sqrt{2} \sqrt{d} \sqrt{f_2}},~~f_6=\frac{4 \left( a^2-a\right) f_4^2}{3 (2 a-1)^2 f_2}, \end{aligned}$$

and substituting these values into eq.(13), we get the many different JEF dominant solutions of Eq. (4) as,

$$\begin{aligned} \phi (\rho )=a+\frac{2 (a-1) a f_4 \Omega (\rho )^4}{(2 a-1) f_2 \left( g_{1} \Omega (\rho )^2+g_{2}\right) }. \end{aligned}$$
(14)

Type 1: When \(k_{1}=1\),   \(k_{2}=-(1+N^{2})\),    \(k_{3}=N^{2}\), then \(\Omega (\rho )=sn(\rho )\) or \(\Omega (\rho )=cd(\rho )\) then we have JEF dominant solutions as,

$$\begin{aligned} U_{1,N}(\rho )=a+\frac{2 (a-1) a f_4 sn(\rho )^4}{(2 a-1) f_2 \left( g_{1} sn (\rho )^2+g_{2}\right) }, \end{aligned}$$
(15)

or

$$\begin{aligned} U_{2,N}(\rho )=a+\frac{2 (a-1) a f_4 cd(\rho )^4}{(2 a-1) f_2 \left( g_{1} cd (\rho )^2+g_{2}\right) }, \end{aligned}$$
(16)

where \(g_{1}\) and \(g_{2}\) as,

$$\begin{aligned} g_{1}= & {} \frac{f_4 \left( -f_2-N^2-1\right) }{\left( -f_2-N^2-1\right) {}^2-2 \left( -N^2-1\right) \left( -f_2-N^2-1\right) +3 N^2}, \\ g_{2}= & {} \frac{3 f_4}{\left( -f_2-N^2-1\right) {}^2-2 \left( -N^2-1\right) \left( -f_2-N^2-1\right) +3 N^2}, \end{aligned}$$

solutions using constraint conditions as,

$$\begin{aligned}{} & {} f_{4}^{2}((-1-N^{2})-f_{2})[9N^{2}-((-1-N^{2})-f_{2})(-2(1+N^{2})+f_{2})]\\{} & {} \quad +3f_{6}[3N^{2}-((1+N^{2})^2-f_{2}^2)]^2=0. \end{aligned}$$

Case 1: For \(N\rightarrow 1\) we obtained soliton-solutions as,

$$\begin{aligned}{} & {} \phi _{1,1}(x,t)\nonumber \\{} & {} \quad =\left( a+\frac{2 (a-1) a f_4 \tanh ^4\left( s t-\frac{\sqrt{a-1} \sqrt{a} x}{\sqrt{2} \sqrt{d} \sqrt{f_2}}\right) }{(2 a-1) f_2 \left( g_{1} \tanh ^2\left( s t-\frac{\sqrt{a-1} \sqrt{a} x}{\sqrt{2} \sqrt{d} \sqrt{f_2}}\right) +g_{2}\right) }\right) e^{\sigma W-\frac{\sigma ^2}{2}}. \end{aligned}$$
(17)

Case 2: For \(N\rightarrow 0\) we get periodic wave solutions as,

$$\begin{aligned} \phi _{1,0}(x,t)=\left( a+\frac{2 (a-1) a f_4 \sin ^4\left( s t-\frac{\sqrt{a-1} \sqrt{a} x}{\sqrt{2} \sqrt{d} \sqrt{f_2}}\right) }{(2 a-1) f_2 \left( g_{1} \sin ^2\left( s t-\frac{\sqrt{a-1} \sqrt{a} x}{\sqrt{2} \sqrt{d} \sqrt{f_2}}\right) +g_{2}\right) }\right) e^{\sigma W-\frac{\sigma ^2}{2}}. \end{aligned}$$
(18)

Type 2: When \(k_{1}=1-N^{2}\),   \(k_{2}=2N^{2}-1\),    \(k_{3}=-N^{2}\), then \(\Omega (\rho )=cn(\rho )\) then JEF dominant solutions as,

$$\begin{aligned} U_{3,N}(\rho )=a+\frac{2 (a-1) a f_4 cn(\rho )^4}{(2 a-1) f_2 \left( g_{1} cn (\rho )^2+g_{2}\right) }, \end{aligned}$$
(19)

where \(g_{1}\) and \(g_{2}\) are taking as,

$$\begin{aligned} g_{1}= & {} \frac{f_4 \left( -f_2+2 N^2-1\right) }{\left( -f_2+2 N^2-1\right) {}^2-2 \left( 2 N^2-1\right) \left( -f_2+2 N^2-1\right) -3 \left( 1-N^2\right) N^2},\\ g_{2}= & {} \frac{3 f_4 \left( 1-N^2\right) }{\left( -f_2+2 N^2-1\right) {}^2-2 \left( 2 N^2-1\right) \left( -f_2+2 N^2-1\right) -3 \left( 1-N^2\right) N^2}, \end{aligned}$$

solutions using constraint conditions as,

$$\begin{aligned}{} & {} f_{4}^{2}((2N^{2}-1)-f_{2})[(9N^{4}-9N^{2})-((2N^{2}-1)-f_{2})((4N^{2}-2)+f_{2})] \\{} & {} \quad +3f_{6}[(3N^{4}-3N^{2})-((2N^{2}-1)^2-f_{2}^2)]^2=0. \end{aligned}$$

Case 1: For \(N\rightarrow 1\) we obtained soliton-solutions as,

$$\begin{aligned} \phi _{3,1}(x,t)=\left( a+\frac{2 (a-1) a f_4 \text {sech}^4\left( s t-\frac{\sqrt{a-1} \sqrt{a} x}{\sqrt{2} \sqrt{d} \sqrt{f_2}}\right) }{(2 a-1) f_2 \left( g_{1} \text {sech}^2\left( s t-\frac{\sqrt{a-1} \sqrt{a} x}{\sqrt{2} \sqrt{d} \sqrt{f_2}}\right) +g_{2}\right) }\right) e^{\sigma W-\frac{\sigma ^2}{2}}. \end{aligned}$$
(20)

Case 2: For \(N\rightarrow 0\) we get periodic solitary wave solutions as,

$$\begin{aligned} \phi _{3,0}(x,t)=\left( a+\frac{2 (a-1) a f_4 \text {cos}^4\left( s t-\frac{\sqrt{a-1} \sqrt{a} x}{\sqrt{2} \sqrt{d} \sqrt{f_2}}\right) }{(2 a-1) f_2 \left( g_{1} \text {cos}^2\left( s t-\frac{\sqrt{a-1} \sqrt{a} x}{\sqrt{2} \sqrt{d} \sqrt{f_2}}\right) +g_{2}\right) }\right) e^{\sigma W-\frac{\sigma ^2}{2}}. \end{aligned}$$
(21)

Type 3: When \(k_{1}=N^{2}-1\),   \(k_{2}=2-N^{2}\), \(k_{3}=-1\), then \(\Omega (\rho )=dn(\rho )\) then JEF solution as,

$$\begin{aligned} U_{4,N}(\rho )=a+\frac{2 (a-1) a f_4 dn(\rho )^4}{(2 a-1) f_2 \left( g_{1} dn(\rho )^2+g_{2}\right) }, \end{aligned}$$
(22)

where \(g_{1}\) and \(g_{2}\) as,

$$\begin{aligned} g_{1}= & {} \frac{f_4 \left( -f_2-N^2+2\right) }{\left( -f_2-N^2+2\right) {}^2-2 \left( 2-N^2\right) \left( -f_2-N^2+2\right) -3 \left( N^2-1\right) },\\ g_{2}= & {} \frac{3 f_4 \left( N^2-1\right) }{\left( -f_2-N^2+2\right) {}^2-2 \left( 2-N^2\right) \left( -f_2-N^2+2\right) -3 \left( N^2-1\right) }, \end{aligned}$$

solutions using constraint conditions as,

$$\begin{aligned}{} & {} f_{4}^{2}((2-N^{2})-f_{2})[-9(N^{2}-1)-((2-N^{2})-f_{2})(2(2-N^{2})+f_{2})] \\{} & {} \quad +3f_{6}[-3(N^{2}-1)-((2-N^{2})^2-f_{2}^2)]^2=0. \end{aligned}$$

Case 1: For \(N\rightarrow 1\) then we get solitary wave solutions as

$$\begin{aligned} \phi _{4,1}(x,t)=\left( a+\frac{2 (a-1) a f_4 \text {sech}^4\left( s t-\frac{\sqrt{a-1} \sqrt{a} x}{\sqrt{2} \sqrt{d} \sqrt{f_2}}\right) }{(2 a-1) f_2 \left( g_{1} \text {sech}^2\left( s t-\frac{\sqrt{a-1} \sqrt{a} x}{\sqrt{2} \sqrt{d} \sqrt{f_2}}\right) +g_{2}\right) }\right) e^{\sigma W-\frac{\sigma ^2}{2}}. \end{aligned}$$
(23)

Type 4: When \(k_{1}=N^{2}\),   \(k_{2}=(-1-N^{2})\),    \(k_{3}=1\), then \(\Omega (\rho )=ns(\rho )\) or \(\Omega (\rho )=dc(\rho )\) then we have JEF dominant solutions as,

$$\begin{aligned} U_{5,N}(\rho )=a+\frac{2 (a-1) a f_4 ns(\rho )^4}{(2 a-1) f_2 \left( g_{1} ns(\rho )^2+g_{2}\right) }, \end{aligned}$$
(24)

or

$$\begin{aligned} U_{6,N}(\rho )=a+\frac{2 (a-1) a f_4 dc(\rho )^4}{(2 a-1) f_2 \left( g_{1} dc(\rho )^2+g_{2}\right) }, \end{aligned}$$
(25)

where \(g_{1}\) and \(g_{2}\) are taking as,

$$\begin{aligned} g_{1}= & {} \frac{f_4 \left( -f_2+N^2-1\right) }{\left( -f_2+N^2-1\right) {}^2-2 \left( N^2-1\right) \left( -f_2+N^2-1\right) +3 N^2},\\ g_{2}= & {} \frac{3 f_4 N^2}{\left( -f_2+N^2-1\right) {}^2-2 \left( N^2-1\right) \left( -f_2+N^2-1\right) +3 N^2}, \end{aligned}$$

solutions using constraint conditions as,

$$\begin{aligned}{} & {} f_{4}^{2}((-1-N^{2})-f_{2})[9N^{2}-((-1-N^{2})-f_{2})(-2(1+N^{2})+f_{2})]\\{} & {} \quad +3f_{6}[3N^{2}-((1+N^{2})^2-f_{2}^2)]^2=0. \end{aligned}$$

Case 1: For \(N\rightarrow 1\) then we get soliton-solutions as

$$\begin{aligned} \phi _{6,1}(x,t)=\left( a+\frac{2 (a-1) a f_4 \coth ^4\left( s t-\frac{\sqrt{a-1} \sqrt{a} x}{\sqrt{2} \sqrt{d} \sqrt{f_2}}\right) }{(2 a-1) f_2 \left( g_{1} \coth ^2\left( s t-\frac{\sqrt{a-1} \sqrt{a} x}{\sqrt{2} \sqrt{d} \sqrt{f_2}}\right) +g_{2}\right) }\right) e^{\sigma W-\frac{\sigma ^2}{2}}. \end{aligned}$$
(26)

Case 2: For \(N\rightarrow 0\) then we get solitary wave solutions as

$$\begin{aligned} \phi _{5,0}(x,t)=\left( a+\frac{2 (a-1) a f_4 \csc ^4\left( s t-\frac{\sqrt{a-1} \sqrt{a} x}{\sqrt{2} \sqrt{d} \sqrt{f_2}}\right) }{(2 a-1) f_2 \left( g_{1} \csc ^2\left( s t-\frac{\sqrt{a-1} \sqrt{a} x}{\sqrt{2} \sqrt{d} \sqrt{f_2}}\right) +g_{2}\right) }\right) e^{\sigma W-\frac{\sigma ^2}{2}}. \end{aligned}$$
(27)

or

$$\begin{aligned} \phi _{6,0}(x,t)=\left( a+\frac{2 (a-1) a f_4 \cos ^4\left( s t-\frac{\sqrt{a-1} \sqrt{a} x}{\sqrt{2} \sqrt{d} \sqrt{f_2}}\right) }{(2 a-1) f_2 \left( g_{1} \cos ^2\left( s t-\frac{\sqrt{a-1} \sqrt{a} x}{\sqrt{2} \sqrt{d} \sqrt{f_2}}\right) +g_{2}\right) }\right) e^{\sigma W-\frac{\sigma ^2}{2}}. \end{aligned}$$
(28)

Type 5: when \(k_{1}=-N^{2}\),   \(k_{2}=2N^{2}-1\),    \(k_{3}=1-N^{2}\), then \(\Omega (\rho )=nc(\rho )\) then we have JEF dominant solutions as,

$$\begin{aligned} U_{7,N}(\rho )=a+\frac{2 (a-1) a f_4 nc(\rho )^4}{(2 a-1) f_2 \left( g_{1} nc(\rho )^2+g_{2}\right) }, \end{aligned}$$
(29)

where \(g_{1}\) and \(g_{2}\) are taking as,

$$\begin{aligned} g_{1}= & {} \frac{f_4 \left( -f_2+2 N^2-1\right) }{\left( -f_2+2 N^2-1\right) {}^2-2 \left( 2 N^2-1\right) \left( -f_2+2 N^2-1\right) +3 \left( 1-N^2\right) N^2},\\ g_{2}= & {} \frac{3 f_4 N^2}{\left( -f_2+2 N^2-1\right) {}^2-2 \left( 2 N^2-1\right) \left( -f_2+2 N^2-1\right) +3 \left( 1-N^2\right) N^2}, \end{aligned}$$

solutions using constraint conditions as,

$$\begin{aligned}{} & {} f_{4}^{2}((2N^{2}-1)-f_{2})[(9N^{4}-9N^{2})-((2N^{2}-1)-f_{2})((4N^{2}-2)+f_{2})] \\{} & {} \quad +3f_{6}[(3N^{4}-3N^{2})-((2N^{2}-1)^2-f_{2}^2)]^2=0. \end{aligned}$$

Case 1: For \(N\rightarrow 1\) then we get solitary wave solutions as

$$\begin{aligned} \phi _{7,1}(x,t)=\left( a+\frac{2 (a-1) a f_4 \cosh ^4\left( s t-\frac{\sqrt{a-1} \sqrt{a} x}{\sqrt{2} \sqrt{d} \sqrt{f_2}}\right) }{(2 a-1) f_2 \left( g_{1} \cosh ^2\left( s t-\frac{\sqrt{a-1} \sqrt{a} x}{\sqrt{2} \sqrt{d} \sqrt{f_2}}\right) +g_{2}\right) }\right) e^{\sigma W-\frac{\sigma ^2}{2}}. \end{aligned}$$
(30)

Case 2: For \(N\rightarrow 0\) then we get periodic wave solutions as

$$\begin{aligned} \phi _{7,0}(x,t)=\left( a+\frac{2 (a-1) a f_4 \sec ^4\left( s t-\frac{\sqrt{a-1} \sqrt{a} x}{\sqrt{2} \sqrt{d} \sqrt{f_2}}\right) }{(2 a-1) f_2 \left( g_{1} \sec ^2\left( s t-\frac{\sqrt{a-1} \sqrt{a} x}{\sqrt{2} \sqrt{d} \sqrt{f_2}}\right) +g_{2}\right) }\right) e^{\sigma W-\frac{\sigma ^2}{2}}. \end{aligned}$$
(31)

Type 6: When \(k_{1}=1\),   \(k_{2}=2-N^{2}\),    \(k_{3}=(1-N^{2})\), then \(\Omega (\rho )=sc(\rho )\) then we have JEF dominant solutions as,

$$\begin{aligned} U_{8,N}(\rho )=a+\frac{2 (a-1) a f_4 sc(\rho )^4}{(2 a-1) f_2 \left( g_{1}sc(\rho )^2+g_{2}\right) }, \end{aligned}$$
(32)

where \(g_{1}\) and \(g_{2}\) are taking as,

$$\begin{aligned} g_{1}= & {} \frac{f_{4}((2-N^{2})-f_{2})}{((2-N^{2})-f_{2})^2+3(1-N^{2})-2(2-N^{2})((2-N^{2})-f_{2})},\\ g_{2}= & {} \frac{3f_{4}}{((2-N^{2})-f_{2})^2+3(1-N^{2})-2(2-N^{2})((2-N^{2})-f_{2})}, \end{aligned}$$

solutions using constraint conditions as,

$$\begin{aligned}{} & {} f_{4}^{2}((2-N^{2})-f_{2})[+9(1-N^{2})-((2-N^{2})-f_{2})(2(2-N^{2})+f_{2})]\\{} & {} \quad +3f_{6}[3(1-N^{2})-((2-N^{2})^2-f_{2}^2)]^2=0. \end{aligned}$$

Case 1: For \(N\rightarrow 1\) then we get soliton-solutions as

$$\begin{aligned} \phi _{8,1}(x,t)=\left( a+\frac{2 (a-1) a f_4 \sinh ^4\left( s t-\frac{\sqrt{a-1} \sqrt{a} x}{\sqrt{2} \sqrt{d} \sqrt{f_2}}\right) }{(2 a-1) f_2 \left( g_{1} \sinh ^2\left( s t-\frac{\sqrt{a-1} \sqrt{a} x}{\sqrt{2} \sqrt{d} \sqrt{f_2}}\right) +g_{2}\right) }\right) e^{\sigma W-\frac{\sigma ^2}{2}}. \end{aligned}$$
(33)

Case 2: For \(N\rightarrow 0\) then we get solitary wave solutions as

$$\begin{aligned} \phi _{8,0}(x,t)=\left( a+\frac{2 (a-1) a f_4 \tan ^4\left( s t-\frac{\sqrt{a-1} \sqrt{a} x}{\sqrt{2} \sqrt{d} \sqrt{f_2}}\right) }{(2 a-1) f_2 \left( g_{1} \tan ^2\left( s t-\frac{\sqrt{a-1} \sqrt{a} x}{\sqrt{2} \sqrt{d} \sqrt{f_2}}\right) +g_{2}\right) }\right) e^{\sigma W-\frac{\sigma ^2}{2}}. \end{aligned}$$
(34)

Type 7: when \(k_{1}=1\),   \(k_{2}=2N^{2}-1\),    \(k_{3}=-N^{2}(1-N^{2})\), then \(\Omega (\rho )=sd(\rho )\) then we have JEF dominant solutions as,

$$\begin{aligned} U_{9,N}(\rho )=a+\frac{2 (a-1) a f_4 sd(\rho )^4}{(2 a-1) f_2 \left( g_{1}sd(\rho )^2+g_{2}\right) }, \end{aligned}$$
(35)

where \(g_{1}\) and \(g_{2}\) are,

$$\begin{aligned} g_{1}= & {} \frac{f_{4}((2N^{2}-1)-f_{2})}{((2N^{2}-1)-f_{2})^2+3N^{2}(N^{2}-1)-2(2N^{2}-1)((2N^{2}-1)-f_{2})},\\ g_{2}= & {} \frac{3f_{4}}{((2N^{2}-1)-f_{2})^2+3N^{2}(N^{2}-1)-2(2N^{2}-1)((2N^{2}-1)-f_{2})}, \end{aligned}$$

solutions using constraint conditions as,

$$\begin{aligned}{} & {} f_{4}^{2}((2N^{2}-1)-f_{2})[(9N^{4}-9N^{2})-((2N^{2}-1)-f_{2})((4N^{2}-2)+f_{2})] \\{} & {} \quad +3f_{6}[(3N^{4}-3N^{2})-((2N^{2}-1)^2-f_{2}^2)]^2=0. \end{aligned}$$

Case 1: For \(N\rightarrow 1\) then we get solitary wave solutions as,

$$\begin{aligned} \phi _{9,1}(x,t)=\left( a+\frac{2 (a-1) a f_4 \sinh ^4\left( s t-\frac{\sqrt{a-1} \sqrt{a} x}{\sqrt{2} \sqrt{d} \sqrt{f_2}}\right) }{(2 a-1) f_2 \left( g_{1} \sinh ^2\left( s t-\frac{\sqrt{a-1} \sqrt{a} x}{\sqrt{2} \sqrt{d} \sqrt{f_2}}\right) +g_{2}\right) }\right) e^{\sigma W-\frac{\sigma ^2}{2}}. \end{aligned}$$
(36)

Case 2: For \(N\rightarrow 0\) then we get periodic wave solutions as

$$\begin{aligned} \phi _{9,0}(x,t)=\left( a+\frac{2 (a-1) a f_4 \sin ^4\left( s t-\frac{\sqrt{a-1} \sqrt{a} x}{\sqrt{2} \sqrt{d} \sqrt{f_2}}\right) }{(2 a-1) f_2 \left( g_{1} \sin ^2\left( s t-\frac{\sqrt{a-1} \sqrt{a} x}{\sqrt{2} \sqrt{d} \sqrt{f_2}}\right) +g_{2}\right) }\right) e^{\sigma W-\frac{\sigma ^2}{2}}. \end{aligned}$$
(37)

Type 8: when \(k_{1}=1-N^{2}\),   \(k_{2}=2-N^{2}\),    \(k_{3}=1\), then \(\Omega (\rho )=cs(\rho )\) then we have JEF dominant solutions as,

$$\begin{aligned} U_{10,N}(\rho )=a+\frac{2 (a-1) a f_4 cs(\rho )^4}{(2 a-1) f_2 \left( g_{1}cs(\rho )^2+g_{2}\right) }, \end{aligned}$$
(38)

where \(g_{1}\) and \(g_{2}\) are,

$$\begin{aligned} g_{1}= & {} \frac{f_{4}((2-N^{2})-f_{2})}{((2-N^{2})-f_{2})^2+3(1-N^{2})-2(2-N^{2})((2-N^{2})-f_{2})},\\ g_{2}= & {} \frac{3(1-N^{2})f_{4}}{((2-N^{2})-f_{2})^2+3(1-N^{2})-2(2-N^{2})((2-N^{2})-f_{2})},\ \end{aligned}$$

solutions using constraint conditions as,

$$\begin{aligned}{} & {} f_{4}^{2}((2-N^{2})-f_{2})[+9(1-N^{2})-((2-N^{2})-f_{2})(2(2-N^{2})+f_{2})]\\{} & {} \quad +3f_{6}[3(1-N^{2})-((2-N^{2})^2-f_{2}^2)]^2=0. \end{aligned}$$

Case 1: For \(N\rightarrow 1\) then we get soliton-solutions as,

$$\begin{aligned}{} & {} \phi _{10,N}(x,t)\nonumber \\{} & {} \quad =\left( a+\frac{2 (a-1) a f_4 \text {csch} ^4\left( s t-\frac{\sqrt{a-1} \sqrt{a} x}{\sqrt{2} \sqrt{d} \sqrt{f_2}}\right) }{(2 a-1) f_2 \left( g_{1} \text {csch} ^2\left( s t-\frac{\sqrt{a-1} \sqrt{a} x}{\sqrt{2} \sqrt{d} \sqrt{f_2}}\right) +g_{2}\right) }\right) e^{\sigma W-\frac{\sigma ^2}{2}}. \end{aligned}$$
(39)

Case 2: For \(N\rightarrow 0\) then we get solitary wave solutions as,

$$\begin{aligned} \phi _{10,N}(x,t)=\left( a+\frac{2 (a-1) a f_4 \text {cot} ^4\left( s t-\frac{\sqrt{a-1} \sqrt{a} x}{\sqrt{2} \sqrt{d} \sqrt{f_2}}\right) }{(2 a-1) f_2 \left( g_{1} \text {cot} ^2\left( s t-\frac{\sqrt{a-1} \sqrt{a} x}{\sqrt{2} \sqrt{d} \sqrt{f_2}}\right) +g_{2}\right) }\right) e^{\sigma W-\frac{\sigma ^2}{2}}. \end{aligned}$$
(40)

Type 9: when \(k_{1}=-N^{2}(1-N^{2})\),   \(k_{2}=2N^{2}-1\),    \(k_{3}=1\), then \(\Omega (\rho )=ds(\rho )\) then we have JEF dominant solutions as,

$$\begin{aligned} U_{11,N}(\rho )=a+\frac{2 (a-1) a f_4 ds(\rho )^4}{(2 a-1) f_2 \left( g_{1}ds(\rho )^2+g_{2}\right) }, \end{aligned}$$
(41)

where \(g_{1}\) and \(g_{2}\) are,

$$\begin{aligned} g_{1}= & {} \frac{f_{4}((2N^{2}-1)-f_{2})}{((2N^{2}-1)-f_{2})^2+3N^{2}(N^{2}-1)-2(2N^{2}-1)((2N^{2}-1)-f_{2})},\\ g_{2}= & {} \frac{-3N^{2}(1-N^{2})f_{4}}{((2N^{2}-1)-f_{2})^2+3N^{2}(N^{2}-1)-2(2N^{2}-1)((2N^{2}-1)-f_{2})}, \end{aligned}$$

solutions using constraint conditions as,

$$\begin{aligned}{} & {} f_{4}^{2}((2N^{2}-1)-f_{2})[(9N^{4}-9N^{2})-((2N^{2}-1)-f_{2})((4N^{2}-2)+f_{2})] \\{} & {} \quad +3f_{6}[(3N^{4}-3N^{2})-((2N^{2}-1)^2-f_{2}^2)]^2=0. \end{aligned}$$

Case 1: For \(N\rightarrow 1\) then we get solitary wave solutions as,

$$\begin{aligned} \phi _{11,1}(x,t)=\left( a+\frac{2 (a-1) a f_4 \text {csch}^4\left( s t-\frac{\sqrt{a-1} \sqrt{a} x}{\sqrt{2} \sqrt{d} \sqrt{f_2}}\right) }{(2 a-1) f_2 \left( g_{1} \text {csch}^2\left( s t-\frac{\sqrt{a-1} \sqrt{a} x}{\sqrt{2} \sqrt{d} \sqrt{f_2}}\right) +g_{2}\right) }\right) e^{\sigma W-\frac{\sigma ^2}{2}}. \end{aligned}$$
(42)

Case 2: For \(N\rightarrow 0\) then we get periodic wave solutions as,

$$\begin{aligned} \phi _{11,0}(x,t)=\left( a+\frac{2 (a-1) a f_4 \text {csc}^4\left( s t-\frac{\sqrt{a-1} \sqrt{a} x}{\sqrt{2} \sqrt{d} \sqrt{f_2}}\right) }{(2 a-1) f_2 \left( g_{1} \text {csc}^2\left( s t-\frac{\sqrt{a-1} \sqrt{a} x}{\sqrt{2} \sqrt{d} \sqrt{f_2}}\right) +g_{2}\right) }\right) e^{\sigma W-\frac{\sigma ^2}{2}}. \end{aligned}$$
(43)

Type 10: When \(k_{1}=\frac{1-N^{2}}{4}\),   \(k_{2}=\frac{1+N^{2}}{2}\),    \(k_{3}=\frac{1-N^{2}}{4}\), then \(\Omega (\rho )=nc(\rho )\pm sc(\rho )\) or \(\frac{cn(\rho )}{1\pm sn(\rho )}\) then we have JEF dominant solutions as,

$$\begin{aligned} U_{12,N}(\rho )=a+\frac{2 (a-1) a f_4 (nc(\rho )\pm sc(\rho ))^4}{(2 a-1) f_2 \left( g_{1}(nc(\rho )\pm sc(\rho ))^2+g_{2}\right) }, \end{aligned}$$
(44)

or

$$\begin{aligned} U_{13,N}(\rho )=a+\frac{2 (a-1) a f_4 (\frac{cn(\rho )}{1\pm sn(\rho )})^4}{(2 a-1) f_2 \left( g_{1}(\frac{cn(\rho )}{1\pm sn(\rho )})^2+g_{2}\right) }, \end{aligned}$$
(45)

where \(g_{1}\) and \(g_{2}\) are,

$$\begin{aligned} g_{1}= & {} \frac{f_{4}\left( \frac{1+N^{2}}{2}-f_{2}\right) }{\left( \frac{1+N^{2}}{2}-f_{2}\right) ^2+3\left( \frac{(1-N^{2})^{2}}{16}\right) -\left( 1+N^{2}\right) \left( \frac{1+N^{2}}{2}-f_{2}\right) },\\ g_{2}= & {} \frac{3\left( \frac{1-N^{2}}{4}\right) f_{4}}{\left( \frac{1+N^{2}}{2}-f_{2}\right) ^2+3\left( \frac{(1-N^{2})^{2}}{16}\right) -\left( 1+N^{2}\right) \left( \frac{1+N^{2}}{2}-f_{2}\right) }, \end{aligned}$$

solutions using constraint conditions as,

$$\begin{aligned}{} & {} f_{4}^{2}\left( \frac{1+N^{2}}{2}-f_{2}\right) \left[ 9\left( \frac{(1-N^{2})^{2}}{16}\right) -\left( \frac{1+N^{2}}{2}-f_{2}\right) \left( (1+N^{2}) +f_{2}\right) \right] \\{} & {} \quad +3f_{6}\left[ 3\left( \frac{(1-N^{2})^{2}}{16}\right) -\left( \frac{\left( 1+N^{2}\right) ^{2}}{4}-f_{2}^2\right) \right] ^2=0. \end{aligned}$$

Case 1: For \(N\rightarrow 1\) then we get soliton-solutions as,

$$\begin{aligned}{} & {} \phi _{12,1}(x,t)\nonumber \\{} & {} \quad =\left( a+\frac{2 (a-1) a f_4 \left( \sinh \left( s t-\frac{\sqrt{a-1} \sqrt{a} x}{\sqrt{2} \sqrt{d} \sqrt{f_2}}\right) \pm \cosh \left( s t-\frac{\sqrt{a-1} \sqrt{a} x}{\sqrt{2} \sqrt{d} \sqrt{f_2}}\right) \right) {}^4}{(2 a-1) f_2 \left( g_{1} \left( \sinh \left( s t-\frac{\sqrt{a-1} \sqrt{a} x}{\sqrt{2} \sqrt{d} \sqrt{f_2}}\right) \pm \cosh \left( s t-\frac{\sqrt{a-1} \sqrt{a} x}{\sqrt{2} \sqrt{d} \sqrt{f_2}}\right) \right) {}^2+g_{2}\right) }\right) \nonumber \\{} & {} \qquad e^{\sigma W-\frac{\sigma ^2}{2}}. \end{aligned}$$
(46)

or

$$\begin{aligned} \phi _{13,1}(\rho )= & {} \left( a+\frac{32 (a-1) a f_4 \text {sech}^4\left( s t-\frac{\sqrt{a-1} \sqrt{a} x}{\sqrt{2} \sqrt{d} \sqrt{f_2}}\right) }{(2 a-1) f_2 \left( 4 g_{1} \text {sech}^2\left( s t-\frac{\sqrt{a-1} \sqrt{a} x}{\sqrt{2} \sqrt{d} \sqrt{f_2}}\right) +g_{2}\right) }\right) \nonumber \\{} & {} e^{\sigma W-\frac{\sigma ^2}{2}}. \end{aligned}$$
(47)

Case 2: For \(N\rightarrow 0\) then we get solitary wave solutions as,

$$\begin{aligned}{} & {} \phi _{12,0}(\rho )\nonumber \\{} & {} \quad =\left( a+\frac{2 (a-1) a f_4 \left( \sec \left( s t-\frac{\sqrt{a-1} \sqrt{a} x}{\sqrt{2} \sqrt{d} \sqrt{f_2}}\right) \pm \tan \left( s t-\frac{\sqrt{a-1} \sqrt{a} x}{\sqrt{2} \sqrt{d} \sqrt{f_2}}\right) \right) {}^4}{(2 a-1) f_2 \left( g_{1} \left( \sec \left( s t-\frac{\sqrt{a-1} \sqrt{a} x}{\sqrt{2} \sqrt{d} \sqrt{f_2}}\right) \pm \tan \left( s t-\frac{\sqrt{a-1} \sqrt{a} x}{\sqrt{2} \sqrt{d} \sqrt{f_2}}\right) \right) {}^2+g_{2}\right) }\right) \nonumber \\{} & {} \qquad e^{\sigma W-\frac{\sigma ^2}{2}}. \end{aligned}$$
(48)

or

$$\begin{aligned}{} & {} \phi _{13,0}(\rho )\nonumber \\{} & {} \quad =\left( a+\frac{2 (a-1) a f_4 \cos ^4\left( s t-\frac{\sqrt{a-1} \sqrt{a} x}{\sqrt{2} \sqrt{d} \sqrt{f_2}}\right) }{(2 a-1) f_2 \left( \sin \left( s t-\frac{\sqrt{a-1} \sqrt{a} x}{\sqrt{2} \sqrt{d} \sqrt{f_2}}\right) +1\right) {}^4 \left( \frac{g_{1} \cos ^2\left( s t-\frac{\sqrt{a-1} \sqrt{a} x}{\sqrt{2} \sqrt{d} \sqrt{f_2}}\right) }{\left( \sin \left( s t-\frac{\sqrt{a-1} \sqrt{a} x}{\sqrt{2} \sqrt{d} \sqrt{f_2}}\right) +1\right) {}^2}+g_{2}\right) }\right) \nonumber \\{} & {} \qquad e^{\sigma W-\frac{\sigma ^2}{2}}. \end{aligned}$$
(49)

Type 11: when \(k_{1}=-\frac{(1-N^{2})^{2}}{4}\),   \(k_{2}=\frac{1+N^{2}}{2}\),    \(k_{3}=-\frac{1}{4}\), then \(\Omega (\rho )=N cn(\rho )\pm dn(\rho )\) then we have JEF dominant solutions as,

$$\begin{aligned} U_{14,N}(\rho )=\frac{2 (a-1) a f_4 (N cn(\rho )\pm dn(\rho ) )^4}{(2 a-1) f_2 \left( g_{1} (N cn(\rho )\pm dn(\rho ) )^2+g_{2}\right) }+a, \end{aligned}$$
(50)

where \(g_{1}\) and \(g_{2}\) are,

$$\begin{aligned} g_{1}= & {} \frac{f_{4}\left( \frac{1+N^{2}}{2}-f_{2}\right) }{\left( \frac{1+N^{2}}{2}-f_{2}\right) ^2+3\left( \frac{(1-N^{2})^{2}}{16}\right) -\left( 1+N^{2}\right) \left( \frac{1+N^{2}}{2}-f_{2}\right) },\\ g_{2}= & {} \frac{-3\left( \frac{(1-N^{2})^{2}}{4}\right) f_{4}}{\left( \frac{1+N^{2}}{2}-f_{2}\right) ^2+3\left( \frac{(1-N^{2})^{2}}{16}\right) -\left( 1+N^{2}\right) \left( \frac{1+N^{2}}{2}-f_{2}\right) }, \end{aligned}$$

solutions using constraint conditions as,

$$\begin{aligned}{} & {} h_{4}^{2}\left( \frac{1+m^{2}}{2}-h_{2}\right) \left[ 9\left( \frac{(1-N^{2})^{2}}{16}\right) -\left( \frac{1+N^{2}}{2}-f_{2}\right) \left( (1+N^{2}) +f_{2}\right) \right] \\{} & {} \quad +3f_{6}\left[ 3\left( \frac{(1-N^{2})^{2}}{16}\right) -\left( \frac{\left( 1+N^{2}\right) ^{2}}{4}-f_{2}^2\right) \right] ^2=0. \end{aligned}$$

Case 1: For \(N\rightarrow 1\) then we get solitary wave solutions as,

$$\begin{aligned}{} & {} \phi _{14,1}(x,t)\nonumber \\{} & {} \quad =\left( a+\frac{2 (a-1) a f_4 \left( \text {sech}\left( s t-\frac{\sqrt{a-1} \sqrt{a} x}{\sqrt{2} \sqrt{d} \sqrt{f_2}}\right) \pm \text {sech}\left( s t-\frac{\sqrt{a-1} \sqrt{a} x}{\sqrt{2} \sqrt{d} \sqrt{f_2}}\right) \right) {}^4}{(2 a-1) f_2 \left( g_{1} \left( \text {sech}\left( s t-\frac{\sqrt{a-1} \sqrt{a} x}{\sqrt{2} \sqrt{d} \sqrt{f_2}}\right) \pm \text {sech}\left( s t-\frac{\sqrt{a-1} \sqrt{a} x}{\sqrt{2} \sqrt{d} \sqrt{f_2}}\right) \right) {}^2+g_{2}\right) }\right) \nonumber \\{} & {} \qquad e^{\sigma W-\frac{\sigma ^2}{2}}. \end{aligned}$$
(51)

Type 12: when \(k_{1}=\frac{1}{4}\),   \(k_{2}=\frac{1-2N^{2}}{2}\),    \(k_{3}=\frac{1}{4}\), then \(\Omega (\rho )=\frac{sn(\rho )}{1\pm cn(\rho )}\) then we have JEF dominant solutions as,

$$\begin{aligned} U_{15,N}(\rho )=a+\frac{2 (a-1) a f_4 (\frac{sn(\rho )}{1\pm cn(\rho )})^4}{(2 a-1) f_2 \left( g_{1} (\frac{sn(\rho )}{1\pm cn(\rho )} )^2+g_{2}\right) }, \end{aligned}$$
(52)

where \(g_{1}\) and \(g_{2}\) are,

$$\begin{aligned} g_{1}= & {} \frac{f_{4}\left( \frac{1-2N^{2}}{2}-f_{2}\right) }{\left( \frac{1-2N^{2}}{2}-f_{2}\right) ^2+\left( \frac{3}{16}\right) -\left( 1-2N^{2}\right) \left( \frac{1-2N^{2}}{2}-f_{2}\right) },\\ g_{2}= & {} \frac{\left( \frac{3}{4}\right) f_{4}}{\left( \frac{1-2N^{2}}{2}-f_{2}\right) ^2+\left( \frac{3}{16}\right) -\left( 1-2N^{2}\right) \left( \frac{1-2N^{2}}{2}-f_{2}\right) }, \end{aligned}$$

solutions using constraint conditions as,

$$\begin{aligned}{} & {} f_{4}^{2}\left( \frac{1-2N^{2}}{2}-f_{2}\right) \left[ \left( \frac{9}{16}\right) -\left( \frac{1-2N^{2}}{2}-f_{2}\right) \left( (1-2N^{2})+f_{2}\right) \right] \\{} & {} \quad +3f_{6}\left[ \left( \frac{3}{16}\right) -\left( \frac{\left( 1-2N^{2}\right) ^{2}}{4}-f_{2}^2\right) \right] ^2=0. \end{aligned}$$

Case 1: For \(N\rightarrow 1\) then we get solitary wave solutions as

$$\begin{aligned}{} & {} \phi _{15,1}(x,t)\nonumber \\{} & {} \quad =\left( a+\frac{2 (a-1) a f_4 \tanh ^4\left( s t-\frac{\sqrt{a-1} \sqrt{a} x}{\sqrt{2} \sqrt{d} \sqrt{f_2}}\right) }{(2 a-1) f_2 \left( \text {sech}\left( s t-\frac{\sqrt{a-1} \sqrt{a} x}{\sqrt{2} \sqrt{d} \sqrt{f_2}}\right) +1\right) {}^4 \left( \frac{g_{1} \tanh ^2\left( s t-\frac{\sqrt{a-1} \sqrt{a} x}{\sqrt{2} \sqrt{d} \sqrt{f_2}}\right) }{\left( \text {sech}\left( s t-\frac{\sqrt{a-1} \sqrt{a} x}{\sqrt{2} \sqrt{d} \sqrt{f_2}}\right) +1\right) {}^2}+g_{2}\right) }\right) \nonumber \\{} & {} \qquad e^{\sigma W-\frac{\sigma ^2}{2}}. \end{aligned}$$
(53)

Case 2: For \(N\rightarrow 0\) then we get periodic wave solutions as

$$\begin{aligned}{} & {} \phi _{15,0}(x,t)\nonumber \\{} & {} \quad =\left( a+\frac{2 (a-1) a f_4 \sin ^4\left( s t-\frac{\sqrt{a-1} \sqrt{a} x}{\sqrt{2} \sqrt{d} \sqrt{f_2}}\right) }{(2 a-1) f_2 \left( \text {cos}\left( s t-\frac{\sqrt{a-1} \sqrt{a} x}{\sqrt{2} \sqrt{d} \sqrt{f_2}}\right) +1\right) {}^4 \left( \frac{g_{1} \sin ^2\left( s t-\frac{\sqrt{a-1} \sqrt{a} x}{\sqrt{2} \sqrt{d} \sqrt{f_2}}\right) }{\left( \text {cos}\left( s t-\frac{\sqrt{a-1} \sqrt{a} x}{\sqrt{2} \sqrt{d} \sqrt{f_2}}\right) +1\right) {}^2}+g_{2}\right) }\right) \nonumber \\{} & {} \qquad e^{\sigma W-\frac{\sigma ^2}{2}}. \end{aligned}$$
(54)

Type 13: When \(k_{1}=\frac{1}{4}\),   \(k_{2}=\frac{1+N^{2}}{2}\),    \(k_{3}=\frac{(1-N^{2})^{2}}{4}\), then \(\Omega (\rho )=\frac{sn(\rho )}{cn(\rho )\pm dn(\rho )}\) then we have JEF solutions

$$\begin{aligned} U_{16,N}(x,t)=a+\frac{2 (a-1) a f_4 (\frac{sn(\rho )}{cn(\rho )\pm dn(\rho )})^4}{(2 a-1) f_2 \left( g_{1}(\frac{sn(\rho )}{cn(\rho )\pm dn(\rho )} )^2+g_{2}\right) }, \end{aligned}$$
(55)

where \(g_{1}\) and \(g_{2}\) are,

$$\begin{aligned} g_{1}= & {} \frac{f_{4}\left( \frac{1+N^{2}}{2}-f_{2}\right) }{\left( \frac{1+N^{2}}{2}-f_{2}\right) ^2+3\left( \frac{(1-N^{2})^{2}}{16}\right) -\left( 1+N^{2}\right) \left( \frac{1+N^{2}}{2}-f_{2}\right) },\\ g_{2}= & {} \frac{3\left( \frac{1}{4}\right) f_{4}}{\left( \frac{1+N^{2}}{2}-f_{2}\right) ^2+3\left( \frac{(1-N^{2})^{2}}{16}\right) -\left( 1+N^{2}\right) \left( \frac{1+N^{2}}{2}-f_{2}\right) }, \end{aligned}$$

solutions using constraint conditions as,

$$\begin{aligned}{} & {} f_{4}^{2}\left( \frac{1+N^{2}}{2}-f_{2}\right) \left[ 9\left( \frac{(1-N^{2})^{2}}{16}\right) -\left( \frac{1+N^{2}}{2}-f_{2}\right) \left( (1+N^{2})+f_{2}\right) \right] \\{} & {} \quad +3f_{6}\left[ 3\left( \frac{(1-N^{2})^{2}}{16}\right) -\left( \frac{\left( 1+N^{2}\right) ^{2}}{4}-f_{2}^2\right) \right] ^2=0. \end{aligned}$$

Case 1: For \(N\rightarrow 1\) then we get soliton-solutions as,

$$\begin{aligned}{} & {} \phi _{16,1}(x,t)\nonumber \\{} & {} \quad =\left( a+\frac{2 (a-1) a f_4 \tanh ^4\left( s t-\frac{\sqrt{a-1} \sqrt{a} x}{\sqrt{2} \sqrt{d} \sqrt{f_2}}\right) }{(2 a-1) f_2 \left( \text {sech}\left( s t-\frac{\sqrt{a-1} \sqrt{a} x}{\sqrt{2} \sqrt{d} \sqrt{f_2}}\right) +\text {sech}\left( s t-\frac{\sqrt{a-1} \sqrt{a} x}{\sqrt{2} \sqrt{d} \sqrt{f_2}}\right) \right) {}^4 \left( J+g_{2}\right) }\right) \nonumber \\{} & {} \qquad e^{\sigma W-\frac{\sigma ^2}{2}}, \end{aligned}$$
(56)

where \(J=\frac{g_{1} \tanh ^2\left( s t-\frac{\sqrt{a-1} \sqrt{a} x}{\sqrt{2} \sqrt{d} \sqrt{f_2}}\right) }{\left( \text {sech}\left( s t-\frac{\sqrt{a-1} \sqrt{a} x}{\sqrt{2} \sqrt{d} \sqrt{f_2}}\right) \pm \text {sech}\left( s t-\frac{\sqrt{a-1} \sqrt{a} x}{\sqrt{2} \sqrt{d} \sqrt{f_2}}\right) \right) {}^2}.\) Case 2: For \(N\rightarrow 0\) then we get periodic wave solutions as,

$$\begin{aligned}{} & {} \phi _{16,0}(x,t)\nonumber \\{} & {} \quad =\left( a+\frac{2 (a-1) a f_4 \sin ^4\left( s t-\frac{\sqrt{a-1} \sqrt{a} x}{\sqrt{2} \sqrt{d} \sqrt{f_2}}\right) }{(2 a-1) f_2 \left( \text {cos}\left( s t-\frac{\sqrt{a-1} \sqrt{a} x}{\sqrt{2} \sqrt{d} \sqrt{f_2}}\right) +1\right) {}^4 \left( \frac{g_{1} \sin ^2\left( s t-\frac{\sqrt{a-1} \sqrt{a} x}{\sqrt{2} \sqrt{d} \sqrt{f_2}}\right) }{J}+g_{2}\right) }\right) \nonumber \\{} & {} \qquad e^{\sigma W-\frac{\sigma ^2}{2}}, \end{aligned}$$
(57)

where \(J=\text {cos}\left( s t-\frac{\sqrt{a-1} \sqrt{a} x}{\sqrt{2} \sqrt{d} \sqrt{f_2}}\right) \pm 1.\)

4 Results and discussion

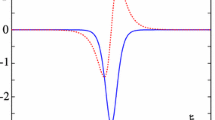
The Fitz Hugh-Nagumo model is the precursor of the excitable system (e.g., neurons). The geometrical structure from Figures (1, 2, 3, 4, 5 and 6) encodes the behavior of the electrically excited cells in the living organism under the effects of noise. Due to the presence of the stochastic term the formation of the perturbed current signals in neurons is demonstrated with the help of surface and contour plots. In short, all the figures presented the emulation of electrically excitable cells especially neurons (that have to transmit information). The abrupt spikes in graphs represent the noise term in the mathematical model but physically they can be related to the pattern of signals used by the neurons to transmit the data. Our main purpose of this study is to find the exact solitons of stochastic FHN. These results are very helpful for a better understanding of the behavior of population growth under the sea bed. We find the JEF solutions and it gives us the solitary wave solutions and solitons. In the ocean, these results are very applicable because they have randomness with consistent behavior such as solitons. in ocean and engineering.

The population growth, and neuron diffusion models are related to the FHN equation and this model has serious significance in applications. The current study describes the multiple solutions for such problems in different environments depending on the choice of the parameters, but the fundamental contribution is that we consider the FHN equation under the influence of the noise which leads to more physical problems and the solution provides the sufficient information of the solution and true behavior of the species growth as well as neuron mobility. In any environment under the sea bed as well as on the common surface. Eichinger et al. considered the stochastic FHN equation with additive noise and analyzed the stability of traveling-pulse solutions (Eichinger et al. 2022). Tuckwell and Rodriguez worked on the stochastic FHN equation under Gaussian white noise with analytical noise (Tuckwell and Rodriguez 1998). Tuckwell used the numerical technique to gain the solution of the stochastic FHN equation (Tuckwell 2008). The authors used the Chebyshev spectral collocation for the computational solution (Singh and Saha Ray 2022). Bonaccorsi et al. worked on the FHN equation with stochastic boundary conditions and they proved the global well-posedness (Marinelli and Scarpa 2022). The authors considered the stochastic FHN equation and analyzed its solution (Beneš et al. 2021). But in this, study we used the \(\phi ^6\)-model expansion method. The method under consideration is providing us with the solutions for the Jacobi elliptic function (JEFs). Solitons and solitary wave solutions are the two sorts of solutions that JEFs can produce. By using the \(\phi ^6\)-model expansion technique, several soliton solutions can be found, including dark, bright, singular, combo, and exact solitary wave solutions. Figure (1) is drawn for the solutions \(\phi _{1,1}(x,t)\) that will give us the dark soliton solution. The subfigures (1a, d) are drawn for the \(\sigma\) zero, and that will provide us the dark solution while we increase the value of \(\sigma =0.3\) and our solution shows the randomness in their behavior that are dispatched in subfigures (1b, e) and subfigures (1c, f) for \(\sigma =0.5\). Figures (2,4) are drawn for the solutions \(\phi _{1,0}(x,t)\) and \(\phi _{2,0}(x,t)\) respectively that will provide us the solitary wave solutions clearly and the noise is shown in their corresponding subfigures as well. Figure (3,5) are drawn for the solutions \(\phi _{2,1}(x,t)\) and \(\phi _{3,1}(x,t)\) that will gives us the bright soliton solutions. Figure (6) is drawn for the solution \(\phi _{13,1}(x,t)\) that gives us the dark-bright solution solution.

Fig. 1
figure 1

Dark soliton solution for the solution \(\phi _{1,1}(x,t)\) for the different choices of parameters

Full size image
Fig. 2
figure 2

Solitary wave solution for the solution \(\phi _{1,0}(x,t)\) for the different choices of parameters

Full size image
Fig. 3
figure 3

Bright soliton solution for the solution \(\phi _{2,1}(x,t)\) for the different choices of parameters

Full size image
Fig. 4
figure 4

Solitary wave solution for the solution \(\phi _{2,0}(x,t)\) for the different choices of parameters

Full size image
Fig. 5
figure 5

Bright soliton solution for the solution \(\phi _{3,1}(x,t)\) for the different choices of parameters

Full size image
Fig. 6
figure 6

Dark-Bright soliton solution for the solution \(\phi _{13,1}(x,t)\) for the different choices of parameters

Full size image

5 Conclusion

In this research, we studied the stochastic Fitz-Hugh Nagumo (FHN) equation analytically. The multiple soliton solutions of the FHN model are successfully constructed. This model is widely used in flame propagation, branching Brownian motion process, autocatalytic chemical reaction, nuclear reactor theory, and mobility in neuroscience that expresses the pulse behavior of neurons and the population growth model. So, it is directly connected with the ocean and engineering as well as where in the sea. To construct the soliton-solutions of this model we adopted the \(\phi ^6\)-model expansion method. If these solutions are considered as the population growth under the sea bed, these solutions will represent the population growth in an environment where the solutions are very important for the people who are working in the framework of ocean engineering. So Brownian motion or other processes play a fundamental role in the dynamics of the population which is governed by this model. For example certain stages you have sudden increases or decreases in the population growth. So, these solutions are successfully constructed under the stochastic behavior or Brownian motion and, hopefully, are used in the wave motions that are directly connected to sea and ocean engineering. Using this model we constructed the new families of the solitary wave solutions successfully in different forms. Under the different constraint conditions, the existence of these solutions to the pulse behavior of neurons is also observed in the form of hyperbolic, trigonometric, and rational forms. The graphical behaviors are also depicted for different values of parameters in 3D and corresponding contour shapes. The nature is full of random behavior. As classical models can not incorporate the fluctuation of the environment, or in the system, it is necessary to consider the classical model under the effect of the noise. The effect of the noise is controlled with the Borel function. Moreover, the underlying model has vast applications in neuroscience that express the pulse behavior of neurons. In general, different kinds of noise have an effect on neurons, e.g., oscillations in the opening and closing of ion stations within the cell membrane and the fluctuations of the different conductivities in the system. This fluctuation creates a sequence of stochastic excitation. A similar procedure can be adopted to observe the impact of noise on the classical models.