New exact solutions of the (3+1)-dimensional double sine-Gordon equation by two analytical methods

Abstract

The (3+1)-dimensional double sine-Gordon equation plays a crucial role in various physical phenomena, including nonlinear wave propagation, field theory, and condensed matter physics. However, obtaining exact solutions to this equation faces significant challenges. In this article, we successfully employ a modified $\left( \dfrac{G'}{G^2}\right)$-expansion and improved $\tan \left( \dfrac{\phi \left( \xi \right) }{2}\right)$-expansion methods to construct new analytical solutions to the double sine-Gordon equation. These solutions can be divided into four categories like trigonometric function solutions, hyperbolic function solutions, exponential solutions, and rational solutions. Our key findings include a rich spectrum of soliton solutions, encompassing bright, dark, singular, periodic, and mixed types, showcasing the (3+1)-dimensional double sine-Gordon equation ability to model diverse wave behaviors. We uncover previously unreported complex wave structures, revealing the potential for complex nonlinear interactions within the (3+1)-dimensional double sine-Gordon equation framework. We demonstrate the modified $\left( \dfrac{G'}{G^2}\right)$-expansion and improved $\tan \left( \dfrac{\phi \left( \xi \right) }{2}\right)$-expansion methods effectiveness in handling higher-dimensional nonlinear partial differential equations, expanding their applicability in mathematical physics. These method offers enhanced flexibility and broader solution categories compared to conventional approaches.

1 Introduction

The (3+1)-dimensional double sine-Gordon equation, a well-known nonlinear partial differential equation with many applications in mathematical physics, describes the evolution of complex wave patterns in multidimensional space and time. Evolution equations, which include both ordinary and partial differential equations, describe how systems change over time, while nonlinear partial differential equations are involved partial derivatives and emphasize nonlinear connections among variables, setting them apart within the realm of evolution equations (Al-Ali 2013; Zheng 2004; Evans 2022). In many branches of mathematical physics, including field theory, condensed matter physics, and nonlinear wave propagation, the (3+1)-dimensional double sine-Gordon equation is the gold standard. However, it has shown to be a challenging task to uncover its secrets through exact solutions. In this paper, we explore into the analytical solutions of this interesting equation, uncovering new perspectives into its behaviour by the implementation of a modified $\left( \dfrac{G'}{G^2}\right)$-expansion and improved $\tan \left( \dfrac{\phi \left( \xi \right) }{2}\right)$-expansion methods.

In space-time dimension, the classical Sine-Gordon equation is a significant nonlinear evolution partial differential equation. It has a significant history (Harrison 1999), includes a wide range of solutions, and exhibits complex dynamics. They have revealed usage in several disciplines of physics (Kivshar and Malomed 1989; Dauxois and Peyrard 2006). In past years, more attention has been paid to the impact of inhomogeneities on the spread of solitons (Kumar and Kumar 2022; Yang et al. 2019). Solitons flow with constant speed and shape as an integrable solution in the classical sine-Gorden model. Solitons may, display more complex motion with varying velocity and structure under various situations due to the inhomogeneities inside the medium (Contoyiannis et al. 2021). This might be a useful impact for quick communication, quick movement, or perhaps a potential soliton cannon (Ekomasov et al. 2018; Manoranjan 2021). The exact soliton solutions for the sine-Gordon equation were found in Hirota (1973) using Hirota’s approach (Zagrodziński 1979) using Lamb’s method, Leibbrandt (1978) using the Backlund transformation (Kaliappan and Lakshmanan 1979). Other authors have taken a variety of different approaches based on various ways to solve the equation.

There are exact solutions for many different variations of the sine-Gordon equation, which is a significant nonlinear partial differential equation in mathematical physics with various applications (Gani et al. 2019; Gul et al. 2018; Joseph 2020a, b; Mohammadi and Riazi 2019). There are numerous applications for the sinh-Gordon equation and its modifications, and a number of the precise solutions for these equations utilizing the Lie group and the straightforward equation methods may be found in Magalakwe et al. (2015, 2022), Faridi et al. (2024), Akbar et al. (2023), Eslami and Rezazadeh (2016), Eslami et al. (2014), Asghari et al. (2023a), Asghari et al. (2023b), Inan et al. (2017), Duran et al. (2012), Uddin et al. (2011), Inan et al. (2011) and Asghari et al. (2023).

The group of $\left( \dfrac{G'}{G}\right)$-expansion methods is special and gives nonlinear evolution equations approximately exact solutions. Li and Liu (2008) developed the $\left( \dfrac{G'}{G}\right)$-expansion method to construct new traveling wave solutions to nonlinear evolution equations related issues. The extended $\left( \dfrac{G'}{G}\right)$-expansion method, which Zayed and Gepreel (2009) presented in 2009, successfully confirmed the effectiveness and accuracy of the $\left( \dfrac{G'}{G}\right)$-expansion method. The two variables $\left( \dfrac{G'}{G}, \dfrac{1}{G}\right)$-expansion method can be used to create traveling wave solutions of nonlinear evolution equations, as has occasionally been shown by many scientists and mathematicians. The concept was first presented forward by Li et al. (2010) in the year 2010. Recently, several writers have suggested the $\left( \dfrac{G'}{G^2}\right)$-expansion method to obtain novel soliton solutions for numerous nonlinear evolution equations. The modified $\left( \dfrac{G'}{G^2}\right)$-expansion method, which has more unknown parameters, is the penultimate innovation of the $\left( \dfrac{G'}{G^2}\right)$-expansion approach.

The $\tan \left( \dfrac{\phi \left( \xi \right) }{2}\right)$-expansion method has a wide range of applications. For various nonlinear fractional physical models, Manafian and Farshbaf Zinati (2020) use the $\tan \left( \dfrac{\phi \left( \xi \right) }{2}\right)$-expansion approach to find trigonometric function, hyperbolic function, exponential function and rational function solutions. Ugurlu et al. (2017) obtained traveling wave solutions of the potential KdV equation (pKdV), and the (3+1)-dimensional shallow water wave equation (SWWE) with the help of the $\tan \left( \dfrac{\phi \left( \xi \right) }{2}\right)$- expansion method. The (2+1)-dimensional Kadomtsev–Petviashvili–Benjamin–Bona–Mahony (KP-BBM) wave equation was solved using this method by Khan et al. (2018), who got several different types of exact solutions. Abundant soliton solutions for Radhakrishnan–Kundu–Laksmanan (RKL) equation with Kerr law non-linearity by Akram et al. (2021) and Younis et al. (2021) using the suggested method.

The main advantage of these approaches is their ability to provide exact analytical solutions for various kinds of nonlinear partial differential equations. These are particularly helpful since they provide researchers with closed-form expressions that highlight the functional forms of the solutions. These methods follow a structured and systematic approaches. Researchers can easily access the approaches due to their systematic nature, which also helps to organise the solution process. Nonlinear partial differential equations are common in mathematical physics and other scientific fields, and these techniques are specifically made to deal with them. These are especially useful for solving equations with nonlinear terms, providing insight into the behavior of complex systems. These approaches have the disadvantage that, although they are effective for particular classes of nonlinear partial differential equations, their ability to be generalised may be restricted in other situations. Certain forms of nonlinear partial differential equations, particularly those with incredibly complicated or irregular solutions, may provide difficulties for the approaches to handle. Numerical techniques or other analytical methods might be better suitable in these situations.

2 Description of the methods

Consider a nonlinear partial differential equation

$$\begin{aligned} P\left( \psi ,\psi _x,\psi _y,\psi _z,\psi _{xy},\psi _{xz},\psi _{yt}, \cdots \right) , \end{aligned}$$

(2.1)

where $\psi = \psi (x,y,z,t)$ is unknown variable, x, y, z, and t are denoted partial derivatives. Now we introduce the wave transformation

$$\begin{aligned} \psi (x,y,z,t) = \Phi \left( \xi \right) , \,\,\,\,\,\,\,\xi = x+y+z-vt, \end{aligned}$$

(2.2)

where v is wave speed. The following nonlinear ordinary differential equation is obtained after substituting Eqs. 2.2 into 2.1

$$\begin{aligned} W\left( \Phi ,\Phi ',-v\,\Phi ', v^2\,\Phi '', \cdots \right) = 0, \end{aligned}$$

(2.3)

where prime denotes derivatives.

2.1 The modified $\left( \frac{G'}{G^{2}}\right)$-expansion method

Step 1. Assume the solution of Eq. 2.3 has the following form

$$\begin{aligned} \Phi \left( \xi \right) = M_0 + \sum ^{N}_{j=1} \left[ M_j \left( \dfrac{G'}{G^2} \right) ^j M_{-j} \left( \dfrac{G'}{G^2} \right) ^{-j} \right] , \end{aligned}$$

(2.4)

where $G = G\left( \xi \right)$.

$$\begin{aligned} \left( \dfrac{G'}{G^2} \right) ' = {\sigma } + {\theta } \left( \dfrac{G'}{G^2} \right) + {\chi } \left( \dfrac{G'}{G^2} \right) ^2, \end{aligned}$$

(2.5)

where ${\sigma }, {\theta },$ and ${\chi }$ are constant coefficients, while $M_0, M_j$ and $M_{-j} \, (j = 1, 2, \cdots , N)$ are unknown constants. Additionally, only one of $M_j$ or $M_{-j}$ can be zero at once; neither $M_j$ nor $M_{-j}$ can be zero simultaneously. Using the homogeneous balance principle on Eq. 2.3, we can calculate the value of the real number N.

Step 2. A system of algebraic equations is obtained by inserting Eqs. 2.4 and 2.5 into 2.3, gathering all coefficients that have the same power of $\left( \dfrac{G'}{G^2} \right) ^j$ where $\left( j = 0,1,2,\cdots \right)$ equal to zero. The system of algebraic equations can be solved by Maple software.

Step 3. The ordinary differential Eq. 2.5 has five possible types of solutions, as described in the following:

Type 1: If ${\sigma } {\chi } > 0$ and ${\theta } = 0$ then

$$\begin{aligned} \left( \dfrac{G'}{G^2}\right) = \dfrac{\sqrt{|{\sigma } {\chi }|}\bigg [\Omega _{{1}}\cos \left( \sqrt{ |{\sigma } {\chi }|}\xi \right) +\Omega _{{2}}\sin \left( \sqrt{|{\sigma } {\chi }|}\xi \right) \bigg ]}{\chi \bigg [ { \Omega _{{2}}\cos \left( \sqrt{|{\sigma } {\chi }|}\xi \right) -\Omega _{{1}}\sin \left( \sqrt{|{\sigma } {\chi }|}\xi \right) } \bigg ]}. \end{aligned}$$

(2.6)

Type 2: If ${\sigma } {\chi } < 0$ and ${\theta } = 0$ then

$$\begin{aligned} \left( \dfrac{G'}{G^2}\right) = - \dfrac{\sqrt{|{\sigma } {\chi }|}\bigg [\Omega _{{1}}\sinh \left( 2 \sqrt{|{\sigma } {\chi }|}\xi \right) +\Omega _{{1}}\cosh \left( 2\sqrt{|{\sigma } {\chi }|}\xi \right) +\Omega _{2} \bigg ]}{\chi \bigg [ { \Omega _{{1}}\cosh \left( 2 \sqrt{|{\sigma } {\chi }|} \xi \right) +\Omega _{{1}}\sinh \left( 2 \sqrt{|{\sigma } {\chi }|}\xi \right) }- \Omega _{2} \bigg ]}. \end{aligned}$$

(2.7)

Type 3: If ${\sigma } = 0, {\chi } \ne 0$ and ${\theta } = 0$ then

$$\begin{aligned} \left( \dfrac{G'}{G^2}\right) = - \dfrac{\Omega _1}{{\chi } \left( \Omega _{{1}} \xi + \Omega _2 \right) }. \end{aligned}$$

(2.8)

Type 4: If ${\theta } \ne 0$ and $\lambda \ge 0$ then

$$\begin{aligned} \left( \dfrac{G'}{G^2}\right) =- \dfrac{{\theta }}{2{\chi }} - \dfrac{\sqrt{\lambda } \left( \Omega _{{1}}\cosh \left( \dfrac{\sqrt{\lambda }}{2}\xi \right) +\Omega _{2}\, \sinh \left( \dfrac{\sqrt{\lambda }}{2}\xi \right) \right) }{2{\chi } \left( \Omega _2\, \cosh \left( \dfrac{\sqrt{\lambda }}{2}\xi \right) + \Omega _1\, \sinh \left( \dfrac{\sqrt{\lambda }}{2}\xi \right) \right) }. \end{aligned}$$

(2.9)

Type 5: If ${\theta } \ne 0$ and $\lambda < 0$ then

$$\begin{aligned} \left( \dfrac{G'}{G^2}\right) =- \dfrac{{\theta }}{2{\chi }} - \dfrac{\sqrt{-\lambda } \left( \Omega _{{1}}\cos \left( \dfrac{\sqrt{-\lambda }}{2}\xi \right) -\Omega _{2}\, \sin \left( \dfrac{\sqrt{-\lambda }}{2}\xi \right) \right) }{2{\chi } \left( \Omega _2\, \cos \left( \dfrac{\sqrt{-\lambda }}{2}\xi \right) + \Omega _1\, \sin \left( \dfrac{\sqrt{-\lambda }}{2}\xi \right) \right) }, \end{aligned}$$

(2.10)

where $\Omega _1, \Omega _2$ are arbitrary real numbers and $\lambda = {\theta }^2 - 4 {\sigma } {\chi }$.

Step 4. The exact solutions of Eq. 2.1 can be obtained by inserting the values of $M_0, M_j, M_{-j}$ and $\dfrac{G'}{G^2}$ into Eq. 2.4 and then putting into Eq. 2.2.

2.2 The improved $\tan \left( \frac{\phi (\xi )}{2}\right)$-expansion method

Step 1. Suppose the solution of Eq. 2.3 has the following form Manafian and Farshbaf Zinati (2020), Khan et al. (2018) and Akram et al. (2021)

$$\begin{aligned} \Phi \left( \xi \right) = \sum ^{N}_{j=0} M_j \left( k + \tan \left( \dfrac{\phi \left( \xi \right) }{2}\right) \right) ^j + \sum ^{N}_{j=1} M_{-j} \left( k + \tan \left( \dfrac{\phi \left( \xi \right) }{2}\right) \right) ^{-j}, \end{aligned}$$

(2.11)

where $M_j$ and $M_{-j}$ are unknown constants, such that both $M_j \ne 0$ and $M_{-j} \ne 0$ and $\phi (\xi )$ satisfies the following ordinary differential equation

$$\begin{aligned} \phi ^{'}\left( \xi \right) = {\sigma }\, \sin \left( \phi \left( \xi \right) \right) + {\theta }\, \cos \left( \phi \left( \xi \right) \right) + {\chi }, \end{aligned}$$

(2.12)

for sake of simplicity we convert $\sin \left( \phi \left( \xi \right) \right)$ and $\cos \left( \phi \left( \xi \right) \right)$ into $\tan \left( \phi \left( \xi \right) /2\right)$, so we can write

$$\begin{aligned} \sin \left( \phi \left( \xi \right) \right) = \dfrac{2\, \tan \left( \phi \left( \xi \right) /2\right) }{1+\tan ^2\left( \phi \left( \xi \right) /2\right) },\,\,\,\,\, \,\,\,\,\,\, \cos \left( \phi \left( \xi \right) \right) = \dfrac{1- \tan ^2\left( \phi \left( \xi \right) /2\right) }{1+\tan ^2\left( \phi \left( \xi \right) /2\right) }. \end{aligned}$$

(2.13)

Step 2. Inserting Eqs. 2.11, along with  2.12, 2.13 into Eq. 2.3, then setting the coefficients of same powers of $\left( \tan \left( \dfrac{\phi \left( \xi \right) }{2}\right) \right) ^j$, where $\left( j = 0,1,2,\cdots \right)$ equal to zero, we obtained a system of algebraic equations.

We will consider the following special solutions of Eq. 2.12:

Type 1: If $\lambda = {\sigma }^2 + {\theta }^2 - {\chi }^2 < 0$ and ${\theta } - {\chi } \ne 0$ then

$$\begin{aligned} \phi \left( \xi \right) =2\,\tan ^{-1} \bigg [ {\frac{{\sigma }}{{\theta }-{\chi }}}-{\frac{\sqrt{-\lambda }}{{\theta }-{\chi }}\tan \left( \dfrac{\sqrt{-\lambda }}{2} {\hat{\xi }} \right) } \bigg ]. \end{aligned}$$

(2.14)

Type 2: If $\lambda = {\sigma }^2 + {\theta }^2 - {\chi }^2 > 0$ and ${\theta } - {\chi } \ne 0$ then

$$\begin{aligned} \phi \left( \xi \right) =2\,\tan ^{-1} \bigg [ {\frac{{\sigma }}{{\theta }-{\chi }}}+{\frac{\sqrt{\lambda }}{{\theta }-{\chi }}\tanh \left( \dfrac{\sqrt{\lambda }}{2} {\hat{\xi }} \right) } \bigg ]. \end{aligned}$$

(2.15)

Type 3: If $\lambda = {\sigma }^2 + {\theta }^2 - {\chi }^2 > 0, {\theta } \ne 0$ and ${\chi } = 0$ then

$$\begin{aligned} \phi \left( \xi \right) =2\,\tan ^{-1} \bigg [ {\frac{{\sigma }}{{\theta }}}+{\frac{\sqrt{{\theta }^2+{\sigma }^2}}{{\theta }}\tanh \left( \dfrac{\sqrt{{\theta }^2+{\sigma }^2}}{2} {\hat{\xi }} \right) } \bigg ]. \end{aligned}$$

(2.16)

Type 4: If $\lambda = {\sigma }^2 + {\theta }^2 - {\chi }^2 < 0, {\chi } \ne 0$ and ${\theta } = 0$ then

$$\begin{aligned} \phi \left( \xi \right) =2\,\tan ^{-1} \bigg [ {-\frac{{\sigma }}{{\chi }}}+{\frac{\sqrt{{\chi }^2-{\sigma }^2}}{{\chi }}\tan \left( \dfrac{\sqrt{{\chi }^2-{\sigma }^2}}{2} {\hat{\xi }} \right) } \bigg ]. \end{aligned}$$

(2.17)

Type 5: If $\lambda = {\sigma }^2 + {\theta }^2 - {\chi }^2 > 0, {\theta }-{\chi } \ne 0$ and ${\sigma } = 0$ then

$$\begin{aligned} \phi \left( \xi \right) =2\,\tan ^{-1} \bigg [\sqrt{\frac{{\theta }+{\chi }}{{\theta }-{\chi }}} \tanh \left( \dfrac{\sqrt{{\theta }^2-{\chi }^2}}{2} {\hat{\xi }} \right) \bigg ]. \end{aligned}$$

(2.18)

Type 6: If ${\sigma } = 0$ and ${\chi } = 0$ then

$$\begin{aligned} \phi \left( \xi \right) = \tan ^{-1} \bigg [\frac{e^{2{\theta }{\hat{\xi }}}-1}{e^{2{\theta }{\hat{\xi }}} +1},\, \frac{2e^{{\theta }{\hat{\xi }}}}{e^{2{\theta }{\hat{\xi }}}+1} \bigg ]. \end{aligned}$$

(2.19)

Type 7: If ${\theta } = 0$ and ${\chi } = 0$ then

$$\begin{aligned} \phi \left( \xi \right) = \tan ^{-1} \bigg [\frac{2e^{{\sigma }{\hat{\xi }}}}{e^{2{\sigma }{\hat{\xi }}} +1},\, \frac{e^{2{\sigma }{\hat{\xi }}}-1}{e^{2{\sigma }{\hat{\xi }}}+1} \bigg ]. \end{aligned}$$

(2.20)

Type 8: If ${\sigma }^2+{\theta }^2 = {\chi }^2$ then

$$\begin{aligned} \phi \left( \xi \right) = 2\,\tan ^{-1} \bigg [\frac{{\sigma }{\hat{\xi }}+2}{\left( {\theta }-{\chi }\right) {\hat{\xi }}}\bigg ]. \end{aligned}$$

(2.21)

Type 9: If ${\sigma } = {\theta } = {\chi } = s{\sigma }$ then

$$\begin{aligned} \phi \left( \xi \right) = 2\,\tan ^{-1} \bigg [e^{s{\sigma }{\hat{\xi }}}-1\bigg ]. \end{aligned}$$

(2.22)

Type 10: If ${\sigma } = {\chi } = s{\sigma }$ and ${\theta } = -s{\sigma }$ then

$$\begin{aligned} \phi \left( \xi \right) = -2\,\tan ^{-1} \bigg [\dfrac{e^{s{\sigma }{\hat{\xi }}}}{-1+ e^{s{\sigma }{\hat{\xi }}}}\bigg ]. \end{aligned}$$

(2.23)

Type 11: If ${\chi } = {\sigma }$ then

$$\begin{aligned} \phi \left( \xi \right) = -2\,\tan ^{-1} \bigg [\dfrac{\left( {\sigma }+{\theta }\right) e^{{\theta }{\hat{\xi }}} -1}{\left( {\sigma }-{\theta }\right) e^{{\theta }{\hat{\xi }}}-1} \bigg ]. \end{aligned}$$

(2.24)

Type 12: If ${\sigma } = {\chi }$ then

$$\begin{aligned} \phi \left( \xi \right) = 2\,\tan ^{-1} \bigg [\dfrac{\left( {\theta }+{\chi }\right) e^{{\theta }{\hat{\xi }}} +1}{\left( {\theta }-{\chi }\right) e^{{\theta }{\hat{\xi }}}-1} \bigg ]. \end{aligned}$$

(2.25)

Type 13: If ${\chi } = -{\sigma }$ then

$$\begin{aligned} \phi \left( \xi \right) = 2\,\tan ^{-1} \bigg [\dfrac{e^{{\theta }{\hat{\xi }}} + {\theta }-{\sigma }}{e^{{\theta }{\hat{\xi }}}-{\theta }-{\sigma }} \bigg ]. \end{aligned}$$

(2.26)

Type 14: If ${\theta } = -{\chi }$ then

$$\begin{aligned} \phi \left( \xi \right) = 2\,\tan ^{-1} \bigg [\dfrac{{\sigma } e^{{\sigma }{\hat{\xi }}}}{1-{\chi } e^{{\sigma }{\hat{\xi }}}} \bigg ]. \end{aligned}$$

(2.27)

Type 15: If ${\theta } = 0$ and ${\sigma } = {\chi }$ then

$$\begin{aligned} \phi \left( \xi \right) = -2\,\tan ^{-1} \bigg [\dfrac{{\chi }{\hat{\xi }}+2}{{\chi }{\hat{\xi }}} \bigg ]. \end{aligned}$$

(2.28)

Type 16: If ${\sigma } = 0$ and ${\theta } = {\chi }$ then

$$\begin{aligned} \phi \left( \xi \right) = 2\,\tan ^{-1} \bigg [{\chi }{\hat{\xi }}\bigg ]. \end{aligned}$$

(2.29)

Type 17: If ${\sigma } = 0$ and ${\theta } = -{\chi }$ then

$$\begin{aligned} \phi \left( \xi \right) = -2\,\tan ^{-1} \bigg [\dfrac{1}{{\chi }{\hat{\xi }}}\bigg ]. \end{aligned}$$

(2.30)

Type 18: If ${\sigma } = 0$ and ${\theta } = 0$ then

$$\begin{aligned} \phi \left( \xi \right) = {\chi }\xi + C. \end{aligned}$$

(2.31)

Type 19: If ${\theta } = {\chi }$ then

$$\begin{aligned} \phi \left( \xi \right) = 2\,\tan ^{-1} \bigg [\dfrac{e^{{\sigma }{\hat{\xi }}}-{\chi }}{{\sigma }} \bigg ], \end{aligned}$$

(2.32)

where ${\hat{\xi }} = \xi + C$.

Step 4. The exact solutions of Eq. 2.1 are obtained by inserting the values of $M_0, M_j, M_{-j}$ and $\phi \left( \xi \right)$ into Eq. 2.4 and then putting the value of $\varphi (x,y,z,t)$ into Eq. 3.5.

3 Application of the methods

Consider the $(3+1)$ dimensional double sine-Gordon equation Wang (2021) as:

$$\begin{aligned} \psi _{xx}+ 2\psi _{x y}- \psi _{x z} +\psi _{yy}- \psi _{z y} - \psi _{x t} - \psi _{y t} + \psi _{z t}= \sin \psi +\sin 2\psi . \end{aligned}$$

(3.1)

Now

$$\begin{aligned} \varphi \left( x,y,z,t\right) = e^{i\,\psi \left( x,y,z,t\right) }, \end{aligned}$$

(3.2)

$$\begin{aligned} \psi \left( x,y,z,t\right) = \dfrac{1}{i} \ln \varphi \left( x,y,z,t\right) , \end{aligned}$$

(3.3)

Also

$$\begin{aligned} \sin \,\psi = \dfrac{\varphi - \varphi ^{-1}}{2 i}, \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\sin \,2\,\psi = \dfrac{\varphi ^2 - \varphi ^{-2}}{2 i},\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \ \cos \,\psi = \dfrac{\varphi + \varphi ^{-1}}{2}, \end{aligned}$$

(3.4)

$$\begin{aligned} \,\psi \left( x,y,z,t\right) = \cos ^{-1} \left( \dfrac{\varphi \left( x,y,z,t\right) + \varphi ^{-1}\left( x,y,z,t\right) }{2} \right) , \end{aligned}$$

(3.5)

The (3+1)-dimensional sine-Gordon equation is changed to an equivalent nonlinear partial differential equation, which is represented as, by substituting Eqs. 3.3 and 3.4 into Eq. 3.1.

$$\begin{aligned} 2\,\varphi \, \varphi _{xx} \, -\,2 \varphi ^2_x \, +\,4\,\varphi \,\varphi _{xy} \, -\,4 \varphi _x \, \varphi _y \,-\,2\,\varphi \,\varphi _{xz}\,+\, 2\,\varphi _x\, \varphi _z\,+\, 2\varphi \,\varphi _{yy} \,-\,2\varphi ^2_y \,-\,2\varphi \, \varphi _{yz} \,+\,2\, \varphi _y\,\varphi _z\,-\,2\varphi \, \varphi _{xt} \nonumber \\ \,+\,2\varphi _t \,\varphi _x \,-\,2\varphi \, \varphi _{yt} \, +\,2 \varphi _t \,\varphi _y \,+\,2\varphi \, \varphi _{zt} \,-\,2 \varphi _t \,\varphi _z \,-\,\varphi ^{4} \,-\, \varphi ^{3} \,+\,\varphi \,+\,1\,=\,0.\,\,\,\,\,\,\,\,\,\,\,\,\,\, \,\,\,\,\,\,\,\,\,\,\,\, \,\,\,\,\,\,\,\,\,\,\,\, \,\,\,\,\,\,\,\,\,\, \,\,\,\,\,\,\,\,\,\,\,\,\,\, \,\,\,\,\,\,\,\,\,\, \,\,\,\,\,\,\,\,\,\,\,\,\,\, \,\,\,\,\,\,\,\,\,\, \end{aligned}$$

(3.6)

Making wave transformation

$$\begin{aligned} \varphi \, = \Phi \left( {\zeta } \right) , \end{aligned}$$

(3.7)

where $\zeta \,=\, \alpha x+\beta y+ \gamma z\,-\,v\,t$. For sake of simplicity take $\alpha$= $\beta$= $\gamma$ =1. To convert into nonlinear partial differential equation, substitute Eqs. 3.7 into 3.6

$$\begin{aligned} 2\, \left( 2\,+\,v \right) \, \Phi \left( \zeta \right) \, \Phi ^{''}\left( \zeta \right) \, -\,2\, \left( 2\,+\,v \right) \, \left( \Phi ^{'}\left( \zeta \right) \right) ^2 \,-\, \Phi ^{4} \,-\, \Phi ^{3} \left( \zeta \right) \,+\, \Phi \left( \zeta \right) \,+\, 1\,=0, \end{aligned}$$

(3.8)

3.1 Exact solutions by the improved $\left( \frac{G'}{G^{2}}\right)$-expansion method

With $N = 1$, Eq. 2.4 contains the following formal solution

$$\begin{aligned} \Phi \left( \zeta \right) =M_{{0}}\,+\,M_{{1}}\, \left( {\frac{ G'}{ G^2}} \right) \,+\,M_{{-1}}\, \left( {\frac{ G'}{ G^2}} \right) ^{-1}, \end{aligned}$$

(3.9)

Substituting Eqs. 3.9 and  2.5 into Eq. 3.8 and collecting all coefficients that have the same powers of $\left( {\frac{ G'}{ G^2}}\right) ^{i}, i = 0,1,\cdots ,8,$ equals to zero, the following system of algebraic equations is obtained

$$\begin{aligned} {\left\{ \begin{array}{ll} 4\,{{\sigma }}^{2}{M^2_{-1}}\,-\,{M^4_{-1}}\,+\,2\,v\,{{\sigma }}^{2}{M^2_{-1}}\,=\,0,\\ 4\,{\sigma }\,{\theta }\,{M^2_{-1}}\,+\,4\,v\,{{\sigma }}^{2}M_{{0}}M_{{-1}}\,-\,{M^3_{{-1}}}\,+\,8\,{{\sigma }}^{2} M_{{0}}M_{{-1}}\,+\,2\,v\,{\sigma }\,{\theta }\,{M^2_{{-1}}}\,-\,4\,M_{{0}}{M^3_{{-1}}}\,=\,0,\\ 6\,v\,{\sigma }\,{\theta }\,M_{{0}}M_{{-1}}\,-\,3\,M_{{0}}{M^2_{{-1}}}\,-\,4\,M_{1}{M^3_{-1}} \,+\,8\,v\,{{\sigma }}^{2}M_{1}M_{-1} \,+\, 16\,{{\sigma }}^{2}M_{1}M_{-1}\,-\, 6\,{M^2_{0}} {M^2_{-1}} \,+\, 12\,{\sigma }\,{\theta }\,M_{{0}}M_{{-1}} \,=\, 0,\\ -3\,{M^2_{0}}M_{-1} \,-\, 3\,M_{1}{M^2_{-1}} \,-\, 4\,{M^3_{0}}M_{-1} \,+\, 32\,{\sigma }\, {\theta }\,M_{{1}}M_{{-1}}\,+\, 8\,{\sigma }\,{\chi }\,M_{0}M_{-1} \,-\, 4\,{\theta }\,{\chi }\,{M^2_{-1}} \,-\, 2\,v\, {\theta }\,{\chi }\,{M^2_{-1}}\\ \,+\, 4\,v\,{\sigma }\,{\chi }\,M_{0}M_{-1} \,+\, 4\,{{\theta }}^{2}M_{{0}}M_{{-1}} \,+\, M_{-1} \,-\, 12\,M_{0}M_{1}{M^2_{-1}} \,+\, 2\,v\,{{\theta }}^{2}M_{0}M_{-1} \,+\, 16\,v\, {\sigma }\,{\theta }\,M_{1}M_{-1} \,=\, 0,\\ M_{0} \,+\, 4\,{\sigma }\,{\theta }\,M_{0}M_{1} \,+\, 4\,{\theta }\,{\chi }\,M_{0}M_{-1} \,-\, {M^4_{0}} \,-\, 4\,{{\chi }}^{2}{M^2_{-1}} \,+\, 2\,v\,{\sigma }\,{\theta }\,M_{0}M_{1} \,-\, 6\,M_{0}M_{1}M_{-1} \,+\, 2\,v\,{\theta }\,{\chi }\,M_{0}M_{-1}\\ \,+\, 16\,{{\theta }}^{2}M_{1}M_{-1} \,-\, 4\,{{\sigma }}^{2}{M^2_{1}} \,+\, 16\,v\,{\sigma }\,{\chi }\,M_{1}M_{-1} \,-\, {M^3_{0}} \,-\, 2\,v\,{{\sigma }}^{2}{M^2_{1}} \,+\,1 \,+\, 32\,{\sigma }\,{\chi }\,M_{1}M_{-1} \,-\, 12\,{M^2_{0}}M_{1}M_{-1}\\ \,+\, 8\,v\,{{\theta }}^{2} M_{1}M_{-1} \,-\, 6\,{M^2_{1}}{M^2_{-1}} \,-\, 2\,v\,{{\chi }}^{2}{M^2_{-1}} \,=\, 0,\\ 16\,v\,{\theta }\,{\chi }\,M_{1}M_{-1} \,+\, 2\,v\,{{\theta }}^{2}M_{0}M_{1} \,-\, 12\,M_{0}{M^2_{1}} M_{-1} \,+\, M_{1} \,-\, 2\,v\,{\sigma }\,{\theta }\,{M^2_{1}} \,-\, 4\,{\sigma }\,{\theta }\,{M^2_{1}} \,+\, 4\,v\,{\sigma }\,{\chi }\,M_{0}M_{1} \,-\, 3\,{M^2_{0}}M_{1} \\ \,-\, 4\,{M^3_{0}}M_{1} \,+\, 32\,{\theta }\,{\chi }\,M_{1}M_{-1} \,+\, 8\,{\sigma }\,{\chi }\,M_{0}M_{1} \,-\, 3\,{M^2_{1}}M_{-1} \,+\, 4\,{{\theta }}^{2}M_{0}M_{1} \,=\, 0,\\ -3\,M_{0}{M^2_{1}} \,+\, 16\,{{\chi }}^{2}M_{-1}M_{1} \,-\, 6\,{M^2_{0}}{M^2_{1}} \,-\, 4\,{M^3_{1}}M_{-1} \,+\, 12\,{\theta }\,{\chi }\,M_{0}M_{1} \,+\, 8\,v\,{{\chi }}^{2}M_{-1}M_{1} \,+\, 6\,v\,{\theta }\,{\chi }\,M_{0}M_{1} \,=\, 0,\\ 8\,{{\chi }}^{2}M_{0}M_{1} \,+\, 4\,{\theta }\,{\chi }\,{M^2_{1}} \,-\, {M^3_{1}} \,+\, 2\,v\,{\theta }\,{\chi }\,{M^2_{1}} \,+\, 4\,v\,{{\chi }}^{2}M_{0}M_{1}\,-\, 4\,M_{0}{M^3_{1}} \,=\, 0,\\ 2\,v\,{{\chi }}^{2}{M^2_{1}} \,+\, 4\,{{\chi }}^{2}{M^2_{1}} \,-\, {M^4_{1}} \,=\,0. \end{array}\right. } \end{aligned}$$

(3.10)

Solving Eq. 3.10 with the help of Mathematica, we have

$$\begin{aligned}{} & {} M_{{0}}=-\,\dfrac{1}{2} \pm \, {\theta }\,\sqrt{\dfrac{3}{-{{\theta }}^{2}+4\,{\sigma }\,{\chi } }}, \, M_1 = 0, \,\end{aligned}$$

(3.11)

$$\begin{aligned}{} & {} \quad M_{{-1}}=\pm \, {\sigma }\,\sqrt{\dfrac{3}{-{{\theta }}^{2}+4\,{\sigma }\,{\chi } }}, \, v=-\,2-\dfrac{3}{ 2\left( {{\theta }}^{2}-4\,{\sigma }\,{\chi }\right) }. \end{aligned}$$

(3.12)

$$\begin{aligned}{} & {} \quad M_{{0}}=-\,\dfrac{1}{2} \pm \, {\theta }\,\sqrt{\dfrac{3}{-{{\theta }}^{2}+4\,{\sigma }\,{\chi } }}, \, M_1 =\pm \, {\chi }\,\sqrt{\dfrac{3}{-{{\theta }}^{2}+4\,{\sigma }\,{\chi } }}, M_{{-1}}= 0,\, v=-\,2-\dfrac{3}{ 2\left( {{\theta }}^{2}-4\,{\sigma }\,{\chi }\right) }. \end{aligned}$$

(3.13)

Plugging Eq. 3.13 along with Eqs. 3.9 into 3.7 then we obtained following soliton solutions of 3.1,

Type 1: If ${\sigma }\,{\chi }\,>0$ and $\,{\theta }\,=\,0$ then

$$\begin{aligned}{} & {} \psi _{{1,1}}(x,y,z,t) = \cos ^{-1} \left( \dfrac{ \left( -\,\dfrac{1}{2} \pm \dfrac{\sqrt{3}}{2} \left( {\frac{ \Omega _{{2}}\cos \left( \sqrt{{\sigma } {\chi }}\zeta \right) -\Omega _{{1}}\sin \left( \sqrt{{\sigma } {\chi }}\zeta \right) }{\Omega _{{1}}\cos \left( \sqrt{{\sigma } {\chi }} \zeta \right) +\Omega _{{2}}\sin \left( \sqrt{{\sigma } {\chi }}\zeta \right) }} \right) \right) ^2 + 1}{ -\, 1 \pm \sqrt{3} \left( {\frac{ \Omega _{{2}}\cos \left( \sqrt{{\sigma } {\chi }}\zeta \right) -\Omega _{{1}}\sin \left( \sqrt{{\sigma } {\chi }}\zeta \right) }{\Omega _{{1}}\cos \left( \sqrt{{\sigma } {\chi }} \zeta \right) +\Omega _{{2}}\sin \left( \sqrt{{\sigma } {\chi }}\zeta \right) }} \right) } \right) , \end{aligned}$$

(3.14)

$$\begin{aligned}{} & {} \quad \,\psi _{{2,1}}(x,y,z,t) = \cos ^{-1} \left( \dfrac{\left( - \dfrac{1}{2} \pm \dfrac{\sqrt{3}}{2} \left( \dfrac{\Omega _{{1}}\cos \left( \sqrt{{\sigma } {\chi }}\zeta \right) +\Omega _ {{2}}\sin \left( \sqrt{{\sigma } {\chi }}\zeta \right) }{\Omega _{{2}}\cos \left( \sqrt{{\sigma } {\chi }}\zeta \right) -\Omega _{{1}}\sin \left( \sqrt{{\sigma } {\chi }}\zeta \right) } \right) \right) ^2 + 1}{- 1 \pm \sqrt{3} \left( \dfrac{\Omega _{{1}}\cos \left( \sqrt{{\sigma } {\chi }}\zeta \right) +\Omega _ {{2}}\sin \left( \sqrt{{\sigma } {\chi }}\zeta \right) }{\Omega _{{2}}\cos \left( \sqrt{{\sigma } {\chi }}\zeta \right) -\Omega _{{1}}\sin \left( \sqrt{{\sigma } {\chi }}\zeta \right) } \right) } \right) , \end{aligned}$$

(3.15)

where $\zeta = x+y+z-vt.$

Type 2: If ${\sigma }\,{\chi }\,<0$ and $\,{\theta }\,=\,0$ then

$$\begin{aligned} \psi _{{3,2}}(x,y,z,t) = \cos ^{-1} \left( \dfrac{\left( -\dfrac{1}{2} \mp \dfrac{\sqrt{3}}{2}\,\left( {\frac{ \Omega _{{1}}\cosh \left( 2\,\sqrt{ \left| {\sigma } {\chi } \right| }\zeta \right) +\Omega _{{1}}\sinh \left( 2\,\sqrt{ \left| {\sigma } {\chi } \right| }\zeta \right) -\Omega _{{2}} }{\Omega _{{1}}\sinh \left( 2\,\sqrt{ \left| {\sigma } {\chi } \right| }\zeta \right) +\Omega _{{1}}\cosh \left( 2\,\sqrt{ \left| {\sigma } {\chi } \right| }\zeta \right) +\Omega _{{2}}}} \right) \right) ^2 + 1}{- 1 \mp \sqrt{3}\,\left( {\frac{ \Omega _{{1}}\cosh \left( 2\,\sqrt{ \left| {\sigma } {\chi } \right| }\zeta \right) +\Omega _{{1}}\sinh \left( 2\,\sqrt{ \left| {\sigma } {\chi } \right| }\zeta \right) -\Omega _{{2}} }{\Omega _{{1}}\sinh \left( 2\,\sqrt{ \left| {\sigma } {\chi } \right| }\zeta \right) +\Omega _{{1}}\cosh \left( 2\,\sqrt{ \left| {\sigma } {\chi } \right| }\zeta \right) +\Omega _{{2}}}} \right) } \right) , \end{aligned}$$

(3.16)

$$\begin{aligned} \,\psi _{{4,2}}(x,y,z,t) = \cos ^{-1} \left( \dfrac{\left( - \dfrac{1}{2} \mp \dfrac{\sqrt{3}}{2} \left( \frac{ \Omega _{{1}} \sinh \left( 2\,\sqrt{ \left| {\sigma } {\chi } \right| }\zeta \right) +\Omega _{{1}}\cosh \left( 2\,\sqrt{ \left| {\sigma } {\chi } \right| }\zeta \right) +\Omega _{{2}} }{\Omega _{{1}}\cosh \left( 2\,\sqrt{ \left| {\sigma } {\chi } \right| }\zeta \right) +\Omega _{{1}}\sinh \left( 2\,\sqrt{ \left| {\sigma } {\chi } \right| }\zeta \right) -\Omega _{{2}}}\right) \right) ^2 + 1}{- 1 \mp \sqrt{3} \left( \frac{ \Omega _{{1}} \sinh \left( 2\,\sqrt{ \left| {\sigma } {\chi } \right| }\zeta \right) +\Omega _{{1}}\cosh \left( 2\,\sqrt{ \left| {\sigma } {\chi } \right| }\zeta \right) +\Omega _{{2}} }{\Omega _{{1}}\cosh \left( 2\,\sqrt{ \left| {\sigma } {\chi } \right| }\zeta \right) +\Omega _{{1}}\sinh \left( 2\,\sqrt{ \left| {\sigma } {\chi } \right| }\zeta \right) -\Omega _{{2}}}\right) }\right) , \end{aligned}$$

(3.17)

where $\zeta = x+y+z-vt.$ Type 3: If ${\sigma }\,=\,0, {\chi }\,\ne \,0$ and $\,{\theta }\,=\,0$ then

$$\begin{aligned} \psi _{{5,3}}(x,y,z,t) = \cos ^{-1} \left( - \dfrac{5}{2} \right) , \end{aligned}$$

(3.18)

where $\zeta = x+y+z-vt.$ Type 4: If ${\theta }\,\ne \,0$ and $\,\lambda = {\theta }^2-4 {\sigma } {\chi }\,\ge \,0$ then

$$\begin{aligned}{} & {} \psi _{{6,4}}(x,y,z,t) = \cos ^{-1} \left( \dfrac{\left( -\dfrac{1}{2} \mp i \sqrt{\dfrac{3}{\lambda }} \left( {\theta }+ {\frac{2\,{\sigma }\,{\chi } \left( \Omega _{{2}}\cosh \left( \dfrac{\sqrt{\lambda }}{2}\zeta \right) +\Omega _{{1}} \sinh \left( \dfrac{\sqrt{\lambda }}{2}\zeta \right) \right) }{-{\theta }\left( \Omega _{{2}}\cosh \left( \dfrac{\sqrt{\lambda }}{2}\zeta \right) +\Omega _{{1}}\sinh \left( \dfrac{\sqrt{\lambda }}{2}\zeta \right) \right) -\sqrt{\lambda }\left( \Omega _{{1}}\cosh \left( \dfrac{ \sqrt{\lambda }}{2}\zeta \right) +\Omega _{{2}}\sinh \left( \dfrac{\sqrt{\lambda }}{2}\zeta \right) \right) }} \right) \right) ^2 + 1}{-1 \mp i\,2 \sqrt{\dfrac{3}{\lambda }} \left( {\theta }+ {\frac{2\,{\sigma }\,{\chi } \left( \Omega _{{2}}\cosh \left( \dfrac{\sqrt{\lambda }}{2}\zeta \right) +\Omega _{{1}} \sinh \left( \dfrac{\sqrt{\lambda }}{2}\zeta \right) \right) }{-{\theta }\left( \Omega _{{2}}\cosh \left( \dfrac{\sqrt{\lambda }}{2}\zeta \right) +\Omega _{{1}}\sinh \left( \dfrac{\sqrt{\lambda }}{2}\zeta \right) \right) -\sqrt{\lambda }\left( \Omega _{{1}}\cosh \left( \dfrac{ \sqrt{\lambda }}{2}\zeta \right) +\Omega _{{2}}\sinh \left( \dfrac{\sqrt{\lambda }}{2}\zeta \right) \right) }} \right) } \right) , \end{aligned}$$

(3.19)

$$\begin{aligned}{} & {} \quad \psi _{{7,4}}(x,y,z,t) = \cos ^{-1} \left( \dfrac{\left( - \dfrac{1}{2} \mp \dfrac{i}{2} \sqrt{\dfrac{3}{\lambda }} \left( {\theta }-{\frac{\sqrt{\lambda } \left( \Omega _{{1}}\cosh \left( \dfrac{\sqrt{\lambda }}{2}\zeta \right) +\Omega _{{2}}\sinh \left( \dfrac{\sqrt{\lambda }}{2}\zeta \right) \right) }{\Omega _{{2}}\cosh \left( \dfrac{\sqrt{\lambda }}{2}\zeta \right) +\Omega _{{1}}\sinh \left( \dfrac{\sqrt{\lambda }}{2}\zeta \right) }} \right) \right) ^2 + 1}{- 1 \mp i \sqrt{\dfrac{3}{\lambda }} \left( {\theta }-{\frac{\sqrt{\lambda } \left( \Omega _{{1}}\cosh \left( \dfrac{\sqrt{\lambda }}{2}\zeta \right) +\Omega _{{2}}\sinh \left( \dfrac{\sqrt{\lambda }}{2}\zeta \right) \right) }{\Omega _{{2}}\cosh \left( \dfrac{\sqrt{\lambda }}{2}\zeta \right) +\Omega _{{1}}\sinh \left( \dfrac{\sqrt{\lambda }}{2}\zeta \right) }} \right) } \right) , \end{aligned}$$

(3.20)

where $\zeta = x+y+z-vt.$

Type 5: If ${\theta }\,\ne \,0$ and $\,\lambda = {\theta }^2-4 {\sigma } {\chi }\,< \,0$ then

$$\begin{aligned}{} & {} \psi _{{8,5}}(x,y,z,t) = \cos ^{-1} \left( \dfrac{ \left( - \dfrac{1}{2} \pm \sqrt{\dfrac{3}{\lambda }} \left( {\theta }+{\frac{2\,{\sigma }\,{\chi } \left( \Omega _{{2}}\cos \left( \dfrac{\sqrt{-\lambda }}{2}\zeta \right) +\Omega _{{1}}\sin \left( \dfrac{\sqrt{-\lambda }}{2}\zeta \right) \right) }{-{\theta } \left( \Omega _{{2}}\cos \left( \dfrac{\sqrt{-\lambda }}{2}\zeta \right) +\Omega _{{1}}\sin \left( \dfrac{\sqrt{-\lambda }}{2}\zeta \right) \right) -\sqrt{-\lambda } \left( \Omega _{{1}}\cos \left( \dfrac{\sqrt{-\lambda }}{2}\zeta \right) -\Omega _{{2}}\sin \left( \dfrac{\sqrt{-\lambda }}{2}\zeta \right) \right) }} \right) \right) ^2 + 1}{- 1 \pm 2\,\sqrt{\dfrac{3}{\lambda }} \left( {\theta }+{\frac{2\,{\sigma }\,{\chi } \left( \Omega _{{2}}\cos \left( \dfrac{\sqrt{-\lambda }}{2}\zeta \right) +\Omega _{{1}}\sin \left( \dfrac{\sqrt{-\lambda }}{2}\zeta \right) \right) }{-{\theta } \left( \Omega _{{2}}\cos \left( \dfrac{\sqrt{-\lambda }}{2}\zeta \right) +\Omega _{{1}}\sin \left( \dfrac{\sqrt{-\lambda }}{2}\zeta \right) \right) -\sqrt{-\lambda } \left( \Omega _{{1}}\cos \left( \dfrac{\sqrt{-\lambda }}{2}\zeta \right) -\Omega _{{2}}\sin \left( \dfrac{\sqrt{-\lambda }}{2}\zeta \right) \right) }} \right) } \right) , \end{aligned}$$

(3.21)

$$\begin{aligned}{} & {} \quad \psi _{{9,5}}(x,y,z,t) = \cos ^{-1} \left( \dfrac{\left( - \dfrac{1}{2} \mp \dfrac{i}{2}\sqrt{\dfrac{3}{\lambda }} \left( {\theta }-{\frac{\sqrt{-\lambda } \left( \Omega _{{1}}\cos \left( \dfrac{\sqrt{-\lambda } }{2}\zeta \right) -\Omega _{{2}}\sin \left( \dfrac{\sqrt{-\lambda }}{2}\zeta \right) \right) }{\Omega _{{2}}\cos \left( \dfrac{\sqrt{-\lambda }}{2}\zeta \right) +\Omega _{{1}}\sin \left( \dfrac{\sqrt{-\lambda }}{2}\zeta \right) }} \right) \right) ^2 + 1}{- 1 \mp i \sqrt{\dfrac{3}{\lambda }} \left( {\theta }-{\frac{\sqrt{-\lambda } \left( \Omega _{{1}}\cos \left( \dfrac{\sqrt{-\lambda } }{2}\zeta \right) -\Omega _{{2}}\sin \left( \dfrac{\sqrt{-\lambda }}{2}\zeta \right) \right) }{\Omega _{{2}}\cos \left( \dfrac{\sqrt{-\lambda }}{2}\zeta \right) +\Omega _{{1}}\sin \left( \dfrac{\sqrt{-\lambda }}{2}\zeta \right) }} \right) } \right) , \end{aligned}$$

(3.22)

where $\zeta = x+y+z-vt.$

3.2 Exact solutions by the improved $\tan \left( \frac{\phi (\xi )}{2}\right)$-expansion method

Equation 2.11 contains the following formal solution

$$\begin{aligned} \Phi \left( \zeta \right) = M_0 + M_1 \left( k + \tan \left( \dfrac{\phi (\zeta )}{2}\right) \right) + M_{-1} \left( k + \tan \left( \dfrac{\phi (\zeta )}{2}\right) \right) ^{-1}, \end{aligned}$$

(3.23)

Substituting Eqs. 3.23, 2.12 and 2.13 into  3.8 and collecting all coefficients that have the same powers of $\tan \left( \dfrac{\phi (\zeta )}{2} \right) ^{i},\, i = 0,1, \cdots ,8,$ equals to zero, the following result of algebraic equations is solved with the help of Maple

$$\begin{aligned} M_0= & {} \dfrac{\pm \sqrt{3}\left( k\,{\chi }-{\sigma }-k\,{\theta }\right) - \sqrt{ -\left( {\sigma }^2+{\theta }^2-{\chi }^2\right) }}{2\sqrt{-\left( {\sigma }^2+{\theta }^2-{\chi }^2\right) }}, \nonumber \\ \, M_1= & {} \pm \dfrac{\sqrt{3}\left( {\theta }-{\chi }\right) }{2\sqrt{-\left( {\sigma }^2+{\theta }^2-{\chi }^2\right) }},\nonumber \\ M_{-1}= & {} 0,\,v = -\,\dfrac{4\left( {\sigma }^2+{\theta }^2-{\chi }^2\right) +3}{2\left( {\sigma }^2+{\theta }^2-{\chi }^2\right) } \end{aligned}$$

(3.24)

Plugging 3.24 along with Eqs. 3.23 into 3.7 then the soliton solutions of Eq. 3.1 are listed below

Type 1: When $\lambda = {\sigma }^2+{\theta }^2-{\chi }^2 <0$ and ${\theta }-{\chi } \ne 0$ then

$$\begin{aligned} \psi _{{1,1}}(x,y,z,t) = \cos ^{-1} \left( \dfrac{\left( - \dfrac{1}{2} \mp \dfrac{\sqrt{3}}{2} \tan \left( \dfrac{\sqrt{-\lambda }}{2}{\hat{\zeta }} \right) \right) ^2 + 1}{- 1 \mp \sqrt{3} \tan \left( \dfrac{\sqrt{-\lambda }}{2}{\hat{\zeta }} \right) } \right) , \end{aligned}$$

(3.25)

where ${\hat{\zeta }} = \left( x + y + z - vt\right) + C.$

Type 2: When $\lambda = {\sigma }^2+{\theta }^2-{\chi }^2 > 0$ and ${\theta }-{\chi } \ne 0$ then

$$\begin{aligned} \psi _{{2,2}}(x,y,z,t) = \cos ^{-1} \left( \dfrac{ \left( - \dfrac{1}{2} \mp i \dfrac{\sqrt{3}}{2}\, \tanh \left( \dfrac{\sqrt{\lambda }}{2}{\hat{\zeta }} \right) \right) ^2 + 1}{ - 1 \mp i \sqrt{3}\, \tanh \left( \dfrac{\sqrt{\lambda }}{2}{\hat{\zeta }} \right) } \right) , \end{aligned}$$

(3.26)

where ${\hat{\zeta }} = \left( x + y + z - vt\right) + C.$

Type 3: When $\lambda = {\sigma }^2+{\theta }^2-{\chi }^2 > 0$, ${\theta } \ne 0,$ and ${\chi } = 0$ then

$$\begin{aligned} \psi _{{3,3}}(x,y,z,t) = \cos ^{-1} \left( \dfrac{ \left( - \dfrac{1}{2} \mp i \dfrac{\sqrt{3}}{2}\, \tanh \left( \dfrac{\sqrt{{\sigma }^2+{\theta }^2}}{2}{\hat{\zeta }} \right) \right) ^2 + 1}{ - 1 \mp i \sqrt{3}\, \tanh \left( \dfrac{\sqrt{{\sigma }^2+{\theta }^2}}{2}{\hat{\zeta }} \right) } \right) , \end{aligned}$$

(3.27)

where ${\hat{\zeta }} = \left( x + y + z - vt\right) + C.$ Type 4: When $\lambda = {\sigma }^2+{\theta }^2-{\chi }^2 < 0$, ${\chi } \ne 0,$ and ${\theta } = 0$ then

$$\begin{aligned} \psi _{{4,4}}(x,y,z,t) = \cos ^{-1} \left( \dfrac{ \left( - \dfrac{1}{2} \mp \dfrac{\sqrt{3}}{2}\, \tan \left( \dfrac{\sqrt{{\chi }^2-{\sigma }^2}}{2}{\hat{\zeta }} \right) \right) ^2 + 1}{ - 1 \mp \sqrt{3}\, \tan \left( \dfrac{\sqrt{{\chi }^2-{\sigma }^2}}{2}{\hat{\zeta }} \right) } \right) , \end{aligned}$$

(3.28)

where ${\hat{\zeta }} = \left( x + y + z - vt\right) + C.$ Type 5: When $\lambda = {\sigma }^2+{\theta }^2-{\chi }^2 > 0$, ${\theta } - {\chi } \ne 0,$ and ${\sigma } = 0$ then

$$\begin{aligned} \psi _{{5,5}}(x,y,z,t) = \cos ^{-1} \left( \dfrac{ \left( - \dfrac{1}{2} \pm \dfrac{1}{2} \,\sqrt{\dfrac{3}{{\chi } - {\theta }}}\, \tanh \left( \dfrac{\sqrt{{\theta }^2-{\chi }^2}}{2} {\hat{\zeta }} \right) \right) ^2 + 1}{ - 1 \pm \sqrt{\dfrac{3}{{\chi } - {\theta }}}\, \tanh \left( \dfrac{\sqrt{{\theta }^2-{\chi }^2}}{2}{\hat{\zeta }} \right) } \right) , \end{aligned}$$

(3.29)

where ${\hat{\zeta }} = \left( x + y + z - vt\right) + C.$ Type 6: When ${\sigma } = 0,$ and ${\chi } = 0$ then

$$\begin{aligned} \psi _{{6,6}}(x,y,z,t) = \cos ^{-1} \left( \dfrac{ \left( - \dfrac{1}{2} \mp i \dfrac{\sqrt{3}}{2}\, \tan \left( \dfrac{1}{2}\, \tan ^{-1}\left( \dfrac{e^{2{\theta } {\hat{\zeta }}} - 1}{e^{2{\theta }{\hat{\zeta }}} + 1}, \dfrac{2e^{{\theta }{\hat{\zeta }}}}{e^{2{\theta }{\hat{\zeta }}} + 1}\right) \right) \right) ^2 + 1}{- 1 \mp i \sqrt{3}\, \tan \left( \dfrac{1}{2}\, \tan ^{-1}\left( \dfrac{e^{2{\theta }{\hat{\zeta }}} - 1}{e^{2{\theta }{\hat{\zeta }}} + 1}, \dfrac{2e^{{\theta }{\hat{\zeta }}}}{e^{2{\theta }{\hat{\zeta }}} + 1}\right) \right) } \right) , \end{aligned}$$

(3.30)

where ${\hat{\zeta }} = \left( x + y + z - vt\right) + C.$ Type 7: When ${\theta } = 0,$ and ${\chi } = 0$ then

$$\begin{aligned} \psi _{{7,7}}(x,y,z,t) = \cos ^{-1} \left( \dfrac{ \left( \dfrac{-1 \pm i \sqrt{3}}{2} \right) ^2 + 1}{ -1 \pm i \sqrt{3} } \right) . \end{aligned}$$

(3.31)

Type 8: When ${\sigma } = {\theta } = {\chi } = s\,{\sigma }$ then

$$\begin{aligned} \psi _{{8,8}}(x,y,z,t) = \cos ^{-1} \left( \dfrac{ \left( \dfrac{-1 \pm i \sqrt{3}}{2} \right) ^2 + 1}{ -1 \pm i \sqrt{3} } \right) . \end{aligned}$$

(3.32)

Type 9: When ${\sigma } = {\chi } = s\,{\sigma }$ and ${\theta } = - s\,{\sigma }$ then

$$\begin{aligned} \psi _{{9,9}}(x,y,z,t) = \cos ^{-1} \left( \dfrac{ \left( \dfrac{-1 \pm i \sqrt{3}}{2} \mp i \dfrac{\sqrt{3}\, e^{s{\sigma }{\hat{\zeta }}}}{e^{s{\sigma }{\hat{\zeta }}} - 1} \right) ^2 + 1}{-1 \pm i \sqrt{3}\, \mp i \dfrac{2\, \sqrt{3}\, e^{s{\sigma }{\hat{\zeta }}}}{e^{s{\sigma } {\hat{\zeta }}} - 1}} \right) , \end{aligned}$$

(3.33)

where ${\hat{\zeta }} = \left( x + y + z - vt\right) + C.$

Type 10: When ${\chi } = {\sigma }$ then

$$\begin{aligned} \psi _{{10,10}}(x,y,z,t) = \cos ^{-1} \left( \dfrac{ \left( - \dfrac{1}{2} \mp i \dfrac{\sqrt{3}}{2} \left( {\frac{1+ \left( {\sigma }-{\theta } \right) {e}^{{\theta } {\hat{\zeta }} }}{ \left( {\sigma }-{\theta }\right) {e}^{{\theta } {\hat{\zeta }} }-1}}\right) \right) ^2 + 1}{- 1 \mp i \sqrt{3} \left( {\frac{1+ \left( {\sigma }-{\theta } \right) {e}^{{\theta } {\hat{\zeta }} }}{ \left( {\sigma }-{\theta }\right) {e}^{{\theta } {\hat{\zeta }} }-1}}\right) } \right) , \end{aligned}$$

(3.34)

where ${\hat{\zeta }} = \left( x + y + z - vt\right) + C.$

Type 11: When ${\sigma } = {\chi }$ then

$$\begin{aligned} \psi _{{11,11}}(x,y,z,t) = \cos ^{-1} \left( \dfrac{ \left( - \dfrac{1}{2} \mp i \dfrac{\sqrt{3}}{2} \left( {\frac{1+ \left( {\theta }-{\chi } \right) {e}^{{\theta } {\hat{\zeta }} }}{ \left( {\theta }-{\chi }\right) {e}^{{\theta } {\hat{\zeta }} }-1}}\right) \right) ^2 + 1}{- 1 \mp i \sqrt{3} \left( {\frac{1+ \left( {\theta }-{\chi } \right) {e}^{{\theta } {\hat{\zeta }} }}{ \left( {\theta }-{\chi }\right) {e}^{{\theta } {\hat{\zeta }} }-1}}\right) } \right) , \end{aligned}$$

(3.35)

where ${\hat{\zeta }} = \left( x + y + z - vt\right) + C.$ Type 12: When ${\chi } = -{\sigma }$ then

$$\begin{aligned} \psi _{{12,12}}(x,y,z,t) = \cos ^{-1} \left( \dfrac{ \left( - \dfrac{1}{2} \mp i \dfrac{\sqrt{3}}{2} \left( {\frac{{e}^{{\theta } {\hat{\zeta }}} +{\theta }+{\sigma }}{ {e}^{{\theta } {\hat{\zeta }} } -{\theta }-{\sigma }}}\right) \right) ^2 + 1}{- 1 \mp i \sqrt{3} \left( {\frac{{e}^{{\theta } {\hat{\zeta }}} +{\theta }+{\sigma }}{ {e}^{{\theta } {\hat{\zeta }} }-{\theta }-{\sigma }}}\right) } \right) , \end{aligned}$$

(3.36)

where ${\hat{\zeta }} = \left( x + y + z - vt\right) + C.$ Type 13: When ${\theta } = -{\chi }$ then

$$\begin{aligned} \psi _{{13,13}}(x,y,z,t) = \cos ^{-1} \left( \dfrac{ \left( - \dfrac{1}{2} \pm i \dfrac{\sqrt{3}}{2} \left( {1 + \frac{2{\chi }{e}^{{\sigma } {\hat{\zeta }}}}{1-{\chi }{e}^{{\sigma } {\hat{\zeta }} }}}\right) \right) ^2 + 1}{- 1 \pm i \sqrt{3} \left( {1 + \frac{2{\chi }{e}^{{\sigma } {\hat{\zeta }}}}{1-{\chi }{e}^{{\sigma } {\hat{\zeta }} }}}\right) } \right) , \end{aligned}$$

(3.37)

where ${\hat{\zeta }} = \left( x + y + z - vt\right) + C.$ Type 14: When ${\sigma } = 0$ and ${\theta } = 0$ then

$$\begin{aligned} \psi _{{14,14}}(x,y,z,t) = \cos ^{-1} \left( \dfrac{ \left( - \dfrac{1}{2} \mp \dfrac{\sqrt{3}}{2}\tan \left( \dfrac{{\chi }\zeta +\,C}{2}\right) \right) ^2 + 1}{- 1 \mp \sqrt{3} \tan \left( \dfrac{{\chi }\zeta +\,C}{2}\right) } \right) , \end{aligned}$$

(3.38)

where $\zeta = x + y + z - vt.$ Type 15: When ${\theta } = {\chi }$ then

$$\begin{aligned} \psi _{{15,15}}(x,y,z,t) = \cos ^{-1} \left( \dfrac{ \left( \dfrac{-1\pm i \sqrt{3}}{2} \right) ^2 + 1}{-1\pm i \sqrt{3}} \right) . \end{aligned}$$

(3.39)

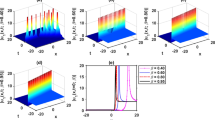
4 The graphical representation

In order to visualize the physical behavior of the solutions and explain the shape of solitons, this part displays the solitions solutions using 3D, and contour graphs.

Fig. 1

3D and contour graphs of $\psi _{3,2}$ for different values of parameters: $\Omega _1=1,\, \Omega _2=-10.2, \,{\sigma }=2,\, {\theta }=0,\, {\chi }=-0.35,\, y=0,\, z=0$

Fig. 2

3D and contour graphs of $\psi _{4,2}$ for different values of parameters: $\Omega _1=0.5,\, \Omega _2=0.002, \,{\sigma }=1.9,\, {\theta }=0,\, {\chi }=-0.65,\, y=0,\, z=0$

Fig. 3

3D and contour graphs of $\psi _{6,4}$ for different values of parameters: $\Omega _1=4.2,\, \Omega _2=1.2, \,{\sigma }=5,\, {\theta }=1.5,\, {\chi }=0.19,\, y=0,\, z=0$

Fig. 4

3D and contour graphs of $\psi _{7,4}$ for different values of parameters: $\Omega _1=14.2,\, \Omega _2=4.2, \,{\sigma }=5,\, {\theta }=1.5,\, {\chi }=0.19,\, y=0,\, z=0$

Fig. 5

3D and contour graphs of $\psi _{9,5}$ for different values of parameters: $\Omega _1=-15.29,\, \Omega _2=7.02, \,{\sigma }=4.03,\, {\theta }=6.5,\, {\chi }=1.89,\, y=0,\, z=0$

Fig. 6

3D and contour graphs of $\psi _{2,2}$ for different values of parameters: ${\sigma }=2,\, {\theta }=0,\, {\chi }=-0.35,\, C=-0.005,\, y=0,\, z=0$

Fig. 7

3D and contour graphs of $\psi _{5,5}$ for different values of parameter: ${\sigma }=0,\, {\theta }=1.5,\, {\chi }=1,\, C=-5,\, y=0,\, z=0$

Fig. 8

3D and contour graphs of $\psi _{9,9}$ for different values of parameters: ${\sigma }=-3.03,\, {\theta }=2.02,\, {\chi }=0.05,\, C=-102.5,\, j=-0.05,\, y=0,\, z=0$

Fig. 9

3D and contour graphs of $\psi _{10,10}$ for different values of parameters: ${\sigma }=100.03,\, {\theta }=-2.02,\, {\chi }=100.03,\, C=-0.005,\, y=0,\, z=0$

Fig. 10

3D and contour graphs of $\psi _{11,11}$ for different values of parameters: ${\sigma }=0,\, {\theta }=3.2,\, {\chi }=0.52,\, C=-0.5,\, y=0,\, z=0$

Fig. 11

3D and contour graphs of $\psi _{12,12}$ for different values of parameter: ${\sigma }=118.03,\, {\theta }=2.02,\, {\chi }=-118.03,\, C=-0.005,\, y=0,\, z=0$

Fig. 12

3D and contour graphs of $\psi _{13,13}$ for different values of parameters: ${\sigma }=5,\, {\theta }=0.35,\, {\chi }=-0.35,\, C=-1.5,\, y=0,\, z=0$

5 Physical interpretation

We explained the 3D and contour plots that are shown in the graphical representation part in this section. These graphs have the goal to illustrate the wave function’s structure and the physical characteristics of the obtained solutions. We discuss the interpretation of these graphs and their importance in understanding the characteristics of the solutions. The wave function can be visualised using both the 3D graph and the contour graph, which can reveal details about the dynamics of the system and help understand its behaviour. They are useful in determining whether solitons, nonlinear effects, and other interesting wave function characteristics are present. The Figs. 1, 2, 3 and 4 display combination of periodic and singular soliton solutions. Similarly, the Fig. 5 display periodic solutions. Furthermore, the Figs. 8, 9, 10, 11 and 12 display combination of periodic and rational solution, and Figs. 6, 7 display combination of periodic and dark soliton solution.

6 Conclusion

This research investigated the modified $\left( \dfrac{G'}{G^2}\right)$-expansion and the improved $\tan \left( \dfrac{\phi \left( \xi \right) }{2}\right)$ expansion, two novel expansion techniques for the analysis of the $(3+1)$-dimensional double sine-Gordon equation. Every technique offers a wide range of solutions, including rational, hyperbolic, exponential, and trigonometric functions, each with complex physical explanations and possible practical uses. After applying these two techniques, we came to the conclusion that modified $\left( \dfrac{G'}{G^2}\right)$-expansion has a wider application range, a simpler study of soliton interactions, and is more easily applied to nonlinear partial differential equations. $\left( \dfrac{G'}{G^2}\right)$ technique provides only a few different kinds of solutions. While, the improved $\tan \left( \dfrac{\phi \left( \xi \right) }{2}\right)$ -expansion offers a wider range of options, some of which are inaccessible through the modified $\left( \dfrac{G'}{G^2}\right)$ -expansion. This method use is more complex and results in certain excessive solutions. However, the resulting soliton solutions of this method improve our knowledge of nonlinear wave processes by providing insight into physical phenomena such as ocean waves. Both expansion techniques solve the $(3+1)$-dimensional double sine-Gordon equation with amazing efficiency and may be used to solve other kinds of nonlinear partial differential equations. This work provides an important starting point for future investigations into the $(3+1)$-dimensional double sine-Gordon equation and provides fascinating new perspectives on nonlinear wave phenomena and the capabilities of creative analytical techniques. In the future, we will examine soliton interactions in more detail, including multi-soliton structures and higher-order interactions. We will also utilise this equation to simulate real-world systems that have extra complexity, such as impurities and external potentials. We can better understand complex physical systems and create even more powerful tools for solving the challenges of nonlinear research by following the indicated future directions.