Comprehensive soliton solutions of fractional stochastic Kraenkel–Manna–Merle equations in ferromagnetic materials

Abstract

The inner characteristics of numerous nonlinear phenomena that arise in real-life problems are stated through nonlinear partial differential equations. This exploration is conducted with fractional stochastic Kraenkel–Manna–Merle model in ferromagnetic materials and achieved ample soliton solutions by adapting enhanced rational $({G}^{\prime}/G)$-expansion and improved tanh schemes. Ferromagnetic materials play a vital role in telecommunications applications, data storage, and manipulation. A new wave variable in the sense of confirmable fractional derivative is utilized to convert the governing model into the ordinary system. The motions of ultra-short-wave pulses in ferrite’s materials are analyzed by showing the effects of fractional derivatives and noise terms on the Brownian motion through multiple diverse 3D, 2D and contour plots. Periodic, singular periodic, kink, anti-kink etc. are visualized under the different parameter’s values involved in the obtained solitary wave solutions. The outcomes made available in the current study might play vital role to depict relevant intricate nonlinear phenomena and inspire the researchers to consider the utilized techniques in further studies.

1 Introduction

Distinct nonlinear partial models are used to illustrate respective phenomena arising in various branches of science and technology such as mathematical physics, biology, plasma physics, chemical science, mechanical engineering, solid state physics, finance, nonlinear optics etc. The study on ferromagnetic materials has taken a major place in the literature for high-density and massive data storages. It is substantial to comprehend more about the properties of supermicro- and micro-structures in nanoscale ferromagnetic materials (Lorestaniweiss and Rashidian 2017; Newman et al. 2006; Ciornei et al. 2011). Many researchers have established numerous powerful and efficient methods to extract nonlinear evolution equations, for example, new auxiliary equation method (Mamun et al. 2023), enhanced rational $({G}{\prime}/G)$-expansion scheme (Islam et al. 2021), improved $P$-expansion approach (Almatrafi 2023a), Riccati-Bernoulli sub-ODE approach (Alharbi and Almatrafi 2020), Bilinear residual network method (Zhang and Li 2022), first-integral method (Feng 2002), inverse scattering transform tool (Ablowitz and Segur 1981), Jacobi elliptic function method (Almatrafi and Alharbi 2023; Muniyappan et al. 2022, 2024), improved tanh approach (Islam et al. 2022), modified extended tanh function method (Muniyappan et al. 2021; Mamun et al. 2020; Mamun et al. 2021a), improved modified extended tanh-function method (Mamun et al. 2022a; Almatrafi 2023b), sine–cosine method (Wazwaz 2004), Sine–Gordon expansion method (Mamun et al. 2022b), Bilinear neural network method (Zhang and Bilige 2019; Zhang et al. 2021a, b, c, d, 2022, 2023), the advanced exp(− ϕ(ψ))-expansion method (Mamun et al. 2022c), improved auxiliary equation technique (Islam et al. 2023a), improved exp $(-F\left(\eta \right))$-expansion approach (Alharbi and Almatrafi 2022), tanh-coth approach (Mamun et al. 2022d), Hirota direct method (Hirota 2004), exp-function approach (He and Wu 2006), mapping method (Mohammed et al. 2022), Jacobi elliptic function expansion technique (Liu et al. 2001), $(G{\prime}/G,1/G)$-expansion method (Mamun et al. 2021b), generalized Kudryashov scheme (Gaber et al. 2019), $\left( {G^{\prime } /G} \right)$-expansion method (Muniyappan et al. 2023), $\left({G}{\prime}/{G}^{2}\right)$-expansion method (Mamun et al. 2021c), fractional sub-equation approach (Meng and Feng 2013), Bifurcation (Ahmed and Almatrafi 2023; Khan and Almatrafi 2023; Berkal and Almatrafi 2023) etc.

In this study, we consider the space fractional stochastic Kraenkel–Manna–Merle system as follows (Mohammed et al. 2023):

$${\mathfrak{D}}_{x}^{\alpha }{\mathcal{Q}}_{t}-\mathcal{Q}{\mathfrak{D}}_{x}^{\alpha }\mathcal{R}+\nu {\mathfrak{D}}_{x}^{\alpha }\mathcal{R}=\sigma {\mathfrak{D}}_{x}^{\alpha }\mathcal{Q}{\mathcal{B}}_{t},$$

$${\mathfrak{D}}_{x}^{\alpha }{\mathcal{R}}_{t}-\mathcal{Q}{\mathfrak{D}}_{x}^{\alpha }\mathcal{Q}=\sigma {\mathfrak{D}}_{x}^{\alpha }\mathcal{R}{\mathcal{B}}_{t},$$

(1.1)

where $\alpha \in (0,\left.1\right]$ stands for the conformable derivative operator ${\mathfrak{D}}_{x}^{\alpha }$; the magnetized function $\mathcal{Q}(x,t)$ and the function $\mathcal{R}(x,t)$ representing external magnetic field are associated to the ferrite, $\nu$ describes the damping parameter, $\sigma$ is the intensity of noise, $\mathcal{B}$ represents the Brownian motion, and ${\mathcal{B}}_{t}=\frac{\partial \mathcal{B}}{\partial t}$. Equation (1.1) illustrates nonlinear phenomena related to ferromagnetic materials demonstrating a spontaneous net magnetization at the atomic level, even where external magnetic field is not present. The ferromagnetic materials are firmly magnetized in the direction of the field when placed in an external magnetic field. Earlier, many scholars have studied the stated governing model in the sense of integer order as well as different fractional order. Mohammad et al. have investigated the time fractional KMM system in ferromagnetic materials with a M-truncated derivative by using the $F$-expansion technique (Alshammari et al. 2023), the generalized projective Riccati equations scheme and modified auxiliary equation technique have been used to examine the space and time fractional KMM system for wave solution for $\beta$-derivative (Arshed et al. 2021). If we put $\sigma =0$ and $\alpha =1$ in Eq. (1.1), then the Kraenkel–Manna–Merle system (KMMS) is appeared as.

$${\mathcal{Q}}_{xt}-\mathcal{Q}{\mathcal{R}}_{x}+\nu {\mathcal{R}}_{x}=0,$$

$${\mathcal{R}}_{xt}-\mathcal{Q}{\mathcal{Q}}_{x}=0,$$

(1.2)

where $\mathcal{R}(x,t)$ and $\mathcal{Q}(x,t)$ represent the external magnetic field and the magnetization connected to ferrite respectively while $x$ is space variable and $t$ represents time variable. This integer order model has been studied by many researchers with the aid of a variety of methods, such as auxiliary equation method (Li and Ma 2018a), symbolic computational with ansatz function and logarithmic transformation technique (Rizvi et al. 2023), consistent tanh expansion (Jin and Lin 2020a), Darboux transformation technique (Ma and Li 2022), extended Fun-sub equation scheme (Bilal et al. 2023), extended sinh-Gordon equation expansion and $({G}{\prime}/{G}^{2})$-expansion function methods (Younas et al. 2022a), generalized Darboux transformation technique (Wu et al. 2023), generalized $({G}{\prime}/G$)-expansion approach (Li and Ma 2018b), inverse scattering transformed method (Tchidjo et al. 2019; Tchokouansi et al. 2022), new extended direct algebraic scheme (Rehman et al. 2021), $N$-fold Darboux transformation technique (Shen et al. 2023a), truncated Painlevé method (Li and Ma 2021), bilinear method (Si and Li 2018; Jin and Lin 2020b), new sub-equation and modified Khater schemes (Tripathy et al. 2023), ${\Phi }^{6}$-model expansion technique (Younas et al. 2022b), multi-scale expansion method and short-wave approximation (Shen et al. 2023b).

The above contents motivate us to explore innovative wave solutions of the considered governing model Eq. (1.1). This exploration is appeared with a new analysis of ultra short-waves depending on the fractional operator and the intensity of noise. Multiple 3D, 2D and contour plots have brought out how the noise and fractional derivatives affect the Brownian motion. The outcomes are interesting and might be helpful to illustrate the underlying nature of short-wave pulses in ferrite’s materials. There are several fractional derivatives in the literature, like Caputo fractional derivative, Riemann–Leoville fractional derivative, beta derivative, M-truncated derivative, conformable derivative etc. We use the conformable derivative stated below (Khalil et al. 2014).

For$\left.\alpha \in (\mathrm{0,1}\right]$, the conformable derivative of a function $p : {\mathbb{R}}^{+}\to {\mathbb{R}}$ is defined as

$${\mathfrak{D}}_{x}^{\alpha }p\left(y\right)=\underset{h\to 0}{{\text{lim}}}\frac{p\left(y+h{y}^{1-\alpha }\right)-p(y)}{h}.$$

This derivative has the subsequent features. If we assume that $p , q : {\mathbb{R}}^{+}\to {\mathbb{R}}$ are differentiable and $\alpha$-differentiable functions of $y$ where$\left.\alpha \in (\mathrm{0,1}\right]$, then.

• (i) ${\mathfrak{D}}_{x}^{\alpha }[\left.{d}_{1}p\left(y\right)+{d}_{2}q\left(y\right)\right]={d}_{1}{\mathfrak{D}}_{x}^{\alpha }p\left(y\right)+{d}_{2}{\mathfrak{D}}_{x}^{\alpha }q\left(y\right),$

• (ii) ${\mathfrak{D}}_{x}^{\alpha }[\left.{d}_{1}\right]=0,$

• (iii) ${\mathfrak{D}}_{x}^{\alpha }\left(p\circ q\right)\left(y\right)={y}^{1-\alpha }{q}{\prime}\left(y\right){p}{\prime}\left(q\left(y\right)\right),$

• (iv) ${\mathfrak{D}}_{x}^{\alpha }[\left.{x}^{n}\right]=n{x}^{n-\alpha },$

• (v) ${\mathfrak{D}}_{x}^{\alpha }p\left(x\right)={x}^{1-\alpha }\frac{dp}{dx},$

where ${d}_{1}$ and ${d}_{2}$ are any real constants. We now intend to define the Brownian motion as follows (Calin 2015).

The Brownian motion $\left\{\mathcal{B}\left(t\right)\right\}{}_{t\ge 0}$ is a stochastic process and fulfills:

• (i) $\mathcal{B}\left(0\right)=0,$

• (ii) $\mathcal{B}\left(t\right)$ is continuous for $t\ge 0$,

• (iii) $\mathcal{B}\left({t}_{2}\right)-\mathcal{B}\left({t}_{1}\right)$ is independent for ${t}_{2}>{t}_{1}$,

• (iv) $\mathcal{B}\left({t}_{2}\right)-\mathcal{B}\left({t}_{1}\right)$ has a normal distribution $N(0,{t}_{2}-{t}_{1})$.

We also need to follow an axiom in this study which is stated as below (Calin 2015):

$$ {\mathbb{E}}\left( {e^{{\rho {\mathcal{B}}\left( t \right)}} } \right) = e^{{\frac{1}{2}\rho^{2} t}} ,\;{\text{where}}\;\rho \ge 0. $$

(1.3)

2 Outline of schemes

In this section, we describe the procedures of the directed approaches. Consider a nonlinear partial model as a polynomial $\mathcal{H}$ containing a wave variable $\mathcal{R}$ and its partial derivatives depending on the spatial variables $x,y,z,\dots$ and temporal variable $t$ as follows:

$$\mathcal{H}(\mathcal{R},{D}_{x}^{\alpha }\mathcal{R},{D}_{y}^{\alpha }\mathcal{R},{D}_{z}^{\alpha }\mathcal{R},{D}_{t}^{\alpha }\mathcal{R},\dots ,{D}_{xx}^{\alpha }\mathcal{R},{D}_{xt}^{\alpha }\mathcal{R},{D}_{zt}^{\alpha }\mathcal{R},\dots )=0.$$

(2.1)

For reducing Eq. (2.1) to an ordinary differential equation we require a new wave variable stated as

$$ {\mathcal{R}}\left( {x,y,z, \ldots ,t} \right) = q\left( \xi \right),\;{\text{where}}\;\xi = \frac{1}{\alpha }\left( {x^{\alpha } + y^{\alpha } + z^{\alpha } + \ldots + t^{\alpha } } \right). $$

(2.2)

Subsequently, the following ODE is obtained.

$$\overline{\mathcal{H} }(\mathcal{R},{\mathcal{R}}{\prime},{\mathcal{R}}^{{\prime}{\prime}},\mathcal{R}{^{\prime}}{^{\prime}}{^{\prime}},\dots )=0,$$

(2.3)

where the primes on $\mathcal{R}$ represent the order of derivative of $\mathcal{R}$ regarding the single independent variable $\xi$. The following guidelines of the suggested methods are brought out in the next ways.

2.1 Enhanced rational $({{\varvec{G}}}^{\boldsymbol{^{\prime}}}/{\varvec{G}})$-expansion scheme

According to this approach, the solution is supposed to be the subsequent form (Islam et al. 2021).

$$q\left(\xi \right)=\frac{{\sum }_{i=0}^{e}{\iota }_{i}{\left(\frac{{G}{\prime}\left(\xi \right)}{G\left(\xi \right)}\right)}^{i}+{\sum }_{i=1}^{e}{\epsilon }_{1}{\left(\frac{{G}{\prime}\left(\xi \right)}{G\left(\xi \right)}\right)}^{-i}}{{\sum }_{i=0}^{e}{\tau }_{i}{\left(\frac{{G}{\prime}\left(\xi \right)}{G\left(\xi \right)}\right)}^{i}+{\sum }_{i=1}^{e}{\varepsilon }_{1}{\left(\frac{{G}{\prime}\left(\xi \right)}{G\left(\xi \right)}\right)}^{-i}},$$

(2.1.1)

where the involved constants are calculated through some operations. The function $\left({G}{\prime}(\xi )/G(\xi )\right)$ is a solution of the ordinary differential equation

$${G}^{{\prime}{\prime}}\left(\xi \right)+\gamma {G}{\prime}\left(\xi \right)+\varsigma G\left(\xi \right)=0,$$

(2.1.2)

providing the solutions,

$$\frac{{G}{\prime}(\xi )}{G(\xi )}=\frac{\left\{-\gamma +\sqrt{{\gamma }^{2}-4\varsigma }\mathrm{ tanh}\left(0.5\sqrt{{\gamma }^{2}-4\varsigma } \xi \right)\right\}}{2},{\gamma }^{2}-4\varsigma >0,$$

$$\frac{{G}{\prime}(\xi )}{G(\xi )}=\frac{\left\{-\gamma +\sqrt{{\gamma }^{2}-4\varsigma }\mathrm{ coth}\left(0.5\sqrt{{\gamma }^{2}-4\varsigma } \xi \right)\right\}}{2},{\gamma }^{2}-4\varsigma >0,$$

$$\frac{{G}{\prime}(\xi )}{G(\xi )}=\frac{1}{\xi }-\frac{\gamma }{2}, {\gamma }^{2}-4\varsigma =0,$$

$$\frac{{G}{\prime}(\xi )}{G(\xi )}=\frac{\left\{-\gamma -\sqrt{4\varsigma -{\gamma }^{2}}\mathrm{ tan}\left(0.5\sqrt{4\varsigma -{\gamma }^{2}} \xi \right)\right\}}{2},{\gamma }^{2}-4\varsigma <0,$$

$$\frac{{G}^{\mathrm{^{\prime}}}(\xi )}{G(\xi )}=\frac{\left\{-\gamma +\sqrt{4\varsigma -{\gamma }^{2}}{\text{cot}}\left(0.5\sqrt{4\varsigma -{\gamma }^{2}} \xi \right)\right\}}{2},{\gamma }^{2}-4\varsigma <0.$$

The guidelines of the above-mentioned technique are available in earlier study (Islam et al. 2023b).

2.2 The improved tanh method

This competent tool defines the solution as (Islam et al. 2022)

$$q\left(\xi \right)=\frac{{\lambda }_{0}+\sum_{i=1}^{e}\left({\lambda }_{i}{Y}^{i}\left(\xi \right)+{\mu }_{i}{Y}^{-i}\left(\xi \right)\right)}{{\sigma }_{0}+\sum_{i=1}^{e}\left({\sigma }_{i}{Y}^{i}\left(\xi \right)+{\tau }_{i}{Y}^{-i}\left(\xi \right)\right)},$$

(2.2.1)

whose unknown free parameters are revealed hereafter. The value of $e$ is estimated by using the homogeneous balance theme. The function $Y=Y\left(\xi \right)$ satisfies

$${Y}{\prime}\left(\xi \right)=\rho +{Y}^{2}\left(\xi \right),$$

(2.2.2)

where $\rho$ is an arbitrary parameter. Equation (2.2.2) provides the solutions.

$Y\left(\xi \right)=-\sqrt{-\rho }\mathrm{ tanh}(\sqrt{-\rho }\xi )$ and $Y\left(\xi \right)=-\sqrt{-\rho }\mathrm{ coth}\left(\sqrt{-\rho }\xi \right), \rho <0,$

$Y\left(\xi \right)=\sqrt{\rho }\mathrm{ tan}(\sqrt{\rho }\xi )$ and $Y\left(\xi \right)=-\sqrt{\rho }\mathrm{ cot}\left(\sqrt{\rho }\xi \right),\rho >0$

$$Y\left(\xi \right)=-1/\xi , \rho =0.$$

The working procedures of the above stated scheme are noticeable in the previous study (Islam and Akter 2021).

3 The traveling wave solutions of the FSKMMS

Regarding dumping effect as zero $(\nu =0)$, we employ the new wave variable conversion

$$ {\mathcal{Q}}\left( {x,t} \right) = q\left( \xi \right)e^{{\sigma {\mathcal{B}}\left( t \right) - \frac{1}{2}\sigma^{2} t}} ,\;{\mathcal{R}}\left( {x,t} \right) = r\left( \xi \right)e^{{\sigma {\mathcal{B}}\left( t \right) - \frac{1}{2}\sigma^{2} t}} ,\;\xi = \frac{1}{\alpha }lx^{\alpha } + mt, $$

(3.1)

where $q(\xi )$ and $r(\xi )$ represent real-valued functions, $l$ and $m$ are nonzero arbitrary parameters. Then we generate the following wave equations:

$$ {\mathfrak{D}}_{x}^{\alpha } {\mathcal{Q}} = lq^{\prime}e^{{\sigma {\mathcal{B}}\left( t \right) - \frac{1}{2}\sigma^{2} t}} ,\;{\mathfrak{D}}_{x}^{\alpha } {\mathcal{Q}}_{t} = \left( {lmq^{\prime\prime} + \sigma lq^{\prime}{\mathcal{B}}_{t} } \right)e^{{\sigma {\mathcal{B}}\left( t \right) - \frac{1}{2}\sigma^{2} t}} , $$

(3.2)

$$ {\mathfrak{D}}_{x}^{\alpha } {\mathcal{R}} = lr^{\prime}e^{{\sigma {\mathcal{B}}\left( t \right) - \frac{1}{2}\sigma^{2} t}} ,\;{\mathfrak{D}}_{x}^{\alpha } {\mathcal{R}}_{t} = \left( {lmr^{\prime\prime} + \sigma lr^{\prime}{\mathcal{B}}_{t} } \right)e^{{\sigma {\mathcal{B}}\left( t \right) - \frac{1}{2}\sigma^{2} t}} . $$

(3.3)

Inserting Eq. (3.1) into Eq. (1.1) and utilizing (3.2) and (3.3), we get

$$lm{q}^{{\prime}{\prime}}-lq{r}{\prime}{e}^{\sigma \mathcal{B}\left(t\right)-\frac{1}{2}{\sigma }^{2}t}=0,$$

$$lm{r}^{\mathrm{^{\prime}}\mathrm{^{\prime}}}-lq{q}^{\mathrm{^{\prime}}{e}^{\sigma \mathcal{B}\left(t\right)-\frac{1}{2}{\sigma }^{2}t}}=0.$$

(3.4)

Taking the expectation on both sides, we have

$$m{q}^{{\prime}{\prime}}-q{r}^{{\prime}{e}^{-\frac{1}{2}{\sigma }^{2}t}}{\mathbb{E}}{e}^{\sigma \mathcal{B}\left(t\right)}=0,$$

$$m{r}^{\mathrm{^{\prime}}\mathrm{^{\prime}}}-q{q}^{\mathrm{^{\prime}}{e}^{-\frac{1}{2}{\sigma }^{2}t}}{\mathbb{E}}{e}^{\sigma \mathcal{B}\left(t\right)}=0.$$

(3.5)

Using Eq. (1.3), where $\mathcal{B}\left(t\right)$ is a normal process with ${\mathbb{E}}\left({e}^{\sigma \mathcal{B}\left(t\right)}\right)={e}^{\frac{1}{2}{\sigma }^{2}t}$, Eq. (3.5) becomes

$$m{q}^{{\prime}{\prime}}-q{r}{\prime}=0,$$

$$m{r}^{{\prime}{\prime}}-q{q}{\prime}=0.$$

(3.6)

Integrating the second equation of the Eq. (3.6), we have

$${r}{\prime}=\frac{1}{2m}{q}^{2}+\frac{k}{m}.$$

(3.7)

The anti-derivative of Eq. (3.7) yields

$$r=\frac{1}{6m}{q}^{3}+\frac{k}{m}q+p,$$

(3.8)

where $k$ and $p$ are integral constants. Now, substituting Eq. (3.7) into the first equation in Eq. (3.6), we get

$${q}^{{\prime}{\prime}}+{d}_{1}{q}^{3}+{d}_{2}q=0,$$

(3.9)

where ${d}_{1}=-\frac{1}{2{m}^{2}}$ and ${d}_{2}=-\frac{k}{{m}^{2}}$. The highest order linear term ${q}^{{\prime}{\prime}}$ and highest nonlinear term ${q}^{3}$ are brought under homogeneous balance rule and found $e=1$. Considering this balancing value, we construct the following appropriate wave solutions.

3.1 Wave solutions via enhanced rational $({{\varvec{G}}}^{\boldsymbol{^{\prime}}}/{\varvec{G}})$-expansion approach

This tool represents the wave solution as

$$q\left(\xi \right)=\frac{{\iota }_{0}+{\iota }_{1}({G}{\prime}(\xi )/G(\xi ))+{\epsilon }_{1}{\left({G}{\prime}(\xi )/G(\xi )\right)}^{-1}}{{\tau }_{0}+{\tau }_{1}({G}{\prime}(\xi )/G(\xi ))+{\varepsilon }_{1}{\left({G}{\prime}(\xi )/G(\xi )\right)}^{-1}},$$

(3.1.1)

where ${\epsilon }_{1}$ and ${\varepsilon }_{1}$ are not zero simultaneously. A polynomial is formed by combining Eq. (3.1.1) and Eq. (2.1.2) with Eq. (3.9). Thereupon, set each term of the polynomial to zero and solve them by utilizing computational software Maple to produces the following results:

Case I: ${\epsilon }_{1}=\frac{\left(2{\iota }_{0}-\gamma {\iota }_{1}\right)\gamma }{4}$, ${\tau }_{0}=\mp \frac{{\iota }_{1}\left({\gamma }^{2}-4\varsigma \right)}{2\sqrt{-2k\left({\gamma }^{2}-4\varsigma \right)}}$, ${\tau }_{1}=0$,${\varepsilon }_{1}=\pm \frac{(\gamma {\iota }_{1}-2{\iota }_{0})({\gamma }^{2}-4\varsigma )}{4\sqrt{-2k\left({\gamma }^{2}-4\varsigma \right)}},$

$$m=\pm \frac{\sqrt{-2k\left({\gamma }^{2}-4\varsigma \right)}}{{\gamma }^{2}-4\varsigma }.$$

Case II: ${\iota }_{1}=0$, ${\tau }_{0}=\pm \frac{\gamma {\iota }_{0}-2{\epsilon }_{1}}{\sqrt{-2k\left({\gamma }^{2}-4\varsigma \right)}}$, ${\tau }_{1}=0$, ${\varepsilon }_{1}=\mp \frac{\gamma {\epsilon }_{1}-2\varsigma {\iota }_{0}}{\sqrt{-2k\left({\gamma }^{2}-4\varsigma \right)}}$, $m=\pm \frac{\sqrt{-2k\left({\gamma }^{2}-4\varsigma \right)}}{{\gamma }^{2}-4\varsigma }.$

Case III: ${\iota }_{0}=2m\gamma {\tau }_{0}$, ${\iota }_{1}=2m{\tau }_{0}$, ${\epsilon }_{1}=2m\varsigma {\tau }_{0}$, ${\tau }_{1}=0$, ${\varepsilon }_{1}=\frac{\gamma {\tau }_{0}}{2}$, $k={m}^{2}\left({\gamma }^{2}-4\varsigma \right).$

Case IV: ${\iota }_{1}=0$, ${\epsilon }_{1}=\frac{\gamma {l}_{0}}{2}$, ${\tau }_{0}=0$,${\tau }_{1}=0$, ${\varepsilon }_{1}=\pm \frac{{\iota }_{0}\sqrt{2k\left(4\varsigma -{\gamma }^{2}\right)}}{4k}$, $m=\mp \frac{\sqrt{2k\left(4\varsigma -{\gamma }^{2}\right)}}{4\varsigma -{\gamma }^{2}}.$

Case V: ${\epsilon }_{1}=\frac{\left(2{\iota }_{0}-\gamma {\iota }_{1}\right)\gamma }{4}$, ${\tau }_{0}=\pm \frac{{\iota }_{1}\left({\gamma }^{2}-4\varsigma \right)}{2\sqrt{-2k\left({\gamma }^{2}-4\varsigma \right)}}$, ${\tau }_{1}=0$,${\varepsilon }_{1}=\mp \frac{\left(\gamma {\iota }_{1}-2{\iota }_{0}\right)\left({\gamma }^{2}-4\varsigma \right)}{4\sqrt{-2k\left({\gamma }^{2}-4\varsigma \right)}},$

$$m=\pm \frac{\sqrt{-2k\left({\gamma }^{2}-4\varsigma \right)}}{{\gamma }^{2}-4\varsigma }.$$

Case VI: ${\iota }_{1}=0$, ${\tau }_{0}=\mp \frac{{\gamma \iota }_{0}{-2\epsilon }_{1}}{\sqrt{-2k\left({\gamma }^{2}-4\varsigma \right)}}$, ${\tau }_{1}=0$, ${\varepsilon }_{1}=\pm \frac{\gamma {\epsilon }_{1}-2\varsigma {\iota }_{0}}{\sqrt{-2k\left({\gamma }^{2}-4\varsigma \right)}}$, $m=\pm \frac{\sqrt{-2k\left({\gamma }^{2}-4\varsigma \right)}}{{\gamma }^{2}-4\varsigma }.$

Case VII: ${\iota }_{0}=-2m\gamma {\tau }_{0}$, ${\iota }_{1}=-2{m\tau }_{0}$, ${\epsilon }_{1}=m{\tau }_{0}(2\varsigma -{\gamma }^{2})$, ${\tau }_{1}=0$, ${\varepsilon }_{1}=\frac{{\gamma \tau }_{0}}{2},$

$$k=2{m}^{2}\left(4\varsigma -{\gamma }^{2}\right).$$

Case VIII: ${\iota }_{0}=-2m\gamma {\tau }_{0}$, ${\iota }_{1}=-2m{\tau }_{0}$, ${\epsilon }_{1}=-2m\varsigma {\tau }_{0}$, ${\tau }_{1}=0$, ${\varepsilon }_{1}=\frac{\gamma {\tau }_{0}}{2}$, $k={m}^{2}\left({\gamma }^{2}-4\varsigma \right).$

Case IX: ${\iota }_{0}=2m\gamma {\tau }_{0}$, ${\iota }_{1}=2{m\tau }_{0}$, ${\epsilon }_{1}=m{\tau }_{0}({\gamma }^{2}-2\varsigma )$, ${\tau }_{1}=0$,${\varepsilon }_{1}=\frac{\gamma {\tau }_{0}}{2},$

$$k=2{m}^{2}\left(4\varsigma -{\gamma }^{2}\right).$$

Case X: ${\iota }_{0}=\pm m{\tau }_{0}\sqrt{4\varsigma -{\gamma }^{2}}$, ${\iota }_{1}=0$, ${\epsilon }_{1}=\mp \frac{m{\tau }_{0}\sqrt{4\varsigma -{\gamma }^{2}}(-\gamma \pm \sqrt{4\varsigma -{\gamma }^{2}})}{2}$, ${\tau }_{1}=0,$

$${\varepsilon }_{1}=\frac{{\tau }_{0}(\gamma \pm \sqrt{4\varsigma -{\gamma }^{2}})}{2}, k=\frac{{m}^{2}\left(4\varsigma -{\gamma }^{2}\right)}{2}.$$

We might insert the constant’s values appeared in the above cases in Eq. (3.1.1) and then construct huge wave solutions with the aid of the solutions of Eq. (2.1.2). For better representations of the current study, we consider only the first four cases and gain the following accurate traveling wave solutions.

Solution group 1 Due to case I, we attain

$${q}_{1}\left(\xi \right)=\frac{\sqrt{2k\left(4\varsigma -{\gamma }^{2}\right)}(\gamma +2({G}{\prime}(\xi )/G(\xi )))}{4\varsigma -{\gamma }^{2}},$$

(3.1.2)

$${r}_{1}\left(\xi \right)=p-k\left(\gamma +2\left(\frac{{G}^{\mathrm{^{\prime}}}\left(\xi \right)}{G\left(\xi \right)}\right)\right)+\frac{k{\left(\gamma +2\left(\frac{{G}^{\mathrm{^{\prime}}}\left(\xi \right)}{G\left(\xi \right)}\right)\right)}^{3}}{3\left({\gamma }^{2}-4\varsigma \right)}.$$

(3.1.3)

Equation (3.1.2) and Eq. (3.1.3) alongside Eq. (3.1) and the solutions of Eq. (2.1.2) ensure the succeeding exact wave solutions.

Under the agreement ${\gamma }^{2}-4\varsigma >0$, the wave solutions are

$${\mathcal{Q}}_{1}^{1}\left(\xi \right)=-\sqrt{-2k}\mathrm{ tanh}\left(0.5\sqrt{{\gamma }^{2}-4\varsigma } \xi \right){e}^{\sigma \mathcal{B}\left({\text{t}}\right)-\frac{1}{2}{\sigma }^{2}t},$$

(3.1.4)

$${\mathcal{R}}_{1}^{1}\left(\xi \right)=\left\{p-k\sqrt{{\gamma }^{2}-4\varsigma }\mathrm{ tanh}\left(0.5\sqrt{{\gamma }^{2}-4\varsigma } \xi \right)+\frac{k\sqrt{{\gamma }^{2}-4\varsigma }{{\text{tanh}}}^{3}\left(0.5\sqrt{{\gamma }^{2}-4\varsigma } \xi \right)}{3}\right\}{e}^{\sigma \mathcal{B}\left({\text{t}}\right)-\frac{1}{2}{\sigma }^{2}t},$$

(3.1.5)

$${\mathcal{Q}}_{1}^{2}\left(\xi \right)=-\sqrt{-2k}\mathrm{ coth}\left(0.5\sqrt{{\gamma }^{2}-4\varsigma } \xi \right){e}^{\sigma \mathcal{B}\left({\text{t}}\right)-\frac{1}{2}{\sigma }^{2}t},$$

(3.1.6)

$${\mathcal{R}}_{1}^{2}\left(\xi \right)=\left\{p-k\sqrt{{\gamma }^{2}-4\varsigma }\mathrm{ coth}\left(0.5\sqrt{{\gamma }^{2}-4\varsigma } \xi \right)+\frac{k\sqrt{{\gamma }^{2}-4\varsigma }{{\text{coth}}}^{3}\left(0.5\sqrt{{\gamma }^{2}-4\varsigma } \xi \right)}{3}\right\}{e}^{\sigma \mathcal{B}\left({\text{t}}\right)-\frac{1}{2}{\sigma }^{2}t},$$

(3.1.7)

where $\xi =\frac{1}{\alpha }l{x}^{\alpha }\pm \sqrt{\frac{-2k}{{\gamma }^{2}-4\varsigma }}t$.

The wave solutions for the condition ${\gamma }^{2}-4\varsigma <0$ are

$${\mathcal{Q}}_{1}^{3}\left(\xi \right)=-\sqrt{2k}\mathrm{ tan}\left(0.5\sqrt{4\varsigma -{\gamma }^{2}} \xi \right){e}^{\sigma \mathcal{B}\left({\text{t}}\right)-\frac{1}{2}{\sigma }^{2}t},$$

(3.1.8)

$${\mathcal{R}}_{1}^{3}\left(\xi \right)=\left\{p+k\sqrt{4\varsigma -{\gamma }^{2}}\mathrm{ tan}\left(0.5\sqrt{4\varsigma -{\gamma }^{2}} \xi \right)+\frac{k\sqrt{4\varsigma -{\gamma }^{2}}{{\text{tan}}}^{3}\left(0.5\sqrt{4\varsigma -{\gamma }^{2}} \xi \right)}{3}\right\}{e}^{\sigma \mathcal{B}\left({\text{t}}\right)-\frac{1}{2}{\sigma }^{2}t},$$

(3.1.9)

$${\mathcal{Q}}_{1}^{4}\left(\xi \right)=\sqrt{2k}\mathrm{ cot}\left(0.5\sqrt{4\varsigma -{\gamma }^{2}} \xi \right){e}^{\sigma \mathcal{B}\left({\text{t}}\right)-\frac{1}{2}{\sigma }^{2}t},$$

(3.1.10)

$${\mathcal{R}}_{1}^{4}\left(\xi \right)=\left\{p-k\sqrt{4\varsigma -{\gamma }^{2}}\mathrm{ cot}\left(0.5\sqrt{4\varsigma -{\gamma }^{2}} \xi \right)-\frac{k\sqrt{4\varsigma -{\gamma }^{2}}{{\text{cot}}}^{3}\left(0.5\sqrt{4\varsigma -{\gamma }^{2}} \xi \right)}{3}\right\}{e}^{\sigma \mathcal{B}\left({\text{t}}\right)-\frac{1}{2}{\sigma }^{2}t},$$

(3.1.11)

where $\xi =\frac{1}{\alpha }l{x}^{\alpha }\pm \sqrt{\frac{-2k}{{\gamma }^{2}-4\varsigma }}t$.

Solution group 2 According to case II,

$${q}_{2}\left(\xi \right)=\frac{\sqrt{2k\left(4\varsigma -{\gamma }^{2}\right)}({\epsilon }_{1}+{\iota }_{0}({G}{\prime}(\xi )/G(\xi )))}{2\varsigma {\iota }_{0}-\gamma {\epsilon }_{1}+(\gamma {\iota }_{0}-2{\epsilon }_{1})({G}{\prime}(\xi )/G(\xi ))},$$

(3.1.12)

$${r}_{2}\left(\xi \right)=p+\frac{k({\gamma }^{2}-4\varsigma )({\epsilon }_{1}+{\iota }_{0}({G}^{\mathrm{^{\prime}}}(\xi )/G(\xi )))}{2\varsigma {\iota }_{0}-\gamma {\epsilon }_{1}+(\gamma {\iota }_{0}-2{\epsilon }_{1})({G}^{\mathrm{^{\prime}}}(\xi )/G(\xi ))}-\frac{k{\left({\gamma }^{2}-4\varsigma \right)}^{2}{\left({\epsilon }_{1}+{\iota }_{0}\left(\frac{{G}^{\mathrm{^{\prime}}}\left(\xi \right)}{G\left(\xi \right)}\right)\right)}^{3}}{3{\left(2\varsigma {\iota }_{0}-\gamma {\epsilon }_{1}+\left(\gamma {\iota }_{0}-2{\epsilon }_{1}\right)\left(\frac{{G}^{\mathrm{^{\prime}}}\left(\xi \right)}{G\left(\xi \right)}\right)\right)}^{3}}.$$

(3.1.13)

Equation (3.1.12) and Eq. (3.1.13) together with Eq. (3.1) and the solutions of Eq. (2.1.2) confirm the next appropriate wave solutions.

The assumption ${\gamma }^{2}-4\varsigma >0$ provides the results

$${\mathcal{Q}}_{2}^{1}\left(\xi \right)=\frac{\sqrt{2k\left(4\varsigma -{\gamma }^{2}\right)}(2{\epsilon }_{1}-{\iota }_{0}(\gamma -\sqrt{{\gamma }^{2}-4\varsigma }\mathrm{ tanh}(0.5\sqrt{{\gamma }^{2}-4\varsigma } \xi )))}{\left(4\varsigma -{\gamma }^{2}\right){\iota }_{0}+(\gamma {\iota }_{0}-2{\epsilon }_{1})\sqrt{{\gamma }^{2}-4\varsigma }\mathrm{ tanh}(0.5\sqrt{{\gamma }^{2}-4\varsigma } \xi )}{e}^{\sigma \mathcal{B}\left({\text{t}}\right)-\frac{1}{2}{\sigma }^{2}t},$$

(3.1.14)

$${\mathcal{R}}_{2}^{1}\left(\xi \right)=\{p+\frac{k\left({\gamma }^{2}-4\varsigma \right)(2{\epsilon }_{1}-{\iota }_{0}(\gamma -\sqrt{{\gamma }^{2}-4\varsigma }\mathrm{ tanh}(0.5\sqrt{{\gamma }^{2}-4\varsigma } \xi )))}{\left(4\varsigma -{\gamma }^{2}\right){\iota }_{0}+(\gamma {\iota }_{0}-2{\epsilon }_{1})\sqrt{{\gamma }^{2}-4\varsigma }\mathrm{ tanh}(0.5\sqrt{{\gamma }^{2}-4\varsigma } \xi )}$$

$$-\frac{k{\left({\gamma }^{2}-4\varsigma \right)}^{2}{\left(2{\epsilon }_{1}-{\iota }_{0}\left(\gamma -\sqrt{{\gamma }^{2}-4\varsigma }{\text{tanh}}\left(0.5\sqrt{{\gamma }^{2}-4\varsigma } \xi \right)\right)\right)}^{3}}{3{\left(\left(4\varsigma -{\gamma }^{2}\right){\iota }_{0}+\left(\gamma {\iota }_{0}-2{\epsilon }_{1}\right)\sqrt{{\gamma }^{2}-4\varsigma }{\text{tanh}}\left(0.5\sqrt{{\gamma }^{2}-4\varsigma } \xi \right)\right)}^{3}}\}{e}^{\sigma \mathcal{B}\left({\text{t}}\right)-\frac{1}{2}{\sigma }^{2}t},$$

(3.1.15)

$${\mathcal{Q}}_{2}^{2}\left(\xi \right)=\frac{\sqrt{2k\left(4\varsigma -{\gamma }^{2}\right)}(2{\epsilon }_{1}-{\iota }_{0}(\gamma -\sqrt{{\gamma }^{2}-4\varsigma }\mathrm{ coth}(0.5\sqrt{{\gamma }^{2}-4\varsigma } \xi )))}{\left(4\varsigma -{\gamma }^{2}\right){\iota }_{0}+(\gamma {\iota }_{0}-2{\epsilon }_{1})\sqrt{{\gamma }^{2}-4\varsigma }\mathrm{ coth}(0.5\sqrt{{\gamma }^{2}-4\varsigma } \xi )}{e}^{\sigma \mathcal{B}\left({\text{t}}\right)-\frac{1}{2}{\sigma }^{2}t},$$

(3.1.16)

$${\mathcal{R}}_{2}^{2}\left(\xi \right)=\{p+\frac{k\left({\gamma }^{2}-4\varsigma \right)(2{\epsilon }_{1}-{\iota }_{0}(\gamma -\sqrt{{\gamma }^{2}-4\varsigma }\mathrm{ tanh}(0.5\sqrt{{\gamma }^{2}-4\varsigma } \xi )))}{\left(4\varsigma -{\gamma }^{2}\right){\iota }_{0}+(\gamma {\iota }_{0}-2{\epsilon }_{1})\sqrt{{\gamma }^{2}-4\varsigma }\mathrm{ tanh}(0.5\sqrt{{\gamma }^{2}-4\varsigma } \xi )}$$

$$-\frac{k{\left({\gamma }^{2}-4\varsigma \right)}^{2}{\left(2{\epsilon }_{1}-{\iota }_{0}\left(\gamma -\sqrt{{\gamma }^{2}-4\varsigma }{\text{tanh}}\left(0.5\sqrt{{\gamma }^{2}-4\varsigma } \xi \right)\right)\right)}^{3}}{3{\left(\left(4\varsigma -{\gamma }^{2}\right){\iota }_{0}+\left(\gamma {\iota }_{0}-2{\epsilon }_{1}\right)\sqrt{{\gamma }^{2}-4\varsigma }{\text{tanh}}\left(0.5\sqrt{{\gamma }^{2}-4\varsigma } \xi \right)\right)}^{3}}\}{e}^{\sigma \mathcal{B}\left({\text{t}}\right)-\frac{1}{2}{\sigma }^{2}t},$$

(3.1.17)

where $\xi =\frac{1}{\alpha }l{x}^{\alpha }\pm \sqrt{\frac{-2k}{{\gamma }^{2}-4\varsigma }}t$.

According to the assignment ${\gamma }^{2}-4\varsigma <0$, we produce the solutions

$${\mathcal{Q}}_{2}^{3}\left(\xi \right)=\frac{\sqrt{2k\left(4\varsigma -{\gamma }^{2}\right)}(2{\epsilon }_{1}+{\iota }_{0}(\gamma +\sqrt{4\varsigma -{\gamma }^{2}}\mathrm{ tan}(0.5\sqrt{4\varsigma -{\gamma }^{2}} \xi )))}{\left(\gamma {\iota }_{0}-2{\epsilon }_{1}\right)\sqrt{4\varsigma -{\gamma }^{2}}\mathrm{ tan}(0.5\sqrt{4\varsigma -{\gamma }^{2}} \xi )-\left(4\varsigma -{\gamma }^{2}\right){\iota }_{0}}{e}^{\sigma \mathcal{B}\left({\text{t}}\right)-\frac{1}{2}{\sigma }^{2}t},$$

(3.1.18)

$${\mathcal{R}}_{2}^{3}\left(\xi \right)=\{p+\frac{k(4\varsigma -{\gamma }^{2})({\iota }_{0}(\gamma +\sqrt{4\varsigma -{\gamma }^{2}}\mathrm{ tan}(0.5\sqrt{4\varsigma -{\gamma }^{2}} \xi ))-2{\epsilon }_{1})}{\left(4\varsigma -{\gamma }^{2}\right){\iota }_{0}-(\gamma {\iota }_{0}-2{\epsilon }_{1})\sqrt{4\varsigma -{\gamma }^{2}}\mathrm{ tan}(0.5\sqrt{4\varsigma -{\gamma }^{2}} \xi )}$$

$$-\frac{k{\left(4\varsigma -{\gamma }^{2}\right)}^{2}{\left({\iota }_{0}\left(\gamma +\sqrt{4\varsigma -{\gamma }^{2}}{\text{tan}}\left(0.5\sqrt{4\varsigma -{\gamma }^{2}} \xi \right)\right)-2{\epsilon }_{1}\right)}^{3}}{3{\left(\left(\gamma {\iota }_{0}-2{\epsilon }_{1}\right)\sqrt{4\varsigma -{\gamma }^{2}}{\text{tan}}\left(0.5\sqrt{4\varsigma -{\gamma }^{2}} \xi \right)-\left(4\varsigma -{\gamma }^{2}\right){\iota }_{0}\right)}^{3}}\}{e}^{\sigma \mathcal{B}\left({\text{t}}\right)-\frac{1}{2}{\sigma }^{2}t},$$

(3.1.19)

$${\mathcal{Q}}_{2}^{4}\left(\xi \right)=\frac{\sqrt{2k\left(4\varsigma -{\gamma }^{2}\right)}(2{\epsilon }_{1}-{\iota }_{0}(\gamma -\sqrt{4\varsigma -{\gamma }^{2}}\mathrm{ cot}(0.5\sqrt{4\varsigma -{\gamma }^{2}} \xi )))}{\left(4\varsigma -{\gamma }^{2}\right){\iota }_{0}+\left(\gamma {\iota }_{0}-2{\epsilon }_{1}\right)\sqrt{4\varsigma -{\gamma }^{2}}\mathrm{ cot}(0.5\sqrt{4\varsigma -{\gamma }^{2}} \xi )}{e}^{\sigma \mathcal{B}\left({\text{t}}\right)-\frac{1}{2}{\sigma }^{2}t},$$

(3.1.20)

$${\mathcal{R}}_{2}^{4}\left(\xi \right)=\{p+\frac{k(4\varsigma -{\gamma }^{2} )({\iota }_{0}(\gamma -\sqrt{4\varsigma -{\gamma }^{2}}\mathrm{ cot}(0.5\sqrt{4\varsigma -{\gamma }^{2}} \xi ))-2{\epsilon }_{1})}{\left(4\varsigma -{\gamma }^{2}\right){\iota }_{0}+\left(\gamma {\iota }_{0}-2{\epsilon }_{1}\right)\sqrt{4\varsigma -{\gamma }^{2}}\mathrm{ cot}(0.5\sqrt{4\varsigma -{\gamma }^{2}} \xi )}$$

$$-\frac{k{\left(4\varsigma -{\gamma }^{2}\right)}^{2}{\left(2{\epsilon }_{1}-{\iota }_{0}\left(\gamma -\sqrt{4\varsigma -{\gamma }^{2}}{\text{cot}}\left(0.5\sqrt{4\varsigma -{\gamma }^{2}} \xi \right)\right)\right)}^{3}}{3{\left(\left(4\varsigma -{\gamma }^{2}\right){\iota }_{0}+\left(\gamma {\iota }_{0}-2{\epsilon }_{1}\right)\sqrt{4\varsigma -{\gamma }^{2}}{\text{cot}}\left(0.5\sqrt{4\varsigma -{\gamma }^{2}} \xi \right)\right)}^{3}}\}{e}^{\sigma \mathcal{B}\left({\text{t}}\right)-\frac{1}{2}{\sigma }^{2}t},$$

(3.1.21)

where $\xi =\frac{1}{\alpha }l{x}^{\alpha }\pm \sqrt{\frac{-2k}{{\gamma }^{2}-4\varsigma }}t$.

Solution group 3 Due to case III,

$${q}_{3}\left(\xi \right)=\frac{4m(\varsigma +\gamma ({G}{\prime}(\xi )/G(\xi ))+{({G}{\prime}(\xi )/G(\xi ))}^{2})}{\gamma +2\left({G}{\prime}(\xi )/G(\xi )\right)},$$

(3.1.22)

$${r}_{3}\left(\xi \right)=\frac{32{m}^{2}{(\varsigma +\gamma ({G}^{\mathrm{^{\prime}}}(\xi )/G(\xi ))+{({G}^{\mathrm{^{\prime}}}(\xi )/G(\xi ))}^{2})}^{3}}{3{(\gamma +2({G}^{\mathrm{^{\prime}}}(\xi )/G(\xi )))}^{3}}+\frac{4{m}^{2}({\gamma }^{2}-4\varsigma )(\varsigma +\gamma ({G}^{\mathrm{^{\prime}}}(\xi )/G(\xi ))+{({G}^{\mathrm{^{\prime}}}(\xi )/G(\xi ))}^{2})}{\gamma +2({G}^{\mathrm{^{\prime}}}(\xi )/G(\xi ))}+p.$$

(3.1.23)

The condition ${\gamma }^{2}-4\varsigma >0$ yields the outcomes

$${\mathcal{Q}}_{3}^{1}\left(\xi \right)=-\frac{m\left(4\varsigma -{\gamma }^{2}\right)\left({{\text{tanh}}}^{2}\left(0.5\sqrt{{\gamma }^{2}-4\varsigma } \xi \right)-1\right)}{\sqrt{{\gamma }^{2}-4\varsigma }{\text{tanh}}\left(0.5\sqrt{{\gamma }^{2}-4\varsigma } \xi \right)}{e}^{\frac{1}{2}{\sigma }^{2}t-\sigma \mathcal{B}\left({\text{t}}\right)},$$

(3.1.24)

$${\mathcal{R}}_{3}^{1}\left(\xi \right)=\{p-\frac{{m}^{2}(4\varsigma -{\gamma }^{2})\sqrt{{\gamma }^{2}-4\varsigma }({{\text{tanh}}}^{2}(0.5\sqrt{{\gamma }^{2}-4\varsigma } \xi )-1)}{{\text{tanh}}(0.5\sqrt{{\gamma }^{2}-4\varsigma } \xi )}$$

$$+\frac{{m}^{2}{({\gamma }^{2}-4\varsigma )}^{2}{({\text{tanh}}(0.5\sqrt{{\gamma }^{2}-4\varsigma } \xi )+1)}^{3}{({\text{tanh}}(0.5\sqrt{{\gamma }^{2}-4\varsigma } \xi )-1)}^{3}}{6\sqrt{{\gamma }^{2}-4\varsigma }{{\text{tanh}}}^{3}(0.5\sqrt{{\gamma }^{2}-4\varsigma } \xi )}\}{e}^{\sigma \mathcal{B}\left({\text{t}}\right)-\frac{1}{2}{\sigma }^{2}t},$$

(3.1.25)

$${\mathcal{Q}}_{3}^{2}\left(\xi \right)=-\frac{m\left(4\varsigma -{\gamma }^{2}\right)\left({{\text{coth}}}^{2}\left(0.5\sqrt{{\gamma }^{2}-4\varsigma } \xi \right)-1\right)}{\sqrt{{\gamma }^{2}-4\varsigma }{\text{coth}}\left(0.5\sqrt{{\gamma }^{2}-4\varsigma } \xi \right)}{e}^{\frac{1}{2}{\sigma }^{2}t-\sigma \mathcal{B}\left({\text{t}}\right)},$$

(3.1.26)

$${\mathcal{R}}_{3}^{2}\left(\xi \right)=\{p-\frac{{m}^{2}(4\varsigma -{\gamma }^{2})\sqrt{{\gamma }^{2}-4\varsigma }({{\text{coth}}}^{2}(0.5\sqrt{{\gamma }^{2}-4\varsigma } \xi )-1)}{{\text{coth}}(0.5\sqrt{{\gamma }^{2}-4\varsigma } \xi )}$$

$$+\frac{{m}^{2}{({\gamma }^{2}-4\varsigma )}^{2}{({\text{coth}}(0.5\sqrt{{\gamma }^{2}-4\varsigma } \xi )+1)}^{3}{({\text{coth}}(0.5\sqrt{{\gamma }^{2}-4\varsigma } \xi )-1)}^{3}}{6\sqrt{{\gamma }^{2}-4\varsigma }{{\text{coth}}}^{3}(0.5\sqrt{{\gamma }^{2}-4\varsigma } \xi )}\}{e}^{\sigma \mathcal{B}\left({\text{t}}\right)-\frac{1}{2}{\sigma }^{2}t},$$

(3.1.27)

where $\xi =\frac{1}{\alpha }l{x}^{\alpha }+mt$.

For the condition ${\gamma }^{2}-4\varsigma <0$, the wave solutions are

$${\mathcal{Q}}_{3}^{3}\left(\xi \right)=-\frac{m\sqrt{4\varsigma -{\gamma }^{2}}\left({{\text{tan}}}^{2}\left(0.5\sqrt{4\varsigma -{\gamma }^{2}} \xi \right)+1\right)}{{\text{tan}}\left(0.5\sqrt{4\varsigma -{\gamma }^{2}} \xi \right)}{e}^{\sigma \mathcal{B}\left({\text{t}}\right)-\frac{1}{2}{\sigma }^{2}t},$$

(3.1.28)

$${\mathcal{R}}_{3}^{3}\left(\xi \right)=\{p+\frac{{m}^{2}{\left(4\varsigma -{\gamma }^{2}\right)}^{3/2}({{\text{tan}}}^{2}(0.5\sqrt{4\varsigma -{\gamma }^{2}} \xi )+1)}{{\text{tan}}(0.5\sqrt{4\varsigma -{\gamma }^{2}} \xi )}$$

$$-\frac{{m}^{2}{{\left({\gamma }^{2}-4\varsigma \right)}^{2}\left({{\text{tan}}}^{2}\left(0.5\sqrt{4\varsigma -{\gamma }^{2}} \xi \right)+1\right)}^{3}}{6\sqrt{4\varsigma -{\gamma }^{2}}{{\text{tan}}}^{3}\left(0.5\sqrt{4\varsigma -{\gamma }^{2}} \xi \right)}\}{e}^{\sigma \mathcal{B}\left({\text{t}}\right)-\frac{1}{2}{\sigma }^{2}t},$$

(3.1.29)

$${\mathcal{Q}}_{3}^{4}\left(\xi \right)=\frac{m\sqrt{4\varsigma -{\gamma }^{2}}({{\text{cot}}}^{2}(0.5\sqrt{4\varsigma -{\gamma }^{2}} \xi )+1)}{{\text{cot}}(0.5\sqrt{4\varsigma -{\gamma }^{2}} \xi )}{e}^{\sigma \mathcal{B}\left({\text{t}}\right)-\frac{1}{2}{\sigma }^{2}t},$$

(3.1.30)

$${\mathcal{R}}_{3}^{4}\left(\xi \right)=\{p-\frac{{m}^{2}{(4\varsigma -{\gamma }^{2})}^{3/2}({{\text{cot}}}^{2}(0.5\sqrt{4\varsigma -{\gamma }^{2}} \xi )+1)}{{\text{cot}}(0.5\sqrt{4\varsigma -{\gamma }^{2}} \xi )}$$

$$+\frac{{m}^{2}{{\left({\gamma }^{2}-4\varsigma \right)}^{2}({{\text{cot}}}^{2}(0.5\sqrt{4\varsigma -{\gamma }^{2}} \xi )+1)}^{3}}{6\sqrt{4\varsigma -{\gamma }^{2}}{{\text{cot}}}^{3}(0.5\sqrt{4\varsigma -{\gamma }^{2}} \xi )}\}{e}^{\sigma \mathcal{B}\left({\text{t}}\right)-\frac{1}{2}{\sigma }^{2}t},$$

(3.1.31)

where $\xi =\frac{1}{\alpha }l{x}^{\alpha }+mt$.

Solution group 4 For case IV,

$${q}_{4}\left(\xi \right)=\frac{\sqrt{2k}(\gamma +2({G}{\prime}(\xi )/G(\xi )))}{\sqrt{4\varsigma -{\gamma }^{2}}},$$

(3.1.32)

$${r}_{4}\left(\xi \right)=p-k\left(\gamma +2\left(\frac{{G}^{\mathrm{^{\prime}}}\left(\xi \right)}{G\left(\xi \right)}\right)\right)+\frac{k{\left(\gamma +2\left(\frac{{G}^{\mathrm{^{\prime}}}\left(\xi \right)}{G\left(\xi \right)}\right)\right)}^{3}}{3\left({\gamma }^{2}-4\varsigma \right)}.$$

(3.1.33)

The postulate ${\gamma }^{2}-4\varsigma >0$ generates the solutions

$${\mathcal{Q}}_{4}^{1}\left(\xi \right)=\sqrt{-2k}\mathrm{ tanh}\left(0.5\sqrt{{\gamma }^{2}-4\varsigma } \xi \right){e}^{\sigma \mathcal{B}\left({\text{t}}\right)-\frac{1}{2}{\sigma }^{2}t},$$

(3.1.34)

$${\mathcal{R}}_{4}^{1}\left(\xi \right)=\left\{p-k\sqrt{{\gamma }^{2}-4\varsigma }\mathrm{ tanh}\left(0.5\sqrt{{\gamma }^{2}-4\varsigma } \xi \right)+\frac{k\sqrt{{\gamma }^{2}-4\varsigma }{{\text{tanh}}}^{3}\left(0.5\sqrt{{\gamma }^{2}-4\varsigma } \xi \right)}{3}\right\}{e}^{\sigma \mathcal{B}\left({\text{t}}\right)-\frac{1}{2}{\sigma }^{2}t},$$

(3.1.35)

$${\mathcal{Q}}_{4}^{2}\left(\xi \right)=\sqrt{-2k}\mathrm{ coth}\left(0.5\sqrt{{\gamma }^{2}-4\varsigma } \xi \right){e}^{\sigma \mathcal{B}\left({\text{t}}\right)-\frac{1}{2}{\sigma }^{2}t},$$

(3.1.36)

$${\mathcal{R}}_{4}^{2}\left(\xi \right)=\left\{p-k\sqrt{{\gamma }^{2}-4\varsigma }\mathrm{ coth}\left(0.5\sqrt{{\gamma }^{2}-4\varsigma } \xi \right)+\frac{k\sqrt{{\gamma }^{2}-4\varsigma }{{\text{coth}}}^{3}\left(0.5\sqrt{{\gamma }^{2}-4\varsigma } \xi \right)}{3}\right\}{e}^{\sigma \mathcal{B}\left({\text{t}}\right)-\frac{1}{2}{\sigma }^{2}t},$$

(3.1.37)

where $\xi =\frac{1}{\alpha }l{x}^{\alpha }\pm \sqrt{\frac{-2k}{{\gamma }^{2}-4\varsigma }}t$.

According to the condition ${\gamma }^{2}-4\varsigma <0$, we attain

$${\mathcal{Q}}_{4}^{4}\left(\xi \right)=-\sqrt{2k}\mathrm{ tan}\left(0.5\sqrt{4\varsigma -{\gamma }^{2}} \xi \right){e}^{\sigma \mathcal{B}\left({\text{t}}\right)-\frac{1}{2}{\sigma }^{2}t},$$

(3.1.38)

$${\mathcal{R}}_{4}^{4}\left(\xi \right)=\left(p+k\sqrt{4\varsigma -{\gamma }^{2}}{\text{tan}}\left(0.5\sqrt{4\varsigma -{\gamma }^{2}} \xi \right)+\frac{k\sqrt{4\varsigma -{\gamma }^{2}}{{\text{tan}}}^{3}(0.5\sqrt{4\varsigma -{\gamma }^{2}} \xi ))}{3}\right){e}^{\sigma \mathcal{B}\left({\text{t}}\right)-\frac{1}{2}{\sigma }^{2}t},$$

(3.1.39)

$${\mathcal{Q}}_{4}^{5}\left(\xi \right)=\sqrt{2k}\mathrm{ cot}\left(0.5\sqrt{4\varsigma -{\gamma }^{2}} \xi \right){e}^{\sigma \mathcal{B}\left({\text{t}}\right)-\frac{1}{2}{\sigma }^{2}t},$$

(3.1.40)

$${\mathcal{R}}_{4}^{5}\left(\xi \right)=\left(p-k\sqrt{4\varsigma -{\gamma }^{2}}{\text{cot}}\left(0.5\sqrt{4\varsigma -{\gamma }^{2}} \xi \right)-\frac{k\sqrt{4\varsigma -{\gamma }^{2}}{{\text{cot}}}^{3}\left(0.5\sqrt{4\varsigma -{\gamma }^{2}} \xi \right)}{3}\right){e}^{\sigma \mathcal{B}\left({\text{t}}\right)-\frac{1}{2}{\sigma }^{2}t},$$

(3.1.41)

where $\xi =\frac{1}{\alpha }l{x}^{\alpha }\pm \sqrt{\frac{-2k}{{\gamma }^{2}-4\varsigma }}t$.

3.2 Solutions via improved tanh method

This technique defines the solution as

$$q\left(\xi \right)=\frac{{\lambda }_{0}+{\lambda }_{1}Y\left(\xi \right)+{\mu }_{1}{Y\left(\xi \right)}^{-1}}{{\sigma }_{0}+{\sigma }_{1}Y\left(\xi \right)+{\tau }_{1}{Y\left(\xi \right)}^{-1}}.$$

(3.2.1)

Equation (3.9) is turned into a polynomial with the help of Eqs. (3.2.1) and (2.2.2). Equate the terms of found polynomial to zero and solve them by employing the computational software Maple to generate the following values:

Case I: ${\lambda }_{0}=0$, ${\lambda }_{1}=2m{\sigma }_{0}$, ${\mu }_{1}=-\frac{k{\sigma }_{0}}{2m}$, ${\sigma }_{1}=0$, ${\tau }_{1}=0$, $\rho =-\frac{k}{4{m}^{2}}$.

Case II: ${\lambda }_{0}=2m{\tau }_{1}$, ${\lambda }_{1}=0$, ${\mu }_{1}=-\frac{k{\sigma }_{0}}{m}$, ${\sigma }_{1}=0$, $\rho =\frac{k}{2{m}^{2}}$.

Case III: ${\lambda }_{0}=2m{\tau }_{1}$, ${\lambda }_{1}=2m{\sigma }_{0}$, ${\mu }_{1}=0$, ${\sigma }_{1}=0$, $\rho =\frac{k}{2{m}^{2}}$.

Case IV: ${\lambda }_{0}=0$, ${\lambda }_{1}=2m{\sigma }_{0}$, ${\mu }_{1}=-\frac{k{\sigma }_{0}}{4m}$, ${\sigma }_{1}=0$, ${\tau }_{1}=0$, $\rho =\frac{k}{8{m}^{2}}$.

Case V: ${\lambda }_{0}=0$, ${\lambda }_{1}=-2m{\sigma }_{0}$, ${\mu }_{1}=\frac{k{\sigma }_{0}}{4m}$, ${\sigma }_{1}=0$, ${\tau }_{1}=0$, $\rho =\frac{k}{8{m}^{2}}$.

Case VI: ${\lambda }_{0}=0$, ${\lambda }_{1}=-2{m\sigma }_{0}$, ${\mu }_{1}=\frac{k{\sigma }_{0}}{2m}$, ${\sigma }_{1}=0$, ${\tau }_{1}=0$,$\rho =-\frac{k}{4{m}^{2}}$.

Case VII: ${\lambda }_{0}=-2m{\tau }_{1}$, ${\lambda }_{1}=0$, ${\mu }_{1}=\frac{k{\sigma }_{0}}{m}$, ${\sigma }_{1}=0$, $\rho =\frac{k}{2{m}^{2}}$.

Case VIII: ${\lambda }_{0}=-2m{\tau }_{1}$, ${\lambda }_{1}=-2m{\sigma }_{0}$, ${\mu }_{1}=0$, ${\sigma }_{1}=0$, $\rho =\frac{k}{2{m}^{2}}$.

The above cases produce abundant wave solutions. To represent the present work in a concise manner, we take into account only the first three cases.

Solution group 1 According to case I,

$${q}_{1}\left(\xi \right)=2mY\left(\xi \right)-\frac{k}{2m}{Y\left(\xi \right)}^{-1},$$

(3.2.2)

$${r}_{1}\left(\xi \right)=\frac{(4{m}^{2}{\left(Y\left(\xi \right)\right)}^{2}-k{)}^{3}}{48{m}^{4}{(Y(\xi ))}^{3}}+\frac{k(4{m}^{2}{\left(Y\left(\xi \right)\right)}^{2}-k)}{2{m}^{2}Y(\xi )}+p,$$

(3.2.3)

where $\xi =\frac{1}{\alpha }l{x}^{\alpha }+mt$. Afterward, the accurate wave solutions are given below.

$$ {\mathcal{Q}}_{1}^{1} \left( \xi \right) = \frac{{4m^{2} \rho \tanh^{2} \left( {\sqrt { - \rho } \xi } \right) + k}}{{2m\sqrt { - \rho } {\text{ tanh}}\left( {\sqrt { - \rho } \xi } \right)}} \times e^{{\sigma {\mathcal{B}}\left( {\text{t}} \right) - \frac{1}{2}\sigma^{2} t}} ,\;\rho < 0 $$

(3.2.4)

$${\mathcal{R}}_{1}^{1}\left(\xi \right)=\left\{p+\frac{k\left(4{m}^{2}\rho {{\text{tanh}}}^{2}\left(\sqrt{-\rho }\xi \right)+k\right)}{2{m}^{2}\sqrt{-\rho }{\text{tanh}}\left(\sqrt{-\rho }\xi \right)}+\frac{{\left(4{m}^{2}\rho {{\text{tanh}}}^{2}\left(\sqrt{-\rho }\xi \right)+k\right)}^{3}}{48{m}^{4}{\left(\sqrt{-\rho }{\text{tanh}}\left(\sqrt{-\rho }\xi \right)\right)}^{3}}\right\}{e}^{\sigma \mathcal{B}\left({\text{t}}\right)-\frac{1}{2}{\sigma }^{2}t}, \rho <0,$$

(3.2.5)

$${\mathcal{Q}}_{1}^{2}\left(\xi \right)=\frac{4{m}^{2}\rho {{\text{coth}}}^{2}\left(\sqrt{-\rho }\xi \right)+k}{2m\sqrt{-\rho }\mathrm{ coth}\left(\sqrt{-\rho }\xi \right)}\times {e}^{\sigma \mathcal{B}\left({\text{t}}\right)-\frac{1}{2}{\sigma }^{2}t}, \rho <0,$$

(3.2.6)

$${\mathcal{R}}_{1}^{2}\left(\xi \right)=\left\{p+\frac{k\left(4{m}^{2}\rho {{\text{coth}}}^{2}\left(\sqrt{-\rho }\xi \right)+k\right)}{2{m}^{2}\sqrt{-\rho }{\text{coth}}\left(\sqrt{-\rho }\xi \right)}+\frac{{\left(4{m}^{2}\rho {{\text{coth}}}^{2}\left(\sqrt{-\rho }\xi \right)+k\right)}^{3}}{48{m}^{4}{\left(\sqrt{-\rho }{\text{coth}}\left(\sqrt{-\rho }\xi \right)\right)}^{3}}\right\}{e}^{\sigma \mathcal{B}\left({\text{t}}\right)-\frac{1}{2}{\sigma }^{2}t}, \rho <0,$$

(3.2.7)

$${\mathcal{Q}}_{1}^{3}\left(\xi \right)=\frac{4{m}^{2}\rho {{\text{tan}}}^{2}\left(\sqrt{\rho }\xi \right)-k}{2m\sqrt{\rho }\mathrm{ tan}\left(\sqrt{\rho }\xi \right)}\times {e}^{\sigma \mathcal{B}\left({\text{t}}\right)-\frac{1}{2}{\sigma }^{2}t}, \rho >0,$$

(3.2.8)

$${\mathcal{R}}_{1}^{3}\left(\xi \right)=\left\{p+\frac{k\left(4{m}^{2}\rho {{\text{tan}}}^{2}\left(\sqrt{\rho }\xi \right)-k\right)}{2{m}^{2}\sqrt{\rho }{\text{tan}}\left(\sqrt{\rho }\xi \right)}+\frac{{\left(4{m}^{2}\rho {{\text{tan}}}^{2}\left(\sqrt{\rho }\xi \right)-k\right)}^{3}}{48{m}^{4}{\left(\sqrt{\rho }{\text{tan}}\left(\sqrt{\rho }\xi \right)\right)}^{3}}\right\}{e}^{\sigma \mathcal{B}\left({\text{t}}\right)-\frac{1}{2}{\sigma }^{2}t}, \rho >0,$$

(3.2.9)

$${\mathcal{Q}}_{1}^{4}\left(\xi \right)=\frac{k-4{m}^{2}\rho {{\text{cot}}}^{2}\left(\sqrt{\rho }\xi \right)}{2m\sqrt{\rho }\mathrm{ cot}\left(\sqrt{\rho }\xi \right)}\times {e}^{\sigma \mathcal{B}\left({\text{t}}\right)-\frac{1}{2}{\sigma }^{2}t}, \rho >0,$$

(3.2.10)

$${\mathcal{R}}_{1}^{4}\left(\xi \right)=\left\{p+\frac{k\left(k-4{m}^{2}\rho {{\text{cot}}}^{2}\left(\sqrt{\rho }\xi \right)\right)}{2{m}^{2}\sqrt{\rho }\mathrm{ cot}\left(\sqrt{\rho }\xi \right)}+\frac{{\left(k-4{m}^{2}\rho {{\text{cot}}}^{2}\left(\sqrt{\rho }\xi \right)\right)}^{3}}{48{m}^{4}{\left(\sqrt{\rho }\mathrm{ cot}\left(\sqrt{\rho }\xi \right)\right)}^{3}}\right\}{e}^{\sigma \mathcal{B}\left({\text{t}}\right)-\frac{1}{2}{\sigma }^{2}t}, \rho >0$$

(3.2.11)

$${\mathcal{Q}}_{1}^{5}\left(\xi \right)=\frac{k{\xi }^{2}-4{m}^{2}}{2m\xi }\times {e}^{\sigma \mathcal{B}\left({\text{t}}\right)-\frac{1}{2}{\sigma }^{2}t}, \rho =0,$$

(3.2.12)

$${\mathcal{R}}_{1}^{5}\left(\xi \right)=\left\{p+\frac{k\left(k{\xi }^{2}-4{m}^{2}\right)}{2{m}^{2}\xi }+\frac{{\left(k{\xi }^{2}-4{m}^{2}\right)}^{3}}{48{m}^{4}{\xi }^{3}}\right\}{e}^{\sigma \mathcal{B}\left({\text{t}}\right)-\frac{1}{2}{\sigma }^{2}t}, \rho =0,$$

(3.2.13)

where $\xi =\frac{1}{\alpha }l{x}^{\alpha }+mt$.

Solution group 2 Due to case II,

$${q}_{2}\left(\xi \right)=\frac{2{m}^{2}{\tau }_{1}-{\sigma }_{0}k{Y\left(\xi \right)}^{-1}}{m\left({\sigma }_{0}+{\tau }_{1}{Y\left(\xi \right)}^{-1}\right)},$$

(3.2.14)

$${r}_{2}\left(\xi \right)=\frac{(2{m}^{2}{\tau }_{1}Y\left(\xi \right)-{\sigma }_{0}k{)}^{3}}{6{m}^{2}{\left({\sigma }_{0}Y\left(\xi \right)+{\tau }_{1}\right)}^{3}}+\frac{k\left(2{m}^{2}{\tau }_{1}Y\left(\xi \right)-{\sigma }_{0}k\right)}{{m}^{2}({\sigma }_{0}Y\left(\xi \right)+{\tau }_{1})}+p,$$

(3.2.15)

where $\xi =\frac{1}{\alpha }l{x}^{\alpha }+mt$. Accordingly, the subsequent pivotal wave solutions are constructed.

$${\mathcal{Q}}_{2}^{1}\left(\xi \right)=\frac{2{m}^{2}{\tau }_{1}\sqrt{-\rho }\mathrm{ tanh}\left(\sqrt{-\rho }\xi \right)+k{\sigma }_{0}}{m({\sigma }_{0}\sqrt{-\rho }\mathrm{ tanh}\left(\sqrt{-\rho }\xi \right)-{\tau }_{1})}\times {e}^{\sigma \mathcal{B}\left({\text{t}}\right)-\frac{1}{2}{\sigma }^{2}t}, \rho <0,$$

(3.2.16)

$${\mathcal{R}}_{2}^{1}\left(\xi \right)=\left\{p+\frac{k\left(2{m}^{2}{\tau }_{1}\sqrt{-\rho }\mathrm{ tanh}\left(\sqrt{-\rho }\xi \right)+{k\sigma }_{0}\right)}{{m}^{2}\left({\sigma }_{0}\sqrt{-\rho }\mathrm{ tanh}\left(\sqrt{-\rho }\xi \right)-{\tau }_{1}\right)}+\frac{{\left(2{m}^{2}{\tau }_{1}\sqrt{-\rho }\mathrm{ tanh}\left(\sqrt{-\rho }\xi \right)+{k\sigma }_{0}\right)}^{3}}{6{m}^{4}{\left({\sigma }_{0}\sqrt{-\rho }\mathrm{ tanh}\left(\sqrt{-\rho }\xi \right)-{\tau }_{1}\right)}^{3}}\right\}{e}^{\sigma \mathcal{B}\left({\text{t}}\right)-\frac{1}{2}{\sigma }^{2}t}, \rho <0,$$

(3.2.17)

$${\mathcal{Q}}_{2}^{2}\left(\xi \right)=\frac{2{m}^{2}{\tau }_{1}\sqrt{-\rho }\mathrm{ coth}\left(\sqrt{-\rho }\xi \right)+k{\sigma }_{0}}{m\left({\sigma }_{0}\sqrt{-\rho }\mathrm{ coth}\left(\sqrt{-\rho }\xi \right)-{\tau }_{1}\right)}\times {e}^{\sigma \mathcal{B}\left({\text{t}}\right)-\frac{1}{2}{\sigma }^{2}t}, \rho <0,$$

(3.2.18)

$${\mathcal{R}}_{2}^{2}\left(\xi \right)=\left\{p+\frac{k\left(2{m}^{2}{\tau }_{1}\sqrt{-\rho }\mathrm{ coth}\left(\sqrt{-\rho }\xi \right)+{k\sigma }_{0}\right)}{{m}^{2}\left({\sigma }_{0}\sqrt{-\rho }\mathrm{ coth}\left(\sqrt{-\rho }\xi \right)-{\tau }_{1}\right)}+\frac{{\left(2{m}^{2}{\tau }_{1}\sqrt{-\rho }\mathrm{ coth}\left(\sqrt{-\rho }\xi \right)+{k\sigma }_{0}\right)}^{3}}{6{m}^{4}{\left({\sigma }_{0}\sqrt{-\rho }\mathrm{ coth}\left(\sqrt{-\rho }\xi \right)-{\tau }_{1}\right)}^{3}}\right\}{e}^{\sigma \mathcal{B}\left({\text{t}}\right)-\frac{1}{2}{\sigma }^{2}t}, \rho <0,$$

(3.2.19)

$${\mathcal{Q}}_{2}^{3}\left(\xi \right)=\frac{2{m}^{2}{\tau }_{1}\sqrt{\rho }{\text{tan}}\left(\sqrt{\rho }\xi \right)-k{\sigma }_{0}}{m\left({\tau }_{1}+{\sigma }_{0}\sqrt{\rho }{\text{tan}}\left(\sqrt{\rho }\xi \right)\right)}\times {e}^{\sigma \mathcal{B}\left({\text{t}}\right)-\frac{1}{2}{\sigma }^{2}t}, \rho >0,$$

(3.2.20)

$${\mathcal{R}}_{2}^{3}\left(\xi \right)=\left\{p+\frac{k\left(2{m}^{2}{\tau }_{1}\sqrt{\rho }{\text{tan}}\left(\sqrt{\rho }\xi \right)-k{\sigma }_{0}\right)}{{m}^{2}\left({\tau }_{1}+{\sigma }_{0}\sqrt{\rho }{\text{tan}}\left(\sqrt{\rho }\xi \right)\right)}+\frac{{\left(2{m}^{2}{\tau }_{1}\sqrt{\rho }{\text{tan}}\left(\sqrt{\rho }\xi \right)-k{\sigma }_{0}\right)}^{3}}{6{m}^{4}{\left({\tau }_{1}+{\sigma }_{0}\sqrt{\rho }{\text{tan}}\left(\sqrt{\rho }\xi \right)\right)}^{3}}\right\}{e}^{\sigma \mathcal{B}\left({\text{t}}\right)-\frac{1}{2}{\sigma }^{2}t}, \rho >0,$$

(3.2.21)

$${\mathcal{Q}}_{2}^{4}\left(\xi \right)=\frac{2{m}^{2}{\tau }_{1}\sqrt{\rho }\mathrm{ cot}\left(\sqrt{\rho }\xi \right)+{k\sigma }_{0}}{m\left({\sigma }_{0}\sqrt{\rho }\mathrm{ cot}\left(\sqrt{\rho }\xi \right)-{\tau }_{1}\right)}\times {e}^{\sigma \mathcal{B}\left({\text{t}}\right)-\frac{1}{2}{\sigma }^{2}t}, \rho >0,$$

(3.2.22)

$${\mathcal{R}}_{2}^{4}\left(\xi \right)=\left\{p+\frac{k\left(2{m}^{2}{\tau }_{1}\sqrt{\rho }\mathrm{ cot}\left(\sqrt{\rho }\xi \right)+{k\sigma }_{0}\right)}{{m}^{2}\left({\sigma }_{0}\sqrt{\rho }\mathrm{ cot}\left(\sqrt{\rho }\xi \right)-{\tau }_{1}\right)}+\frac{{\left(2{m}^{2}{\tau }_{1}\sqrt{\rho }\mathrm{ cot}\left(\sqrt{\rho }\xi \right)+{k\sigma }_{0}\right)}^{3}}{6{m}^{4}{\left({\sigma }_{0}\sqrt{\rho }\mathrm{ cot}\left(\sqrt{\rho }\xi \right)-{\tau }_{1}\right)}^{3}}\right\}{e}^{\sigma \mathcal{B}\left({\text{t}}\right)-\frac{1}{2}{\sigma }^{2}t}, \rho >0,$$

(3.2.23)

$${\mathcal{Q}}_{2}^{5}\left(\xi \right)=\frac{2{{m}^{2}\tau }_{1}+k{\sigma }_{0}\xi }{m\left({\sigma }_{0}-{\tau }_{1}\xi \right)}\times {e}^{\sigma \mathcal{B}\left({\text{t}}\right)-\frac{1}{2}{\sigma }^{2}t}, \rho =0.$$

(3.2.24)

$${\mathcal{R}}_{2}^{5}\left(\xi \right)=\left\{p+\frac{k\left(2{{m}^{2}\tau }_{1}+k{\sigma }_{0}\xi \right)}{{m}^{2}\left({\sigma }_{0}-{\tau }_{1}\xi \right)}+\frac{{\left(2{{m}^{2}\tau }_{1}+k{\sigma }_{0}\xi \right)}^{3}}{6{m}^{4}{\left({\sigma }_{0}-{\tau }_{1}\xi \right)}^{3}}\right\}{e}^{\sigma \mathcal{B}\left({\text{t}}\right)-\frac{1}{2}{\sigma }^{2}t}, \rho =0,$$

(3.2.25)

where $\xi =\frac{1}{\alpha }l{x}^{\alpha }+mt$.

Solution group 3 For case III,

$${q}_{3}\left(\xi \right)=2mY\left(\xi \right),$$

(3.2.26)

$${r}_{3}\left(\xi \right)=\frac{4}{3}{m}^{2}{\left(Y\left(\xi \right)\right)}^{3}+2kY\left(\xi \right)+p,$$

(3.2.27)

where $\xi =\frac{1}{\alpha }l{x}^{\alpha }+mt$. Thereupon, the accurate form significant wave solutions are generated as follows:

$${\mathcal{Q}}_{3}^{1}\left(\xi \right)=-2m\sqrt{-\rho }\mathrm{ tanh}\left(\sqrt{-\rho }\xi \right){e}^{\sigma \mathcal{B}\left({\text{t}}\right)-\frac{1}{2}{\sigma }^{2}t}, \rho <0,$$

(3.2.28)

$${\mathcal{R}}_{3}^{1}\left(\xi \right)=\left\{p-2k\sqrt{-\rho }{\text{tanh}}\left(\sqrt{-\rho }\xi \right)-\frac{4}{3}{{m}^{2}\left(\sqrt{-\rho }{\text{tanh}}\left(\sqrt{-\rho }\xi \right)\right)}^{3}\right\}{e}^{\sigma \mathcal{B}\left({\text{t}}\right)-\frac{1}{2}{\sigma }^{2}t}, \rho <0,$$

(3.2.29)

$${\mathcal{Q}}_{3}^{2}\left(\xi \right)=-2m\sqrt{-\rho }\mathrm{ coth}\left(\sqrt{-\rho }\xi \right){e}^{\sigma \mathcal{B}\left({\text{t}}\right)-\frac{1}{2}{\sigma }^{2}t}, \rho <0,$$

(3.2.30)

$${\mathcal{R}}_{3}^{2}\left(\xi \right)=\left\{p-2k\sqrt{-\rho }{\text{coth}}\left(\sqrt{-\rho }\xi \right)-\frac{4}{3}{{m}^{2}\left(\sqrt{-\rho }{\text{coth}}\left(\sqrt{-\rho }\xi \right)\right)}^{3}\right\}{e}^{\sigma \mathcal{B}\left({\text{t}}\right)-\frac{1}{2}{\sigma }^{2}t}, \rho <0,$$

(3.2.31)

$${\mathcal{Q}}_{3}^{3}\left(\xi \right)=2m\sqrt{\rho }\mathrm{ tan}\left(\sqrt{\rho }\xi \right){e}^{\sigma \mathcal{B}\left({\text{t}}\right)-\frac{1}{2}{\sigma }^{2}t}, \rho >0,$$

(3.2.32)

$${\mathcal{R}}_{3}^{3}\left(\xi \right)=\{p+2k\left(\sqrt{\rho }\mathrm{ tan}\left(\sqrt{\rho }\xi \right)+\frac{4}{3}{{m}^{2}\left(\sqrt{\rho }{\text{tan}}\left(\sqrt{\rho }\xi \right)\right)}^{3}\right\}{e}^{\sigma \mathcal{B}\left({\text{t}}\right)-\frac{1}{2}{\sigma }^{2}t}, \rho >0,$$

(3.2.33)

$${\mathcal{Q}}_{3}^{4}\left(\xi \right)=-2m\sqrt{\rho }\mathrm{ cot}\left(\sqrt{\rho }\xi \right){e}^{\sigma \mathcal{B}\left({\text{t}}\right)-\frac{1}{2}{\sigma }^{2}t}, \rho >0,$$

(3.2.34)

$${\mathcal{R}}_{3}^{4}\left(\xi \right)=\{p-2k\left(\sqrt{\rho }\mathrm{ cot}\left(\sqrt{\rho }\xi \right)-\frac{4}{3}{{m}^{2}\left(\sqrt{\rho }{\text{cot}}\left(\sqrt{\rho }\xi \right)\right)}^{3}\right\}{e}^{\sigma \mathcal{B}\left({\text{t}}\right)-\frac{1}{2}{\sigma }^{2}t}, \rho >0,$$

(3.2.35)

$${\mathcal{Q}}_{3}^{5}\left(\xi \right)=\frac{-2m}{\xi }{e}^{\sigma \mathcal{B}\left({\text{t}}\right)-\frac{1}{2}{\sigma }^{2}t}, \rho =0,$$

(3.2.36)

$${\mathcal{R}}_{3}^{5}\left(\xi \right)=\left\{p-\frac{2k}{\xi }-\frac{4{m}^{2}}{3{\xi }^{3}}\right\}{e}^{\sigma \mathcal{B}\left({\text{t}}\right)-\frac{1}{2}{\sigma }^{2}t}, \rho =0,$$

(3.2.37)

where $\xi =\frac{1}{\alpha }l{x}^{\alpha }+mt$.

4 Results discussion and graphical representations

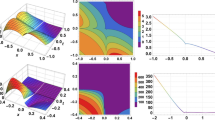
Nonlinear intricate phenomena arising in nature-world are explained through the nonlinear partial model. Researchers have intended to extract nonlinear evolution equations for exact wave solutions which are helpful to analyze the nonlinear phenomena. The exploration is successful in making available huge interesting and significant wave solutions with newness and generality. The achieved solutions are distinct and novel than the existing results in the literature (Mohammed et al. 2023). We figure out some of the achieved solutions to illustrate the dynamic behavior of nonlinear waves in ferromagnetic materials. The effects of noise on the Brownian motion as well as the effects of fractional operator are highlighted in plotting the wave solutions. Figure 1: A soliton of solution Eq. (3.1.6) is found as singular periodic shape for the values $\alpha =1$, $l=0.25$, $k=1.5$, $p=\varsigma =1$ and $\gamma =4$ within $-10\le x,t\le 10$, and 2D plots are described at $t=0.1$. The effects of noise $(\sigma =0.0, 0.2, 0.4)$ on the Brownian motion through 3D, 2D and contour plots are highlighted in a good manner in this figure. Figure 2: The singular periodic shape soliton for solution Eq. (3.1.6) is appeared for $l=0.25$, $k=1.5$, $p=\varsigma =1$, $\gamma =4$ and $\sigma =0$ in $-10\le x,t\le 10$, and 2D plots are labelled at $t=0.1$. In this case, the effects of fractional operator $(\alpha =1.0, 0.7, 0.3)$ are highlighted clearly. Figure 3: The soliton for solution Eq. (3.1.28) is periodic type under $\alpha =1$, $l=m=0.5$, $k=5$, $\varsigma =4$ and $\gamma =3$ in the interval $0\le x,t\le 10$, and 2D plots are explained at $t=6.9$. This figure brings out the effects of noise $(\sigma =0.0, 0.2, 0.4)$ on the Brownian motion. Figure 4: Solution Eq. (3.1.28) represents periodic soliton for $l=m=0.5$, $\varsigma =4$, $\gamma =4$ and $\sigma =0$ within the range $0\le x,t\le 10$, and 2D plots are portrayed at $t=6.9$. The effects of fractional operator $(\alpha =1.0000, 0.9985, 0.9969)$ are appeared in this figure. Figure 5: Anti-kink type soliton of solution Eq. (3.1.37) is illustrated for $\alpha =p=1$, $l=k=\varsigma =2$ and $\gamma =6$ in $-10\le x,t\le 10$, and 2D plots are described at $t=0.1$. The effects of noise $(\sigma =0.0, 0.1, 0.2)$ on the Brownian motion are visualized in this figure. Figure 6: Anti-kink shape soliton of solution Eq. (3.1.37) is appeared under $p=1$, $l=k=\varsigma =2$, $\gamma =6$ and $\sigma =0$ within the interval $-10\le x,t\le 10$, and 2D plots are depicted at $t=0.1$. The effects of fractional operator $(\alpha =1.00, 0.76, 0.51)$ are made visible in this figure. Figure 7: Solution Eq. (3.2.20) gives periodic shape soliton with the values $\alpha =1$, $k=m=0.25$, $l=0.5$, ${\tau }_{1}=5$ and ${\sigma }_{0}=2$ in the range $0\le x,t\le 10$, and 2D plots are described at $t=5$. The effects of noise $(\sigma =0.0, 0.4, 0.8)$ on the Brownian motion are highlighted in this plot. Figure 8: A soliton for solution (3.2.20) is periodic for $k=m=0.25$, $l=0.5$, ${\tau }_{1}=5$, $\sigma =0$ and ${\sigma }_{0}=2$ in $0\le x,t\le 10$, and 2D plots are described at $t=5$. Periodic shape soliton of solution Eq. (3.2.20) with the effects of fractional operator $(\alpha =1.0000, 0.9988, 0.9976)$ are made visible in this figure. Figure 9: Solution Eq. (3.2.29) represents kink type soliton $\alpha =l=m=1$, $p=50$ and $k=-10$ in the interval $0\le x,t\le 10$, and 2D plots are given at $t=5$. The effects of noise $(\sigma =0.0, 0.2, 0.4)$ on the Brownian motion are emphasized in this plot. Figure 10: kink shape soliton of solution Eq. (3.2.29) is obtained for the values $l=m=1$, $p=10$, $k=-10$ and $\sigma =0$ within the range $0\le x,t\le 10$, and 2D plots are described at $t=5$. The effects of fractional operator $(\alpha =1.0, 0.7, 0.3)$ are made visible in this figure.

Fig. 1

Singular periodic soliton with noise effects of Eq. (3.1.6) under $\alpha =1$, $l=0.25$, $k=1.5$, $p=\varsigma =1$ and $\gamma =4$

Fig. 2

Singular periodic soliton with fractional operator effects of (3.1.6) for $l=0.25$, $k=1.5$, $p=\varsigma =1$, $\gamma =4$ and $\sigma =0$

Fig. 3

Periodic soliton of Eq. (3.1.28) with noise effects for $\alpha =1$, $l=m=0.5$, $k=5$, $\varsigma =4$ and $\gamma =3$

Fig. 4

Periodic soliton of Eq. (3.1.28) with the effects of fractional operator for $l=m=0.5$, $\varsigma =4$, $\gamma =4$ and $\sigma =0$

Fig. 5

Anti-kink shape soliton of Eq. (3.1.37) with noise effects for $\alpha =p=1$, $l=k=\varsigma =2$ and $\gamma =6$

Fig. 6

Anti-kink shape soliton of Eq. (3.1.37) with the effects of fractional operator for $p=1$, $l=k=\varsigma =2$, $\gamma =6$ and $\sigma =0$

Fig. 7

Periodic soliton of Eq. (3.2.20) with the noise effects under $\alpha =1$, $k=m=0.25$, $l=0.5$, ${\tau }_{1}=5$ and ${\sigma }_{0}=2$

Fig. 8

Periodic soliton of Eq. (3.2.20) with the effects of fractional operator for $k=m=0.25$, $l=0.5$, ${\tau }_{1}=5$, $\sigma =0$ and ${\sigma }_{0}=2$

Fig. 9

Kink soliton of Eq. (3.2.29) with noise effects under $\alpha =l=m=1$, $p=50$ and $k=-10$

Fig. 10

Kink soliton of Eq. (3.2.29) with the effects of fractional operator for $l=m=1$, $p=10$, $k=-10$ and $\sigma =0$

5 Conclusion

Our desire was to explore appropriate soliton solutions of the space fractional stochastic Kraenkel–Manna–Merle model in ferromagnetic materials. This investigation has adapted two efficient techniques, namely enhanced rational $({G}{\prime}/G)$-expansion and improved tanh which provided remarkable solitary wave solutions. The constructed solutions have significantly been highlighted throughout the graphical representations. Diverse multiple plots in contour, 2D and 3D outlines have been visualized to express the underlying nature of nonlinear dynamic ultra short-waves in ferromagnetic materials. It has been observed that the effects of noise on the Brownian motion and the effects of fractional operator have characterized the ultra-short-wave pulses through graphical representations in a crucial way. Ferromagnetic materials are mainly utilized in two technological applications, as flux multipliers forming the nucleus of electromagnetic machines and as stores of either information or energy. The exploration might be a new addition in the literature regarding its outcomes and used competent techniques.