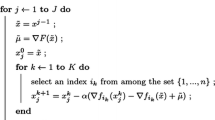Abstract
This paper focuses on tomographic reconstruction for nuclear medicine imaging, where a classical approach consists to maximize the likelihood of Poisson distributed data using the iterative Expectation Maximization algorithm. In this context and when the quantity of acquired data is low and produces low signal-to-noise ratio in the images, a step forward consists to incorporate a total variation prior on the solution into a MAP-EM formulation. This prior is not differentiable. The novelty of the paper is to propose a convergent and efficient numerical scheme to compute the MAP-EM optimizer, alternating regular maximum likelihood maximization steps and TV-denoising solved using the convex-duality principle of Fenchel-Rockafellar. The main theoretical result is the proof of stability and convergence of this scheme. We also present some numerical experiments where we compare the proposed algorithm with some other algorithms from the literature.








Similar content being viewed by others
Data availability
Data sharing not applicable to this article as no datasets were generated or analyzed during the current study.
References
Lange, K., Carson, R.: EM reconstruction algorithms for emission and transmission tomography. J. Comput. Assist. Tomogr. 8(2), 306–316 (1984)
Vardi, Y., Shepp, L.A., Kaufman, L.: A statistical model for positron emission tomography. J. Am. Stat. Assoc. 80(389), 8–20 (1985)
Hudson, H.M., Larkin, R.S.: Accelerated image reconstruction using ordered subsets of projection data. IEEE Transactions on Medical Imaging 13(4), 601–609 (1994)
Browne, J., De Pierro, A.B.: A row-action alternative to the EM algorithm for maximizing likelihood in emission tomography. IEEE Transactions on Medical Imaging 15(5), 687–699 (1996)
Sitek, A.: Representation of photon limited data in emission tomography using origin ensembles. Physics in Medicine & Biology 53(12), 3201 (2008)
Kaufman, L.: Implementing and accelerating the EM algorithm for positron emission tomography. IEEE Transactions on Medical Imaging 6(1), 37–51 (1987)
Snyder, D.L., Miller, M.I., Thomas, L.J., Politte, D.G.: Noise and edge artifacts in maximum-likelihood reconstructions for emission tomography. IEEE Transactions on Medical Imaging 6(3), 228–238 (1987)
Silverman, B., Jones, M., Wilson, J., Nychka, D.: A smoothed EM approach to indirect estimation problems, with particular, reference to stereology and emission tomography. Journal of the Royal Statistical Society. Series B (Methodological) 52(2), 271–324 (1990)
Veklerov, E., Llacer, J., Hoffman, E.: MLE reconstruction of a brain phantom using a Monte Carlo transition matrix and a statistical stopping rule. IEEE Transactions on Nuclear Science 35(1), 603–607 (1988)
Snyder, D.L., Miller, M.I.: The use of sieves to stabilize images produced with the EM algorithm for emission tomography. IEEE Transactions on Nuclear Science 32(5), 3864–3872 (1985)
Stute, S., Comtat, C.: Practical considerations for image-based PSF and blobs reconstruction in PET. Physics in Medicine and Biology 58(11), 3849 (2013)
Fessler, J.A., Rogers, W.L.: Spatial resolution properties of penalized-likelihood image reconstruction: space-invariant tomographs. IEEE Transactions on Image Processing 5(9), 1346–1358 (1996)
Nuyts, J., Fessler, J.A.: A penalized-likelihood image reconstruction method for emission tomography, compared to postsmoothed maximum-likelihood with matched spatial resolution. IEEE Transactions on Medical Imaging 22(9), 1042–1052 (2003)
Sidky, E.Y., Kao, C.-M., Pan, X.: Accurate image reconstruction from few-views and limited-angle data in divergent-beam CT. Journal of X-ray Science and Technology 14(2), 119–139 (2006)
Beck, A., Teboulle, M.: Fast gradient-based algorithms for constrained total variation image denoising and deblurring problems. IEEE Transactions on Image Processing 18(11), 2419–2434 (2009). https://doi.org/10.1109/TIP.2009.2028250
Rudin, L.I., Osher, S., Fatemi, E.: Nonlinear total variation based noise removal algorithms. Physica D: Nonlinear Phenomena 60(1–4), 259–268 (1992)
Sawatzky, A., Brune, C., Wubbeling, F., Kosters, T., Schafers, K., Burger, M.: Accurate EM-TV algorithm in PET with low SNR. In: Nuclear Science Symposium Conference Record, 2008. NSS’08. pp. 5133–5137. IEEE (2008)
Yan, M., Chen, J., Vese, L.A., Villasenor, J., Bui, A., Cong, J.: EM+TV based reconstruction for cone-beam CT with reduced radiation. In: Advances in Visual Computing, pp. 1–10. Springer (2011). https://doi.org/10.1007/978-3-642-24028-7_1
Anthoine, S., Aujol, J.-F., Boursier, Y., Melot, C.: Some proximal methods for Poisson intensity CBCT and PET. Inverse Problems & Imaging 6(4), 565–598 (2012)
Sawatzky, A., Brune, C., Koesters, T., Wuebbeling, F., Burger, M.: EM-TV methods for inverse problems with Poisson noise. In: Level Set and PDE Based Reconstruction Methods in Imaging, pp. 71–142. Springer, (2013). https://doi.org/10.1007/978-3-319-01712-9_2
Mikhno, A., Angelini, E.D., Bai, B., Laine, A.F.: Locally weighted total variation denoising for ringing artifact suppression in PET reconstruction using PSF modeling. In: 2013 IEEE 10th International Symposium on Biomedical Imaging (ISBI), pp. 1252–1255 (2013)
Panin, V.Y., Zeng, G.L., Gullberg, G.T.: Total variation regulated EM algorithm. IEEE Transactions on Nuclear Science 46(6), 2202–2210 (1999). https://doi.org/10.1109/23.819305
Persson, M., Bone, D., Elmqvist, H.: Total variation norm for three-dimensional iterative reconstruction in limited view angle tomography. Physics in Medicine & Biology 46(3), 853 (2001)
Green, P.J.: Bayesian reconstructions from emission tomography data using a modified EM algorithm. IEEE Transactions on Medical Imaging 9(1), 84–93 (1990). https://doi.org/10.1109/42.52985
Ahn, S., Fessler, J.A.: Globally convergent image reconstruction for emission tomography using relaxed ordered subsets algorithms. IEEE Transactions on Medical Imaging 22(5), 613–626 (2003)
Chambolle, A., Pock, T.: A first-order primal-dual algorithm for convex problems with applications to imaging. Journal of Mathematical Imaging and Vision 40(1), 120–145 (2011). https://doi.org/10.1007/s10851-010-0251-1
Ehrhardt, M.J., Markiewicz, P., Schönlieb, C.-B.: Faster pet reconstruction with non-smooth priors by randomization and preconditioning. Physics in Medicine & Biology 64(22), 225019 (2019)
Kereta, Ž, Twyman, R., Arridge, S., Thielemans, K., Jin, B.: Stochastic EM methods with variance reduction for penalised PET reconstructions. Inverse Problems 37(11), 115006 (2021)
Dempster, A.P., Laird, N.M., Rubin, D.B.: Maximum likelihood from incomplete data via the EM algorithm. Journal of the Royal Statistical Society. Series B (Methodological) 39, 1–38 (1977)
Sidky, E.Y., Jørgensen, J.H., Pan, X.: Convex optimization problem prototyping for image reconstruction in computed tomography with the Chambolle-Pock algorithm. Physics in Medicine and Biology 57(10), 3065–3091 (2012). https://doi.org/10.1088/0031-9155/57/10/3065
Iusem, A.N.: A short convergence proof of the EM algorithm for a specific Poisson model. Brazilian J. Probab. Stat. 6(1), 57–67 (1992)
Chambolle, A.: An algorithm for total variation minimization and applications. J. Math. Imag. Vision 20(1–2), 89–97 (2004)
Yan, M., Bui, A.A., Cong, J., Vese, L.A.: General convergent expectation maximization (EM)-type algorithms for image reconstruction. Inverse Problems & Imaging 7(3), 1007–1029 (2013)
Hiriart-Urruty, J.-B., Lemaréchal, C.: Fundamentals of Convex Analysis. Springer, Berlin (2004)
Beck, A., Teboulle, M.: A fast iterative shrinkage-thresholding algorithm for linear inverse problems. SIAM Journal on Imaging Sciences 2(1), 183–202 (2009)
Chambolle, A., Dossal, C.H.: On the convergence of the iterates of “Fast Iterative Shrinkage/Thresholding Algorithm’’. Journal of Optimization Theory and Applications 166(3), 25 (2015)
Bardsley, J.M., Goldes, J.: Regularization parameter selection methods for ill-posed Poisson maximum likelihood estimation. Inverse Problems 25(9), 095005 (2009)
Bertero, M., Boccacci, P., Talenti, G., Zanella, R., Zanni, L.: A discrepancy principle for Poisson data. Inverse Problems 26(10), 105004 (2010). https://doi.org/10.1088/0266-5611/26/10/105004
Hohage, T., Werner, F.: Inverse problems with Poisson data: statistical regularization theory, applications and algorithms. Inverse Problems 32(9), 093001 (2016). https://doi.org/10.1088/0266-5611/32/9/093001
Lucka, F., Proksch, K., Brune, C., Bissantz, N., Burger, M., Dette, H., Wübbeling, F.: Risk estimators for choosing regularization parameters in ill-posed problems - properties and limitations. Inverse Problems & Imaging 12(5), 1121–1155 (2018)
Acknowledgements
This work was partially funded by the French National Research Agency (ANR) under grant ANR-20-CE45-0020 and by the LABEX PRIMES (ANR-11-LABX-0063) of Université de Lyon within the program “Investissements d’Avenir” (ANR-11-IDEX-0007).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflicts of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A: Proof of Lemma 1
For a given \(\varvec{\lambda }^{\prime }\in D\) and any \(\varvec{\lambda }\in D\), we denote \(K(\varvec{\lambda }\vert \varvec{\lambda }^{\prime })= F(\varvec{\lambda })-U(\varvec{\lambda }\vert \varvec{\lambda }^{\prime })\). Let us start with some results concerning \(K(\varvec{\lambda }\vert \varvec{\lambda }^{\prime })\). We have:
Since \(\sum \limits _{i=1}^{I} \sum \limits _{j=1}^{J} t_{ij}\lambda _{j} = \sum \limits _{j=1}^{J} s_{j}\lambda _{j}\), thus
The partial derivatives of \(K(\cdot \vert \varvec{\lambda }^{\prime })\) are:
We recall that \(\overline{\varvec{\lambda }^{\prime }}\) is the vector with entries \(\overline{\lambda ^{\prime }}_{j} = \displaystyle \frac{\lambda ^{\prime }_{j}}{s_{j}}\sum _{i=1}^{I}\frac{t_{ij}y_{i}}{\sum _{k} t_{ik}\lambda ^{\prime }_{k}}\). This implies that for all \(\varvec{\lambda }^{\prime }\in D\)
The logarithm being a concave function, by the Jensen inequality we obtain for all \(i\in \{1,\dots ,I\}\) that:
thus which implies that for all \(\varvec{\lambda },\varvec{\lambda }^{\prime }\),
Proof of Lemma 1
Let \(\varvec{\lambda }^{*}\) be a minimum of F. From (A3), for all \(\varvec{\lambda }\in D\), \(K(\varvec{\lambda }\vert \varvec{\lambda }^{*})\le K(\varvec{\lambda }^{*}\vert \varvec{\lambda }^{*})\) thus \(U(\varvec{\lambda }\vert \varvec{\lambda }^{*})\ge U(\varvec{\lambda }^{*}\vert \varvec{\lambda }^{*})\) and (16) is verified. Conversely, if \(\varvec{\lambda }^{*}\) verifies (16) then \(0\in \partial U(\cdot \,\vert \varvec{\lambda }^{*})(\varvec{\lambda }^{*}) = \partial F(\varvec{\lambda }^{*})-\nabla K(\cdot \vert \varvec{\lambda }^{*})(\varvec{\lambda }^{*})\). From (A2), \(\nabla K(\cdot \vert \varvec{\lambda }^{*})(\varvec{\lambda }^{*}) =0\), thus \(0\in \partial F(\varvec{\lambda }^{*})\) and \(\varvec{\lambda }^{*}\) is a minimum of F. \(\square \)
Appendix B: Proof of Theorem 2
Proof
-
(i)
From the definition of K and from (A3) it follows that
$$ \begin{array}{ll} F(M(\varvec{\lambda }^{\prime })) &{}= U(M(\varvec{\lambda }^{\prime })\vert \varvec{\lambda }^{\prime }) + K(M(\varvec{\lambda }^{\prime })\vert \varvec{\lambda }^{\prime }) \\ &{}\le U(M(\varvec{\lambda }^{\prime })\vert \varvec{\lambda }^{\prime }) + K(\varvec{\lambda }^{\prime }\vert \varvec{\lambda }^{\prime }). \end{array} $$Then from (18) and again the definition of K we obtain the result.
-
(ii)
If \(\varvec{\lambda }^{*}\) is a fixed point of M then \(U(M(\varvec{\lambda }^{*})\vert \varvec{\lambda }^{*}) = U(\varvec{\lambda }^{*}\vert \varvec{\lambda }^{*})\). Equation (19) follows from Definition 1. The reciprocal is obvious by the definition of M.
-
(iii)
This property immediately follows from (ii) and Lemma 1.
\(\square \)
Appendix C: Proof of Theorem 3
Proof
(i) The fact that the sequence \((F(\varvec{\lambda }^{(n)}))\) is non-increasing is a direct consequence of Theorem 2(i). It is clear that \((\varvec{\lambda }^{(n)})\) is bounded. Indeed, if this would not be the case, a sub-sequence \((\varvec{\lambda }^{(n_{k})})\) such that \(\lim _{k\rightarrow +\infty }\Vert \varvec{\lambda }^{(n_{k})}\Vert =+\infty \) may be extracted. Since F is coercive, the sequence \((F(\varvec{\lambda }^{(n_{k})}))\) would not be bounded either, which comes in contradiction with the fact that \((F(\varvec{\lambda }^{(n)}))\) is non-increasing and bounded below by the minimum of F. Let \((\varvec{\lambda }^{(n_{k})})\) be a convergent sub-sequence of \((\varvec{\lambda }^{(n)})\) with limit \(\varvec{\lambda }^{*}\). Then the sub-sequence \((\varvec{\lambda }^{(n_{k}+1)})\) is also convergent and tends to \(M(\varvec{\lambda }^{*})\). The sequence \((F(\varvec{\lambda }^{(n)}))\) being non-increasing and bounded below, it converges and
thus \(F(M(\varvec{\lambda }^{*}))=F(\varvec{\lambda }^{*})\). From Theorem 2(i) we then deduce that
and from the same theorem it results that \(\varvec{\lambda }^{*}\) is a fixed point of M and \(\varvec{\lambda }^{*}\in \mathop {\mathrm {arg\,min\,}}\lbrace F(\varvec{\lambda })\,:\, \varvec{\lambda }\in X\rbrace \). Thus
(ii) As an immediate consequence of the proof of (i) we have:
(iii) If F is strictly convex there is an unique
From (ii), any convergent sub-sequence of \((\varvec{\lambda }^{(n)})\) has to converge to \(\varvec{\lambda }^{*}\), thus the sequence converges to the same limit. \(\square \)
Appendix D: Proof of Lemma 4
Proof
From the definition of the Fenchel-Legendre transform we have:
If for some \(j\in \{1,\dots ,J\}\), \(p_{j}\ge s_{j}\) then
By taking all other entries of \(\varvec{u}\) as ones, it can be seen that \(H^{*}(\varvec{p})\) is infinite. In the case \({\varvec{p}}<\varvec{s}\) component-wise, the resolution of the Euler equation associated to the optimization problem shows that
Finally, we have
with \(C=\left\langle \log (\varvec{s}\widetilde{\varvec{\lambda }})-\varvec{1},\varvec{s}\widetilde{\varvec{\lambda }}\right\rangle \) independent from \(\varvec{p}\). \(\square \)
Appendix E: Proof of Lemma 5
Proof The Fenchel-Legendre transform of the total variation G is (see [32]):
where \( K = \lbrace \textrm{div}_{d} \varvec{\varphi }{:} \varvec{\varphi }\in Z \text { such that } \vert \varphi _{j}\vert \le 1, \ j=1,\dots ,J \rbrace ,\) and \(\delta \) is the indicator function,
Thus the solution \(\varvec{p}^{*}\) of the dual problem can be expressed as \(\varvec{p}^{*} = -\alpha \textrm{div}_{d} \varvec{\varphi }^{*}\), and the conclusion follows now from Lemma 4.
Appendix F: Proof of Lemma 6
Proof
If \(\varvec{\varphi }\in S\), we have \(\Vert \textrm{div}_{d} \varvec{\varphi }\Vert _{\infty } \le 4\) and then for \(\alpha < s_{\textrm{min}}/4\) we obtain
The function h is thus finite and continuous on the compact set S. h is thus bounded and \(\varvec{\varphi }^{*}\) exists. The positivity of \(\varvec{u}^{*}\) is obvious from the previous inequality. \(\square \)
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Maxim, V., Feng, Y., Banjak, H. et al. Tomographic reconstruction from Poisson distributed data: a fast and convergent EM-TV dual approach. Numer Algor 94, 701–731 (2023). https://doi.org/10.1007/s11075-023-01517-w
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11075-023-01517-w