1 Introduction

Chaos is one of the major nonlinear phenomena in the microelectromechanical systems. The chaotic dynamic behavior of such systems can be promising in various applications. One of the prominent applications of chaos is the generation of pseudo-random numbers and chaotic signals in the encryption of data for secure communications [1,2,3]. Chaos is also employed in ultra-sensitive sensors [4,5,6] such as mass sensor. As the chaotic regime is highly sensitive to the changes in the system parameters, it can offer an ideal platform for identification of the parameters. Yin et al. [6] experimentally measured ultra-small changes in the mass of a cantilever beam as a highly sensitive mass sensor by detecting changes in its chaotic behavior. Regarding their sensitivity to initial conditions, chaotic oscillators can also be utilized to detect very weak signals with a high noise to signal ratio in resonant sensor applications [7, 8]. The most important studies in the field of chaos prediction and control in MEMS can be found in Refs. [9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25]. Haghighi et al. [9] examined the chaotic dynamics in MEMS resonators based on straight microbeams under parallel-plates electrostatic excitation. They presented an analytical criterion for homoclinic chaos using the Melnikov function. Their numerical studies indicated the significant effect of the excitation amplitude on the transition of system dynamics to chaos. Luo et al. [10] also addressed the prediction and control of chaos in a similar model. Dynamic analysis based on phase-plane and bifurcation diagrams and Lyapunov exponents showed that chaotic behavior is highly dependent on system parameters and initial conditions of MEMS resonators. Initially curved microbeams have gained a prominent position in MEMS due to their unique nonlinear characteristics and behaviors, such as bi-stability, snap-through motion, the ability of large displacements and high sensitivity. However, a limited number of studies have investigated the chaotic dynamics of such microstructures. Tajaddodianfar et al. [11] explored the chaotic vibrations of an initially curved microbeam under parallel-plates electrostatic actuation. Using proper numerical tools such as Poincare sections and Fourier spectrum, they investigated the effects of various parameters, including the initial curvature of the microbeam, on the formation of chaotic regions. Period-doubling bifurcation is one of the most well-known routes to chaos [17,18,19,20,21,22,23, 26, 27]. In this regard, De et al. [17] investigated the nonlinear dynamics of electrostatic microelectromechanical systems under superharmonic excitations. With the increase of AC voltage, a period-doubling cascade was observed, which finally led to the chaotic regime. Najar et al. [18] studied the chaotic dynamics of electrostatic micro-actuators. Using the finite difference method, they showed the cyclic-fold and period-doubling bifurcations in the frequency–response curves and reported the cascade of period-doubling bifurcations and chaos in the studied model. Liu et al. [19] also examined period-doubling and chaos in an electrostatically actuated microcantilever beams using Poincare map. Concerning the solving method of nonlinear equations, the nonlinear vibrations of the beam have been successfully analyzed in Refs. [28,29,30] using the extended Galerkin method.

The pull-in instability is one of the most important concerns in MEMS resonators based on parallel-plates electrostatic actuation. The use of fringing-field electrostatic actuation in microelectromechanical systems is very promising as it prevents pull-in instability and increases the lifelong of the devices. Based on the literature review, no study has so far addressed the chaotic dynamics of initially curved microbeams under fringing-field electrostatic actuation. Regarding the advantages of this MEMS structure, the analysis of the chaotic dynamics of such resonators is highly important.

For the first time, this paper is aimed to comprehensively investigate the chaotic dynamics of MEMS resonators based on piezoelectrically laminated initially curved microbeam exposed to fringing-field electrostatic actuation. The nonlinear equation of the motion accounting for the electrostatic and geometric nonlinearities have been discretised to yield a reduced order model and the resultant is numerically integrated over the time for the time response. The frequency response curve along with the bifurcation points are determined using the combination of shooting and continuation techniques and types of the bifurcation points are examined using the loci of the associated multipliers with respect to the unit circle on the complex plane. It has been illustrated that the cascade of period doubling bifurcations end up with the so-called period doubling route to chaos which has been identified by means of developing the Poincaré sections and the associated frequency spectrum of the time response. The chaotic response of the system has been regularised by applying an appropriate piezoelectric excitation.

2 Mathematical modeling

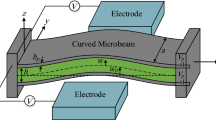
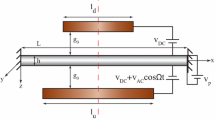
Clamped–clamped microbeam with initial curvature \({w}_{0}\) under simultaneous piezoelectric and fringing-field electrostatic actuation is considered as shown in Fig. 1. The initially curved microbeam has the length \(L\), width \(a\) and thickness \(h\). The microbeam is assumed to be made of isotropic linear elastic material with Young’s modulus \({E}_{b}\), Poisson’s ratio \({\upsilon }_{b}\) and density \({\rho }_{b}\). As the width of the microbeam is much larger than its thickness the plane strain condition holds and therefore, the effective Young’s modulus \({\widetilde{E}}_{b}={E}_{b}/\left(1-{{\upsilon }_{b}}^{2}\right)\) [31] is considered. For the sake of simplicity, the sign of tilda (\(\sim \)) on the effective modulus of elasticity has been dropped. For piezoelectric actuation, the microbeam is sandwiched with two thin layers of PZT throughout the entire length of the microbeam. Piezoelectric layers have thickness \({h}_{p}\), density \({\rho }_{p}\), Young’s modulus \({E}_{p}\) and Poisson’s ratio \({\upsilon }_{p}\). Moreover, two stationary electrodes with the length of \({L}_{e}\) and the same width and thickness as of the microbeam are symmetrically placed on both sides of the microbeam for the fringing-field electrostatic actuation. The horizontal distance between the actuation electrodes and the edges of the microbeam on the \(xy\) plane is g.

Fig. 1
figure 1

Double-clamped initially curved microbeam under simultaneous piezoelectric and fringing-field electrostatic actuation

Full size image

Upon applying DC voltage \({V}_{p}\) to each of the piezoelectric patches, the resulting axial force is applied along the length to the microbeam as follows[32, 33]

$${F}_{p}=-2{e}_{31}{V}_{p}a$$
(1)

Where \({e}_{31}\) denotes the piezoelectric voltage constant. Depending on the polarity of the piezoelectric voltage, the axial force can be tensile or compressive. Moreover, the potential difference \(V\) is applied between the microbeam and the lateral actuation electrodes. The asymmetry of the electric fringing-fields leads to the application of an out-of-plane electric force along the z-axis to the microbeam. Using the finite element simulation, the electrostatic force per unit of length can be expressed as [34]

$${f}_{e}=-\frac{rsinh\left(q\left({w}_{0}+w\right)\right)\times {V}^{2}}{{cosh}^{s}\left(q\left({w}_{0}+w\right)\right)}H\left(x-\frac{L-{L}_{e}}{2}\right)H\left({L}_{e}+\frac{L-{L}_{e}}{2}-x\right)$$
(2)

where \(r\), \(q\) and \(s\) are the fitting parameters. Furthermore, \(H\left(x\right)\) is the Heaviside step function and \(V=\left[{V}_{DC}+{V}_{AC}cos\left(\Omega t\right)\right]\), in which \({V}_{DC}\) is the direct current voltage and \({V}_{AC}\) and \(\Omega \) are the amplitude and frequency of the alternating current voltage, respectively.

With the axial force and the fringing-field electrostatic force in hand, the governing equation of the motion and the associated boundary conditions considering the assumptions of Euler–Bernoulli for shallow beam can be derived by means of minimization of the Hamiltonian [34,35,36]

$${\left(EI\right)}_{eq}\frac{{\partial }^{4}w}{\partial {x}^{4}}+{\left(\rho A\right)}_{eq}\frac{{\partial }^{2}w}{\partial {t}^{2}}+{C}_{d}\frac{\partial w}{\partial t}=\left[{F}_{p}+\frac{{\left(EA\right)}_{eq}}{2L}{\int }_{0}^{L}\left({\left(\frac{\partial w}{\partial x}\right)}^{2}+2\frac{\partial w}{\partial x}\frac{d{w}_{0}}{dx}\right)dx\right]\left[\frac{{\partial }^{2}w}{\partial {x}^{2}}+\frac{{d}^{2}{w}_{0}}{d{x}^{2}}\right]+{f}_{e}$$
(3)

where

$$ \begin{gathered} \left( {EI} \right)_{eq} = E_b I_b + E_p I_p = E_b \frac{ah^3 }{{12}} + E_p a\left( {h_p h\left( {\frac{h}{2} + h_p } \right) + \frac{2h_p^3 }{3}} \right) \hfill \\ \left( {\rho A} \right)_{eq}\, = \,\rho_b A_b + \rho_p A_p = \rho_b ah + 2\rho_p ah_p \left( {EA} \right)_{eq} = E_b A_b + E_p A_p = E_b ah + 2E_p ah_p \hfill \\ \end{gathered} $$
(4)

\({A}_{b}\) and \({A}_{p}\) are the cross section of microbeam and piezoelectric layers, respectively. \({I}_{b}\) and \({I}_{p}\) also denote the moment of inertia of the cross-section of microbeam and piezoelectric layers, respectively. In Eq. (3), \({C}_{d}\) is the viscous damping coefficient and \({w}_{0}\left(x\right)={b}_{0}\left(1-cos\left(2\pi x/L\right)\right)/2\), in which \({b}_{0}\) shows the initial elevation of the midpoint of the microbeam. The boundary conditions associated with Eq. (3) are given as

$$w\left(0,t\right)=0 , w\left(L,t\right)=0 , \frac{\partial w\left(0,t\right)}{\partial x}=0 , \frac{\partial w\left(L,t\right)}{\partial x}=0$$
(5)

For convenience, the following nondimensional parameters are introduced

$$\widehat{w}=\frac{w}{h} , {\widehat{w}}_{0}=\frac{{w}_{0}}{h} , \widehat{x}=\frac{x}{L} , {\widehat{L}}_{e}=\frac{{L}_{e}}{L} , \widehat{t}=\frac{t}{\widetilde{t}} , \widetilde{\Omega }=\Omega \widetilde{t}$$
(6)

where, \(\widetilde{t}=\sqrt{{\left(\rho A\right)}_{eq}{L}^{4}/{\left(EI\right)}_{eq}}\). Therefore, the nondimensional equation of motion can be obtained as follows, the over hat (^) has been dropped for simplicity

$$\frac{{\partial }^{4}w}{\partial {x}^{4}}+\frac{{\partial }^{2}w}{\partial {t}^{2}}+C\frac{\partial w}{\partial t}=\left[P+{\alpha }_{1}{\int }_{0}^{1}\left({\left(\frac{\partial w}{\partial x}\right)}^{2}+2\frac{\partial w}{\partial x}\frac{d{w}_{0}}{dx}\right)dx\right]\left[\frac{{\partial }^{2}w}{\partial {x}^{2}}+\frac{{d}^{2}{w}_{0}}{d{x}^{2}}\right]-{\alpha }_{2}\frac{sinh\left(q\left({w}_{0}+w\right)\right)}{{cosh}^{s}\left(q\left({w}_{0}+w\right)\right)}H\left(x-\frac{1-{L}_{e}}{2}\right)H\left({L}_{e}+\frac{1-{L}_{e}}{2}-x\right)$$
(7)

The dimensionless parameters in Eq. 7 are

$$C=\frac{{C}_{d}{L}^{4}}{\widetilde{t}{\left(EI\right)}_{eq}} , P=\frac{{F}_{p}{L}^{2}}{{\left(EI\right)}_{eq}} , {\alpha }_{1}=\frac{{h}^{2}{\left(EA\right)}_{eq}}{2{\left(EI\right)}_{eq}} , {\alpha }_{2}=\frac{r{L}^{4}{V}^{2}}{{\left(EI\right)}_{eq}h}$$
(8)

The dimensionless viscous damping coefficient \(C\) is related to the damping ratio \(\xi \) as \(C=2\xi \omega \), where \(\omega \) shows the nondimensional fundamental natural frequency. The nondimensional boundary conditions associated with Eq. (7) are given as

$$w\left(0,t\right)=0 , w\left(1,t\right)=0 , \frac{\partial w\left(0,t\right)}{\partial x}=0 , \frac{\partial w\left(1,t\right)}{\partial x}=0$$
(9)

To obtain the reduced order model (ROM), the Galerkin decomposition method is implemented considering the normalized mode shapes \({\varphi }_{i}\left(x\right)\) as admissible functions. Accordingly, the deflection of the microbeam is expressed as

$$w\left(x,t\right)=\sum_{i=1}^{M}{u}_{i}\left(t\right){\varphi }_{i}\left(x\right)$$
(10)

where \({u}_{i}\left(t\right)\) are unknown generalized coordinates. By substituting Eq. (10) in Eq. (7), multiplying both sides of the equation by \({\varphi }_{i}\left(x\right)\) and integrating the resultant over the beam domain \(x=\left[\mathrm{0,1}\right]\), the reduced order model can be derived as follows

$${\ddot{u}}_{n}+C{\dot{u}}_{n}+\sum_{i=1}^{M}{u}_{i}\left(t\right){\int }_{0}^{1}{{\varphi }_{i}}^{\left(iv\right)}{\varphi }_{n}dx-P\left(\sum_{i=1}^{M}{u}_{i}\left(t\right){\int }_{0}^{1}{{\varphi }_{i}}^{"}{\varphi }_{n}dx+{\int }_{0}^{1}{{w}_{0}}^{"}{\varphi }_{n}dx\right)$$
$$-{\alpha }_{1}\left(\begin{array}{c}\sum_{i=1}^{M}\sum_{j=1}^{M}\sum_{k=1}^{M}{u}_{i}{u}_{j}{u}_{k}{\int }_{0}^{1}{{\varphi }_{i}}{\prime}{{\varphi }_{j}}{\prime}dx{\int }_{0}^{1}{{\varphi }_{k}}^{"}{\varphi }_{n}dx+\sum_{i=1}^{M}\sum_{j=1}^{M}{u}_{i}{u}_{j}{\int }_{0}^{1}{{\varphi }_{i}}{\prime}{{\varphi }_{j}}{\prime}dx{\int }_{0}^{1}{{w}_{0}}^{"}{\varphi }_{n}dx\\ +2\sum_{i=1}^{M}\sum_{j=1}^{M}{u}_{i}{u}_{j}{\int }_{0}^{1}{{\varphi }_{i}}{\prime}{{w}_{0}}{\prime}dx{\int }_{0}^{1}{{\varphi }_{j}}^{"}{\varphi }_{n}dx+2\sum_{i=1}^{M}{u}_{i}{\int }_{0}^{1}{{\varphi }_{i}}{\prime}{{w}_{0}}{\prime}dx{\int }_{0}^{1}{{w}_{0}}^{"}{\varphi }_{n}dx\end{array}\right)$$
$$=-{\alpha }_{2}{\int }_{0}^{1}\frac{sinh\left(q\left({w}_{0}+\sum_{i=1}^{M}{u}_{i}{\varphi }_{i}\right)\right){\varphi }_{n}\left(x\right)}{{cosh}^{s}\left(q\left({w}_{0}+\sum_{i=1}^{M}{u}_{i}{\varphi }_{i}\right)\right)}H\left(x-\frac{1-{L}_{e}}{2}\right)H\left({L}_{e}+\frac{1-{L}_{e}}{2}-x\right)dx$$
(11)

Such that \(n=\mathrm{1,2},3,\dots ,M\).

3 Results and discussion

To perform first validation, the results of this paper are compared with those presented in Ref. [37]. For this purpose, the microbeam with an initial curvature under the fringing-field electrostatic actuation with the properties studied in Ref. [37] is considered. The variations of the first three natural frequencies with respect to the applied \({V}_{DC}\) for the present paper, along with the results of Tausiff et al. are depicted in Fig. 2. A very good agreement can be seen between the results.

Fig. 2
figure 2

Variation of the first three natural frequencies with DC voltage: validation of the current model

Full size image

To perform second validation, the results presented in this paper are compared with the results of Ref. [38]. Considering VDC = 80V, VAC = 40V, \(\xi =0.01\) and the geometric and mechanical properties in Ref. [38], the frequency response curves in the vicinity of the third natural frequency for the present study along with the results of Ouakad et al. are presented in Fig. 3, which suggests a very good agreement.

Fig. 3
figure 3

The frequency response curve in the vicinity of the third natural frequency: validation of the current model

Full size image

The material and geometrical properties of the studied model are given in Table 1 as follows:

Table 1 Geometrical and material properties of the studied model
Full size table

The fitting parameters for the electrostatic force, obtained through the minimization of the square root of the errors, are introduced in Table 2 as follows.

Table 2 Fitting parameters of the electrostatic force
Full size table

Variation of the first three natural frequencies with respect to the applied VDC is illustrated in Fig. 4.

Fig. 4
figure 4

Variation of the first three natural frequencies versus the applied electrostatic voltage

Full size image

The electrostatic force implicitly influences the stiffness of the microbeam. This implies that the microbeam's stiffness results from the combination of its elastic stiffness and the superimposed electrical stiffness. It has been demonstrated that when the fringing field electrostatic force is applied, the first three natural frequencies begin to decrease. This behavior is reminiscent of the parallel plate excitation, where applying a voltage VDC leads to a reduction in the natural frequency due to the softening nature of the electrostatic force [39]. As the VDC increases, the softening effect intensifies, causing a further drop in the natural frequency. Beyond a certain voltage for each individual natural frequency, denoted as 93.12, 96.01 and 128.9V, the electrostatic voltage begins to stiffen the system, resulting in a corresponding recovery and increase in the associated natural frequency.

In the present study, considering VDC = 180V, VAC = 100V and \(\xi =0.06\), we investigate the nonlinear dynamics of the system in the vicinity of the third natural frequency where the system exhibits strong nonlinear behavior and undergoes various nonlinear bifurcations i.e. period doubling which eventually yields in chaotic response through the cascade of various period doubling bifurcations. Figure 5 represents the frequency response curve in the region of the interest.

Fig. 5
figure 5

The frequency response curve in the domain of strong nonlinear behavior

Full size image

As illustrated, while \(\Omega \) is swept from 75, the system undergoes a Neimark-Sacker (NS) or Secondary Hopf bifurcation where the two complex conjugate Floquet multipliers exit the unit circle away from the real axis on the complex plane [40]. Here the bifurcation solution introduces a new frequency in addition to the one prior to the bifurcation point. The dynamics of the bifurcated solution has not been the focus of this study and it requires a separated dedicated investigation. Immediately after the NS bifurcation point, the stable branch loses its stability and transforms into an unstable branch. This continues until another NS bifurcation point is reached, beyond which stability is restored. Further increase in the frequency yields in a period doubling bifurcation (PD1) where the Floquet multipliers exit the unit circle through −1 [34]. The stable solution loses stability as the bifurcation point is passed over. The unstable branch of the solution undergoes another PD bifurcation namely PD2 rightward of which the stability is regained. Though a sequence of NS and PD bifurcations occurs on the frequency response curve beyond PD2, our focus, in this case, has been on the period-doubled branches of the frequency response curves originating from PD1 and PD2. This is depicted in more detail in Fig. 6 and comprehensively discussed in the following section.

Fig. 6
figure 6

Frequency response curves for VP = 0V, VDC = 180V, VAC = 100V, \(\xi =0.06\) (a): period-2, (b) and (c): period-4

Full size image

Figure 6a illustrates the period-doubled branch of the frequency response curve originating from PD1 (\(\Omega =131.5\)) which eventually intersects with the original branch of solution throughout a subcritical period doubling bifurcation (PD2 (\(\Omega =128.9\))) where an unstable branch of period-doubled solution is destroyed. Starting from PD1 on the period-doubled branch, the solution is unstable indicating that PD1 is of subcritical type. As travelling along the period-doubled branch, the response undergoes a cyclic fold bifurcation (CF (\(\Omega =110.5\))) where the stable and unstable manifolds of the solution are both originated from the same point. Here the Floquet multipliers exit the unit circle throughout + 1 on the complex plane. Passing over the first CF bifurcation on the period-doubled branch, various PD, CF and NS bifurcations take place up until the period-doubled branch intersects with the original branch at PD2. We explored the period-quadrupled branches which originate from the Period-doubling bifurcation points. We concluded that the Period-quadrupled branches originating from PD4 (\(\Omega =129.4\)) and PD6 (\(\Omega =152.1\)) intersect with the period-doubled branch at PD5 (\(\Omega =149.1\)) and PD7 (\(\Omega =168.2\)) respectively; the associated period-quadrupled solutions are depicted in Figs. 6(b) and (c). The occurrence of successive period-doubling bifurcations suggests the potential for a cascade of such bifurcations leading to chaotic behavior. Capturing this cascade of period-doubled branches was challenging, requiring significant runtime to record the higher-order branches. From now on we have focused on the response of the system with the excitation frequency between 152.1 and 168.2 which are associated with the frequencies of PD6 and PD7. We believe the cascade of the period-doubling bifurcations occurs along this branch.

We have explored the response of the system prior to the PD8 (\(\Omega =158.9\)) bifurcation point. Here the response settles on the period-quadrupled branch. The associated time response, phase plane, Poincaré section and the frequency spectrum are depicted in Fig. 7.

Fig. 7
figure 7

Response for \(\Omega =158\) (a): Time response, (b): Phase plane, (c): Poincare section, (d): FFT

Full size image

The time response corresponding to a complete single period has been illustrated as an inset in Fig. 7a. The time response, phase plane, Poincaré section and the frequency spectrum of the response at \(\Omega =159\), are represented in Fig. 8. The excitation frequency here is slightly after the PD8 bifurcation point.

Fig. 8
figure 8

Response for \(\Omega =159\) (a): Time response, (b): Phase plane, (c): Poincare section, (d): Frequency spectrums

Full size image

Exciting the system with the frequency \(\Omega =159\) implies that the associated period (T) is 0.0395. However, the response has completed one period in 8 times the value of T. This is because the response settles on the third consecutive period-doubled branch resulting in the duration of \({2}^{3}T\) for a single period. The time response corresponding to a complete single period has been illustrated as an inset in Fig. 8a. The system has various orders on nonlinearity including quadratic, cubic (from geometry), fifth and seventh orders (coming from electrostatic force) which justifies the existence of the dominant frequency \({M}^{r}{N}^{o}\Omega \) where M and N are the any of the orders of nonlinearity and r and o can be any integer. The ratio of the maximum dominant frequency to the frequency spectrum \({\omega }_{s}\) for \(\Omega =159\) are given in Table 3.

Table 3 Frequency ratios for \(\Omega =159\)
Full size table

To extract the Poincaré section, we have applied the sampling rate associated with the highest frequency present in the frequency spectrum of the response and this yields in 12 intersection points between the phase trajectories and the Poincaré section which are depicted in Fig. 8c. The number 12 is significant because it represents the least common multiple of the contributing frequency ratios listed in Table 3. When additional nonlinear frequency components are introduced, it can potentially lead to a larger common multiple, thereby increasing the number of intersection points on the Poincaré section. In extreme cases, this can result in the formation of a chaotic strange attractor.

Exciting the system with the frequency \(\Omega =160\) reveals that a broad range of frequencies emerge on the frequency spectrum and the Poincare section exhibits the formation of a complex geometry so-called as strange attractor in the literature of chaotic dynamics.

To identify chaotic behavior, we didn't solely rely on the presence of infinite points in the Poincaré section. In cases where the frequency components of the time response have incommensurable ratios, they can generate intricate patterns within the Poincaré section. Therefore, we qualitatively assessed chaotic dynamics not only by examining the Poincaré section but also by analyzing the frequency spectrum of the time response. This approach ensured that the strange geometry observed in the Poincaré section was not solely a result of the incommensurable frequency ratios within the response.

The time response, phase plane, Poincaré section and the frequency spectrum of the steady state response for \(\Omega =162\), \(\Omega =164\) and \(\Omega =166\) are illustrated in Figs. 10, 11, 12.

As depicted in Figs. 9, 10, 11, 12, the chaotic response occurs for \(159.4<\Omega <166.6\) where the cascade of period doubling bifurcations occur. Figure 13 illustrates the bifurcation diagram for the excitation frequencies varying in the range of 145–175. Starting from \(\Omega =145\), as the frequency is swept, the period-2 branch undergoes a transformation into a period-4 branch via a super critical period doubling bifurcation denoted as PD6. Further sweep of the excitation frequency yields in the cascade of super critical period doubling bifurcations and accordingly emergence of the chaotic region in the bifurcation diagram. As the frequency is swept even further the cascade of subcritical period doubling bifurcations take place, ultimately leading to a return to regular response for frequencies beyond 166.6.

Fig. 9
figure 9

Response for \(\Omega =160\) (a): Time response, (b): Phase plane, (c): Poincare section, (d): FFT

Full size image
Fig. 10
figure 10

Response for \(\Omega =162\) (a): Time response, (b): Phase plane, (c): Poincare section, (d): FFT

Full size image
Fig. 11
figure 11

Response for \(\Omega =164\) (a): Time response, (b): Phase plane, (c): Poincare section, (d): FFT

Full size image
Fig. 12
figure 12

Response for \(\Omega =166\) (a): Time response, (b): Phase plane, (c): Poincare section, (d): FFT

Full size image
Fig. 13
figure 13

The bifurcation diagram

Full size image

For more clarity referring to Fig. 7, (\(\Omega =158\)) there are 6 points on the Poincaré section, and these specific points have been highlighted in Fig. 13.

Assuming \({S}_{\Omega }=\left\{{S}_{1}, {S}_{2}, \dots ,{S}_{N}\right\}\) represents the N-member-sequence of the samples on the Poincaré section for a specific excitation frequency, the values of the samples depend on the time that the first sample is taken. Consequently, there is not a unique sequence of samples associated with a given frequency. The sequence can comprise any N points taken from the trajectory with a fixed sampling time provided that the transient response, in the case of regular response, has decayed.

Figure 14 represents the time history, phase plane, Poincaré section, and the frequency spectrum associated with the excitation frequency of \(\Omega =167.\) The excitation frequency here is slightly before the PD9 (\(\Omega =167.2\)) bifurcation point. The time response of a one single period of the motion is depicted as an inset in Fig. 14a.

Fig. 14
figure 14

Response for \(\Omega =167\) (a): Time response, (b): Phase plane, (c): Poincare section, (d): FFT

Full size image

In this section, an appropriate voltage is applied to the piezoelectric layers which has accordingly regularized the chaotic response of the micro beam. Figure 15 illustrates the time response, phase plane, Poincaré section and the frequency spectrum of the time response for \(\Omega =164\) and VP =  + 0.3V.

Fig. 15
figure 15

Response for \(\Omega =164\), VP =  + 0.3V (a): Time response, (b): Phase plane, (c): Poincare section, (d): FFT

Full size image

As illustrated, the previously chaotic response shown in Fig. 11 has been regularized. This can be attributed to the application of voltage to the piezoelectric layers, which generates an axial force along the length of the microbeam. This axial force shifts the frequency response curve along the horizontal axis, consequently affecting the chaotic regime. As a result, the excitation frequency is pushed outside the chaotic regime, leading to a regulated response; however, the response has fallen into the third consecutive period-doubled regular region. Consequently, despite exciting the system with an excitation \(\Omega =164\), which is associated with T = 0.038, the system exhibits an 8T period. Here the least common factor associated with the dominant frequency ratios present in the frequency spectrum is 12 and accordingly twelve intersections between the trajectory and the Poincaré section have been recorded.

Figure 16 depicts the response of the system similar to those of Fig. 15 but with a negative polarity of the piezoelectric voltage, VP = -0.3V.

Fig. 16
figure 16

Response for \(\Omega =164\), VP = −0.3V (a): Time response, (b): Phase plane, (c): Poincare section, (d): FFT

Full size image

Applying piezoelectric voltage with negative polarity generates a compressive force. As a result, the frequency response curve shifts to the left, causing the excitation frequency to move outside the chaotic zone. In this case, the excitation falls within the 2T period response, and consequently, the system response exhibits a period equal to twice of the excitation frequency. Here, the least common multiple of the contributing frequency ratios in the time response is 3, which results in 3 intersection points between the trajectory and the Poincaré section.

To investigate the impact of piezoelectric actuation on the bifurcation diagram, the diagrams corresponding to VP =  + 0.3V and VP = −0.3V are depicted in Figs. 17 and 18, respectively. It is noteworthy that in the case of VP =  + 0.3V, the period doubling route did not culminate in a chaotic response. However, for the negative polarity, the chaotic region persisted but shifted backward along the frequency axis.

Fig. 17
figure 17

The bifurcation diagram for VP =  + 0.3V

Full size image
Fig. 18
figure 18

The bifurcation diagram for VP = −0.3V

Full size image

4 Conclusion

In this paper the nonlinear and chaotic dynamics of a piezoelectrically actuated initially curved microbeam exposed to lateral fringing-field electrostatic actuation was investigated. The nonlinear differential equation of the motion accounting for the geometric and fringing-field electrostatic nonlinearity was discretized to a finite degree of freedom model and then the resultant nonlinear ODEs were numerically integrated over the time to reveal the time response of the system. The frequency response curves were determined using the combination of shooting and continuation methods and the stability of the periodic solutions were assessed based on the eigen values of the associated monodromy matrix. Assuming the excitation frequency as the control parameter, the bifurcations on the frequency domain were determined and their types were examined based on the loci of the associated eigen values with respect to the unit circle on the complex plane. The bifurcation points consisted of Neimark-Sacker (NS) or Secondary Hopf, cyclic fold and period-doubling types. It was observed that period-doubling bifurcations occurred in a cascade, ultimately leading to chaotic behavior through a period-doubling route. The chaotic response was qualitatively identified by capturing the corresponding Poincare section and the associated frequency spectrum. The geometry on the Poincare section was a complex geometry of fractional dimension; this could have occurred not necessarily due to the chaotic response but due to incommensurable ratios of the contents of the frequency spectrum; The frequency spectrum was developed to explore the cause of the strange attractors. It was observed that a broad range of frequencies existed on the frequency spectrum and accordingly it was concluded that the system exhibits a chaotic response. The piezoelectric actuation was applied to generate an axil force along the microbeam which accordingly shifted the frequency response curves along the frequency axis and regularized the chaotic response of the system. The outcomes of the present study are genuinely promising for the design and fabrication of MEMS large-amplitude resonators.