Skip to main content
SpringerLink
Log in

A 2+1 dimensional Volterra type system with nonzero boundary conditions via Dbar dressing method

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

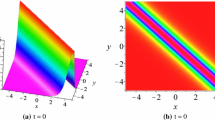
A 2+1 dimensional Volterra type system with nonzero boundary conditions is considered. The Dbar dressing method based on a single-valued variable is discussed. The explicit solutions, including line-solitons and rational solutions of the Volterra type system are considered on certain new variables.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

Data availability

Data will be made availability on reasonable request.

References

  1. Mikhailov, A.V.: Integrability of a two-dimensional gemeralization of the Toda chain. Sov. Phys.-JETP Lett. 30, 443–448 (1979)

  2. Villarroel, J., Chakravarty, S., Ablowitz, M.J.: On a 2+1 Volterra system. Nonlinearity 9, 1113–1128 (1996). https://doi.org/10.1088/0951-7715/9/5/004

    Article  MathSciNet  MATH  Google Scholar 

  3. Zhang, Y.N., He, Y., Tam, H.W.: One variant of a (2+1)-dimensional Volterra system and its (1+1)-dimensional reduction. Front. Math. China 8, 1085–1097 (2013). https://doi.org/10.1007/s11464-013-0308-8

    Article  MathSciNet  MATH  Google Scholar 

  4. Sahadevan, R., Khousalya, S.: Similarity reduction of a (2+1) Volterra system. J. Phys. A Math. Gen. 33, L171–L176 (2000). https://doi.org/10.1088/0305-4470/33/19/102

    Article  MathSciNet  MATH  Google Scholar 

  5. Huang, Q., Gao, Y., Jia, S., Wang, Y., Deng, G.: Bilinear Bäcklund transformation, soliton and periodic wave solutions for a (3+1)-dimensional variable-coefficient generalized shallow water wave equation. Nonlinear Dyn. 87, 2529–2540 (2017). https://doi.org/10.1007/s11071-016-3209-z

    Article  MATH  Google Scholar 

  6. Cao, Y., He, J., Mihalache, D.: Families of exact solutions of a new extended (2+1)-dimensional Boussinesq equation. Nonlinear Dyn. 91, 2593–2605 (2018). https://doi.org/10.1007/s11071-017-4033-9

    Article  Google Scholar 

  7. Foroutan, M., Manafian, J., Ranjbaran, A.: Lump solution and its interaction to (3+1)-D potential-YTSF equation. Nonlinear Dyn. 92, 2077–2092 (2018). https://doi.org/10.1007/s11071-018-4182-5

    Article  Google Scholar 

  8. Zhang, Y., Rao, J., Porsezian, K., He, J.: Rational and semi-rational solutions of the Kadomtsev-Petviashvili-based system. Nonlinear Dyn. 95, 1133–1146 (2019). https://doi.org/10.1007/s11071-018-4620-4

    Article  MATH  Google Scholar 

  9. Li, B., Ma, Y.: Interaction dynamics of hybrid solitons and breathers for extended generalization of Vakhnenko equation. Nonlinear Dyn. 102, 1787–1799 (2020). https://doi.org/10.1007/s11071-020-06024-4

    Article  Google Scholar 

  10. Zhang, R., Li, C., Yin, H.: Rogue wave solutions and the bright and dark solitons of the (3+1)-dimensional Jimbo-Miwa equation. Nonlinear Dyn. 103, 1071–1079 (2021). https://doi.org/10.1007/s11071-020-06112-5

    Article  Google Scholar 

  11. Mukam, S., Souleymanou, A., Kuetche, V., Bouetou, T.: Generalized Darboux transformation and parameter-dependent rogue wave solutions to a nonlinear Schrödinger system. Nonlinear Dyn. 93, 373–383 (2018). https://doi.org/10.1007/s11071-018-4198-x

    Article  MATH  Google Scholar 

  12. Xu, S., He, J., Mihalache, D.: Rogue waves generation through multiphase solutions degeneration for the derivative nonlinear Schrödinger equation. Nonlinear Dyn. 97, 2443–2452 (2019). https://doi.org/10.1007/s11071-019-05140-0

    Article  MATH  Google Scholar 

  13. Ji, T., Zhai, Y.: Soliton, breather and rogue wave solutions of the coupled Gerdjikov-Ivanov equation via Darboux transformation. Nonlinear Dyn. 101, 619–631 (2020). https://doi.org/10.1007/s11071-020-05790-5

    Article  Google Scholar 

  14. McAnally, M., Ma, W.: Explicit solutions and Darboux transformations of a generalized D-Kaup-Newell hierarchy. Nonlinear Dyn. 102, 2767–2782 (2020). https://doi.org/10.1007/s11071-020-06030-6

    Article  Google Scholar 

  15. Geng, X., Li, Y., Xue, B.: A second-order three-wave interaction system and its rogue wave solutions. Nonlinear Dyn. 105, 2575–2593 (2021). https://doi.org/10.1007/s11071-021-06727-2

    Article  Google Scholar 

  16. Ablowitz, M.J., Yaacov, D.B., Fokas, A.S.: On the inverse spectral transform for the Kadomtsev-Petviashvili equation. Stud. Appl. Math. 69, 135–143 (1983). https://doi.org/10.1002/sapm1983692135

    Article  MathSciNet  MATH  Google Scholar 

  17. Beals, R., Coifman, R.R.: The D-bar approach to inverse scattering and nonlinear evolutions. Phys. D 18, 242–249 (1986). https://doi.org/10.1016/0167-2789(86)90184-3

    Article  MathSciNet  MATH  Google Scholar 

  18. Gilbert, R.P.: Remarks on matrix hierarchies, d bar dressing, and the spectral transform. Appl. Anal. 51, 1–33 (1993). https://doi.org/10.1080/00036819308840201

    Article  MathSciNet  Google Scholar 

  19. Zakharov, V., Manakov, S.V.: Construction of higher-dimensional nonlinear integrable systems and of their solutions. Func. Anal. Appl. 19, 89–101 (1985). https://doi.org/10.1007/BF01078388

    Article  MATH  Google Scholar 

  20. Konopelchenko, B.G.: Introduction to multidimensional integrable equations: the inverse spectral transform in 2+1-dimensions. Plenum press, New York and London (1992)

    Book  MATH  Google Scholar 

  21. Manakov, S.V.: The inverse scattering transform for the time-dependent Schrödinger equation and Kadomtsev-Petviashvili equation. Phys. D 3, 420–427 (1981). https://doi.org/10.1016/0167-2789(81)90145-7

    Article  MathSciNet  MATH  Google Scholar 

  22. Beals, R., Coifman, R.R.: Linear spectral problems, non-linear equations and the \({\bar{\partial }}\)-method. Inverse Problems 5, 87–130 (1989). https://doi.org/10.1088/0266-5611/5/2/002

    Article  MathSciNet  MATH  Google Scholar 

  23. Bogdanov, L.V., Manakov, S.V.: The non-local \({\bar{\partial }}\) problem and (2+1)-dimensional soliton equations. J. Phys. A: Math. Gen. 21, L537–L544 (1988). https://doi.org/10.1088/0305-4470/21/10/001

  24. Dubrovsky, V.G.: The construction of exact multiple pole solutions of some (2+1)-dimensional integrable nonlinear evolution equations via the \({\bar{\partial }}\)-dressing method. J. Phys. A Math. Gen. 32, 369–390 (1999). https://doi.org/10.1088/0305-4470/32/2/011

    Article  MathSciNet  MATH  Google Scholar 

  25. Dubrovsky, V.G., Topovsky, A.V.: Multi-lump solutions of KP equation with integrable boundary via \({\bar{\partial }}\)-dressing method. Phys. D 414, 132740 (2020). https://doi.org/10.1016/j.physd.2020.132740

    Article  MathSciNet  MATH  Google Scholar 

  26. Dubrovsky, V.G., Topovsky, A.V.: Multi-soliton solutions of KP equation with integrable boundary via \({\bar{\partial }}\)-dressing method. Phys. D 428, 133025 (2021). https://doi.org/10.1016/j.physd.2021.133025

    Article  MathSciNet  MATH  Google Scholar 

  27. Dubrovsky, V.G., Topovsky, A.V., Basalaev, M.Y.: New exact solutions of two-dimensional integrable equations using the \({\bar{\partial }}\)-dressing method. Theoret. Math. Phys. 167, 725–739 (2011). https://doi.org/10.1007/s11232-011-0057-3

    Article  MathSciNet  Google Scholar 

  28. Konopelchenko, B.G., Dubrovsky, V.G.: Inverse spectral transform for the modified Kadomtsev-Petviashvili equation. Stud. Appl. Math. 86, 219–268 (1992). https://doi.org/10.1002/sapm1992863219

    Article  MathSciNet  Google Scholar 

  29. Konopelchenko, B.G., Matkarimov, B.T.: Inverse spectral transform for the nonlinear evolution equation generating the Davey-Stawartson and Ishimori equation. Stud. Appl. Math. 82, 319–359 (1990). https://doi.org/10.1002/sapm1990824319

    Article  MathSciNet  MATH  Google Scholar 

  30. Kuang, Y.H., Zhu, J.Y.: A three-wave interaction model with self-consistent sources: the \({\bar{\partial }}\)-dressing method and solutions. J. Math. Anal. Appl. 426, 783–793 (2015). https://doi.org/10.1016/j.jmaa.2015.01.072

    Article  MathSciNet  MATH  Google Scholar 

  31. Luo, J.H., Fan, E.G.: Dbar-dressing method for the Gerdjikov-Ivanov equation with nonzero boundary conditions. Appl. Math. Lett. 120, 107297 (2021). https://doi.org/10.1016/j.aml.2021.107297

    Article  MathSciNet  MATH  Google Scholar 

  32. Wang, X.R., Zhu, J.Y.: Dbar-approach to coupled nonlocal NLS equation and general nonlocal reduction. Stud. Appl. Math. 148, 433–456 (2022). https://doi.org/10.1111/sapm.12445

    Article  MathSciNet  Google Scholar 

  33. Wang, X.R., Zhu, J.Y., Qiao, Z.J.: New solutions to the differential-difference KP equation. Appl. Math. Lett. 113, 106836 (2021). https://doi.org/10.1016/j.aml.2020.106836

    Article  MathSciNet  MATH  Google Scholar 

  34. Wang, Z.Y., Tian, S.F., Cheng, J.: The \({\bar{\partial }}\)-dressing method and soliton solutions for the three-component coupled Hirota equations. J. Math. Phys. 62, 093510 (2021). https://doi.org/10.1063/5.0046806

    Article  MathSciNet  MATH  Google Scholar 

  35. Yurova, M.: Application of dressing method for long wave-short wave resonance interaction equation. J. Math. Phys. 48, 053516 (2007). https://doi.org/10.1063/1.2719562

    Article  MathSciNet  MATH  Google Scholar 

  36. Zhu, J.Y., Geng, X.G.: A hierarchy of coupled evolution equations with self-consistent sources and the dressing method. J. Phys. A Math. Theor. 46, 035204 (2013). https://doi.org/10.1088/1751-8113/46/3/035204

    Article  MathSciNet  MATH  Google Scholar 

  37. Zhu, J.Y., Geng, X.G.: The AB equations and the \({\bar{\partial }}\)-dressing method in semi-characteristic coordinates. Math. Phys. Anal. Geo. 17, 49–65 (2014). https://doi.org/10.1007/s11040-014-9140-y

  38. Zhu, J.Y.: Line-soliton and rational solutions to (2+1)-dimensional Boussinesq equation by Dbar-problem. arXiv: 1704.02779

  39. Zhu, J.Y., Jiang, X.L., Wang, X.R.: Dbar dressing method to nonlinear Schrödinger equation with nonzero boundary conditions. arXiv: 2011.09028

  40. Dai, H.H., Geng, X.G.: Decomposition of a 2+1-dimensional Volterra type lattice and its quasi-periodic solutions. Chaos Soliton. Fract. 18, 1031–1044 (2003). https://doi.org/10.1016/s0960-0779(03)00061-4

Download references

Funding

The author declares that no funds were received during the preparation of this manuscript.

Author information

Authors and Affiliations

  1. School of Mathematics and Statistics, Zhengzhou University, Zhengzhou, 450001, Henan, China

    Tengfei Liu

Authors
  1. Tengfei Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Tengfei Liu.

Ethics declarations

Conflict of interest

The author declares that he has no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix

Appendix

Here, we deduce the 2+1 dimensional Volterra type system (2). Acting E and \(E^{-1}\) to (14) follow that

$$\begin{aligned} \begin{aligned} \partial _y\ln E\chi ^{(0)}_n&=\frac{2E^2\chi ^{(1)}_n}{E^2\chi ^{(0)}_n}-\frac{2E\chi ^{(1)}_n}{E\chi ^{(0)}_n},\\ \partial _y\ln E^{-1}\chi ^{(0)}_n&=\frac{2\chi ^{(1)}_n}{\chi ^{(0)}_n}-\frac{2E^{-1}\chi ^{(1)}_n}{E^{-1}\chi ^{(0)}_n}. \end{aligned} \end{aligned}$$
(A.1)

Substituting (14) and (A.1) into (12), we have

$$\begin{aligned} b_n=a_n\partial _y[\ln (\chi ^{(0)}_n\cdot E\chi ^{(0)}_n)], \end{aligned}$$
(A.2)

and it is clear to find that

$$\begin{aligned} a_nb_{n-1}-b_na_{n-1}=(a_na_{n-1})_y, \end{aligned}$$

which is the second equation of (2).

Acting E to (15) follows that

$$\begin{aligned}&\frac{2\partial _yE\chi ^{(1)}_n}{E\chi ^{(0)}_n}+\frac{\chi ^{(0)}_n}{E^2\chi ^{(0)}_n}\nonumber \\&+\frac{4E\chi ^{(2)}_n}{E\chi ^{(0)}_n}-\frac{4E^2\chi ^{(2)}_n}{E^2\chi ^{(0)}_n}-1=0, \end{aligned}$$
(A.3)

substituting (15) and (A.3) into (16), we have

$$\begin{aligned}&\partial _t\ln \chi ^{(0)}_n+2-\frac{2E^{-1}\chi ^{(0)}_n}{E\chi ^{(0)}_n} -\frac{2\partial _y\chi ^{(1)}_n}{\chi ^{(0)}_n}-\frac{2\partial _yE\chi ^{(1)}_n}{E\chi ^{(0)}_n}\nonumber \\&+\frac{4E\chi ^{(1)}_n}{E\chi ^{(0)}_n}{[\frac{E^2\chi ^{(1)}_n}{E^2\chi ^{(0)}_n}-\frac{\chi ^{(1)}_n}{\chi ^{(0)}_n}]}=0, \end{aligned}$$
(A.4)

noting that

$$\begin{aligned} \begin{aligned} \partial _y(\frac{\chi ^{(1)}_n}{\chi ^{(0)}_n})&=\frac{\partial _y\chi ^{(1)}_n}{\chi ^{(0)}_n}-\frac{\chi ^{(1)}_n}{\chi ^{(0)}_n}\cdot \partial _y\ln \chi ^{(0)}_n,\\ \partial _y(\frac{E\chi ^{(1)}_n}{E\chi ^{(0)}_n})&=\frac{\partial _yE\chi ^{(1)}_n}{E\chi ^{(0)}_n}-\frac{E\chi ^{(1)}_n}{E\chi ^{(0)}_n}\cdot \partial _y\ln E\chi ^{(0)}_n. \end{aligned} \end{aligned}$$
(A.5)

Substituting (A.1), (A.5) into (A.4) and acting \(1-E\) to (A.4) afterwards, we have

$$\begin{aligned} \begin{aligned}&\partial _t\ln (\frac{\chi ^{(0)}_n}{E\chi ^{(0)}_n})+\frac{2\chi ^{(0)}_n}{E^2\chi ^{(0)}_n}-\frac{2E^{-1}\chi ^{(0)}_n}{E\chi ^{(0)}_n}\\&+2\partial _y(\frac{E^2\chi ^{(1)}_n}{E^2\chi ^{(0)}_n}-\frac{\chi ^{(1)}_n}{\chi ^{(0)}_n})\\&+(\frac{2E\chi ^{(1)}_n}{E\chi ^{(0)}_n}-\frac{2\chi ^{(1)}_n}{\chi ^{(0)}_n})\partial _y\ln \chi ^{(0)}_n\\&+(\frac{2E\chi ^{(1)}_n}{E\chi ^{(0)}_n}-\frac{2E^2\chi ^{(1)}_n}{E^2\chi ^{(0)}_n})\partial _y\ln E\chi ^{(0)}_n=0, \end{aligned} \end{aligned}$$
(A.6)

according to (14) and (A.1), we have

$$\begin{aligned} \begin{aligned}&(\frac{2E\chi ^{(1)}_n}{E\chi ^{(0)}_n}-\frac{2\chi ^{(1)}_n}{\chi ^{(0)}_n})\partial _y\ln \chi ^{(0)}_n\\&+(\frac{2E\chi ^{(1)}_n}{E\chi ^{(0)}_n}-\frac{2E^2\chi ^{(1)}_n}{E^2\chi ^{(0)}_n})\partial _y\ln E\chi ^{(0)}_n\\ =&(\frac{2E^2\chi ^{(1)}_n}{E^2\chi ^{(0)}_n}-\frac{2\chi ^{(1)}_n}{\chi ^{(0)}_n})(\partial _y\ln \chi ^{(0)}_n-\partial _y\ln E\chi ^{(0)}_n). \end{aligned} \end{aligned}$$
(A.7)

Substituting (A.7) and (11) into (A.6), we get

$$\begin{aligned}&\partial _t\ln a_n+2a_na_{n+1}-2a_na_{n-1}+2\partial _y(\frac{E^2\chi ^{(1)}_n}{E^2\chi ^{(0)}_n}\nonumber \\&-\frac{\chi ^{(1)}_n}{\chi ^{(0)}_n})+(\frac{2E\chi ^{(1)}_n}{E\chi ^{(0)}_n}-\frac{2\chi ^{(1)}_n}{\chi ^{(0)}_n})\partial _y\ln a_n=0, \end{aligned}$$
(A.8)

then (A.8) multiplies \(a_n\) and substituting (12) into the result, we can obtain

$$\begin{aligned} a_{n,t}+b_{n,y}=2a^2_n(a_{n-1}-a_{n+1}), \end{aligned}$$

which is the first equation of (2).

Rights and permissions

Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Liu, T. A 2+1 dimensional Volterra type system with nonzero boundary conditions via Dbar dressing method. Nonlinear Dyn 111, 671–682 (2023). https://doi.org/10.1007/s11071-022-07855-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-022-07855-z

Keywords

Mathematics Subject Classification

Search

Navigation