Energy–momentum integration and analysis for sliding contact coupling dynamics in large flexible multibody system

Abstract

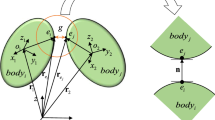
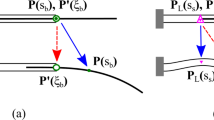
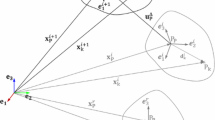
This paper studies the energy–momentum conserving integration for large flexible dynamic systems combining the node-to-element sliding contact pair, which suffers strong coupling between deformation modes and large-scale sliding motion. Unlike node-to-node contact, the sliding contact pair places higher demands on smoothness of geometry description and reduction of material nonlinearity as the contact generally occurs on lines or surfaces. To maintain contact transition continuity, it is necessary to cautiously implement the interpolation of relative kinematic constraints. Moreover, the numerical treatment of auxiliary non-generalized variable influences the accuracy and stability in solving differential-algebraic system. To solve these problems, this paper has made improvements from the two aspects of flexibility description based on the rotationless director triad and isogeometric interpolation, and energy–momentum conserving integration. The treatment of sliding parameter derived from constraint equations is synchronized with that of the generalized variables in differential-algebraic system. Compared with three commonly used numerical methods, this integration shows advantages in strong robustness, conservation properties and convergence verified by typical numerical examples. Novel results are obtained for the sliding joint flexible multibody system revealing the performance of accuracy and robustness in complex dynamics.

Appendix A Proof of invariance of discrete strain measure

Define the generalized coordinates ${{\varvec{q}}^\#}=\{ {\varvec{\varphi }}^\#, {\varvec{d}}^\#_I \}$ in a new configuration after superimposing the rigid body motion $( {\varvec{\varphi }}_{R}, {\varvec{\Lambda }}_{R} )$ as

$$\begin{aligned} ({\varvec{\varphi }}^A)^\#= & {} {\varvec{\varphi }}_{R} + {\varvec{\Lambda }}_{R}{\varvec{\varphi }}^A , \nonumber \\ ({\varvec{d}}^A_I)^\#= & {} {\varvec{\Lambda }}_{R} {\varvec{d}}^A_I \end{aligned}$$

(A1)

Inserting this transformation into Eqs. (47) and (48), the newly approximated position gives:

$$\begin{aligned} ({\varvec{\varphi }}^{\mathrm{{h}}})^\#= & {} \sum \limits _{A = 1}^{ne} {{N}^A(s)}({\varvec{\varphi }^{A}})^\# \nonumber \\= & {} \sum \limits _{A = 1}^{ne} {{N}^A(s)} \left( {\varvec{\varphi }}_{R} + {\varvec{\Lambda }}_{R}{\varvec{\varphi }}^A \right) , \end{aligned}$$

(A2)

and the triad vectors become

$$\begin{aligned} ({\varvec{d}}_I^{\mathrm{{h}}})^\#= & {} \sum \limits _{A = 1}^{ne} {{N}^A(s)}({\varvec{d}_I^{A}})^\# \nonumber \\= & {} \sum \limits _{A = 1}^{ne} {{N}^A(s)}{\varvec{\Lambda }}_{R}{\varvec{d}^{A}_{I}} \end{aligned}$$

(A3)

Employing Eq. (A2), the axial generalized strain component in Eq. (19) is re-formulated as:

$$\begin{aligned} {({\varepsilon }^{\mathrm{{h}}}) ^\#}= & {} {\frac{1}{2} \left[ \left( {\varvec{\varphi }^{\mathrm{{h}}}_{,s}}\right) ^\# \cdot \left( {\varvec{\varphi }^{\mathrm{{h}}}_{,s}}\right) ^\# - 1 \right] } \nonumber \\= & {} \frac{1}{2} \left[ \sum \limits _{A,B = 1}^{ne} {{N}_s^{A}} {{N}_s^{B}} \left( {\varvec{\varphi }_R} + {\varvec{\Lambda }_R}{\varvec{\varphi }^A}\right) \cdot \right. \nonumber \\&\left. \left( {\varvec{\varphi }_R} + {\varvec{\Lambda }_R}{\varvec{\varphi }^B}\right) - 1 \right] \end{aligned}$$

(A4)

Likewise, the other scalar-valued strain components are:

$$\begin{aligned} {({\gamma }^{\mathrm{{h}}}_{\alpha }) ^\#}= & {} \sum \limits _{A,B = 1}^{ne} {{N}_s^{A}} {{N}^{B}} \left( {\varvec{\varphi }_R} + {\varvec{\Lambda }_R} {\varvec{\varphi }^A}\right) \cdot {\varvec{\Lambda }_R} {\varvec{d}_{\alpha }^{B}} \end{aligned}$$

(A5)

$$\begin{aligned} {({\kappa }^{\mathrm{{h}}}_{1}) ^\#}= & {} \sum \limits _{A,B = 1}^{ne} {{N}_s^{A}} {{N}^{B}} {\varvec{\Lambda }_R} {\varvec{d}_{2}^{A}} \cdot {\varvec{\Lambda }_R} {\varvec{d}_{3}^{B}} \end{aligned}$$

(A6)

$$\begin{aligned} {({\kappa }^{\mathrm{{h}}}_{\alpha }) ^\#}= & {} \sum \limits _{A,B = 1}^{ne} {{N}_s^{A}} {{N}_s^{B}} \left( {\varvec{\varphi }_R} + {\varvec{\Lambda }_R}{\varvec{\varphi }^A}\right) \cdot {\varvec{\Lambda }_R} {\varvec{d}_{\beta }^{B}} \end{aligned}$$

(A7)

Considering the superimposed rotation tensor satisfies ${ {\varvec{\Lambda }^{\mathrm{{T}}}_R} {\varvec{\Lambda }_R} = {\varvec{I}} }$, Eqs. (A4) and (A5) are derived as:

$$\begin{aligned} {({\varepsilon }^{\mathrm{{h}}})^{\#}}= & {} \frac{1}{2} \left\{ \sum \limits _{A,B = 1}^{ne} {{N}_s^{A}} {{N}_s^{B}} \left( {\varvec{\varphi }_R} \!\cdot \! {\varvec{\varphi }_R} + {\varvec{\Lambda }_R}{\varvec{\varphi }^A} \!\cdot \! {\varvec{\varphi }_R} \right. \right. \nonumber \\&\left. \left. + {\varvec{\varphi }_R} \!\cdot \! {\varvec{\Lambda }_R}{\varvec{\varphi }^B} + {\varvec{\varphi }^A} \!\cdot \! {\varvec{\varphi }^B} \right) - 1 \right\} \end{aligned}$$

(A8)

$$\begin{aligned} {({\gamma }^{\mathrm{{h}}}_{\alpha }) ^\#}= & {} \sum \limits _{A,B = 1}^{ne} {{N}_s^{A}} {{N}^{B}} \left( {\varvec{\varphi }_R} \cdot {\varvec{\Lambda }_R} {\varvec{d}_{\alpha }^{B}} + {\varvec{\varphi }^A} \cdot {\varvec{d}_{\alpha }^{B}} \right) \end{aligned}$$

(A9)

$$\begin{aligned} {({\kappa }^{\mathrm{{h}}}_{1}) ^\#}= & {} \sum \limits _{A,B = 1}^{ne} {{N}_s^{A}} {{N}^{B}} {\varvec{d}_{2}^{A}} \cdot {\varvec{d}_{3}^{B}} \end{aligned}$$

(A10)

$$\begin{aligned} {({\kappa }^{\mathrm{{h}}}_{\alpha }) ^\#}= & {} \sum \limits _{A,B = 1}^{ne} {{N}_s^{A}} {{N}_s^{B}} \left( {\varvec{\varphi }_R} \cdot {\varvec{\Lambda }_R} {\varvec{d}_{\alpha }^{B}} + {\varvec{\varphi }^A} \cdot {\varvec{d}_{\alpha }^{B}} \right) \end{aligned}$$

(A11)

The B-spline basis function is the partition of unity given by ${\sum \limits _{A = 1}^{ne} {{N}^{A}} = 1}$, which leads to the evolved partial derivative condition:

$$\begin{aligned} {\sum \limits _{A = 1}^{ne} {{N}_s^{A}} \cdot {\varvec{\varphi }_R} = {\varvec{0}}} \end{aligned}$$

(A12)

Substituting Eq. (A12) into Eqs. (A8)–(A11), the objectivity relation ${\varvec{\epsilon }^{\mathrm{{h}}} ( {\varvec{q}} ^\# ) = \varvec{\epsilon }^{\mathrm{{h}}} ( {\varvec{q}} )}$ is confirmed:

$$\begin{aligned} {({\varepsilon }^{\mathrm{{h}}}) ^\#}= & {} \frac{1}{2} \left\{ \sum \limits _{A,B = 1}^{ne} {{N}_s^{A}} {{N}_s^{B}} {\varvec{\varphi }^A} \cdot {\varvec{\varphi }^B} - 1 \right\} = {\varepsilon }^{\mathrm{{h}}} \nonumber \\ {({\gamma }^{\mathrm{{h}}}_{\alpha }) ^\#}= & {} \sum \limits _{A,B = 1}^{ne} {{N}_s^{A}} {{N}^{B}} {\varvec{\varphi }^A} \cdot {\varvec{d}_{\alpha }^{B}} = {\gamma }^{\mathrm{{h}}}_{\alpha } \nonumber \\ {({\kappa }^{\mathrm{{h}}}_{1}) ^\#}= & {} \sum \limits _{A,B = 1}^{ne} {{N}_s^{A}} {{N}^{B}} {\varvec{d}_{2}^{A}} \cdot {\varvec{d}_{3}^{B}} = {\kappa }^{\mathrm{{h}}}_{1} \nonumber \\ {({\kappa }^{\mathrm{{h}}}_{\alpha }) ^\#}= & {} \sum \limits _{A,B = 1}^{ne} {{N}_s^{A}} {{N}_s^{B}} {\varvec{\varphi }^A} \cdot {\varvec{d}_{\beta }^{B}} = {\kappa }^{\mathrm{{h}}}_{\alpha } \end{aligned}$$

(A13)