Parametric instability of a vertically driven magnetic pendulum with eddy-current braking by a flat plate

Abstract

The vertically driven pendulum is one of the classical systems where parametric instability occurs. We study its behavior with an additional electromagnetic interaction caused by eddy currents in a nearby thick conducting plate that are induced when the bob is a magnetic dipole. The known analytical expressions of the induced electromagnetic force and torque acting on the dipole are valid in the quasistatic limit, i.e., when magnetic diffusivity of the plate is sufficiently high to ensure an equilibrium between magnetic field advection and diffusion. The equation of motion of the vertically driven pendulum is derived assuming that its magnetic dipole moment is aligned with the axis of rotation and that the conducting plate is horizontal. The vertical position of the pendulum remains an equilibrium with the electromagnetic interaction. Conditions for instability of this equilibrium are derived analytically by the harmonic balance method for the subharmonic and harmonic resonances in the limit of weak electromagnetic interaction. The analytical stability boundaries agree with the results of numerical Floquet analysis for these conditions but differ substantially when the electromagnetic interaction is strong. The numerical analysis demonstrates that the area of harmonic instability can become doubly connected. Bifurcation diagrams obtained numerically show the co-existence of stable periodic orbits in such conditions. For moderately strong driving, chaotic motions can be maintained for the subharmonic instability.

1 Introduction

Electromagnetic induction is essential for applications such as motors, generators and transformers [1]. Electromagnetic wheel brakes are used in trains and industrial vehicles. Magnetic fields are also applied for controlling the flow of conducting liquids in casting equipment or crystal growth [2, 3]. In most of these applications, the induced currents, secondary magnetic fields and Lorentz force cannot be calculated analytically because either the magnet system, the conductor or (for a fluid conductor) the relative motion are too complicated. For the rare cases where this is nonetheless possible, it is therefore appealing to construct simple electromechanical models described by ordinary differential equations. These are interesting in their own right since their behavior can be fairly easily analyzed and understood. By that, such models could serve as instructive examples for realistic systems that require numerically expensive solutions of Maxwell’s equations.

In a recent work, Priede et al. [4] obtained an analytical solution for the induced force and torque on a magnetic dipole moving or rotating parallel to a conducting plate in the limit of low magnetic Reynolds number. This work was motivated by the practical example of inductive flow measurement with a magnetic flywheel [5, 6]. We have used these results to study the parametric instability [7] of a magnetic pendulum when the nearby horizontal conducting plate performs a vertical oscillation. Conditions for parametric instability exist when the magnetic dipole moment is parallel to the rotation axis of the pendulum or it is in the plane of motion with vertical or horizontal alignment when the pendulum is at rest. In these cases, the plate does not only brake the pendulum, but the plate motion can also destabilize it provided that the magnetic moment as well as frequency and amplitude of the plate’s oscillation satisfy certain constraints [8]. The assumption of a magnetic dipole field for the magnetic bob is not unrealistic since a uniformly magnetized sphere has the same field distribution [9]. However, the finite size of the spherical magnet was neglected in [8].

In the present work, we consider a modified setup which leaves the electromagnetic induction problem principally unchanged, i.e., the pivot performs a vertical sinusoidal oscillation while the plate is fixed. By the modulation of the effective gravitational acceleration, the forcing and braking of the pendulum are no longer directly linked by the strength of the electromagnetic interaction between magnet and plate. Although a damping effect of the electromagnetic interaction is always present, it also modifies the parametric mechanical forcing and could even enhance it. This possibility and its consequences are of particular interest in the present work. In addition, the finite radius of the magnetic bob is incorporated, and the limiting case when the bob passes directly over the plate is considered.

The electromagnetic torque on our vertically driven pendulum is strongly dependent on the vertical distance between magnet and plate and described by two nondimensional parameters. This constitutes the main difference to the case with frictional resistance considered by various authors, e.g., [10, 11]. The velocity-dependent damping and parametric forcing in our case are absent in other magnetic pendulums interacting with exterior electromagnets [12]. Numerical solutions reveal numerous interesting bifurcation phenomena in such systems at subharmonic frequency ratios [13]. Moreover, magnetic pendulums that are excited by time-dependent fields were recently studied experimentally [14, 15]. The corresponding mathematical models, which can reproduce the fully nonlinear behavior successfully, include additional terms for a damping element with elasticity and friction. In contrast to our case, these effects are not caused by the electromagnetic interaction and require the introduction of several empirical parameters. Such investigations are also extended to other nonlinear oscillators with one degree of freedom and magnetic interactions [16]. A strongly localized forcing of a pendulum without dissipation is also obtained by an electrostatic rather than magnetic interaction, e.g., when the bob and an external body are electrically charged. Such cases were recently studied for idealized setups [17, 18].

The structure of this paper is as follows. Section 2 describes the mathematical formulation of the problem and the derivation of equation of motion of the vertically driven pendulum including its electromagnetic interaction with the conducting plate. The linearized equation of motion is also obtained in order to study analytically the behavior close to the vertical equilibrium. In sect. 3, we analyze the stability limits of the equilibrium state by the harmonic balance method for weak electromagnetic interaction between the magnet and the plate. The cases of subharmonic and harmonic resonances are considered. These results are verified and extended to stronger electromagnetic interaction by numerical Floquet analysis in sect. 4. This is followed by sect. 5 presenting numerical investigations of the nonlinear dynamics for finite driving amplitudes of the pendulum. The last section summarizes our findings and provides suggestions for future work.

Fig. 1

Sketch of the vertically driven magnetic pendulum in the presence of a horizontal conducting plate

2 Problem definition

2.1 Geometry and physical properties

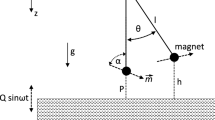
We consider a simple pendulum as sketched in Fig. 1 that is located above a thick stationary plate with electric conductivity $\sigma$. It is assumed that the pendulum motion is confined to the (x, z)-plane. The bob is a sphere of mass $m_b$ and radius R, which is connected to the pivot by a massless, inextensible and inflexible rod. The pendulum length l corresponds to the distance between pivot and the center of the spherical bob. The bob is magnetic with a magnetic field distribution corresponding to a magnetic point dipole. Its dipole moment with modulus $M=\Vert {\mathbf {m}}\Vert$ is parallel to the y-direction, which is indicated by the cross mark in Fig. 1.

The distance P between the center of the magnet and plate corresponds to a vertical pendulum pointing along the z-axis and a fixed pivot $z_0=0$. The pendulum is vertically driven, i.e., the pivot position $z_0$ changes periodically in time t with amplitude Q and frequency $\omega$ according to the equation

$$\begin{aligned} z_0 (t) = - Q \sin \omega t . \end{aligned}$$

2.2 Derivation of equation of motion

The motion of the pendulum has one degree of freedom and is characterized by the displacement angle $\theta (t)$ around the y-axis. The displacement angle $\theta =0$ corresponds to the pendulum pointing in positive z-direction. The motion is caused by the gravity force, the kinematic excitation $z_0(t)$ of the pivot and the electromagnetic interaction between the magnetic bob and the conducting plate. This interaction, as will be discussed in the next section, generates an electromagnetic torque $T_{em}$ acting on the pendulum in y-direction.

The horizontal component of the bob’s velocity is

$$\begin{aligned} u_x=\frac{d}{dt} \left( l \sin {\theta } \right) = l \, {\dot{\theta }} \, \cos {\theta } , \end{aligned}$$

(1)

where ${\dot{\theta }}$ with the dot symbol denoting the time derivative is the angular velocity of the pendulum.

The vertical position of the center of the magnet is given by $z_0+l\cos \theta$. To prevent collisions with the plate, the sum of this distance and the radius R must always be less or equal than $z_p=l+P$, which corresponds to the plate surface. This requires $P\ge Q+R$. The distance h between the center of the spherical magnet and the plate surface is therefore

$$\begin{aligned} h\!=\!z_p-(z_0+ l\cos \theta )\!=\!l +P+Q\sin \omega t- l \cos \theta .\nonumber \\ \end{aligned}$$

(2)

The vertical velocity of the magnet is

$$\begin{aligned} u_z=-\frac{dh}{dt}=-\omega Q\cos \omega t - l \, {\dot{\theta }} \, \sin \theta . \end{aligned}$$

(3)

To derive the equation of motion of the harmonically driven pendulum, it is convenient to use the Lagrange’s equation of the second kind with a generalized force caused by the electromagnetic torque about the fixed pivot point

$$\begin{aligned} \frac{d}{dt} \frac{\partial {{\mathcal {L}}}}{\partial {\dot{\theta }}} - \frac{\partial {{\mathcal {L}}}}{\partial \theta } = T_{em} . \end{aligned}$$

(4)

The Lagrangian ${{\mathcal {L}}}={{\mathcal {T}}}-{{\mathcal {U}}}$ is defined as the difference between the kinetic and the potential energies of the system. The kinetic energy ${{\mathcal {T}}}$ consists of translational and rotational parts

$$\begin{aligned} {{\mathcal {T}}}(t, \theta , {\dot{\theta }}) = \frac{1}{2} m_b \left( u_x^2 + u_z^2 \right) + \frac{1}{2} J_b {\dot{\theta }}^2 , \end{aligned}$$

where $J_b = \frac{2}{5} m_b R^2$ is the moment of inertia of the spherical bob. The potential energy ${{\mathcal {U}}}(t, \theta ) = m_b g h$ is associated with gravity relative to the plate surface, where g is the gravitational acceleration. After writing the Lagrangian using Eqs. (1), (2) and (3), the Lagrange’s Eq. (4) leads to the following equation of motion

$$\begin{aligned} \left( m_b l^2 + \frac{2}{5} m_b R^2 \right) \ddot{\theta }+ m_b l \left( g - Q \omega ^2 \sin \omega t \right) \sin \theta = T_{em}.\nonumber \\ \end{aligned}$$

(5)

Obviously, the kinematic excitation of the pivot results in a further acceleration in addition to gravity, i.e., $g-\ddot{z}_0(t)$.

2.3 Electromagnetic torque

The equation of motion requires the computation of the electromagnetic torque $T_{em}$ acting on the pendulum about the pivot point. When the magnetic moment is aligned with the rotation axis, the electromagnetic interaction by the motion of the dipole causes two in-plane components $F_x$, $F_z$ of the force on the magnet. They read [4]

$$\begin{aligned} F_x= & {} -\frac{\mu _0^2 M^2 \sigma u_x}{512 h^3}, \end{aligned}$$

(6)

$$\begin{aligned} F_z= & {} -\frac{\mu _0^2 M^2 \sigma u_z}{128 h^3}, \end{aligned}$$

(7)

where $\mu _0$ is the vacuum permeability. We note that the rotation of the magnet with angular velocity ${\dot{\theta }}$ does not give rise to a force or torque on it since the magnetic field in the conductor remains unchanged by a rotation of the magnet around the y-axis. More general expressions for force and torque components in the case of arbitrary orientation of the magnetic dipole moment are given in [4, 8]. Like Eqs. (6) and (7), they are valid in the quasistatic limit, i.e., when the magnetic diffusivity is sufficiently high to ensure an equilibrium of magnetic field advection and diffusion.

As a result of the action of the force components $F_x$, $F_z$ on the magnetic bob, the total electromagnetic torque on the pendulum is

$$\begin{aligned} T_{em}=l\cos \theta \, F_x-l\sin \theta \, F_z. \end{aligned}$$

(8)

By using Eqs. (6) and (7) as well as Eqs. (1), (2) and (3) in Eq. (8), we finally obtain

$$\begin{aligned} \begin{aligned} T_{em} =&- \frac{\mu _0^2 M^2 \sigma }{128\pi } \frac{\omega Q l \cos \omega t }{\left( l + P+Q\sin \omega t - l\cos \theta \right) ^3}\, \sin \theta \\&- \frac{\mu _0^2 M^2 \sigma }{512\pi } \frac{l^2 \left( 1+3\sin ^2\theta \right) }{\left( l + P+Q\sin \omega t - l\cos \theta \right) ^3}\, {\dot{\theta }}. \end{aligned} \end{aligned}$$

(9)

The electromagnetic torque vanishes for $\theta ={\dot{\theta }}=0$, i.e., the vertical position remains an equilibrium as in the non-magnetic case.

2.4 Nondimensional equation of motion and its linearization

Without the electromagnetic torque and for a fixed pivot, the eigenfrequency of the simple gravity pendulum is

$$\begin{aligned} \Omega _0=\sqrt{\frac{ |g| }{L}}, \end{aligned}$$

with a modified (effective) length of the pendulum

$$\begin{aligned} L=l + \frac{2}{5} \frac{R^2}{l}. \end{aligned}$$

For convenience, we define a nondimensional time and five nondimensional parameters, i.e.,

$$\begin{aligned} {\tilde{t}}= & {} \frac{\omega t}{2}, \quad A = \frac{4 \Omega _0^2 }{\omega ^2} , \quad B=\frac{2 Q }{L}, \quad S = \frac{2 P }{L },\\ D= & {} \frac{2 R }{L },\quad C=\frac{\mu _0^2 M^2 \sigma }{16\pi \,m_b \, \omega \, L^3 }. \end{aligned}$$

Small values of A correspond to high excitation frequencies and negative A to an inverted pendulum. The parameter $C\ge 0$ can be regarded as a ratio between electromagnetic and inertial forces. The geometry parameters B, S and D only need to satisfy the restriction $S\ge B+D$ to avoid collisions between magnet and plate.

In the following, we shall only consider the limiting case, when the distance between the spherical pendulum and the plate is minimal for avoiding collisions, i.e., we take

$$\begin{aligned} S=B+D \end{aligned}$$

to reduce the number of parameters to four.

Using these parameters and taking into account Eqs. (5) and (9), the nonlinear equation of motion in nondimensional form is

$$\begin{aligned}&\ddot{\theta }+ \gamma \, C \frac{1+3 \sin ^2\theta }{2 \left( 2\gamma \left( 1-\cos \theta \right) +S+B\sin 2t\right) ^3} \, {\dot{\theta }} \nonumber \\&+\left( A -2 B\sin \left( 2t\right) + C \frac{2 B\cos 2t}{\left( 2\gamma \left( 1-\cos \theta \right) +S+B\sin 2t\right) ^3} \right) \nonumber \\&\sin \theta =0, \end{aligned}$$

(10)

where the tilde over t is suppressed for convenience.

The coefficient

$$\begin{aligned} \gamma = \frac{l}{L}=\frac{1}{2}\left( 1+\sqrt{1-\frac{2 D^2}{5}}\right) , \quad 0<\gamma <1 \end{aligned}$$

depends only on the ratio D of the magnet diameter 2R to the effective length L of the pendulum.

Since we are interested in the behavior close to the equilibrium $\theta =0$, the equation of motion (10) can be linearized with respect to $\theta$. For the electromagnetic torque $T_{em}$ in Eq. (9), the linearized expression consists of the superposition of two leading terms proportional to the displacement angle $\theta$ and the angular velocity ${\dot{\theta }}$, respectively, $T_{em}= \theta \, T^{\left( 0\right) } + {\dot{\theta }}\, T^{\left( 1\right) }$. It is easy to see that the first contribution vanishes for $\theta =0$, which is necessary for a vertical equilibrium.

The linearized nondimensional equation of motion for small $\theta$ is

$$\begin{aligned} \ddot{\theta }+ {\dot{\theta }}\, C \, f_1(t) +\theta \left( A - 2 B\sin 2t - C \,f_2(t)\right) =0.\nonumber \\ \end{aligned}$$

(11)

The $\pi$-periodic functions $f_1(t)$ and $f_2(t)$ are

$$\begin{aligned} f_1(t)= & {} \frac{\gamma }{2 \left( D+B\left( 1+\sin 2t\right) \right) ^3}, \\ f_2(t)= & {} - \frac{2 B\cos 2t}{\left( D+B\left( 1+\sin 2t\right) \right) ^3 } . \end{aligned}$$

In the configuration considered, when the conducting plate is fixed and the pivot is periodically driven, there is an additional modulation of the gravitational acceleration, which is manifested by the forcing term $2 B\sin 2t$ in Eq. (11). The terms proportional to C are due to the electromagnetic torque. The analysis of the complementary configuration made in [8] shows that when the pivot is fixed, the oscillations of the conducting plate play a dual role as forcing as well as damping. This means that the B-term disappears from the equation of motion.

3 Analytical stability results

For $C=0$, the problem reduces to the vertically driven simple pendulum without damping. Parametric instability of the equilibrium point $\theta =0$ is described by the linear classical Mathieu equation. The stability limits for this problem can be determined by the harmonic balance method [7]. It is based on seeking for time-periodic solutions in the form of a Fourier series

$$\begin{aligned} \theta = a_0 + \sum _{n=1}^\infty \left( a_n \cos nt+ b_n \sin n t \right) . \end{aligned}$$

The series is truncated at some order and substituted into the Mathieu equation. Subsequent trigonometric reduction leads to a homogeneous linear system for the coefficients $a_n$ and $b_n$. Non-trivial solutions exist when the determinant of this truncated system is equal to zero, which determines a relation B(A) as the boundary between stable and unstable parameter regions. Zeros of B(A) occur at the resonant frequency ratios corresponding to $A_k=k^2$ with integer k. We note that the result is an approximation on account of the truncation, which does not work for large values of A. It can be improved by including more terms, which leads to increasingly complicated algebraic expressions. Alternatively, the unstable regions in the (A, B) parameter plane (also called tongues) can be found by numerical Floquet analysis [7].

In the present problem for $C>0$, we apply the harmonic balance method and treat both B and C as small parameters. Specifically, only the leading-order terms in C will be taken into account. Since the linear systems for the unknown coefficients are obtained by trigonometric reduction, the functions $f_1$ and $f_2$ have to be expressed as Fourier series. This was already done in our previous work. They are of the form

$$\begin{aligned} \begin{aligned} f_1(t)&= d_0 + d_1 \sin 2t+ d_2 \cos 4 t,\\ f_2(t)&= e_1 \cos 2t+ e_2 \sin 4 t. \end{aligned} \end{aligned}$$

(12)

Terms of higher order are omitted. The coefficients $d_0$, $d_1$, $d_2$ and $e_1$, $e_2$ are typically square roots of rational functions of the parameters B and S and are given in Appendix A.

3.1 Condition for subharmonic instability

We limit our consideration to the simplest representation

$$\begin{aligned} \theta =a_0+ a_1 \cos t+ b_1 \sin t \end{aligned}$$

(13)

in order to find the behavior close to the subharmonic resonance with $\Omega _0\approx \omega /2$, i.e., $A\approx 1$. Eq. (13) is substituted into Eq. (11) with Eq. (12) for $f_1$ and $f_2$. Using the Mathematica software [19], one can easily carry out the necessary trigonometric reductions to pure sine and cosine terms. Omitting the higher frequency terms, the result is

$$\begin{aligned} 0= & {} 2 a_0 A \!+\!\left[ (2A \!-\!2 \!-\!C(d_1\!+\!e_1)) a_1\!+\! 2 (C d_0\!-\!B) b_1\right] \cos t \nonumber \\&+\left[ - 2 (C d_0 \!+\!B) a_1 +(2A -2 +C(d_1+e_1)) b_1\right] \sin t. \end{aligned}$$

The coefficients of the constant term and the sine and cosine terms must vanish, which leads to a homogeneous linear system for $a_0$, $a_1$ and $b_1$. Clearly, $a_0=0$ is needed for the case $A\approx 1$, and we are left with the linear system for $a_1$ and $b_1$. The condition that its determinant vanishes is

$$\begin{aligned} \varepsilon ^2 -B^2 + \frac{C^2}{4}\left( 4d_0^2-\left( d_1+e_1\right) ^2\right) =0, \end{aligned}$$

(14)

where $\varepsilon =A-1$. Figure 2 shows these stability boundaries in the (A, B) parameter plane for several values of C and D. The magnetic damping causes deviations from $B=\pm \varepsilon$, which diminish for larger values of $|\varepsilon |$.

Fig. 2

Stability boundaries for subharmonic instability obtained from the harmonic balance method for (a) $D = 0.01$ and (b) $D = 0.1$

3.2 Condition for harmonic instability

For the harmonic resonance with $\Omega _0\approx \omega$, i.e., $A\approx 4$, we choose the solution form

$$\begin{aligned} \theta = a_0+ a_2 \cos 2t + b_2\sin 2t{+} a_4 \cos 4t {+} b_4\sin 4t\nonumber \\ \end{aligned}$$

(15)

and substitute it into Eq. (11) with Eq. (12) for $f_1$ and $f_2$. The representation (15) excludes odd multiples of t since these decouple from the even multiples as for the classical Mathieu equation. The order of $f_1$ and $f_2$ in Eq. (12) matches with Eq. (15), which is required for consistency. The trigonometric reduction leads to the expression

$$\begin{aligned} 0= & {} A a_0 -C \left( d_1+\frac{e_1}{2}\right) a_2-B b_2+ C\left( 2d_2-\frac{e_2}{2}\right) b_4\\&+\left[ -C e_1 a_0+\left( A-4\right) a_2 + C \left( d_2+2d_0-\frac{e_2}{2}\right) b_2 \right. \\&\left. -C \left( 2d_1+\frac{e_1}{2}\right) a_4 -B b_4\right] \cos 2t \\&+\left[ -2B a_0+C \left( d_2-2d_0-\frac{e_2}{2}\right) a_2 \right. \\&\left. +(A-4)b_2+ B a_4 - C \left( 2 d_1 +\frac{e_1}{2}\right) b_4 \right] \sin 2t\\&+ \left[ C \left( d_1 -\frac{e_1}{2}\right) a_2 +B b_2 \right. \\&\left. +(A-16)a_4 +4C d_0 b_4\right] \cos 4t\\&+\bigg [ -C e_2 a_0 -B a_2 + C \left( d_1 -\frac{e_1}{2}\right) b_2 \\&-4 C d_0 a_4 +(A-16) b_4\bigg ] \sin 4t. \end{aligned}$$

Nonzero solutions for the coefficients $a_0$, $a_2$, $b_2$, $a_4$ and $b_4$ exist if the determinant of the corresponding linear system vanishes. Since we wish to consider the limiting case of small C only, we first recall the case $C=0$ as a starting point. The leading approximation for small B in this case is found by putting $\varepsilon =A-4$ and expanding the determinant in powers of $\varepsilon$ using the Mathematica software. If we keep powers in $\varepsilon$ up to second order, and, in addition, retain only the leading terms in the coefficients (which depend on B), we find

$$\begin{aligned} 144 \varepsilon ^2 - 48 B^2 \varepsilon - 5 B^4=0. \end{aligned}$$

The solutions are

$$\begin{aligned} \varepsilon _{1,2} = \frac{B^2}{6 }\pm \frac{B^2}{4 }. \end{aligned}$$

(16)

For $0<C\ll 1$, we proceed in a similar way, i.e., neglect cubic and higher terms in $\varepsilon$ and retain only the leading terms in the coefficients of $\varepsilon$ that now also depend on C. It turns out that only the term $\varepsilon ^0$ changes, i.e.,

$$\begin{aligned} 144 \varepsilon ^2 \!-\! 48 B^2 \varepsilon \!-\! 5 B^4 \!+\! 36 C^2\left( 16 d_0^2\!-\!\left( 2d_2\!-\!e_2\right) ^2\right) \!=\!0.\nonumber \\ \end{aligned}$$

(17)

As for the subharmonic case, this equation can be solved analytically for $\varepsilon$ but not for B when $C\ne 0$. Figure 3 shows these stability boundaries in the (A, B) parameter plane for several values of C and D. The magnetic damping causes deviations from the solution (16), which increase with C but diminish for larger values of $|\varepsilon |$.

Fig. 3

Stability boundaries for harmonic instability obtained from the harmonic balance method for (a) $D = 0.01$ and (b) $D = 0.1$

3.3 Minimum values of B for instability

Fortunately, it is not necessary to find the minimum of the implicitly given function $B(\varepsilon )$ for the subharmonic and harmonic instability numerically. In both cases, $dB/d\varepsilon =0$ occurs where the two solution branches of the quadratic equation for $\varepsilon (B)$ meet, i.e., where the discriminant vanishes.

In the subharmonic case, the minimum of B is located at $\varepsilon =0$, i.e., $A_\text {min}=1$, and satisfies the equation following from Eq. (14)

$$\begin{aligned} B^2_\text {min} = \frac{C^2}{4}\left( 4d_0^2-\left( d_1+e_1\right) ^2\right) = C^2\, G_s(B_\text {min},D). \end{aligned}$$

In the harmonic case, the minimum of B is located at $\varepsilon =B^2/6$, i.e., $A_\text {min}=4+B^2_\text {min}/6$, and satisfies the equation following from Eq. (17)

$$\begin{aligned} B^4_\text {min} {=}4C^2\left( 16 d_0^2-\left( 2d_2-e_2\right) ^2\right) {=}C^2\, G_h(B_\text {min},D). \end{aligned}$$

In both cases, one can directly solve for $C(B_\text {min})$. In the limiting cases $B\ll D \ll 1$ and $D\ll B\ll 1$ one can also solve approximately for $B_\text {min}(C)$ because the functions $G_s$ and $G_h$ are then simplified drastically.

For $B\ll D \ll 1$, when the amplitude of pivot oscillations is small in comparison with the bob’s radius, we obtain

$$\begin{aligned} G_s \sim \frac{1}{4 D^6}, \qquad G_h \sim \frac{16}{ D^6} \end{aligned}$$

in the leading order. Likewise, for $D\ll B \ll 1$ when contrarily the radius is smaller than the amplitude, we obtain

$$\begin{aligned} G_s \sim \frac{3}{256 D^4 B^2},\qquad G_h \sim \frac{3}{B^2 D^4}. \end{aligned}$$

For the subharmonic case, it follows that

$$\begin{aligned} \begin{aligned}&B_\text {min} \sim \frac{C}{2 D^3} \qquad (C\ll D^4),\\&B_\text {min}\sim \frac{3^{1/4}C^{1/2}}{ 4 D} \quad (D^4 \ll C\ll D^2 ) \end{aligned} \end{aligned}$$

(18)

The corresponding power laws for the harmonic case are

$$\begin{aligned} \begin{aligned}&B_\text {min} \sim \frac{2C^{1/2}}{ D^{3/2}} \qquad (C\ll D^5),\\&B_\text {min} \sim \frac{3^{1/6}C^{1/3}}{ D^{2/3}} \quad (D^5 \ll C\ll D^2 ). \end{aligned} \end{aligned}$$

(19)

Figure 4 shows the dependence of the minimum value of B for instability as function of C for two values of D in the subharmonic and harmonic cases. The power laws (18) and (19) provide a good approximation in the respective intervals for C.

Fig. 4

Minimum values of B for instability as functions of C from the harmonic balancing method for (a) subharmonic and (b) harmonic cases. The approximate power laws (18) and (19) are shown as thin solid and dashed straight lines

3.4 Stability for negative A

The inverted system, i.e., configuration of the conducting plate fixed over the inverted pendulum with movable pivot, corresponds to the negative value of g in the equation of motion (5), which results in negative values of A. Without the plate, the vertical oscillations of the pivot can stabilize the inverted pendulum [20]. The limit of the stable region is found from the same representation (15) as for harmonic instability. For $C=0$, the leading terms of the determinant in A and B near $A=B=0$ are

$$\begin{aligned} 32 A+ 16 B^2 =0, \end{aligned}$$

i.e., the stability boundary is $B=\sqrt{-2 A}$. When $C>0$ is retained in leading order, we get an additional term independent of A, i.e.,

$$\begin{aligned} 32 A\!+\! 16 B^2\!+\!C^2\big (4 e_1(2d_1\!+\!e_1) \!+\!e_2(-4d_2\!+\!e_2)\big )\!=\!0. \end{aligned}$$

The coefficient of $C^2$ can be expanded into a power series at $B=0$, which reads

$$\begin{aligned} 4 e_1(2d_1+e_1) +e_2(-4d_2+e_2)\!\sim \! B^2\left( \frac{16}{D^6}+\frac{24\gamma }{D^7}\right) . \end{aligned}$$

The necessary amplitude for stability is therefore reduced when $C>0$, i.e.,

$$\begin{aligned} B\sim \left( \frac{-2A}{1+C^2 \left( \frac{1}{D^6}+\frac{3\gamma }{2 D^7}\right) }\right) ^{1/2}. \end{aligned}$$

4 Numerical results from the linear stability analysis

According to the Floquet theorem, the linear stability boundary corresponds to the set of parameters, where largest eigenvalue $\lambda _m$ of the monodromy matrix

$$\begin{aligned} {\mathbf {M}}={\mathbf {G}}(0)^{-1}{\mathbf {G}}(\pi ) \end{aligned}$$

(20)

has modulus $|\lambda _m|=1$. In Eq. (20), the matrix ${\mathbf {G}}$ is defined as

$$\begin{aligned} {\mathbf {G}}(t)=\left( \begin{matrix} \theta _{1}(t) &{} {\dot{\theta }}_1(t) \\ \theta _{2}(t) &{} {\dot{\theta }}_2(t) \\ \end{matrix} \right) , \end{aligned}$$

where $\theta _1$ and $\theta _2$ are two linearly independent solutions of the linearized equation of motion. These solutions are calculated numerically over the period $\pi$ using MATLAB’s ode45 solver [21] with a low relative error tolerance.

We want to confirm the validity of our analytical results from the previous section in the limit of small B by the numerical Floquet analysis. It will also show the limitations of the analytical approximation.

Fig. 5

Stability boundaries for (a) subharmonic and (b) harmonic instabilities obtained from the harmonic balance method (analytic) and the numerical Floquet analysis (numeric) for $D=0.1$ in the region of small values of B

Fig. 6

Stability boundaries for harmonic instability obtained from the numerical Floquet analysis for (a) $D=0.1$ and (b) $D=0.01$

Figure 5 presents isolines $|\lambda _m|=1$ for $D=0.1$ and two different values of C near the subharmonic and harmonic resonances. For comparison, the analytical results shown above in Figs. 2 and 3 are also plotted here. We see that there is good agreement between analytical and numerical curves near the minimum of B(A) for the smaller value of C, which verifies the numerical method. The differences increase as B grows. We also note that the symmetry about $A=1$ is lost for larger values of B in the subharmonic case (Fig. 5a). The minimum $B_{\text {min}}$ is shifted slightly to the right from $A=1$. For the harmonic case and $C=10^{-3}$, the difference between analytical and numerical results becomes significant even at the minimum of B(A) because $B \approx 0.5$ is no longer small compared to unity (Fig. 5b).

Larger values of C can significantly affect the stability limits for values of A and B outside the regions of subharmonic and harmonic resonances of Mathieu’s equation. This is shown in Fig. 6a,b for parameters $D=0.1$ and $D=0.01$. For both cases, the neutral stability curves $|\lambda _m|=1$ are deformed in a similar way when C increases. They become flatter near $A=1$, which can lead to a non-monotonic dependence of the critical value B(C) for instability at values of A sufficiently far away from $A=1$. Near the harmonic resonance $A=4$, the neutral curves are mainly shifted upwards upon increasing C. Remarkably, they are also pinched such that an island of instability develops near $A=5$ and below the connected region when C is sufficiently large. This is particularly apparent in Fig. 6b, where the island has not been completely formed. The behavior of B(C) for a fixed $A\approx 5$ can therefore not only be non-monotonic but also non-unique.

Both the flattening and the formation of an island of instability are indications that the pivot’s vertical motion, i.e., the term $f_2(t)$ in Eq. (11), contributes a significant driving rather than braking electromagnetic torque for these parameters.

Fig. 7

Minimum values of B (a, c) and corresponding A (b, d) for subharmonic instability as functions of C from numerical Floquet analysis: (a, b) $D=0.1$ and (c, d) $D=0.01$. The analytical results from the harmonic balance method are shown in solid lines for comparison

We shall now examine the dependence of the instability minimum $(A_\text {min}, B_\text {min})$ on the parameter C. As in Fig. 4, two values of $D=0.1$ and $D=0.01$ are considered. Figure 7a–d show the results for the minimum position in the subharmonic case. The minimum value $B_\text {min}$ taken over the subharmonic range of A shows a monotonic increase with C (Fig. 7a,c). The corresponding position $A_\text {min}$ has a non-monotonic dependence on C and becomes a decreasing function for large values of C. Generally, the analytical results agree remarkably well with the numerical results for small values of C. For $D=0.1$, the analytical solution deviates from the numerical one starting from $C \gtrsim 10^{-2}$.

The behavior for $D=0.01$ is qualitatively similar, but the deviation from the analytical results appears already for $C \gtrsim 10^{-5}$. In the interval $10^{-5} \lesssim C \lesssim 10^{-3}$, $B_\text {min}$ is overpredicted by the analytical solution.

Fig. 8

Minimum values of B (a, b) and corresponding A b, d for harmonic instability as functions of C from numerical Floquet analysis: (a, b) $D=0.1$ and (c, d) $D=0.01$. The analytical results from the harmonic balance method are shown in solid lines for comparison

Figure 8 shows the results for the positions $B_\text {min}$ and $A_\text {min}$ in the harmonic case. In contrast to Fig. 7a,c, $B_\text {min}$ is now a non-monotonic function of C, which is related to the pinching and/or splitting of the neutral curve. Eventually, $B_\text {min}$ resumes the growth with C when $C\gtrsim D$, cf. Fig. 8a,c. The agreement with the analytical prediction is here limited to significantly smaller values than for the subharmonic case. Figure 8a,b show that the results for both $B_\text {min}$ and $A_\text {min}$ deviate visibly from the analytical prediction for $C \gtrsim 10^{-3}$ in the case $D=0.1$. For $D=0.01$, this threshold is in the interval $10^{-6} \lesssim C \lesssim 10^{-5}$ (Fig. 8c,d).

There are at least two sources for the observed differences. The analytical predictions are based on the assumption of $B\ll 1$ and $C\ll 1$. Typically, the former condition no longer holds when the differences appear. The influence of D on the threshold value for C, where the analytical prediction ceases to be valid, is presumably caused by the quality of approximation of the functions $f_1$ and $f_2$ by the leading terms of their Fourier expansion. When B becomes comparable to D, this approximation becomes more and more inaccurate.

5 Pendulum motions with finite amplitude

In this section, we examine the effect of varying B at a fixed value $D=0.1$ and two values of A in the subharmonic and harmonic instability intervals. Specifically, we choose $A=1.3$ and $A=5$. In addition, we consider several values of C that should reveal non-monotonic behavior of the stability threshold B.

To explore the qualitative behavior, we compute bifurcation diagrams that display the angular velocity ${\dot{\theta }}$ at times $t_n=n\pi$, i.e., multiples of the fundamental period, as function of the oscillation amplitude B of the pivot. This is done by solving Eq. (10) in MATLAB using the ode45 routine. The parameter B is either increased or decreased by small increments. The final state from the previous B value is used as initial condition. The values of ${\dot{\theta }}$ are plotted only after a large number of cycles has been completed at the given B to exclude transients. We also note that the signs of ${\dot{\theta }}$ in the bifurcation diagrams depend on the initial conditions. The opposite signs can also be obtained.

5.1 Subharmonic cases

Fig. 9

Bifurcation diagrams based on the angular velocity ${\dot{\theta }}$ at times $t_n=n\pi$ as a function of (a) increasing and (b) decreasing value of B for the parameter values $A=1.3$, $C=10^{-4}$ and $D=0.1$

Fig. 10

Phase planes ${\dot{\theta }}(\theta )$ for increasing values of B and fixed values of $A=1.3$, $C=10^{-4}$ and $D=0.1$

In this subsection, we set $A=1.3$ and vary B in the interval $0\le B\le 1.2$. The first bifurcation diagrams shown in Fig. 9 correspond to $C=10^{-4}$. For increasing B (Fig. 9a), the initial condition is close to the equilibrium and decays to zero while $B\lesssim 0.3$ (cf. Fig. 2b). For larger values, we find a continuously rotating state illustrated by the phase plane for $B=0.5$ in Fig. 10a. This solution undergoes a period doubling but remains continuously rotating as shown in Fig. 10b. It is followed near $B=0.66$ by apparently chaotic behavior with oscillations and overturning motion in both clockwise and counterclockwise senses of rotation (Fig. 10c). Around $B=0.7$, the solution becomes periodic with a closed orbit, which involves two cycles of rotation with a reversal in between (Fig. 10d). After another interval of apparently chaotic behavior, there is again a window of regular motion close to $B=1$. At $B=1.014$, the pendulum performs a rotating motion with a short reversal every two cycles (Fig. 10e). For $B=1.034$, we find a period doubling of this particular rotating state (Fig. 10f). Regular motion is no longer observed upon increasing B further up to $B=1.2$. The solution at $B=1.034$ corresponds to the opposite sense of overall rotation than at $B=1.014$. Both states are separated by a narrow chaotic B-interval.

The bifurcation diagram for decreasing B in Fig. 9b shows the same states apart from the period doubling near $B=1.034$. It also demonstrates hysteresis, e.g., the regular motion interval near $B=0.7$ overlaps hardly with the corresponding B-interval in Fig. 9a. The first non-trivial solution shown in Fig. 10a can be traced down to very small positive values of B.

Fig. 11

Bifurcation diagrams based on the angular velocity ${\dot{\theta }}$ at times $t_n=n\pi$ as a function of (a) increasing and (b) decreasing value of B for the parameter values $A=1.3$, $C=10^{-3}$ and $D=0.1$

Fig. 12

Phase planes ${\dot{\theta }}(\theta )$ for (a) increasing and (b) decreasing values of B and fixed values of $A=1.3$, $C=10^{-3}$ and $D=0.1$

The results for $C=10^{-3}$ are shown in Figs. 11 and 12. For increasing B, the bifurcation diagram Fig. 11a is qualitatively similar to $C=10^{-4}$ up to the second bifurcation. There is a short and presumably transient chaotic window at $B\approx 0.65$, which is absent in Fig. 11b. Another short interval with a second period doubling appears at $B=0.69$. The continuously rotating solution is shown in Fig. 12a. From $B\approx 0.7$ on, the solutions are chaotic. A periodic window near $B=0.7$ observed at $C=10^{-4}$ is absent.

The bifurcation diagram for decreasing B in Fig. 11b shows that the first bifurcation at $C=10^{-3}$ is again subcritical since this solution can be continued down to $B<0.1$. Otherwise it is rather similar to the one for increasing B. Only the second period doubling is missing. In addition, there is a short periodic window at $B \approx 1$. This solution with three full rotations between reversals is shown in Fig. 12b.

Fig. 13

Bifurcation diagrams based on the angular velocity ${\dot{\theta }}$ at times $t_n=n\pi$ as a function of (a) increasing and (b) decreasing value of B for the parameter values $A=1.3$, $C=10^{-2}$ and $D=0.1$

Fig. 14

Phase planes ${\dot{\theta }}(\theta )$ for increasing values of B and fixed values of $A=1.3$, $C=10^{-2}$ and $D=0.1$

Another tenfold increase of C to $C=10^{-2}$ leads to the behavior shown in Figs. 13 and 14. For increasing B, the initial bifurcation from the equilibrium $\theta =0$ appears at $B\approx 0.2$ in Fig. 13a. It leads to an oscillation with small amplitude illustrated by the phase planes in Fig. 14a,b rather than a full rotation of the pendulum at the lower values of C. The second bifurcation near $B\approx 0.34$ provides a similar oscillation but with significantly increased amplitude (Fig. 14c). This is followed by a chaotic interval and a periodic window near $B=0.67$ (Fig. 14d) until chaotic behavior largely persists above $B=0.7$. The bifurcation diagram Fig. 13b for decreasing B is very similar except that the solution obtained from the second bifurcation persists down to $B\approx 0.12$.

5.2 Harmonic cases

In this subsection, we set $A=5$ and vary B in the interval $0.1\le B\le 3$. As before, the initial condition is set to a nonzero value close to the equilibrium as long as the trivial solution $\theta =0$ persists after a long integration time. Otherwise, the solution from the previous B is used.

Fig. 15

Bifurcation diagrams based on the angular velocity ${\dot{\theta }}$ at times $t_n=n\pi$ as a function of (a) increasing and (b) decreasing value of B for the parameter values $A=5$, $C=10^{-4}$ and $D=0.1$

Fig. 16

Phase planes ${\dot{\theta }}(\theta )$ for increasing values of B and fixed values of $A=5$, $C=10^{-4}$ and $D=0.1$

In our parametric study, we again first consider $C=10^{-4}$. Figure 15 shows the bifurcation diagrams. The first bifurcation for increasing B occurs near $B=1.7$. The phase plot for $B=2$ in Fig. 16a shows that it is a continuous rotation with two full rotations between the sampling times. A second bifurcation causes a tripling of the period near $B=2.6$ before the solution becomes chaotic. A further increase of B then leads to a periodic solution with one rotation between reversals shown in Fig. 16b. It persists at least up to $B=3$. The bifurcation diagram for decreasing B in Fig. 15b shows essentially only the rotating solution that emerges after the first bifurcation when B increases. It persists down to $B\approx 0.2$. A short interval with period tripling appears near $B=2.6$.

Fig. 17

Bifurcation diagrams based on the angular velocity ${\dot{\theta }}$ at times $t_n=n\pi$ as a function of B for the parameter values $A=5$, $C=10^{-2}$ and $D=0.1$. Directions of increasing or decreasing B values are indicated by arrows

Fig. 18

Phase planes ${\dot{\theta }}(\theta )$ for increasing values of B and fixed values of $A=5$, $C=10^{-2}$ and $D=0.1$

A significant change in the dynamics is observed for $C=10^{-2}$. The bifurcation diagrams for increasing and decreasing B are shown together in Fig. 17. The first bifurcation for increasing B near 1.8 leads to a finite-amplitude oscillation, i.e., with reversals (Fig. 18a). Increasing B further results in two period doublings (Fig. 18b). This is finally followed by a bifurcation that leads to the same periodic motion with one full rotation between reversals as found out for $B=2.88$ with $C=10^{-4}$. Decreasing B shows that this solution persists down to $B\approx 1.9$, where it reverses to the simple oscillation without overturning. This branch extends down to $B\approx 0.6$ where the trivial solution reappears.

Fig. 19

Bifurcation diagrams based on the angular velocity ${\dot{\theta }}$ at times $t_n=n\pi$ as a function of B for the parameter values $A=5$, $C=10^{-1}$ and $D=0.1$. Directions of increasing or decreasing B values are indicated by arrows

Fig. 20

Phase planes ${\dot{\theta }}(\theta )$ for an (a) increasing and (b) decreasing value of $B=1.5$ and fixed values of $A=5$, $C=10^{-1}$ and $D=0.1$

Finally, we consider the case $C=0.1$. Figure 19 shows that the first bifurcation appears already near $B=0.9$ and is now supercritical. It leads to a small-amplitude oscillation. This solution jumps to another branch with large oscillation amplitude near $B=1.8$. For $B=2.6$, there is a period doubling of the oscillatory solution. Decreasing B from $B=3$ demonstrates that the oscillation with larger amplitude persists down to $B\approx 1.5$. The lower and upper branch solutions at $B=1.5$ are shown in Fig. 20a,b.

6 Conclusions

We have studied the parametric instability of a vertically driven pendulum with a spherical magnetic bob located above a thick conducting plate. For simplicity, we assumed that the bob’s magnetic moment is parallel to the axis of rotation. The induction of eddy currents in the plate by the magnet’s motion provides an electromagnetic torque that depends on the pendulum’s displacement angle and angular velocity as well as on the time. By comparison with the ordinary vertically driven pendulum, this torque causes a modulation of the damping and stiffness coefficients. The latter includes the effects of both mechanical driving of the pivot as well as an electromagnetic contribution. The electromagnetic damping and stiffness contributions are identical to the case with fixed pivot and vertically oscillating conducting plate studied earlier, where the mechanical driving of the pendulum is absent. In addition, the magnet’s finite radius is taken into account (size parameter D) and it is assumed that the smallest possible separation between plate and magnet surface is zero. Further nondimensional parameters are the frequency parameter A, the driving amplitude B, and the electromagnetic interaction parameter C. The stability of the vertical equilibrium position was determined analytically by the harmonic balance method in the limits $B\ll 1$ and $C\ll 1$ for the ranges of A, where subharmonic and harmonic resonances occur. The calculation provides approximate power-law dependencies between necessary driving amplitude $B_\text {min}$ for instability and interaction parameter C when the conditions $B\ll D\ll 1$ or $D\ll B\ll 1$ apply. The numerical Floquet analysis was also performed, where these restrictions do not apply. In the subharmonic case, the minimal amplitude $B_\text {min}$ for instability grows monotonically with C. By contrast, $B_\text {min}$ can decrease with increasing C in the harmonic resonance case when C is fairly large. This is associated with the electromagnetic contribution to the stiffness coefficient, which can support the mechanical driving. For fixed C and D, the harmonically unstable region in the (A, B)-plane can therefore become pinched and even disconnected. A similar behavior was reported in [22] for a higher resonance of a damped linear torsion-spring oscillator with a square-wave modulation of its moment of inertia.

The nonlinear behavior was illustrated by bifurcation diagrams with variation of B for several values C and two values of A near the subharmonic and harmonic resonance. In both cases, the primary bifurcation from the trivial state could be shifted to smaller B and changed from sub- to supercritical by increasing C. In these cases with large C, the former primary bifurcations seem to occur as secondary bifurcations at roughly the same B values as before. Chaotic motion is present in all the cases in the subharmonic instability range but largely absent for those in the harmonic range except for the lowest C. It may well appear for $B>3$, which could be explored further as well as a variation of the parameter D. The periodic orbits obtained in the bifurcation diagrams could also be continued numerically into the unstable parameter range by a shooting method as done in [14]. This could highlight common structures of the solution branches between different values of C further.

We also note that our idealized model configuration must probably be extended to include the mass of the connecting rod and friction in the bearing in order to compare it with experiments. Nonetheless, the chosen values $D=0.1$ and C up to $10^{-2}$ would be fairly realistic for a table-top experiment. For an effective pendulum length of $L=0.1\, \text {m}$, the magnet radius would be $R=5 \, \text {mm}$. The magnetic moment of the spherical magnet is the product of its magnetization and volume [9], i.e.,

$$\begin{aligned} M=\frac{4\pi R^3 B_r}{3\mu _0}, \end{aligned}$$

where $B_r$ is the remanence of the magnetic material. The parameter C then reads

$$\begin{aligned} C= \frac{D^3}{\tau \omega }\qquad \text {with} \qquad \tau =\frac{96\varrho }{B_r^2\sigma }, \end{aligned}$$

where the time constant $\tau$ depends only on the material properties of the bob and the plate. The remanence of typical permanent magnets is in the range between $0.2\, \text {T}\le B_r\le 1.3\, \text {T}$ and their densities $\varrho$ in the interval $5 \times \, 10^3\,\text {kg}\,\text {m}^{-3}\le \varrho \le 8 \times \, 10^3\, \text {kg}\,\text {m}^{-3}$. For a copper plate with conductivity $\sigma \approx 6\times 10^7\,\text {S}\,\text {m}^{-1}$, the time constant can take values $8\, \text {ms} \le \tau \le 200 \, \text {ms}.$ For harmonic resonance, the excitation frequency $\omega$ is approximately the eigenfrequency $\Omega _0\approx 10/\text {s}$. With these assumptions, we find that the interaction parameter takes values $0.0005 \le C\le 0.0125$.

The limitation of the quasistatic approximation [23, 24] is hard to overcome. In principle one has to solve the time-dependent induction equation in the plate to find the eddy currents. When a thin plate is assumed, it may be possible to use Maxwell’s receding image solution for the induced currents [25, 26]. The electromagnetic torque at a given instant would then be a functional of the earlier time-dependent position and velocity of the magnet.

A Leading Fourier coefficients of the functions \(f_1\) and \(f_2\)

For the case of spanwise dipole moment together with the limiting geometric constraint $S=B+D$

$$\begin{aligned} d_0= & {} \gamma \,\frac{B^2+2 (B+D)^2}{4 (D (2 B+D))^{5/2}},\\ d_1= & {} -\gamma \,\frac{3 B (B+D)}{2 (D (2 B+D))^{5/2}},\\ d_2= & {} -\gamma \, \frac{3 B^2}{2 (D (2 B+D))^{5/2}},\\ e_1= & {} -\frac{2 B}{(D (2 B+D))^{3/2}},\\ e_2= & {} \frac{8}{B^2} +\frac{4 (B+D) \left( B^2-4 B D-2 D^2\right) }{B^2 (D (2 B+D))^{3/2}}, \end{aligned}$$

where $\gamma = \frac{1}{2}\left( 1+\sqrt{1-\frac{2 D^2}{5}}\right)$.