Distributed robust control for a class of semilinear fractional-order reaction–diffusion systems

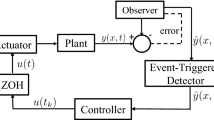
Abstract

This paper is devoted to considering the problem of distributed robust Mittag–Leffler (M–L) stabilization for a class of semilinear fractional-order reaction–diffusion systems (FRDSs), in which the controllers and sensors are discretely distributed in space. In the case of the controllers and the sensors being collocated, the distributed robust control law is directly designed according to the measurements of the corresponding sensors. However, when they are non-collocated, i.e., the measurement information of the sensors cannot be directly used in the control design, which brings additional difficulties to the design of the controllers. To overcome the previous difficulties, an extended Luenberger-type observer is constructed, and then, based on the observer measurement information, a distributed robust controller is designed. For the above two cases, sufficient conditions are all presented in terms of linear matrix inequalities (LMIs) to ensure the M–L stability of the closed-loop system. Finally, simulation results on the control of the semilinear FRDSs illustrate the effectiveness of the proposed design method.

Appendix A

Before proving Lemma 2.1, a few definitions that need to be used are given first.

Definition A.1

(See [39].) The fractional integral of order $\alpha$ with the lower limit zero for a function f is defined as:

$$\begin{aligned}&I^{\alpha }f(t)=\frac{1}{\Gamma (\alpha )}\int _{0}^{t}(t-s)^{\alpha -1}f(s)ds,\\&\quad t\ge 0, \quad 0<\alpha <1, \end{aligned}$$

provided the right-hand side is pointwise defined on $[0,\infty )$, where $\Gamma (\cdot )$ is the Gamma function.

Definition A.2

(See [39]) Riemann–Liouville derivative of order $\alpha$ with the lower limit zero for a function f can be written as: as

$$\begin{aligned}&{}^{L}D^{\alpha }f(t)=\frac{1}{\Gamma (1-\alpha )}\frac{d}{dt}\int _{0}^{t}(t-s)^{-\alpha }f(s)ds,\\&\quad t\ge 0, \quad 0<\alpha <1. \end{aligned}$$

Definition A.3

(See [40]) The Caputo derivative of order $\alpha$ for a function f can be written as:

$$\begin{aligned}&{}^{c}D^{\alpha }f(t)= {^{L}D^{\alpha }}(f(t)-f(0)), \\&\quad t\ge 0, \quad 0<\alpha <1. \end{aligned}$$

Proof of Lemma 2.1: As cited in [17], by using the definitions of operator ${\mathcal {A}}$ and ${\textbf {B}}$, the abstract evolution equations of (1)–(3) in ${\mathcal {H}}$ can be written as:

$$\begin{aligned} _{0}^{c} D_{t}^{\alpha }v(\cdot ,t)&={\mathcal {A}}v(\cdot ,t)+f(v(\cdot ,t))\nonumber \\&\quad +{\textbf {B}}{} {\textbf {u}}(t), t>0, , \end{aligned}$$

(A.1)

$$\begin{aligned}&v(\cdot ,0)=v_{0}. \end{aligned}$$

(A.2)

The following proof consists of two parts:

Part 1. According [41] and the Definition A.1–Definition A.3, it is suitable to rewrite the problem (A.1)–(A.2) in the equivalent integral equation

$$\begin{aligned} v(\cdot ,t)&= v_{0}+\frac{1}{\Gamma (\alpha )}\int _{0}^{t}(t-s)^{\alpha -1}\nonumber \\&\quad \bigg [{\mathcal {A}}v(\cdot ,s)+f(v(\cdot ,s))+{\textbf {B}}{} {\textbf {u}}(s)\bigg ]ds, \end{aligned}$$

(A.3)

provided that the integral in (A.3) exists. According to Lemma 2.1 in [41], we have a conclusion that if (A.3) holds, then

$$\begin{aligned}&v(\cdot ,t)=\int _{0}^{\infty }\vartheta _{\alpha }(\zeta )\Phi (t^{\alpha }\zeta )d\zeta v_{0}\nonumber \\&\qquad +\alpha \int _{0}^{t}\int _{0}^{\infty }\frac{\zeta \vartheta _{\alpha }(\zeta )\Phi ((t-\tau )^{\alpha }\zeta )}{(t-\tau )^{1-\alpha }}d\zeta (f(v(\cdot ,\tau ))\nonumber \\&\qquad +{\textbf {B}}{} {\textbf {u}}(\tau ))d\tau , \end{aligned}$$

(A.4)

that is, the expression (5) is the mild solution of (A.1)–(A.2), where $\vartheta _{\alpha }(t)=\alpha ^{-1}t^{-1-\frac{1}{\alpha }}\psi _{\alpha }(t^{-\frac{1}{\alpha }})$ and $\psi _{\alpha }(t)$ is the one-side stable probability density and can be chosen as: $\psi _{\alpha }(t)=\sum _{n=1}^{+\infty }\frac{(-1)^{n-1}\sin (n\alpha \pi )\Gamma (n\alpha +1)}{\pi t^{\alpha n+1}n!},t>0$ (see [42]).

Next, we give the proof of (A.4) by using the method in [39,40,41].

Set $\breve{v}(\lambda )=\int _{0}^{\infty }e^{-\lambda t}v(\cdot ,t)dt$, $\breve{f}(\lambda )=\int _{0}^{\infty }e^{-\lambda t} f(v(\cdot ,t))dt$, $\breve{{\textbf {u}}}(\lambda )=\int _{0}^{\infty }e^{-\lambda t}{} {\textbf {u}}(t)dt$. Utilizing the similar method in [44] and applying the Laplace transform to (A.3), we have

$$\begin{aligned} \breve{v}(\lambda )=\frac{1}{\lambda }v_{0}+\frac{1}{\lambda ^{\alpha }}{\mathcal {A}}\breve{v}(\lambda )+\frac{1}{\lambda ^{\alpha }}\breve{f}(\lambda )+\frac{1}{\lambda ^{\alpha }}{} {\textbf {B}}\breve{{\textbf {u}}}(\lambda ), \end{aligned}$$

then

$$\begin{aligned}&\breve{v}(\lambda )=\lambda ^{\alpha -1}(\lambda ^{\alpha }I-{\mathcal {A}})^{-1}v_{0}\nonumber \\&\qquad +(\lambda ^{\alpha }I-{\mathcal {A}})^{-1}\breve{f}(\lambda )+(\lambda ^{\alpha }I-{\mathcal {A}})^{-1}{} {\textbf {B}}\breve{{\textbf {u}}}(\lambda )\nonumber \\&\quad =\lambda ^{\alpha -1}\int _{0}^{\infty }e^{-\lambda ^{\alpha }s}\Phi (s)v_{0}ds\nonumber \\&\qquad +\int _{0}^{\infty }e^{-\lambda ^{\alpha }s}\Phi (s)\breve{f}(\lambda )ds\nonumber \\&\qquad +\int _{0}^{\infty }e^{-\lambda ^{\alpha }s}\Phi (s){\textbf {B}}\breve{{\textbf {u}}}(\lambda )ds, \end{aligned}$$

(A.5)

where I is the identity operator.

Consider the one-side stable probability density [42]

$$\begin{aligned} \psi _{\alpha }(t)=\sum _{n=1}^{+\infty }\frac{(-1)^{n-1}\sin (n\alpha \pi )\Gamma (n\alpha +1)}{\pi t^{\alpha n+1}n!},t>0, \end{aligned}$$

whose Laplace transform is given by

$$\begin{aligned}&\int _{0}^{\infty }e^{-\lambda s}\psi _{\alpha }(s)ds\nonumber \\&\quad =e^{-\lambda ^{\alpha }}, \alpha \in (0,1). \end{aligned}$$

(A.6)

Thus, we get

(A.7)

and

(A.8)

Similarly, we have

$$\begin{aligned}&\int _{0}^{\infty }e^{-\lambda ^{\alpha }s}\Phi (s){\textbf {B}}\breve{{\textbf {u}}}(\lambda )ds\nonumber \\&\quad =\int _{0}^{\infty }e^{-\lambda t}\nonumber \\&\qquad \bigg (\alpha \int _{0}^{t} \int _{0}^{\infty }\frac{(t-\theta )^{\alpha -1}}{s^{\alpha }} \psi _{\alpha }(s)\Phi \nonumber \\&\qquad \bigg (\frac{(t-\theta )^{\alpha }}{s^{\alpha }}\bigg ){\textbf {B}}{} {\textbf {u}}(\theta )ds d\theta \bigg )dt. \end{aligned}$$

(A.9)

Substituting (A.7)–(A.9) into (A.5), it gives

$$\begin{aligned} \breve{v}(\lambda )&=\int _{0}^{\infty }e^{-\lambda t}\bigg (\int _{0}^{\infty }\psi _{\alpha }(s)\Phi \bigg (\frac{t^{\alpha }}{s^{\alpha }}\bigg )v_{0}ds\nonumber \\&\quad +\alpha \int _{0}^{t} \int _{0}^{\infty }\frac{(t-\theta )^{\alpha -1}}{s^{\alpha }} \psi _{\alpha }(s)\Phi \bigg (\frac{(t-\theta )^{\alpha }}{s^{\alpha }}\bigg )\nonumber \\&f(v(\cdot ,\theta ))ds d\theta \nonumber \\&\quad +\alpha \int _{0}^{t} \int _{0}^{\infty }\frac{(t-\theta )^{\alpha -1}}{s^{\alpha }} \psi _{\alpha }(s)\Phi \bigg (\frac{(t-\theta )^{\alpha }}{s^{\alpha }}\bigg )\nonumber \\&{\textbf {B}}{} {\textbf {u}}(\theta )ds d\theta \bigg )dt. \end{aligned}$$

(A.10)

Taking the inverse Laplace transform of (A.10), then, it gives

$$\begin{aligned} v(\cdot ,t)&= \int _{0}^{\infty }\psi _{\alpha }(s)\Phi \bigg (\frac{t^{\alpha }}{s^{\alpha }}\bigg )v_{0}ds\\&\quad +\alpha \int _{0}^{t} \int _{0}^{\infty }\frac{(t-\theta )^{\alpha -1}}{s^{\alpha }} \psi _{\alpha }(s)\Phi \bigg (\frac{(t-\theta )^{\alpha }}{s^{\alpha }}\bigg )\\&\quad \bigg (f(v(\cdot ,\theta ))+{\textbf {B}}{} {\textbf {u}}(\theta )\bigg )ds d\theta \\&=\int _{0}^{\infty }\vartheta _{\alpha }(\zeta )\Phi (t^{\alpha }\zeta )d\zeta v_{0}\\&\quad +\alpha \int _{0}^{t}\int _{0}^{\infty }\frac{\zeta \vartheta _{\alpha }(\zeta )\Phi ((t-\tau )^{\alpha }\zeta )}{(t-\tau )^{1-\alpha }}d\zeta (f(v(\cdot ,\tau ))\\&\quad +{\textbf {B}}{} {\textbf {u}}(\tau ))d\tau , \end{aligned}$$

where $\vartheta _{\alpha }(t)=\alpha ^{-1}t^{-1-\frac{1}{\alpha }}\psi _{\alpha }(t^{-\frac{1}{\alpha }})$.

Part 2. There is a unique $v(\cdot ,t)$ such that Eq. (A.4) holds.

First, the operator ${\mathcal {F}}$ is defined as ${\mathcal {F}}: C([0,T]; L^{2}(0,1))\rightarrow C([0,T]; L^{2}(0,1))$, then (A.4) can be written as:

$$\begin{aligned}&({\mathcal {F}}v)(t)={\mathcal {P}}(t) v_{0}+\alpha \int _{0}^{t}{\mathcal {Q}}(t-\tau ) (f(v(\cdot ,\tau ))\nonumber \\&\qquad +{\textbf {B}}{} {\textbf {u}}(\tau ))d\tau , \ \ t\in [0,T], \end{aligned}$$

(A.11)

where ${\mathcal {P}}(t)\triangleq \int _{0}^{\infty }\vartheta _{\alpha }(\zeta )\Phi (t^{\alpha }\zeta )d\zeta$ and ${\mathcal {Q}}(t)\triangleq \int _{0}^{\infty }\frac{\zeta \vartheta _{\alpha }(\zeta )\Phi (t^{\alpha }\zeta )}{t^{1-\alpha }}d\zeta$.

Since semigroup $\Phi (t)$ is uniformly bounded analytic semigroup, there exists $\bar{{\mathcal {M}}}>0$ such that $\parallel \Phi (t)\parallel \le \bar{{\mathcal {M}}}$ (see [45]), Meanwhile, we have $\vartheta _{\alpha }(\zeta )>0$ and $\int _{0}^{\infty }\zeta \vartheta _{\alpha }(\zeta )d\zeta =\frac{1}{\Gamma (1+\alpha )}$ (see [46]). Then, when ${\textbf {u}}(t)=0$, for any $u, v \in C([0,T]; L^{2}(0,1))$,

$$\begin{aligned}&\parallel ({\mathcal {F}}u)(t)-({\mathcal {F}}v)(t)\parallel _{L^2(0,1)}\nonumber \\&\quad \le \frac{\alpha \chi \bar{{\mathcal {M}}}}{\Gamma (1+\alpha )}\nonumber \\&\quad \int _{0}^{t}(t-\tau )^{\alpha -1}\parallel u(\cdot ,\tau )-v(\cdot ,\tau )\parallel _{L^2(0,1)} d\tau \nonumber \\&\quad \le \frac{\alpha \bar{{\mathcal {M}}}\chi \parallel u-v\parallel _{C([0,T];L^2(0,1))}}{\Gamma (1+\alpha )}\nonumber \\&\quad \int _{0}^{t}(t-\tau )^{\alpha -1}d\tau \nonumber \\&\quad \le \frac{\bar{{\mathcal {M}}}\chi T^{\alpha }}{\Gamma (1+\alpha )}\parallel u-v\parallel _{C([0,T];L^2(0,1))}, \end{aligned}$$

(A.12)

where $T\le (\frac{\Gamma (1+\alpha )}{\bar{{\mathcal {M}}}\chi })^{\frac{1}{\alpha }}$ and $\chi >0$ is the Lipschitz constant. Then, by (A.12), one can derive $\Vert {\mathcal {F}}u-{\mathcal {F}}v\Vert _{C([0,T],L^2(0,1))}\le \frac{\bar{{\mathcal {M}}}\chi T^{\alpha }}{\Gamma (1+\alpha )}\Vert u-v\Vert _{C([0,T],L^2(0,1))}$.

Thus, according to the Banach fixed-point theorem—the contraction mapping principle [47], there exists unique fixed point $v\in C([0,T]; L^{2}(0,1))$ such that ${\mathcal {F}}v=v$, namely, Eq. (A.4) has a unique solution $v\in C([0,T];L^2(0,1))$. Based on the Lemma on the extension of solutions, it can be concluded that Eq. (A.4) exists unique solution on $(0, +\infty )$. So this proves the existence and uniqueness of solutions to equation (A.1)–(A.2). When ${\textbf {u}}(t)\ne 0$, define the operator ${\mathfrak {c}}\in \mathrm {L}({\mathcal {H}}, {\mathbb {R}}^{m})$ as ${\mathfrak {c}}v(\cdot ,t)\triangleq \int _{0}^{1}{\varvec{c}}(s)v(s,t)ds$. Evidently, the operator ${\textbf {B}}{\varvec{K}}{\mathfrak {c}}$ is a bounded one. With the help of the idea in [48, 49], we can get the conclusion according to the similar proof process above, so it is omitted. In this way, we have completed the proof.