Nonlinear vibrations of a misaligned bladed Jeffcott rotor

Abstract

This paper describes the numerical and experimental investigation of the nonlinear vibration of a bladed Jeffcott rotor. The nonlinearity in the system is due to discontinuities caused by multiple contacts with an outer ring as well as the nonlinear deformation of the massless blades. Contacts occur since the rotor shaft is initially misaligned by displacing the outer ring in one direction. The aim of the paper is to develop a simple model of bladed rotor and verify whether the global dynamics of the numerical simulations can be observed experimentally. The experimental rig and data acquisition are presented in detail together with the experimental procedures. The results between the numerical simulation and experiments are compared in terms of bifurcation diagrams and waterfall plots. An overall correlation is observed between the numerical and experimental study in the case of stiff blades, with differences mainly in localized frequency ranges due to parameter variation.

1 Introduction

Rotor-to-stator rubbing is a malfunction that can occur in rotordynamics due to small clearances of the system. The main property of this interaction is an intermittent stiffness change since multiple contacts occur during operation. It is known that very complex dynamic behaviour can occur in the case of non-smooth nonlinearities. It can even lead to a high level of vibrations or machine failure in the worst-case scenario. As a result, it is necessary to model and verify experimentally the different types of dynamics that can appear in rotating machinery.

In rotating systems, most of the rotor-to-stator rubbing has been studied by assuming cylinder-to-cylinder rubbing. The experimental validation of numerical simulations has usually been observed on simple mathematical models. Karpenko et al. [1–3] found a positive correlation between analytical, numerical and experimental bifurcation diagrams of a Jeffcott rotor with a preloaded snubber ring. Gonsalves et al. [4] developed a model of discontinuous Jeffcott rotor subjected to mass-unbalance forces. As a preliminary study, they found that the orbit plots and waterfall diagrams of the experimental rig and numerical simulations were similar. Chu and Lu [5] observed experimentally different types of motion for a rotor-to-stator full rub in single and multi-discs rotors. Qin et al. [6] investigated the contact of an overhung rotor as function of rotating speed, unbalance and external damping using the transfer matrix method. Behzad et al. [7] developed a model of rigid rotor contacting a discretized stator using the Lagrange multiplier technique to solve the constraint equation during contact. Roques et al. [8] also investigated rubbing caused by accidental unbalance using a Lagrange multiplier approach and prediction-correction marching procedure. In general, the experimental study confirms the numerical simulation for simple models, but a comparison of bifurcation diagrams is rarely performed in order to obtain the whole system’s behaviour.

Contrary to cylinder-to-cylinder rubbing, fewer studies have been performed in the case of the blade tip–rub interaction. Padovan and Choy [9] developed a blade-to-stator contact model with large linear kinematics where they investigated the influence of several parameters such as friction, blade stiffness and unbalance. When the blade tip exceeds the clearance, Sinha [10] modelled a radial force by applying a summation of compressive buckling loads for a simple beam column. In this case, the transient response of a decelerating rotor is calculated and rubbing occurs momentarily when going through resonance. This study gives an upper bound of the order of the magnitude of impact loads. Legrand et al. [11] also provided complete finite element model that describes contacts between the blades and casing due to modal interaction of each structure combined with small clearances. Legrand et al. [12] developed another model with three dimensional kinematics of the contact phenomenon by using the Lagrange multiplier and B-splines of the contact surface. Jacquet-Richardet et al. [13] gave a review of these models and results which synthesize blade tip–rub interaction and rotor-to-stator contacts. Chen [14] evaluated the blade-casing rubbing fault by studying the effects of the number of blades on the casing signal’s characteristics. The results can be used to detect faults when blade contacts occur in rotating machines.

In general, these models can be used to analyse a rotor system with a fixed set of parameters due to the complex modelling, but it lacks the information of global dynamics that can occur in bladed rotors. It also misses the experimental verification of these numerical models. Nonetheless, a rubbing Jeffcott rotor with three blades has been developed by Aidanpää and Lindkvist [15]. In this model, the elastic and massless blades enter in contact with an outer ring due to an initial misalignment of the rotor. It was shown that complex dynamics can occur below the natural frequency at integer fractions of $\omega _{n}/3$. Thiery and Aidanpää [16] developed a simpler model with rigid blades contacting a massless ring. They showed that the same characteristics occur with only differences in localized frequency ranges. This paper describes in details the nonlinear beam contact model and verifies experimentally the global properties of a simple bladed rotor found numerically. The experimental data have been collected using Labview which allows to create the FFT spectra, time series, orbit plots, Poincaré sections, and most importantly waterfall plots and bifurcation diagrams that are compared with the numerical simulations.

Fig. 1

a Jeffcott rotor. b Top view of the bladed model. c Blade impact geometry

2 Model description

2.1 Simplified Jeffcott rotor

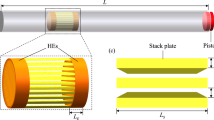
The model of the bladed Jeffcott rotor is given in Fig. 1a, b. The mass of the rotor is m with external damping c and stiffness $k_{s}$ for the shaft. The three massless blades are equally spaced and of length L, Young’s modulus E and area moment of inertia I. The blades rotate in a fixed rigid ring of radius R, while the rotor has an angular velocity $\omega$. When the blades enter in contact with the outer ring, the contact forces are described by a force F normal to the circle delimited by the ring, and a tangential force $\mu F$ at the contact point where $\mu$ is a friction coefficient (Coulomb friction). The blades are supposed to remain elastic during contact and do not enter plasticity. The choice of using a Jeffcott rotor with massless blades is determined by different reasons. First of all, the usefulness of the Jeffcott model is to decrease the number of degrees of the system to the minimum possible without losing the fundamental properties of a rotor. Hence, it allows to perform fast simulations and to scale the equations of motion with regard to the fundamental mode of vibration. Secondly, the main advantage of using massless blades is to avoid the influence of parametric excitation induced by rotating beams in order to focus on the nonlinear vibrations induced by the multiples contacts of the nonlinear spring modelling of the beam.

2.2 Contact forces model

The contact forces during blade impacts will be derived in the fixed coordinate system (O,$\mathbf {i}$,$\mathbf {j}$). A contact occurs for the kth blade when $\Vert \mathbf r _{k}\Vert =R$ due to the geometrical limitation from the stator. The position of the tip of the blade is given by:

$$\begin{aligned} \mathbf r _{k}= & {} (x+(L-\delta ) \cos (\varphi _{k})+\Delta \sin (\varphi _{k}))\mathbf i \nonumber \\&+(y+y_{0}+(L-\delta ) \sin (\varphi _{k})-\Delta \cos (\varphi _{k}))\mathbf j \end{aligned}$$

(1)

where $\Delta$ and $\delta$ are the transversal and axial deformation necessary to keep the blades within the stator, $y_{0}$ is the initial misalignment of the rotor, and $\varphi _{k} = \omega t+2\pi (k-1)/n_{\textsf {blade}}$ is the phase of the kth blade where $n_{\textsf {blade}}$ is the number of blades in the system. The deformation of the cantilever blade is given by the nonlinear beam theory as follows

$$\begin{aligned} w''(\varepsilon )=\dfrac{F}{E I} (1+w'(\varepsilon )^{2})^{3/2} ((\Delta -w(\varepsilon ))+\mu (L-\varepsilon -\delta )) \end{aligned}$$

(2)

where the symbol $'$ denotes differentiation with respect to $\varepsilon$, with the beam being clamped at one side ($\varepsilon =0$), and subjected to F and $\mu F$ at the free end ($\varepsilon =L-\delta$). A detailed description of the impact formulation is given in Fig. 1c. The process used to find the contact forces can be described as follows:

• Step 0: For a fixed set of parameters of the blade, the nonlinear beam equation Eq. (2) is integrated numerically. The displacements $\delta$ and $\Delta$ can be described as a function of F, i.e $\delta = g_{1}(F)$ and $\Delta =g_{2}(F)$. An example of these two numerical functions can be seen in Fig. 2. They also depend on the blade geometry and material properties, so that these functions should be re-calculated when changing the blade dimensions.

• Step 1: For the rotating bladed system, the contact condition of the k-th blade is found when $\Vert \mathbf r _{k}\Vert =R$. This creates a force F initialized to a small, but strictly positive value.

• Step 2: From the initial value of F, the displacements $\delta$ and $\Delta$ can be found by interpolating the function $g_{1}(F)$ and $g_{2}(F)$ using Fig. 2.

• Step 3: The norm of the position of the blade tip $\Vert \mathbf r _{k}(\delta ,\Delta )\Vert$ is calculated using Eq. (1) to verify whether the beam length geometrically fits the outside ring (Fig. 1c) using the couple of displacements $(\delta ,\Delta )$ found in Step 2.

  If $\Vert \mathbf r _{k}(\delta ,\Delta )\Vert > R$, the force is updated with $F \leftarrow F+dF$ where dF is a small increment and we return to Step 2 using this new force F.

• Final step: The process is iterated until $\Vert \mathbf r _{k}(\delta ,\Delta )\Vert = R$. When this condition is achieved, the latest increment of the force F will be used in the calculation of the normal and tangential force applied to the Jeffcott rotor.

Fig. 2

Representation of the axial displacement $\delta$ and transversal displacement $\Delta$ as function of the force F

In our model, we assume that the angle $\alpha = \varphi _{k}-\Phi$ is small so that the normal force points towards O (see “Appendix”). As a result, one can write the normal force $\mathbf {F_{n}}=F \, \mathbf n$ with $\mathbf n$ as a normal unit vector pointing outwards from the centre of the ring. $\mathbf n$ can be written $\mathbf n =\mathbf r _{k}/\Vert \mathbf r _{k}\Vert$ in the fixed coordinate system. The tangential force is a Coulomb frictional force $\mathbf {F_{t}}=-\mu \;{\mathrm {sgn}}(v_{c_{k}}) F \, \mathbf t$ where $\mathbf t$ is the tangential unit vector at the contact point obtained from a rotation of angle $+\pi /2$ of $\mathbf n$. The tangential contact velocity is obtained from $v_{c_{k}}= \dot{\mathbf {r}} \cdot \mathbf t$. The resulting forces for the kth blade in the x and y direction are derived by projecting the normal and tangential forces on $\mathbf {i}$ and $\mathbf {j}$, respectively, i.e.

$$\begin{aligned} \left\{ \begin{aligned} F_{x_{k}}=(\mathbf F _{n}^{k}+\mathbf F _{t}^{k})\cdot \mathbf i = F \; \mathbf n \cdot \mathbf i - \mu \;{\mathrm {sgn}}(v_{c_{k}}) F \; \mathbf t \cdot \mathbf i \\ F_{y_{k}}= (\mathbf F _{n}^{k}+\mathbf F _{t}^{k})\cdot \mathbf j = F \; \mathbf n \cdot \mathbf j - \mu \;{\mathrm {sgn}}(v_{c_{k}}) F \; \mathbf t \cdot \mathbf j \end{aligned} \right. \nonumber \\ \end{aligned}$$

(3)

where F corresponds to the last iteration performed which satisfies $\Vert \mathbf r _{k}(\delta ,\Delta )\Vert = R$ as described in the iteration process. For a total number of blades $n_{\textsf {blade}}$, and assuming that several blades can enter in contact at the same time, the equation of motion can be written

$$\begin{aligned} \left\{ \begin{aligned} \ddot{x}+2 \zeta \omega _{n} \dot{x}+\omega _{n}^{2} x= -\dfrac{1}{m}\sum _{k=1}^{n_{\textsf {blade}}} F_{x_{k}} \\ \ddot{y}+2 \zeta \omega _{n} \dot{y}+\omega _{n}^{2} y= -\dfrac{1}{m}\sum _{k=1}^{n_{\textsf {blade}}} F_{y_{k}} \\ \end{aligned} \right. \end{aligned}$$

(4)

where $\omega _{\textsf {n}}=\sqrt{k/m}$ is the natural frequency of the rotor and $\zeta =c/(2\sqrt{km})$ the damping ratio. During free flight motion, the forces $F_{x_{k}}$ and $F_{y_{k}}$ are set to 0. Equation (4) is then normalized with regard to the bending mode of vibration of the Jeffcott rotor and ready to be numerically solved.

Fig. 3

Bifurcation diagram of the bladed Jeffcott rotor with nonlinear beam deformation with $R=0.11, L=0.1, \delta _{c}=0.01, m=1,\omega _{n}=10, \zeta =0.1, \mu =0.1, E=206 \times 10^{9}, I=0.01 \times 0.001^{3}/12$ and $y_{0}=0.01001$

2.3 Simulation methods and general results

Equation (4) is written in the state-space form and solved using a fourth-order Runge–Kutta integration with adaptive time step in-house code implemented in Fortran. For bifurcation diagrams, 100 Poincaré sections were collected after simulating 200 periods for a given normalized frequency $\varOmega =\omega /\omega _{n}$. In this model, the state-space dimension is 5 ($\mathbb {R}^{4} \times \mathbb {S}$) with displacements x and y, velocities $\dot{x}$ and $\dot{y}$, and the phase $\varphi =\varOmega t$. The Poincaré sections are retrieved at a constant phase $\theta _{p}=2 \pi$ in the state space. To plot the bifurcation diagrams, 1000 steps are used for the normalized frequency range. The final state vector of a simulation at a given frequency is used as the initial condition for the following one in order to find stable solutions over the whole studied range. When the parameters are not specified, the following values have been used by default: $R=0.11, L=0.1, \delta _{c}=0.01, m=1, \omega _{n}=10, \zeta =0.1, \mu =0.1, E=206 \times 10^{9},I=0.01 \times 0.001^{3}/12$ and $y_{0}=0.01001$. The bifurcation diagram in Fig. 3 shows four dominant regions. A periodic region $\textcircled {1}$ appears until 1 / 3 of the natural frequency. Since the displacements are low in this region, the first zoom view allows to distinguish different types of motion depending on the rotor speed. From $\varOmega \simeq 1/3$, the periodic region continues with an increase in forces and displacements until it reaches a chaotic region $\textcircled {2}$ with intermittent periodic motions inside. Another periodic region $\textcircled {3}$ appears leading to chaotic region $\textcircled {4}$ by a period-doubling bifurcation at exactly 2 / 3 of the natural frequency. The second zoom view helps to identify the period doubling in Fig. 3. A small parameter variation can locally change the behaviour in any of the region $\textcircled {1}$–$\textcircled {4}$, but the global dynamics remain similar. A numerical simulation shown in Fig. 4a performed for the model developed by [16] with rigid blades impacting a massless ring shows that the system behaves similarly for a damping value $\zeta \le 0.15$. However, a low damping can increase region $\textcircled {2}$ and shorten region $\textcircled {3}$. It can also reveal small chaotic areas in region $\textcircled {1}$. On the contrary, a high damping value tends to attenuate chaotic regions $\textcircled {2}$ and $\textcircled {4}$ until they disappear for higher damping ratios. In Fig. 4b, it is observed that the friction coefficient only locally influences the dynamics of the system with an appearance of chaotic motion in region $\textcircled {1}$ for $0.01 \le \mu \le 0.2$, but the global dynamics properties stay unchanged. From an experimental point of view, unbalance is always present in the rotor even if well-balanced. As a result, additional numerical simulations are performed by taking into account both the misalignment and unbalance forces. The magnitude is increased according to the following values $me = [0; 1 \cdot 10^{-6}; 1 \cdot 10^{-5}; 5 \cdot 10^{-5}; 1 \cdot 10^{-4}]$ kg m corresponding respectively to the cases 1–5 in Fig. 4c. It can be observed that the four regions are still visible for a small unbalance. When the unbalance force is increased, the trigger property at 2/3 of the normalized frequency starts to disappear. A new chaotic region is created in region $\textcircled {3}$, until an entire chaotic region is formed and composed of the three regions $\textcircled {2}$, $\textcircled {3}$ and $\textcircled {4}$. However, the trigger property at 1/3 is always present independently of the unbalance force. A summary of the influence of these parameters on the global behaviour of the rotor is available in Table 1. Since the numerical modelling gives dynamic similarities independently of several parameters, it is of interest to verify whether these inherent properties—such as the threshold values at 1/3 and 2/3 of the normalized frequency and the different regions—can be found experimentally.

Fig. 4

Three dimensional bifurcation diagram: a as function of rotating speed and damping ratio $\xi = [0.05;0.075;0.10;0.125;0.15;0.175]$, b as function of rotating speed and friction $\mu =[0.01;0.05;0.09;0.13;0.17;0.21]$, c as function of rotating speed and unbalance $me = [0; 1 \times 10^{-6}; 1\,\times \,10^{-5}; 5\,\times \,10^{-5}; 1 \times 10^{-4}]$ kg m

Table 1 Influence of different parameters on the dynamics of the rotor

3 Experimental set-up

3.1 Set-up overview

The experimental rig set-up shown in Fig. 5 is composed of a vertical Jeffcott rotor on which a cylinder with three blades is attached. The rotor is supported at both ends on seven-ball bearings manufactured by SKF with reference number 619/8-2RS1. The electric rotor is taken from the Bently Nevada Rotor Kit Model RK 4 equipment, as well as the proximity probes 3300 XL NsV and the asset condition monitoring. The output voltages are read in a NI 9205 Analog Input Module designed by National Instruments connected to a Labview Data Acquisition System. Four proximity probes are installed on the set-up: the first one is used as a speed controller, the second as a key phaser, and the last two are used to record the x and y displacements of the rotor. These displacements measurements are taken at the base of the rotor where an additional cylinder has been placed to avoid the probes interacting with each other. The influence of this cylinder is negligible in terms of dynamical modifications of the system. This cylinder is placed 13 cm above the lower bearing to capture the whole range of displacement at once for the bifurcation diagram. An imposed displacement of 1 mm at the middle of the rotor produces a displacement of 0.45 mm at the measurement cylinder. As a result, the displacement can be scaled approximately by a factor of 2.2 between the bladed cylinder and the measurement cylinder.

Fig. 5

Drawing of the experimental set up

3.2 Parameters insight

As seen in the description, the experimental rotor differs slightly from the numerical model due to assembly and manufacturing reasons, such as the insertion of blades and measurement improvements. The notation is the same as the numerical model, with extra parameters given in Fig. 5. The following parameters have been used in this study: $R=62.5\, \hbox {mm}, L=40\, \hbox {mm}, b=12.7\, \hbox {mm}, h=0.5\, \hbox {mm}, R_{c}=20\, \hbox {mm}, t_{c}=30\, \hbox {mm}, R_{m}=10\, \hbox {mm}, t_{m}=20\, \hbox {mm}, L_{s}=650\, \hbox {mm}, R_{s}=8\, \hbox {mm}$. The misalignment $y_{0}$ is introduced by offsetting the stator with side screws until a slight contact with the blade occurs. The blades are inserted in their respective notches in the cylinder that allows for changing the blade length and clearance. The three blades are adjusted by hand until all of them have the same contact on the left side of the outer ring in Fig. 6. The rotor has to be properly balanced so that the unbalance force generated by the midspan rotor is reasonable to keep the blades in contact with the ring during the entire experiment. The bending frequency and damping ratio associated with the first mode are found by processing the free vibration response. The first natural is equal to $f_{1} \simeq 30.23\, \hbox {Hz}= 1814$ RPM with a damping ratio $\zeta \simeq 0.052$. The friction coefficient is assumed to be $\mu \le 0.2$. Only approximate ranges of these parameters are necessary to ensure the global dynamic properties of the numerical model.

Fig. 6

Top view of the experimental bladed rotor. The side screws allow to displace the outer ring in order to obtain a slight contact area between the blade and the casing on the left side. One screw revolution corresponds to a displacement of 1/10th of a millimetre

Initially, a thickness of 1 mm was chosen to conduct the experiments, but a thick blade would cause high contact forces that could result in the failure of the rotor or the blade due to high stresses. Since the operation is hazardous, it was decided to decrease the blade thickness. Under a value of 0.4 mm, the contact between the blades and the casing would be too smooth, resulting in a disappearance of the chaotic regions. Moreover, in the flexible blade configuration, the overall dynamical properties are more influenced by parameters such as clearance, damping and initial contact condition. As a result, the blade thickness was set to 0.5 mm to reduce the risks of failure during operation, with the advantage of obtaining the specific dynamics of bladed rotors. In this configuration, neither the clearance nor the initial eccentricity plays a major role in the general behaviour of the system. The axial and transversal force-displacement curves for these particular blades are shown in Fig. 2. From a practical point of view, the sharp corners of the blades have been rounded to avoid them from being stuck in the outer casing.

4 Experimental results

To keep the experimental study close to the numerical simulation, the bifurcation diagram was recorded by increasing the rotor speed step by step. The recording process of the displacements has been performed for several rotational speeds within the range [250–1500] RPM by small increments when possible. At each speed, after the transient response dies out, 20 s of recording has been processed corresponding to a minimum of 82 Poincaré sections for the lower speed and 465 for the higher speed. As the rotating speed was not perfectly constant through the simulation due to the blade contacts, the speed was averaged with help of the keyphasor record. The rotating speed can vary between $\pm 3.09$ RPM for the lower case and until $\pm 166.7$ RPM for the upper case, which is not ideal when assuming a constant speed for numerical simulations. Moreover, in some regions, the impacts are more severe. This might cause wear on both the blades and the inner section of the outer ring. These effects might have a significant influence on the friction coefficient.

The first region of periodic motion appears for $\varOmega \in [0.137-0.333]$ in Fig. 7b, c with an appearance of chaotic motion for a low speed at $\varOmega =0.181$. The transition from $\textcircled {1}$ to $\textcircled {2}$ at 1 / 3 of the natural frequency can be observed as suggested in the numerical simulation, even if it enters the chaotic region as a lower speed than expected. The transition between Fig. 7c at $\varOmega =0.34$ and $\varOmega =0.35$ in Fig. 7d also occurs instantaneously rather than with a gradual increase in amplitude. After the periodic motion, a region of chaotic motion is observed for $\varOmega \in [0.35-0.55]$. The maximum displacement is greater at the beginning of the region and tends to decrease afterwards. The region $\textcircled {3}$ starts with a periodic motion, but suddenly jumps to an unexpected region of chaotic motion in the range [0.55–0.58] as seen in Fig. 8a until a periodic region takes over for $\varOmega =0.72$ in Fig. 8b. A last region of chaotic motion is observed for $\varOmega \in [0.65-0.80]$ corresponding to the region $\textcircled {4}$ starting around 2 / 3 of the natural frequency as predicted. There is also a very abrupt increase in displacement for this second transition from Fig. 8c to d, and it continues to grow with the rotation speed. It can be observed that for $\varOmega =0.72$, the displacement becomes too high and cannot be measured because the measurement cylinder is too close to the probes. Hence, the experimental study was stopped at a speed $\varOmega =0.80$ due to the saturated signals. Since the contacts forces in region $\textcircled {4}$ are high, the tip of the blades can lose a lot of material. After performing the bifurcation diagram, we observed that the initial contact was $-0.1$ mm which confirms the material loss. Since the clearance has increased during the experimental procedure, the displacement in Fig. 10a2 has not been normalized with the clearance as for Fig. 10a1. The types of transition found numerically—such as the period doubling at 2/3 of the natural frequency—are impossible to identify since they occur on short range. The comparison of the system dynamics in terms of orbit plots and Poincaré sections is not relevant as a difference in any of the parameters such as unbalance and material loss can give a different behaviour in a localized range. However, a display of the orbits is available in Fig. 9 corresponding to the numerical simulation in each of the four regions with the experimental blades dimensions. One can distinguish two periodic orbits at $\varOmega =0.304$ and $\varOmega =0.605$ and two chaotic orbits at $\varOmega =0.4$ and $\varOmega =0.74$ similarly to Figs. 7 and 8.

Fig. 7

On the left side: plot of the x displacement as function of the time. In the middle: plot of the orbit motion where the Poincaré sections are specified with red dots. On the right side: Fast Fourier Transform of the displacement signal in the x direction. The different cases correspond to the following normalized rotating speeds: a $\varOmega =0.187$, b $\varOmega =0.304$, c $\varOmega =0.335$, d $\varOmega =0.347$

Fig. 8

On the left side: plot of the x displacement as function of the time. In the middle: plot of the orbit motion where the Poincaré sections are specified with red dots. On the right side: Fast Fourier Transform of the displacement signal in the x direction. The different cases correspond to the following normalized rotating speeds: a $\varOmega =0.567$, b $\varOmega =0.605$, c $\varOmega =0.653$, d $\varOmega =0.669$

Fig. 9

Plot of the numerical orbits with experimental blades dimensions at $\varOmega =0.304,\varOmega =0.4,\varOmega =0.605, \varOmega =0.74$ corresponding to the four different regions

In order to compare the waterfall plots and bifurcation diagrams of the numerical simulation and experimental test, an additional numerical simulation is performed corresponding to the experimental conditions. The following parameters have been used: $\delta = 0.35$ mm, $\zeta =5.0\,\%$, with an initial contact $y_{0}\simeq 0.01$ mm. The bifurcation diagrams and waterfall plots of the experimental rotor are given in Fig. 10a2–b2. The rotating speed is normalized with the first experimental bending frequency $\omega _{1}=1814$ RPM. As the Poincaré sections look unclear, the maximum displacement is shown to get a better indication of the type of motion and to compare the results with numerical diagrams. The numerical bifurcation diagram of the 0.5 mm blade in Fig. 10a displays dynamics which are similar to Fig. 3. The properties at 1/3 and 2/3 are visible as well as the four dominant regions. The comparison of the numerical waterfall plot in Fig. 10b1 and the experimental waterfall plot in Fig. 10b2 gives similarities for the global vibration properties. The appearance of a chaotic motion in region $\textcircled {3}$ can be due to unbalance forces as it is shown in Fig. 4c. In Fig. 10b1, the 1$\times$ line refers to the synchronous line excitation since the main peak in the FFT is equal to the rotating speed. Similarly, the 3$\times$ line represents the $3\cdot \varOmega$ excitation line. The appearance of a high peak when entering region $\textcircled {2}$ along the 3$\times$ line is visible in both cases. Moreover, the broadband excitation in the chaotic region $\textcircled {2}$ is centred between the 1$\times$ line and 2$\times$ line. The main difference lies in the appearance of the 1$\times$ excitation line in the experimental diagram due to unbalance forces, but the two chaotic and periodic regions are clearly visible. To reproduce the experiment with the same conditions, new blades need to be used since the clearance has been increased by the material loss. The results usually show a similar behaviour (same order of magnitude for the maximum displacement curve), but the second periodic region is narrow compared with Fig. 10a1. As a general conclusion—for the same experimental conditions—we could observe regions $\textcircled {1}$, $\textcircled {2}$ and $\textcircled {4}$ in most cases as well as the trigger property at 1/3 and 2/3 of the natural frequency of the system. The main differences occur in region $\textcircled {3}$ where the periodicity range changes from one experimental test to another. This difference may be due to the accuracy of the setting of the blades, the initial misalignment or even to a greater material loss during operation.

Fig. 10

(a1) Numerical bifurcation diagram with experimental conditions. The (–) line represents the maximum displacement curve. (b1) Numerical waterfall with experimental conditions, (a2) Experimental bifurcation diagram. The ($-\blacksquare -$) line represents the maximum displacement curve, (b2) Experimental waterfall diagram

5 Conclusion

The aim of this paper was to correlate the global behaviour of a simple bladed rotor both numerically and experimentally. The nonlinearity of the system is due to the blades making multiple contacts with the outer ring as well as the nonlinear deformation of the blade itself. The results presented in this paper are mainly applicable to rotors that run undercritically, i.e. with a rotating speed lower than the frequency of the fundamental mode of vibration. It is typically the case of hydropower rotors which have a low operating speed [17, 18]. Despite the differences between the numerical and experimental case, the sudden jump from periodic to chaotic motion at 1/3 and 2/3 of the natural frequency was observable in both cases. The regions $\textcircled {1}$, $\textcircled {2}$ and $\textcircled {4}$ can be distinguished on the experimental study, but the periodic region $\textcircled {3}$ gives way to a chaotic motion which indicates that unbalance can mostly influence the dynamics of this region without affecting the others. Even if the unbalance force is not desired to evaluate the properties of initially misaligned rotors, it helps to keep contact between the blades and the stator by compensating for the clearance increase due to material loss. Even though the model does not fully describe the blade contact problem due to disregarding the effect of the beam vibration, the parametric excitation induced by the rotating mass or the change of dynamic friction during contact, the simplified model used here still allows to obtain the periodic and chaotic motions with the same FFT signature for the studied speed range. The numerical and experimental waterfall diagrams show that the blade-rubbing response has a specific FFT signal with a broadband excitation close to the natural frequency of the rotor for the second chaotic region, while the beginning of the first chaotic can be observed by the presence of a large peak at a frequency equal to three times the rotating speed. This result is primordial as it can help to diagnose blade rubbing in on-site condition monitoring and to stop the rotor before extreme vibrations occur. Moreover, the identification of periodic regions can be useful when designing new rotors by choosing an appropriate operating speed in order to avoid severe contacts.

Fig. 11

Geometry of a blade submitted to a follower Force $F^{*}$

It should be noted that the present study is more relevant for thick blades. Weak blades—in comparison with the rotor stiffness—tend to change the global inherent properties with the disappearance of the first chaotic region and second chaotic region, but keep the increase in displacement at 1/3 and 2/3 of $\omega _{n}$. For thin blades, initial parameters such as clearance and initial contact also have a great influence on the system dynamics. Several other simplifications can modify the results between the mathematical and experimental model. First of all, the gyroscopic effects and influence of the measurement cylinder are discarded in the mathematical model. Secondly, the blades were assumed to deform elastically through the entire process. Moreover, the vibration of the beam after contact with the casing was not included in the model with the massless assumption, but it would result in a more complicated modelling and longer computational simulations. Thirdly, the wear of the blades and inner part of the outer ring were disregarded. However, the friction coefficient does not play a major role in terms of global behaviour of the rotor. Finally, the material loss at the blade tip increases continuously throughout the experimental procedure which was not modelled numerically. However, since this study is focused on the global behaviour of the system over a wide speed range, no specific comparison was performed between orbit plots and Poincaré sections between the numerical and experimental study. This could be done by improving blade contact modelling as suggested or by using Finite Element models described in the references, and to verify experimentally the model for only a few speeds since parameters can vary when performing bifurcation diagrams. Additional tests can be performed since the same behaviour of global vibrational behaviour can be found numerically for 5, 10 or 50 blades by scaling the rotational speed with the number of blades [19]. An experimental study on a rotor with more blades could be of interest to verify whether the properties found for a three-bladed rotor can be applied to any type of bladed rotor system.

Appendix: Proof of assumption of loads in constant direction

A beam is deformed axially by $\delta$ and laterally by $\Delta$ due to a force $F^{*}$. The beam is subjected to the follower force $F^{*}$ during the whole deformation. However, the analyses of the deformations $\delta$ and $\Delta$ are performed by assuming a non-rotating force. Therefore, it is essential to show that we can assume F to be a non-rotating force. The beam in Fig. 11 is displaced axially by z and compressed axially by $\delta$ due to a force $F^{*}$. The force $F^{*}$ will also cause a transversal displacement.

Using geometrical relations, the angle of rotation $\alpha$ between $F^{*}$ and F is given by:

$$\begin{aligned} \left\{ \begin{aligned} \cos (\alpha )= \dfrac{1}{\sqrt{1+\Big ( \dfrac{\Delta }{z+L-\delta }\Big )^{2}}} \\ \sin (\alpha )= \dfrac{\Delta }{\sqrt{1+\Big ( \dfrac{\Delta }{z+L-\delta }\Big )^{2}}} \\ \end{aligned} \right. \end{aligned}$$

(5)

With the assumption $\Delta<< (z+L-\delta )$, we get $\cos (\alpha ) \approx 1$ and $\sin (\alpha ) \approx 0$. Hence, as long as $\Delta$ is much smaller than the length of the beam L, one can assume that the rotation of the contact force can be neglected. As an example, in the experimental section, we used a blade of length $L=40$ mm, height $h=0.5$ mm and thickness $b=12.7$ mm. The lateral displacement is about 0.001 mm at maximum amplitude of 0.008 m. The numerical application gives $\sin (\alpha )= 7.8*10^{-3}$ and $\cos (\alpha )= 0.98$ for the largest displacements.