Nonsynchronous bifurcation of SIRS epidemic model with birth pulse and pulse vaccination

Abstract

In this paper, we construct an SIRS epidemic model with birth pulse and pulse vaccination at the different fixed moment. The stability of the infection-free periodic solution is obtained by using the Poincaré map. The existence of nontrivial periodic solution bifurcated from the infection-free periodic solution is discussed by means of the bifurcation theory. It is shown that once a threshold is reached, a nontrivial periodic solution emerges via a supercritical bifurcation. Furthermore, some numerical simulations are given, which are in good accordance with the theoretical results.

1 Introduction

Man has been facing a threat of many diseases, such as severe acute respiratory syndrome (SARS) affected in 2003, because environmental destruction is increasingly aggravated. Therefore, it is urgent for us to reveal the propagation mechanism of disease and find an effective prevention measure.

Epidemic models of the impulsive differential equation have been formulated by many researchers [1–5] in the past few years. Zeng [1] studied the epidemic model with the impulsive vaccination and obtained the condition for which infection-free periodic solution was globally asymptotically stable. Pei [2] investigated two delayed SIR models with the impulsive vaccination and a generalized nonlinear incidence. They obtained the sufficient conditions for the eradication and permanence of the disease, respectively. Li [3] formulated SIR and SVS epidemic models with the vaccination and obtained the basic reproduction number determining whether the disease died out or persisted eventually. An impulsive vaccination strategy of the epidemic model with the nonlinear incidence rate $\beta S^2I$ was considered in [4]. Using the discrete dynamical system determined by the stroboscopic map, they obtained the infection-free periodic solution that was globally asymptotically stable. An $SIS$ epidemic model with the impulsive vaccination was investigated in [5], and some results were obtained for the global stability of the infection-free periodic solution and the existence of the nontrivial periodic solution.

In population model, population births are usually assumed to be continuous and time independent. However, population growth rate mostly depends on the numbers of reproducing offsprings, and these births are seasonal or occur in regular pulse. Hence, the continuous reproduction is removed from the model and replaced with an annual birth pulse [6–9]. In [9], authors formulated the following the model:

$$\begin{aligned} \begin{array}{ll} \left. \begin{array}{l@{\quad }l} \frac{\hbox {d}S}{\hbox {d}t}=\sigma S-\beta SI+\delta R,\\ \frac{\hbox {d}I}{\hbox {d}t}=\beta SI-(\gamma +\sigma )I,\\ \frac{\hbox {d}R}{\hbox {d}t}=\gamma I-(\delta +\sigma )I,\\ \end{array} \right\} t\ne nT, \\ \left. \begin{array}{l@{\quad }l} \Delta S=(b-cN)N-pS,\\ \Delta I=0,\\ \Delta R=pS,\\ \end{array} \right\} t\ne nT, \end{array} \end{aligned}$$

(1.1)

where $\Delta S=S(t^+)-S(t),\Delta I=I(t^+)-I(t),\Delta R=R(t^+)-R(t)$, $c=r(b-d)$, $N=S+I+R$. $S(t), I(t)$ and $R(t)$ denote the numbers of susceptible, infective, and removed individual at time $t$, respectively. $\sigma$ is the natural death rate, $\delta$ is the rate at which infective individual loses immunity and returns to the susceptible class, and $\gamma$ is the natural recovery rate of the infective population. Susceptible become infectious at a rate $\beta I$, where $\beta$ is the contact rate. $d$ is the maximum death rate, $r$ is a parameter reflecting the relative importance of density-dependent population regulating through birth and death, and $b$ is the maximum birth rate. At each vaccination time, a constant fraction $p(0<p<1)$ of susceptible population is vaccinated under the impulsive vaccination strategy, and $T$ is the impulsive period. They investigated the existence and stability of the infection-free periodic solution and the nontrivial periodic solution [9].

Recently, many impulsive effects are assumed to occur at the same fixed moment [10–12] for simplicity. Correspondingly, synchronous bifurcation has also been investigated in [10–12]. In fact, all kinds of impulsive effects [13–15] occur at the different fixed moment. Liu [13] introduced an nonsynchronous pulse into $SI$ epidemic model and obtained the disease-free periodic solution that was globally asymptotically attractive. Zhao [14] investigated the inshore–offshore fishing model with the impulsive diffusion and pulsed harvesting at the different fixed time. The existence and stability of both the trivial periodic solution and the positive periodic solution are obtained in [14]. Zhang et al. [15] formulated the integrated pest management of the spraying pesticides and releasing natural enemies at the different fixed moment, and they investigated the stability of the pest-eradication periodic solution and nontrivial periodic solution emerging via a supercritical bifurcation. From the point of the above paper [10–15], nonsynchronous bifurcation is investigated only for two state variables. In this paper, we will investigate the nonsynchronous bifurcation of the three state variables by the impulsive bifurcation theory.

Motivated by [9–15], we introduce the nonsynchronous pulse into the following model:

$$\begin{aligned} \begin{array}{llll} \left. \begin{array}{ll} \!\!\!\displaystyle \frac{\hbox {d}S}{\hbox {d}t}=-\sigma S\!-\!\beta SI\!+\!\delta R,\\ \!\!\!\displaystyle \frac{\hbox {d}I}{\hbox {d}t}=\beta SI\!-\!(\gamma \!+\!\sigma )I,\\ \!\!\!\displaystyle \frac{\hbox {d}R}{\hbox {d}t}=\gamma I-(\delta +\sigma )R,\\ \end{array}\!\!\! \right\} &{} t\ne nT, \quad t\ne (n\!+\!l\!-\!1)T,\!\!\!\\ \left. \begin{array}{ll} \!\!\!\Delta S(t)=bN\hbox {e}^{-N},\\ \!\!\!\Delta I(t)=0,\\ \!\!\!\Delta R(t)=0,\\ \end{array} \right\} &{} t=(n+l-1)T,\\ \left. \begin{array}{ll} \!\!\!\Delta S=-pS,\\ \!\!\!\Delta I=0,\\ \!\!\!\Delta R=pS,\\ \end{array} \right\}&t=nT, \end{array} \end{aligned}$$

(1.2)

$l(0<l<1)$ and $b$ are the positive constants. The meanings of other parameters are the same as system (1.1).

2 The stability of the infection-free periodic solution

Firstly, we give some basic properties about the following subsystem of system (1.2)

$$\begin{aligned} \begin{array}{ll} \left. \begin{array}{ll}\!\!\!\dot{S}(t)=-\sigma S+\delta R, \\ \!\!\!\dot{R}(t)=-(\delta +\sigma )R, \\ \end{array} \right\} &{} t\ne (n+l-1)T,\quad t\ne nT,\!\!\!\\ \left. \begin{array}{ll} \!\!\!\Delta S =bN\hbox {e}^{-N},\\ \!\!\!\Delta R =0,\\ \end{array} \right\} &{} t=(n+l-1)T,\\ \left. \begin{array}{ll} \!\!\!\Delta S =-pS,\\ \!\!\!\Delta R =pS,\\ \end{array} \right\} &{} t=nT,\\ \end{array} \end{aligned}$$

(2.1)

or

$$\begin{aligned} \begin{array}{ll} \left. \begin{array}{ll}\!\!\!\dot{N}(t)=-\sigma N, \\ \!\!\!\dot{R}(t)=-(\delta +\sigma )R, \\ \end{array} \right\} &{} t\ne (n+l-1)T,\quad t\ne nT,\!\!\!\\ \left. \begin{array}{ll} \!\!\!\Delta N =bN\hbox {e}^{-N},\\ \!\!\!\Delta R =0,\\ \end{array} \right\} &{} t=(n+l-1)T,\\ \left. \begin{array}{ll} \!\!\!\Delta N =0,\\ \!\!\!\Delta R =p(N-R),\\ \end{array} \right\} &{} t=nT.\\ \end{array} \end{aligned}$$

(2.2)

We can easily obtain the analytical solution of the system (2.2) on the interval $((n-1)T,nT].$

$$\begin{aligned} \left\{ \begin{array}{lll} N(t)=\left\{ \begin{array}{ll} N((n-1)T^+) \hbox {e}^{-\sigma (t-(n-1)T)}, &{}\quad \quad \quad (n-1)T<t\le (n+l-1)T,\\ (1+ b\exp (-N((n-1)T^+)\hbox {e}^{-\sigma lT})\\ \quad \times N((n-1)T^+)\hbox {e}^{-\sigma (t-(n-1)T)}, &{} \quad \quad \quad (n+l-1)T<t\le nT,\\ \end{array} \right. \\ \begin{array}{ll} R(t)=R((n-1)T^+)\hbox {e}^{-(\sigma +\delta )(t-(n-1)T)},&{}\quad \quad \quad \quad \quad (n-1)T< t\le nT, \end{array} \end{array}\right. \end{aligned}$$

(2.3)

Denote $N(nT^+)=N_{nT},N((n-1)T^+)=N_{(n-1)T}, R(nT^+)=R_{nT},R((n-1)T^+)=R_{(n-1)T},$ we have:

$$\begin{aligned} \left\{ \begin{array}{lll} N_{nT}&{}=&{}N_{(n-1)T}(1+b\exp (-N_{(n-1)T}\hbox {e}^{-\sigma lT}))\hbox {e}^{-\sigma T},\\ R_{nT}&{}=&{}(1-p)R_{(n-1)T}\hbox {e}^{-(\sigma +\delta )T}\\ &{}&{} +\,pN_{(n-1)T}(1+b\exp (-N_{(n-1)T}\hbox {e}^{-\sigma lT}))\hbox {e}^{-\sigma T},\\ \end{array}\right. \nonumber \\ \end{aligned}$$

(2.4)

Equations (2.4) are difference equations. Difference system (2.4) has two fixed points $(0,0)$ and $(N^*, R^*),$ where $N^*=\displaystyle \hbox {e}^{\sigma lT}\ln \frac{b}{\hbox {e}^{\sigma T}-1}$, $R^*=\frac{pN^*}{1-(1-p)\hbox {e}^{-(\sigma +\delta )T}}.$ For each fixed point of difference equations, there is an associated periodic solution of system (2.2) and vice versa. Therefore, the dynamical behavior of system (2.3) is determined through the dynamical behavior of system (2.4) coupled with system (2.3). Thus, in the following, we will focus our attention on the system (2.3) and (2.4).

Next, we consider the stability of the fixed point by means of the characteristic equation. Firstly, the stability of the fixed point $(0,0)$ is determined by the following characteristic equation,

$$\begin{aligned} \left| \begin{array}{ll} \lambda -(1+b)\hbox {e}^{-\sigma \tau } &{}\quad 0\\ -p(1+b)\hbox {e}^{-\sigma \tau } &{}\quad \lambda -(1-p)\hbox {e}^{-(\delta +\sigma )\tau } \end{array} \right| =0. \end{aligned}$$

We obtain $\lambda _1=(1+b)\hbox {e}^{-\sigma \tau },\lambda _2=(1-p)\hbox {e}^{-(\delta +\sigma )\tau },$ $0<\lambda _2<1$ and $0<\lambda _1<1$ for $b<\hbox {e}^{\sigma T}-1.$ Hence, the fixed point $(0,0)$ is stable if $b<\hbox {e}^{\sigma T}-1.$ Similarly, for the fixed point $(N^*, R^*)$, we have

$$\begin{aligned} \left| \begin{array}{ll} \lambda -1+(1-\hbox {e}^{-\sigma \tau })\ln \frac{b}{\hbox {e}^{\sigma \tau }-1} &{}\quad 0\\ * &{}\quad \lambda -(1-p)\hbox {e}^{-(\delta +\sigma )\tau } \end{array} \right| =0, \end{aligned}$$

where the asterisk does not influence on calculating the characteristic root; therefore, there is no need to calculate. From the above characteristic equation, we have $\lambda _3=1-(1-\hbox {e}^{-\sigma \tau })\ln \frac{b}{\hbox {e}^{\sigma \tau }-1},$ $\lambda _4=(1-p)\hbox {e}^{-(\delta +\sigma )\tau }$. It is easy to compute that $0<\lambda _4<1$ and $-1<\lambda _3<1$ hold for $b<(\hbox {e}^{\sigma T}-1)\ln \frac{2}{1-\hbox {e}^{-\sigma T}}$ and $b>\hbox {e}^{\sigma T}-1.$ Therefore, the fixed point $(N^*, R^*)$ is stable for $\hbox {e}^{\sigma T}-1<b<(\hbox {e}^{\sigma T}-1)\ln \frac{2}{1-\hbox {e}^{-\sigma T}}.$ Correspondingly, the infection-free periodic solution $(N*(t), 0, R^*(t))$ of system (1.2) is given by the following form:

$$\begin{aligned} \left\{ \begin{array}{lll} N^*(t)=\left\{ \begin{array}{ll} \displaystyle \hbox {e}^{\sigma lT}\ln \frac{b}{\hbox {e}^{\sigma T}-1} \hbox {e}^{-\sigma (t-(n-1)T)}, &{} \quad (n-1)T<t\le (n+l-1)T,\\ \displaystyle \hbox {e}^{\sigma (l+1)T}\ln \frac{b}{\hbox {e}^{\sigma T}-1}\hbox {e}^{-\sigma (t-(n-1)T)}, &{} \quad (n+l-1)T<t\le nT,\\ \end{array} \right. \\ R^*(t)=\displaystyle \frac{p\hbox {e}^{\sigma l\tau }\ln \frac{b}{\hbox {e}^{\sigma T}-1}}{1-(1-p)\displaystyle \hbox {e}^{-(\delta +\sigma )T}}\hbox {e}^{-(\sigma +\delta )(t-(n-1)T)},\quad (n-1)T< t\le nT, \end{array}\right. \end{aligned}$$

(2.5)

Therefore, we have:

Theorem 2.1

The infection-free periodic solution $(N^*(t)$, $0, R^*(t))$ of system (1.2) is stable for $\hbox {e}^{\sigma T}-1<b<(\hbox {e}^{\sigma T}-1)\ln \frac{2}{1-\hbox {e}^{-\sigma T}}$.

3 The bifurcation of the nontrivial periodic solution

In the following, we will view $b$ as a bifurcation parameter and investigate the bifurcation of the positive periodic solution near the infection-free periodic solution $(N^*(t), 0, R^*(t)).$ From system (1.2) and $N(t)=S(t)+I(t)+R(t),$ system (1.2) may be rewritten as

$$\begin{aligned} \left\{ \begin{array}{llll} \left. \begin{array}{ll} \frac{\hbox {d}R}{\hbox {d}t}=\gamma I-(\delta +\sigma )R,\\ \frac{\hbox {d}I}{\hbox {d}t}=\beta (N-I-R)I\\ \quad \quad \quad -(\gamma +\sigma )I,\!\!\!\\ \end{array} \right\} &{} t\ne nT, \ \ t\!\ne \! (n+l\!-\!1)T,\!\!\\ \left. \begin{array}{ll} \Delta R(t)=0,\\ \Delta I(t)=0,\\ \end{array} \right\} &{} t=(n+l-1)T,\\ \left. \begin{array}{ll} \Delta R=p(N-I),\\ \Delta I=0,\\ \end{array} \right\}&t=nT. \end{array}\right. \end{aligned}$$

(3.1)

To this purpose, we shall employ a fixed point argument. We denote by $\Phi (t, U_0)$ the solution of the (unperturbed) system consisting of the first two equations of (1.2) for the initial data $U_0=(u_0^1,u_0^2);$ also, $\Phi =(\Phi _1, \Phi _2).$ We define the mapping $I_1, I_2: R^2\rightarrow R^2$ by

$$\begin{aligned} I_1(x_1, x_2)&= (x_1, x_2), \\ I_2(x_1, x_2)&= (x_1-px_2+pN, x_2) \end{aligned}$$

and the mapping $F=(F_1, F_2): R^2\rightarrow R^2$ by

$$\begin{aligned} F_1(x_1, x_2)&= \gamma x_2-(\delta +\sigma )x_1,\\ F_2(x_1, x_2)&= \beta (N-x_2-x_1)x_2-(\gamma +\sigma )x_2. \end{aligned}$$

Furthermore, let us define $\Psi : [0, \infty )\times R^2\rightarrow R^2$ by

$$\begin{aligned} \Psi (T, U_0)&= I_2(\Phi ((1-l)T, I_1(\Phi (lT, U_0)))); \\ \Psi (T, U_0)&= (\Psi _1(T,U_0), \Psi _2(T,U_0)). \end{aligned}$$

It is easy to see that $\Psi$ is actually the stroboscopic mapping associated with the system (3.1), which puts in the correspondence the initial data at $0_+$ with the subsequent state of the system $\Psi (T^+, U_0)$ at $T_+,$ where $T$ is the stroboscopic time snapshot.

We reduce the problem of finding a periodic solution of (3.1) to a fixed problem. Here, $U$ is a periodic solution of period $T$ for (3.1) if and only if its initial value $U(0)=U_0$ is a fixed point for $\Psi (T, \cdot )$. Consequently, to establish the existence of nontrivial periodic solutions of (3.1), one needs to prove the existence of the nontrivial fixed point of $\Psi .$

We are interested in the bifurcation of nontrivial periodic solution near $(R^*(t), 0).$ Assume that $X_0=(x_0,0)$ is starting point for the trivial periodic solution $(R^*(t), 0),$ where $x_0=R^*(0^+).$ To find a nontrivial periodic solution of period $\tau$ with initial value $X,$ we need to solve the fixed point problem $X=\Psi (\tau , X),$ or denoting $\tau =T+\widetilde{\tau }, X=X_0+\widetilde{X},$

$$\begin{aligned} X_0+\widetilde{X}= \Psi (T+\widetilde{\tau }, X_0+\widetilde{X}). \end{aligned}$$

Let us define

$$\begin{aligned} N\left( \widetilde{\tau }, \widetilde{X}\right)&= X_0+\widetilde{X}-\Psi \left( T+\widetilde{\tau }, X_0+\widetilde{X}\right) \nonumber \\&= \left( N_1\left( \widetilde{\tau }, \widetilde{X}\right) ,N_1\left( \widetilde{\tau }, \widetilde{X}\right) \right) . \end{aligned}$$

(3.2)

At the fixed point $N(\widetilde{\tau }, \widetilde{X})=0.$ Let us denote

$$\begin{aligned} D_XN(0, (0,0))=\left( \begin{array}{lll} a_0' &{}\quad b_0'\\ c_0' &{}\quad d_0'\\ \end{array} \right) . \end{aligned}$$

It follows that

$$\begin{aligned} a'_0&= 1-\exp (-(\sigma +\delta )T)>0,\end{aligned}$$

(3.3)

$$\begin{aligned} b'_{0}&= \displaystyle -\gamma \left[ \hbox {e}^{-(\delta +\sigma )T}\int _0^{lT} \hbox {e}^{\int _0^s (\beta N(\tau )-\beta R^*(\tau )-\gamma -\sigma )\hbox {d}\tau }\hbox {d}s\right. \nonumber \\&\left. +\,\hbox {e}^{-(\delta +\sigma )(1-l)T}\hbox {e}^{-(\gamma +\sigma )u-\int _0^u( \beta N(\tau )-\beta R^*(\tau ))\hbox {d}\tau }du\right] ,\nonumber \\ \end{aligned}$$

(3.4)

$$\begin{aligned} c_0'&= 0, \end{aligned}$$

(3.5)

$$\begin{aligned} d'_0&= \displaystyle 1- \exp \int _0^{T} (\beta N(t)-\beta R^*(t)-\gamma -\sigma )\hbox {d}t. \end{aligned}$$

(3.6)

(see Appendix $A_1$ for details). A necessary condition for the bifurcation of nontrivial periodic solution near $(R^*(t), 0)$ is then

$$\begin{aligned} \det [D_XN(0, (0,0))]=0. \end{aligned}$$

Since $D_XN(0, (0,0))$ is an upper triangular matrix and $1-\exp (-(\delta +\sigma )T)>0$, it consequently follows that $d_0'=0$ is necessary for the bifurcation. It is easy to see that $d_0'=0$ is equivalent to

$$\begin{aligned}&b=(\hbox {e}^{\sigma T}\!-\!1)\exp \left( \frac{(\sigma +\gamma )T}{\frac{\beta (\hbox {e}^{\sigma T}-1)}{\sigma }+\frac{p\beta \hbox {e}^{\sigma lT} (1-\hbox {e}^{-(\delta +\sigma )T})}{(\delta +\sigma )(1-(1-p)\hbox {e}^{-(\delta +\sigma )T})}}\right) \\&\quad \mathop {=}\limits ^{\Delta }b^*. \end{aligned}$$

It now remains to show that this necessary condition is also sufficient. This assertion represents the statement of the following theorem, which is our main result.

Theorem 3.1

A supercritical bifurcation occurs at $b=b^*$ in system (1.2), in the sense, for $\varepsilon >0$ such that $b\in (b^*,b^*+\varepsilon )$ there is a nontrivial periodic solution.

Proof

With the above notations, it is that

$$\begin{aligned} \dim (\hbox {Ker}[D_XN(0, (0,0))])=1, \end{aligned}$$

and a basis in $\hbox {Ker}[D_XN(0, (0,0))]$ is $(-\frac{b_0'}{a_0'},1).$ Then, the equation $N(\widetilde{\tau }, \widetilde{X})=0$ is equivalent to

$$\begin{aligned} N_1(\widetilde{\tau }, \alpha Y_0+zE_0)=0, N_2(\widetilde{\tau }, \alpha Y_0+zE_0)=0, \end{aligned}$$

where $E_0=(1,0), \ Y_0=(-\frac{b_0'}{a_0'},1).$ $\widetilde{X}=\alpha Y_0+zE_0$ represents the direct sum decomposition of $\widetilde{X}$ using the projections onto $\hbox {Ker}[D_XN(0,(0,0))]$ (the central manifold) and $\hbox {Im}[D_X N(0,(0,0))]$ (the stable manifold).

Let us define

$$\begin{aligned} f_1(\widetilde{\tau }, \alpha , z)&= N_1(\widetilde{\tau }, \alpha Y_0+zE_0), \\ f_2(\widetilde{\tau }, \alpha , z)&= N_2(\widetilde{\tau }, \alpha Y_0+zE_0). \end{aligned}$$

Firstly, we see that

$$\begin{aligned} \frac{\partial f_1}{\partial z}(0,0,0)=\frac{\partial N_1}{\partial x_1}(0,(0,0))=a_0'\ne 0. \end{aligned}$$

Therefore, by the implicit function theorem, one may solve the equation $f_1(\widetilde{\alpha }, \alpha , z)=0$ near $(0,0,0)$ with respect to $z$ as a function of $\widetilde{\tau }$ and $\alpha$ and find $z=z(\widetilde{\tau },\alpha )$ such that $z(0,0)=0$ and

$$\begin{aligned} f_1(\widetilde{\tau },\alpha , z(\widetilde{\tau },\alpha ))=N_1(\widetilde{\tau }, \alpha Y_0+ z(\widetilde{\tau },\alpha )E_0)=0.\nonumber \\ \end{aligned}$$

(3.7)

Moreover,

$$\begin{aligned}&\frac{\partial N_1}{\partial x_1}(0,(0,0))\cdot \left( -\frac{b_0'}{a_0'}\right) + \frac{\partial N_1}{\partial x_2}(0,(0,0)) \\&\quad +\,\frac{\partial N_1}{\partial x_1}(0,(0,0))\cdot \frac{\partial z}{\partial \alpha }(0,0)=0 \end{aligned}$$

and consequently,

$$\begin{aligned} a_0'\left( -\frac{b_0'}{a_0'}\right) +b_0'+a_0'\frac{\partial z}{\partial \alpha }(0,0)=0. \end{aligned}$$

Hence, we obtain that

$$\begin{aligned} \frac{\partial z}{\partial \alpha }(0,0)=0. \end{aligned}$$

Next, we compute $\frac{\partial z}{\partial \widetilde{\tau }}(0,0).$

$$\begin{aligned}&\frac{\partial x_1}{\partial z}\frac{\partial z}{\partial \widetilde{\tau }}(0,0)=\frac{\partial I_2}{\partial x_1}\frac{\partial \Phi _1}{\partial \widetilde{\tau }}((1-l)T,I_1(lT, X_0 )) \\&\quad \cdot \,(1-l)+\frac{\partial I_2}{\partial x_1}\frac{\partial \Phi _1}{\partial x_1}((1-l)T,I_1(\Phi (lT, X_0)))\\&\quad \cdot \left( \frac{\partial \Phi _1}{\partial \widetilde{\tau }}(lT, X_0)\cdot l+ \frac{\partial \Phi _1}{\partial x_1}(lT,X_0)\cdot \frac{\partial z}{\partial \widetilde{\tau }}(0,0)\right) \\&\quad +\,\frac{\partial I_2}{\partial x_1}\frac{\partial \Phi _1}{\partial x_2}((1-l)T,I_1(\Phi (lT, X_0)))\\&\quad \cdot \left( \frac{\partial \Phi _2}{\partial \widetilde{\tau }}(lT, X_0)\cdot l +\frac{\partial \Phi _2}{\partial x_1}(lT, X_0)\frac{\partial z}{\partial \widetilde{\tau }}(0,0)\right) . \end{aligned}$$

We may obtain

$$\begin{aligned}&\frac{\partial z}{\partial \widetilde{\tau }} (0,0)\cdot \left( 1-\frac{\partial \Phi _1}{\partial x_1}((1-l)T,I_1(\Phi (lT, X_0))) \frac{\partial \Phi _1}{\partial x_1}(lT, X_0)\right) \\&\qquad =\frac{\partial \Phi _1}{\partial \widetilde{\tau }}\left( (1-l)T,I_1(\Phi (lT, X_0))\right) \cdot (1-l)\\&\quad \qquad +\,\frac{\partial \Phi _1}{\partial x_1}((1-l)T,I_1(\Phi (lT,X_0)))\frac{\partial \Phi _1}{\partial \widetilde{\tau }}(lT, X_0)\cdot l, \end{aligned}$$

therefore, we have

$$\begin{aligned} \displaystyle \frac{\partial z}{\partial \widetilde{\tau }}(0,0)&= \frac{1}{a_0'}[-(\delta +\sigma )R^*(T)(1-l)\\&+\,\hbox {e}^{-(\delta +\sigma )(1-l)T}R^*(lT)l]\\&= -\displaystyle \frac{\delta +\sigma }{a_0'}R^*(T). \end{aligned}$$

Then $N(\widetilde{\tau },\widetilde{X})=0$ if and only if

$$\begin{aligned} f_2\left( \widetilde{\tau },\alpha \right) =N_2\left( \widetilde{\tau }, \left( -\frac{b_0'}{a_0'}\alpha +z\left( \widetilde{\tau },\alpha \right) , \alpha \right) \right) =0.\nonumber \\ \end{aligned}$$

(3.8)

Equation (3.8) is called the “determining equation,” and the number of its solutions equals the number of periodic solutions of (1.2). We now proceed to solving (3.8). Let us denote

$$\begin{aligned} f(\widetilde{\tau },\alpha )=f_2(\widetilde{\tau },\alpha , z). \end{aligned}$$

Firstly, it is easy to see that $f(0,0)=N_2(0,(0,0))=0.$ We determine the Taylor expansion of $f$ around $(0,0).$ For this, we compute the first-order partial derivatives $\frac{ \partial f}{\partial \widetilde{\tau }}(0,0)$ and $\frac{ \partial f}{\partial \alpha }(0,0)$ and observe that

$$\begin{aligned} \frac{ \partial f}{\partial \widetilde{\tau }}(0,0)=\frac{ \partial f}{\partial \alpha }(0,0)=0. \end{aligned}$$

(see Appendix $A_2$ for the proof of this fact). Furthermore, it is observed in Appendix $A_3$ that

$$\begin{aligned} A&= \frac{\partial ^2 f(0,0)}{\partial \widetilde{\tau }^2}, \ B=\frac{\partial ^2f(0,0)}{\partial \alpha \partial \widetilde{\tau }}<0, \\ C&= \frac{\partial ^2f(0,0)}{\partial \alpha ^2}>0, \end{aligned}$$

and hence

$$\begin{aligned} f\left( \widetilde{\tau }, \alpha \right)&= \frac{\partial ^2f(0,0)}{\partial \alpha \partial \widetilde{\tau } }\alpha \widetilde{\tau }+ \frac{\partial ^2f(0,0)}{\partial \widetilde{\tau }^2} \frac{\alpha ^2}{2}\\&+\,o\left( \widetilde{\tau },\alpha \right) \left( \widetilde{\tau }^2+\alpha ^2\right) . \end{aligned}$$

For $\frac{\partial ^2 f}{\partial \alpha \widetilde{\tau }}(0,0)<0,$ by denoting $\widetilde{\tau }=l\alpha$ (where $l=l(\alpha )$), we obtain that (3.7) is equivalent to

$$\begin{aligned} Bl+C \frac{l^2}{2}+o(l\alpha ,\alpha )(1+l^2)=0. \end{aligned}$$

Since $B<0$ and $C>0$, this equation is solvable with respect to $l$ as a function of $\alpha .$ Moreover, here, $l\approx -\frac{2B}{C}>0,$ which implies that there is a supercritical bifurcation to a nontrivial periodic solution near a period $T$ which satisfies the sufficient condition for the bifurcation $b=b^{*}$. $\square$

4 Discussion

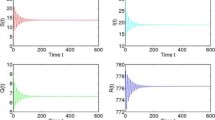
In this paper, an SIRS epidemic model with birth pulse and pulse vaccination is discussed by means of a Poincaré map and bifurcation theory. We obtain the trivial periodic solution that is stable (see Fig. 1) for the birth rate $b<\hbox {e}^{\sigma T}-1,$ which means population tends to extinction, and infection-free periodic solution $(S^*(t),0,R^*(t))$ is asymptotically stable for $\hbox {e}^{\sigma T}-1<b<(\hbox {e}^{\sigma T}-1)\ln \frac{2}{(1-\hbox {e}^{-\sigma T})},$ which is simulated in Fig. 2. Next, the bifurcation of nontrivial periodic solution via a projection method is investigated in Sect. 3, and there is a supercritical bifurcation of a nontrivial periodic solution which satisfies the sufficient condition for the bifurcation $b=b^*$. In Fig. 3, a nontrivial periodic solution is simulated for $b^*=0.636.$

Fig. 1

Graph describes the trivial periodic solution, $\sigma =0.7, \beta =0.8, \delta =1, \gamma =1,b=2,p=0.3, T=2.5,l=0.5$. a Time series of the susceptible population. b Time series of the infectious population. c Time series of the Removed population. d Phase space of the trivial periodic solution

Fig. 2

The graph describes the infection-free periodic solution, $\sigma =0.7, \beta =0.8, \delta =1, \gamma =1,b=8,p=0.3, T=2,l=0.5$. a Time series of the susceptible population. b Time series of the infectious population. c Time series of the removed population. d Phase space of the infection-free periodic solution

Fig. 3

Graph describes the nontrivial periodic solution, $\sigma =0.7, \beta =0.8, \delta =1, \gamma =1,b=13.4,p=0.3, T=2,l=0.5$. a Time series of the susceptible population. b Time series of the infectious population. c Time series of the removed population. d Phase space of the nontrivial periodic solution

Appendices

Appendix $A_1$: The first-order partial derivatives of $\Phi _1, \Phi _2$

By formally deriving the equation

$$\begin{aligned} \frac{\hbox {d}}{\hbox {d}t}(\Phi (t, X_0))=F(\Phi (t, X_0)), \end{aligned}$$

which characterized the dynamics of the unperturbed flow associated with the first two equations in (1.2), one obtains that

$$\begin{aligned} \frac{\hbox {d}}{\hbox {d}t}[D_X\Phi (t, X_0)]=D_XF(\Phi (t,X_0))D_X\Phi (t, X_0). \nonumber \\ \end{aligned}$$

(5.1)

This relation will be integrated in what follows in order to compute the components of $D_X\Phi (t, X_0)$ explicitly. Firstly, it is clear that

$$\begin{aligned} \Phi (t, X_0)=(\Phi _1(t,X_0),0). \end{aligned}$$

Then we deduce that (5.1) takes the particular form

$$\begin{aligned}&\frac{\hbox {d}}{\hbox {d}t}\left( \begin{array}{l@{\quad }l} \dfrac{\partial \Phi _1}{\partial x_1} &{} \dfrac{\partial \Phi _1}{\partial x_2}\\ \dfrac{\partial \Phi _2}{\partial x_1} &{} \dfrac{\partial \Phi _2}{\partial x_2}\\ \end{array} \right) (t,X_0)\nonumber \\&\quad = \left( \begin{array}{l@{\quad }l} -(\delta +\sigma )&{} \gamma \\ 0 &{} \beta N(t)-\beta R^*(t)-\gamma -\sigma \\ \end{array} \right) \nonumber \\&\quad \qquad \times \left( \begin{array}{l@{\quad }l} \dfrac{\partial \Phi _1}{\partial x_1} &{} \dfrac{\partial \Phi _1}{\partial x_2}\\ \dfrac{\partial \Phi _2}{\partial x_1} &{} \dfrac{\partial \Phi _2}{\partial x_2}\\ \end{array} \right) (t,X_0), \end{aligned}$$

(5.2)

the initial condition for (5.2) at $t=0$ being

$$\begin{aligned} D_X\Phi (0, X_0)=I_2. \end{aligned}$$

(5.3)

Here, $I_2$ is the identity matrix in $M_2(R).$ It follows that

$$\begin{aligned} \frac{\partial \Phi _2(t, X_0)}{\partial x_1}&= \exp \left( \int _0^t(\beta N(s)-\beta R^*(s)-\gamma -\sigma )\hbox {d}s\right) \nonumber \\&\times \frac{\partial \Phi _2(0,X_0)}{\partial x_1}. \end{aligned}$$

This implies, using the initial condition (5.3), that

$$\begin{aligned} \frac{\partial \Phi _2(t,X_0)}{\partial x_1}=0, \ \ for \ \ t\ge 0. \end{aligned}$$

(5.4)

To compute $\frac{\partial \Phi _1(t, X_0)}{\partial x_1}, \frac{\partial \Phi _1(t, X_0)}{\partial x_2}$ and $\frac{\partial \Phi _2(t, X_0)}{\partial x_2,}$, from (5.2), one obtains that

$$\begin{aligned} \frac{\hbox {d}}{\hbox {d}t}\left( \frac{\partial \Phi _1(t, X_0)}{\partial x_1}\right)&= -\, (\delta +\sigma )\frac{\partial \Phi _1(t,X_0)}{\partial x_1},\\ \frac{\hbox {d}}{\hbox {d}t}\left( \frac{\partial \Phi _1(t, X_0)}{\partial x_2}\right)&= -\, (\delta +\sigma )\frac{\partial \Phi _1(t,X_0)}{\partial x_2}\\&+\,\gamma \frac{\partial \Phi _2(t,X_0)}{\partial x_2},\\ \frac{\hbox {d}}{\hbox {d}t}\left( \frac{\partial \Phi _2(t, X_0)}{\partial x_2}\right)&= ( \beta N(t)-\beta R^*(t)-\gamma -\sigma )\\&\times \frac{\partial \Phi _2(t,X_0)}{\partial x_2}. \end{aligned}$$

According to the initial condition, we obtain that

$$\begin{aligned} \frac{\partial \Phi _1(t,X_0)}{\partial x_1}&= \hbox {e}^{-(\delta +\sigma )t},\\ \frac{\partial \Phi _1(t,X_0)}{\partial x_2}&= \hbox {e}^{-(\delta +\sigma )t}\int _0^t\gamma \hbox {e}^{\int _0^s( \beta N(t)-\beta R^*(t)-\gamma -\sigma )\hbox {d}t}\hbox {d}s,\\ \frac{\partial \Phi _2(t, X_0)}{\partial x_2}&= \hbox {e}^{\int _0^t\beta N(s)-\beta R^*(s)-\gamma -\sigma )\hbox {d}s}. \end{aligned}$$

From (3.1), we obtain that

$$\begin{aligned} D_XN(0,(0,0))=I_2-D_X\psi (T,X_0), \end{aligned}$$

which implies

$$\begin{aligned} D_XN(0, (0,0))=\left( \begin{array}{ll} a_0' &{}\quad b_0'\\ 0 &{}\quad d_0' \end{array} \right) , \end{aligned}$$

with $a'_0, b'_0, d'_0$ given by

$$\begin{aligned} a'_0&= 1-\frac{\partial \Phi _1}{\partial x_1}((1-l)T,I_1(\Phi _1(lT, X_0)))\nonumber \\&\times \frac{\partial \Phi _1(lT,X_0)}{\partial x_1}, \end{aligned}$$

(5.5)

$$\begin{aligned} b'_0&= -\left[ \frac{\partial \Phi _1}{\partial x_1}((1-l)T,I_1(\Phi _1(lT, X_0)))\right. \nonumber \\&\left. \times \frac{\partial \Phi _1(lT,X_0)}{\partial x_2}+\frac{\partial \Phi _1}{\partial x_2}((1-l)T,\right. \nonumber \\&\left. I_1(\Phi _1(lT, X_0)))\frac{\partial \Phi _2}{\partial x_2}(lT,X_0)\right] , \end{aligned}$$

(5.6)

$$\begin{aligned} d'_0&= 1-\frac{\partial \Phi _2}{\partial x_2}((1-l)T,I_1(\Phi _1(lT, X_0)))\nonumber \\&\times \frac{\partial \Phi _2(lT,X_0)}{\partial x_2}. \end{aligned}$$

(5.7)

Appendix $A_2$: The first partial derivatives of $f$

By (3.1) and (3.7), it is easy to see that

$$\begin{aligned}&\frac{\partial f}{\partial \alpha }(\overline{\tau }, \alpha )\nonumber \\&\quad =\frac{\partial }{\partial \alpha }[\alpha -\psi _2(T+\overline{\tau }, X_0+\alpha Y_0+z(\overline{\tau }, \alpha )E_0 )]\nonumber \\&\quad =1-\frac{\partial }{\partial \alpha }[\Phi _2((1-l)(T+\overline{\tau }),I_1(\Phi (l(T+\overline{\tau }),X_0\nonumber \\&\quad \quad +\,\alpha Y_0+z(\overline{\tau },\alpha )E_0) )))]\nonumber \\&\quad =1-\frac{\partial \Phi _2}{\partial x_1}((1-l)(T+\overline{\tau }), I_1(\Phi (l(T+\overline{\tau }), X_0 \nonumber \\&\quad \quad +\,\alpha Y_0\!+\!z(\overline{\tau },\alpha )E_0))\times \left( \frac{\partial \Phi _1 }{\partial x_1}(l(T\!+\!\overline{\tau }),X_0\!+\!\alpha Y_0 \right. \nonumber \\&\quad \quad +z(\overline{\tau }, \alpha ))\left( -\frac{b'_0}{a'_0}+\frac{\partial z }{\partial \alpha }(\overline{\tau }, \alpha )\right) \nonumber \\&\quad \quad \left. +\,\frac{\partial \Phi _1}{\partial x_2}(l(T+\overline{\tau }, X_0+\alpha Y_0+z(\overline{\tau }, \alpha )E_0))\right) \nonumber \\&\quad \quad -\,\frac{\partial \Phi _2 }{\partial x_2}((1-l)(T+\overline{\tau }), I_1(\Phi (l(T+\overline{\tau }, X_0 \nonumber \\&\quad \quad +\,\alpha Y_0+z(\overline{\tau }, \alpha )E_0)))\left( \frac{\partial \Phi _2}{\partial x_1}(l(T+\overline{\tau }),X_0 \right. \nonumber \\&\quad \quad +\,\alpha Y_0+z(\overline{\tau }, \alpha )E) \left( -\frac{b'_0}{a'_0}+\frac{\partial z}{\partial \alpha }(\widetilde{\tau },\alpha )\right) \nonumber \\&\quad \quad \left. +\frac{\partial \Phi _2}{\partial x_2}(l(T+\overline{\tau }, X_0+\alpha Y_0+z(\overline{\tau },\alpha )E_0))\right) .\nonumber \\ \end{aligned}$$

(6.1)

It then follows that

$$\begin{aligned} \frac{\partial f(0,0)}{\partial \alpha }&= 1-\frac{\partial \Phi _2}{\partial x_2}\left( (1-l)T, I_1(\Phi (lT,X_0))\right) \\&\left( \frac{\partial \Phi _2}{\partial x_1}(lT,X_0)\left( -\frac{b'_0}{a'_0}+\frac{\partial z }{\partial \alpha }(0,0)\right) \right. \\&\left. +\frac{\partial \Phi _2}{\partial x_2}(lT, X_0 )\right) . \end{aligned}$$

Since

$$\begin{aligned} \begin{aligned}&\frac{\partial \Phi _2}{\partial \widetilde{\tau }}(lT, X_0)=0,\\&\frac{\partial \Phi _2}{\partial x_1}(lT, X_0)=0,\\ \end{aligned} \end{aligned}$$

(6.2)

it is seen that

$$\begin{aligned} \frac{\partial f}{\partial \alpha }(0,0)&= 1-\frac{\partial \Phi _2 }{\partial x_2}((1-l)T, I_1(\Phi (lT,X_0)))\\&\times \frac{\partial \Phi _2}{\partial x_2}(lT, X_0)\\&= d'_0=0. \end{aligned}$$

Using (3.1) and (3.7), it is seen that

$$\begin{aligned}&\frac{\partial f}{\partial \overline{\tau }}(\overline{\tau },\alpha )\nonumber \\&\quad = \frac{\partial }{\partial \overline{\tau } }\left[ \alpha -\Psi _2(T+\overline{\tau },X_0+\alpha Y_0+z(\overline{\tau }, \alpha )E_0)\right] \nonumber \\&\quad = -\frac{\partial }{\partial \overline{\tau } }\left[ \Phi _2((1-l)(T+\overline{\tau }),I_1(\Phi (l(T+\overline{\tau }), X_0 \right. \nonumber \\&\quad \quad \left. +\,\alpha Y_0 +z(\overline{\tau }, \alpha )E_0))))\right] \nonumber \\&\quad = - \frac{\partial \Phi _2}{\partial \overline{\tau }}((1-l)(T+\overline{\tau }), I_1(\Phi (l(T+\overline{\tau }),X_0 \nonumber \\&\quad \quad +\,\alpha Y_0+z(\overline{\tau },\alpha )E_0)))(1-l)\nonumber \\&\quad \quad -\,\frac{\partial \Phi _2}{\partial x_1}((1-l)(T+\overline{\tau }), I_1(\Phi (l(T+\overline{\tau }),X_0 \nonumber \\&\quad \quad +\,\alpha Y_0+z(\overline{\tau },\alpha )E_0)))\cdot \left( \frac{\partial \Phi _1}{\partial \overline{\tau }}(l(T+\overline{\tau }),X_0\right. \nonumber \\&\quad \quad +\,\alpha Y_0+z(\overline{\tau },\alpha )E_0)\cdot l +\,\frac{\partial \Phi _1}{\partial \overline{\tau }}(l(T+\overline{\tau }), X_0 \nonumber \\&\quad \quad \left. +\,\alpha Y_0+z(\overline{\tau },\alpha )E_0)\frac{\partial z}{\partial \overline{\tau }}(\overline{\tau },\alpha )\right) \nonumber \\&\quad \quad -\,\frac{\partial \Phi _2}{\partial x_2}((1-l)(T+\overline{\tau }), I_1(\Phi (l(T+\overline{\tau }), X_0 \nonumber \\&\quad \quad +\,\alpha Y_0+z(\overline{\tau },\alpha )E_0 )))(1-q)\nonumber \\&\quad \quad \cdot \, \left( \frac{\partial \Phi _2}{\partial \overline{\tau }}(l(T+\overline{\tau }),X_0 \right. +\,\alpha Y_0\nonumber \\&\quad \quad +\,z(\overline{\tau },\alpha )E_0)\cdot l+\,\frac{\partial \Phi _2}{\partial x_1}(l(T+\overline{\tau }), X_0 \nonumber \\&\quad \quad \left. +\,\alpha Y_0+z(\overline{\tau },\alpha )E_0 )\frac{\partial z}{\partial \overline{\tau }}(\overline{\tau },\alpha )\right) . \end{aligned}$$

(6.3)

Therefore,

$$\begin{aligned}&\frac{\partial f}{\partial \overline{\tau }}(0,0)\nonumber \\&\quad =-\frac{\partial \Phi _2}{\partial \overline{\tau }}((1-l)T,I_1(\Phi (lT, X_0))) (1-l) \\&\quad \quad -\,\frac{\partial \Phi _2}{\partial x_1}((1-l)T, I_1(\Phi (lT,X_0)))\\&\quad \quad \cdot \, \left( \frac{\partial \Phi _1}{\partial \overline{\tau }}(lT, X_0)\cdot l +\frac{\partial \Phi _1}{\partial x_1}(lT,X_0)\frac{\partial z}{\partial \overline{\tau }}(0,0)\right) \\&\quad \quad -\,\frac{\partial \Phi _2}{\partial x_2}((1-l)T,I_1(\Phi (lT, X_0)))\\&\quad \quad (1-q)\left( \frac{\partial \Phi _2}{\partial \overline{\tau }}(lT,X_0)\cdot l+\,\frac{\partial \Phi _2}{\partial \overline{\tau }}(lT,X_0)\frac{\partial z}{\partial \overline{\tau }}(0,0)\right) . \end{aligned}$$

Since

$$\begin{aligned}&\frac{\partial \Phi _2}{\partial \overline{\tau } }((1-l)T,I_1(lT, X_0))=0, \end{aligned}$$

(6.4)

$$\begin{aligned}&\frac{\partial \Phi _2}{\partial x_1}((1-l)T,I_1(\Phi (lT, X_0)))=0, \end{aligned}$$

(6.5)

it follows that

$$\begin{aligned} \frac{\partial f}{\partial \overline{\tau }}(0,0)=0. \end{aligned}$$

Appendix $A_3$: The second-order partial derivatives of $\Phi _2$

Again, by formally deriving

$$\begin{aligned} \frac{\hbox {d}}{\hbox {d}t}(\Phi (t, X_0))=F(\Phi (t,X_0)), \end{aligned}$$

as done in appendix $A_1$, we may get $\frac{\partial ^2 \Phi _2}{\partial x_1^2}(t,X_0)$, $\frac{\partial ^2 \Phi _2}{\partial x_2^2}(t,X_0), \frac{\partial ^2 \Phi _2}{\partial x_1\partial x_2}(t,X_0)$ as the solutions of certain initial value problems.

$$\begin{aligned}&\frac{\hbox {d}}{\hbox {d}t}\left( \frac{\partial ^2 \Phi _2}{\partial x_1^2}(t, X_0)\right) \\&\quad = \left( \beta N(t)-\beta \Phi _1(t,X_0)-\gamma -\sigma \right) \frac{\partial ^2 \Phi _2}{\partial x_1^2}\\&\quad \quad -\,\beta \frac{\partial \Phi _1}{\partial x_1}(t,X_1)\frac{\partial \Phi _2}{\partial x_1}(t,X_0) \end{aligned}$$

and since

$$\begin{aligned} \frac{\partial \Phi _2}{\partial x_1}(t,X_0)=0 \ \ \ for \ \ \ t\ge 0. \end{aligned}$$

It then follows that

$$\begin{aligned}&\frac{\partial ^2 \Phi _2}{\partial x_1^2}(t, X_0)\\&\quad =\hbox {e}^{\int _0^t(\beta N(s)-\beta \Phi _1(s,X_0)-\gamma -\sigma )\hbox {d}s}\frac{\partial ^2 \Phi _2}{\partial x_1^2}(0, X_0). \end{aligned}$$

Since $\frac{\partial ^2 \Phi _2}{\partial x_1^2}(0, X_0)=0,$ this implies that

$$\begin{aligned} \frac{\partial ^2 \Phi _2}{\partial x_1^2}(t, X_0)=0 \ \ for \ \ t\ge 0. \end{aligned}$$

By similar method, we have

$$\begin{aligned}&\frac{\hbox {d}}{\hbox {d}t}\left( \frac{\partial ^2 \Phi _2}{\partial x_2^2}(t, X_0)\right) \\&\quad =\left( \beta N(t)-\beta \Phi _1(t,X_0)-\gamma -\sigma \right) \frac{\partial ^2 \Phi _2}{\partial x_2^2}(t, X_0)\\&\quad \quad -\,\beta \frac{\partial \Phi _2}{\partial x_2}(t, X_0)\frac{\partial \Phi _1}{\partial x_2}(t, X_0). \end{aligned}$$

Since

$$\begin{aligned} \frac{\partial ^2 \Phi _2}{\partial x_2^2}(0, X_0)=0, \end{aligned}$$

we have

$$\begin{aligned} \displaystyle \frac{\partial ^2 \Phi _2}{\partial x_2^2}(t, X_0)&= -\beta \hbox {e}^{\int _0^t(\beta N(s)-\beta \Phi _1(s,X_0)-\gamma -\sigma )\hbox {d}t}\\&\times \int _0^t\frac{\partial \Phi _1 }{\partial x_2}(s,X_0)\hbox {d}s. \end{aligned}$$

Similarly, we may compute

$$\begin{aligned}&\displaystyle \frac{\hbox {d}}{\hbox {d}t}\left( \frac{\partial ^2 \Phi _2}{\partial x_1\partial x_2}(t, X_0)\right) \\&\quad =(\beta N(t)-\beta \Phi _1(t,X_0)-\gamma -\sigma )\frac{\partial ^2 \Phi _2}{\partial x_1\partial x_2}(t, X_0)\\&\quad \quad -\,\beta \frac{\partial \Phi _1}{\partial x_2 }(t,X_0)\frac{\partial \Phi _2}{\partial x_1 }(t,X_0). \end{aligned}$$

According to $\frac{\partial ^2 \Phi _2}{\partial x_1\partial x_2}(t,X_0)=0,$ we get

$$\begin{aligned} \frac{\partial ^2 \Phi _2}{\partial x_1\partial x_2}(t, X_0)&= - \beta \hbox {e}^{\int _0^t(\beta N(t)-\beta \Phi _1(t,X_0)-\gamma -\sigma )\hbox {d}t}\\&\times \int _0^t\frac{\partial \Phi _1 }{\partial x_1}(s,X_0)\hbox {d}s. \end{aligned}$$

We note that

$$\begin{aligned}&\frac{\partial ^2 \Phi _2}{\partial x_1\partial \overline{\tau }}((1-l)T, I_1(\Phi (lT, X_0)))=0, \end{aligned}$$

(7.1)

$$\begin{aligned}&\frac{\partial ^2 \Phi _2}{\partial x_1^2}((1-l)T, I_1(\Phi (lT, X_0)))=0, \end{aligned}$$

(7.2)

$$\begin{aligned}&\frac{\partial ^2 \Phi _2}{\partial x_1^2}(lT,X_0)=0. \end{aligned}$$

(7.3)

Considering (7.1)–(7.3) with (6.2)–(6.5), we obtain

$$\begin{aligned} \frac{\partial ^2 f}{\partial \overline{\tau }^2}(0,0)=-\frac{\partial ^2 \Phi _2}{\partial \overline{\tau }^2}((1-l)T, I_1(\Phi (lT, X_0)))(1-l)^2. \end{aligned}$$

Since

$$\begin{aligned} \frac{\partial ^2 \Phi _2}{\partial \overline{\tau }^2}((1-l)T, I_1(\Phi (lT, X_0)))=0, \end{aligned}$$

we have

$$\begin{aligned} \frac{\partial ^2 f}{\partial \overline{\tau }^2}(0,0)=0. \end{aligned}$$

We then compute $\frac{\partial ^2 f}{\partial \alpha ^2}(0,0).$ By (6.1), we have

$$\begin{aligned}&\displaystyle \frac{\partial ^2 f}{\partial \alpha ^2}(\widetilde{\tau },\alpha )\\&\quad =\frac{\partial ^2}{\partial \alpha ^2} \left( \alpha - \Psi _2(T+\widetilde{\tau },X_0 +\alpha Y_0+z(\widetilde{\tau },\alpha )E_0)\right) \\&\quad =-\frac{\partial ^2}{\partial \alpha ^2} \left( \Phi _2((1-l)(T+\widetilde{\tau }),I_1(\Phi (T+\widetilde{\tau })l,X_0 \right. \\&\quad \quad \left. +\,\alpha Y_0+z(\widetilde{\tau }, \alpha )E_0 ))\right) \\&\quad =-\frac{\partial }{\partial \alpha }\left[ \frac{\partial \Phi _2}{\partial x_1}\left( (1-l)(T+\widetilde{\tau }),I_1(\Phi ((T+\widetilde{\tau })l,X_0 \right. \right. \\&\quad \quad \left. \left. +\,\alpha Y_0+z(\widetilde{\tau },\alpha )E_0 ))\right) \right] \times \,\left( \frac{\partial \Phi _1 }{\partial x_1}((T+ \widetilde{\tau })l, X_0 \right. \\&\quad \quad +\,\alpha Y_0+z(\widetilde{\tau }, \alpha )E_0)\left( -\frac{b_0'}{a_0'}+\frac{\partial z}{\partial \alpha }(\widetilde{\tau },\alpha )\right) \\&\quad \quad +\,\frac{\partial \Phi _1 }{\partial x_2}((T+\widetilde{\tau })l,X_0 \left. +\alpha Y_0+z(\widetilde{\tau },\alpha )E_0)\right) \\&\quad \quad -\,\frac{\partial \Phi _2}{\partial x_1}\left( (1-l)(T+\widetilde{\tau }),I_1 \left( \Phi \left( (T+\widetilde{\tau })l,X_0 \right. \right. \right. \\&\quad \quad \left. \left. \left. +\,\alpha Y_0+z(\widetilde{\tau }, \alpha )E_0 \right) \right) \right) \times \,\frac{\partial }{\partial \alpha }\left[ \frac{\partial \Phi _1}{\partial x_1}((T+\widetilde{\tau })l,X_0 \right. \\&\quad \quad +\,\alpha Y_0+z(\widetilde{\tau },\alpha )E_0)\left( -\frac{b_0'}{a_0'}+\frac{\partial z }{\partial \alpha }(\widetilde{\tau },\alpha )\right) \\&\quad \quad +\,\frac{\partial \Phi _1}{\partial x_2}((T+\widetilde{\tau })l,X_0 \left. +\alpha Y_0+z(\widetilde{\tau },\alpha )E_0)\right] \\&\quad \quad -\,\frac{\partial }{\partial \alpha }\left[ \frac{\partial \Phi _2 }{\partial x_2}((1-l)(T+\widetilde{\tau }), I_1(\Phi (T+\widetilde{\tau })l,X_0 \right. \\&\quad \quad \left. +\,\alpha Y_0+z(\widetilde{\tau },\alpha )E_0))\right] \times \left( \frac{\partial \Phi _1 }{\partial x_1}((T+\widetilde{\tau })l,X_0 \right. \\&\quad \quad +\,\alpha Y_0+z(\widetilde{\tau },\alpha )E_0)\left( -\frac{b_0'}{a_0'}+\frac{\partial z }{\partial \alpha }(\widetilde{\tau },\alpha )\right) \\&\quad \quad +\,\frac{\partial \Phi _1 }{\partial x_2}((T+\widetilde{\tau })l,X_0 \left. +\,\alpha Y_0+z(\widetilde{\tau },\alpha )E_0)\right) \\&\quad \quad -\,\frac{\partial \Phi _2}{\partial x_2}((1-l)(T+\widetilde{\tau }),I_1((T+\widetilde{\tau })l,X_0 \\&\quad \quad +\,\alpha Y_0+z(\widetilde{\tau },\alpha )E_0 ))\times \,\frac{\partial }{\partial \alpha }\left[ \frac{\partial \Phi _2}{\partial x_1}((T+\widetilde{\tau })l,X_0 \right. \\&\quad \quad +\,\alpha Y_0+z(\widetilde{\tau }, \alpha )E_0)\left( -\frac{b_0'}{a_0'}+\frac{\partial z}{\partial \alpha }(\widetilde{\tau },\alpha )\right) \\&\quad \quad +\,\frac{\partial \Phi _2}{\partial x_2 }((T+\widetilde{\tau })l,X_0 \left. +\alpha Y_0+z(\widetilde{\tau },\alpha )E_0)\right] . \end{aligned}$$

After a few computations, we derive that

$$\begin{aligned}&\displaystyle \frac{\partial ^2 f}{\partial \alpha ^2}(0,0) \\&\quad =-\frac{\partial }{\partial \alpha }\left[ \frac{\partial \Phi _2}{\partial x_1}((1-l)(T+\overline{\tau }),I_1(\Phi (l(T+\overline{\tau }), \right. \\&\quad \quad \left. X_0+\,\alpha Y_0+z(\overline{\tau },\alpha )E_0)))\right] |_{(\overline{\tau },\alpha )=(0,0)}\\&\quad \quad \times \left( \frac{\partial \Phi _1}{\partial x_1}(lT,X_0)\left( -\frac{b'_0}{a'_0}+\frac{\partial z}{\partial \alpha }(0,0)\right) \right. \\&\quad \quad \left. +\,\frac{\partial \Phi _1}{\partial x_2}(lT, X_0 )\right) -\,\frac{\partial }{\partial \alpha }\left[ \frac{\partial \Phi _2}{\partial x_1}((1-l)(T+\overline{\tau }),\right. \\&\quad \quad \left. I_1(\Phi (l(T+\overline{\tau }),X_0 \right. +\,\alpha Y_0\\&\quad \quad \left. +\,z(\overline{\tau },\alpha )E_0)))\right] \Big |_{(\overline{\tau },\alpha )=(0,0)}\\&\quad \quad \times \left( -\frac{b'_0}{a'_0}+\frac{\partial z}{\partial \alpha }(0,0)\right) +\,\frac{\partial \Phi _2}{\partial x_2}\left( lT,X_0 \right) )\\&\quad \quad -\,\frac{\partial \Phi _2}{\partial x_2}\left( (1-l)T, I_1(\Phi (lT,X_0))\right) \\&\quad \quad \times \,\frac{\partial }{\partial \alpha }\left[ \frac{\partial \Phi _2}{\partial x_1}(l(T+\overline{\tau }),X_0 \right. +\,\alpha Y_0+z(\overline{\tau },\alpha )E_0)\\&\quad \quad \times \left( -\frac{b'_0}{a'_0}+\frac{\partial z}{\partial \alpha }(0,0)\right) +\,\frac{\partial \Phi _2 }{\partial x_2 }(l(T+\overline{\tau },X_0 \\&\quad \quad \left. +\,\alpha Y_0+z(\overline{\tau },\alpha )E_0)))\right] |_{(\overline{\tau },\alpha )=(0,0)}. \end{aligned}$$

Using again (7.2) and $\frac{\partial z}{\partial \alpha }(0,0)=0$, it follows that

$$\begin{aligned}&\frac{\partial ^2 f}{\partial \alpha ^2}(0,0)\\&\quad =-2\frac{\partial ^2 \Phi _2}{\partial x_1\partial x_2}((1-l)T, I_1(\Phi (lT,X_0)))\\&\quad \quad \times \,\left( \frac{\partial \Phi _1}{\partial x_1}(lT,X_0)\left( -\frac{b'_0}{a'_0}\right) +\,\frac{\partial \Phi _1}{\partial x_2 }(lT, X_0)\right) \\&\quad \quad \times \frac{\partial \Phi _2}{\partial x_2 }(lT, X_0) -\,\frac{\partial ^2 \Phi _2}{\partial x_2^2}((1-l)T,I_1(\Phi (lT,X_0))) \\&\quad \quad \!\times \left( \frac{\partial \Phi _2}{\partial x_2}(lT, X_0)\right) ^2\!-\!\frac{\partial \Phi _2}{\partial x_2 }\left( (1\!-\!l)T, I_1(\Phi (lT,X_0))\right) \\&\quad \quad \!\times \,\left[ 2\frac{\partial ^2 \Phi _2 }{\partial x_2\partial x_1}(lT,X_0)\left( -\frac{b'_0}{a'_0}\right) +\frac{\partial ^2 \Phi _2}{\partial x_2 ^2}(lT,X_0)\right] . \end{aligned}$$

Obviously, it can be deduced from above that

$$\begin{aligned} \frac{\partial ^2 f}{\partial \alpha ^2}(0,0)>0. \end{aligned}$$

It is also seen that

$$\begin{aligned}&\frac{\partial ^2 f}{\partial \alpha \partial \overline{\tau }}(0,0)\\&\quad = - \frac{\partial ^2\Phi _2}{\partial x_2\partial \widetilde{\tau }} ((1\!-\!l)T,I_1(\Phi (lT, X_0))) \frac{\partial \Phi _2}{\partial x_2}(lT,X_0)(1\!-\!l)\\&\quad \quad -\,\frac{\partial ^2 \Phi _2}{\partial x_1\partial x_2 }((1-l)T,I_1(\Phi (lT, X_0))) \frac{\partial \Phi _2}{\partial x_2}(lT,X_0)\\&\quad \quad \times \, \left( \frac{\partial \Phi _1}{\partial \widetilde{\tau }}(lT, X_0)l+\frac{\partial \Phi _1}{\partial x_1}(lT, X_0)\frac{\partial z}{\partial \widetilde{\tau }}(0,0)\right) \\&\quad \quad -\,\frac{\partial \Phi _2}{\partial x_2}((1-l)T,I_1(lT, X_0)) \\&\quad \quad \times \,\left( \frac{\partial ^2 \Phi _2}{\partial x_2\partial \widetilde{\tau }}(lT, X_0)+\frac{\partial ^2\Phi _2}{\partial x_1\partial x_2}(lT,X_0)\frac{\partial z}{\partial \widetilde{\tau }}(0,0)\right) . \end{aligned}$$

Now, we compute the right-hand side of the equation above. It is showed that

$$\begin{aligned}&-\frac{\partial ^2 \Phi _2}{\partial x_2\partial \widetilde{\tau }}((1-l)T,I_1(\Phi (lT,X_0)))\frac{\partial \Phi _2 }{\partial x_2}(lT,X_0)(1-l)\\&\qquad = -\left( \beta N(T)-\beta R^*(T)-\gamma -\sigma \right) (1-l),\\&-\,\frac{\partial ^2\Phi _2}{\partial x_2\partial x_1}((1-l)T,I_1(\Phi (lT,X_0))) \frac{\partial \Phi _2}{\partial x_2}(lT,X_0)\\&\qquad =\displaystyle \int _0^{(1-l)T}\gamma \hbox {e}^{-(\delta +\sigma )t}\hbox {d}t,\\&\frac{\partial \Phi _1}{\partial \widetilde{\tau }}(lT, X_0)l+\frac{\partial \Phi _1}{\partial x_1}(lT,X_0)\frac{\partial z }{\partial \widetilde{\tau }}(0,0)\\&\qquad =\displaystyle -(\delta +\sigma )R^*(lT)l+\frac{\hbox {e}^{-(\delta +\sigma )lT}(-(\delta +\sigma )R^*(T))}{a_0'}\\&\qquad =-(\delta +\sigma )(R^*(lT)l+\frac{\hbox {e}^{-(\delta +\sigma )lT}R^*(T)}{a'_0}),\\&- \frac{\partial \Phi _2}{\partial x_2}((1-l)T,I_1(\Phi (lT,X_0))) \left( \frac{\partial ^2\Phi _2}{\partial x_2\partial \widetilde{\tau }}(lT,X_0)l\right. \\&\quad \quad \left. +\,\frac{\partial ^2\Phi _2}{\partial x_1\partial x_2 }(lT,X_0)\frac{\partial z }{\partial \widetilde{\tau } }(0,0)\right) \\&\quad = - \frac{\partial \Phi _2}{\partial x_2}((1-l)T,I_1(\Phi (lT,X_0))) ((\beta N(lT)\\&\quad \quad -\,\beta R^*(lT)-\gamma -\sigma )\frac{\partial \Phi _2 }{\partial x_2}(lT,X_0)l\\&\quad \quad -\,\left( \frac{\partial \Phi _2 }{\partial x_2}(lT,X_0)\int _0^{lT}\gamma \hbox {e}^{-(\delta +\sigma )s}\hbox {d}s\right) \frac{\partial z }{\partial \widetilde{\tau }}(0,0))\\&\quad = -\left[ \displaystyle (\beta N(lT)-\beta R^*(lT)-\gamma -\sigma )l\right. \\&\quad \quad \left. +\,\int _0^{lT}\gamma \hbox {e}^{-(\delta +\sigma )s}\hbox {d}s\frac{(\delta +\sigma )R^*(T) }{a_0'}\right] . \end{aligned}$$

Hence, it is concluded that

$$\begin{aligned} \frac{\partial ^2f}{\partial \alpha \partial \widetilde{\tau }}(0,0)&= -(\beta N(T)-\beta R^*(T)-\gamma -\sigma )(1-l)\\&-(\delta \!+\!\sigma )\left( R^*(lT)l\!+\!\frac{\hbox {e}^{-(\delta +\sigma )lT}R^*(T)}{a'_0} \right) \\&\times \displaystyle \int _0^{(1-l)T}\gamma \hbox {e}^{-(\delta +\sigma )t}\hbox {d}t\\&-\,\left[ \displaystyle (\beta N(lT)-\beta R^*(lT)-\gamma -\sigma )l\right. \\&\left. +\int _0^{lT}\gamma \hbox {e}^{-(\delta +\sigma )s}\hbox {d}s\frac{(\delta +\sigma )R^*(T) }{a_0'}\right] . \end{aligned}$$

It follows from $\frac{\hbox {d}S}{\hbox {d}t}>0$ and $\int _0^T(\beta (N(s)-R^*(s))-\gamma -\sigma )\hbox {d}s=\int _0^T(\beta S(u)-\gamma -\sigma )du=0$, we have $\frac{1}{T}\int _0^{T}(\beta (N(s)-R^*(s))-\gamma -\sigma )\hbox {d}s<\beta S(lT)l-(\gamma +\sigma )l+\beta S(T)(1-l)-(\gamma +\sigma )(1-l).$ Consequently, one notes that $\frac{\partial ^2f}{\partial \alpha \partial \widetilde{\tau }}(0,0)<0.$